Punktweise Grenzwerte Analytischer Funktionen

Seminararbeit

Punktweise Grenzwerte Analytischer Funktionen

Markus Tempelmayr 1. Februar 2017

1 Einleitung

1.1 Definition. Sei G ⊆ C offen. Eine Funktion f : G → C heißt analytisch auf G, falls sie an jedem Punkt in G stetig komplex differenzierbar ist. Die Menge aller auf G analytischen Funktionen bezeichnen wir mitH(G).

Die Stetigkeit der Ableitung muss dabei nicht vorausgesetzt werden sondern ist im Fall der komplexen Differenzierbarkeit automatisch erf¨ullt, wie z.B. in [A2, Satz 11.9.2] gezeigt wird.

1.2 Definition. Sei G ⊆ C und f :G → C. Eine Folge von Funktionen f_n : G → C, n ∈ N, konvergiert lokal gleichm¨aßig gegen f, wenn f¨ur jede kompakte Teilmenge K ⊆ G die Folge (fn|_K)n∈N gleichm¨aßig gegenf|_K konvergiert.

1.3 Lemma. SeiG⊆C offen und fn:G→C, n∈N, eine Folge analytischer Funktionen, die lokal gleichm¨aßig gegen eine Funktion f :G→Ckonvergiert. Dann ist auch f analytisch.

Beweis. Siehe [A2, Lemma 11.8.13]. k

Dass punktweise Konvergenz i.A. nicht ausreicht um Analytizit¨at einer Funktionenfolge zu erhalten, sondern lokal gleichm¨aßige Konvergenz der Folge (f_n)n∈N tats¨achlich notwendig ist, soll folgendes Beispiel verdeutlichen:

1.4 Beispiel . Ziel ist es, eine Funktionenfolge F_n : C→ C, n ∈ N, analytischer Funktionen zu konstruieren, die punktweise gegen eine nicht analytische FunktionF :C→Ckonvergiert.

F¨ur jedesa >0 seiH_a:=

z∈C : <(z)> a,|=(z)|< π ,γ_a:=∂H_a undf :C→C, z7→exp(exp(z)).

Abbildung 1:H_a Wegen

f(x±iπ) = exp(exp(x±iπ)) = exp(exp(x) exp(±iπ)) = exp(−exp(x)) = 1

f(x) ∀x∈R, gilt f¨urz /∈γ_a und damitd(γ_a, z)>0

Z

γa

f(ζ) ζ−z

dζ = Z

{a}×(−π,π)

f(ζ) ζ−z

dζ+ Z

(a,+∞)×{π}

f(ζ) ζ−z

dζ+ Z

(a,+∞)×{−π}

f(ζ) ζ−z

dζ ≤

1 d(γa, z)

Z

(−π,π)

|f(a+iζ)|dζ+ Z

(a,+∞)

|f(ζ+iπ)|dζ+ Z

(a,+∞)

|f(ζ−iπ)|dζ

!

= 1

d(γ_a, z) Z

(−π,π)

|f(a+iζ)|dζ+ 2 Z

(a,+∞)

1 f(ζ)

dζ

!

<+∞.

2 2 POSITIVE RESULTATE Deshalb ist eine Funktion I_a:C\γ_a→Cwohldefiniert durch

Ia(z) := 1 2πi

Z

γa

f(ζ) ζ−zdζ.

Die Funktion Ia ist nach [A3, Lemma 15.2.9] analytisch auf (γa)^c und wegen |I_a(z)| ≤ _d(γ^C

a,z)

gilt

I_a(tz)^t→∞−→ 0 f¨urz /∈R⁺ und |I_a(tz)|<Ce f¨urt≥0, z ∈R⁺. (1) F¨ura < b undz /∈γa∪γb gilt außerdem

I_b(z)−I_a(z) = 1 2πi

Z

∂(Ha∩H_b^c)

f(ζ)

ζ−zdζ=f(z)1Ha∩H_b^c(z), (2) denn f¨ur z ∈ Ha∩H_b^c gilt die Cauchy’sche Integralformel, siehe [A2, Satz 11.8.9], und f¨ur z /∈ H_a∩H_b^c wird ¨uber den Rand eines einfach zusammenh¨angenden Gebietes integriert, und damit verschwindet das Integral, siehe [A2, Korollar 11.8.7].

F¨ura < b stimmenIa undIb aufH_a^cuberein, und weiters gilt¨ S

a>0H_a^c=C. Damit k¨onnen wir folgende Funktion definieren:I :C→C, z7→I_a(z) aufH_a^c. Mit (1) und

∀x∈Ha∩R⁺, a < x < b:I(x)^Def.= Ib(x)⁽²⁾= Ia(x)

| {z }

beschr.

wegen (1)

+f(x)^x→∞−→ ∞,

gilt nun f¨ur die FunktionF :C→C, z7→exp(−I(z)) folgendes Grenzwertverhalten:

F(tz)^t→∞−→

0 , z∈R⁺ 1 ,sonst.

Definiert man nun die Funktionenfolge F_n :C→C, z7→ F(nz), n ∈N, so ist jedes Folgenglied als Komposition analytischer Funktionen wieder analytisch und konvergiert gegen die nicht einmal stetige Grenzfunktion

z7→

0 , z∈R⁺ 1 ,sonst.

//

2 Positive Resultate

Ziel dieses Abschnittes ist es zu zeigen, dass bei punktweiser Konvergenz einer analytischen Funktionenfolge die Analytizit¨at zumindest auf einer dichten Teilmenge des Definitionsbereiches erhalten bleibt. Daf¨ur ben¨otigen wir einige aus der Analysis bekannte Definitionen und eine Variante des Satzes von Arzela-Ascoli.

2.1 Definition. SeiF eine Familie von Funktionen auf einer MengeG. Dann heißtF

• punktweise beschr¨ankt, wenn gilt: ∀z∈G: sup

|f(z)| : f ∈ F <∞,

• gleichgradig stetig bei w∈G, wenn gilt:

∀ >0 ∃δ >0 (∀f ∈ F ∀z∈G:|z−w|< δ=⇒ |f(z)−f(w)|< ),

• lokal beschr¨ankt, wenn gilt: ∀z₀ ∈G ∃δ >0 : sup

|f(z)| : f ∈ F, z∈U_δ(z₀) <∞.

2.2 Satz (von Arzela-Ascoli). Sei G ⊆C offen und F ⊆ C(G,C). Weiters sei F punktweise beschr¨ankt und gleichgradig stetig bei jedem w ∈ G. Dann hat jede Folge in F eine lokal gleichm¨aßig konvergente Teilfolge.

Beweis. Sei {x₁, x2, . . .} eine abz¨ahlbare und dichte Teilmenge von G. Als solche Men- ge kann beispielsweise die Menge aller Punkte aus G mit rationalem Real- und Imagin¨arteil gew¨ahlt werden. F¨ur jedes z ∈ G definiere X(z) :=

f(z) : f ∈ F . Weil F punktweise beschr¨ankt ist, ist die Menge X(z) ⊆C kompakt. Aus dem Satz von Tychonoff [F, Satz 1.3.1]

folgt dass auch die Menge Y :=Q∞

i=1X(xi) kompakt ist.

Sei nun (f_n)n∈Neine beliebige Folge aus F. Dann ist ((f_n(x_i))i∈N)n∈N eine Folge inY und weil Y kompakt ist, existiert eine konvergente Teilfolge ((f_nk(x_i))i∈N)k∈N.

Sei K ⊆ G kompakt und > 0, wir zeigen nun dass die Folge (fnk)k∈N auf K gleichm¨aßig konvergiet. W¨ahle eine kompakte Menge K_N ⊆ G mit K ⊆ K_N^◦, z.B.

K_n = K_n(0) ∩

z ∈ G : d(z, G^c) ≥ ¹_n mit geeignetem n ∈ N. Da (f_nk)k∈N nach Voraussetzung auch auf K_N^◦ gleichgradig stetig ist, w¨ahleδ >0 sodass

∀z, w∈K_N^◦ ∀k∈N:|z−w|< δ⇒ |f_nk(z)−fn_k(w)|< . DaK_N^◦ offen und

x_i : i∈N dicht inGist existiert zu jedemy∈K einδ >0 mitx_i(y)∈K_N^◦ und y ∈ Uδ(x_i(y)). Diese Kugeln ¨uberdecken K, also gibt es endlich viele Kugeln Uδ(xij) mit xij ∈K_N^◦, j = 1. . . n, dieK ¨uberdecken. Nachdem (fn_k)k∈Nan den Punkten (xi)i∈Nkonvergiert, w¨ahleM ∈Nsodass

∀k, l≥M, j= 1. . . n:|f_nk(x_ij)−f_nl(x_ij)|< . Sei nun x∈K beliebig. W¨ahle j sodass x∈U_δ(xij), dann gilt f¨urk, l≥M

|f_nk(x)−f_nl(x)| ≤ |f_nk(x)−f_nk(x_ij)|+|f_nk(x_ij)−f_nl(x_ij)|+|f_nl(x_ij)−f_nl(x)|<3.

Damit ist (f_nk)k∈N eine gleichm¨aßig konvergente Folge, d.h. (f_n)n∈Nhat eine lokal gleichm¨aßig

konvergente Teilfolge. k

2.3 Satz(von Montel).SeiG⊆Coffen und F ⊆H(G). Weiters seiF lokal beschr¨ankt. Dann hat jede Folge inF eine lokal gleichm¨aßig konvergente Teilfolge.

2.4 Bemerkung . Der Satz von Montel ist das Analogon zum Satz von Arzela-Ascoli f¨ur analytische Funktionen. Man beachte, dass die etwas st¨arkere Bedingung der lokalen Be- schr¨anktheit gefordert wird, daf¨ur die Forderung der gleichgradigen Stetigkeit fallen gelassen werden kann.

Beweis. Wir zeigen dass beide Voraussetzung aus Satz 2.2 erf¨ullt sind. Aus lokaler Be- schr¨anktheit folgt sicherlich punktweise Beschr¨anktheit, bleibt also noch die gleichgradige Stetigkeit zu zeigen.

Sei w ∈ G, r > 0 sodass K_r(w) ⊆ G und z₁, z₂ ∈ U^r

2(w). Dann gilt nach der Cauchy’schen

4 2 POSITIVE RESULTATE Integralformel [A2, Satz 11.8.9]

|f(z₁)−f(z₂)| = 1 2π

Z

∂Ur(w)

f(ζ) ζ−z1

dζ− Z

∂Ur(w)

f(ζ) ζ−z2

dζ

= 1

2π Z

∂Ur(w)

f(ζ)(z₁−z₂) (ζ−z1)(ζ−z2)dζ

≤ 1 2π

Z

∂Ur(w)

f(ζ)(z₁−z₂) (ζ−z1)

| {z }

≥^r₂

(ζ−z2)

| {z }

≥^r₂

dζ

≤ 1 2π

4

r² |z₁−z2| Z

∂Ur(w)

|f(ζ)|dζ ≤ 1 2π

4

r² |z₁−z2|2πr max

ζ∈∂Ur(w)

|f(ζ)|

= 4

r |z₁−z2| max

ζ∈∂Ur(w)

|f(ζ)| ≤ 4M

r |z₁−z2| mitM := sup

|f(ζ)| : ζ ∈∂U_r(w), f ∈ F . F¨urr klein genug istM wegen der Voraussetzung

an F endlich, undF daher gleichgradig stetig beiw∈G. k

F¨ur das n¨achste Resultat ben¨otigen wir den Satz von Baire in einer Variante, die in den Analysis bzw. Funktionalanalysis Vorlesungen nicht behandelt wurde. Deshalb ist nachfolgend der Satz inkl. Beweis angef¨uhrt.

2.5 Satz (von Baire). Sei (X,T) ein lokalkompakter Hausdorff Raum, und seien Vn, n ∈ N, offene und dichte Teilmengen von X. Dann ist auch T

n∈NV_n dicht in X.

Beweis. Sei (Vn)n∈N eine beliebige Folge von offenen, dichten Teilmengen von X. Wir zeigen, dass der Schnitt einer beliebigen nicht leeren offenen Menge U mitV :=T

n∈NVnnicht leer ist. Dazu konstruieren wir induktiv eine Folge (U_n)^∞_n=0von nicht leeren, offenen Teilmengen von X mit der Eigenschaft, dass f¨ur alle n∈N0 gilt

Uj+1 ⊆Vj+1∩Uj f¨ur 0≤j≤n, Uj kompakt f¨ur 1≤j≤n. (3) F¨urn= 0 ist mitU0 :=U die Forderung (3) erf¨ullt. Seien nun f¨ur einn∈N0 nicht leere offene MengenU₀, . . . , U_n⊆X so konstruiert, dass (3) erf¨ullt ist. Da V_n+1 inX dicht ist gibt es einen Punktx_n∈U_n∩V_n+1. DaX lokalkompakt ist undU_n∩V_n+1 eine Umgebung vonx_nist, gibt es eine kompakte UmgebungK von xn mitK⊆Un∩Vn+1. Dann istUn+1 :=K^◦ offen, nicht leer und es gilt (3). Setzen wir nun A:= T

n∈NU_n so folgt wegen der Kompaktheit der U_n aus der endlichen Durchschnittseigenschaft kompakter Mengen [A2, Proposition 12.11.2] dass A 6= ∅.

Nach Konstruktion gilt

∅ 6=A⊆ \

n∈N

(Vn∩U) =V ∩U.

k Insbesondere gilt unter den Voraussetzungen aus Satz 2.5 dass T

n∈NV_n 6= ∅. Geht man nun zu den Komplementen ¨uber erh¨alt man folgendes Resultat.

2.6 Korollar. Sei (X,T) ein lokalkompakter Hausdorff Raum, und seien A_n, n ∈ N, abge- schlossene Teilmengen von X mit leerem Inneren. Dann hat auchS

n∈NA_n leeres Inneres.

Beweis. Aus [A2, Fakta 12.2.12] folgt (A^◦_n)^c = A^c_n. Als Komplemente abgeschlossener

Mengen sind alleA^c_noffen, und wegenX= (A^◦_n)^c=A^c_nsind auch alle A^c_n dicht inX. Aus Satz 2.5 folgt dass T

n∈NA^c_n dicht inX ist. Also gilt X= \

n∈N

A^c_n

= [

n∈N

A_nc

= [

n∈N

A_n◦c

,

und somit (S

n∈NAn)^◦=∅. k

2.7 Lemma. Sei G ⊆ C offen und F ⊆ C(G,C) punktweise beschr¨ankt. Dann existiert eine maximale, offene, dichte Menge Gb⊆G sodass F |

Gb lokal beschr¨ankt ist.¹ Beweis. F¨ur jedes n ∈ N sei K_n :=

z ∈ G : sup_f∈F|f(z)| ≤ n und Gb := S

n∈NK_n^◦. Wir zeigen nun dassGb die gew¨unschten Eigenschaften besitzt.

Als Vereinigung offener Mengen ist Gb offen. Außerdem ist F |

Gb lokal beschr¨ankt. Um dies einzusehen w¨ahlez∈G. Nach Konstruktion existiert einb N ∈N mitz∈K_N^◦, und wir haben

sup

|f(w)| : w∈K_N^◦, f ∈ F ≤N.

Gb ist auch gr¨oßtm¨oglich. Denn ist Ge eine weitere offene Teilmenge von G, sodass F |

Ge lo- kal beschr¨ankt ist und z ∈ G, dann existiert eine offene Mengee O und ein N ∈ N sodass sup

|f(w)| : w∈O, f ∈ F ≤N und damitz∈O ⊆K_N^◦, d.h. Ge⊆G.b

Um zu zeigen dassGbinGdicht ist, seiU ⊆Goffen und nicht leer. Da alle Funktionenf ∈ F ste- tig sind ist jedesK_n abgeschlossen bzgl. der Spurtopologie inG. WeilF punktweise beschr¨ankt ist gilt auch S

n∈NKn = G. Deshalb ist Kn∩U abgeschlossen bzgl. der Spurtopologie in U und S

n∈N(K_n∩U) =U. Da die Menge U offen ist, hat sie nicht leeres Inneres. Aus Korollar 2.6, angewandt auf den Raum (U,E|_U) und die Mengen K_n∩U, folgt dass es ein N ∈N mit (KN ∩U)^◦ 6=∅ gibt, wobei das Innere bzgl. der Spurtopologie inU zu verstehen ist. Also gibt es eine offene und nicht leere Menge O⊆K_N∩U und weil O offen ist, gilt auchO ⊆K_N^◦ ∩U. Insbesondere gilt

∅ 6=O⊆K_N^◦ ∩U ⊆ [

n∈N

K_n^◦∩U =Gb∩U,

womit Gb dicht inGist. k

2.8 Korollar (Satz von Osgood). Sei G ⊆ C offen und (f_n)n∈N eine Folge analytischer Funktionen auf G, die punktweise gegen eine Funktion f :G → C konvergiert. Dann existiert eine offene und inGdichte Teilmenge Gb auf der die Funktionenfolge (fn)n∈N lokal gleichm¨aßig gegen f konvergiert. Insbesondere giltf ∈H(G).b

Beweis. Die Menge F :=

fn : n ∈ N ist punktweise beschr¨ankt, da (fn)n∈N punkt- weise gegen f konvergiert. Nach Lemma 2.7 existiert eine offene und in G dichte Menge Gb sodass F |

Gb lokal beschr¨ankt ist. Aus dem Satz von Montel, Satz 2.3, folgt dass eine lokal gleichm¨aßig konvergente Teilfolge (fnk|

Gb)k∈N existiert. Wegen der punktweisen Konvergenz muss der Grenzwert dieser Teilfolge gleich f|

Gb sein. Als lokal gleichm¨aßiger Grenzwert ist wegen Lemma 1.3 auch die Grenzfunktion f|

Gb analytisch. W¨urde die Folge (f_n|

Gb)n∈N nicht lokal gleichm¨aßig konvergieren, g¨abe es eine kompakte Menge K ⊆G, einb > 0, eine Teilfolge (f_nm)m∈N und Punkte z_m∈K sodass |f_nm(z_m)−f(z_m)| ≥f¨urm≥1. Dann kann aber keine Teilfolge von (fnm)m∈N aufK gleichm¨aßig gegenf konvergieren, ein Widerspruch. k

1F |

Gb:=

f|Gb : f∈ F

6 3 LAVRIENTIEV’S RESULTATE

3 Lavrientiev’s Resultate

Im folgenden Abschnitt m¨ochten wir darauf eingehen, ob bei gegebener punktweise konver- genten Funktionenfolge (f_n)n∈N auf einer offenen Menge G⊆ C eine dichte Teilmenge Gb jene gr¨oßtm¨ogliche Menge sein kann, auf der (f_n)n∈Nlokal gleichm¨aßig konvergiert. Eine notwendige und hinreichende Bedingung an die Menge Gb hat M. A. Lavrientiev in [L] gegeben. Allerdings sind diese Bedingungen sehr unhandlich, weshalb wir nicht n¨aher darauf eingehen, sondern zwei einfachere (und unserer Meinung nach sch¨onere) Resultate vorstellen m¨ochten.

Daf¨ur ben¨otigen wir ein Maximumprinzip f¨ur analytische Funktionen.

3.1 Satz(Maximumprinzip). SeiG⊆C offen und f ∈H(G). Dann gilt:

(i) Sei zus¨atzlichGzusammenh¨angend. Existiert ein Punkt a∈Gmit|f(a)| ≥ |f(z)|, z∈G, so ist f konstant.

(ii) Sei Gbeschr¨ankt und f stetig bis zum Rand, d.h. f ∈H(G)∩C(G). Dann gilt sup

z∈G

|f(z)|= max

z∈∂G|f(z)|.

Beweis.

(i) Sei angenommenf nicht konstant unda∈G. Wegen dem Satz von der offenen Abbildung [K, Proposition 5.2.1 (iv)] enth¨alt f(G) eine ganze Umgebung von f(a), also sicher auch Punkte mit gr¨oßerem Betrag.

(ii) Daf stetig ist undG kompakt gibt es eine Stelle a∈G mit|f(a)|= max_z∈G|f(z)|. An- genommena∈G, dann ist wegen(i) die Funktionf auf der Zusammenhangskomponente Gˆ von Gwelche a enth¨alt konstant. Nun ist ∂Gˆ ⊆∂G da C lokal zusammenh¨angend ist, und wir schließen dass es einen Punkt ˆa∈ ∂G gibt mit |f(ˆa)|= |f(a)|. Es folgt dass |f|

sein Maximum sicher auch am Rand annimmt, also sup

z∈G

|f(z)| ≤ max

z∈∂G|f(z)|.

Die umgekehrte Ungleichung gilt wegen der Stetigkeit vonf.

k

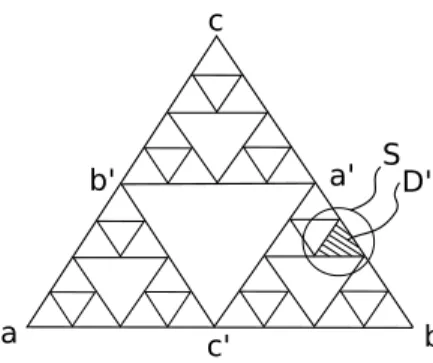
Beim ersten Resultat handelt es sich um eine Aussage ¨uber das Sierpinski Dreieck.

3.2 Beispiel .Sei G⊆C offen. Wir konstruieren nun ein sogenanntes Sierpinski Dreieck. Dazu w¨ahle in einer offenen Kugel inGdrei Punktea,bundcwelche die Eckpunkte eines gleichseitigen Dreiecks bilden. SeiD0 der Rand dieses Dreiecks. Nun sei c⁰ der Mittelpunkt der Strecke ab,b⁰ der Mittelpunkt der Streckeacunda⁰ Mittelpunkt der Streckebc. SeiD₁der Rand des Dreiecks mit den Eckpunkten a⁰, b⁰ und c⁰. Damit ergeben sich vier gleichseitige Dreiecke, deren Rand D0∪D1 ist. Nun wiederhole dieses Verfahren in den ¨außeren drei Dreiecken und fahre immer weiter so fort. Das Sierpinski DreieckD ist die kompakte MengeD₀∪D₁∪ · · ·.

Abbildung 2: Ersten Konstruktionsschritte eines Sierpinski Dreiecks

Nach Konstruktion ist Gb:=G\D offen und dicht inG. //

Nun kann man sich folgende Frage stellen: Gibt es eine analytische Funktionenfolge auf G die punktweise konvergiert und f¨ur die Gb die gr¨oßtm¨ogliche offene und dichte Menge ist, auf der die Folge lokal gleichm¨aßig konvergiert? Wie wir sehen werden l¨asst sich solch eine Funktionenfolge nicht finden.

3.3 Lemma. Sei G ⊆ C offen, Gb und das Sierpinski Dreieck D wie in Beispiel 3.2. Dann existiert keine Funktionenfolge (f_n)n∈N analytischer Funktionen die auf G punktweise gegen eine Grenzfunktionf konvergiert und f¨ur dieGb die gr¨oßtm¨ogliche offene und dichte Menge ist, auf der (fn)n∈N lokal gleichm¨aßig gegen f konvergiert.

Beweis. Angenommen (fn)n∈N und f existieren. F¨urz∈Gsei cn(z) := sup

|f_n(z)−fm(z)| : m≥n (∈R), Un:=

z∈G : cn(z)>1 (⊆G).

Die MengenU_nsind offen f¨ur jedes n∈Ndenn entweder giltU_n=∅oder es existiert ein Punkt z0 ∈ Un sodass |f_n(z0)−fm(z0)|>1 f¨ur ein m ≥n. Weil aberfn und fm insbesondere stetig sind gilt f¨ur hinreichend kleinesδ >0 auch

|f_n(z)−f_m(z)|>1 ∀z∈U_δ(z₀).

Also giltU_δ(z₀)⊆U_n womit U_n offen ist.

Da (fn)n∈N als konvergente Folge in C eine Cauchyfolge ist gilt cn(z) ^n→∞−→ 0 f¨ur jedes z ∈ G.

Also istT

n∈NU_n=∅. Aus dem Satz von Baire f¨ur vollst¨andig metrische R¨aume, [F, Satz 4.1.1], angewandt auf den Raum (D, d₂) und die in der Spurtopologie von Doffenen Mengen U_n∩D folgt dass f¨ur mindestens einen Index N ∈ N die Menge UN ∩D nicht dicht in D sein kann.

Also existiert eine nicht leere und inD offene MengeV ⊆D mitV ∩U_N =∅, d.h. es existiert eine offene Kugel S⊆CmitS∩D6=∅und

∀z∈S∩D: sup

|f_N(z)−fm(z)| : m≥N ≤1.

Da f_N als stetige Funktion auf dem Kompaktum D beschr¨ankt ist, ist (f_n)n∈N gleichm¨aßig beschr¨ankt auf S∩D. W¨ahlt man nun ein in S liegendes dreieckiges Gebiet D⁰ so, dass ∂D⁰ ein gewisses bei der Konstruktion von D vorkommendes Di ist, so gilt ∂D⁰ ⊆ S ∩D. Daher ist (f_n)n∈N auch auf ∂D⁰ gleichm¨aßig beschr¨ankt und nach dem Maximumprinzip f¨ur analy- tische Funktionen, Satz 3.1, auch auf D⁰. Sei (f_nk|_D⁰)k∈N eine Teilfolge von (f_n|_D⁰)n∈N. Aus dem Satz von Montel, Satz 2.3, folgt die Existenz einer lokal gleichm¨aßig konvergenten Teilfolge (f_nkl|_D⁰)l∈N. Nachdem die Folge (f_n)n∈N punktweise gegen f konvergiert, muss der Grenzwert

8 3 LAVRIENTIEV’S RESULTATE von (f_nkl|_D⁰)l∈N mitf|_D⁰ ubereinstimmen. Also konvergiert (f¨ _n|_D⁰)n∈Ngegen f|_D⁰. WeilGb ma- ximal ist muss gelten

D⁰⊆Gb=G\D.

Das kann aber nicht sein, denn es liegen Punkte in D⁰ welche auch inD liegen. k Auch das zweite und letzte Resultat ist dem Vorigen sehr ¨ahnlich.

3.4 Lemma.SeiG⊆Cein einfach zusammenh¨angendes Gebiet. Weiters sei C ⊆Geine bzgl.

Gabgeschlossene, nicht leere und nirgends dichte Teilmenge sodass Gb :=G\C eine dichte und offene Teilmenge von G ist die sich als disjunkte Vereinigung offener Kugeln schreiben l¨asst, d.h. Gb = S∞

i=1Ui(xi). Dann existiert keine Funktionenfolge (fn)n∈N analytischer Funktionen die auf G punktweise gegen eine Grenzfunktion f konvergiert und f¨ur die Gb die gr¨oßtm¨ogliche offene und dichte Menge ist, auf der (fn)n∈N lokal gleichm¨aßig gegen f konvergiert.

Beweis. Angenommen (f_n)n∈N und f existieren. Bezeichne die Kugeln U_i(x_i) mit S_i. Da fn|_C punktweise gegen f|_C konvergiert ist

fn|_C : n ∈ N punktweise beschr¨ankt. Nach Lemma 2.7 existiert eine bzgl. der Spurtopologie auf C offene und dichte Teilmenge Cb ⊆ C sodass

f_n|

Cb : n∈N lokal beschr¨ankt ist. Daher gibt es einz₀∈C,r >0 und M >0 sodass

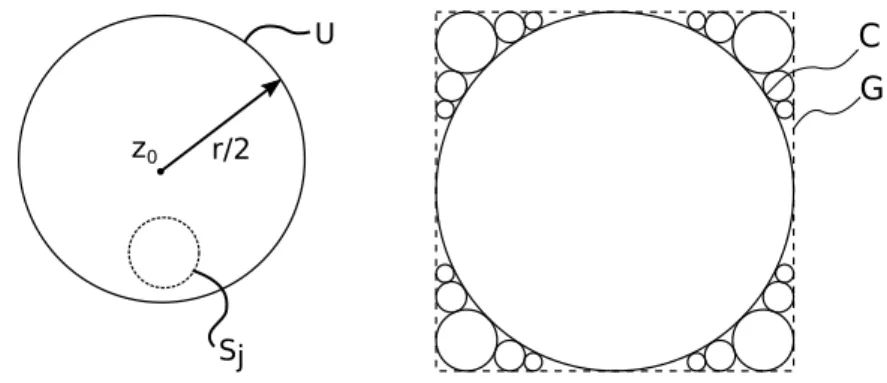
|f_n(z)| ≤M ∀n∈N, ∀z∈Ur(z0)∩C. (4) Setze U := U^r

2(z₀). Um jeden Punkt z ∈ C, insbesondere z₀, findet man nach Voraussetzung eine beliebig kleine Kugel Sj. Also existiert ein j ∈N sodass Sj∩U 6=∅ und Sj einen Radius kleinergleich ₄^r hat.

Abbildung 3: Links:U und Sj. Rechts: Veranschaulichung einer m¨oglichen Wahl vonGund C, wobei vonC nur endlich viele Kreise dargestellt sind.

Es kann aber nur endlich viele KugelnSi1, . . . , Sim geben dieU schneiden und einen Radius gr¨oßer als ^r₄ haben. Setze R := U \ {S_i1∪˙ . . .∪S˙ _im}. Weil mindestens eine Kugel mit Radius kleinergleich ^r₄ die Kugel U schneidet und alle S_i paarweise disjunkt sind gilt R 6=∅ und sogar R^◦6=∅. Nun zeigen wir dass f¨urz∈R gilt

|f_n(z)| ≤M ∀n∈N, (5)

denn f¨urz∈R tritt genau einer der folgenden beiden F¨alle ein:

• z∈U ∩S_j und S_j hat Radius kleinergleich ^r₄: Dann gilt∂S_j ⊆U_r(z₀)∩C. Aus (4) folgt

|f_n(w)| ≤M ∀n∈N, w∈∂S_j.

Aus dem Maximumprinzip, Satz 3.1, folgt nun sogar

|f_n(w)| ≤M ∀n∈N, w ∈S_j, also insbesondere (5).

• z∈U ∩C: Wegen U ∩C ⊆Ur(z0)∩C folgt (5) wieder aus (4).

Insbesondere haben wir gezeigt dass sup

|f_n(z)| : n ∈ N, z ∈ R < ∞. Aus dem Satz von Montel, Satz 2.3, folgt dass eine auf R gegen f lokal gleichm¨aßig konvergente Teilfolge (f_nk)k∈N existiert. Wie im Beweis von Korollar 2.8 zeigt man dass dann auch (f_n)n∈N auf R lokal gleichm¨aßig konvergiert. WeilGb maximal ist muss gelten

R^◦⊆G,b

was geometrisch aber nicht m¨oglich ist. Denn Gb ist eine Vereinigung disjunkter Kugeln, also m¨usste sich R^◦ als Vereinigung disjunkter Kugeln schreiben lassen, R^◦ ist aber eine Kugel

geschnitten mit Komplementen endlich vieler Kugeln. k

10 LITERATUR

Literatur

[A1] Michael Kaltenb¨ack:Analysis 1, Vorlesungsskriptum Version WS 2014/2015 [A2] Michael Kaltenb¨ack:Analysis 2, Vorlesungsskriptum Version SS 2015 [A3] Michael Kaltenb¨ack:Analysis 3, Vorlesungsskriptum Version WS 2015/2016

[F] Harald Woracek, Michael Kaltenb¨ack und Martin Bl¨umlinger:Funktionalana- lysis, Vorlesungsskriptum, 10. Auflage, Februar 2015

[K] Harald Woracek:Komplexe Analysis, Vorlesungsskriptum Version SS 2015

[L] M.A. Lavrientiev: Sur les fonctioins d’une variable complexes representables par des series de polynomes, Hermann & Cie, Paris 1936

[D] K.R. Davidson:Pointwise Limits of Analytic Functions, Amer. Math. Monthly, Vol. 90, 391-394

[P] M.J. Pelling:Letters to the Editor, Amer. Math. Monthly, Vol. 95, 535-536

[BM] A.F. Beardon, D. Minda: On the Pointwise Limit of Complex Analytic Functions, Amer. Math. Monthly, Vol. 110, 289-297

[A] Ernst Albrecht:Topologie, Vorlesungsskriptum SS 2007,

www.math.uni-sb.de/ag/albrecht/ss07/top/files/TKap5.pdf, Stand 09.01.2017