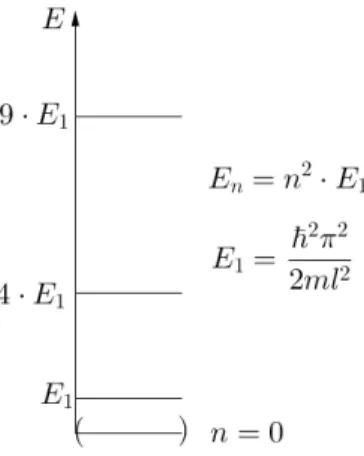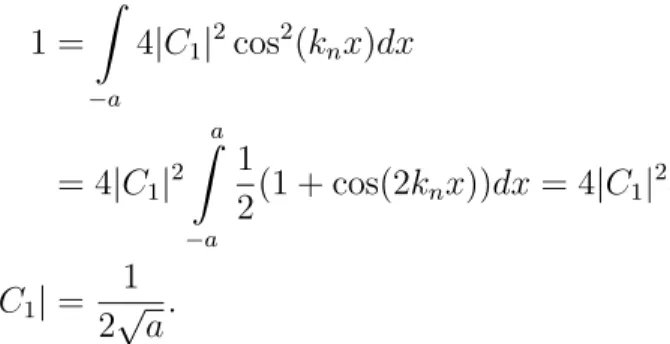2.7.1 Wahrscheinlichkeitsamplitude und Unsch¨ arfe

Eigenschaften der Schr¨odingergleichung: Betrachten wir ein paar Eigenschaften der oben besprochenen Schr¨odingergleichung.

1. Die L¨osung hat die Form

ψE(r, t) =e^−~iE·tψE(r)

2. Die Linearit¨at der Schr¨odingergleichung liefert das Superpositionsprinzip. Sind also ψ1

und ψ2 L¨osungen der Schr¨odingergleichung, so ist auch ψ =c₁ψ₁+c₂ψ₂

mit beliebigen komplexen Koeffizientenc1, c2 ∈C L¨osung der Schr¨odingergleichung.

3. Wegen der Normierungsbedingung Z

|ψ(r)|²d³r = 1

erh¨alt die Schr¨odingergleichung die Teilchenzahl. Dies ist die globale Teilchenzahlerhal- tung. In Analogie zur Elektrodynamik betrachten wir nun eine lokale Teilchenzahlbilanz bzw. Wahrscheinlichkeitsdichtebilanz. In der Elektrodynamik galt:

∂ρL

∂t + divj_L= 0,

wobei ρL die Ladungsdichte und j_L die Ladungsstromdichte bezeichnen. Wir beweisen nun die folgende Behauptung.

Behauptung: Ist ρ die Wahrscheinlichkeitsdichte und j(r, t) die Wahrscheinlichkeits- stromdichte, mit

j(r, t) = ~

2mi(ψ^∗∇ψ−ψ∇ψ^∗), so erf¨ullen ρ und j die Kontinuit¨atsgleichung.

Beweis:

∂

∂tρ= ∂

∂t(ψψ^∗) = ˙ψψ^∗+ψψ˙^∗ Die komplex konjugierte Schr¨odingergleichung ist:

−i~ψ˙^∗ =

−~²

2m∇²+V

ψ^∗.

Setzt man diese und die urspr¨ungliche Schr¨odingergleichung oben ein, so erh¨alt man:

∂

∂ρ=−i

~

ψ^∗

− ~²

2m∇²+V

ψ−ψ

−~²

2m∇²+V

ψ^∗

=− i~ 2m

ψ^∗∇²ψ−ψ∇²ψ^∗

=− i~

2m[∇(ψ^∗∇ψ−ψ∇ψ^∗)−(∇ψ^∗∇ψ− ∇ψ∇ψ^∗)]

=− i~

2mdiv(−ψ^∗∇ψ+ψ∇ψ^∗).

Dies war zu zeigen.

Wir fassen zusammen:

2.5. DIE SCHR ¨ODINGERGLEICHUNG 39

Die Wahrscheinlichkeitsdichteρ und die Wahrscheinlichkeitsstromdichte j mit:

ρ(r, t) =ψ(r, t)ψ^∗(r, t) (2.16) j(r, t) = ~

2mi(ψ^∗∇ψ−ψ∇ψ^∗) (2.17) erf¨ullen die Kontinuit¨atsgleichung:

∂

∂tρ+ divj = 0 (2.18)

4. Die Schr¨odingergleichung istreversibel(zeitumkehr-invariant), wie auch die Gleichungen der klassischen Mechanik und der Elektrodynamik. Betrachte hierzu die L¨osung:

ψ(r, t) = ψE(r)e^−iE~t Die Ersetzung

t → −t f¨uhrt dann zu

ψ →ψ^∗.

Hierbei tritt nur eine ¨Anderung der Phase auf, welche nicht messbar ist. Die messbare Wahrscheinlichkeitsdichte ¨andert sich nicht, ρ(r, t) → ρ(r,−t). Die ebenfalls messbare Stromdichte ¨andert allerdings ihr Vorzeichen,j(r, t)→ −j(r,−t), wie man direkt aus der Definition (2.17) ersehen kann⁵. Damit bleibt auch die Kontinuit¨atsgleichung invariant gegen¨uber Zeitumkehr.

5. Wir k¨onnen die Schr¨odingergleichung auch in Operatorform schreiben, wenn wir den sogenannten Hamiltonoperatordefinieren:

Hˆ =−~²

2m∇²+V(r) (2.19)

Dieser ist die quantenmechanische Verallgemeinerung der Hamilton-Funktion. Hieraus kann man den Operator der kinetischen Energie ablesen:

Tˆ=−~²

2m∇². (2.20)

Wegen der Analogie zur klassischen Mechanik erwarten wir ˆT = _2m^pˆ2 und k¨onnen den Impulsoperator ablesen:

ˆ p= ~

i∇. (2.21)

Die Schr¨odingergleichung in Operatorform sieht dann wie folgt aus:

i~∂

∂tψ(r, t) = ˆHψ(r, t)

5Dies ist analog zum Vorzeichenwechsel der elektrischen Stromdichte und h¨angt mit der Richtungs¨anderung der Geschwindigkeit zusammen.

6. Betrachten wir nun die station¨are Schr¨odingerlgleichung in Operatorform:

Hψˆ E(r, t) =EψE(r, t). (2.22) Hierbei ist ψE die station¨are L¨osung zum Parameter E. Gleichung (2.22) ist also eine Eigenwertgleichungder Hamiltonoperators ˆH. Die L¨osungen f¨ur eine solche Gleichung sind Paare einer EigenfunktionψE(r, t) und einem EigenwertE:

{E, ψE}

Die Interpretation ist nun, dass die EigenwerteE die m¨oglichen Energiewerte sind, die zu der zugeh¨origen Eigenfunktion ψE(r, t), die die jeweilige Ortswahrscheinlichkeit angibt, korrespondieren. Nun gibt es zwei F¨alle:

(a) Die Energiewerte sind diskret verteilt. Dies tritt z.B. im H-Atom auf (gebundene Zust¨ande), in denen die diskreten Bohrschen Bahnen (ihre Verallgemeinerung) streng aus der L¨osung des Eigenwertproblems folgen.

(b) Die Energieverteilung ist kontinuierlich. Ein freies Teilchen kann beispielsweise jede Energie annehmen.

7. Wir m¨ussen noch einige physikalische bzw. mathematische Anforderungen an ψ stellen, damit wir dem Wahrscheinlichkeitscharakter von ψ und damitρ gerecht werden.

(a) Die L¨osung muss f¨ur gegebene Anfangs-und Randbedingungen eindeutig sein.

(b) Wir erwarten Stetigkeit von ψ und ∇ψ, damit auch ρ und j stetig sind.

(c) Da wirψ als Wahrscheinlichkeitsamplitude verstehen, muss Reψ <∞, Imψ <∞ gelten.

(d) Da mit der Normierung in einem Volumen V f¨ur alle Zeitent Z

ρ(r, t)dr= 1,

gilt, umfasst die Menge aller ψ nur quadrat-integrable-Funktionen.

8. Da aufgrund der statistischen Natur der Quantenmechanik nur Mittelwerte von Gr¨oßen physikalische Relevanz haben und wir solchen Gr¨oßen einen Operator zuordnen k¨onnen, ist der Mittelwert einer Gr¨oße A wie folgt zu berechnen⁶:

hAˆi= Z

ψ^∗(r) ˆA ψ(r)d³r.

2.6 Zeitverhalten eines freien Quanten-Teilchens

Wir betrachten in diesem Abschnitt ein Teilchen, welches nicht mit einem Potential wechsel- wirkt, also giltV(r) = 0, und die Schr¨odinger-Gleichung nimmt folgende Form an:

i~∂ψ(r, t)

∂t =− ~²

2m∇²ψ(r, t).

6Dies zeigen wir genauer im n¨achsten Kapitel.

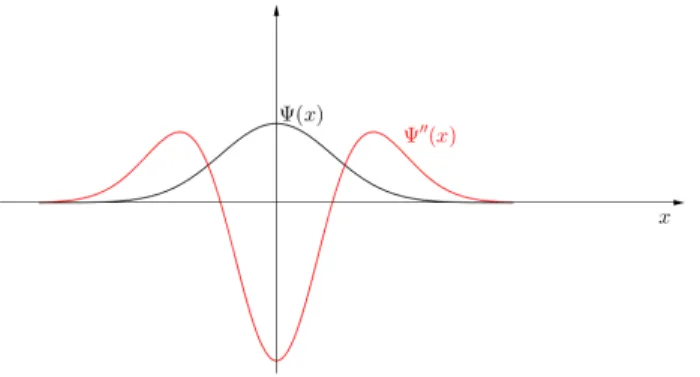
2.6. ZEITVERHALTEN EINES FREIEN QUANTEN-TEILCHENS 41 Bei t = 0 sei die Wahrscheinlichkeitsamplitude durch ψ0(r) gegeben. Uns interessiert nun die Zeitentwicklung. Bevor wir diese errechnen, ¨uberlegen wir uns das qualitative Verhalten. Auf der rechten Seite der obigen Schr¨odinger-Gleichung tritt im eindimensionalen Fall die zweite Ableitung der Funktionψ auf. Die zweite Ableitung einer Funktion stellt ihre Kr¨ummung (mal

−1) dar. Im unten stehenden Bild sind zur Illustration eine gaußf¨ormige Funktion und ihre zweite Ableitung skizziert.

Abbildung 2.9: Gaußf¨ormige (reelle) Wellenfunktion und ihre zweite Ableitung

Betrachten wir nun die linke Seite der Schr¨odinger-Gleichung und schauen wir uns den Grenz- wert f¨ur große Zeiten an, bei dem die zeitliche ¨Anderung verschwindet, so muss f¨ur allergelten:

t→∞lim

∂

∂tψ(r, t) = 0.

Also ist im Endzustand die erste Ableitung der Wellenfunktion im Ortsraum konstant (1- dimensionaler Fall):

t→∞lim

∂

∂xψ(x, t) = const.

Im Zeitverlauf reduziert sich also die Kr¨ummung unserer Wellenfunktion immer mehr.

Abbildung 2.10: Verbreiterung der Wellenfunktion im Ortsraum

Die asymptotische L¨osung sollte also eine flache Kurve sein, die Wellenfunktion “zerfließt”.

2.6.1 L¨ osung im Fourier-Raum

Bei der genauen Berechnung der Wellenfunktion eines freien Teilchen k¨onnen wir auf die Fourier-Transformation zur¨uckgreifen. Wir wissen bereits vom Doppelspalt, dass ψ0 in der Form einer ebenen Welle die beobachte Interferenz am Doppelspalt erkl¨art und gleichzeitig die Schr¨odingergleichung l¨ost. Die Gesamtheit der ebenen Wellen bildet ein vollst¨andiges abge- schlossenes Funktionensystem (s. Analysis). Man kann also jede L¨osung der Schr¨odingergleichung

aus unendlich vielen Partialwellen ¨uberlagern. Zum Beispiel k¨onnen wir die Gaußfunktion in Abbildung 2.9 als ¨Uberlagerung von Partialwellen darstellen. Eine solche Funktion stellt eine gute Modellvorstellung eines freien Teilchens dar, das den klassischen Limes (Punktteilchen ergibt sich bei Breite gegen Null) direkt enth¨alt. Umgekehrt entspricht eine ebene Welle dem Limes Breite gegen Unendlich. Es bleibt zu kl¨aren, wie die Breite des Wellenpaketes mit phy- sikalischen Eigenschaften des Teilchens zusammenh¨angt.

Transformieren wir also die Ortsabh¨angigkeit in den Fourier-Raum (Wellenzahl-Raum), wobei wir uns auf eine Dimension beschr¨anken⁷:

ψ(x, t) = Z∞

−∞

1

2πψ(k, t)e˜ ^ikxdk.

Dies setzen wir in die obige Schr¨odinger-Gleichung ein:

i~∂

∂t Z∞

−∞

1

2πψ(k, t)e˜ ^ikxdk =− ~² 2m

∂²

∂x² Z∞

−∞

1

2πψ(k, t)e˜ ^ikxdk i~

Z∞

−∞

1 2πe^ikx ∂

∂tψ(k, t)dk˜ =− ~² 2m

Z∞

−∞

1

2πψ(k, t)˜ ∂

∂x²e^ikxdk

i~ Z∞

−∞

1 2πe^ikx ∂

∂tψ(k, t)dk˜ = ~² 2m

Z∞

−∞

k²

2πψ(k, t)e˜ ^ikxdk i~∂

∂tψ(k, t) =˜ ~²k²

2m ψ(k, t)˜ .

Beim letzten Schritt haben wir ausgenutzt, dass Exponentialfunktionen zu verschiedenen k unabh¨angig voneinander sind (orthogonales Funktionensystem). Das bedeutet, dass linke und rechte Seite f¨ur jedeskseparat ¨ubereinstimmen m¨ussen. Dann k¨onnen wir das Integral und den gemeinsamen e-Faktor weglassen.

Die Schr¨odinger-Gleichung imk-Raum ist also entkoppelt, d.h. L¨osungen f¨ur unterschiedlichek sind voneinander unabh¨angig (das ist eine Konsequenz der Linearit¨at der Schr¨odingergleichung).

Die zeitabh¨angige L¨osung dieser entkoppelten Differentialgleichung finden wir nun wieder ein- fach ¨uber einen e-Ansatz:

ψ(k, t) =˜ A(k)·e^−iω(k)t,

wobeiA undω zun¨achst unbestimmte Koeffizienten sind, die jedoch von unserem Parameterk abh¨angen k¨onnen. Einsetzen liefert:

i~(−i)ω(k)·A(k)·e^−iω(k)t= ~²k²

2m A(k)·e^−iω(k)t

~ω(k) = ~²k² 2m

Damit haben wir wieder die Dispersionsrelation eines nichtrelativstischen Teilchens reprodu- ziert. Nun m¨ussen wir noch den Vorfaktor A(k) aus der Anfangsbedingung gewinnen. Zur Zeit t= 0 gilt im Ortsraum:

ψ(x, t= 0) =ψ0(x)

7Die Wahl des Faktor _2π¹ ist nicht eindeutig. Bei unserer Wahl taucht in der R¨ucktransformation der Faktor 1 auf. Alternativ werden h¨aufig in beiden Transformationen symmetrische Faktoren _(2π¹₎₁/2 verwendet.

2.6. ZEITVERHALTEN EINES FREIEN QUANTEN-TEILCHENS 43 Setzen wir diese Gr¨oße in die Fourier-Transformation ein, so erhalten wir die Anfangsbedingung im k-Raum:

ψ(k, t˜ = 0) = ˜ψ0(k)

Mit t = 0 kann man ˜ψ0(k) mit dem Vorfaktor A(k) identifizieren, so dass die zeitabh¨angige L¨osung im k-Raum die Form

ψ(k, t) = ˜˜ ψ₀(k)·e^−iω(k)t,

erh¨alt. F¨ur die zeitabh¨angige L¨osung im Ortsraum ist nun ˜ψ(k, t) zur¨uck zu transformieren.

Die R¨ucktransformation geben wir hier in drei Dimensionen an:

ψ(r, t) =

Z d³k

(2π)³ψ˜₀(k)ei{k◦r−ω(k)t}.

2.6.2 L¨ osung f¨ ur eine Gauss-Anfangsbedingung

Beschr¨anken wir uns nun wieder auf den eindimensionalen Fall einer ebenen Welle inx-Richtung.

Die Fouriertransformation von oben nimmt dann die Form ψ(x, t) =

Z∞

−∞

dk

2πψ˜0(k)ei{kx−ω(k)t},

an mit der Dispersionsrelation ω(k) = ^~_2m^k2. Als Beispiel behandeln wir nun ein Gauss-f¨ormiges Wellenpaket im Impulsraum,

ψ˜₀(k) = Ce^{−14σ2(k−k0)2−ikx0}, (2.23) mit der zugeh¨origen Wahrscheinlichkeitsdichte im k-Raum

˜

ρ(k)≡ |ψ˜0(k)|² =|C|²e^{−σ22(k−k0)2}

Die Gauss-Verteilung beschreibt eine ¨Uberlagerung monochromatischer Wellen, die umk0 zen- triert sind, wobei die Breite der Verteilung durch σ⁻¹ gegeben ist. Setzen wir die Anfangsbe- dingung (2.23) in die Fourier-Transformation ein, so erhalten wir die folgende zeitabh¨angige L¨osung im Ortsraum:

ψ(x, t) = C 2π

Z∞

−∞

dk

2π e^{−σ42(k−k0)2+i[k(x−x0−ω(k)t]}.

Wir entwickeln nun ω(k) um die Frequenz am Peak, k =k0 (die “Tr¨agerfrequenz”). Die Tay- lorreihe ist nach dem quadratischen Term bereits exakt, da die dritte Ableitung von ω nach k gleich Null ist.

ω(k) = ~k²

2m =ω(k0) + dω dk k0

(k−k0) + 1 2

d²ω dk² k0

(k−k0)²

=ω₀+vG(k−k₀) +β(k−k₀)² Hierbei wurden die folgenden Gr¨oßen definiert:

ω0 = ~k²₀ 2m, vG= ~k0

m , β= 1

2

~ m,

wobei vG die ¨ubliche Gruppengeschwindigkeit einer Welle bezeichnet. Damit schreibt man die Wellenfunktion mit der Substitutionk^′ =k−k0 zu:

ψ(x, t) = C 2π

Z∞

−∞

e

−

σ² 4 +iβt

| {z }

:=a

k^′2+ik^′[(x−x₀)−vGt]

| {z }

:=b ·e^{i[k0(x−x0)−ω0t]}dk^′

Die zweite e-Funktion des obigen Integrals stellt die monochromatische Tr¨ager-Welle dar. Ist der Realteil von a gr¨oßer als Null, so gilt:

Z∞

−∞

e^−ax2+bxdx= Z∞

−∞

e^−a(^x−2a^b)²e^b4a2dx=

√π a e^b4a2. Benutzt man dieses Integral, so folgt:

ψ(x, t) = C

2πe^{i[k0(x−x0)−ω0t]}

s π

σ²

4 +iβte⁻

((x−x0)−vGt)2

σ2+4iβt (2.24)

Im Grenzfall, dass 4βt gegen die ¨ubrigen Terme vernachl¨assigt werden kann, identifizieren wir die Phasengeschwindigkeit vph durch:

k0(x−x0)−ω0 = const ⇒vph = ω0

k0

(2.25) und dieGruppengeschwindigkeitvG als die Geschwindigkeit, mit der sich die Gauß-f¨ormige Funktion verschiebt.

Berechnen wir nun die Wahrscheinlichkeitsdichte im Ortsraum. Das Betragsquadrat von Glei- chung (2.25) ergibt

|ψ(x, t)|² = |C|² 4π

1 qσ⁴

16 +β²t² e⁻²

(x−x0−vGt)2 σ4+(4βt)2 σ²

= |C|² π

1

pσ⁴+ 16β²t²e^{−2σ2 (}

x−x0−vGt)2 σ4+16β2t2 .

Die Wahrscheinlichkeitsdichte im Ortsraum ist also auch Gauß-f¨ormig. Das Maximum, bezie- hungsweise der Schwerpunkt des Wellenpaketes, verschiebt sich mit der Gruppengeschwindig- keit vG gleichf¨ormig:

xmax−x0−vGt= 0

xmax(t) =x0 +vGt

Die Breite der Wahrscheinlichkeitsdichte, ∆x, nimmt mit der Zeit zu. Das Wellenpaket zerfließt also. Ein Vergleich mit

ψ(x, t) = 1

p2π(∆x)²e⁻

(x−x0−vGt)2 2(∆x(t))2 , liefert durch Ablesen f¨ur die doppelte Varianz

2(∆x)² = σ⁴+ 16β²t² 2σ² ,

woraus sich die Standardabweichung (“Unsch¨arfe”) des Ortes im Zustand ψ(x, t) ergibt:

∆x(t) = rσ²

4 + 4β²

σ² t². (2.26)

2.7. ENDLICHE R ¨AUMLICHE AUSDEHNUNG VON MIKROTEILCHEN 45 Die Breite des Wellenpaketes nimmt also mit der Zeit t zu, das Wellenpaket “zerfließt”, wie bereits zu Beginn vermutet. F¨ur große Zeiten w¨achst die Standardabweichung linear mit der Zeit, genauso wie bei der Diffusion eines klassischen Teilchens.

Aufgabe: Man bestimme die Unsch¨arfe im Orts- und Impulsraum und untersuche die Heisenberg- Unsch¨arfe-Relation. Wie h¨angt das Unsch¨arfeprodukt von k0 und von der Zeit ab?

2.7 Endliche r¨ aumliche Ausdehnung von Mikroteilchen

Wir hatten bereits in Abschnitt 1.1 gesehen, dass sich die Probleme der klassischen Beschrei- bung von Mikroteilchen beheben lassen, wenn die Teilchen eine endliche Ausdehnung besitzen w¨urden. Mathematisch kann dies durch ein Wellenpaket dargestellt werden. Den Zusammen- hang zwischen Breite des Paketes im Orts- und Impulsraum diskutieren wir im n¨achsten Ab- schnitt. Die physikalische Ursache dieser endlichen Breite

2.7.1 Wahrscheinlichkeitsamplitude und Unsch¨ arfe

Wir wollen qualitativ noch einmal den Begriff der Unsch¨arfe aufgreifen.

A) klassisches Teilchen: F¨ur ein klassisches Teilchen lassen sich “im Prinzip” die Orts- unsch¨arfe (oder Ortsungenauigkeit) ∆r und die Impulsunsch¨arfe ∆p beliebig verkleinern (im Rahmen der klassischen Mechanik wird angenommen, dass der aktuelle Phasenraumpunkt ei- nes Teilchens beliebig genau bestimmbar ist). Dies ist mit der oben betrachteten L¨osung der Schr¨odingergleichung f¨ur das (typische) Beispiel eines Gaußschen Wellenpaktetes nicht verein- bar.

B) freies Mikroteilchen: Unsere erste Beschreibung eines freien Mikroteilchens hatten wir an Hand des Doppelspaltexperiments mit einer ebenen Welle realisiert. Nun betrachten wir eine ebene Lichtwelle:

E(x, t) = E₀e^−iωt+ikx Hierbei haben wir nur einen freien Parameter, da

ω(k) = c·k

als L¨osbarkeitsbedingung f¨ur die Maxwell-Gleichung folgte. Wir bestimmen nun die Frequenzω und die Wellenzahlkf¨ur Mikroteilchen und bringen die Interferenzbilder f¨ur Licht und Teilchen f¨ur alle x, z und t zur Deckung. Nun variieren wir die Beschleunigungsspannung U und damit auch die kinetische Energie. Als Resultat erhalten wir folgende ebene Welle:

ψfrei(x, t) = ψ0e^{−iE(p)~ t+ip~x} (2.27) Hieraus folgt dann E =~ω und p=~k. Man erh¨alt also das gleiche Resultat wie f¨ur Photonen (vergleiche hierzu Einsteins Erkl¨arung der Photoeffekts). Diskutieren wir nun die Darstellung durch Gleichung (2.27). Die Aufenthaltswahrscheinlichkeitsdichte ist gegeben durch:

ρfrei(x, t) = |ψfrei|² =|ψ0|². (2.28) Wir haben also eine orts- und zeitunabh¨angige Aufenthaltswahrscheinlichkeitsdichte. Die Im- pulsunsch¨arfe ist gleich 0, da der Impuls in (2.27) fixiert ist. Da jedoch alle Aufenthaltsorte gleich wahrscheinlich sind, gilt f¨ur die Ortsunsch¨arfe:

∆x→ ∞.

Hierzu sind noch einige Bemerkungen zu machen. Die obige ebene Welle beschreibt eine un- endlich ausgedehnte Wahrscheinlichkeitsamplitude, die dar¨uber hinaus auch f¨ur alle Zeiten,

−∞< t <∞existiert. Dies ist ein Modell, welches physikalisch nicht realisierbar ist (Vergleiche hierzu die divergente Energie einer ebenen monochromatischen Welle in der Elektrodynamik).

Auch ist f¨ur Gleichung (2.28) die Normierung problematisch. Die korrekte L¨osung besprechen wir sp¨ater. Wenden wir uns nun dem realistischen Fall C) zu.

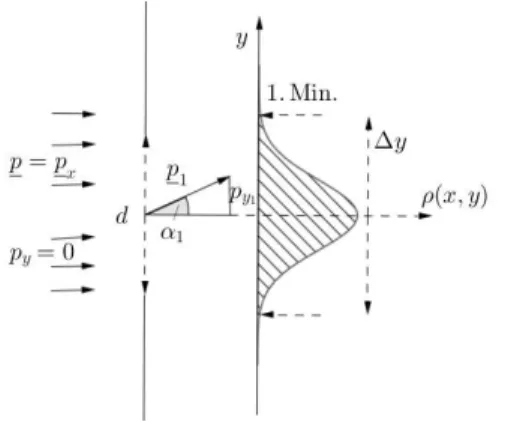
C) R¨aumlich lokalisiertes Teilchen: Betrachten wir nun ein Mikroteilchen, welches wir r¨aumlich lokalisieren k¨onnen. Dies konnten wir ja zum Beispiel nach der Beugung am Spalt.

Abbildung 2.11: r¨aumliche Lokalisierung eines Mikroteilchens bei der Beugung am Spalt Vor der Beugung liegt der gesamte Impuls inx-Richtung vor und wir haben keine Komponente in y-Richtung. Daf¨ur ist y-Komponente vor der Beugung unscharf. Nach der Beugung k¨onnen wir den Impuls nur noch durch

0≤ |py1| ≤py(α1) = ∆py

absch¨atzen. Das heißt, indem wir die Ortsunsch¨arfe auf ∆y begrenzt haben, hat sich die Im- pulsunsch¨arfe auf ∆py vergr¨oßert. Aus der Wellenoptik wissen wir:

sinα1 = λ d , und es gilt auch:

py1

|p₁| = sinα₁.

Mit Sicherheit gilt auch ∆y&d. Damit haben wir folgende Absch¨atzung:

∆y·∆py &d·p1sinα1

=d·~·kλ d

=~k2π k

Wir erhalten also den Spezialfall des allgemeines Gesetzes der Unsch¨arfe von Heisenberg:

∆y·∆py &h (2.29)

Eine geringere Unsch¨arfe ist also nicht m¨oglich⁸. Dies ist kein Defizit der Messapparatur oder der Messmethode, sondern eine Eigenschaft der Mikroteilchen. Also auch eine Eigenschaft der

8Diese Absch¨atzung ist noch grob. Die genaue Rechnung, sowie die Anwendung auf ein Gaußsches Wellen- paket unten zeigen, dass die korrekte untere Grenze der Unsch¨arfe~/2 betr¨agt

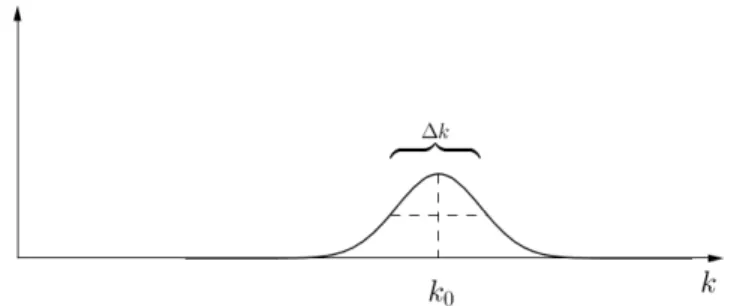
2.7. ENDLICHE R ¨AUMLICHE AUSDEHNUNG VON MIKROTEILCHEN 47 Natur. Diese Eigenschaft der Unsch¨arfe hat jede Welle. Wir m¨ussen hierf¨ur nur obenpdurch ^k_~ ersetzen. Man kann die Unsch¨arfe als Eigenschaft der Fourier-Transformation sehen. Sie folgt aus dem Zusammenhang zwischen dem direkten und dem Fourier-Raum. Schauen wir uns hierzu noch einmal eine monochromatische Welle f¨ur ein festes t an.

Abbildung 2.12: Monochromatische Welle f¨ur ein festes t.

Die Fourier-Transformation liefert eine scharfe Wellenzahl k0.

Abbildung 2.13: Spektrum einer monochromatischen Welle im k-Raum

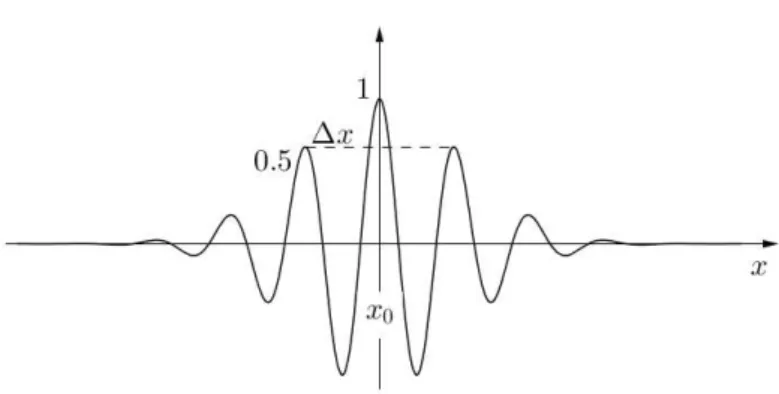
Die Fourier-Transformation in den Variablent undω verl¨auft analog. Betrachten wir nun nicht mehr eine monochromatische Welle, sondern eine ¨Uberlagerung aus mehreren monochroma- tischen Wellen mit unterschiedlichen Wellenl¨angen so ergibt sich ein Wellenpaket mit einer endlichen Breite in x-Richtung.

Abbildung 2.14: Nicht-monochromatisches Wellenpaket

Dieses hat im Fourier-Raum ebenfalls eine endliche Breite.

Abbildung 2.15: Gaußf¨ormige Verteilung im k-Raum F¨ur den Zusammenhang der beiden Breiten folgt:

∆x·∆k = 2π

Analog gilt f¨ur den Zusammenhang des Zeit- und Frequenzraums:

∆t·∆ω= 2π

Wir sehen also, dass der Zusammenhang der Breiten im Orts- und Impulsraum eine direkte Kon- sequenz der Fouriertransformation ist (Ort und Wellenzahl bzw. Zeit und Frequenz sind Fourier- konjugierte Gr¨oßen). Aus diesem Grund ist auch die Heisenberg-Unsch¨arfe-Relation kein spezi- fisches quantenmechanisches Ph¨anomen sondern eine Konsequenz der Fourier-Transformation.

2.7.2 Ursache der endlichen Ausdehnung von Mikroteilchen

Wie wir im Abschnitt 1.1 gesehen haben, gibt es keine M¨oglichkeit, die Ph¨anomene der Mi- krowelt mit einem klassischen Modell zu verstehen, das die Teilchen als “punkt-f¨ormig” an- sieht. Dies w¨urde unweigerlich zum Kollaps der Elektronen im Atom f¨uhren (Divergenz der Wechselwirkung-Energie), die in der Natur nicht beobachtet wird. Die nat¨urliche L¨osung des Problems erfolgt dadurch, dass die Teilchen – zus¨atzlich zur attraktiven Wechselwirkung mit den Atomkernen – eine kinetische Energie besitzen, die den Kollaps zu einem Punkt (der die potentielle Energie minimieren w¨urde) verhindert. Betrachten wir dazu die rechte Seite der Schr¨odingergleichung eines freien Teilchens (V = 0), die nichts anderes als den Operator der kinetischen Energie, angewendet auf die Wellenfunktion, darstellt (ein-dimensionaler Fall),

T ψ(x) =ˆ − ~² 2m

∂²ψ(x)

∂x² ∼ −K(x). (2.30)

Dieser Ausdruck ist proportionoal zur lokalen Kr¨ummung K(x) (mal −1). F¨ur die charak- teristische Form eines Wellenpaketes, das wir oben betrachtet haben, ist die Kr¨ummung im zentralen Bereich, der die Hauptbeitr¨age zur Wahrscheinlichkeitsdichte enth¨alt, ¨uberall negativ und dieser Ausdruck daher immer positiv, vergleiche Abb. 2.9. Die kinetische Energie (hier die r¨aumlich delokalisierte Dichte der kinetischen Energie) ist also positiv, wie aus der klassischen Mechanik bekannt. Interessanterweise besitzt ein quantenmechanisches Teilchen aber – anders als ein klassisches Teilchen – bereits eine kinetische Energie, wenn es sich in Ruhe befindet. Diese Energie verschwindet nur, wenn die Kr¨ummung verschwindet, also bei unendlicher Ausdehnung des Teilchens (was physikalisch nicht m¨oglich ist). Umgekehrt w¨urde f¨ur ein klassisches Punkt- teilchen die Kr¨ummung unbegrenzt wachsen und die kinetische Energie divergieren. Auch dies ist nicht m¨oglich, da die Natur (spontan) nur Zust¨ande realisiert, die die Energie minimieren.

F¨ur ein Elektron in der N¨ahe des Atomkerns (attraktive potentielle Energie) Vek < 0 ergibt sich also eine Gesamtenergie H =Vek+T, die sich als r¨aumliches Mittel ¨uber die ausgedehnte

2.8. TEILCHEN IM 1D-KASTENPOTENTIAL 49 Wellenfunktion ergibt,

H = Z ∞

−∞

dx ψ^∗(x)

Vek(x) +

− ~² 2m∂_x²²

ψ(x). (2.31)

W¨ahrend der erste Term negativ ist, ist der zweite positiv, und die Wellenfunktion nimmt die Form an, die diese Gesamtenergie minimiert (im Grundzustand). Dies f¨uhrt auf die bekannten Wellenfunktionen des Elektrons im Atom, die eine Ausdehnung der Gr¨oßenordnung des Bohr- Radius aufweisen. Gleichzeitig wird das unendliche Auseinanderfließen wie bei einem freien Teilchen hier durch das attraktive Kernpotential verhindert.

Durch diese einfache L¨osung sind alle fundamentalen Problem der klassischen Beschreibung behoben. Diese qualitativen Betrachtungen werden in den folgenden Kapiteln durch strenge Rechnungen im Rahmen der Schr¨odingergleichung best¨atigt.

Abschließend noch eine Bemerkung zum h¨aufig diskutierten“Welle-Teilchen-Dualismus”⁹. Die- ser wird oft missverstanden als ein Verhalten, das entweder durch Teilchen- oder durch Wel- leneigenschaften charakterisiert ist, wo sich das Objekt zu einer Zeit wie eine Welle, zu einer anderen wie ein Teilchen verh¨alt. Dies ist falsch. Charakteristisch f¨ur die Mikrowelt ist dagegen die fundamentale Eigenschaft einer endlichen r¨aumlichen Ausdehnung aller Objekte. Die Pro- pagation als Wellenpaket tr¨agt dabei Z¨uge der Dynamik klassischer Teilchen. Die Superposition ebener monochromatischer Wellen im Wellenpaket enth¨altgleichzeitig die M¨oglichkeit zur Inter- ferenz. Wie stark Welleneigenschaften ausgepr¨agt sind und wie groß die r¨aumliche Ausdehnung ist, h¨angt eintscheidend von der Umgebung des Teilchens, also von den Randbedingungen und

¨außeren Einfl¨ussen – externen Potentialen oder Feldern – ab. Die mathematische Antwort auf diese Fragen ist durch die Schr¨odingergleichung gegeben.

2.8 Teilchen im Kastenpotential. Diskretes und kontinuierliches Energie-Spektrum

Wir kommen nun zur ersten physikalischen Anwendung der station¨aren Schr¨odinger-Gleichung, bei der wir ein Mikroteilchen in einem externen Potential V(x) betrachten. Um dies zu moti- vieren, geben wir zun¨achst einige Beispiele.

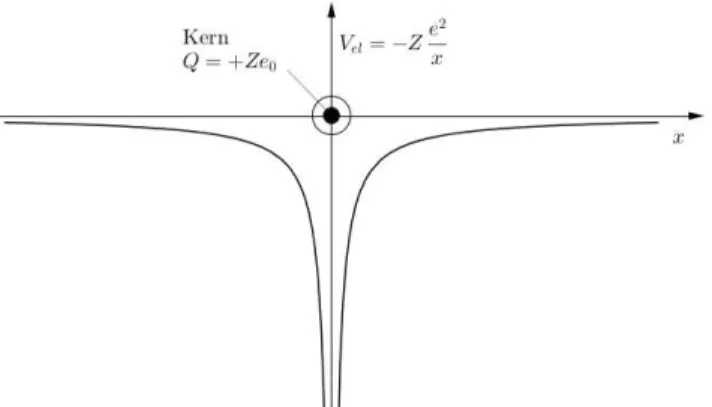
1. Die Elektronen im Atom wechselwirken mit dem Potential, welches durch die Coulomb- wechselwirkung mit dem Kern erzeugt wird.

Abbildung 2.16: Wechselwirkungspotential Vei(x) des Elektrons mit dem Atomkern (eindimen- sionales Modell)

9Genausowenig existiert ein “Welle-Teilchen-Dualismus” beim Licht. Auch hier treten beide Eigenschaften simultan auf und werden durch die Maxwell-Gleichungen f¨ur das quantisierte elektromagnetische Feld beschrie- ben.

2. Auch Elektronen in Halbleiter-Nanostrukturen erfahren charakteristische Potentiale mit Bindungscharakter.

Abbildung 2.17: Halbleiter-Heterostruktur und zugeh¨origes Potential (schematisch) 3. Atome in kalten Gasen in einem confinement-Potential oder optischem Gitter (durch

interferierende Laser erzeugt).

4. Ein weiteres Beispiel sind Quarks, die durch die starke Wechselwirkung in den Baryonen lokalisiert sind (bag model).

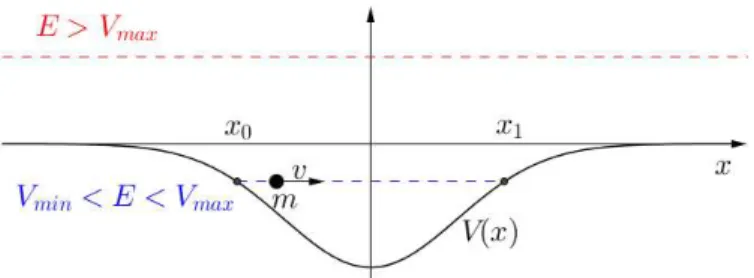
Was ist zu erwarten? Wir werden kurz unsere Erwartungen besprechen, wobei wir auf klassische Teilchen in einem externen Potential und auf Licht in einem Resonator eingehen.

1. Klassisches Teilchen: Hier gilt die Energieerhaltung, also:

E = m

2v²+V(x) = const.

Zeichnen wir ein typisches Potential wie in der Abbildung unten, so gibt es klassisch 3 M¨oglichkeiten (nur zwei sind realisierbar).

(a) Wenn die Gesamtenergie gr¨oßer als das Maximum des Potentials ist, so liegt eine ungebundene Bewegung vor.

E > Vmax

(b) Liegt die Gesamtenergie auf H¨ohe des Potentials so gibt es eine gebundene Bewegung und in Folge dessen Oszillationen mit den Wendepunkten x0 und x1.

Vmin < E < Vmax

(c) Der Fall

E < Vmin

ist aufgrund der Energieerhaltung nicht m¨oglich, da die kinetische Energie keine negativen Werte annehmen kann.

Abbildung 2.18: M¨ogliche klassische Zust¨ande eines Teilchens in einem Potential V(x).

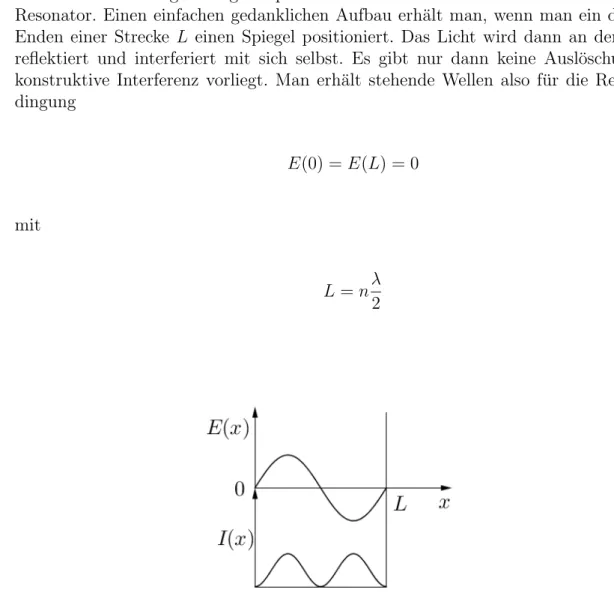
2.8. TEILCHEN IM 1D-KASTENPOTENTIAL 51 2. Resonator:Wie angek¨undigt besprechen wir nun noch kurz das Verhalten von Licht im Resonator. Einen einfachen gedanklichen Aufbau erh¨alt man, wenn man ein den beiden Enden einer Strecke L einen Spiegel positioniert. Das Licht wird dann an den Spiegeln reflektiert und interferiert mit sich selbst. Es gibt nur dann keine Ausl¨oschung, wenn konstruktive Interferenz vorliegt. Man erh¨alt stehende Wellen also f¨ur die Resonanzbe- dingung

E(0) =E(L) = 0

mit

L=nλ 2

Abbildung 2.19: Stehende Welle des elektromagnetischen Feldes und ihre Intensit¨atsverteilung in einem Resonator f¨ur den Fall undurchdringlicher (vollst¨andig reflektierender) W¨ande.

Wir werden im Folgenden verschiedene relevante Varianten des eindimensionalen Kastenpoten- tials besprechen.

2.8.1 A) Eindimensionaler Potentialkasten mit unendlich hohen W¨ anden

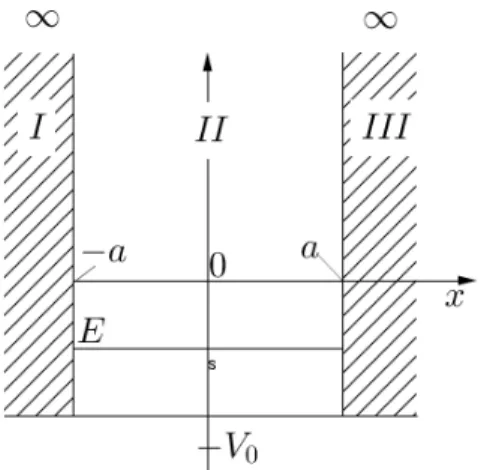
Wir betrachten zun¨achst den einfachsten Fall—ein Potential der Form (s. Abb. 2.20):

V(x) =







−V₀ , x∈[−a, a]

∞ , sonst

Abbildung 2.20: Eindimensionaler Potentialkasten mit unendlich hohen W¨anden. Die Energie- Eigenwerte E werden relativ zum Boden des Potentials angegeben, d.h. V0 →0.

Die Breite des Kasten ist also L = 2a. Die Bereiche I und III sind nicht zug¨anglich, da das Teilchen nicht in eine unendlich hohe Barriere eindringen kann. Wir m¨ussen also nur den Bereich II untersuchen. Dort hat der Hamilton-Operator folgende Gestalt:

Hˆ =−~² 2m

∂²

∂x² −V₀

Damit wird die station¨are Schr¨odinger-Gleichung im Intervall [−a, a] zu:

− ~² 2m

∂²

∂x² −V0

ψE(x) = E·ψE(x)

−~²

2mψ^′′_E(x) = (V0+E)ψE

ψ_E^′′(x) +αEψE = 0, mit αE = (V0 +E)2m

~² ≥0.

Hierbei ist V0+E =E−(−V0) der Energieabstand vonE zuV0. An die L¨osung ψE der obigen Differentialgleichung stellen wir folgende Bedingungen:

• Wie bereits erw¨ahnt, sind die Bereiche I und III nicht zug¨anglich. Damit ist f¨ur x /∈ [−a, a]ψE(x)≡0. Da die Wellenfunktion aber stetig sein soll, muss gelten:

ψE(−a) =ψE(a) = 0

• Außerdem gelte wie ¨ublich die Normierungsbedingung:

Za

−a

ψ_E^∗(x)·ψE(x)dx= 1.

Die L¨osung dieser Differentialgleichung erfolgt ¨uber einen e-Ansatz:

ψE(x) = Ce^µx

Hierbei ist C =const. und µ ein zu berechnender Parameter. Einsetzen in die Differential- Gleichung ergibt:

µ²+αE = 0 µ² =−αE

µ=±i√αE

2.8. TEILCHEN IM 1D-KASTENPOTENTIAL 53 Die allgemeine L¨osung muss eine Linearkombination dieser beiden L¨osungen sein. Setze noch kE =√αE:

ψE(x) =C₁e^ikEx+C₂e^−ikEx.

Hierbei sindC1, C2 ∈Czun¨achst unabh¨angige Konstanten. Man hat nun noch drei unbekannte Gr¨oßen in dieser Funktion zu spezifizieren. Zum Einen sind nat¨urlichC1 undC2 zu bestimmen.

Zum Anderen wissen wir auch noch nicht, welche Werte E annehmen kann. In Folge dessen ist also auch noch kE unbestimmt. Diese Unbestimmtheiten lassen sich nun aus den oben auf- gef¨uhrten Randbedingungen und der Normierungsbedingung berechnen. Nutzen wir zun¨achst die Randbedingungen:

0 =C1e^ikEa+C2e^−ikEa, 0 =C1e^−ikEa+C2e^ikEa.

Dies ist ein lineares homogenes Gleichungssystem f¨ur C1 und C2. Es besitzt genau dann nicht- triviale L¨osungen (C1, C2 6= 0), wenn die Determinante der Koeffizientenmatrix gleich Null ist:

det

e^ikEa e^−ikEa e^−ikEa e^ikEa,

!

= 0

und damit folgt:

0=^! e^2ikEa−e^−2ikEa = 2isin 2kEa.

Also erhalten wir die L¨osbarkeitsbedingung zu:

kn = nπ 2a = nπ

L , (2.32)

mit n= 0,±1,±2, .... Hierbei haben wir kE →kn vorgenommen, um deutlich zu machen, dass die Energie aufgrund der L¨osbarkeitsbedingung nur diskrete Werte annehmen kann:

αn = (V0+En)2m

~² =nπ 2a

2

. Die diskreten Energie-(Eigen)Werte erh¨alt man also zu:

En= ~² 2m

n²π² L² −V0.

Setzt man den Energie-Nullpunkt so, dass V0 = 0 gilt, erh¨alt man:

En= ~² 2m

n²π²

L² . (2.33)

In der Skizze 2.21 sind die m¨oglichen Energien eingezeichnet. Man beachte, dass die Abst¨ande nicht ¨aquidistant sind. Die Energie, die zu n = 0 geh¨ort, ist eingeklammert, weil wir jetzt feststellen werden, dass dieser Eigenwert nicht m¨oglich ist.

Abbildung 2.21: Diskretes Energie-Spektrum im eindimensionalen Kasten mit unendlich hohen W¨anden (Fall A).

F¨ur n= 0 gilt n¨amlich

Ψ0(x) =C1+C2 = const.

Wir m¨ussen aber nicht nur die Randbedingungen, sondern auch die Normierungsbedingung beachten:

1 = Za

−a

|C1+C2|²dx.

Hieraus folgt, dass nicht gleichzeitig C1 = 0 und C2 = 0 gelten kann. Dies widerspricht aber zum Beispiel der RandbedingungψE(a) = 0. Der Zustand mitn= 0 ist also nicht m¨oglich. Das Teilchen besitzt also immer eine positive (kinetische) Energie E >0. In unserem Fall folgt f¨ur das endliche Energieminimum

Emin =E1 >0,

und damit auch ein endliches Minimum des Impuls-Eigenwertes:

pmin = ~π l .

Dies ist ein fundamentaler Unterschied zur klassischen Mechanik, in der Energie und Impuls gleich 0 sein k¨onnen. DieseNullpunktsfluktuation ist ein reiner Quanteneffekt und findet sich in allen Quantensystemen wieder. Wir k¨onnen sie in Zusammenhang mit derUnsch¨arfe erkl¨aren.

Zuvor definieren wir den Begriff der Unsch¨arfe noch etwas genauer.

Unter Unsch¨arfe einer Gr¨oße A (Zufallsprozess) verstehen wir die Standardabweichung σA

(Wurzel aus der Varianz) dieser Gr¨oße. F¨ur einen Zufallsprozess (und die Quantenmechanik beschreibt Zufallsprozesse) ist die Standardabweichung einer Gr¨oße A gegeben durch (wir ge- ben die beiden gebr¨auchlichen Notationen an):

σA = ∆A=p

h(A− hAi)²i.

Da die Mittelwertbildung linear ist, gilt f¨ur das Argument der Wurzel (die Varianz):

σ_A² =hA²−2AhAi+hAi²i=hA²i − hAi².

2.8. TEILCHEN IM 1D-KASTENPOTENTIAL 55 Hierbei verstehen wir unter dem Mittelwert des Quadrats der Gr¨oße A:

hA²i= Z

ψ^∗(x)A²ψ(x)dx. (2.34)

Da – wie wir im folgenden Kapitel sehen werden – in der Quantenmechanik physikalische Gr¨oßen durch Operatoren beschrieben werden, sind in diesen Definitionen die Funktionen A und A² durch die Operatoren ˆA bzw. ˆA² zu ersetzen.

Kommen wir nun zur¨uck zur Frage, was die Nullpunktenergie mit der Unsch¨arfe zu tun hat.

Die Position des Teilchens ist innerhalb des Kastens unbestimmt. Die Ortsunsch¨arfe ist also von der Ordnung ∆x = L. Die Impulsunsch¨arfe ist nun eben dieser minimal m¨ogliche Impuls

∆p = pmin (f¨ur den Zustand ψ1, mit der minimalen Energie, sonst gr¨oßer). Das Produkt der Unsch¨arfen ist dann:

∆x·∆p=

(pmin·L= ^h₂ , n = 1

pmin·L > ^h₂ , n >1 (2.35) Man bezeichnet den Zustand mit der minimalen Energie auch als Grundzustand und alle wei- teren Zust¨ande mit h¨oheren Energien als angeregte Zust¨ande¹⁰.

Wir finden nun die Eigenzust¨ande ψn(x) zu diesen m¨oglichen Energien En. Hierzu nutzen wir die Symmetrie des Systems aus, um die Rechnung zu erleichtern. Das Potential ist achsensym- metrisch bez¨uglich x= 0:

V(−x) =V(x).

Wir erwarten deshalb dieselbe Symmetrie bei allen physikalisch messbaren Gr¨oßen. Insbeson- dere gilt also f¨ur die Wahrscheinlichkeitsdichte:

ρ(x) =ρ(−x).

Da die Wahrscheinlichkeitsdichte aber gerade das Betragsquadrat der Wellenfunktion ist, exi- stieren 2 Typen von L¨osungen f¨ur die Wellenfunktion, die wir mit + f¨ur eine gerade Parit¨at und − f¨ur eine ungerade Parit¨at bezeichnen:

1. ψ+(−x) = ψ+(x), 2. ψ−(−x) = −ψ−(x).

Ist die Wellenfunktion gerade (Fall 1), so folgt aus der Konstruktion von ψ:

C1 =C2. Ist die Wellenfunktion dagegen ungerade (Fall 2), so gilt:

C1 =−C2. Hieraus ergibt sich:

1. F¨ur gerade Parit¨at haben die Eigenfunktionen die Form ψn+ = 2C1cos(knx).

Damit hier noch die Bedingung ψn+(a) = 0 erf¨ullt ist, muss n ungerade sein¹¹.

10Dies ist analog zu stehenden Wellen, wo ¨uberblicherweise die Bezeichnung Grundschwingung und Ober- schwingungen verwendet wird.

11Man ¨uberpr¨ufe dies an der Definition vonkn.

2. F¨ur ungerade Parit¨at erhalten wir analog

ψn₋(x) = 2iC1sin(knx),

wobei hiern gerade sein muss, um die Randbedingungen zu erf¨ullen.

Nun ist nur nochC1 aus der Normierung zu finden. F¨ur die geraden L¨osungen folgt 1 =

Za

−a

4|C₁|²cos²(knx)dx

= 4|C₁|² Za

−a

1

2(1 + cos(2knx))dx= 4|C₁|²a

|C1|= 1 2√

a.

Man kann sich leicht davon ¨uberzeugen, dass dies nicht nur f¨ur alle ungeraden n gilt, sondern auch f¨ur die ungeraden L¨osungen (f¨ur alle geraden n) und damit f¨ur alle n ∈N. Da die Phase der Konstanten C₁ irrelevant f¨ur alle Observablen ist, setzen wir diese zu Null und k¨onnen allgemein

Cn=C = 1 2√a

schreiben. In Abbildung 2.22 sind die Eigenfunktionen zu den verschiedenen Eigenwerten En

skizziert.

Abbildung 2.22: Eigenfunktionen ψn, Parit¨at und Energieeigenwert am eindimensionalen Potential-Kasten unendlicher Tiefe.

Hat ein Zustand mehr Knoten (Nullstellen) in [−a, a], so besitzt er eine h¨ohere Kr¨ummung und damit, nach der Schr¨odinger-Gleichung, eine gr¨oßere kinetische Energie. Wir haben nun also die vollst¨andige L¨osung des Problems gefunden:

{(E1, ψ1),(E2, ψ2), ...}

2.8. TEILCHEN IM 1D-KASTENPOTENTIAL 57 Nun verbleibt die Frage, welcher der Zust¨ande realisiert wird. Alle Paare (En, ψn) sind gleichbe- rechtigte L¨osungen der station¨aren Schr¨odinger-Gleichung. Aus der Linearit¨at ebendieser ergibt sich mit dem Superpositionsprinzip die allgemeine L¨osung zu:

Ψ(x) = X∞ n=1

Dnψn(x), (2.36)

mit Dn ∈C. Die allgemeine L¨osung ist also ein Superpositions-Zustand. Der Spezialfall Dn = δn,l wird alsreiner Zustand bezeichnet. Da die Zust¨ande aber eine Orthogonalsystem in [−a, a]

bez¨uglich des Skalarproduktes

ψn◦ψm = Z a

−a

ψ_n^∗(x)·ψm(x)dx,

bilden (das trifft hier zu, andernfalls sind die Eigenzust¨ande leicht orthogonalisierbar), gilt:

Z a

−a

ψ^∗_n(x)ψm(x)dx=δn,m. Wegen der Normierungsbedingung folgt:

1 = Z a

−a|Ψ(x)|²dx= X∞ n=1

|Dn|² Z a

−a|ψn(x)|²dx

| {z }

=1

,

und damit ist |Dn|² die Wahrscheinlichkeit der Realisierung (der Besetzung) des Zustandes n.

Die aktuellen Werte dieser Wahrscheinlichkeiten sind abh¨angig von der Pr¨aparation im Expe- riment.

Die allgemeine zeitabh¨angige L¨osung ist schließlich gegeben durch:

Ψ(x, t) = X∞ n=1

Dnψn(x)e^{−iEn~ t}.

Man beachte, dass jede Funktion in dieser Superposition ihren eigenen e-Faktor hat. Die zu- geh¨orige Wahrscheinlichkeitsdichte weist also, i.a. Interferenzterme auf.

Aufgabe: Berechnen Sie das Unsch¨arfeprodukt von Ort und Impuls im Grundzustand mit Hilfe der Mittelwertformeln (2.34) und vergleichen Sie mit der Absch¨atzung (2.35).

2.8.2 B) Eindimensionaler Potentialkasten mit endlicher Tiefe

Der zuvor besprochene Fall mit unendlich hohen W¨anden war ein Modellfall, der einige Effek- te ausschließt. So kann das Teilchen den Kasten nicht verlassen, und es sind nur gebundene Bewegungen m¨oglich. Wir kommen nun zum allgemeineren Fall einer endlichen Potentialh¨ohe/

-tiefe. Zur mathematischen Erleichterung behalten wir aber die als senkrecht angenommene Form des Potentials bei¹². Definieren wir nun also ein Potential der Form:

V(x) =−V₀Θ(a− |x|) =







−V0 , −a≤x≤a 0 , x /∈[−a, a]

12Nat¨urlich tr¨agt dies Modellcharakter. Diese Einschr¨ankung werden wir sp¨ater fallen lassen, wenn wir uns mit dem harmonischen Oszillator besch¨aftigen.