g-Tensoren in naheentarteten Zust
anden
von zweiatomigen Verbindungen
am Beispiel des AlO-Molek
uls
Diplomarbeit
von
Natalie Gilka
aus
Bydgoszz (Polen)
Dusseldorf, im August 2003
g-Tensoren in naheentarteten Zust
anden
von zweiatomigen Verbindungen
am Beispiel des AlO-Molek
uls
von
Natalie Gilka
DiplomarbeitinChemie
angefertigt am
Institut fur Theoretishe Chemieund Computerhemie
vorgelegt der
Mathematish-Naturwissenshaftlihen Fakultat
der Heinrih-Heine-UniversitatDusseldorf
August 2003
angegebenen Quellenund Hilfsmittelbenutzt sowie Zitatekenntlih gemaht habe.
Dusseldorf, den 25.08.2003
Referentin: Frau Prof. Dr. ChristelM. Marian
Korreferent: Herr Prof.Dr. Karl Kleinermanns
nahzudenken. Es hatte keinenSinn. Es ist besser, zulernen.
Konfuzius
Einleitung 1
I Theoretishe Grundlagen 3
1 Nihtrelativistishe Quantenhemie 5
1.1 Die Shrodingergleihung . . . 5
1.1.1 DieBorn-Oppenheimer-Naherung . . . 6
1.1.2 Dieelektronishe Wellenfunktion . . . 8
1.2 Naherungsverfahren . . . 10
1.2.1 Variationsverfahren . . . 11
1.2.1.1 Hartree-Fok . . . 11
1.2.1.2 Weiterentwiklungen: CI, MRCI, MCSCF, CASSCF . 12 1.2.2 Storungstheorie: Ausfuhrungen zur Entartung . . . 14
2 Relativistishe Quantenhemie 17 2.1 Ausgangspunkt: Die Dira-Gleihung . . . 17
2.1.1 DerBreit-Pauli-Operator . . . 21
2.2 Der Spin-Bahn-Operator . . . 24
2.2.1 Bemerkungen zur Gauge-Invarianz . . . 25
3 Zweiatomige Molekule 27 3.1 Grundlagen . . . 27
3.1.1 Drehimpuls . . . 27
3.1.2 Punktgruppen . . . 29
3.2 Atomare und molekulareZustande . . . 30
3.2.1 Folgender Verwendung von Untergruppen . . . 31
3.3 Spin-Bahn-Kopplung, auereMagnetfelder . . . 33
3.4 Auswertung vonMatrixelementen . . . 34
3.4.1 Auswahlregeln . . . 34
3.4.2 Wigner-Ekart-Theorem . . . 35
3.5 Molekulshwingungen . . . 36
4 Der g-Tensor 39 4.1 Betrahtung von ESR-Experimenten . . . 39
4.2 Storungstheoretishe Behandlung . . . 41
4.2.1.2 Notwendigkeitvonvibronishen Zustanden. . . 49
4.2.2 Weitere Korrekturterme . . . 53
II Anwendungen 55 5 Charakteristika des Systems 57 5.1 Elektronishe Zustande . . . 57
5.2 Eektder Spin-Bahn-Kopplung . . . 60
5.2.1 Folgen furden g-Tensor . . . 63
6 Die elektronishe Basis 65 6.1 Methodik . . . 65
6.2 Wahlder Parameter . . . 68
6.2.1 Molekulorbitale . . . 69
6.2.2 Potentialfunktionen . . . 72
6.2.2.1 Anzahl anZustanden. . . 72
6.2.2.2 Referenzraum . . . 80
6.2.2.3 Selektionsshwellenwert . . . 83
6.3 Diskussionder Berehnung . . . 87
6.3.1 Asymmetrieder Zustande . . . 88
6.3.2 Ionizitatder Zustande . . . 89
6.4 Vergleihmitdem Experiment . . . 91
7 Der g-Tensor 97 7.1 Methodik . . . 97
7.1.1 Diskussionder PT-Matrixelemente . . . 98
7.2 Matrixelemente uber ^ H SO , ^ L . . . 99
7.3 Analyse . . . 106
7.3.1 Elektronishe Basis . . . 106
7.3.2 Vibronishe Zustande . . . 113
7.3.3 Gesamtvergleih. . . 117
7.4 Qualitatder Berehnung . . . 118
7.4.1 Vibronishe Funktionen . . . 118
7.4.2 Einuder Beshreibung der elektronishen Funktionen. . . 120
7.4.3 Beitrage untershiedlihen Vorzeihens . . . 123
7.4.4 Beitrage hoherer Zustande . . . 124
Zusammenfassung und Ausblik 129
A Notation 131
Abbildungsverzeihnis 141
Literaturverzeihnis 146
Danksagung 147
Elektronen-Spin-Resonanz-Experimente (ESR) messen dieals Zeeman-Eekt bezeih-
neteAufspaltungvonSpinzustandenradikalisherSystemeineinemexternenMagnet-
feld.Eineinzelnes freies Elektron erfahrt imFeldeine Aufspaltung,die direkt propor-
tionalzum sog.g-Faktorg
e
des freien Elektrons ist,wahrend ingebundenen Systemen
Abweihungen von dieser Groe auftreten. Hauptsahlihe Ursahe besagter Abwei-
hungensind inder Spin-Bahn-Kopplungzu suhen, alsoder KopplungvonSpin-und
Bahndrehimpuls von Elektronen. Die Auswirkung der Spin-Bahn-Kopplung auf die
Zeeman-Aufspaltungwird durh dieGroe des sogenannten g-Tensorsg ausgedrukt.
DieBestimmungdesg-Tensorserlaubtprinzipielleine Aussage
uberdieSymmetriedes
betrahtetenelektronishenZustandes,dieWehselwirkungmitanderenelektronishen
ZustandenoderauhdienahereUmgebungdesRadikals.Sowurdez.B.derAnsatzver-
folgt,zurUntersuhung desReaktionsmehanismus' vonPhotosystemen eine Messung
des g-Tensors des paramagnetishen Mg-Atoms, welhes Teil des Reaktionszentrums
ist,durhzufuhren [1℄.
In den letztenJahren wurden bezuglihder Berehnung des g-Tensors zwei-und drei-
atomigerSystemeerhebliheFortshritteerzielt[2,3,4℄.DennohwareninEinzelfallen
deutlihe Abweihungen des theoretishen vom experimentellen Wert feststellbar, die
aufprinzipielleShwierigkeitenderBehandlung einzelnerMolekulehindeuten.AlsAn-
satz wurde zumeist die Verwendung niht-entarteter Storungstheorie gewahlt, wobei
eine geringe Abhangigkeit des g-Tensors vom interatomaren Abstand angenommen
wurde. Dies legitimierte die Naherung des g-Tensors des niedrigsten vibronishen Ni-
veaus durh eine Berehnung dieser Groe am Potentialminimum des elektronishen
Grundzustandes selbst.
Zu den erwahnten problematishen Systemen lat sih das AlO-Molekul zahlen. Die
Vorhersagen vershiedener theoretisher Betrahtungen zeigen groe Streuungen un-
tereinander, des weiteren ist ein Vergleih mit dem Experiment nur bedingt moglih,
da zum einen lediglih Werte aus Matrixmessungen vorliegen, zum anderen eine Be-
stimmung des g-Tensorshohe Anforderungenan das Experimentstellt.
AlO zeigt einen 2
+
-Grundzustand (X 2
+
), der in nahster Nahe zum Potentialmi-
nimum von einem 2
-Zustand (A 2
) durhkreuzt wird. Unter Beruksihtigung von
Spin-Bahn-Eektentritt eine Kopplungdieser beiden Zustandeauf. Damitverbunden
zeigtder g-Tensorals Ausdruk furdieGroe der Spin-Bahn-Kopplungvermutlihei-
ne starke Abhangigkeit von der Nahe zum Kreuzungspunkt, d. h. vom interatomaren
Abstand Al{O. Des weiteren ist die Legitimation niht-entarteter Storungstheorie im
Fallenahe-entarteter Zustande fragwurdig.
Zumindest imFalle des AlO-Molekulslat sih somit dieShwierigkeit in der Bereh-
nung des g-Tensors vermutlih aufdie starkeKopplung von X 2
+
- und A 2
-Zustand
zurukfuhren.
In der vorliegenden Arbeit sollen die Grenzen der bisherigen Vorgehensweise unter-
suht und alternative Behandlungsmoglihkeiten dargestellt werden. Hierbei ist zum
einen die Verwendung quasi-entarteter Storungstheorie (QDPT) anstelle von niht-
entarteter Storungstheorie denkbar, zum anderen eine Durhfuhrung der Berehnung
des g-Tensors bezogen auf Shwingungszustande anstelle einer Berehnung amPoten-
tialminimum des elektronishen Grundzustandes.
Theoretishe Grundlagen
Nihtrelativistishe Quantenhemie
1.1 Die Shrodingergleihung
1
Der Beginn des 20. Jahrhunderts war, wissenshaftlih gesehen, mit groen
Ande-
rungen verbunden: Das bisherige Weltbild, basierend auf der klassishen Mehanik,
begann,imWiderspruhzu experimentellenBeobahtungenzu stehen. Einsteinzeigte
einenWegaus dieserProblematikdurh dieErklarungdes Photoelektrishen Eektes
basierend auf der Quantisierung des Lihtes in Form von Photonen. Dies stellte den
Beginn der Quantenmehanik dar. Es zeigte sih, da das Prinzip der Quantisierung
auh auf energetishe Zustande angewandt werden mute. So postulierte Bohr 1913
die Existenz diskreter Zustande in Atomen, um das Linienspektrum des Wasserstos
zu erklaren, und leitete ausgehend davon sein Atommodell ab. Mit der Formulierung
der Shrodingergleihung imJahre 1926 durh ihren Namensgeber Erwin Shrodinger
gelang es, Elektronen und Atomkerne quantenmehanish geshlossen zu beshreiben
undbeobahtbareEektewiedieerwahnten diskreten
Ubergangeaufeinetheoretishe
Basiszu stellen.
In zeitabhangiger Form wird dieShrodingergleihung geshrieben als 2
:
^
Hj i=i~
t
j i; (1.1)
mit~ h
2
mitdem Plankshen Wirkungsquantum h
Dersog.Hamiltonoperator
^
HwirktaufdieWellenfunktionj i,diealsZustandsfunkti-
ondesSystemsAussagen
uberPositionundBewegungderbeteiligtenTeilhenerlaubt.
EinephysikalisheInterpretationder Wellenfunktionistlediglih
uberihrBetragsqua-
drat moglih, welhes als Wahrsheinlihkeitsdihte des Elektrons verstanden werden
kann, so da sih die Aufenthaltswahrsheinlihkeit des Elektrons imIntervalldx be-
rehnet
uber:
dx=j (x)j 2
dx: (1.2)
1
ZurVerfassungdesKapitelsderNihtrelativistishenQuantenhemiewurdedieLiteratur[5,6,7℄
herangezogen.
2
Eswurdediein AnhangAgegebeneNotationfurmathematisheGroenverwendet.
DieWellenfunktionwird
ubliherweisenormiert,d.h.dieWahrsheinlihkeit,dasElek-
tron aneiner beliebigenStelle im Raum anzutreen, aufeins gesetzt:
Z
dx
=h j i =1: (1.3)
Im Falle eines zeitunabhangigen Hamiltonoperators
^
H ist eine Separation von zeit-
und ortsabhangigem Anteil der Wellenfunktion moglih, so da die zeitunabhangige
Shrodingergleihung erhalten wird:
^
Hj
n i=E
n j
n
i: (1.4)
Mathematish istdies einEigenwertproblem,dessen Losung auf diequantisiertensta-
tionaren Zustande j
n
i mitden Energien E
n
fuhrt. Die Energie E
n
stellt demzufolge
den Eigenwert der Gleihung dar und kann durh Bildung des Erwartungswertes
uber
^
H berehnet werden:
E
n
=h
n j
^
Hj
n
i: (1.5)
Im Falleeines molekularen Systems vonN Kernen und n Elektronen unter Beshran-
kungaufdieBetrahtungreinelektrostatisherWehselwirkugenbeinhaltetderHamil-
tonoperator
^
H Terme,diezum einendiekinetishe Energie
^
T
K bzw.
^
T
e
derbeteiligten
Atomkerne bzw. Elektronen beshreiben, zum anderen die potentielle Energie
^
V, die
durh dieCoulomb-Wehselwirkung zwishen den geladenen Teilhen bestimmtwird:
^
H =
^
T
K +
^
T
e +
^
V
KK +
^
V
ee +
^
V
Ke
(1.6)
= N
X
I 1
2M
I r
2
I n
X
i 1
2 r
2
i +
N
X
I N
X
J>I Z
I Z
J
r
IJ
N
X
I n
X
j Z
I
r
Ij +
n
X
i n
X
j>i 1
r
ij
; (1.7)
mit der Summation
uber die Atomkerne I, J und Elektronen i, j, dem Laplae-
Operator r 2
k
=
2
x 2
k +
2
y 2
k +
2
z 2
k
eines Teilhens k sowie der Kernmasse M
I
von Kern
I. Obiger Hamiltonoperator ist in atomaren Einheiten formuliert, die sih von SI-
Einheiten untersheiden durh: e = 1, m = 1, ~ = 1, 4
0
= 1 mit der Ladung des
Elektrons e, seiner Masse m und der Dielektrizitatskonstantedes Vakuums
0 .
Durh die Kopplung der Bewegungen der Ladungstrager ist eine prinzipielle Losung
derShrodingergleihungbeiBetrahtungvonmehralszweiwehselwirkendenTeilhen
niht moglih.
Aufgabe der Quantenhemie ist somit, zuverlassige Naherungslosungen zur exakten
Shrodingergleihung zu entwikeln. Diegrundlegende Naherung, auf der die
uberwie-
gende Mehrheit der Losungsansatze basiert, ist die sogenannte Born-Oppenheimer-
Naherung.
1.1.1 Die Born-Oppenheimer-Naherung
Die Wellenfunktion wird im allgemeinen angesetzt als Produkt eines kern- und eines
1.1. DIESCHRODINGERGLEICHUNG 7
auh:Die Wellenfunktionwirdinder Basisvonelektronisher undKernwellenfunktion
expandiert:
(frg;fRg)= 1
X
m;n
m(n)
(fRg)
n
(frg;fRg); (1.8)
mit der elektronishen Wellenfunktion
n
(frg;fRg) des elektronishen Zustandes n
und der Kernwellenfunktion
m(n)
(fRg) des Kernzustandes m im elektronishen Zu-
standn, dievondem Satz der Kernkoordinaten fRgabhangig sind.
Bei Einsetzen dieses Losungsansatzes in die Shrodingergleihung tauhen Terme der
Ableitungder elektronishenWellenfunktionnahdenKernkoordinatenauf.Innerhalb
derBO-NaherungwerdendieseTermenun vernahlassigtunterderAnnahme, dasih
dieElektronenbewegung instantan andieKernbewegung anpat,soda eine Betrah-
tungderElektronenbewegung alsineinemfesten Kernsystemstattndendzulassigist.
DiesemAnsatz liegt das Prinzipzugrunde, da dieBewegung der Elektronen, bedingt
durh ihre geringere Masse, im allgemeinen deutlih shneller erfolgt als die Kernbe-
wegung selbst.
Man erhalt die sogenannte elektronishe Shrodingergleihung, die lediglih von den
Elektronenkoordinaten abhangigeTerme enthalt:
^
H =
^
T
e +
^
V
ee +
^
V
Ke
: (1.9)
Die BO-Naherung ermogliht somit eine Separation von Elektronen- und Kernbewe-
gung. Die Wellenfunktion formuliert sih nun als einfahes Produkt einer Kern- und
einerelektronishen Funktion:
mn
(frg;fRg) =
m(n
(fRg)
n
(frg;f
Rg): (1.10)
DieelektronisheWellenfunktionzeigtnebenderAbhangigkeitvondemSatzderElek-
tronenkoordinatenfrgzudemeineparametrisheAbhangigkeitvondenKernkoordina-
tenfRg,indiziertdurhdenQuerbalken.DieProblemstellungwirdaufdieBerehnung
der elektronishen Wellenfunktion beifester Kerngeometrie reduziert.Der Beitragder
Kerne kann nah Losung der elektronishen Shrodingergleihung unter Verwendung
des Kern-Hamilton-Operators mitgeringem Aufwand bestimmt werden: Der Energie-
beitragdesKern-Hamilton-Operatorssetztsihzusammenaus derkinetishenEnergie
derKerne,der potentiellenEnergie resultierendaus Kern-Kern-Wehselwirkungenun-
ter Annahmefester Kerngeometrie,sowie der Wehselwirkung der xierten Kernemit
dem durh dieElektronen erzeugten Potential.
DieBorn-Oppenheimer-Naherung versagt,wenn dieelektronishe Wellenfunktioneine
starke
Anderung mit dem Kernabstand erfahrt. Dies kann z. B. der Fall sein, wenn
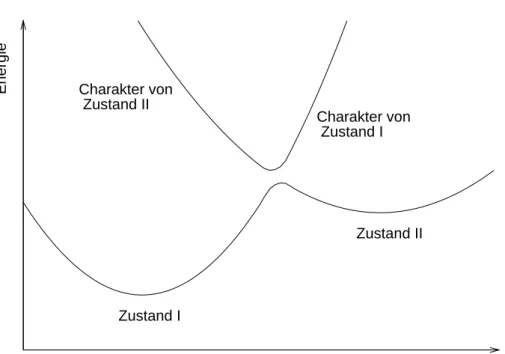
elektronisheZustandegleiher SymmetrieeinevermiedeneKreuzungeingehen:Solhe
BereihezeihnensihdurheinenWehseldesCharaktersderFunktionimKreuzungs-
Energie
Radius Zustand I
Zustand II Charakter von
Zustand II
Charakter von Zustand I
Abbildung1.1: Versagen der BO-Naherung
InAbbildung1.1.1isteinsolherFallskizziert,wobeidieDarstellungsihausGrunden
der
UbersihtlihkeitaufdieBetrahtungderWehselwirkungzweierAtomebeshrankt.
Das erhaltene Bild der Potentialkurven spiegelt naturlih niht die physikalishe Rea-
litatwider,dadiezugrundeliegendenBerehnungen aufderindiesemFallenihtmehr
gultigenBO-Naherungbasieren.Vielmehrmussennundiesog.niht-adiabatishenMa-
trixelementeh
m j
R
i j
n
ider elektronishen Zustande
n ,
m
Beruksihtigungnden,
dieimRahmen der BO-Naherung alsvershwindend angenommenwurden.
1.1.2 Die elektronishe Wellenfunktion
In der genaherten Losung der Shrodingergleihung gestaltet sih die Vorgehensweise
prinzipiellderart,dazuersteinplausibelersheinender AnsatzfurdieWellenfunktion
gewahlt wird.Ausgehend vondiesemAnsatz wird,zum Teildurh iterativeVerfahren,
die Energie des Systems berehnet. Der Ansatz der Wellenfunktion ist jedoh zwei
Beshrankungen unterworfen, dieauf fundamentalenPrinzipien der Quantenmehanik
beruhen:
Bei dem ersten Prinzip handelt es sih um die Heisenbergshe Unsharferelation. Sie
ist eine direkte Folge der zentralen Aussage der Quantenmehanik, da Observablen,
alsomebareGroenwiederImpulsoderderOrt,inderQuantenmehanik nihtmehr
notwendigerweise miteinanderkommutieren:
^ xp^
x 6=p^
x
x :^ (1.11)
Diese Observablen konnen somit niht mehr einfahe Funktionen der Zeit darstellen,
1.1. DIESCHRODINGERGLEICHUNG 9
Der Kommutator von zwei Operatoren
^
A,
^
B erlaubt eine Aussage daruber, ob diese
Groen gekoppelt sind und wird eingefuhrtals:
h
^
A ;
^
B i
=
^
A
^
B
^
B
^
A: (1.12)
DieHeisenbergsheUnsharferelationformulierteineBeziehungzwishendemKommu-
tator zweier Operatoren
^
A,
^
B und der Unsharfe A,B, mitder diese Observablen
gemessen werden konnen:
h(A) 2
ih(B) 2
i 1
4 jh[
^
A;
^
B℄ij 2
: (1.13)
Die Moglihkeit, zwei Observablen exakt zu bestimmen, ist somit davon abhangig, ob
diese beiden Observablen miteinanderkommutieren.Dies istfurden gleihgerihteten
Ortund Impuls eines Teilhensnihtder Fall,dennder Kommutatorfurdiese Groen
lautet:
[^x ;p^
x
℄=i~: (1.14)
DieMessungvonOrtundImpulseinesElektronsistalsostetsmiteinerinderQuanten-
mehanikbegrundetenUngenauigkeitverbunden.FureinSystemmiteinanderwehsel-
wirkenderElektronen,wieesz.B.ineinemMolekulvorliegt,bedeutetdies,daesniht
moglih ist, den Weg der einzelnen Elektronen zu messen, sie sind also niht vonein-
anderzu untersheiden.DieWellenfunktionmudemzufolgebezuglihjedes Elektrons
identish sein.
Das zweite fundamentale Prinzip betritdas Verhalten eines Systems von identishen
Teilhen unter Permutation:FunktionenvonElementarteilhen halbzahligenSpins,zu
denen Elektronen mit einem Spin von einhalb zahlen, sind bezuglih Vertaushung
von zwei beliebigen Teilhen ungerade, wahrend Funktionen von Elementarteilhen
ganzzahligenSpinsgerade, alsosymmetrish,sind. Dieserlegt der elektronishenWel-
lenfunktiondie Bedingungauf, da sihdas Vorzeihen bei Vertaushung der Koordi-
natenzweierbeliebigerElektronen
andert.DesweiterenlatsihausderForderungder
Antisymmetrie fermionisher Systeme bezuglih Teilhenvertaushung die historishe
Formulierungdes Pauli-Prinzips verstehen, welhe besagt, da keine zwei Elektronen
einesAtoms oder MolekulsdenselbenZustand einnehmendurfen: EinFunktion,inder
zwei identishe Zustande auftauhen, istnotwendigerweise symmetrish bezuglih der
beiden Elektronen, diediese Zustandebesetzen.
Der einfahste Ansatz, der die obigen beiden Bedingungen erfullt, ist der Ansatz der
elektronishen Wellenfunktion als sogenannte Slater-Determinante, die fur ein Sy-
stem von n Elektronen dieallgemeine Form hat:
(x
1
;x
2
;x
3
;:::;x
n
)=(n!) 1
2
i (x
1 )
j (x
1 )
k (x
1
) :::
l (x
1 )
i (x
2 )
j (x
2 )
k (x
2
) :::
l (x
2 )
.
.
.
.
.
. .
.
.
i (x
n )
j (x
n )
k (x
n
) :::
l (x
n )
; (1.15)
mitderKoordinatex
i
vonElektroniunddennbesetztenSpinorbitalen
m
.Verwendet
wird alskompaktere Darstellung desselben Ausdruks auh:
(x
1
;x
2
;x
3
;;x
n )=j
i
j
k :::
n
i: (1.16)
1.2 N
aherungsverfahren
Die untershiedlihen Ansatze zur approximativen Losung der Shrodingergleihung
lassen sih zumeist auf zwei Prinzipien zurukfuhren: Den Variationsansatz und die
Storungstheorie. Der Variationsansatzgeht vomRitzshen Variationsprinzipaus, wel-
hes besagt, da fur eine beliebige Wellenfunktion j
trial
i der Eigenwert E
trial
=
h
trial j
^
Hj
trial i=h
trial j
trial
i niht geringer sein kann als die exakte Grundzustands-
energieE
0
=h
0 j
^
Hj
0
i der exakten Wellefunktion j
0 i:
h
trial j
^
Hj
trial i
h
trial j
trial i
E
0
: (1.17)
Der imNenner auftretende Term h
trial j
trial
i dient der Normierung der Wellenfunk-
tion.
DasRitzshe VariationsprinzipermoglihteinenAnsatzderWellenfunktioninFormei-
nerparametrishenAbhangigkeitvonFaktoren
i
.DurhVariationdieserParameterim
HinblikaufeineMinimierungderEnergieE
trial
wirddieunterderLimitierungbedingt
durh den gewahltenAnsatz bestmoglihe Grundzustandsenergieerhalten. Der Eigen-
wert E
trial
stellt somit eine obere Shranke furdieGroe der exakten Grundzustands-
energiedar.
Ubliherweise wird das lineareVariationsverfahrenverwendet,welhes die
Wellenfunktionj
trial
iallgemeinalsSummeeinesProduktesvonVariationsparametern
i
und parameterlosen Funktionenj
i
i ansetzt:
j
trial i=
X
i
i j
i
i: (1.18)
Das zweite Prinzip, welhes weite Anwendung ndet, ist die Storungstheorie. Hier-
bei wird der exakte Hamiltonoperator
^
H des betrahteten Systems, dessen Losungen
unbekannt sind, aufgesplittet in einen sogenannten ungestorten Operator
^
H 0
mit be-
kannten Eigenwerten E (0)
i
und Eigenkets j (0)
i
i des elektronishen Zustandes i sowie
einen Storoperator
^
V,dessen Starke mitdem Storparameter skaliert wird:
^
H =
^
H 0
+
^
V: (1.19)
DieStorgroe und somit dieWirkung von
^
V aufdieEigenzustande von
^
H 0
wird als
relativ gering angenommen. Die Eigenfunktion j
i
i des Hamilton-Operators
^
H wird,
ebenso wie seine Eigenwerte E
i
, angesetzt alsReihenentwiklung in :
E
i
= E (0)
i
+E (1)
i +
2
E (2)
i +
3
E (3)
i
+:::; (1.20)
j
i
i = j (0)
i
i+j (1)
i
i+ 2
j (2)
i
i+ 3
j (3)
i
i+:::: (1.21)
Der Subindex i bezieht sih auf den elektronishen Zustand, wahrend der Superin-
dex (j) den Grad, auh bezeihnet als Ordnung, der Storentwiklung angibt. Setzt
man diese Ansatze in Gleihung (1.19) ein, so erhaltman nah einigen Umformungen
dieStorfunktion j (j)
i
i der Ordnung j ausgedrukt als Linearkombinationungestorter
Wellenfunktionen j
l i;j
m i;j
n i;:::.
1.2. NAHERUNGSVERFAHREN 11
1.2.1 Variationsverfahren
1.2.1.1 Hartree-Fok
DaselementarsteVerfahrenderQuantenhemiezurnaherungsweisenLosungderShro-
dingergleihung,welheszudemmeisteinenAusgangspunktfurweitergehendeLosungs-
ansatze darstellt, ist das Hartree-Fok Self-Consistent-Field-Verfahren (HF-SCF). In
diesem Verfahren wird die elektronishe Wellenfunktion in der einfahst moglihen
Form des in Kapitel 1.1.2 beshriebenen Ein-Determinanten-Ansatzes (Gl. 1.15) ge-
wahlt. Die Spin-Molekulorbitale (MOs)
j
werden im Sinne des linearen Variations-
verfahrensangesetzt (Gl.1.18),wobeiessihbeiden verwendeten Funktionennun um
Atomorbitale (AOs) handelt. Diese Verfahrensweise wird als Entwiklung der Spin-
MOsin einer BasisvonAOs bezeihnet.
Im Rahmen dieses Ansatzes erfolgt eine Variation der Spinorbitale hinsihtlih einer
Minimierung der Energie mit der Nebenbedingung der Orthonormierung dieser Orbi-
tale.
Formal wird hierbei eine Ein-Elektronen-Eigenwertgleihung erhalten, die als Fok-
Gleihung bezeihnet wird und sih fur Elektron 1 an Ort x
1
in Orbital
a
shreibt
als:
^
f(1)
a (x
1 )=
a
a (x
1
): (1.22)
Der Fok-Operator
^
f(1) ist deniert als Summeaus dem Ein-Elektronen-Operator
^
h,
der die Terme der kinetishen Energie der Elektronen und der Coulomb-Wehselwir-
kung Elektron-Kern beinhaltet, sowie dem sogenannten Hartree-Fok-Potential ^v HF
:
^
f(1) =
^
h(1)+v^ HF
(1) (1.23)
= 1
2 r
2
1 X
A Z
A
r
A1 +^v
HF
(1); (1.24)
mit
^ v
HF
(1)
a (x
1 ) =
X
b6=a h
^
J
b (1)
^
K
b (1)
i
a (x
1
) (1.25)
= X
b6=a Z
dx
2
b (x
2 )
1
r
12
b (x
2 )
a (x
1 )
X
b6=a Z
dx
2
b (x
2 )
1
r
12
a (x
2 )
b (x
1
): (1.26)
In diesem Ausdruk wird zum einen deutlih, da die Fok-Eigenwertgleihung fur
das Spinorbital
a
Abhangigkeiten von den anderen Spinorbitalen
b
durh die Aus-
druke des Coulomboperators
^
J
b
und des Austaushoperators
^
K
b
zeigt. Es liegt also
ein gekoppeltes Gleihungssystem der Spinorbitale
i
vor, welhes nur iterativ losbar
ist. Zum anderen stellt das Hartree-Fok-Potential ^v HF
eine Naherung an die elek-
tronishe Shrodingergleihung dar:Der Coulomboperator
^
J
b
beshreibt diegemittelte
Coulomb-Wehselwirkung eines Elektrons in miteiner Ladung an der Position x .
DasProblemvonnmiteinanderinWehselwirkungstehendenElektronenwirdeffektiv
durh die Wehselwirkung eines Elektrons mit einem gemittelten Potential genahert.
Esistoensihtlih,dadieseNaherungeinegrobeBeshreibungderRealitatdarstellt,
in der die Bewegung eines Elektrons niht unabhangig ist von der instantanen Posi-
tion der anderen Elektronen des Systems. Dies wird als Fehler in der Korrelation der
Bewegung aller Elektronen miteinander bezeihnet. Allgemein untersheidet man hier
zwishenfehlendenBeitragenvondynamisherundstatisherKorrelation.Alsdynami-
she Korrelation wird die ungenugende Beshreibung von kurzreihweitigen Elektron-
Elektron-Wehselwirkungen angesehen, wahrend sihdie statishe Korrelation aufdie
BeruksihtigunglangreihweitigerWehselwirkungenbezieht.StatisheKorrelationist
zum einen zur korrekten Beshreibung des Dissoziationsverhaltens molekularerSyste-
me notwendig, aber auh in der Betrahtung von elektronishen Zustanden, die eine
starke Wehselwirkung miteinander zeigen, so da man von einer \Mishung" dieser
Zustandespriht.Fehlende dynamisheKorrelationzeigtsihu.a.inverlangertenBin-
dungsabstanden, wahrend Mangel in der statishen Korrelation verkurzte Bindungen
zur Folge haben. Somitkann beiVerwendung von SCFeine partielleFehlerkompensa-
tion auftreten.
DurhWeiterentwiklungenausgehendvomHF-Verfahrenwirdversuht, denFehlerin
der Elektronenkorrelationzu kompensieren.
1.2.1.2 Weiterentwiklungen: CI, MRCI, MCSCF, CASSCF
EinenAnsatz zur Behandlung der imHF-VerfahrenvernahlassigtenElektronenkorre-
lationstellt das CI-Verfahren (onguration interation)dar. DurhLosung der Fok-
Gleihungen wird ein Satz von besetzten und virtuellen Spinorbitalen erhalten. Die
CI-Wellenfunktionwirdnun alsLinearkombinantionvonSlater-Determinanten 3
unter-
shiedliher BesetzungendieserSpinorbitaleangesetzt, gewihtet durhdieVariations-
parameter
i :
j
CI i =
X
i j
i
i (1.27)
=
0 j
0 i+
1
1!
2
X
a X
r
r
a j
r
a i+
1
2!
2
X
a;b X
r;s
rs
ab j
rs
ab
i+:::: (1.28)
j
0
i ist hier die HF-Grundzustands-Wellenfunktion, in der in einem n-Elektronen-
System die n energetish tiefsten Spinorbitale besetzt sind, j r
a
i stellt eine Wellen-
funktion dar, in der ein Elektron aus dem imGrundzustand besetzten Spinorbital
a
entfernt und in das zuvor unbesetzte Spinorbital
r
transferiert wurde (sog. Einfah-
anregung), j rs
ab
i leitet sih analog durh Besetzung der Orbitale
r
;
s
anstelle der
Orbitale
a
;
b
ab(sog. Doppelanregung),usw. Mitder CI-Wellenfunktionerfolgteine
variationelleLosungder Shrodingergleihung.Inder Praxisistman naturlihaufeine
3
Umgenauzusein,werdenhiernihteinzelneSlater-Determinantenverwendet,sondernbestimmte
LinearkombinationenvonSlater-Determinanten,diealsCSFs(onguration statefuntions) bezeih-
netwerden.EinekurzeErklarungderCSFsisterstnahEinfuhrungdesSpinsmoglihunderfolgtin
1.2. NAHERUNGSVERFAHREN 13
endlihe Expansionder Wellenfunktioninj
i
i und einenendlihen Satz vonSpinorbi-
talen f
j
g beshrankt.
HaugeVerwendungndetdas sogenannteSingles-Doubles-CI(SDCI):NahWahldes
Satzesder Spinorbitalewerden fur dienahfolgende CI-Rehnung diejenigenKongu-
rationen verwendet, die sih durh Einfah- und Doppelanregungen aus dem Grund-
zustand, der auh als Referenzzustand bezeihnet wird, heraus ergeben. Der Beitrag
hoherer Anregungen zur Wellenfunktion wird somit vernahlassigt. Diese Limitierung
auf Einfah- und Doppelanregungen ist besonders dann problematish, wenn die Be-
rehnung hoher angeregter Zustandeintendiert wird.
DassogenannteMRCI-Verfahren (multireferene-CI)bietet einenAlternative:ImSin-
ne des CI-Verfahrens wird dieWellenfunktionalsLinearkombinationuntershiedliher
AnregungenangesetztunddieEnergiefurdieseLinearkombinationvariationellbereh-
net. Als Spezialfall des CI-Verfahrens bildet jetzt allerdings, im Gegensatz z. B. zum
SDCI, welhes auh als singlereferene-Verfahren bezeihnet wird, ein Satz von Wel-
lenfunktionen vershiedener Anregungden Ausgangspunkt fur dieErzeugung weiterer
Kongurationen durh Anregung der Elektronen. Man arbeitet im MRCI also mit
mehreren Referenzfunktionen, deren Gesamtheit als Referenzraum bezeihnet wird.
Hierdurhistdie Berehnung der Energienangeregter Zustande inzumGrundzustand
annaherndvergleihbarer Qualitatmoglih.
Eine Beshrankung der Groe der Rehnung ist zum einen durh Beshrankung des
Grads der Anregung, zum anderen durh die sog. Kongurationsselektion moglih:
AusgehendvondenKongurationendes Referenzraumswird zuerstdurhn-fahe An-
regungaus den Referenzzustanden dieMenge der moglihen Funktionenfur dienah-
folgendeCI-Rehnung,dersog.CI-Raum,generiert.EineEinshrankungderGroedes
CI-Raums erfolgt durh storungstheoretishe Abshatzung des Beitrags der einzelnen
Kongurationen zur jeweiligen Wurzel, d. h. zum jeweiligen elektronishen Zustand.
Abhangig von dem fur die Groe dieses Beitrags gewahlten Selektionsshwellenwert
wird die betrahtete Kongurationaus dem Raum entfernt oder in der CI-Rehnung
beruksihtigt. Im Anshlu an die Rehnung kann der Beitrag der vernahlassigten
Kongurationenstorungstheoretish ermitteltund zur berehneten MRCI-Energiead-
diert werden. Somit lat sih die Groe des Beitrags dieser Korrektur als Indiz der
Gute der Berehnungen ansehen, da sie naherungsweise die Dierenz der berehne-
tenCI-Energie zu einerFull-CI-Rehnung (FCI),diesih durh Beruksihtigungaller
Anregunginnerhalb des gewahltenRaums der Molekulorbitaleauszeihnet, angibt.
DerAnsatz der Wellenfunktionbasierend aufden HF-Spinorbitalen istunter anderem
kritish, wenn der Grundzustand nur unzureihend durh eine einzige Konguration
beshrieben wird. Dies kann z. B. der Fall sein, wenn elektronishe Zustande glei-
her Symmetrie nahe beieinander liegen, so da eine Methode benotigt wird, die der
statishen Korrelation Rehnung tragt. In diesem Falle kann das MCSCF-Verfahren
(multionguration-SCF)Anwendung nden: DieGrundzustands-Wellenfunktion wird
imSinne einer CI-Wellenfunktionals Linearkombinationvonzumeist einigen wenigen
Slater-Determinantenangesetzt.ImUntershiedzurCI-Wellenfunktionerfolgtnuneine
Variation sowohl der ExpansionskoeÆzienten
i
als auh der in den Wellenfunktionen
auftretenden Spinorbitale selbst hinsihtlih einer Minimierung der Energie. Dadurh
enthalt bereits dieGrundzustands-Wellenfunktionj i Beitrage hoherer Anregungen.
Einen Spezialfall des MCSCF-Verfahrens stellt das CASSCF (omplete ative spae-
SCF) dar, in dem, zumeist basierend auf einer vorangehenden HF-Rehnung und den
hierbei erhaltenen Spinorbitalen, ein Satz von aktiven Orbitalen deniert wird, der
sih imRegelfallaus hohen besetzten und tieiegendenunbesetzten Spinorbitalenzu-
sammensetzt.Die furdieCASSCF-Rehnung verwendeten Kongurationenleiten sih
durh die moglihen Verteilungen der Elektronen des aktiven Raumes auf die aktiven
Orbitaleselbst ab.
1.2.2 Storungstheorie: Ausfuhrungen zur Entartung
In der Storungstheorie wird, wie bereits in Kapitel 1.2 ausgefuhrt, der Hamilton-
Operators
^
H alsSummeeinesungestortenOperators
^
H 0
undeinesStorterms
^
V formu-
liertundsowohldieEnergieE
i
des elektronishenZustandesialsauhdieWellenfunk-
tion j
i
ials Expansion ineinem Storparameter angesetzt. Im Falleniht-entarteter
Zustande i werden durh Einsetzen in die Shrodingergleihung
^
H =
^
H 0
+
^
V nah
Umformung Energie und Wellenfunktionerhalten als:
E
i
= E (0)
i
+E (1)
i +
2
E (2)
i
+::: (1.29)
= E (0)
i +
^
V
ii
2 X
k6=i
^
V
ki
2
E (0)
k E
(0)
i
+:::; (1.30)
j
i
i = j (0)
i
i+j (1)
i
i+ 2
j (2)
i
i+::: (1.31)
= j (0)
i
i
X
k6=i j
(0)
k i
^
V
ki
E (0)
k E
(0)
i
+
2 0
B
X
k6=i X
l 6=i
j (0)
k i
^
V
kl
^
V
l i
(E (0)
k E
(0)
i )(E
(0)
l E
(0)
i )
X
k6=i j
(0)
k i
^
V
ki
^
V
ii
E (0)
k E
(0)
i
2 1
C
A
+:::;(1.32)
mitden Matrixelementen
^
V
st
= h (0)
s j
^
Vj (0)
t i
= Z
dx (0)
s (x)
^
V (0)
t (x):
Fur den Fall entarteter Zustande erkennt man, da obige Gleihungen keine Losung
darstellen konnen, da sie eine Summation
uber Zustande gleiher Energie beinhalten
wurden, so da, bedingt durh den Energieausdruk im Nenner, Singularitaten auf-
traten.
In der entarteten Storungstheorie wird ebenfallsein Ansatz von Energie und Wellen-
funktionalsEntwiklungingewahlt,allerdingswirdhiereineTrennungdesentarteten
vom niht-entarteten Raum durh Einfuhrung von entsprehenden Projektionsopera-
toren durhgefuhrt. Fur nahere Ausfuhrungen seiauf [5℄verwiesen.
AlsErgebnissollfestgehaltenwerden,dabeiVorliegenentarteterZustandedieStorener-
gieersterOrdnungE (1)
l
desgestortenZustandesj
l
idurhDiagonalisierungdesStorope-
rators
^
V im Raum der entarteten Zustande erhalten wird. Es erfolgtalso dieAufstel-
^
1.2. NAHERUNGSVERFAHREN 15
entarteten Funktionenj (0)
m
i sind:
0
B
h
(0)
1 j
^
Vj (0)
1
i h (0)
1 j
^
Vj (0)
2
i :::
h (0)
2 j
^
Vj (0)
1
i h (0)
2 j
^
Vj (0)
2
i :::
.
.
.
.
.
.
.
.
. 1
C
A 0
B
1
2
.
.
. 1
C
A
=E (1)
l 0
B
1
2
.
.
. 1
C
A
: (1.33)
DurhLosung des Matrix-Eigenwertproblems werden dieStorenergienerster Ordnung
alsEigenwerte,diekorrektenStorzustandenullterOrdnungj (0)
l
ialsEigenketsinForm
einerLinearkombination der entarteten Zustande j (0)
m
i erhalten:
j (0)
l
i=
1 j
(0)
1 i+
2 j
(0)
2
i+:::: (1.34)
Sind die Eigenkets j (0)
l
i bereits bekannt, so kann die Storenergie E (1)
l
des Zustandes
j (0)
l
i direkt als Erwartungswert
uberden Storoperatorberehnet werden:
E (1)
l
=h (0)
l j
^
Vj (0)
l
i: (1.35)
Auh im Falle nahezu entarteter Zustande tritt die Problematik der Annaherung an
Singularitatenauf,soda bezuglihderquasientartetenZustandeeineVorgehensweise
analog entarteter Storungstheorie angebraht ist. Die Durhfuhrung einer Diagonali-
sierungdes Storoperatorsinder Basisvon energetish nahe liegenden Zustanden wird
alsquasi-entarteteStorungstheorie (QDPT) bezeihnet.
Relativistishe Quantenhemie
2.1 Ausgangspunkt: Die Dira-Gleihung
1
Wenngleihmitder Einfuhrungder Shrodingergleihungvielen experimentellenBe-
obahtungen, die bis dato keine Beshreibung fanden, Rehnung getragen wurde, so
waren dennoh die Grenzen dieser Gleihung oensihtlih: Zum einen stand sie im
Widerspruhzu einerweiterenErrungenshaftEinsteins,derRelativitatstheorie.Nah
der SpeziellenRelativitatstheorie bildenOrt und Zeit dieBasis des vierdimensionalen
Raumes.Physikalishe Gesetzesolltenunabhangig vomgewahlten Inertialsystemsein,
was sih darin ausdrukt, da Transformationen dieser Basis, also Transformationen
von Raum und Zeit untereinander, keine Auswirkung auf die Gultigkeitdieser Geset-
ze haben. Manbezeihnet diese Transformationenauh als Lorentz-Transformationen
und fordert die Lorentz-Invarianz physikalisher Gleihungen. In der Shrodingerglei-
hung tauhtder Rauminder zweiten,dieZeit jedohinder erstenAbleitungauf,die
Shrodingergleihung ist also niht symmetrish bezuglih Raum und Zeit und kann
deshalbnihtLorentz-invariantsein. Zumanderen fandsih keinUrsprungfurdievon
W.Paulipostulierte vierte Quantenzahl des Elektrons, namlih den Spin.
Esgalt somit,eine relativistishe Beshreibung des Elektrons, diein der Lage ist,den
Spin alsintrinsishe Eigenshaft zu beshreiben, zu nden.
Einerster Ansatz fur eine Gleihung, dieRelativistikund Quantenmehanik verband,
gingvomrelativistishen,niht-quantenmehanishen AusdrukderEnergieeinesTeil-
hens der Masse m und der Ladung q unter Wirkung der elektromagnetishen Poten-
tiale Aund aus 2
:
E =(m 2
2
+ 2
) 1
2
+q; (2.1)
mitdem mehanishen Moment =p qAmit dem Impuls p.
DerAnsatz bestanddarin, nah Umformung der Gleihung dieQuantenmehanik ein-
zufuhren durh Substitutionder Energie E und des Impulses p,die inder klassishen
Mehanik multiplikative Groen darstellen, durh ihr quantenmehanishes Pendant
1
Die AusfuhrungendesKapitelsderRelativistishenQuantenhemiesindengan[8℄angelehnt.
2
IndiesemKapitelndenSI-EinheitenVerwendung,daeinTeilderGleihungennihtquantenme-
hanisherNaturistundubliherweise inSI-Einheitenformuliertwird.
alsOperatoren:
^
E = i~
t
; (2.2)
^
p = i~
^
r: (2.3)
Dies fuhrte auf dieKlein-Gordon-Gleihung:
(
^
E+e) 2
= 2
(m 2
2
+^ 2
); (2.4)
mitder Ladung eund der Masse m des Elektrons.
Es zeigte sih, da dieser Ansatz ebenfalls keine gultige Beshreibung des Elektrons
darstellt, da auh die Klein-Gordon-Gleihung niht in der Lage ist, dem Spin des
Elektrons Rehnung zu tragen.
Ausgehend von der
Uberlegung, da notwendige Bedingung fur die Lorentz-Invarianz
einer relativistishen Gleihung eine symmetrishe Beruksihtigung von Raum und
Zeitist,zumanderen LosungendieserGleihungebenfallsLosungenderKlein-Gordon-
Gleihung,dieshlielihengmitdem klassishen Ausdruk verknupftist,seinsollten,
postulierte P. A.M.Dira 1928eine relativistishe quantenmehanishe Gleihungdes
Elektrons. Die sogenannte Dira-Gleihung ist gultig fur ein einzelnes Elektron im
elektromagnetishen Potential, A:
h
^ p
0 +
e
^
^
^
m
i
=0; (2.5)
mitp^
0
=
^
E
.
DieDira-Operatoren^ und
^
=^
0
erfullendieAntikommutatorbeziehungenf^
i
;^
j g
=^
i
^
j +^
j
^
i
=2Æ
ij
miti;j =0;x;y;zund demKroneker-DeltaÆ
ij
,welhesdeniert
ist
uber:
Æ
ij
=
1 fur i=j
0 fur i6=j
: (2.6)
Die Dira-Operatoren shreiben sihin der Standard-Darstellung als:
^
= 0
B
B
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
1
C
C
A
; (2.7)
^ =
0 ^
^
0
; (2.8)
mitden Pauli-Matrizen ^
i
(i=x;y;z) als Komponenten des Vektors :^
^
x
=
0 1
1 0
; ^
y
=
0 i
i 0
; ^
z
=
1 0
0 1
: (2.9)
Bei Reduktion der Dira-Gleihung auf den nihtrelativistishen Fall erhalt man die
bereits bekannte Shrodingergleihung eines Elektrons imelektromagnetishen Poten-
der Wehselwirkung eines intrinsishen Drehmomentes mit dem
aueren Magnetfeld
interpretiert werden kann:
^
H
nihtrel :Limit
= e+
^ 2
2m +
e~
2m
^ B =
^
H
SG +
e~
2m
^
B: (2.10)
Das damitassoziierte magnetishe Moment des Elektrons
s ist:
s
= e~
2m
= 2
B
s; (2.11)
mit dem Bohrshen Magneton
B
= e~
2m
und dem intrinsishen Drehimpuls des Elek-
trons ~s =
~
2
. Die Dira-Gleihung ist alsotatsahlih in der Lage, in
Ubereinstim-
mung mitExperimenten eine gultige Beshreibung des Elektronszu liefern.
Durhden konkreten Ausdruk der Dira-Operatoren inFormvon44-Matrizenlat
sihbereitserkennen, dadieDira-GleihunginMatrixformebenfallsals44-Matrix
dargestellt werden mu, die notwendigerweise auf eine vierkomponentige Wellenfunk-
tion wirkt:
= 0
B
B
1
2
3
4 1
C
C
A
: (2.12)
Nah dem Paulishen Elektronenbildware eine zweikomponentige Funktion zu erwar-
tengewesen, entsprehend denbeidenmoglihenelektronishen Zustandenmit -und
-Spin.DiezweizusatzlihenKomponentenlassensihLosungennegativerEnergiezu-
ordnen,dieeinemTeilhenderMasse des Elektrons,jedohderLadung+e,alsoeinem
Positron, entsprehen. Die Losungen positiver Energie
1
;
2
sind mit den Losungen
negativer Energie
3
;
4
durh den Dira-Operatorgekoppelt.
Ubliherweise istman lediglih anden Losungen positiverEnergie interessiert, soda
es von Vorteil ware, den Rehenaufwand in der Losung der Dira-Gleihung durh
Reduktionauf eine zweikomponentige Form zu minimieren.
EinmoglihesPrinzip der EntkopplungvonLosungen positiverund negativer Energie
beruht auf einer Einteilung der Terme der Dira-Gleihung in sogenannte gerade und
ungerade Operatoren E bzw. O. Gerade Operatoren E zeihnen sihdadurh aus, da
sieLosungen positiverund negativerEnergie niht miteinanderkoppeln, wahrendun-
geradeOperatorenOUrsahevonKopplungstermenzwishen
1
;
2
aufdereinenund
3
;
4
aufderanderen Seitesind.DerDira-Hamilton-OperatorkannnunineinerRei-
henentwiklung expandiert werden; der Beitragder einzelnen Terme zur Energie wird
uber ihre Ordnung in der Expansionsgroe abgeshatzt. Praktish wird die Reihen-
entwiklung durh eine sukzessive Transformation des Hamilton-Operators erhalten,
wobei durh jede Transformation ungerade Terme niedrigerer Ordnung durh gerade
Terme niedrigerer Ordnung sowie ungeraden Terme hoherer Ordnung ersetzt werden.
Bezeihnet man allgemeindie Expansionsgroe alsk und dieOrdnung der Terme ink
alsn bzw. m, so erhalt man alsodurh Transformation:
n n m>n
Durh Vernahlassigung der ungeraden Terme niedrigerer Ordnung erhalt man einen
genaherten Hamilton-Operator, dessen Genauigkeit sih aus der hohsten Ordnung
n, in der die geraden Terme noh Beruksihtigung nden, bestimmt. Mit steigender
Anzahl an durhgefuhrten Transformationen wahst die Genauigkeit des Hamilton-
Operators,jedoh nimmtauh dieKomplexitatder Umformungen zu.
Die hier skizzierte Transformation der Dira-Gleihung zu einer zweikomponentigen
Gleihung,dieeineinzelnesElektronimelektromagnetishenPotentialbeshreibt,wird
alsFoldy-Wouthuysen-Transformationbezeihnet.AlsExpansionsparameterderFoldy-
Wouthuysen-TransformationhatsihdieWahlderFeinstrukturkonstantealssinnvoll
erwiesen:
= e
2
0
2h
; (2.14)
mitder Permeabilitatskonstantedes Vakuums
0 .
Die Feinstrukturkonstante bietet den Vorteil der Dimensionslosigkeitund somit der
Unabhangigkeitvomgewahlten Masystem;dieeinzelnenTermesowohldes Dira-als
auh des transformierten Hamilton-Operators lassen sih durh m 2
n
uber die Ord-
nung nin klassizieren (O(m 2
n
)).Nah sukzessiver DurhfuhrungvondreiFoldy-
Wouthuysen-Transformationen wird der genaherte relativistishe Hamilton-Operator
einesElektronsimelektromagnetishenPotentialfurZustandepositiverEnergieerhal-
ten, der zur Ordnung vonm 2
5
Gultigkeithat:
^
H =m
2
e+
^ 2
2m
(a)
+ e~
m
(^sB) (b)
e~
4m 2
2
^
s(^ E E)^ ()
^ 4
8m 3
2
e~
2m 3
2
(^sB)^ 2
(d)
+ e~
2
8m 2
2
(
^
rE) (e)
+O(m 2
6
):
(2.15)
Die einzelnen Terme lassen sih interpretierenals:
(a) ErsterTerm istAusdruk der RuheenergieeinesElektrons,der zweite beshreibt
die Energie eines Elektrons in einem elektrishen Potential , der dritte seine
kinetishe Energie,
(b) Zeeman-Term, der die Energie eines Elektrons resultierend aus der Wehselwir-
kung des mitdem Spinassoziierten magnetishenMomentes
s
miteinem
aue-
ren Magnetfeld beshreibt,
() Wehselwirkung eines bewegten Elektrons miteinem
aueren elektrishen Feld:
elektrishen Feldes bewegte Ladung in seinem eigenen Ruhesystem ein Magnet-
feld,welhes in diesemFall mitdem intrinsishen magnetishen Moment
s des
Elektronsin Wehselwirkung tretenkann 3
,
(d) Relativistishe Korrekturen zur kinetishen Energie und zum Zeeman-Term,
(e) Darwin-Term (entbehrt eines klassishen Analogons).
Eine vollstandige Entkopplung der Losungen positiver und negativer Energie ist, bis
auf Spezialfalle wie den des freien Elektrons, niht moglih,so da der transformierte
Hamilton-Operatorstets nur naherungsweise korrekt ist.
In der Praxis hat sih zur Beshreibung von Mehrelektronen-Systemen, die approxi-
mativ relativistishe Eekte beruksihtigen, die Verwendung von zwei vershiedenen
Operatoren durhgesetzt. Bei dem ersten Operator handelt es sih um den sogenann-
tenBreit-Pauli-Operator
^
H
BP
,aufdenimfolgendenKapiteleingegangenwird,dadies
derjenige Operator ist, der in der vorliegenden Arbeit Verwendung ndet. Der zweite
Operator ist der no-pair-Hamilton-Operator
^
H
np
. Fur eine ausfuhrlihe Beshreibung
diesesOperators seiauf [9℄ verwiesen.
2.1.1 Der Breit-Pauli-Operator
ImFolgenden solldieAbleitungdes Breit-Pauli-Operatorsangedeutetsowie eineInter-
pretationdereinzelnenTermegegebenwerden.DerhierdargestellteWegistjedohnur
eine von mehreren Moglihkeiten, den Ausdruk des Breit-Pauli-Hamilton-Operators
zu erhalten. Sowurde der Breit-Pauli-Operator z. B. bereits vor der Postulierung der
Dira-Gleihung1927 durhPaulieingefuhrt[12℄; eine weitere Moglihkeitder Herlei-
tungsowohlvonBreit-Pauli-, alsauh vonno-pair-Hamilton-Operatorgeht direktvon
der Quantenelektrodynamik (QED) aus [13℄. Die Quantenelektrodynamik formuliert
einegenauere Beshreibung der Wehselwirkungen inSystemengeladenerTeilhen,da
siezusatzlih dieQuantisierung elektromagnetisher Potentiale beruksihtigt.
Ausgehend vom zweikomponentigen, naherungsweise relativistishen Hamilton-Ope-
rator eines Elektrons (Gl. 2.15) lat sih prinzipiell ein zweites Elektron einfuhren,
indemalsUrsahe der aufgefuhrtenelektromagnetishen Potentiale einElektron 2der
Ladung e
2
mit dem Impuls p
2
angenommen wird. Die durh die Gegenwart dieses
Elektrons bedingten Potentiale
1 , A
1
amOrt von Elektron 1mussen nun durh ihre
relativistishenAusdrukesubstituiertwerden,diesihausder BetrahtungderWeh-
selwirkungenzweier bewegter Ladungen ergeben. Hierdurh werden Termeeingefuhrt,
dieeineAbhangigkeitvomAbstandr
12
derbeidenLadungenvoneinanderzeigen.Wei-
terhin mu beruksihtigt werden, da elektromagnetishe Potentiale niht nur durh
dieLadung des Elektrons verursaht werden, sondern ebenfallsdurh das mit seinem
Spin assoziierte magnetishe Moment. Hieraus resultieren weitere Terme, dienun eine
AbhangigkeitvomSpindrehimpuls zeigen.
Neben der Tatsahe, da die relativistishen Ausdruke der elektromagnetishen Po-
tentiale eines Systems von zwei miteinander wehselwirkenden bewegten Ladungen
3
Dieser Term ist alleinige Ursahe der sog. Spin-Bahn-Kopplung, auf die explizit in Kapitel 2.2
nurnaherungsweiseermitteltwerdenkonnen,istdieHerleitungeinesZwei-Elektronen-
Hamilton-Operatorsmittels dieses Vorgehens mitInkonsistenzen verbunden. Die end-
gultige Form des Operators lat sih nur durh Vergleih mit Ausdruken, die auf
anderem Wege abgeleitet wurden, verizieren. Der geshilderte Ansatz bietet jedoh
den Vorteil, da sih dieauftretenden Terme der Interpretationbezuglih ihrer physi-
kalishen Ursahe ershlieen.
Der zweikomponentige Hamilton-Operator eines Systems von zwei bewegten Elektro-
nenindenexternenelektromagnetishenPotentialen
i ,A
i
bzw.denexternenFeldern
E
i , B
i
an der Position von Elektron i ergibt sih nah Durhfuhrung der Ableitung
zu:
^
H =
X
i=1;2 h
m
i
2
e
i
i +
^ 2
i
2m
i +
e
i
~
m
i (^
s
i B
i )
e
i
~
4m 2
i
2
^ s
i (^
i E
i E
i ^
i )
^ 4
i
8m 3
i
2
e
i
~
2m 3
i
2 (^s
i B
i )^
2
i +
e
i
~ 2
8m 2
i
2 (
^
rE
i )
i
(a)
+ e
1 e
2
4
0 r
12
(b)
e
1 e
2
~
8
0 m
1 m
2
2
^
1
^
2
r
12
+(^
1 r^
12 )
1
r 3
12 (^r
12 ^
2 )
()
e
1 e
2
~
8
0
2
r 3
12
^ s
1
(^r
12 ^
1 )
m 2
1
^ s
2
(^r
12 ^
2 )
m 2
2
(d)
+ e
1 e
2
~
4
0 m
1 m
2
2
r 3
12 [^
s
1 (^r
12
^
2 )
^
s
2 (^r
12
^
1
)℄ (e)
+ e
1 e
2
~ 2
4
0 m
1 m
2
2
^
s
1
^
s
2
r 3
12
3(^
s
1 r^
12 )
1
r 5
12 (^r
12
^
s
2 )
8
3 Æ(r
12 )(^
s
1
^
s
2 )
(f)
e
1 e
2
~ 2
8
0
2 Æ(r
12 )
1
m 2
1 +
1
m 2
1
(g)
+O(m 2
5
):
(2.16)
Elektromagnetishe Potentiale und Felder, deren Ursahe die Elektronen selbst sind,
wurden bereits durh die konkreten, furdie Wehselwirkung von zwei bewegten Elek-
tronengultigen, Ausdruke ersetzt.
Die Summe(a)beinhaltet Beitrage,die ledigliheine Abhangigkeitvoneiner Elektro-
nenkoordinate zeigen und entspriht dem genaherten relativistishen Hamilton-Ope-
rator eines einzelnen Elektrons (Gl. 2.15), summiert uber Elektron 1 und 2, wahrend
dieTerme(b)-(f)aus Elektron-Elektron-Wehselwirkungenresultieren.IhreUrsahen
lassen sihinterpretierenals:
() Bahn-Bahn-Wehselwirkung: Die Bahnbewegung eines Elektrons ist Ursahe ei-
nesMagnetfeldes, welhes auf einebewegte Ladung,namentlihdas zweite Elek-
tron,wirkt, und umgekehrt,
(d) Spin-Same-Orbit-Term:Mit dem Spin eines Elektrons assoziiertisteinmagneti-
shes Moment
s
.Wie bereits erwahnt,wirktaufeine bewegte Ladung ineinem
elektrishen Feldinihrem eigenenReferenzsystem einMagnetfeld. Im vorliegen-
den Term ist das zweite Elektron Ursahe eines elektrishen Feldes, so da das,
bedingt durh seine eigene Bahnbewegung, vom ersten Elektron gespurte Mag-
netfeld mit seinem eigenen magnetishen Moment
s
wehselwirkt. Diese Art
der Wehselwirkung wird auh als Kopplung von Spin- und Bahndrehimpuls ei-
nes Elektrons bezeihnet,
(e) Spin-Other-Orbit-Term: Dieser Term lat sih zusammengesetzt denken aus ei-
nemBeitrag,der denSpineinesElektronsalsUrsaheeinesMagnetfeldesansieht
unddieWirkung diesesFeldes aufeine bewegte Ladung(Elektron 2)beshreibt,
sowie einem Beitrag, der die Bahnbewegung eines Elektrons als Ursahe eines
Magnetfeldes ansieht und die Wirkung auf den Spin des zweiten Elektrons be-
shreibt. Insgesamt resultiert eine Kopplung von Bahndrehimpulsdes einen mit
Spindrehimpulsdes anderen Elektrons,
(f) Spin-Spin-Wehselwirkung: Die ersten beiden Terme beshreiben die klassishe
Dipol-Dipol-Wehselwirkung,dieanalogzurBahn-Bahn-WehselwirkungalsWir-
kung des durh den Spindrehimpuls des ersten Elektrons verursahten Magnet-
feldesauf dasmagnetishe Spinmoment deszweiten Elektronsangesehen werden
kann. Der letzte Term wird als Fermi-Kontakt-Wehselwirkung bezeihnet und
beruksihtigt alsFolge des Antisymmetrieprinzips dieTatsahe, da keine zwei
Elektronen identishen Spins dasselbe Raumelement einnehmen durfen. In der
Gesamtheitbewirkt dieserAusdruk eineKopplungder SpinszweierElektronen,
(g) Darwin-Term.
Es sollte erwahnt werden, da durh eine alternative Herleitung dieses naherungs-
weise relativistishen Zwei-Elektronen-Hamilton-Operators
uber einen vierkomponen-
tigen Zwei-Elektronen-Operator (Breit-Operator) deutlih wird, da die Einfuhrung
der Elektron-Elektron-Wehselwirkung unter Verwendung von Storungstheoriedurh-
gefuhrt werden mu. Dies hat zur Folge, da der Breit-Pauli-Operator selbst nur zur
hier gegebenen Ordnung entwikelt werden darf und seine Gultigkeit auf langsame
Elektronenbeshrankt ist.
AufdemWegzummolekularenAnalogenobigenZwei-Elektronen-Hamilton-Operators
mu zum einen eine Ausdehnung auf Mehrelektronensysteme, zum anderen die Ein-
fuhrungvonAtomkerneninFormvonentsprehendenElektron-Atomkern-Wehselwir-
kungen durhgefuhrt werden.
Der
Ubergang zum Mehrelektronensystem wird durh Summation der Terme (b) bis
(f)
uber alle Elektronen bewerkstelligt, so da eektiv eine Addition der Elektron-
DieseVorgehensweise vernahlassigtTerme,diedieBewegungdreier(odermehr)Elek-
tronenkoppeln; es latsihjedoh aus der QEDzeigen,da biszu einer Ordnung von
O(m 2
4
) keine solhen Terme auftauhen [10℄.
DieEinfuhrungvonAtomkernenkann durhdieInterpretationihrer LadungalsUrsa-
he des externenFeldes vollzogen werden.
AmEndedieserShrittestehtderBreit-Pauli-Operator,einzweikomponentigerOpera-
tor,derGultigkeitfurdieBeshreibungmolekularerSystemehat.FureineBetrahtung
der einzelnen Terme dieses Operators seiauf [15℄ verwiesen.
2.2 Der Spin-Bahn-Operator
Die vorliegende Arbeit konzentriert sih auf Eekte, die durh Spin-Bahn-Kopplung
der Elektronen verursaht werden. Dies beinhaltet sowohl Spin-Same-, als auh Spin-
Other-Orbit-Wehselwirkungen, entsprehend den Termen (d) und (e) der Gl. 2.16,
wobei erstere in Form von Elektron-Elektron- und Elektron-Kern-Wehselwirkungen
auftretenkonnen.
DerzurBeshreibung dieserWehselwirkungennotwendigeBreit-Pauli-Spin-Bahn-Ha-
milton-Operatorin Abwesenheit externer Felder ist somit:
^
H SO
BP
= e
2
~ 2
8
0 m
2
2
X
i;I Z
I
r 3
iI
^
s
i (^r
iI
^
p
i ) (a)
e 2
~ 2
8
0 m
2
2
X
i;j6=i 1
r 3
ij
^ s
i (^r
ij p^
i ) (b)
+ e
2
~ 2
4
0 m
2
2
X
i;j6=i 1
r 3
ij
^ s
i (^r
ij p^
j
) ():
(2.17)
Die Summationerfolgt
uber Elektroneni, j und Kerne I.
Term(a)beruksihtigtSpin-Same-Orbit-Wehselwirkungen,dieeinElektronaufgrund
seinerBewegungimelektrishenFeldderKerneerfahrt,Term(b)stellt dieSpin-Same-
Orbit-Wehselwirkungen aufgrund der Ladung anderer Elektronen dar, Term () be-
shreibt dieSpin-Other-Orbit-Wehselwirkungen der Elektronen untereinander.
In der Betrahtung der Spin-Bahn-Kopplung werden Terme, die die Wehselwirkung
des Kernspins I mit den Elektronen beruksihtigen,
ubliherweise vernahlassigt,
ebenso wie dieSpin-Spin-Kopplung,daallgemeinangenommenwird, da dieBeitrage
dieser Terme von deutlih kleinerer Groenordnung sind als die Spin-Bahn-Kopplung
selbst. So wird z. B. fur die Vernahlassigung der sog. Hyperfein-Kopplung, die das
Analogonzur Spin-Spin-Kopplungfurden FallKernspin-Elektronenspin darstellt,von
Launila und Jonsson [22℄ von einem mittleren Fehler RMS von 0.022 m 1
im Fit
ihrerRotationszustandefurdas SystemAlOberihtet. DieserFehlerreduziertsihun-
ter Beruksihtigung der Hyperfein-Wehselwirkung auf 0.002 m 1
. In der vorliegen-
den Arbeit werden Shwingungszustande betrahtet, die Energiedierenzen von etwa
600 m 1
zeigen, so da eine Vernahlassigung dieser zusatzlihen Terme im Bereih
Inden imRahmendieser Studiedurhgefuhrten Berehnungen wurde derBreit-Pauli-
Spin-Bahn-Operator unter Beruksihtigung zweier wesentliher Naherungen verwen-
det, die eine deutlihe Verkurzung der Rehenzeit bewirken: Zum einen wurden die
Elektron-Elektron-Wehselwirkungen durh gemittelte Spin-Bahn-Wehselwirkungen
einesElektronsmitallenanderenElektronenersetzt,sodaeektiveinEin-Elektronen-
Operatorresultiert, der alsSOMF (spin-orbit mean-eld)[14℄ Hamiltonianbezeihnet
wird.Zumanderenwurden IntegralezwishenElektronen, dieanvershiedenen Atom-
kernenzentriertsind, vernahlassigt.DieRehtfertigungfurdiese Vorgehensweiseliegt
inder Abhangigkeitdes Spin-Bahn-Operators
^
H
SO
vomAbstandrzur Potenzvonmi-
nusdrei,sodaeinrapiderAbfallderSO-Wehselwirkungenmitwahsendem Abstand
vorliegt.DieVerwendung diesersog. Einzentrennaherung hateinedeutliheReduktion
derAnzahl anzu berehnenden Integralenzur Folge. Fur einenahereBetrahtung der
verwendeten Approximationen seiauf [13℄, S.25-35,verwiesen.
2.2.1 Bemerkungen zur Gauge-Invarianz
Allgemein bezeihnet eine Gauge-Transformation eine Vershiebung des Bezugspunk-
tes einer Groe. Im Beispiel eines Ortsvektors entspriht die Gauge-Transformation
einer Vershiebung des Ursprungs des Koordinatensystems, in der Behandlung von
elektromagnetishen Potentialen wird als Gauge-Transformation eine Transformation
der Art:
A 0
= A rf; (2.18)
0
= + f
t
(2.19)
bezeihnet, wobei f eine beliebigeskalare Funktion von Ort und Zeit sein kann. Elek-
trishes und magnetishes FeldE bzw. B sind unabhangig von der Wahlvon f.
Es ist oensihtlih, da eine Vershiebung des Bezugspunktes keinen Eekt auf die
Aussageeinerphysikalishen Gleihunghaben darf,und tatsahlihsindsowohlShro-
dinger- als auh Dira- und Breit-Pauli-Gleihung Gauge-invariant bezuglih einer
Transformationder elektromagnetishen Potentiale.Werden jedoh atomareoder mo-
lekulare Eigenshaften unter Beshrankung auf die Verwendung bestimmter Terme
dieserGleihungenberehnet, ist esmoglih,da darauseine Gauge-Abhangigkeitre-
sultiert: Wenn bei Durhfuhrung einer Gauge-Transformation eine Ausloshung von
Beitragen, die aus Transformation vershiedener Terme resultieren, erfolgt, und nur
einTeildieser Termeinder Berehnung Beruksihtigung ndet,istoensihtlih,da
keine Invarianz bezuglih der Transformation mehr vorliegen kann. DieserPunkt wird
beider Behandlung der Berehnung von g-Tensoren aufgegrien.
Zweiatomige Molek
ule
3.1 Grundlagen
3.1.1 Drehimpuls
Inder Quantenmehanik wird allgemeinder Operator
^
J des DrehimpulsesJ
uberdie
Kommutatorbeziehungenseiner Komponenten deniert:
h
^
J
i
;
^
J
j i
=i~
ijk
^
J
k
; (3.1)
furRotationen um dieAhsen i;j;k mitdem Levi-Civita-Symbol
ijk mit:
123
=
231
=
312
= 1;
132
=
213
=
321
= 1; (3.2)
alleweiteren
ijk
= 0:
DerOperator des Betragsquadrats des Drehimpulses
^
J 2
=
^
J
^
J ist gegeben durh:
^
J 2
^
J
x
^
J
x +
^
J
y
^
J
y +
^
J
z
^
J
z
; (3.3)
soda:
h
^
J 2
;
^
J
k i
=0; k =1;2;3: (3.4)
Eskann gezeigt werden, da furmiteinander kommutierende Operatoren gemeinsame
Eigenzustandegewahltwerdenkonnen[5℄.Nunkommutiertzwar
^
J 2
mitjederderKom-
ponenten
^
J
k
, jedoh kommutieren diese Komponenten niht untereinander. Somit ist
eslediglihmoglih,Zustandezu wahlen,dieEigenfunktionenvon
^
J 2
sowieeinerseiner
Komponenten sind;
ubliherweise wird hierbei
^
J
z
gewahlt. Die Eigenfunktionen jj;mi
dieserOperatorenwerdennundurhihreEigenwertej,m,dieauhalsQuantenzahlen
bezeihnet werden,harakterisiert mit:
^
J 2
jj;mi = j(j+1)~ 2
jj;mi; (3.5)
^
J
z
jj;mi = m~jj;mi: (3.6)
DieQuantenzahlmkannhierbeidieWertem = j; j+1;:::;+j 1;+j annehmen.
DieAnzahl der Zustande gleiherj-Quantenzahlistsomitgegeben durh N
j
=2j+1,
entsprehend der Anzahl mogliher m-Quantenzahlen.
Weiterhin werden dieLeiteroperatoren
^
J
+ und
^
J eingefuhrt mit:
^
J
=
^
J
x i
^
J
y
: (3.7)
Die Wirkung der Operatoren
^
J
auf Eigenzustande jj;mi von
^
J 2
und
^
J
z
ist nun fol-
gendermaen gegeben:
^
J
jj;mi= p
j(j+1) m(m1)~jj;(m1)i: (3.8)
Ein Eigenzustand des Operators
^
J
z
wird also in einen benahbarten Eigenzustand
diesesOperatorsuberf uhrt, der jedohder gleihe Eigenzustandvon
^
J 2
ist.Ausdieser
Wirkung, zusammen mit der Beshrankung der m-Quantenzahl auf die Werte j
m+j, ergibtsih, da gelten mu:
^
J
+
jj;m=+ji=0;
^
J jj;m= ji=0: (3.9)
Wirdein System durh mehr alseinen Drehimpuls harakterisiert, somussen die wir-
kenden Drehimpulse miteinander gekoppelt werden. Als Beispiele fur solhe Systeme
seien zwei freieElektronen genannt,vondenen jedes einen Spinrehimpulsvon s=1=2
aufweist oder der Falleinesatomaren Elektrons, welhes sowohlBahndrehimpuls` als
auh Spindrehimpuls s besitzt. Die Kopplung der Operatoren
^
J
1 ,
^
J
2
zweier Drehim-
pulse J
1 , J
2
soll im Folgenden skizziert werden: Eine Kopplung von
^
J
1 und
^
J
2 zum
Gesamtdrehimpuls
^
J erfolgt durh vektorielle Addition:
J =J
1 +J
2
: (3.10)
Das gekoppelte System lat sih nun durh die Quantenzahlen m und j beshreiben
mit:
m = m
1 +m
2
; (3.11)
jj
1 j
2
j j j
1 +j
2
: (3.12)
Ausder Kopplung vonj
1 und j
2
resultieren N ZustandemitN =(2j
1
+1)(2j
2 +1),
wobeimitjeder j-Quantenzahlwiederum(2j+1)Zustandeuntershiedliher m-Werte
assoziiert sind. Die eindeutige Charakterisierung jedes Zustandes lat sih durh die
AngabederQuantenzahleneinesSatzesvonOperatoren,diemiteinanderkommutieren,
durhfuhren. Hierfur bietensih zwei Moglihkeiten:
Die Zustande des gekoppelten Systems lassen sih als Eigenzustande der Ope-
ratoren
^
J 2
1 ,
^
J 2
2 ,
^
J
1z und
^
J
2z
wahlen und konnen somit durh die Bezeihnung
jj
1 j
2
;m
1 m
2
i eindeutig beshrieben werden.
DieZustandedesgekoppeltenSystemslassensihalsEigenzustandederOperato-
ren
^
J 2
,
^
J 2
,
^
J 2
und
^
J
z
wahlenundwerdendemzufolgealsjj
1 j
2
;jmiharakterisiert.