Die Analyse von Proportionen:



und Logistic Regression

Jonathan Harrington

Die Analyse von Proportionen:

Befehle: proportion.txt

Kontinuierlich

Kontinuierlich und kategorisch

Kategorisch

Was ist die Wahrscheinlichkeit, dass:

F2 von [i:] höher ist als von [] (t-test)

F1 und Dauer von [a] miteinander korreliert sind (Regression)?

Eine steigende Melodie in Aussagen von jugendlichen im Vergleich zu aelteren

Personen verwendet wird?

Ein [r] statt [R] in Bayern im Vergleich zu Schleswig-Holstein verwendet wird?

Was ist die Wahrscheinlichkeit, dass:

In einer kategorischen Analyse werden meistens 2 Proportionen miteinander verglichen.

Die tests dafür: 

und Logistic Regression.

zB wir zählen wie oft steigende Melodien in Aussagen bei jugendlichen (35%) und älteren Leuten (11%)

vorkommen. Sind diese Proportionen (35%, 11%)

signifikant unterschiedlich?

Solche Methoden haben insbesondere in der

Soziolinguistik/phonetik eine Anwendung, in der sehr oft auditiv die Proportionen wahrgenommener Allophone miteinander als Funktion von Alter, Dialekt usw.

verglichen werden, ohne unbedingt die

kontinuierlichen akustischen (oder artikulatorischen) Parameter (Dauer, Formanten usw.) zu analysieren.

(In der Soziolinguistik: Logistic Regression = VARBRUL)

Terminologie: Klassen (Gruppen) und Ebenen (levels)

Was ist die Wahrscheinlichkeit, dass ein silbenfinaler /t/ gelöst wird?

Gruppe = silbenfinaler /t/ mit 2 Ebenen: gelöst oder nicht gelöst.

Was ist die Wahrscheinlichkeit, dass ein silbenfinaler /t/

gelöst, nicht-gelöst oder lenisiert wird?

Gruppe = silbenfinaler /t/ mit 3 Ebenen (gelöst, nicht-gelöst, lenisiert)

Eine Gruppe

Zwei Gruppen

Wird ein silbenfinaler /t/ häufiger in Bayern als in Hessen gelöst?

Gruppe 1: /t/ mit 2 Ebenen (gelöst, nicht-gelöst)

Gruppe 2: Dialekt mit 2 Ebenen (bayerisch, hessisch).

Ist die Verteilung der /t/ Realisierungen – ob sie gelöst, lenisiert oder nicht-gelöst werden – dieselbe in Bayern, Hessen, und Sachsen?

Zwei Gruppen ( /t/ und Dialekt) jeweils mit 3 Ebenen.

Drei Gruppen

Unterscheidet sich die Häufigkeit der //-Vokalisierungen zwischen Männern und Frauen in Bayern und Hessen?

Gruppe 1: // mit 2 Ebenen (vokalisiert oder nicht) Gruppe 2: Geschlecht mit 2 Ebenen: (M, F)

Gruppe 3: Dialekt mit 2 Ebenen (Bayern, Hessen).

Die statistische Analyse von Proportionen

Mehr als 2 Gruppen**

Logistic Regression (kann auch bei 2 Gruppen

eingesetzt werden**, und gibt fast das gleiche Ergebnis wie ein 

-test).

glm() = generalized linear model

(der Name soll an lm() erinnern – da sie miteinander viele Ähnlichkeiten haben)

**eine Gruppe muss 2 Ebenen haben

Eine oder zwei Gruppen

Analyse von Proportionen = 

-test

prop.test() chisq.test()

(aber prop.test() kann nicht eingesetzt werden, wenn beide

Gruppen mehr als 2 Ebenen haben)

1. Eine Gruppe, zwei Ebenen

Ich werfe eine Münze 20 Mal und bekomme 5 Mal Kopf.

Ist die Münze gezinkt?

d.h. weicht die Proportion 5/20 = ¼ signifikant von 10/20 = ½ ab?

prop.test(5, 20, .5)

data: 5 out of 20, null probability 0.5 X-squared = 4.05, df = 1, p-value = 0.04417

alternative hypothesis: true p is not equal to 0.5 95 percent confidence interval:

0.0959326 0.4941155 sample estimates:

p 0.25

Die Münze ist gezinkt: 

(1) = 4.05, p < 0.05

(Gruppe = Münze, Ebenen = Kopf, Zahl)

2 Gruppen jeweils 2 Ebenen

Die Anzahl der glottalisierten silbenfinalen /t/s ist in einem englischen Dialekt getrennt fuer Männer und Frauen gemessen worden.

Männer

glottalisiert nicht-glottalisiert Frauen

110 90

82 108

Kommt die Glottalisierung häufiger bei Männern vor?

n 200 190

Genauer: sind 110/200 und 82/190 voneinander signifikant unterschiedlich?

Silbenfinaler /t/

Geschlecht

Die Frage in eine Proportion umsetzen: unterscheiden sich

die Proportionen der Glottalisierungen zwischen M und F?

prop.test(c(110, 82), c(200, 190))

data: c(110, 82) out of c(200, 190)

X-squared = 5.0034, df = 1, p-value = 0.0253 alternative hypothesis: two.sided

95 percent confidence interval:

0.01473134 0.22211077 sample estimates:

prop 1 prop 2 0.5500000 0.4315789

Männer und Frauen dieses Dialekts unterscheiden sich in der Häufigkeit der silbenfinalen /t/-

Glottalisierung 

(1) = 5.00, p < 0.05.

Männer

glottalisiert nicht-glottalisiert Frauen

110 90

82 108

n 200 190 Silbenfinaler /t/

Geschlecht

Die Verteilung der /l/ Vokalisierungen in einem Dialekt in 4 Altersgruppen ist wie folgt:

2 Gruppen, eine Gruppe mit 2 Ebenen, die andere mit mehr als 2 Ebenen

A20min A20bis30 A31bis40 A41plus vok 58 55 62 38 nicht-vok 34 49 84 59

lvoc

Hat Alter einen signifikanten Einfluss auf /l/-Vokalisiertung?

Alter

/l/

In Proportionen umwandeln – und dazu brauchen wir die jeweiligen Gruppensummen

A20min A20bis30 A31bis40 A41plus vok 58 55 62 38 nicht-vok 34 49 84 59

lvoc

A20min A20bis30 A31bis40 A41plus 92 104 146 97

und vergleichen dann miteinander 58/92, 55/104, 62/146, 38/97 apply(lvoc, 2, sum)

prop.test(c(58, 55, 62, 38), c(92, 104, 146, 97))

prop.test(c(58, 55, 62, 38), c(92, 104, 146, 97))

data: c(58, 55, 62, 38) out of c(92, 104, 146, 97) X-squared = 14.0959, df = 3, p-value = 0.002778

alternative hypothesis: two.sided sample estimates:

prop 1 prop 2 prop 3 prop 4 0.6304348 0.5288462 0.4246575 0.3917526

Alter hat einen signifikanten Einfluss auf //-Vokalisierung,

2(3) = 14.10, p < 0.01

Das gleiche mit chisq.test() chisq.test(lvoc)

X-squared = 14.0959, df = 3, p-value = 0.002778

Wie wird 

berechnet?



ist die Abweichung der tatsächlich vorkommenden (Observed) von den zu erwartenden (Expected)

Verteilungen, unter der Annahme (Null Hypothese) dass die Verteilungen pro Gruppe gleich sind.

A20min A20bis30 A31bis40 A41plus vok 58 55 62 38 nicht-vok 34 49 84 59

Null Hypothese: die Proportion der vokalisierten //s ist in allen 4 Gruppen gleich.

d.h. unter der Null-Hypothese müssten 0.4851936 der /l/s in jeder Altersgruppe vokalisiert sein. zB für A20min:

0.4851936 * sum(lvoc[,1]) [1] 44.63781 [1] 0.4851936

Proportion der vok //s unabhängig vom Alter = sum(lvoc[1,])/sum(lvoc)

Anzahl der vokalisierten /l/s dividiert durch Anzahl aller /l/s.

A20min A20bis30 A31bis40 A41plus

vok 44.63781

nicht-vok 47.36219

A20min A20bis30 A31bis40 A41plus vok 58 55 62 38 nicht-vok 34 49 84 59

Observed

Expected 0.4851936 * sum(lvoc[,1])

r = chisq.test(lvoc) r$expected

A20min A20bis30 A31bis40 A41plus vok 44.63781 50.46014 70.83827 47.06378 nicht-vok 47.36219 53.53986 75.16173 49.93622

(1- 0.4851936) * sum(lvoc[,1])

oder sum(lvoc[,1])- 44.63781

O = lvoc

E = r$expected d = (O - E)^2/E

<20 30s 40s >41 mitvok 3.999928 0.4084483 1.102723 1.745549 ohnevok 3.769844 0.3849535 1.039292 1.645141

Je größer die Abweichung von 0 (Null) umso mehr trägt eine Zelle zum signifikanten Ergebnis bei.

Wie wird 

berechnet?

Wir wollen die Größe der Abweichung, d, zwischen Observed und Expected prüfen (die Null Hypothese: d

= 0).

E E d ( O  )





ist dann einfach die Summe der Abweichungen:

sum(d) 14.0959

d



-Test für einen Trend

In der Standardaussprache von England, RP, wurde von einer vornehmeren Schichte der Gesellschaft vor 50 Jahren 'lost' mit einem hohen Vokal gesprochenen (auch 'often').

pfad = "das Verzeichnis der gespeicherten Datei lost.txt"

lost = as.matrix(read.table(paste(pfad, "lost.txt", sep="/")))

Hier ist die Häufigkeit der Verwendung von /lo:st/

(Vokal = high) oder /lOst/ (Vokal = low) in Sprechern, die in 6 verschiedenen Jahren aufgenommen wurden (hypothetische Daten).

high low 1950 30 5 1960 18 21 1971 15 26 1980 13 20 1993 4 32 2005 2 34

Gibt es einen Trend? d.h.

nimmt die Proportion der /lOst/ Erzeugungen zu?

In 1950 produzierten 30

Sprecher /lo:st/ und 5 /lOst/.

Abbildung

Wir standardisieren die Jahre, sodass 0 = 1950.

jahr = as.numeric(rownames(lost)) jahr = jahr - 1950

# Proportion von /lo:st/ berechnen p = lost[,1]/apply(lost, 1, sum)

plot(jahr, p, type="b")

Test:

prop.trend.test(x, n, score) x: die Anzahl von /lo:st/

n: Gesamtanzahl pro Jahr

score: die X-Achsen Werte, für die wir einen linearen Trend berechnen wollen.

Proportionen von /lo:st/

über 55 Jahre

0 10 20 30 40 50

0.20.40.60.8

jahr

Proportion

prop.trend.test(lost[,1], n, jahr)

# Spalte 1 hat die Anzahl von /lo:st/

x = lost[,1]

# Summe lo:st + lOst getrennt pro Jahr n = apply(lost, 1, sum)

data: lost[, 1] out of n ,

using scores: 0 10 21 30 43 55

X-squared = 54.506, df = 1, p-value = 1.550e-13

Die Proportion von /lo:st/ nimmt in späteren Jahren

signifikant ab (

(1) = 54.5, p < 0.001)

1. Logistic Regression: allgemeine Einführung

Dalgaard, P. (2002) Introductory Statistics with R.

Insbesondere Kap. 11

D. Cook, P. Dixon, W. M. Duckworth, M.S. Kaiser, K. Koehler, W.

Q. Meeker and W. R. Stephenson. Binary Response and Logistic Regression Analysis.

http://www.faculty.sbc.edu/bkirk/Biostatistics/course%20documents%20for

%202006/Logistic%20Regression%20Analysis.doc

Literatur

Baayen, R.H. Analyzing Linguistic Data: A practical introduction to Statistics. S. 213-234

Johnson, Keith (in press). Quantitative Methods in Linguistics.

Blackwell. Kapitel 5.

Verzani, J. (2005). Using R for Introductory Statistics

(Ebook ueber die LMU UB). Kapitel 12

1. Logistic Regression: allgemeine Einführung

Mit logistic Regression wird eine Regressionslinie an Proportionen angepasst werden.

Aus verschiedenen Gründen kann jedoch die lineare (least-squares) Regression nicht auf Proportionen angewandt werden.

Vor allem liegen Proportionen zwischen 0 und 1 während lineare Regression keine solchen Grenzen kennt (und

daher könnte ein lineares Regressionsmodell Proportionen unter 0 oder über 1 vorhersagen).

Außerdem wird in der linearen Regression eine konstante

Varianz angenommen; jedoch kann beweisen werden,

dass je höher der Proportionsdurchschnitt, umso größer

die Varianz.

Diese (und andere) Probleme können überwunden werden:

1. wenn log-odds statt Proportionen modelliert werden

2. Wenn anstatt die Regressionslinie durch den kleinsten Abstand der Linie zu den Werten (=least squares

regression) zu berechnen, die Methode der 'maximum likelihood' eingesetzt wird.

1. Logistic Regression: allgemeine Einführung

y = mx + b

logodds(y) = mx + b

Least-squares Regression Logistic Regression

Es wird nicht angenommen, dass die Werte Stichproben aus einer Normalverteilung sind.

Ein Vorteil von logistic Regression:

Log-odds

p q=1-p Odds = p/q Log-Odds = log(p/q)

0.8 0.2 log(4) = 1.39

0.5 0.5 1 0

4

bedeutet 4:1 (wie im Pferderennen). Die Wahrscheinlichkeit vom Erfolg (p) ist 4 Mal so groß wie Scheitern (q)

p: Proportion 'Erfolg'.

lo:st lOst

32 8

n 40

p 0.8 (prop. lOst)

(prop. lo:st)

0.0 0.2 0.4 0.6 0.8 1.0

-4-2024

Die Logit-Funktion

p (Erfolg)

Log-odds log(p/(1-p))

Log-odds also log (p/q) als Funktion von p Log-odds haben Werte zwischen ±∞

Log-odds

2. Anwendung der logistic Regression in R: glm()

Das Ziel: nach der Anwendung von logistic Regression geben wir einen beliebigen Jahrgang ein, und das Modell soll uns die Proportion von /lo:st/ vorhersagen zB Eingabe 1962, Proportion (lo:st) = ?.

Jahr ist daher in diesem Fall die unabhängige Variable, Proportion von /lo:st/ die abhängige Variable.

In logistic Regression ist die abhängige Variable immer ein kategorialer Wert von 2 Möglichkeiten:

ja oder nein, rot oder grün, 0 oder 1, weiblich oder

männlich, wach oder eingeschlafen, /lo:st/ oder

/lOst/, Erfolg oder Scheitern, usw.

g = glm(lost ~ jahr, binomial) Ergebnis: ein Log-

Odd pro Jahr

unabhängige Variable (der Jahrgang)

bedeutet:

logistic

Regression ('binomial' weil wie in der

binomialen Verteilung wir mit 2 Werten (ja/nein,

Erfolg/Scheitern zu tun haben).

wird modelliert durch Abhängige Variable

Eine 2-spaltige Matrix: Anzahl von 'ja' und 'nein' (hier /lo:st/ und /lOst/)

lost

high low

1950 30 5

1960 18 21

1971 15 26

1980 13 20

1993 4 32

2005 2 34

Da die Ausgabe der Regression in log-odds ist,

müssen wir die Proportionen ebenfalls umwandeln, wenn wir die Regressionslinie sehen wollen.

Die vorhergesagten Werte überlagern

text(jahr, predict(g), "x", col=3)

Eine Abbildung der Daten in diesem Raum:

# Proportion von /lo:st/ berechnen p = lost[,1]/apply(lost, 1, sum)

# log-odds

lodd = log(p/(1-p))

plot(jahr, lodd, type="b")

# Regressionslinie ueberlagern abline(g, col=2)

0 10 20 30 40 50

-3-2-101

jahr

lodd

x

x

x

x

x

x

3. Abbildung der Regressionslinie

Wir können durch die Transformation (2) die

Regressionslinie auch in einem Raum von Jahr x Proportionen abbilden.

Von Proportionen in log-odds

Von log-odds zurück in Proportionen

1 )

log( p L p

  L = log(p/(1-p))

L L

e p e

 

1 p = exp(L)/(1+exp(L))

log(0.8/0.2) [1] 1.386294

exp(1.386294)/(1+ exp(1.386294)) [1] 0.8

Abbildung der Regression

(1)

(2)

logodds(y) = mx + k

Die Regressionslinie in log-odds

Die entsprechende Regression in Proportionen

) (

) (

1 ^{mx k}

k mx

e

y e _



 

coef(g)

(Intercept) jahr 1.10432397 -0.07026313

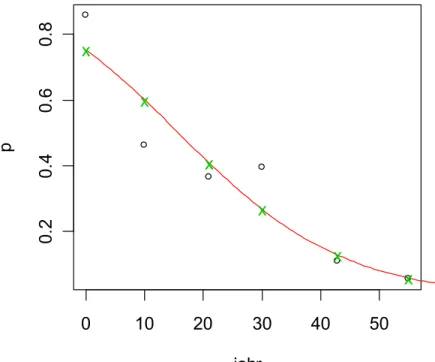
plot(jahr,p)

p = lost[,1]/apply(lost, 1, sum)

curve(exp(m*x + k)/(1+ exp(m*x+k)), xlim=c(0, 60), add=T, col=2)

Abbildung der Regressionslinie

k = coef(g)[1]

m = coef(g)[2]

und die vorhergesagten Werte liegen wieder auf der Linie:

vorher = predict(g)

text(jahr, exp(vorher)/(1+exp(vorher)), "x", col=3)

0 10 20 30 40 50

0.20.40.60.8

jahr

p

x

x

x

x

x

x

Abbildung der Regression

Lineare Regression: R

oder adjusted R

und ein F-test Logistic Regression: G

und ein 

-test.

G

= Null deviance – residual deviance

Für ein signifikantes Ergebnis wollen wir daher, dass Null deviance hoch und Residual deviance klein ist.

wenn dieser Wert 0 wäre, dann wären alle Proportionen in allen Jahren gleich (und die Regressionslinie wäre horizontal)

je höher dieser Wert, umso unwahrscheinlicher ist es, dass die Werte überhaupt durch die Regression

modelliert werden können.

4. Signifikanz-Test

Was ist die Wahrscheinlichkeit, dass die Proportion von

/lo:st/ durch den Jahrgang vorhergesagt werden kann?

69.3634 - 8.2422

[1] 61.1212

G

= Null deviance - residual deviance summary(g)

Null deviance: 69.3634 on 5 degrees of freedom

Residual deviance: 8.2422 on 4 degrees of freedom

…

Der Test mit anova() ist ob G

signifikant von 0 abweicht:

anova(g, test="Chisq")

Df Deviance Resid. Df Resid. Dev P(>|Chi|) NULL 5 69.363 jahr 1 61.121 4 8.242 5.367e-15

Die Proportionen folgen einem Trend (

(1)=61.2, p < 0.001)

5. Zwei unabhängige Variablen.

Hier sind genau dieselben Daten aber zusätzlich nach männlich-weiblich aufgeteilt.

female lost 1950 1960 1971 1980 1993 2005

n n 16 9 8 8 4 1

y n 14 9 7 5 0 1

n y 0 6 10 7 10 15

y y 5 15 16 13 22 19

lost

high low 1950 30 5 1960 18 21 1971 15 26 1980 13 20 1993 4 32 2005 2 34

In 1971 waren 26 Tokens [lost] und 15 [lo:st]

von diesen 26 waren 10 von Männern und 16 von Frauen

erzeugt.

8M, 7F

(a) Gibt es einen Trend?

Also weniger [lo:st] in

späteren Jahren? (b) Ist die Proportion [lost]/[lo:st] in

M und F unterschiedlich verteilt?

female lost 1950 1960 1971 1980 1993 2005

n n 16 9 8 8 4 1

y n 14 9 7 5 0 1

n y 0 6 10 7 10 15

y y 5 15 16 13 22 19

Dies ist ein Problem der mehrfachen Logistic Regression:

logodds (lo:st) = b

+ b

year + b

Geschlecht (also in diesem Fall eine Linie im 3D-Raum)

Geschlecht

Year logodds(lo:st)

Und eine gerade Linie in einem 3D-Raum

(b

ist das Intercept,

b

und b

die Neigungen)

pfad = "das Verzeichnis wo ich lost2.txt gespeichert habe"

lost2 = as.matrix(read.table(paste(pfad, "lost2.txt", sep="/")))

high low 0.0 16 0 10.0 9 6 21.0 8 10 30.0 8 7 43.0 4 10 55.0 1 15 0.1 14 5 10.1 9 15 21.1 7 16 30.1 5 13 43.1 0 22 55.1 1 19

M

W

1950 1960 1971 1980 1993 2005 1950 1960 1971 1980 1993 2005

} }

high = Spalte 1 = /lo:st/

low = Spalte 2 = /lOst/

Daten-Vorbereitung

J = c(jahr, jahr)

G = c(rep("m",6), rep("f", 6)) J

G

[1] 0 10 21 30 43 55 0 10 21 30 43 55

[1] m m m m m m f f f f f f

Zuerst eine Abbildung…

p = lost2[,1]/apply(lost2, 1, sum) interaction.plot(J, G, p)

0. 0 0. 4 0 .8

J

m ea n o f p

0 10 21 30 43 55

G m f

Nimmt die Proportion von

/lo:st/ in späteren Jahren ab?

(Die Unterschiede zwischen m und f ignorieren).

Ja Nein Vielleicht

Unterscheiden sich m und f in der Proportion von /lo:st/?

(Die Unterschiede in den Jahrgängen ignorieren).

Ja Nein Vielleicht

Modell berechnen…

mehrg = glm(lost2 ~ J + G, binomial)

g2 = glm(lost2 ~ J, binomial) anova(g2, test="Chisq")

Analysis of Deviance Table

Df Deviance Resid. Df Resid. Dev P(>|Chi|) NULL 11 89.557 year 1 61.121 10 28.436 5.367e-15

Wenn wir übrigens G weglassen, dann müssten wir

trotz der anderen Aufteilung der Daten das gleiche

Ergebnis wir vorhin bekommen:

Coefficients:

(Intercept) J Gm

0.67472 -0.07524 1.20282

Degrees of Freedom: 11 Total (i.e. Null); 9 Residual Null Deviance: 89.56

Residual Deviance: 15.61 AIC: 51.51

logodds(lo:st) = 0.67472 - 0.07524J+ 1.20282G mehrg = glm(lost2 ~ J + G, binomial)

anova(mehrg, test="Chisq")

Df Deviance Resid.Df Resid. Dev P(>|Chi|) NULL 11 89.557 J 1 61.121 10 28.436 5.367e-15 G 1 12.822 9 15.613 3.425e-04

M und F unterscheiden sich in der Proportion von lo:st/lOst, 

(1) = 12.82, p < 0.001

Die Proportion von 'lo:st' nimmt in späteren Jahren ab,



(1) = 61.12, p < 0.001.

mehrg

Mit 2 oder mehr Variablen soll auch geprüft werden, ob sie miteinander interagieren.

Eine Interaktion zwischen den unabhängigen Variablen – in diesem Fall Geschlecht und Jahrgang – liegt vor, wenn sie eine unterschiedliche Wirkung auf die abhängige

Variable ausüben wie in 1 und 2, aber nicht in 3 und 4

6. Die Interaktion zwischen 2 Variablen

1950 2000

prop(lo:st)

1950 2000 1950 2000 1950

2000 prop(lo:st) prop(lo:st) prop(lo:st)

1 2 3 4

m

f

Wenn eine Interaktion vorliegt, dann können signifikante Ergebnisse in einer der unabhängigen Variablen nicht uneingeschränkt akzeptiert werden.

zB wenn eine Interaktion vorkommt, gibt es vielleicht eine Wirkung von Jahrgang auf die Proportion von /lo:st/ nur in Männern aber nicht in Frauen usw.

Die Interaktion zwischen 2 Variablen

0.00.20.40.60.81.0

year

mean of p

0 10 21 30 43 55

geschl m f

dies scheint aber hier nicht

der Fall zu sein.

Die Interaktion zwischen 2 unabhängigen Variablen, A und B, kann in R mit A:B geprüft werden.

Daher in diesem Fall

g = glm(lost2 ~ J + G + J:G, binomial)

Eine Abkürzung dafür (und mit genau demselben Ergebnis) g = glm(lost2 ~ J * G, binomial)

Die Interaktion zwischen 2 Variablen

anova(g, test="Chisq")

Df Deviance Resid. Df Resid. Dev P(>|Chi|) NULL 11 89.557

J 1 61.121 10 28.436 5.367e-15 G 1 12.822 9 15.613 3.425e-04 J:G 1 0.017 8 15.596 0.896

d.h. die Interaktion ist nicht signifikant und J:G kann

aus dem Regressionsmodell weggelassen werden.

Start: AIC= 53.49 lost2 ~ J * G

Df Deviance AIC - J:G 1 15.613 51.506

<none> 15.596 53.489 Df Deviance AIC

<none> 15.613 51.506 - G 1 28.436 62.328 - J 1 80.018 113.910

Wir bleiben also bei

Call: glm(formula = lost2 ~ J + G, family = binomial) Residual Deviance: 15.61 AIC: 51.51

library(MASS) stepAIC(g)

Dies wird auch durch stepAIC() bestätigt:

AIC wird kleiner wenn wir

J:G weglassen

Aus dem vorigen Beispiel wird auch klar, dass ähnlich wie



Logistic Regression angewandt werden kann, auch wenn die Gruppe nur aus 2 Ebenen besteht.

Gibt es einen signifikanten Unterschied zwischen M und F?

gmf = glm(lost2 ~ G, "binomial") anova(gmf, test="Chisq")

Df Deviance Resid. Df Resid. Dev P(>|Chi|)

NULL 11 89.557 G 1 9.539 10 80.018 0.002

M und F unterscheiden sich in der Proportion von lo:st/lOst (

(1) = 9.5, p < 0.002).

7. Logistic Regression und zwei Ebenen

_{high low}

0.0 16 0 10.0 9 6 21.0 8 10 30.0 8 7 43.0 4 10 55.0 1 15 0.1 14 5 10.1 9 15 21.1 7 16 30.1 5 13 43.1 0 22 55.1 1 19

m = apply(lost2[1:6,], 2, sum) f = apply(lost2[7:12,], 2, sum) mf = rbind(m, f)

rownames(mf) = c(0, 1)

colnames(mf) = c("high", "low") mf

Wir bekommen dasselbe Ergebnis wenn Logistic Regression auf die entsprechende Tabelle

angewandt wird:

lost2

l.mf = c(0,1)

gmf2 = glm(mf ~ l.mf, "binomial") anova(gmf2, test="Chisq")

high low 0 46 48 1 36 90

= (kodiert nur nach M und F)

und man bekommt dann fast das gleiche Ergebnis mit einem 

-Test, der direkt auf die Tabelle angewandt wird:

chisq.test(mf)

Pearson's Chi-squared test with Yates' continuity correction

data: mf

X-squared = 8.6985, df = 1, p-value = 0.003185

Ein 2-Test kann jedoch nicht verwendet

werden, bei einer Gruppenanzahl von > 2 …

lost3 = as.matrix(read.table(paste(pfad, "alter.txt", sep="/"), header=T))

Haben (a) Alter und (b) Geschlecht einen Einfluss auf die Proportion von /lo:st/?

Hier sind dieselben Daten aufgeteilt in 2 Altersgruppen sowie M/F

Gruppe 1 = Vokal = high/low

Gruppe 2 = Geschl = M/F (=0/1) Gruppe 3 = Alter = alt/jung

3 Gruppen jeweils 2 Ebenen

high low alt.0 43 35 alt.1 30 15 jung.0 3 13 jung.1 6 75

lost3

Zuerst eine Abbildung high low alt.0 43 35 alt.1 30 15 jung.0 3 13 jung.1 6 75

# Alter kodieren A = c(0, 0, 1, 1)

# Geschlecht kodieren G = c(0, 1, 0, 1)

prop = lost3[,1]/apply(lost3, 1, sum)

interaction.plot(A, G, prop)

im Geschlecht?

ja nein

Signifikanter Einfluss auf lo:st/lOst?

im Alter? vielleicht

ja nein vielleicht Interaktion zwischen A und G? ja nein vielleicht

0.10.20.30.40.50.6

A

mean of prop

0 1

G

0 1

g = glm(lost3 ~ A * G, binomial) anova(g, test="Chisq")

Df Deviance Resid. Df Resid. Dev P(>|Chi|) NULL 3 67.758 A 1 64.452 2 3.306 9.893e-16 G 1 0.398 1 2.908 0.528 A:G 1 2.908 0 -4.441e-16 0.088

Es gab einen signifikanten Einfluss vom Alter (

(1)=64.2, p <

0.001) aber nicht vom Geschlecht auf die Proportion von

/lo:st/. Die Interaktion zwichen Alter und Geschlecht war nicht

signifikant (p > 0.05).