PRESENCE OF LONG MEMORY 1
by
Walter Kramer and Philipp Sibbertsen
Fachbereich Statistik,Universitat Dortmund, D-44221Dortmund, Germany
VersionJune 2000
Abstract
Wederivethe limitingnulldistributionsofthe standardandOLS{
based CUSUM-tests for structural change of the coecients of a
linearregressionmodelinthecontextoflongmemorydisturbances.
We show that both tests behave fundamentallydierent ina long
memoryenvironment,ascomparedtoshortmemory,andthatlong
memory is easily mistaken for structural change when standard
critical values are employed.
1 Introduction and Summary
It is by now well known that long memory and structural change are easily
confused(Lobatoand Sawin1997,Engleand Smith1999,Grangerand Hyung
1999, Diebold and Inoue 1999 and many others). Therefore it is of interest
to know about both the stochastic properties of procedures for detecting and
measuring long memory when there isonly structural change,and ofthe per-
formance of tests for structural change when there isonly long memory.
1
ResearchsupportedbyDeutscheForschungsgemeinschaft;weare gratefulto A. Zeileis
forexpert computationalassistance.
been rather little work on the latter (Hidalgo and Robinson 1996, Wright
1998). Below we consider the behaviour of the standard and the OLS-based
CUSUM-tests,whose limitingdistributionsare wellunderstoodinthe context
of variousregressor-sequences and iid-orshort memorydisturbances(Kramer
et al. 1988, Ploberger and Kramer 1992, 1996). As shown by Wright (1998)
for theOLS-based CUSUM-test andthe special caseof polynomialregressors,
these limiting distributions are not robust to departures from short memory
- in fact, the OLS-based CUSUM-test has an asymptotic size of unity. The
present paperallows for more generalregressor sequences alsocovers the con-
ventional CUSUM-test based on recursive residuals as well. We show that
Wright's results concerning the behaviour under H
0
essentially go through
with more general regressors, and that similar results hold for the standard
CUSUM-test. This is a rather negative result which conrms related theo-
rems fromthe structural-change-mistaken-for-long-memory-literature:Similar
tostructural changebeingmistaken forlong memory,longmemory islikewise
easily mistaken for structural change, and it is remains an open problem to
eciently discriminate between the two 2
.
2 Two unpleasant theorems
Weconsider the standard linear regression model
y
t
= 0
x
t +"
t
; (t=1;:::;T) (1)
with nonstochastic, xed regressors x
t
and stationary mean zero disturbances
"
t
. We assumethat
1
T T
X
t=1 x
t
! c<1 and (2)
2
There do exist solutionsfor somespecial cases,such asKunsch's (1986)procedure to
discriminate betweenlongmemory and monotonictrends, but ageneral treatment ofthis
problemisstillmissing.
1
T X
t=1 x
t x
0
t
! Q(nite, nonsingular): (3)
Theseare standardassumptions inlinearregression largesampleasymptotics;
theyexcludetrendingdata,whichrequireseparatetreatmentandproofswhich
dier fromthe ones below.
Weare concerned withtesting the model(1) againstthe alternativeof unspe-
cied structural change in the regression coecients . We consider rst the
OLS{based CUSUM{test, asproposed by Ploberger and Kramer (1992).This
test rejects the nullhypothesis of nostructural changefor large values of
TS := sup
0<<1 jC
T
()j; where (4)
C
T
() := T 1
2
^
1
"
[T]
X
t=1 e
t
; (5)
and where e
t :=y
t x
0
t
^
are the OLS{residuals from(1).
The limiting null distribution of TS is well known for white noise and short
memory disturbances. Our rst theorem extends these results to stationary
long memory disturbances, where the "
t
followa stationaryARFIMA(p,d,q){
process:
E("
t
"
t k
)=L(k)k d
; (6)
L(k)slowlyvarying, 0<d<1=2.
Theorem 1 In the regression model (1), with disturbances as in (6) we have
T d
C
T
()!B
d
() c 0
Q 1
(); (7)
where B
d
() is fractional Brownian Motion with self-similarity parameter d
and ()N(0;
2
"
Q).
C
T
() = T 1
2
^
1
"
8
<
: [T]
X
t=1
"
t [T]
X
t=1 x
0
t T
X
t=1 x
t x
0
t
!
1
T
X
t=1 x
t
"
t 9
=
;
; so (8)
T d
C
T
() = (
T d+
1
2
z
[T]
T d+
1
2 [T]
X
t=1 x
0
t T
X
1 x
t x
0
t
!
1
T
X
1 x
t
"
t )
=^
"
; (9)
where z
t
=z
t 1 +"
t , z
0
=0.In viewof
T d
1
2
z
[T]
!
"
B() (see e.g. Marmol 1995); (10)
1
T [T]
X
t=1 x
t
! c; (11)
0
@ 1
T [T]
X
t=1 x
t x
0
t 1
A 1
!
1
Q 1
; (12)
T d
1
2 [T]
X
t=1 x
t
"
t
! () (see Giraitisand Taqqu 1998); (13)
and
^ 2
"
= T
X
t=1 e
2
t
T
= T
X
t=1
"
2
T +o
P
(1)! 2
"
the limiting relationship(7) follows. 2
>From (7), it is immediately seen that TS P
! 1 under H
0
, so the OLS-
based CUSUM{test is extremely non{robust to long{memory disturbances,
in the sense that long memory is easily mistaken for structural change when
conventional criticalvaluesare employed.
Next we consider the standard CUSUM-test based onrecursiveresiduals
~ e
t
= y
t x
0
t
^
(t 1)
f
t
;
^
(t 1)
=
X (t 1)
0
X (t 1)
1
X (t 1)
0
y (t 1)
(14)
f
t
=
1+x 0
t (X
(t 1) 0
X (t 1)
) 1
x
t 1
2
(t=K+1;:::;T); (15)
It rejects for large valuesof
S
T
= sup
0<<1 W
T
()=(1+2): (16)
where
W
T
():=T 1
2
^
1
"
[T]
X
t=K+1
~ e
t
: (17)
Theorem 2 In the regression model (1), with disturbances as in (6) we have
T d
W
T
()!B
d
(); (18)
whereagainB
d
()isfractionalBrownianMotionwithself-similarityparameter
d.
PROOF:Following Kramer et al.(1988), wewrite W
T () as
W
T ()=
1
p
T [T]
X
t=K+1
"
t
[T]
X
t=K+1
^
(t 1)
0
x
t
: (19)
Let Q
j :=
1
T P
j
i=1 x
i x
0
i
.First we showthat
max
KtT jj
^
(t)
t
X
j=K [(y
j x
0
j )x
j ]Q
1
j
jj=o
p
T d+
1
2
(ln ln T) 1
2
:(20)
LetS
t :=
P
t
j=1 (y
j x
0
j )x
j
.Bythe lawofthe iteratedlogarithmforthe sums
of long memory Gaussian random variables we have for some slowly varying
function L(T)
max
1tT
S
t
2
(d+
1
2 )2(d+
1
2 ) 1
T 2(d+
1
2 )
L(T) ln ln(T) 1
2
=O
p
(1); (21)
so (20) follows directlyfrom Lemma3.1 of Jureckova and Sen (1984).
1
p
T [T]
X
t=K+1 (y
t x
0
t
^
(t 1)
)
= 1
p
T [T]
X
t=1 t
X
j=1 c
ij (y
j x
0
j
)+o(T (d+
1
2 )
ln ln T) 1
2
; (22)
where
c
ij
= 8
>
>
>
<
>
>
>
: x
0
j Q
1
(i 1) x
i
i>j
1 i=j
0 i<j
(23)
(see also Sibbertsen, 2000). In viewof a result by Sen (1984) that
X
ji c
2
ij
=1+0(
1
i
) (24)
and theorem 5.1of Taqqu (1975),the theorem now follows from (22). 2
Theorem2showsthatthenulldistributionofthestandard CUSUM-testtends
toinnityaswell,sothestandardCUSUM-testhaslikewiseanasymptoticsize
of unity.
3 Some nite sample Monte Carlo evidence
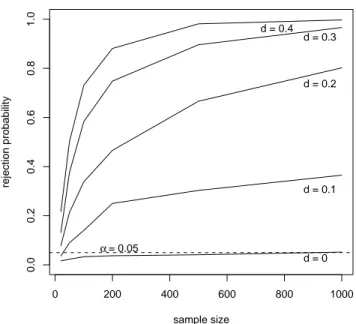
Figure1belowgivestheempiricalrejectionrates,using1000runsandstandard
critical values form the iid-disturbance case, for the OLS-based CUSUM-test.
WhenthedisturbancesareinfactARFIMA(0,d,0).Itconrmesourtheoretical
results:rejectionratesincreasewithdandsamplesize,andproducemisleading
evidence even for smalld and T.
0 200 400 600 800 1000
0.00.20.40.60.81.0
sample size
rejection probability
α= 0.05
d = 0 d = 0.1 d = 0.2 d = 0.3 d = 0.4
Figure 1:Empiricalrejection probabilityof OLS-basedCUSUM-test
0 200 400 600 800 1000
0.00.20.40.60.81.0
sample size
rejection probability
α= 0.05
d = 0 d = 0.1 d = 0.2 d = 0.3 d = 0.4
Figure2:Empiricalrejection probabilityofstandard CUSUM-test
Figure 2 gives the corresponding empirical rejection rates for the standard
CUSUM-test. Notsurprisingly,the empiricalsize isnot as far othe mark as
for the OLS-based CUSUM-test, but the test is misleadinghere as well.
Diebold, F.S. and Inoue, A. (1999): "Long memory and structural
change." Stern Schoolof Business discussion paper.
Engle, R.F. and Smith, A. (1999): "Stochastic permanent breaks." Re-
view of Economics and Statistics
Giraitis, L. and Taqqu, M. (1998): "Convergence of normalized quadra-
tic forms." To appear in Journal of Statistical Planning and Inference
80,15 {35.
Granger, C.W.J. and Hyung, N. (1999): "Occasional structural breaks
and long memory."UCSD discussion paper 99-114.
Hidalgo, J. and Robinson, P.M. (1996): "Testing for structural change
inalong{memoryenvironment."Journal of Econometrics70,159{174.
Jureckova, J. and Sen, P.K. (1984): "On adaptive scale-equivariant M-
estimators in linearmodels."Statistics and Decision 2, 31{ 46.
Kunsch, H. (1986): "Discrimination between monotonic trends and long
range dapendence." Journal of Applied Probability23,1025 { 1030.
Kramer, W.; Ploberger, W. and Alt, R. (1988): "Testing for structu-
ralchangein dynamic models."Econometrica56, 1355 {1369.
Lobato, I.N. and Savin, N.E. (1997): "Real and spurious lon-memory
properties of stock market data (with discussion and reply)." Journal
of Business and Economic Statistics 16,261 {283.
Marmol, F. (1995): "Spurious regression between I(d){processes."Journal
of Time Seies Analysis16,313 {321.
Ploberger, W. and Kramer, W. (1992): "The CUSUM{test with OLS{
residuals." Econometrica 60,271 { 286.
Ploberger, W. and Kramer, W. (1996): "A trend{resistent test for
structuralchange basedonOLS{residuals."Journal of Econometrics70,
175 { 185.
Sibbertsen, Ph. (2000): "Robust CUSUM-M-test in the presence of long
memory disturbances." TechnicalReport 19/2000,SFB 475, Universitat
Dortmund.
Taqqu, M.S. (1975): "Weak convergence of fractionalBrownian Motion to
the Rosenblatt process." Zeitschrift fur Wahrscheinlichkeitstheorie und
verwandte Gebiete 31,287 {302.
long-memory disturbances." Journal of Time Series Analysis 19, 369 {
379.