Halbleiterbauelemente: physikalische Grundlagen und Simulation

Research Collection

Educational Material

Halbleiterbauelemente

physikalische Grundlagen und Simulation

Author(s):

Schenk, Andreas Publication Date:

2001

Permanent Link:

https://doi.org/10.3929/ethz-a-004303105

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Halbleiterbauelemente -

Physikalische Grundlagen und Simulation

Privat-Dozent Dr. rer. nat. Andreas Schenk Integrated Systems Laboratory, ETH Zurich

December 18, 2001

1 Quanten-Transport 2

1.1 Quanten-Bauelemente . . . . 2

1.2 Quanten-Transportgleichungen ^∗ . . . . 19

2 Boltzmann-Gleichung 23 2.1 “Ableitung” . . . . 23

2.2 Methoden der direkten L¨osung . . . . 26

2.2.1 Relaxationszeit-N¨aherung . . . . 26

2.2.2 Monte-Carlo-Methode . . . . 27

3 Momenten-Methode 32 3.1 Hydrodynamische Transportgleichungen, Drift-Diffusions-Modell . . . . 32

3.2 Thermodynamisches Modell ^∗ . . . . 43

4 Numerische Methoden f ¨ur die Simulation von Bauelementen by Bernhard Schmith ¨usen 48 4.1 Skalierte Gleichungen und L¨osungsprozedur . . . . 48

4.1.1 Die Physikalischen Gleichungen . . . . 48

4.1.2 Randwerte . . . . 49

4.1.3 Die skalierten (station¨aren) Gleichungen . . . . 50

4.1.4 Wahl der Variablen . . . . 50

4.1.5 Die L¨osungsprozedur . . . . 51

4.2 Diskretisierung . . . . 52

4.2.1 Allgemeine Diskretisierungsverfahren . . . . 52

4.2.2 Anforderung an Diskretisierung . . . . 53

4.2.3 Diskretisierung der Poissongleichung . . . . 54

4.2.4 Diskretisierung der Kontinuit¨atsgleichungen . . . . 56

4.2.5 Die Diskretisierten Gleichungen . . . . 60

4.3 Gitter . . . . 60

4.3.1 Anforderungen an Gitter . . . . 61

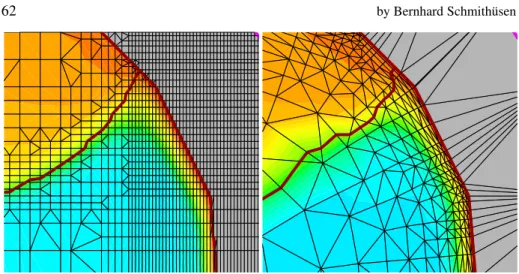
4.3.2 Gitter Adaption . . . . 62

5 Silizium 63 5.1 Bandstruktur . . . . 63

5.2 Zustandsdichte . . . . 79

5.3 Fermi-Dirac-Verteilung ^∗ . . . . 82

5.3.1 System mit konstanter Teilchenzahl (“kanonische Verteilung”) . . . . 82

5.3.2 System mit variabler Teilchenzahl (“grosskanonische Verteilung”) . . . . 86

5.3.3 Fermi-Dirac-Verteilung . . . . 87

i

Contents 1

5.4 Ladungstr¨agerdichten . . . . 89

6 Streuprozesse 95 6.1 S _kk

am Beispiel der Streuung an ionisierten St¨orstellen . . . . 95

6.2 Die wichtigsten Streumechanismen in Silizium . . . 105

6.3 Die Matthiessen-Regel . . . 106

7 Beweglichkeit kalter und heisser Ladungstr¨ager 108 7.1 µ imp und µ ac . . . 108

7.2 Modelle f¨ur die Beweglichkeit kalter Ladungstr¨ager im bulk . . . 109

7.3 Beweglichkeit im MOSFET-Kanal . . . 112

7.4 Beweglichkeit heisser Ladungstr¨ager . . . 116

7.4.1 S¨attigung der Driftgeschwindigkeit . . . 116

7.4.2 Empirische Modelle f¨ur Bauelemente-Simulation . . . 118

8 Strahlungslose Rekombination 121 8.1 Tiefe St¨orstellen . . . 121

8.2 Generations-Rekombinationsraten f¨ur Band-Band- und Band-Trap- ¨ Uberg¨ange . . 125

8.3 Raten-Gleichungen . . . 127

8.4 SRH-Lebensdauern . . . 129

9 Auger-Rekombination 131 10 Stossionisation 135 10.1 Ionisations-Schwellenenergien . . . 135

10.2 Stossionisationsrate und -koeffizienten . . . 138

10.3 Modelle f¨ur die Stossionisationskoeffizienten . . . 140

10.4 Avalanche-Durchbruch . . . 141

11 Metall-Halbleiter (MS)-Kontakt 144 11.1 Energieniveau-Schema vor Einstellung des thermodynamischen Gleichgewichts . 144 11.2 MS-Kontakt im Gleichgewicht, Schottky- und Bardeen-Modell . . . 145

11.3 MS-Kontakt im Nichtgleichgewicht . . . 151

11.4 Kontakt-Randbedingungen in der Bauelemente-Simulation . . . 154

12 Metall-Isolator-Halbleiter (MIS) Struktur 156 12.1 Isolator-Halbleiter (IS)- ¨ Ubergang im Gleichgewicht . . . 156

12.2 MIS-Struktur bei angelegter Spannung . . . 159

12.3 Ladungstransport durch d¨unne Oxide . . . 164

13 Hetero- ¨ Uberg¨ange 166 13.1 Banddiskontinuit¨aten . . . 166

13.2 Potentialverlauf nach Einstellung des Gleichgewichts . . . 167

13.3 Supergitter und Quantum Wells . . . 169

1 Quanten-Transport

1.1 Quanten-Bauelemente

Definition Transport:

Bewegung von Ladungstr¨agern ( = Str¨ome) in einem Bauelement oder einer Halbleiterstruktur infolge ¨ausserer Felder.

dissipativer Transport im bulk:

Energieverlust haupts¨achlich im Innern des Bauelements, mittlere freie Wegl¨ange klein gegen Abmessungen des Bauelements.

ballistischer Transport:

Mittlere freie Wegl¨ange f¨ur dissipative und elastische Streuung ist von der Gr¨ossenordnung der Abmessungen des Bauelements.

quanten-ballistischer Transport:

Zus¨atzlich Quantisierungseffekte durch “confinement” und Interferenz-Effekte infolge verschiedener m¨oglicher Wege.

koh¨arenter ballistischer Transport:

Koh¨arenzl¨ange von derselben Gr¨ossenordnung wie die Struktur, Phase der Elektronenwelle bleibt erhalten.

Quanten-Transport kann man auch nach m¨oglichen Anwendungen in der Nanoelektronik klassifizieren, wobei jeweils typische Quanten-Effekte ausgenutzt werden:

A) Interferenz-Effekte in niedrig-dimensionalen Strukturen, wie Resonant-Tunnel-Dioden (resonant tunnel diodes, RTDs) und Resonant-Tunnel-Transistoren (resonant tunnel transistors, RTTs)

2

1.1 Quanten-Bauelemente 3

B) Coulomb-Blockade in Einzel-Elektron-Transistoren (single electron transistors, SETs) und Quanten-Punkten (quantum dots, QD) C) Mesoskopischer Transport in Quanten-Wellenleitern (quantum

waveguides) A) Interferenz-Effekte

interferencedevices.ID.epsi 99 × 72 mm

single barriers resonant double barrier

quantum well superlattice

chirp superlattice camel transistor

B) Quanten-Dr¨ahte und Quanten-Punkte

confinementdevices.ID.epsi 107 × 60 mm

epitaxial wire modulation-doped deep-etched wire

modulation-doped shallow-etched wire

split-gate wire quantum dot

quantum well GaAs

n-(Al,Ga)As

C) Quanten-Wellenleiter

waveguidedevices.ID.epsi 110 × 26 mm

interference ring device

tapered quantum waveguide

stub device cross-talking

wires

Quantenmechanik (QM): Ultra-Short Course I

In QM werden Observablen ( = Messgr¨ossen) A durch Operatoren ˆ A beschrieben

E −→ H ˆ Hamiltonoperator p −→ p ˆ Impulsoperator x −→ x ˆ Ortsoperator

und die Zust¨ande eines Systems (die in der klassischen Mechanik durch Angabe der Koordinaten und Impulse aller Teilchen eindeutig bestimmt sind) durch Wellenfunktionen ψ( x ) (mathematisch: Vektoren im Hilbert- raum).

1D : H ˆ = p ˆ ²

2 m + V ( x ˆ ) , p ˆ = − i

∂

∂ x . (1.1)

V ( x ˆ ) ist der Operator der potentiellen Energie. Die fundamentale Glei- chung zur Bestimmung von ψ( x ) ist die Schr¨odinger-Gleichung:

station¨ar : H ˆ ψ( x ) = E ψ( x ) , (1.2) zeitabh¨angig : i

∂

∂ t Φ( x , t ) = H ˆ Φ( x , t ) . (1.3) Beispiel: freies Elektron (V ≡ 0)

In der klassischen Physik ist wegen F = p ˙ = 0 v = const , E = m

2 v ² ,

1.1 Quanten-Bauelemente 5

in der QM dagegen muss man die Schr¨odinger-Gleichung ˆ H ψ = E ψ l¨osen. Einsetzen des Hamiltonoperators (es bleibt nur der Operator der kinetischen Energie in einer Dimension) ergibt die Eigenwertgleichung

−

² 2m

∂ ²

∂ x ² ψ( x ) = E ψ( x ) (1.4) oder, mit Einf¨uhrung der sogenannten Wellenzahl k = √

2mE /

∂ ²

∂ x ² + k ²

ψ( x ) = 0 (1.5)

Die allgemeine (von Null verschiedene) L¨osung lautet

ψ( x ) = A e ^ikx + B e ^−ikx (1.6) und beschreibt eine ebene Welle.

= ⇒ Der mathematische Formalismus der QM beschreibt die Wellennatur der Teilchen.

Beispiel: Potentialtopf mit unendlich hohen W¨anden

well1.ID.epsi 45 × 40 mm

V(x)

x

0 d

V ( x ) = ∞ f¨ur x ≤ 0 , x ≥ d V ( x ) = 0 f¨ur x im Innern

Mit diesem Potential erh¨alt man

ψ( x ) = A e ^ikx + B e ^−ikx im Innern ψ( 0 ) = ψ( d ) = 0

da das Elektron in die unendlich hohen Potentialw¨ande nicht eindringen kann. Das Verschwinden der Wellenfunktion an den R¨andern des Poten- tialtopfes f¨uhrt auf zwei Bestimmungsgleichungen f¨ur die unbekannten Koeffizienten A und B

A + B = 0 , A e ^ikd + B e ^{− ikd} = 0

und damit zur Quantisierungsbedingung f¨ur die Wellenzahl k:

sin(kd) = 0 k _n = n π

d , n = 1 , 2 ,... quantisierter Impuls , E n =

² k _n ²

2m =

² π ²

2md ² n ² quantisierte Energie .

Wegen A = − B und k = k _n haben die Wellenfunktionen die Form ψ n ( x ) = C sin ( n π x / d ) . Die Konstante C wird so spezifiziert, dass die (gebunde- nen) Zust¨ande auf Eins normiert sind, also

Z

d 0

dx |ψ n ( x )| ² = 1 .

Die Gr¨osse |ψ n ( x )| ² heisst Aufenthaltswahrscheinlichkeitsdichte des Teilchens im Zustand mit der Quantenzahl n. Die Normierungsbedingung bedeutet damit nichts weiter, als dass sich das Teilchen mit Sicherheit in- nerhalb des Potentialtopfes befindet. Die Auswertung der Normierungs- bedingung ergibt f¨ur die Wellenfunktionen

ψ n ( x ) = 2

d sin n π

d x

stehende Wellen! (1.7)

well2.ID.epsi 43 × 42 mm

E

x

0 d

n = 1 n = 2 n = 3

diskretes Energiespektrum!

Wellenl¨ange λ n = 2d n

Was passiert im Falle a) endlich hoher und b) endlich hoher und endlich dicker Potentialw¨ande?

a) Es gibt nur noch eine endliche Anzahl von gebundenen Zust¨anden.

Wird der Potentialtopf zu flach, kann u.U. ¨uberhaupt kein Teilchen mehr gebunden werden (im Falle asymmetrischer Potentialt¨opfe).

b) Das Teilchen kann mit einer gewissen Wahrscheinlichkeit aus dem

Potentialtopf heraustunneln, d.h. die Lebensdauer des gebunde-

nen Zustandes wird endlich. Wegen der Heisenbergschen Un-

sch¨arferelation

1.1 Quanten-Bauelemente 7

∆ t ∆ E ≥

₂

werden die (f¨ur unendlich dicke Potentialw¨ande) diskreten Energie- niveaus E _n zu Resonanzen mit endlicher Linienbreite “verschmiert”

(Lebensdauer-Verbreiterung). Die Maxima der Resonanzen ver- schieben sich gegen¨uber den E _n zu niedrigeren Energien.

well3.ID.epsi 110 × 34 mm

a) b)

Bei den Resonanzenergien wird die Durchdringungswahrscheinlichkeit f¨ur die Doppel-Barriere gross. Je asymmetrischer die Doppel-Barriere, um so mehr wird die Resonanz ged¨ampft.

Sind die station¨aren Zust¨ande ψ n ( x ) bekannt, kann man sofort die L¨osungen der zeitabh¨angigen Schr¨odinger-Gleichung angeben:

Φ n ( x , t ) = e ^{−i En}

^t ψ n ( x ) . ( Einsetzen , Probe! )

Die zeitabh¨angigen Wellenfunktionen oszillieren mit der Frequenz ω n = E _n /

. Damit sich eine stehende Welle (bzw. scharfe Resonanz) ausbilden kann, muss die entsprechende Zeitkonstante t _n =

/ E _n klein gegen¨uber einer charakteristischen mittleren Streuzeit τ n sein.

Zahlenbeispiel:

E ₁ = 66 meV,

= 6 . 6 × 10 ⁻¹⁶ eVs = ⇒ t _n = 10 ⁻¹⁴ s

Typisches τ n bei Raumtemperatur ist τ n ∼ 2 × 10 ⁻¹⁴ s (f¨ur Streuung von Elektronen an Phononen, den Quanten der Gitterschwingungen).

= ⇒ Interferenz-Bauelemente funktionieren nur bei gen¨ugend tiefen Tem- peraturen! (“gen¨ugend” ist dabei nat¨urlich relativ und h¨angt von der St¨arke der erreichbaren Energie-Quantisierung ab)

Im folgenden werden die Bauelemente-Gruppen A) und B) an den

wichtigsten Beispielen praktisch erl¨autert.

A) Resonant-Tunnel-Diode (RTD) and Resonant-Tunnel-Transistor (RTT)

RTDbandscheme.epsi 124 × 103 mm A

Band-Schema einer RTD. Die Potentialbarrieren werden durch Spr ¨unge der Leitungs- bandkante zwischen dem breitl¨uckigeren Halbleiter AlAs und dem schmall¨uckigeren Halbleiter GaAs erzeugt. Die Energie der Zust¨ande im Potentialtopf ist quanti- siert. Elektronen aus der hochdotierten Quelle, die alle Energieniveaus zwischen der Leitungsbandkante und dem Fermi-Niveau besetzen, k¨onnen nur dann durch die Doppel-Barriere tunneln, wenn ihre Energien mit der der Resonanzniveaus

¨ubereinstimmen. Dazu muss an der Quelle eine Spannung angelegt werden. Die notwendige Energie f¨ur das Hinzuf¨ugen eines (N+1)-ten Elektrons setzt sich aus zwei Anteilen zusammen: der Additionsenergie A und der Anregungsenergie ∆ε. A wird gebraucht, um die elektrostatische Abstossung zwischen dem (N+1)-ten und den N Elektronen zu ¨uberwinden, die sich bereits im Quantentopf befinden. A ist propor- tional zum inversen mittleren Abstand 1/r der Elektronen im Quantentopf, wogegen

∆ε ∼ 1/d ² (siehe Rechnung zum Potentialtopf). Senkrecht zur Quantisierungsrichtung

k¨onnen sich die Elektronen frei ausbreiten, was zu einem relativ grossen r und daher

zu einem kleinen A f¨uhrt. F¨ur eine RTD gilt also A ∆ε. (Im Bild ist A ¨ubertrieben

gross dargestellt.)

1.1 Quanten-Bauelemente 9

RTDoperation.ps 105 × 139 mm

a) Schematischer Querschnitt einer RTD.

b) Bei zu kleiner Source-Drain-Spannung kann kein resonanter Tunnelstrom in der RTD fliessen (“off-state”). Es fliesst lediglich ein Leckstrom, verursacht von thermisch an- geregten Elektronen in der Quelle (um so gr¨osser, je h¨oher die Betriebstemperatur).

c) Resonanz-Situation (“on-state”) . Es fliesst ein resonanter Tunnelstrom, dessen St¨arke

von der Durchdringungswahrscheinlichkeit der Doppelbarriere abh¨angt, d.h. von der

Linienbreite der Resonanz.

RTDkennlinie.ps 101 × 64 mm

A

a) Band-Schema einer RTD bei steigender Source-Drain-Spannung.

b) Strom-Spannungs-Charakteristik. Der Abstand der Peaks entspricht grob der Anre-

gungsenergie ∆ε. Allerdings ist ∆ε selbst eine Funktion der Source-Drain-Spannung, da

sich die Form des Potentials der Struktur st¨andig ¨andert. U.U. kann kein zweiter Peak

auftreten, wenn der deformierte Potentialtopf keinen zweiten gebundenen Zustand mehr

erzeugt.

1.1 Quanten-Bauelemente 11

RTToperation.ps 101 × 141 mm

a) Schematischer Querschnitt eines Resonant-Tunnel-Transistors (lateraler Typ).

b) Das Band-Schema ist ¨ahnlich dem der RTD.

c) Im Unterschied zur RTD existiert eine dritte Elektrode (Gate), mit der man die Lage

der Energie-Niveaus relativ zum Fermi-Niveau in der Quelle ver¨andern kann. Insbeson-

dere kann man bei fester Source-Drain-Spannung durch kontinuierliche ¨ Anderung der

Gate-Spannung die Energie-Niveaus des Quantentopfes in Resonanz mit den besetzten

Zust¨anden in der Quelle bringen. Allerdings werden auch die Potentialbarrieren von der

Gate-Spannung beeinflusst.

B) Quanten-Punkt (QD) und Einzel-Elektron-Transistor (SET)

Quanten-Punkt: Dimensionalit¨at ist in allen drei Richtungen reduziert.

Elektronen sind v¨ollig eingesperrt, d.h. sie haben keinen klassischen Frei- heitsgrad mehr. Die elektronischen Zust¨ande sind in allen drei Dimensio- nen quantisiert. Die Anregungsenergien ∆ε x , ∆ε y und ∆ε z sind gross, ebenso die Additionsenergie A, da der mittlere Elektronenabstand r im Dot durch das einsperrende Potential klein gehalten wird. Die elektro- nische Struktur von Quanten-Punkten kann starke ¨ Ahnlichkeiten mit der von Atomen aufweisen, daher spricht man auch von k¨unstlichen Atomen.

Insbesondere liefern die Austausch-Wechselwirkung und die Elektron- Elektron-Korrelation starke Beitr¨age zur Gesamtenergie. Die Anre- gungsenergien representieren keine Einteilchen-Zust¨ande mehr, sondern Vielteilchenzust¨ande der N Elektronen im Dot.

QDgate.epsi 98 × 43 mm

GaAs AlGaAs 1

QD auf der Basis einer GaAs/AlGaAs Heterostruktur. Das einsperrende Potential wird durch planare metallische Gates erzeugt (Stanford University).

QDox.epsi 90 × 49 mm

QD auf der Basis einer Silicon-On-Insulator (SOI) Heterostruktur. Das einsperrende

Potential wurde durch “pattern-dependent oxidation” eines Silizium-Quantendrahts

erzeugt (Princeton University).

1.1 Quanten-Bauelemente 13

QDflash.epsi 99 × 58 mm

Gate

Channel Dot

Oxide Drain

Source

QD flash memory: Das Speicher-Gate besteht aus einer poly-Si-Insel.

Einzel-Elektron-Transistor: 3-Terminal-Bauelement analog zum gew¨ohnlichen MOSFET. Dimensionalit¨at ist in keiner Richtung (wesentlich) reduziert. Die zentrale Insel des SETs enth¨alt typischer- weise Millionen von Elektronen. Am weitesten verbreitet sind SETs mit metallischen Inseln. Da der Quantisierungseffekt schwach ist oder gar nicht existiert, gilt f¨ur den SET: A ∆ε . Diesen Grenzfall nennt man Coulomb-Blockade, ein rein klassischer Effekt der elektrostatischen Ab- stossung der Elektronen untereinander, der verhindert, dass bei zu kleiner Source-Drain-Spannung ein zus¨atzliches Elektron auf die Insel tunneln kann (daher der Begriff “Blockade”). Ein Strom kann erst einsetzen, wenn die Source-Drain-Spannung die Additionsenergie erreicht. Den Spannungsbereich, wo kein Strom fliessen kann, nennt man Coulomb gap. Die Tunnel-Barrieren verhindern, dass sich Elektronen gleichzei- tig ¨uber Source, Drain und Insel ausbreiten k¨onnen. Deshalb ist der Tunnelprozess immer sequentiell: Ein Elektron muss aus der Insel ins Drain tunneln, bevor das n¨achste von der Source auf die Insel tunneln kann. Man spricht von (r¨aumlich) korreliertem Tunneln. Dieser Vorgang wiederholt sich millionenmal pro Sekunde, so dass ein messbarer Strom durch die Insel fliesst.

Bleibt die Source-Drain-Spannung kleiner als die Additionsenergie,

spricht man vom Coulomb-Blockade-Regime. Durch Anlegen einer

Spannung am Gate kann man die Coulomb-Blockade aufheben und die

Zahl der Elektronen auf der Insel ¨andern, z.B. von N-1 zu N. Dies

geschieht bei bestimmten kritischen Werten der Gate-Spannung, wo sich

gleichzeitig N-1 oder N Elektronen auf der Insel befinden d¨urfen (Ent-

artungspunkte) und bewirkt einen pl¨otzlichen Strom von Source nach

(a)

(b) V

V e

2C _Σ

e 2C _Σ

3e 2C _Σ

5e 2C _Σ

− _2C ^e _Σ

I

I

a) “Coulomb gap” und I-V-Kennlinie eines SETs mit symmetrischen Tunnel-Barrieren.

F¨ur Source-Drain-Spannungen betragsm¨assig kleiner als die halbe Additionsenergie e ² / 2C _Σ kann kein Strom fliessen.

b) Schematische “Coulomb staircase”, die I-V-Kennlinie eines SETs mit stark asym- metrischen Tunnel-Barrieren bei T=0 K. Der Abstand der Stufen ist gleich der Addi- tionsenergie e ² / C _Σ .

Drain, der bei weiterer Erh¨ohung der Gate-Spannung aber sofort wieder verschwindet (wegen der Coulomb-Blockade!). Die Elektronenzahl hat sich dabei auf den Wert N stabilisiert. Der Source-Drain-Strom wird also durch kleinste ¨ Anderungen der Gate-Ladung ein- und ausgeschal- tet. Die dazu n¨otige ¨ Anderung der Gate-Ladung kann eine einzige, ja selbst nur einen Bruchteil der Elementarladung ausmachen, worauf der Name “Einzel-Elektron-Transistor” zur¨uckgeht. Da der Strom auf einzelne Gate-Ladungen reagiert, kann der Verst¨arkungsfaktor (gain) des SETs extrem gross sein!

Physik des SETs: Ultra-Short Course

Um die Form der Kennlinien eines SETs besser zu verstehen, betrach-

ten wir die charakteristischen Energien im einfachsten physikalischen

Modell (dem sogenannten orthodoxen Modell). In diesem Modell wer-

den sowohl Quantisierungseffekte als auch die Vielteilcheneffekte der

1.1 Quanten-Bauelemente 15

ivg.epsi 96 × 48 mm

I-V g -Kennlinie eines SETs im Coulomb-Blockade-Regime bei T > 0 K. Bei den Gate- Spannungen V g = (N − 1/2)e/C g treten Strom-Peaks auf, da die Coulomb-Blockade aufgehoben ist. Die Peaks sind umso sch¨arfer, je tiefer die Temperatur ist. Ihr Abstand ist gleich e/C g . Die H¨ohe h¨angt von der Source-Drain-Spannung und dem Widerstand der Tunnel-Barrieren ab.

Austausch-Wechselwirkung und Korrelation vernachl¨assigt.

Ein System aus N Elektronen hat die Coulomb-Energie U _coul ( N ) =

Z

− eN 0

dQ Φ( Q ) , (1.8)

wobei Φ( Q ) das elektrostatische Potential der Insel mit der Ladung Q unter dem Einfluss externer Gates ist:

Φ( Q ) = Q C _Σ + C _g

C _Σ V _g . (1.9)

C _Σ ist die Summe aus Gate-Kapazit¨at und Insel-Kapazit¨at C _Σ = C _island + C _g . Nach Einsetzen erh¨alt man

U _coul ( N ) = ( eN ) ²

2C _Σ − eN C _g

C _Σ V _g . (1.10)

Im thermodynamischen Sinne ist U _coul ( N ) gleich der freien (Gibbs) En- ergie F ( N ) (im hier betrachteten orthodoxen Modell); der erste Term ist die elektrostatische Energie der Insel, der zweite Term ist die Arbeit, die die Spannungsquelle am Gate verrichtet. Die Differenz

F ( N ) − F ( N − 1 ) = µ ( N ) (1.11)

heisst chemisches Potential und ist gleich der Energie, die aufgebracht

werden muss, um dem (N-1)-Elektronen-System ein weiteres Elektron

zuzuf¨uhren. Man erh¨alt

µ ( N ) = e ² C _Σ

N − 1

2

− e C _g

C _Σ V _g . (1.12)

Die ¨ Anderung des chemischen Potentials mit der Elektronenzahl haben wir oben als Additionsenergie A bezeichnet

µ ( N ) − µ ( N − 1 ) = A = e ² / C _Σ . (1.13) Die Coulomb-Staircase der I-V-Kennlinie und die Strom-Peaks der I-V _g - Kennlinie kann man nun folgendermassen verstehen:

I-V-Kennlinie eines SETs mit stark asymmetrischen Tunnel-Barrieren (Einzel-Elektron-Box):

Generell kann es nur dann zum Strom kommen (Ladungstr¨ager- Austausch zwischen Insel und Source/Drain), wenn die Wahrschein- lichkeit, dass die Insel N Elektronen enth¨alt, gleich der Wahrschein- lichkeit ist, dass sie N - 1 Elektronen enth¨alt. Die Elektronenzahl fluktuiert dann zwischen N und N - 1. Die Gleichheit dieser Wahrschein- lichkeiten f¨uhrt auf die Bedingung

µ ( N ) = E _F , (1.14)

wobei E _F das Fermi-Niveau in Source/Drain ist. Sei E _{F , drain} = 0, dann ist E _{F , source} = eV . Die Gate-Spannung sei Null. Aus Eq. (1.12) und Eq. (1.14) erh¨alt man

V ( N ) = e C _Σ

N − 1

2

(1.15) als diejenigen Spannungen, bei denen sich die Zahl der nicht- kompensierten Elektronen auf der Insel um 1 ¨andert. N = 1 definiert das Coulomb gap. Die Zeitkonstante des korrelierten Tunnelns wird mit steigender Spannung V > V(1) kontinuierlich kleiner, was zu einem kontinuierlichen Anstieg des Stroms in diesem Spannungsbereich f¨uhrt.

Der Anstieg wird vom Widerstand der dicken Tunnel-Barriere bestimmt.

I-V _g -Kennlinie eines SETs bei verschwindend kleiner Source-Drain- Spannung:

In diesem Fall ist E _{F , drain} ≈ E _F,source = 0 (wegen der Wahl des Energie- Nullpunkts) und Eq. (1.12), Eq. (1.14) ergeben

V _g ( N ) = e C _g

N − 1

2

(1.16)

als diejenigen Spannungen, bei denen ein Strom-Peak auftritt.

1.1 Quanten-Bauelemente 17

Free energy F

Charge Q

Gate voltage V _g V

= −( N − 1 )

V

= −( N −

)

V

= −( N −

)

V

= −( N −

)

−( N − 1 ) e

−( N − 1 ) e

−( N − 1 ) e

−( N − 1 ) e

− Ne

− Ne

− Ne

− Ne E

= 0

E

µ ( N )

e

Freie Energie als Funktion der Ladung auf der Insel f ¨ur vier verschiedene Gate-

Spannungen (oben). Bei V g = −(N − 1/2)e/C g existieren zum selben Wert der freien

Energie zwei Ladungszust¨ande (Entartung). Es kann ein Strom fliessen. In dieser Situ-

ation ist das chemische Potential µ(N) gleich dem ¨ausseren Fermi-Niveau (unten).

vertdotall.epsi 133 × 111 mm

(c) (a)

a) Schematische Darstellung eines vertikalen QDs mit unterschiedlichen Barrieren.

b) Energie-Quantisierung und Vielteilcheneffekte bestimmen wesentlich die Kennli- nien. Man erkennt an der I-V g -Kennlinie die Schalenstruktur des Energiespektrums, die ¨ Ahnlichkeit mit der eines zweidimensionalen harmonischen Oszillators aufweist.

Gef¨ullte Schalen gibt es zu den Elektronenzahlen N = 2 , 6 , 12.

c) Coulomb staircase (I-V-Kennlinie).

Prinzipielle und praktische Hindernisse in der Nanoelektronik

- Pr¨azision und Uniformit¨at der Strukturen (Tunnel-Barrieren, In- seln) auf einer Skala von wenigen Nanometern f¨ur zuverl¨assiges und gleichartiges Verhalten einer riesigen Zahl von Bauelementen.

Besonders kritisch ist die exponentielle Sensivit¨at des Tunnelstroms bzgl. Dickenvariationen der Tunnel-Barrieren.

- Hintergrund-Ladungen akkumulieren sich bevorzugt in der N¨ahe

1.2 Quanten-Transportgleichungen ^∗ 19

von QDs und SETs und k¨onnen ihre Funktion v¨ollig ausschalten.

- Auswahl des Halbleiter-Materials: III-V-Heterostrukturen haben glatte und saubere Grenzfl¨achen, aber schwache Potential-Barrieren.

Die Oberfl¨achen lassen sich nicht passivieren und sind deshalb Tr¨ager von Ladungen hoher Dichte, die die Stabilit¨at der Bauele- mente stark beeintr¨achtigen. SiO ₂ als nat¨urlicher Isolator auf Sili- zium ist eine hervorragende Barriere gegen Leckstr¨ome, ist jedoch amorph und hat deshalb eine hohe Defektdichte.

- Betriebstemperatur: F¨ur eine Anwendung von Si SETs bei Raumtemperatur m¨ussen die Inseln Abmessungen von h¨ochstens 10 nm haben. Heutige Quanten-Bauelemente funktionieren deshalb nur bei sehr tiefen Temperaturen.

- Betriebsspannungs-Schwankungen k¨onnen leicht dazu f¨uhren, dass SETs aus der “Resonanz” geraten und so unbeabsichtigt vom “on- state” in den “off-state” umschalten.

1.2 Quanten-Transportgleichungen ^∗

Beispiel: Wigner-Boltzmann-Gleichung

Die allgemeinste Beschreibung eines quantenmechanischen Systems er- folgt mit Hilfe der sogenannten Dichtematrix

ρ ˆ = |ψψ| .

ψ sei die Wellenfunktion eines abgeschlossenen Systems. (Zust¨ande eines Systems, die durch Wellenfunktionen beschrieben werden k¨onnen, heissen reine Zust¨ande. Die Formulierung mittels Dichtematrix erlaubt auch die Beschreibung von gemischten Zust¨anden. Hier seien nur reine Zust¨ande betrachtet.) Die triviale Zeitabh¨angigkeit der Wellenfunktionen gem¨ass Eq. (1.3) wird der K¨urze halber nicht mitgeschrieben.

Wendet man die zeitabh¨angige Schr¨odinger-Gleichung auf die Dichtematrix an, erh¨alt man ihre Bewegungsgleichung

i

∂

∂ t ρ ˆ = H ˆ , ρ ˆ

.

Dabei ist [ a , b ] = ab − ba der Kommutator. Zur sogenannten Ortsdarstel- lung gelangt man nach folgender Vorschrift:

r 2 | ρ| ˆ r 1 = r 2 |ψψ| r 1 ^def = ψ( r 2 ) ψ ^∗ ( r 1 ) .

Durch ¨ Ubergang zu Schwerpunktskoordinaten r ₁ = R + r

2 , r ₂ = R − r 2

und anschliessende Fouriertransformation bzgl. r entsteht die Wigner- Funktion (Wigner, 1932)

f _W ( p , R , t ) = 1 ( 2 π

) ³

Z

d ³ r ψ ^∗ R − r

2 ψ

R + r 2

exp

− i

~

p · r

(1.17) Eigenschaften:

1) f _W ist reell ( f _W = f _W ^∗ ) , aber nicht positiv (eine Konsequenz der Heisenbergschen Unsch¨arferelation, Wigner 1967).

2)

R

d ³ p f W ( p , R , t ) = |ψ( R , t )| ² ist die Aufenthaltswahrscheinlichkeit im Ortsraum (Dichte).

3)

R

d ³ R f _W ( p , R , t ) =

= _{( 2 π} ¹

~

) ³

R

d ³ r

R

d ³ R ψ ^∗ R − r

2 ψ

R + r

2 exp

−

ⁱ

p · r

= _{( 2 π} ¹

~

) ³

R

d ³ r ₁

R

d ³ r ₂ ψ ^∗ ( r ₂ ) ψ ( r ₁ ) exp

−

ⁱ

p · ( r ₁ − r ₂ )

= ψ( p , t ) ψ ^∗ ( p , t ) = |ψ( p , t )| ² ist die Wahrscheinlichkeitsdichte im Impulsraum.

Ableitung der Bewegungsgleichung:

Wir setzen abk¨urzend ψ + = ψ( R + r / 2 ) und ψ ^∗ ₋ = ψ ^∗ ( R − r / 2 ) . Die explizite Zeitableitung der Wigner-Funktion ergibt

∂

∂ t f _W ( p , R , t ) = 1 ( 2 π

) ³

Z

d ³ r ∂ψ ^∗ ₋

∂ t ψ + + ψ ^∗ ₋ ∂ψ ⁺

∂ t

exp

− i

~

p · r

. Die Zeitableitungen auf der rechten Seite werden durch die jeweilige zeitabh¨angige Schr¨odinger-Gleichung ausgedr¨uckt, d.h.

∂ψ ^∗ ₋

∂ t = 1

− i

−

²

2m ∇ ² R + V ( R − r / 2 )

ψ ^∗ ₋

∂ψ +

∂ t = 1 i

−

²

2m ∇ ² R + V ( R + r / 2 )

ψ +

1.2 Quanten-Transportgleichungen ^∗ 21

Nach dem Einsetzen wird die Ableitung bzgl. R auf eine Ableitung bzgl.

r umgew¨alzt, z.B.

∇ ² R ψ ^∗ ₋ ψ + → 4

∇ ² r ψ ^∗ ₋ ψ + ,

und eine partielle Integration nach r durchgef¨uhrt. Dabei verschwinden die Terme im Unendlichen wegen der Annahme, dass die Wellenfunktio- nen dort Null sind und es bleibt

∂

∂ t f _W ( p , R , t ) = 1 ( 2 π

) ³

Z

d ³ r 2i

m ∇rψ ^∗ ₋ ∇r

ψ + e ⁻

ⁱ p · r

−

− 2i

m ∇rψ + ∇r

ψ ^∗ ₋ e ⁻

ⁱ p · r

− i

~

( V ₊ − V ₋ ) ψ ^∗ ₋ ψ + e ⁻

ⁱ p · r . Werden nun die Ableitungen bzgl. r ausgef¨uhrt und kehrt man danach wieder zur Ableitung nach R zur¨uck, folgt

∂

∂ t f _W ( p , R , t ) = − p

m · ∇ ^R f _W ( p , R , t ) −

− i

~

1 ( 2 π

) ³

Z

d ³ r ( V ₊ − V ₋ ) ψ ^∗ ₋ ψ + e ⁻

ⁱ p · r . Um den letzten Term durch die Wigner-Funktion selbst ausdr¨ucken zu k¨onnen, wird das Potential V ( R ± r / 2 ) in eine Taylor-Reihe bzgl. r ent- wickelt:

V ( R ± r / 2 ) = ∑

λ

∂ ^{λ 1 +λ 2 +λ 3} V ( R )

∂ R ^λ ₁ ¹ ∂ R ^λ ₂ ² ∂ R ^λ ₃ ³

r ₁ ^{λ 1} r ^λ ₂ ² r ₃ ^{λ 3} λ 1 ! λ 2 ! λ 3 !

± 1 2

_{λ 1 +λ 2 +λ 3}

. (1.18) Wegen der Differenz V ₊ − V ₋ in der Bewegungsgleichung bleiben nur Glieder ¨ubrig, f¨ur die λ 1 + λ 2 + λ 3 ungerade ist. Beschr¨ankt man sich auf die ersten beiden Terme, also auf λ 1 + λ 2 + λ 3 = 1 und λ 1 + λ 2 + λ 3 = 3, folgt

( V ₊ − V ₋ ) = ∇ R V ( R ) · r + 1

4 ∑

λ 1 +λ 2 +λ 3 =3

∂ ^{λ 1 +λ 2 +λ 3} V ( R )

∂ R ^λ ₁ ¹ ∂ R ^λ ₂ ² ∂ R ^λ ₃ ³

r ^λ ₁ ¹ r ₂ ^{λ 2} r ^λ ₃ ³

λ 1 ! λ 2 ! λ 3 ! .

Nach Einsetzen in die Bewegungsgleichung und Generierung der Kom-

ponenten von r durch partielle Ableitung nach den Komponenten des Im-

pulses p entsteht die endg¨ultige Form der Wigner-Boltzmann-Gleichung

mit erstem nicht-verschwindenden Quanten-Korrekturterm:

∂

∂ t + p

m · ∇ ^R − ∇ ^R V ( R ) · ∇p

f _W ( p , R , t ) + (1.19) +

²

4 ∑

λ 1 +λ 2 +λ 3 = 3

∂ ³ V ( R )

∂ R ^λ ₁ ¹ ∂ R ^λ ₂ ² ∂ R ^λ ₃ ³ 1 λ 1 ! λ 2 ! λ 3 !

∂ ³ f W ( p , R , t )

∂ p ^λ ₁ ¹ ∂ p ^λ ₂ ² ∂ p ^λ ₃ ³ = 0 . Die niedrigste Quantenkorrektur ist ∼

² und verschwindet f¨ur Potentiale, die h¨ochstens quadratisch von den Koordinaten abh¨angen (harmonische Potentiale). In diesem Fall reproduziert sich die klassische, stossfreie Liouville-Gleichung. Symbolisch schreibt man daf¨ur

∂

∂ t + v · ∂

∂ R + F · ∂

∂ p

f = 0 . (1.20)

Der zweite Term beschreibt Diffusionsprozesse, der dritte Driftprozesse.

Die rechte Seite ist Null wegen der Voraussetzung der Stossfreiheit (abgeschlossenes System).

Das Auftreten eines Terms mit dritter Ableitung nach den Koordinaten

in der Wigner-Boltzmann-Gleichung ist Ausdruck der Nicht-Lokalit¨at der

Quantenmechanik.

Boltzmann-Gleichung 2

2.1 “Ableitung”

streuung.epsi 114 × 89 mm

dx dy

dz

x x + dx

in out

v _x v _y

v _z v v’

dv _x dv _y dv _z Streuung

Ziel ist die Aufstellung einer Bilanzgleichung im Phasenraum (drei Orts- koordinaten x, y und z, drei Geschwindigkeitskoordinaten v x , v y und v z ) f¨ur die Zahl der Elektronen (L¨ocher, allgemein: Teilchen), die sich zur Zeit t im Raumelement d ³ r am Ort r und im Geschwindigkeitselement

23

d ³ v zur Geschwindigkeit v befinden. Diese Zahl bezeichnen wir mit f ( r , v , t ) d ³ r d ³ v . (2.1) f ( r , v , t ) ist die klassische Verteilungsfunktion, d.h. Ort und Impuls sind gleichzeitig scharf messbar. Die Teilchen bewegen sich auf klassischen Trajektorien.

Bilanz im Ortsraum:

Die Zahl der Elektronen, die in den infinitesimalen W¨urfel mit den Kan- tenl¨angen dx, dy, dz in x-Richtung an der Stelle x im Zeitintervall dt hin- einfliegen (“in”) und an der Stelle x + dx in diesem Zeitintervall wieder herausfliegen (“out”), ist

in : f ( r , v , t ) d ³ v v _x dt dy dz ,

out : f ( x + dx , y , z , v , t ) d ³ v v _x dt dy dz ,

weil sie in dt die Strecke dx = v _x dt zur¨ucklegen. Der Netto-Zuwachs an Elektronen am Ort r ist dann gleich in − out, d.h.

− v _x [ f ( x + dx , y , z , v , t ) − f ( r , v , t )] d ³ v dy dz dt

= − v x ∂ f

∂ x d ³ v d ³ r dt

oder in 3D : = − v · ∇ r f d ³ v d ³ r dt . (2.2) In analoger Weise betrachtet man die

Bilanz im Geschwindigkeitsraum:

Man erh¨alt einen Netto-Zuwachs an Elektronen mit der Geschwindigkeit v

− v ˙ _x [ f ( r , v _x + dv _x , v _y , v _z , t ) − f ( r , v , t )] d ³ r dv _y dv _z dt

= − v ˙ _x ∂ f

∂ v _x d ³ vd ³ r dt

oder in 3D : = − v ˙ · ∇ v f d ³ v d ³ r dt . (2.3) Die Elektronen werden im Zeitintervall dt unter dem Einfluss eines

¨ausseren Feldes beschleunigt und ¨andern ihre Geschwindigkeit von v nach v + dv. Nach Newton gilt

˙ v = F ₀

m = − eE

m , (2.4)

wobei F ₀ die einwirkende Kraft ist, die im Falle eines elektrischen Feldes

E den Wert − eE hat.

2.1 “Ableitung” 25

Die Zahl der Elektronen mit der Geschwindigkeit v am Ort r kann aber auch auf andere Art ge¨andert werden. Die Elektronen werden gestreut und ¨andern dadurch ihre Geschwindigkeit am Ort r von v nach v (wenn sie aus dem Geschwindigkeitsw¨urfel bei v herausgestreut werden), bzw.

von v nach v (wenn sie hineingestreut werden). Man erh¨alt in : ∑

v

S ( v , v ) f ( r , v , t ) d ³ r d ³ v dt , (2.5) out : − ∑

v

S ( v , v ) f ( r , v , t ) d ³ r d ³ v dt , (2.6) f¨ur die ¨ Anderung der Elektronenzahl im Zeitintervall dt infolge von St¨ossen. Dabei ist S ( v , v ) die Streuwahrscheinlichkeit f¨ur die Streuung v → v (Dimension: s ⁻¹ ). S ist also ein Mass f¨ur die H¨aufigkeit der Streu- ung.

Alles zusammen, d.h. die Ausdr¨ucke (2.2), (2.3), (2.5) und (2.6), ergeben die explizite zeitliche ¨ Anderung der Elektronenzahl im Phasenraumele- ment d ³ r d ³ v w¨ahrend des Zeitintervalls dt, also _∂t ^∂ f ( r , v , t ) d ³ r d ³ v dt

∂

∂ t + v · ∇ r + F ₀ m · ∇ v

f ( r , v , t ) =

= ∑

v

S ( v , v ) f ( r , v , t ) − S ( v , v ) f ( r , v , t )

(2.7) (Ludwig Boltzmann, 1872).

Die Boltzmann-Gleichung (BG) ist eine komplizierte Integro-Differen- tialgleichung. Die “Ableitung” zeigt, dass man implizit r¨aumliche und zeitliche Lokalit¨at annimmt. Zeitliche Lokalit¨at bedeutet, dass die St¨osse instantan sind, r¨aumliche Lokalit¨at bedeutet, dass die St¨osse auf einer Ausdehnung der L¨ange Null stattfinden. In sehr grossen elektrischen Feldern ( > 10 ⁷ V / cm) sind diese Annahmen nicht mehr gerechtfertigt (intra-collisional field effect).

In der Bauelemente-Modellierung werden folgende Erweiterungen gemacht:

- Die Geschwindigkeit wird als Gruppengeschwindigkeit v =

∇ k E ( k )/

verstanden.

- E ( k ) ist durch die realistische Bandstruktur des Halbleiters gegeben.

- F¨ur die Streuwahrscheinlichkeiten S ( v , v ) der einzelnen Streupro-

zesse werden die quantenmechanischen ¨ Ubergangswahrscheinlich-

keiten pro Zeiteinheit verwendet.

- Im Stossterm der BG (rechte Seite) wird f ( r , v , t ) → [ 1 − f ( r , v , t )] f ( r , v , t ) und f ( r , v , t ) → [ 1 − f ( r , v , t )] f ( r , v , t ) ersetzt.

Damit wird das Pauli-Prinzip ber¨ucksichtigt, d.h. die Endzust¨ande d¨urfen beim Stossprozess nicht besetzt sein (Fermi-Statistik).

2.2 Methoden der direkten L¨osung

2.2.1 Relaxationszeit-N¨aherung

- Die Streuwahrscheinlichkeit S sei gerade in allen Geschwindigkeits- komponenten: S ( v , v ) = S (− v , v ) = S ( v , − v ) = S (− v , − v ) . (Gilt nicht f¨ur alle Streuprozesse und f¨ur bestimmte nur n¨aherungsweise.) - Man zerlegt die Verteilungsfunktion f in einen geraden Anteil f ⁽⁰⁾

und einen ungeraden Anteil f ⁽¹⁾

f = f ^{( 0 )} + f ^{( 1 )} , mit f ^{( 0 )} ( v ) = f ^{( 0 )} (− v ) f ^{( 1 )} ( v ) = − f ^{( 1 )} (− v ) . - Einsetzen in den Stossterm der BG ergibt

∑ v

S ( v , v ) f ^{( 0 )} ( r , v , t ) − S ( v , v ) f ^{( 0 )} ( r , v , t )

− S ( v , v ) f ^{( 1 )} ( r , v , t ) Der Term mit f ^{( 1 )} ( r , v , t ) verschwindet, weil f ^{( 1 )} eine ungerade und S eine gerade Funktion in der Geschwindigkeit v ist.

- Im thermodynamischen Gleichgewicht ist f ^{( 0 )} die Gleichgewichts- Verteilungsfunktion (Maxwell-Boltzmann-Verteilung). Die eckige Klammer verschwindet dann wegen des Prinzips der detaillierten Balance (Zahl der herausgestreuten gleich Zahl der hineingestreuten Teilchen).

- Definition totale (mikroskopische) Relaxationszeit:

τ tot ( v ) = 1

∑ v S ( v , v ) - Damit wird der Stossterm symbolisch

∂ f ⁽⁰⁾

∂ t

coll

− f ⁽¹⁾

τ tot ( v ) .

2.2 Methoden der direkten L¨osung 27

Beispiel: Station¨are, homogene BG, linearisiert im elektrischen Feld E Ist das elektrische Feld E hinreichend schwach, kann man die BG in E linearisieren, d.h. f ^{( 0 )} ist dann identisch mit der Gleichgewichts- Verteilung und f ^{( 1 )} h¨angt nur linear von E ab. Beschr¨ankt man sich weiter auf den r¨aumlich und zeitlich homogenen Fall, reduziert sich die BG auf

eE

m · ∇ v f ⁽⁰⁾ ( v ) = f ⁽¹⁾ ( v )

τ tot ( v ) . (2.8)

Zur weiteren Vereinfachung ersetzen wir τ tot ( v ) durch eine Konstante τ tot

und f¨uhren die Gr¨osse Beweglichkeit µ = e τ tot / m ein. F¨ur die Stromdichte der Elektronen folgt

j _n = − e v = − e ∑ _v ^{f ( v ) v = − e} ∑ _v ^{f ( 1 ) ( v ) v = − eµ} ∑ _v ^{v E · ∇ v f ( 0 ) ( v ) .}

Nach partieller Integration erh¨alt man

j _n = eµ ∑ _v ^{f (0) ( v ) E = eµ n E = σ n E , (2.9)}

also das Ohmsche Gesetz. Dazu wurde die Definition der Elektronen- dichte n = ∑v f ⁽⁰⁾ ( v ) und der Leitf¨ahigkeit σ n = eµ n benutzt.

2.2.2 Monte-Carlo-Methode

- Man verfolgt Trajektorien der einzelnen Elektronen und l¨asst sie nach dem Zufallsprinzip streuen.

- Alle zu betrachtenden Streumechanismen (Phononen, St¨orstellen, ...) werden durchindiziert. Die Streurate des α -ten Mechanismus ist

∑ v

S _α ( v , v ) ^def = 1 τ α ( v ) .

- Die Wahrscheinlichkeit, dass ein Elektron bis zur Zeit t + dt nicht gestreut wurde, ist

P ( t + dt ) = P ( t ) P ( dt )

= P ( t )

1 − dt ∑

v

S ( v , v )

.

(dt ∑v S ( v , v ) = dt ∑ α τ ⁻ _α ¹ ( v ) ist die Wahrscheinlichkeit, dass das

Elektron im Zeitintervall dt gestreut wurde.)

trajectory.ID.epsi 111 × 78 mm

x

y trajectory

c) x(t)

t

〈 x 〉 a)

t v(t)

〈 v 〉 b)

Schematische Darstellung der stochastischen Bewegung eines Elektrons im Falle reiner Diffusion (kein Feld). a) x(t)-Diagramm. b) v(t )-Diagramm: Nach jedem Stoss hat die Geschwindigkeit einen neuen, konstanten Wert. c) Trajektorie in der x-y-Ebene.

- Daraus folgt die Differentialgleichung dP

dt = − P ∑

v

S ( v , v ) mit der L¨osung (man beachte, dass P(0) = 1)

P ( t ) = exp

−

Z

t 0

dt ∑

v

S ( v , v )

im Intervall [ 0 , t ] . (2.10) Die Zeit t ist also gleich der freien Flugzeit t _f vom Anfangszeitpunkt t = 0 an gerechnet. P nimmt Werte zwischen 0 und 1 an, ist also eine echte Wahrscheinlichkeit. Sie kann durch Zufallszahlen r f zwischen 0 und 1 beschrieben werden.

- Auf diese Weise kann die zuf¨allige freie Flugzeit t _f eines Elektrons aus

Z

t f

0

dt 1

τ tot ( v ( t )) = − ln r _f (2.11)

2.2 Methoden der direkten L¨osung 29

berechnet werden. Die numerische Aufl¨osung dieser Gleichung nach der oberen Integrationsgrenze t _f verbietet sich jedoch geradezu wegen der komplizierten Gestalt von τ tot ( v ( t )) . Deshalb f¨uhrt man eine fiktive Selbst-Streuung

S _{f ict} ( v , v ) =

Γ − ∑

v

S ( v , v )

δvv , S _{f ict} ( v ) = Γ − 1

τ tot ( v ) ≥ 0 ,

ein, die wegen δvv offenbar den Zustand des Elektrons nicht ver¨andert (daher der merkw¨urdige Name “Selbst-Streuung”). Das Hinzuf¨ugen von S f ict zur BG hat keine Wirkung, da sich in- scattering- und out-scattering-Term kompensieren. Der Sinn der Einf¨uhrung von S _{f ict} wird sofort deutlich: Die Gesamt-Streurate ist nun n¨amlich τ ⁻¹ tot ( v ) + S _{f ict} ( v ) = Γ = const . und Gleichung (2.11) f¨ur die freie Flugzeit vereinfacht sich zu

t f = − ln r _f Γ ,

d.h. der numerische Aufwand reduziert sich auf die Berechnung des Logarithmus der Zufallszahl. In der Praxis nimmt man f¨ur Γ die obere Grenze der Streurate aller realen Prozesse.

- Nach der Zeit t _f wird das Elektron gestreut. Es muss ein bestimmter Streumechanismus ausgew¨urfelt werden. Der α -te Mechanismus (inclusive der Selbst-Streuung) wird mit Hilfe der Zufallszahl r _s

¨uber die Ungleichung

α−1 ∑ _{j=1 τ} ¹ _j ^{< r s Γ <} ∑ _j=1 ^α _τ ¹ _j ^(2.12)

bestimmt. Veranschaulichung:

z . B . α = 2 ( iv ), wenn 1

τ ac < r s Γ <

1 τ ac + 1

τ iv

.

Um so st¨arker ein bestimmter Streumechanismus, um so gr¨osser

1 /τ α und um so gr¨osser die Wahrscheinlichkeit, dass er aus-

gew¨urfelt wird. Die ganze Physik wird also in die Wichtung

gesteckt.

streumech.ID.epsi 100 × 33 mm

ac iv imp ee

1 2 3 4

τ 1 ac

τ 1 iv

τ 1 imp

τ 1 ee j =

Type = Rate =

0 Γ

r s Γ

5 self-scatt.

S _fict

- Der Endzustand nach der Streuung (v ) muss unter den Restriktio- nen der Energie- und Impulserhaltung f¨ur das Gesamtsystem der Stosspartner ausgew¨ahlt werden. Wenn eine Hyperfl¨ache existiert, muss der konkrete v -Vektor ausgew¨urfelt werden, z.B. im Falle der elastischen Streuung ( | v | = | v | ) der Elektronen in Silizium ein be- stimmtes Tal und ein bestimmter Winkel:

endzustand.ID.epsi 61 × 58 mm

v v’

- Die makroskopischen Gr¨ossen, wie mittlere Driftgeschwindigkeit,

Stromdichte, Elektronentemperatur, ... werden nach gewissen

(Beobachtungs-) Zeitintervallen ∆ t durch Ensemble-Mittelung be-

stimmt.

2.2 Methoden der direkten L¨osung 31

mc-flow.epsi 132 × 162 mm

Fluss-Diagramm einer Monte-Carlo-Simulation f¨ur den Fall eines homogenen Halblei-

ters.

3 Momenten-Methode

3.1 Hydrodynamische Transportgleichungen, Drift- Diffusions-Modell

Ziel ist die Ableitung von kinetischen Gleichungen f¨ur Mittelwerte einer Funktion Φ( v )

Φ =

R

d ³ v Φ( v ) f ( r , v , t )

R

d ³ v f ( r , v , t ) = 1 n ( r , t )

Z

d ³ v Φ( v ) f ( r , v , t ) (3.1) aus der Boltzmann-Gleichung. ¹ Dabei geht ein betr¨achtlicher Teil an In- formation verloren (n¨amlich der ¨uber die Geschwindigkeiten der einzel- nen Teilchen), aber die Gleichungen werden einfacher und numerisch schneller l¨osbar. Φ bleibt nat¨urlich eine Funktion von r und t, was wir nicht explizit mitschreiben. Wir betrachten jetzt das Produkt aus Dichte n ( r , t ) und dem Mittelwert Φ und leiten dieses Produkt explizit nach der Zeit ab:

∂

∂ t ( n Φ) = ∂

∂ t

Z

d ³ v Φ( v ) f ( r , v , t ) =

Z

d ³ v Φ( v ) ∂

∂ t f ( r , v , t ) . F¨ur ∂ f /∂ t setzen wir die Boltzmann-Gleichung (2.7) ein, wobei wir den l¨anglichen Stossterm mit der Bezeichnung (∂ f /∂ t ) coll abk¨urzen:

∂

∂ t ( n Φ) =

Z

d ³ v Φ( v )

− v · ∇ r f − F ₀

m · ∇ v f + ∂ f

∂ t

coll

= −∇ r

Z

d ³ v Φ( v ) v f − F ₀ m

Z

d ³ v Φ( v ) ∇ v f + ∂

∂ t

Z

d ³ v Φ f

coll

1

Diese Ableitung folgt der von K. Bløtekjær (IEEE TED 17, 38 (1970)) vorgeschlagenen Methode.

32

3.1 Hydrodynamische Transportgleichungen, Drift-Diffusions-Modell 33

Um alle Terme auf der rechten Seite wieder durch Mittelwerte ausdr¨ucken zu k¨onnen, darf keine Ableitung von f unter dem Integral stehen. Im zweiten Term muss daher eine partielle Integration durchgef¨uhrt werden

Z

d ³ v Φ( v ) ∇ v f = −

Z

d ³ v (∇ v Φ( v )) f

(man beachte, dass f f¨ur | v | → ∞ verschwindet). Benutzt man jetzt die Definition des Mittelwerts (3.1), folgt

∂

∂ t ( n Φ) + ∇ r · ( n v Φ) − n F ₀

m · ∇ v Φ = ∂

∂ t n Φ

coll

, (3.2) was man in verallgemeinerter Form als

∂

∂ t ( n Φ) + ∇ r · j _Φ − n F _Φ = ∂

∂ t n Φ

coll

(3.3) schreiben kann. Diese Gleichung ist eine Bilanzgleichung f¨ur die ver- allgemeinerte Dichte n Φ . Ihre explizite zeitliche ¨ Anderung ist mit der Divergenz einer verallgemeinerten Stromdichte j _Φ = n v Φ und dem Auftreten einer verallgemeinerten treibenden Kraft F _Φ = F ₀ · ∇ v Φ/ m verkn¨upft.

W¨ahlt man Φ( v ) speziell als Potenz der Geschwindigkeit, d.h. v ^m , erh¨alt man eine Hierarchie von Erhaltungss¨atzen f¨ur Teilchendichte (m=0), Teilchen-Stromdichte (m=1), Energiedichte (m=2) und Energie- Stromdichte (m=3).

Man nennt n v ^m das m-te Moment von v und die entsprechende Glei- chung daf¨ur das m-te Moment der Boltzmann-Gleichung.

Sprechen von jetzt ab wieder von Elektronen (Index n).

m = 0

Φ = v ⁰ = 1 j _Φ = n v = − j _n / e F _Φ = 0 .

Einsetzen in Gleichung (3.3) liefert den Erhaltungssatz f¨ur die Elektro- nendichte n (Kontinuit¨ats-Gleichung):

∂ n

∂ t − 1

e ∇ r · j _n = ∂ n

∂ t

coll

, (3.4)

(j _n ist die elektrische Stromdichte).