Rudiger W. Braun

Funktionentheorie

Rudiger W. Braun

Sommersemester 2014

Inhaltsverzeichnis

1 Komplexe Differenzierbarkeit 5

2 Wegintegrale 17

3 Die Umlaufzahl 21

4 Kompakte Mengen 23

5 Der Cauchysche Integralsatz f¨ur konvexe Mengen 25

6 Der Cauchysche Integralsatz 27

7 Der komplexe Logarithmus 29

8 Reihen holomorpher Funktionen 31

9 Die Taylorsche Entwicklung 33

10 Die Laurentsche Entwicklung 35

11 Residuenkalk¨ul 37

12 Das Nullstellenz¨ahlintegral und der Satz von Rouch´e 41

13 Isolierte Singularit¨aten 43

14 Meromorphe Funktionen 45

15 Der Satz von der Gebietstreue 49

16 M¨obiustransformationen 51

17 Die Riemannsche Zahlensph¨are 57

18 Die S¨atze von Arzel`a-Ascoli und Montel 61

19 Der Riemannsche Abbildungssatz 63

Inhaltsverzeichnis

20 Homotope Wege 65

21 Der Abelsche Grenzwertsatz 67

22 Die Euler-Maclaurinsche Summenformel 69

23 Die Riemannsche Zetafunktion 73

4

1 Komplexe Differenzierbarkeit

Erinnerung: Komplexe Zahlen

(a) z=x+iy, w=u+iv∈C, wobeix, y, u, v ∈R. Dannz+w= (x+u) +i(y+v) und zw= (xu−yv) +i(xv+yu).

(b) Furz=x+iymitx, y∈Rbezeichnet manxals Realteil undyals Imaginarteil von z, in Zeichen x = Rez, y = Imz. Die zu z komplex konjugierte Zahl ist z=x−iy.

(c) In C verwenden wir die Norm |z|=p

(Rez)²+ (Imz)²=√ zz.

(d) C ist ein normierter R-Vektorraum. Also konnen Grenzuberlegungen kompo- nentenweise fur Real- und Imaginarteil durchgefuhrt werden. Das ist aber nur in der Anfangsphase notwendig.

(e) Wegen (d) sind topologische Begrie wie \Stetigkeit", \glmg. Stetigkeit" usw.

klar.

1.1 Definition. (a) Sei U ⊂ C oen. Eine Funktion f: U → C heit komplex die- renzierbar inz ∈U, wenn

limh→0

f(z+h) −f(z) h

existiert. Falls er existiert, so bezeichnet man ihn mitf⁰(z).

(b) fheit holomorph inU, wennfin jedem Punkt ausUkomplex dierenzierbar ist.

Manche Leute sagen auch analytisch anstelle von holomorph.

1.2 Satz. Sei U ⊂ C oen. Dann ist f genau dann komplex dierenzierbar in z∈U, wenn es ein L∈C und eine Funktion ψ: {h |z+h∈U}→C gibt, so dass

(a) limh→0ψ(h) =0,

(b) f(z+h) −f(z) =Lh+ψ(h)h fur alle h.

1.3 Bemerkung. Mit genau denselben Beweisen wie in der Analysis I erhalt man (a) Ist f komplex dierenzierbar in z, so ist fstetig in z.

1 Komplexe Dierenzierbarkeit (b) Ist f konstant, so f⁰ =0.

(c) Sind f,g und h komplex dierenzierbar in z mit h(z)6=0, so gelten furα∈C beliebig

(f+g)⁰(z) =f⁰(z) +g⁰(z), (αf)⁰(z) =αf⁰(z), (fg)⁰(z) =f⁰(z)g(z) +f(z)g⁰(z),

f h

⁰

(z) = f⁰(z)h(z) −f(z)h⁰(z) h(z)² . (d) (g^◦f)⁰(z) =g⁰(f(z))f⁰(z), falls fin z und g in f(z) komplex dierenzierbar.

1.4 Satz. Seien U, V ⊂C oen, sei f: U→V holomorph und bijektiv, sei f⁰(z)6=0 fur alle z∈U und sei f⁻¹: V →U stetig. Dann ist f⁻¹ holomorph und

f⁻¹⁰

(w) = 1

f⁰(f⁻¹(w)) fur alle w∈V.

1.5 Bezeichnung. ι: C →R², x+iy7→ (^xy), ist ein R-linearer Homoomorphismus mit kι(z)k₂ =|z|. Wir schreibenU^ι und z^ι fur ι(U) und ι(z).

1.6 Definition. Sei M ⊂ C oen, sei f: M → C, setze u(x, y) = Ref(x +iy) und v(x, y) = Imf(x+iy). Dann bezeichnet man f^ι: M^ι → R², (^xy) 7→

u(x,y) v(x,y)

als das zu fgehorige Vektorfeld.

Die partiellen Ableitungen von u nach x und y bezeichnet man mit ux und uy, dito fur v.

fheit reell dierenzierbar in z, wenn f^ι in z^ι dierenzierbar (im Sinne der Ana- lysis II) ist.

Das ist genau dann der Fall, wenn es eine Matrix A ∈ R^2×2 und eine Abbildung Ψ:{ξ∈R² |ξ+z^ι ∈M^ι}→R² gibt, so dass

f^ι(z^ι+ξ) =f^ι(z^ι) +Aξ+Ψ(ξ) und lim

ξ→0

kΨ(ξ)k kξk =0.

In diesem Fall ist A=J_f^ι(z^ι).

1.7 Satz. Fur fwie oben gilt:f ist genau dann inz komplex dierenzierbar, wenn f^ι in z^ι reell dierenzierbar ist und ux(z^ι) =vy(z^ι) und uy(z^ι) = −vx(ι). In diesem Fall

J_f^ι(z^ι) = Ref⁰(z) −Imf⁰(z) Imf⁰(z) Ref⁰(z)

!

f⁰(z) =u_x(z^ι) +iv_x(z^ι) =u_x(z^ι) −iu_y(z^ι) =v_y(z^ι) +iv_x(z^ι).

1.8 Beispiel. Die Abbildung z7→z ist nicht holomorph.

6

1.9 Bemerkung. (a) Das Dierentialgleichungssystem u_x =v_y, u_y = −v_x bezeich- net man als Cauchy-Riemannsches Dierentialgleichungssystem.

(b) Man deniert noch die beiden folgenden Dierentialoperatoren:

∂f

∂z = 1 2

∂f

∂x −i∂f

∂y

und ∂f

∂z = 1 2

∂f

∂x +i∂f

∂y

.

1.10 Lemma. Eine reell dierenzierbare Abbildung f: G→C ist genau dann kom- plex dierenzierbar, wenn ^∂f_∂z =0. In diesem Fall ist ^∂f_∂z =f⁰.

1.11 Definition. Ein Gebiet ist eine zusammenhangende, oene Menge in C.

Erinnerung: Ein metrischer RaumXheit zusammenhangend, wenn ausX=A∪B fur disjunkte oene Mengen Aund B bereits A=∅ oder B=∅ folgt.

Ein metrischer Raum heit wegzusammenhangend, wenn es zu je zwei Punkten x, y∈X eine stetige Abbildung γ: [0, 1]→X mit γ(0) =x und γ(1) =y gibt.

In der Analysis II oder der Analysis III wird gezeigt: Jeder wegzusammenhangende Raum ist zusammenhangend, und fur oene Teilmengen des Rⁿ gilt auch die Um- kehrung.

Daher ist es in der Denition des Gebietes unerheblich, wenn das Wort \zusam- menhangend" durch das Wort \wegzusammenhangend" ersetzt wird.

1.12 Korollar. Es seiG⊂Cein Gebiet und es sei f: G→Cholomorph mitf⁰(z) =0 fur alle z∈G. Dann ist f konstant.

1.13 Bezeichnung. Wir identizierenCmit demR-VektorraumR² und versehenCmit dem Skalarprodukt hz, wi=xu+yv=Re(zw), wenn z =x+iy und w=u+iv fur x, y, v, w∈R.

1.14 Lemma. Seien z, w ∈C^∗ = C\ {0}. Sie stehen genau dann senkrecht aufein- ander, wenn _w^z rein imaginar ist.

1.15 Definition. Eine bijektive R-lineare Abbildung T:C→C heit winkeltreu, wenn hTw, Tzi

|Tw||Tz| = hw, zi

|w||z| fur alle z, w∈C^∗.

1.16 Lemma. Fur eine bijektive R-lineare Abbildung T: C→C sind aquivalent:

(a) T: C→C ist winkeltreu.

(b) Wenn z und w senkrecht aufeinander stehen, dann auch Tz und Tw. (c) Es gibt a ∈ C^∗, so dass entweder Tz = az fur alle z ∈ C oder Tz = az fur

alle z ∈C.

1 Komplexe Dierenzierbarkeit

(d) Es gibt s > 0, so dass hTz, Twi=shz, wi fur alle z, w∈C.

1.17 Definition. SeiD⊂Coen. Eine reell dierenzierbare Abbildungf: D→Cheit winkeltreu, wenn die reelle Ableitung Df: C→C in jedem Punkt aus D winkeltreu ist.

1.18 Lemma. Ist f: D→C oder f: D→C holomorph mit f⁰(z)6=0 fur alle z∈D, so ist f winkeltreu.

1.19 Definition. f: G→C heit antiholomorph, wenn fholomorph ist.

Bemerkung. f ist genau dann antiholomorph, wenn ^∂f_∂z =0.

1.20 Satz. SeiG⊂C ein Gebiet. Es sei f: G→C reell dierenzierbar mit stetiger Ableitung. Es sind aquivalent

(a) f ist winkeltreu in G.

(b) f⁰(z)6=0 fur alle z∈G und fist holomorph oder antiholomorph in ganz G. 1.21 Bemerkung. Wir hatten in der Analysis I den Begri der Potenzreihe ein- gefuhrt. Ich wiederhole die wichtigsten Aussagen. Wir setzen B_ρ(z₀) = {z ∈ C |

|z−z₀|< ρ}.

Eine Potenzreihe ist eine Reihe der Form P_∞

n=0a_n(z−z₀)ⁿ, a_n, z₀ ∈ C. Zu jeder Potenzreihe existiert ein r ∈ [0,∞) ∪ {∞}, so dass die Reihe fur alle z ∈ B_r(z₀) konvergiert und fur alle z mit |z −z₀| > r divergiert. Die Zahl r bezeichnet man als Konvergenzradius der Reihe. Fur jedesρ < r konvergiert die Reihe gleichmaig und absolut in B_ρ(z₀). Insbesondere deniert die Potenzreihe eine stetige Funktion auf B_r(z₀). Der Konvergenzradius kann beispielsweise mit der Formel von Hadamard bestimmt werden

r= 1

lim supn→∞ ⁿ

p|a_n|. 1.22 Satz. Sei f(z) = P_∞

n=0a_n(z−z₀)ⁿ eine Potenzreihe mit Konvergenzradius r. Dann gelten:

(a) f ist komplex dierenzierbar in Br(z0) mit f⁰(z) =P_∞

n=1nan(z−z0)ⁿ⁻¹. Der Konvergenzradius dieser Reihe ist ebenfalls r.

(b) Fur jedes k∈N ist f k-mal stetig dierenzierbar in B_r(z₀) mit f^(k)(z) =

X∞ n=k

n(n−1). . .(n−k+1)a_n(z−z₀)^n−k.

(c) Fur alle n∈N gilt f⁽ⁿ⁾(z0) =n!an.

8

1.23 Bezeichnung. Jede komplexe Zahl kann dargestellt werden als z = re^iϕ mit r ∈ [0,∞) und ϕ∈(−π, π]. Der Winkel ϕist das Argument von z.

Visualisierung

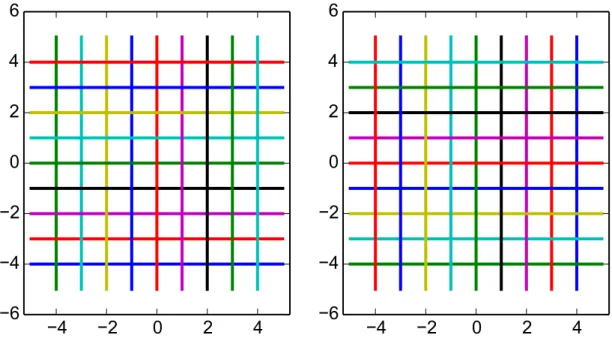
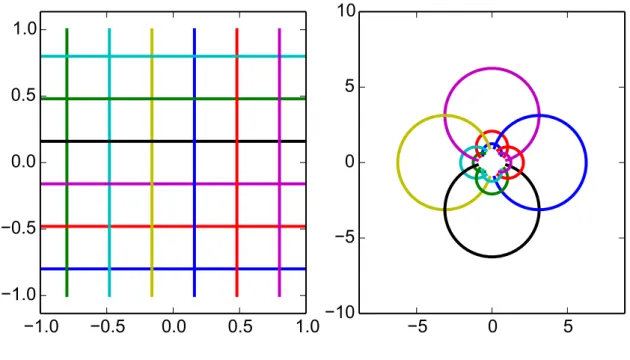
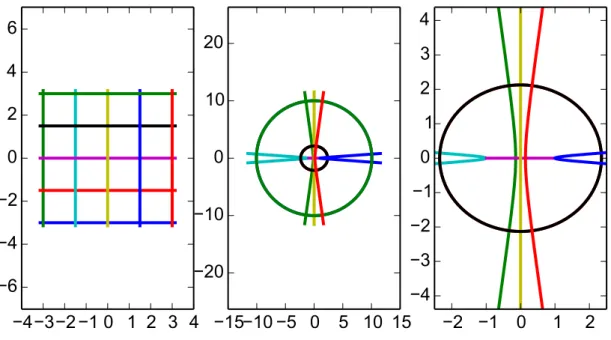
(a) Man zeigt das Bild eines Gitters in Cunter f. Das bezeichne ich als konformes Bild von f. Es ist vor allem nutzlich in Bereichen, in denen fbijektiv ist.

(b) Man zeigt den Graph von |f| als Funktion von Rez und Imz und farbt in Abhangigkeit vom Argument ein. Ich nenne das einen r-ϕ-Plot.

1.24 Beispiel. Polynome sind holomorph. Die Ableitung von z 7→ P_d

n=0a_nzⁿ ist Pd

n=1na_nzⁿ⁻¹. Die Visualisierung der Identitat zeigt Abbildung 1.1.

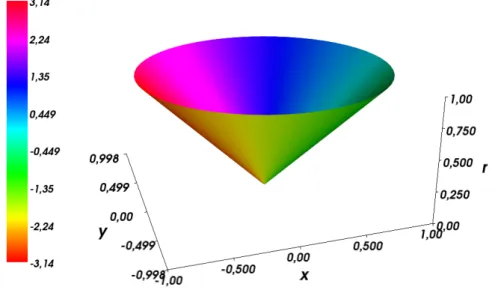
Die Multiplikation mit i entspricht einer Drehung um eine Viertelkreis. Den r-ϕ- Plot zeigt Abbildung 1.2, den konformen Plot zeigt Abbildung 1.3.

Den r-ϕ-Plot der Quadratfunktion zeigt Abbildung 1.4, den der Kubikfunktion zeigt Abbildung 1.5.

Gebrochen rationale Funktionen sind dort holomorph, wo ihre Nenner nicht ver- schwinden. Den r-ϕ-Plot von z 7→ ¹_z zeigt Abbildung 1.6, den konformen Plot zeigt Abbildung 1.7.

1.25 Beispiel. Die Exponentialfunktionf(z) =exp(z)ist holomorph wegen Satz1.22.

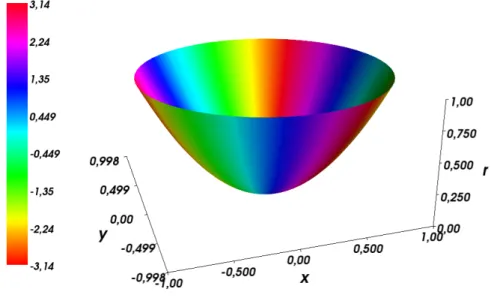
Den r-ϕ-Plot der Exponentialfunktion zeigt Abbildung 1.8, den konformen Plot zeigt Abbildung 1.9.

Den r-ϕ-Plot des Sinus zeigt Abbildung 1.8, den konformen Plot zeigt Abbil- dung 1.9.

1 Komplexe Dierenzierbarkeit

Abbildung 1.1:r-ϕ-Graph der Identitat

Abbildung 1.2:r-ϕ-Graph von z7→iz

10

4 2 0 2 4 6

4 2 0 2 4 6

4 2 0 2 4

6 4 2 0 2 4 6

Abbildung 1.3: Die Funktion z7→iz

Abbildung 1.4:r-ϕ-Graph von z7→z²

1 Komplexe Dierenzierbarkeit

Abbildung 1.5:r-ϕ-Graph von z7→z³

Abbildung 1.6:r-ϕ-Graph vonz 7→ ¹_z

12

1.0 0.5 0.0 0.5 1.0 1.0

0.5 0.0 0.5 1.0

5 0 5

10 5 0 5 10

Abbildung 1.7: Die Funktion z7→ ¹_z

Abbildung 1.8:r-ϕ-Graph der Exponentialfunktion

1 Komplexe Dierenzierbarkeit

4 3 2 1 0 1 2 3 4 4

2 0 2 4

30 20 10 0 10 20 30 30

20 10 0 10 20 30

Abbildung 1.9: Die Exponentialfunktion

Abbildung 1.10:r-ϕ-Graph des Sinus

14

4 3 2 1 0 1 2 3 4 6

4 2 0 2 4 6

15 10 5 0 5 10 15 20

10 0 10 20

2 1 0 1 2

4 3 2 1 0 1 2 3 4

Abbildung 1.11: Der Sinus

2 Wegintegrale

2.1 Definition. Sei f: [a, b] → C eine Funktion, fur welche Ref und Imf Riemann- integrierbar sind. Wir setzen

Zb a

f(t)dt = Zb

a

Ref(t)dt+i Zb

a

Imf(t)dt.

2.2 Bemerkung. Fur fund gmit Riemann-integrierbaren Real- und Imaginarteilen, ζ∈C und a < b < c gelten

(a) R_b

a(f(t) +g(t))dt=R_b

af(t)dt+R_b

ag(t)dt, (b) R_b

aζf(t)dt=ζR_b

af(t)dt, (c) R_c

af(t)dt =R_b

af(t)dt+R_c

bf(t)dt.

2.3 Definition. (a) Eine Funktion γ: [a, b] → C ist ein stuckweiser C¹-Weg, wenn es Zahlen a₀ =a < a₁ < a₂ <· · ·< a_n =b, > 0 und Funktionen g_j: (a_j−1− , a_j+)→C von der Klasse C¹ gibt, so dass γ_j=g_j|[a_j−1, a_j] furj=1, . . . , n. (b) Ein Weg γ: [a, b]→C heit geschlossen, wenn γ(a) =γ(b).

Statt C kann der Zielbereich auch der Rⁿ fur ein n ∈ N sein. Oenbar sind stuckweise C¹-Wege stetig. Polygonzuge sind Beispiele fur stuckweise C¹-Wege.

2.4 Definition. Sei U ⊂ C oen, sei f: U → C stetig und sei γ: [a, b] → U ein stuckweiserC¹-Weg wie in Denition2.3. Man deniert das Integral vonfentlang γ

als Z

γ

f= Z

γ

f(z)dz= Xn

j=1

Zaj

aj−1

f(γ(t))γ⁰(t)dt.

Man bezeichnet dieses Integral auch als Wegintegral.

2.5 Beispiel. f(z) = (z−z₀)^m, z ∈ C\ {z₀}, m ∈ Z, r > 0, γ: [0, 2π] → C\ {z₀}, γ(t) =z₀+re^it. Dann

Z

γ

f= Z2π

0

f(γ(t))γ⁰(t)dt= Z2π

0

r^me^imtrie^itdt=i Z2π

0

r^m+1e^i(m+1)tdt=

0, m 6= −1, 2πi, m = −1.

2 Wegintegrale

2.6 Beispiel. Wir integrieren ¹_z uber den Rand des Quadrats mit den Ecken 1, −i,

−1undi in mathematisch negativer Richtung. Den Weg denieren wir alsγ: [0, 4]→ C\ {0}},

γ(t) =













−ti+1−t, 0≤t < 1,

−(t−1) + (2−t)(−i), 1≤t < 2, (t−2)i− (3−t), 2≤t < 3, (t−3) + (4−t)i, 3≤t ≤4.

Dann Z

γ

dz z =

Z4 0

1

γ(t)γ⁰(t)dt= Z4

0

u(t) +i Z4

0

v(t)dt fur

u(t) =













2t−1

2t²−2t+1, 0≤t < 1,

2t−3

2t²−6t+5, 1≤t < 2,

2t−5

2t²−10t+13, 2≤t < 3,

2t−7

2t²−14t+25, 3≤t ≤4,

und v(t) =













−1

2t²−2t+1, 0≤t < 1,

−1

2t²−6t+5, 1≤t < 2,

−1

2t²−10t+13, 2≤t < 3,

−1

2t²−14t+25, 3≤t≤4.

Wir bestimmen Stammfunktionen Uj von u|(j−1,j) und Vj von v|(j−1,j)

U_j(t) =













1

2log 2t²−2t+1

, j=1,

1

2log 2t²−6t+5

, j=2,

1

2log 2t²−10t+13

, j=3,

1

2log 2t²−14t+25

, j=4,

und V_j(t) =













−arctan(2t−1), j=1,

−arctan(2t−3), j=2,

−arctan(2t−5), j=3,

−arctan(2t−7), j=4.

Man uberzeugt sich nun, dass U_j(j) −U_j(j−1) = 0 und V_j(j) −V_j(j−1) = −^π₂ fur j=1, 2, 3, 4. Damit haben wir gezeigt

Z

γ

dz

z = −2πi.

2.7 Definition. Es sei U ⊂ C oen und es seien f, F: U → C zwei Funktionen. Man bezeichnet F als Stammfunktion von f, wennF⁰ =f.

2.8 Satz. (a) Es sei D ⊂C ein Gebiet. Die Funktion f: D→C besitze Stamm- funktionen F und G. Dann ist F−G konstant.

(b) Es sei U⊂C oen, es sei f: U→C stetig mit Stammfunktion F und es sei γ: [a, b]→U ein stuckweiser C¹-Weg. Dann gilt

Z

γ

f=F(γ(b)) −F(γ(a)).

Speziell gilt R

γ =0, falls γ geschlossen ist.

18

Die beiden Beispiele zeigen, dass es im Gegensatz zum reellen Fall nicht immer eine Stammfunktion gibt.

2.9 Bemerkung. Seiγ: [a, b]→C ein stuckweiser C¹-Weg mita₀, . . . , a_n wie in der Denition. Seine Lange ist gleich

Xn j=1

Zaj

aj−1

|γ⁰(t)|dt.

Das entspricht der Lange von γ, wie sie in der Analysis II deniert worden war, wenn manγ als Weg im R² auffasst.

2.10 Lemma. (a) Sei g: [a, b]→C eine stetige Funktion. Dann

Z_b

a

g(t)dt

≤ Z_b

a

|g(t)|dt.

(b) Sei U⊂C oen, sei γ: [a, b]→U stuckweise C¹, sei fstetig in U und sei L die Lange von γ. Dann

Z

γ

f

≤L max

z∈γ([a,b])|f(z)|.

2.11 Bemerkung. Eigenschaften des Wegintegrals: Fur c, d∈C, f, g: U→ C stetig und einen stuckweisen C¹-Wegγ: [a, b]→U gelten

(a) C-Linearitat: R

γ(cf+dg) =cR

γf+dR

γg.

(b) Wennγ⁻ der zuγentgegengesetzte Weg ist, alsoγ⁻(t) =γ(b+a−t),t ∈[a, b], dann R

γ⁻f= −R

γf.

(c) Anderung der Parametrisierung andert den Wert nicht: Sei g: [a₁, b₁] → R von der Klasse C¹ mit g([a1, b1]) ⊂ [a, b], g(a1) = a und g(b1) = b, dann R

γf=R

γ◦gf.

(d) Dierentiation unter dem Integral: Sei V ⊂Cebenfalls oen, seif: U×V →C stetig und fur jedes ζ ∈ U sei die Funktion z 7→ f(ζ, z) in V holomorph mit Ableitung f_z(ζ, z). Die Abbildung f_z: U×V →C sei ebenfalls stetig. Dann ist die Funktion G(z) =R

γf(ζ, z)dζ holomorph mit G⁰(z) =R

γf_z(ζ, z)dζ.

3 Die Umlaufzahl

3.1 Definition. Sei U⊂Coen. Auf U wird wie folgt eine Aquivalenzrelation erklart:

z₁, z₂ ∈ U sind aquivalent, wenn es einen stuckweisen C¹-Weg in U gibt, der z₁ und z₂ verbindet.

Die Aquivalenzklassen von Uheien Wegzusammenhangskomponenten von U. 3.2 Bemerkung. (a) Fur oenes U sind auch alle Wegzusammenhangskomponen-

ten oen.

(b) Sei γ ein geschlossener stetiger Weg. Dann existiert genau eine unbeschrankte Wegzusammenhangskomponente von C\Bild(γ).

3.3 Definition. Sei γ ein geschlossener, stuckweiser C¹-Weg, sei a /∈ Bild(γ). Dann bezeichnet man

Indγ(a) = 1 2πi

Z

γ

1 z−adz als Index oder Umlaufzahl vonγ bezuglich a.

3.4 Satz. Sei γ ein geschlossener, stuckweiser C¹-Weg, sei w /∈Bild(γ). (a) Indγ(w)∈Z.

(b) Indγ ist konstant in jeder Wegzusammenhangskomponente von C\Bild(γ). (c) Indγ ≡ 0 in der unbeschrankten Wegzusammenhangskomponente von C\

Bild(γ).

3.5 Bezeichnung. Mit ∂B⁺_R(a) bezeichnen wir den Weg γ: [0, 2π] → C, t 7→ a+Re^it. Entsprechend bezeichnet ∂B⁻_R(a) denselben Weg in umgekehrter Richtung.

3.6 Beispiel.

Ind∂B⁺_r(z₀)(a) =

0, |z₀−a|> r, 1, |z₀−a|< r.

3.7 Definition. Seienγ₁, . . . , γ_nstuckweiseC¹-Wege inCundm₁, . . . , m_n∈Z. Formale Summen der Form T = P_n

j=1m_jγ_j heien Ketten. Sie heien Zyklen, wenn alle γ_j geschlossen sind.

3 Die Umlaufzahl

Die Ketten bilden eine abelsche Gruppe, wenn man alle Ketten der FormPn j=10γ_j mit 0 sowie −γ mit γ⁻ identiziert.

3.8 Definition. Es sei T =Pn

j=1m_jγ_j eine Kette. Dann deniert man (a)

Z

T

f= Xn

j=1

m_j Z

γj

f.

(b) Bild(T) =

n

[

j=1 mj6=0

Bild(γ_j).

Ist T sogar ein Zyklus, so setzt man fur z /∈Bild(T) IndT(z) = 1

2πi Z

T

dζ ζ−z =

Xn j=1

m_jIndγj(z).

3.9 Definition. Ein Weg γ: [a, b] → C lauft in einem Gebiet G von Rand zu Rand, wenn folgende Bedingungen erfullt sind

(a) es gibt a≤t₁ < t₂ ≤bmit γ(t₁), γ(t₂)∈∂G und γ(t₁)6=γ(t₂), (b) fur alle t ∈(t₁, t₂) gilt γ(t)∈G,

(c) fur alle t ∈[a, b]\[t1, t2] gilt γ(t)∈/ G,

(d) G\Bild(γ) hat genau zwei Wegzusammenhangskomponenten, und Bild(γ)∩G liegt auf dem Rand dieser beiden Komoponenten.

3.10 Satz. γ: [a, b] → C ein geschlossener, stuckweiser C¹-Weg, B = B_r(z₀) eine Kreisscheibe. γ laufe in B von Rand zu Rand. Seien t₁ und t₂ wie in 3.9, seien z =γ(t₁) und w=γ(t₂). Der Teilweg γ|[t1,t2] werde mit γ₀ bezeichnet, sei σ der positive orientierte Rand von B, sei σ₁ der Kreisbogen von w nach z und σ₂ der Kreisbogen von z nach w, beide in der Durchlaufrichtung von σ. B₁ und B₂ seien die Wegkomponenten von B\Bild(γ), wobei Bild(σ_j)⊂∂B_j, j=1, 2. Dann gilt fur beliebige z1 ∈B1 und z2∈B2

Indγ(z₁) =Indγ(z₂) +1.

22

4 Kompakte Mengen

Ich wiederhole die Begrie \kompakt" und \Haufungspunkt" aus der Analysis III von Herrn Singhof.

4.1 Definition. Ein metrischer RaumX heit kompakt, wenn jede Uberdeckung vonX durch oene Teilmengen eine endliche Teiluberdeckung besitzt.

4.2 Definition. Sei (x_n)_n∈N eine Folge in einem metrischen Raum X. Dann heit a ∈ X Haufungspunkt von (x_n)n∈N, wenn (x_n)n∈N eine Teilfolge besitzt, die gegen a konvergiert.

4.3 Definition. Sei X ein metrischer Raums. Fur j ∈ J sei a_j ∈ X. Man bezeichnet (a_j)j∈J als -Netz von X, wenn X⊂S

j∈JB(a_j).

4.4 Definition. Der Durchmesser einer beschrankten MengeA⊂X ist gleich sup{d(x, y)|x, y∈A}.

4.5 Definition. Sei (U_j)j∈J eine oene Uberdeckung von K. Wenn es ein λ > 0 gibt, so dass alle Teilmengen von K mit Durchmesser < λ in wenigstens einem U_j enthalten sind, dann bezeichnet man λ als Lebesgue-Zahl der Uberdeckung.

Beispiel. Durch U₀ = (−∞, 1) und U_j = (j −1, j+ ¹_j) fur j ∈ N wird eine oene

Uberdeckung(U_j)j∈N0vonRgegeben. Sie besitzt weder eine endliche Teiluberdeckung noch eine Lebesguezahl.

4.6 Satz. Fur einen metrischen Raum X sind gleichwertig:

(a) X ist kompakt.

(b) Jede Folge in X besitzt einen Haufungspunkt in X.

(c) Jede oene Uberdeckung von X besitzt eine Lebesgue-Zahl, und X besitzt zu jedem > 0 ein endliches -Netz.

(d) Wenn (A_j)j∈J ein System abgeschlossener Mengen in X mit T

j∈JA_j =∅ ist, dann gibt es eine endliche Teilmenge{j₁, . . . , j_n}vonJ, so dass Tn

k=1A_jk =∅.

4 Kompakte Mengen

Beispiel. Es sei Xirgendeine unendliche Menge, die mit der diskreten Metrik verse- hen ist

d(x, y) =

0, x=y, 1, x6=y.

Dann ist ({x})x∈X eine oene Uberdeckung von X. Sie besitzt die Lebesguezahl ¹₂, aber X besitzt kein endliches -Netz, falls < 1.

Bemerkung. In der Vorlesung von Herrn Singhof wurde auerdem noch gezeigt, dass die Kompaktheit von X aquivalent ist zu

(e) X ist vollstandig und besitzt zu jedem > 0 ein endliches -Netz.

Eine Teilmenge K eines metrischem Raums X ist genau dann kompakt, wenn sie kompakt ist als metrischer Raum, versehen mit der Einschrankung der Metrik vonX. Daher kann man den Satz auch wie folgt schreiben:

4.7 Korollar. Fur eine Teilmenge K eines metrischen Raums X sind gleichwertig:

(a) Jede oene Uberdeckung von K besitzt eine endliche Teiluberdeckung.

(b) Jede Folge in K besitzt einen Haufungspunkt in K.

(c) Wenn (A_j)j∈J ein System abgeschlossener Mengen in X mit K∩T

j∈JA_j=∅ ist, dann gibt es eine endliche Teilmenge {j₁, . . . , j_n} von J, so dass K∩ Tn

k=1A_jk =∅.

4.8 Satz (Heine-Borel). K ⊂ R^N ist genau dann kompakt, wenn K abgeschlossen und beschrankt ist.

4.9 Korollar. Die kompakten Intervalle sind genau die Intervalla [a, b] mit a, b ∈ R, a≤b.

4.10 Satz. Seien X, Y metrische Raume, f: X → Y stetig und K ⊂ X kompakt.

Dann ist f(X) kompakt.

Damit ist der folgende Satz gezeigt, der bereits in der Analysis II von Herrn Singhof bewiesen worden war.

4.11 Satz. Sei K eine beschrankte und abgeschlossene Teilmenge des Rⁿ und sei f: K→R stetig. Dann nimmt f auf K ihr Maximum und ihr Minimum an.

24

5 Der Cauchysche Integralsatz f¨ ur konvexe Mengen

5.1 Definition. Ein Dreiecksweg ist ein Weg γ: [a, b] →C, fur den es a=a₁ < a₂ <

a₃ < a₄ =b gibt, so dassγ(a) =γ(b) und γ|[aj−1,aj] an ist und fur den die konvexe Hulle von{γ(a₁), γ(a₂), γ(a₃)}in U liegt.

5.2 Satz(Satz von Goursat). Sei U⊂C oen, sei f holomorph in U und sei γ ein Dreiecksweg in U. Dann R

γf=0.

5.3 Satz (Satz von Goursat, punktierte Form). Sei U ⊂ C oen, sei p ∈ U, sei f stetig in U und holomorph in U\ {p} und sei γ ein Dreiecksweg in U. Dann R

γf=0.

5.4 Lemma. Sei U ⊂ C oen und konvex und sei f stetig in U. Wenn fur jeden Dreiecksweg γ in U gilt R

γf=0, dann besitzt f eine Stammfunktion in U. 5.5 Satz (Cauchyscher Integralsatz fur konvexe Mengen). Sei U⊂C oen und kon- vex, sei p∈U, sei f stetig in U und holomorph in U\ {p}. Dann gelten:

(a) f besitzt eine Stammfunktion in U. (b) R

γf=0 fur jeden geschlossenen, stuckweisen C¹-Weg in U.

5.6 Satz (Cauchysche Integralformel fur konvexe Mengen). Sei U ⊂ C oen und konvex, sei f holomorph in U, sei γ ein geschlossener stuckweiser C¹-Weg in U und sei z ∈U\Bild(γ). Dann

(a) f(z)Indγ(z) = 1 2πi

Z

γ

f(ζ) ζ−zdζ.

(b) Fur alle n∈N ist f n-mal stetig komplex dierenzierbar mit f⁽ⁿ⁾(z)Indγ(z) = n!

2πi Z

γ

f(ζ) (ζ−z)ⁿ⁺¹dζ.

5.7 Korollar. SeiU⊂Coen, seifholomorph inU. Dann istfbeliebig oft komplex dierenzierbar.

5 Der Cauchysche Integralsatz fur konvexe Mengen 5.8 Beispiel. Sei γ irgendein Weg mit Indγ(0) =1.

Z

γ

sin(ζ)

ζ⁶ dζ= 2πi 5!

5!

2πi Z

γ

sin(ζ)

(ζ−0)⁶ = 2πi

5! Indγ(0)sin⁽⁵⁾(0) = πi 60.

5.9 Satz (Satz von Morera). Sei U ⊂C oen, sei f: U→ C stetig. Falls fur jeden Dreiecksweg γ in U gilt R

γf=0, so ist f holomorph in U.

5.10 Satz (Cauchysche Abschatzungsformel). Sei f holomorph in B_r(z₀) und sei 0 < ρ < r. Dann gilt fur jedes n∈N0

f⁽ⁿ⁾(z₀) ≤ n!

ρⁿ sup

|z−z₀|=ρ

|f(z)|.

5.11 Definition. Eine auf C holomorphe Funktion heit ganz.

5.12 Satz (Liouville). Ist f ganz und beschrankt, so ist f konstant.

5.13 Lemma. Es sei f ein Polynom vom Grad m ≥1. Dann existieren > 0 und R > 0, so dass fur alle z∈C mit |z| ≥R gilt |f(z)| ≥|z|^m.

5.14 Theorem (Fundamentalsatz der Algebra). Jedes Polynom vom Grad m ≥ 1 besitzt mindestens eine komplexe Nullstelle.

5.15 Bemerkung. Mittels Polynomdivision folgt per vollstandiger Induktion: Zu je- dem Polynom vom Grad m existieren a, z1, . . . , zm ∈ C, a 6= 0, so dass f(z) = aQ_m

j=1(z−zj).

26

6 Der Cauchysche Integralsatz

6.1 Definition. Es sei U⊂C oen.

(a) Ein ZyklusT inUheit nullhomolog inU, (i. Z.T ∼0), wenn fur jedesa∈C\U gilt IndT(a) =0.

(b) Zwei ZyklenT₁undT₂inUheien homolog inU(i. Z.T₁∼T₂), wennT₁−T₂ ∼0. (c) Ein Gebiet G⊂C heit einfach zusammenhangend, wenn jeder Zyklus in G

nullhomolog in Gist.

6.2 Beispiel. (a) U = C \ B_R(0). T = ∂B⁺₁(R + 2) ist nullhomolog in U, aber S = ∂B⁺_R+1(0) ist nicht nullhomolog in U. Speziell ist U nicht einfach zusam- menhangend.

(b) Sternformige Gebiete sind einfach zusammenhangend.

(c) C\(−∞, 0] ist sternformig.

6.3 Lemma. SeiV ⊂Coen, seiXein kompakter metrischer Raum, seig: X×V → Cstetig. Falls fur jedes x∈Xdie komplexe Ableitung g_zvonz 7→g(x, z)existiert, so ist die Funktion g_z stetig auf X×V.

6.4 Satz. Seien U, V ⊂ C oen, sei f: U×V → C stetig und fur jedes ζ ∈ U sei die Funktion z 7→ f(ζ, z) in V holomorph mit Ableitung f_z(ζ, z). Dann ist die Funktion G(z) =R

γf(ζ, z)dζ holomorph mit G⁰(z) =R

γfz(ζ, z)dζ. Fur einen Zyklus T =P_n

j=1m_jγ_j denieren wir BildT =Sn

j=1Bildγ_j.

6.5 Theorem (Cauchyscher Integralsatz). Sei U ⊂C oen, sei f holomorph auf U, sei T ein nullhomologer Zyklus in U. Dann gelten

(a) Fur alle z∈U\Bild(T): f(z)IndT(z) = 1 2πi

Z

T

f(ζ) ζ−zdζ. (b)

Z

T

f=0.

6.6 Satz (Causchysche Integralformel). Sei U ⊂ C oen, sei f holomorph in U, sei T nullhomolog in U und sei z /∈Bild(T). Dann gilt fur alle n∈N⁰

f⁽ⁿ⁾(z)IndT(z) = n!

2πi Z

T

f(ζ) (ζ−z)ⁿ⁺¹dζ.

6 Der Cauchysche Integralsatz

6.7 Satz. Sei G ⊂ C ein Gebiet und sei f holomorph in G. Wenn fur jeden geschlossenen, stuckweisen C¹-Wegγ inG gilt R

γf=0, dann besitzt f in G eine Stammfunktion F. Wenn w∈G beliebig, aber fest gewahlt ist, dann gilt

F(z) = Z

γ

f fur jeden Weg γ von w nach z.

6.8 Korollar. Sei G ein einfach zusammenhangendes Gebiet und sei f holomorph in G. Dann besitzt f eine Stammfunktion.

28

7 Der komplexe Logarithmus

7.1 Definition. Nach Korollar 6.8 gibt es genau eine holomorphe Funktion f: C \ (−∞, 0] → C mit f⁰(z) = ¹_z fur alle z und f(1) = 0. Diese Funktion bezeichnet man als den Hauptzweig des komplexen Logarithmus, i. Z. log(z).

7.2 Bemerkung. (a) Fur z∈C\(−∞, 0] existiert ϕ∈(−π, π), so dass z =|z|e^iϕ. Damit gilt fur den Hauptzweig des Logarithmus logz=log|z|+iϕ. Hierbei ist log|z|der aus der Analysis I bekannte reelle Logarithmus.

(b) Fur z ∈C\(−∞, 0] gilt exp(logz) =z.

(c) Fur z ∈C mit |Imz|< π gelten e^z∈C\(−∞, 0] und log(e^z) =z.

7.3 Definition. SeiG⊂C\{0}ein Gebiet. Eine stetige Funktionf: G→Cheit Zweig des Logarithmus, wenn exp^◦f=idG.

7.4 Bemerkung. SeienG₁, G₂ ⊂C\ {0}zwei Gebiete, in denen jeweils ein Zweig des Logarithmus erklart ist. Seien f₁ und f₂ diese Zweige.

(a) Zu jedem z ∈G1∩G2 existiert einmz∈Z, so dass f2(z) =f1(z) +2πimz. (b) Wenn z1 und z2 in derselben Wegzusammenhangskomponente von G1∩G2 lie-

gen, dann m_z1 =m_z2.

7.5 Satz. Sei G⊂C\ {0} ein Gebiet. Dann sind gleichwertig (a) Auf G existiert ein Zweig des Logarithmus.

(b) Auf G besitzt ¹_z eine Stammfunktion.

(c) Fur jeden geschlossenen, stuckweisen C¹-Weg γ in G gilt Indγ(0) =0. Speziell besitzt jedes einfach zusammenhangende Gebiet G ⊂ C\ {0} einen Zweig des Logarithmus.

7.6 Bemerkung. Mit log: C\(−∞, 0] →C werde der Hauptzweig des Logarithmus bezeichnet.

(a) Fur jedes z ∈C\(−∞, 0] gilt log

1 z

= −log(z).

7 Der komplexe Logarithmus

(b) Fur jedes w ∈ C\(−∞, 0] wird durch z 7→ log(zw) −log(w) ein Zweig des Logarithmus auf G={z∈C|zw /∈(−∞, 0]} gegeben.

(c) Fur z = ^√1

2(−1+i) gilt logz = ³₄πi, aber logz² =log(−i) = −¹₂πi.

30

8 Reihen holomorpher Funktionen

8.1 Definition. SeienX,Y metrische Raume, sei (f_n)n∈N eine Folge stetiger Funktionen f_n: X→Y. Die Folge konvergiert kompakt in X, wenn fur jede kompakte Teilmenge K⊂X die Folge der Einschrankungen(f_n|K)n∈N gleichmaig inK konvergiert.

Eine Reihe P_∞

n=1f_n konvergiert kompakt, wenn die Folge ihrer Partialsummen kompakt konvergiert.

8.2 Bemerkung. (a) Gleichmaige Konvergenz impliziert kompakte Konvergenz.

(b) Sei f_n: C\ {0}, f_n(z) = _nz¹. Dann f_n →0 kompakt.

(c) Sei X ein metrischer Raum derart, dass jeder Punkt x ∈ X eine kompakte Umgebung besitzt. Das ist beispielsweise der Fall, wennXeine oene Teilmenge des Rⁿ oder bereits selber kompakt ist. Wenn alle f_n: X → Y stetig sind und die Folge (f_n)n∈N kompakt gegen f konvergiert, dann ist auch fstetig.

(d) Aus einem Satz der Analysis I folgt die kompakte Konvergenz der Potenzreihen im Inneren ihres Konvergenzkreises.

8.3 Satz. Es sei U⊂C oen und fur n∈Nsei fn: U→C stetig. Die Folge (fn)n∈N

konvergiere kompakt auf U gegen f.

(a) Sei γ ein stuckweiser C¹-Weg in U. Dann

nlim→∞

Z

γ

fn = Z

γ

f.

(b) Wenn alle f_n sogar holomorph sind, dann ist auch fholomorph und (f_n⁰)_n∈N konvergiert kompakt gegen f⁰.

8.4 Korollar. Sei U ⊂ C oen, sei P_∞

n=1f_n eine Reihe holomorpher Funktionen, die kompakt in U konvergiert. Dann istf=P_∞

n=1f_n holomorph mit f⁰ =P_∞

n=1f_n⁰. 8.5 Satz (Identitatssatz fur Potenzreihen). Sei M ⊂ C eine Menge mit Haufungs- punkt z₀. Die Potenzreihen f(z) = P_∞

n=0a_n(z−z₀)ⁿ und g(z) = P_∞

n=0b_n(z−z₀)ⁿ seien in M konvergent, und es gelte f|M =g|M. Dann a_n=b_n fur alle n∈N0.

9 Die Taylorsche Entwicklung

9.1 Satz. Sei U ⊂ C oen, sei z₀ ∈ U. Setze r = ∞, wenn U = C, und r = minz /∈U|z₀ −z| sonst. Sei f: U → C holomorph. Dann existiert eine eindeutig bestimmte Folge (an)n∈N0 in C, so dassf(z) =P_∞

n=0an(z−z0)ⁿ fur alle z∈Br(z0). (Speziell betragt der Konvergenzradius der Potenzreihe mindestensr.) Fur jedes n∈N⁰ gilt

a_n = f⁽ⁿ⁾(z₀) n! .

9.2 Bemerkung. Aus der Cauchyschen Abschatzungsformel folgt fur ρ < r

|a_n| ≤ 1 ρⁿ sup

|z−z₀|=ρ

|f(z)|.

9.3 Beispiel. (a) e^z=

X∞ n=0

zⁿ

n!, cos(z) = X∞

n=0

(−1)ⁿ z²ⁿ

(2n)!, sin(z) = X∞ n=0

(−1)ⁿ z²ⁿ⁺¹ (2n+1)!. (b)

1

1+z² = 1

1− (−z²) = X∞

n=0

(−1)ⁿz²ⁿ. Der Konvergenzradius ist 1.

(c) Sei f: U → C ein Zweig des Logarithmus mit 1 ∈ U. Dann gilt fur alle z mit

|z−1|< 1

f⁰(z) = 1

z = 1

1− (1−z) = X∞ n=0

(1−z)ⁿ= X∞ n=0

(−1)ⁿ(z−1)ⁿ. Also folgt durch Integration

f(z) =f(1) + X∞ n=0

(−1)ⁿ

n+1(z−1)ⁿ⁺¹ =f(1) + X∞

n=1

(−1)ⁿ⁻¹

n (z−1)ⁿ.

Falls es sich beifum den Hauptzweig handelt, istf(1) =0. Der Konvergenzra- dius betragt1, unabhangig von der Wahl von U. Das zeigt, dass das raus dem Satz nur eine untere Abschatzung fur den Konvergenzradius ist.

9 Die Taylorsche Entwicklung

9.4 Satz (Identitatssatz). Sei G⊂ C ein Gebiet, seien f, gG → C holomorph. Sei M⊂G eine Menge, die einen Haufungspunkt in G besitzt. Falls f(z) =g(z) fur alle z ∈M, so gilt f=g.

Bemerkung. Aus dem Identitatssatz folgt, dass die weiter vorne denierten Funktio- nen exp, sin und cos die einzigen holomorphen Funktionen sind, die mit den auf R denierten Funktionen gleichen Namens ubereinstimmen.

34

10 Die Laurentsche Entwicklung

10.1 Definition. M ⊂ C, f_n: M → C fur alle n ∈ Z. Die Reihe P_∞

n=−∞f_n heit konvergent in z ∈M, wenn die Reihen P_∞

n=0f_n und P_∞

n=1f_−n in z konvergieren. In diesem Fall schreibt man P_∞

n=−∞fn=P_∞

n=0fn+P_∞

n=1f−n.

Analog deniert man absolute, gleichmaige bzw. kompakte Konvergenz der Reihe P_∞

n=−∞f_n.

Reihen der FormP_∞

n=−∞a_n(z−z₀)ⁿ heien Laurentreihen. In diesem Fall bezeich- net man P₋₁

n=−∞a_n(z−z₀)ⁿ als Hauptteil und P_∞

n=0a_n(z−z₀)ⁿ als Nebenteil.

10.2 Beispiel. Fur |z|>|z₀| gilt 1

z−z₀ = 1 z

1

1−z₀/z = 1 z

X∞ n=0

z₀ z

n

= X∞ n=0

zⁿ₀ zⁿ⁺¹ =

X−1 m=−∞

z^−m−1₀ z^m.

10.3 Definition. Fur z₀ ∈C, 0≤r₂ < r₁ ≤∞ bezeichnet man RG(z₀, r₁, r₂) ={z ∈C| r₂<|z−z₀|< r₁} als Ringgebiet.

10.4 Bemerkung. (a) P−1

n=−∞a_n(z−z₀)ⁿ konvergiert genau dann in z, wenn die Reihe P_∞

n=1a−nwⁿ in w =1/(z−z0) konvergiert. Sei r der Konvergenzradius der Potenzreihe P_∞

n=1a−nwⁿ. Dann:

(i) Fur allezmit|z−z0|> ¹_r konvergiert die ReiheP₋₁

n=−∞an(z−z0)ⁿabsolut.

(ii) Fur alle z mit |z−z0|< ¹_r divergiert die Reihe P₋₁

n=−∞an(z−z0)ⁿ. (b) SeiP_∞

n=−∞a_n(z−z₀)ⁿeine Laurentreihe. Der Konvergenzradius ihres Nebenteils betrage R, der Konvergenzradius von P_∞

n=1a−nwⁿ sei r. Dann konvergiert die Laurentreihe kompakt in RG(z0, R,¹_r).

10.5 Satz(Laurentsche Entwicklung). f sei holomorph im Ringgebiet RG(z₀, r₁, r₂). (a) Es existiert eine eindeutig bestimmte Folge (a_n)n∈Z, so dass fur alle z ∈

RG(z0, r1, r2)

f(z) = X∞ n=−∞

a_n(z−z₀)ⁿ. (b) Fur r₂ < r < r₁ und n∈Z gilt

a_n = 1 2πi

Z

∂B⁺r(z0)

f(ζ)

(ζ−z₀)ⁿ⁺¹dζ.

10 Die Laurentsche Entwicklung

10.6 Beispiel. (a) f(z) = _z(z−1)⁻¹ ist holomorph aufU=C\{0, 1}. Zum Entwicklungs- punkt z₀ = 0 gibt es zwei verschiedene Entwicklungen in zwei verschiedenen Ringgebieten.

Furz ∈RG(0, 1, 0) gilt

f(z) = 1 z

1

1−z = 1 z

X∞ n=0

zⁿ= X∞ n=−1

zⁿ.

Furz ∈RG(0,∞, 1) gilt

f(z) = −1 z

1

z−1 = −1 z²

1

1−1/z = −1 z²

X∞ n=0

1 z

n

= − X−2 n=−∞

zⁿ.

(b) g(z) =e^z+e^1/z. Fur z∈RG(0, 0,∞) gilt g(z) =

X∞ n=0

zⁿ n! +

X∞ n=0

1

zⁿn! =1+ X∞ n=−∞

zⁿ

|n|!.

36

11 Residuenkalk¨ ul

11.1 Beispiel. Berechne Z

∂B⁺₂(0)

1

(z−5)(z²+1)dz.

Dazu bestimmen wir die Partialbruchzerlegung des Integranden 1

(z−5)(z²+1) = 1

26(z−5) − 1+5i

52(z−i) − 1−5i 52(z+i).

Also Z

∂B⁺₂(0)

1

(z−5)(z²+1)dz =2πi

−1+5i

52 −1−5i 52

= −πi 13. 11.2 Definition. Es sei f(z) = P_∞

n=−∞a_n(z − z₀)ⁿ eine Laurentreihe im Ringgebiet RG(z0, , 0). Dann bezeichnet man a−1 als Residuum von f in z0 und schreibt Resz0(f).

Bemerkung. Fur jedes ρ∈(0, ) gilt Resz0(f) = 1

2πi Z

∂B⁺_ρ(z0)

f(z)dz.

11.3 Satz (Residuensatz). Sei U ⊂ C oen, sei A = {z1, . . . , zn} ⊂ U, sei T ein nullhomologer Zyklus in U mit A∩Bild(T) = ∅ und sei f holomorph in U\A. Dann

1 2πi

Z

T

f= Xn

k=1

IndT(z_k)Reszk(f).

11.4 Bemerkung. (a) Es seif(z) =P_∞

j=−ma_j(z−z₀)^j in RG(z₀, r, 0), wobei m∈N.

Dann

Resz0(f) = 1

(m−1)!_zlim_→z

z6=z₀0

d^m−1

dz^m−1((z−z₀)^mf(z)).

(b) f(z) = _h(z)^g(z), wobei g und h holomorph in einer Umgebung von z0 sind mit h(z0) =0 und h⁰(z0)6=0. Dann

Resz0(f) = g(z₀) h⁰(z0).

11 Residuenkalkul

11.5 Beispiel. In Beispiel 11.1 hatten wir g(z) = 1, h(z) = (z−5)(z²+1) = (z− 5)(z−i)(z+i), U = B₃(0), z₁ = i und z₂ = −i. Dann h⁰(z) = (z−i)(z+i) + (z− 5)(z+i) + (z−5)(z−i), also

Resi(f) = 1

h⁰(i) = 1

(i−5)2i = 1

−2−10i, Res−i(f) = 1

−2+10i

und Z

∂B⁺₂(0)

1

(z−5)(z²+1)dz=2πi

1

−2−10i + 1

−2+10i

= −πi 13.

11.6 Satz. Es sei f eine rationale Funktion (d. h. Quotient zweier Polynome), deren Nenner keine reellen Nullstellen hat. Der Grad des Nenners sei um min- destens 2 groer als der Grad des Zahlers. Seien z₁, . . . , z_n die paarweise ver- schiedenen Nullstellen des Nenners in der oberen Halbebene {Imz > 0}. Dann

Z_∞

−∞

f(x)dx=2πi Xn

k=1

Reszk(f).

11.7 Beispiel. Berechne Z_∞

−∞

x² 1+x⁴dx.

f = ^g_h fur g(z) = z² und h(z) = 1+ z⁴. Die Voraussetzungen sind erfullt. Fur ω=e^iπ/4= ^√1

2+^√i

2 liegen die Nullstellen vong beiω,ω³, ω⁵ undω⁷. Davon liegen ω und ω³ in der oberen Halbebene.

g(ω) =ω² =i, h⁰(ω) =4ω³ =4iω g(ω³) =ω⁶ = −i, h⁰(ω³) =4ω⁹ =4ω.

Resω(f) +Resω³(f) = i

4iω− i 4ω = 1

4 e^−iπ/4−e^iπ/4

= i 2sin

−π 4

= − i 2√

2.

Also Z_∞

−∞

x²

1+x⁴dx=2πi

− i 2√

2

= π

√2.

Man kann diese Aufgabe auch mit Partialbruchzerlegung losen. Dazu benotigt man die Primfaktorzerlegung des Nenners in R[X]:

1+x⁴ = (1+

√

2x+x²)(1−

√

2x+x²).

11.8 Satz. Es sei P(v, w) eine rationale Funktion in den beiden komplexen Varia- blen v und w. Es sei

f(z) =P

z²−1

2iz ,z²+1 2z

.

38

Auf ∂B₁(0) sollen keine Nullstellen des Nenners von f liegen. Dann Z2π

0

P(sin(t),cos(t))dt= Z

∂B⁺₁(0)

f(z) iz dz.

11.9 Beispiel. Es seia > 1. Berechne Z2π

0

dx a+cos(x). Setze P(v, w) = _a+w¹ . Dann

f(z) =P

z²−1

2iz ,z²+1 2z

= 1

a+^z2_2z⁺¹ = 2z z²+2az+1

und f(z)

iz = −2i

z²+2az+1. Die Nullstellen des Nenners liegen bei z₁ = −a+√

a²−1 und z₂ = −a−√

a²−1. Wegen z₁z₂ = 1 ist eine der beiden Zahlen vom Betrag her kleiner und eine vom Betrag her groer als 1, also z₂ <−a < −1 < z₁ < 0. Mit der Formel von oben

Resz1

f(z) iz

= −2i

2z₁+2a = −2i

−2a+2√

a²−1+2a = −i

√

a²−1.

Schlielich Z_2π

0

dx

a+cos(x)dx= 2π

√a²−1.

Maple16 behauptet, die folgende Funktion sei eine Stammfunktion von _a+cos¹ _(x)

F(x) =

2arctan (a−1)tan ^x₂

√a²−1

!

√a²−1 .

Leider ist F in x =π aber unstetig. sympy in Version 0.7.5 ndet folgendes Ergebnis F(x) =

1 q−a−1

a−1 (a−1)

log − r

−a+1

a−1+tanx 2

!

−log r

−a+1

a−1 +tanx 2

!!

.

Diese Funktion ist ebenfalls unstetig. Maple kann das bestimmte Integral berechnen, sympy nicht.

12 Das Nullstellenz¨ ahlintegral und der Satz von Rouch´ e

12.1 Definition. z₀ heit Nullstelle von f, wennf(z₀) =0.

SeiG⊂Cein Gebiet, seifholomorph inG, seifnicht die Nullfunktion, seiz₀∈G. Man sagt, f habe in z0 eine Nullstelle der Ordnung m ∈ N, wenn die Taylorreihe von f in z0 die Form f(z) =P_∞

n=man(z−z0)ⁿ mit am 6=0 besitzt.

12.2 Bemerkung. (a) Fur Polynome stimmt dieser Begri mit dem aus der Alge- bra uberein.

(b) z₀ist genau dann Nullstelle der Ordnungmvonf, wenn es eine inGholomorphe Funktion h gibt mit h(z₀)6=0, so dass f(z) = (z−z₀)^mh(z) fur alle z∈G. 12.3 Satz. Sei U ⊂ C oen, sei γ ein geschlossener, stuckweiser C¹-Weg, der nullhomolog in U ist, so dass C\Bild(γ) aus genau zwei Wegzusammenhangs- komponenten besteht. Die unbeschrankte der beiden heie A2, die andereA1. Es gelte Indγ(z) =1 fur allez∈A1. Ferner seif: U→Ceine holomorphe Funktion, die keine Nullstellen in Bild(γ) besitzt. Dann ist

1 2πi

Z

γ

f⁰ f

gleich der Anzahl der Nullstellen von f in A₁ unter Berucksichtigung der Viel- fachheiten.

12.4 Satz(Satz von Rouche). SeiU⊂Coen, sei γ ein geschlossener, stuckweiser C¹-Weg, der nullhomolog in U ist, so dass C\Bild(γ) aus genau zwei Wegzu- sammenhangskomponenten besteht. Die unbeschrankte der beiden heie A₂, die andere A₁. Es gelte Indγ(z) = 1 fur alle z ∈ A₁. Es seien f, g: U → C zwei holomorphe Funktionen, so dass fur alle z ∈ Bild(γ) gilt |f(z)| > |g(z)|. Dann besitzen f und f+g in A₁ gleich viele Nullstellen unter Berucksichtigung der Vielfachheiten.

12.5 Beispiel. (a) Sei p(z) =Pm

j=0a_jz^j ein Polynom vom Grad m. Sei R > max

m−j

sm|a_j|

|a_m|

0≤j < m

.

12 Das Nullstellenzahlintegral und der Satz von Rouche

Dann besitzt p in B_R(0) genau m Nullstellen unter Berucksichtigung der Viel- fachheiten. Da wir aus der Algebra wissen, dass pnicht mehr alsm Nullstellen hat, liegen folglich alle Nullstellen in B_R(0).

In Lemma 5.13 hatten wir eine ahnliche, aber weniger scharfe Abschatzung gezeigt.

(b) p(z) = z⁵ −4z+2. Setze f(z) = −4z +2, g(z) = z⁵ und γ = ∂B⁺₁(0). Fur z ∈∂B₁(0) gelten |f(z)| ≥ 2 und |g(z)| =1. Also besitzt p in B₁(0) genau eine Nullstelle. Nach Teil (a) gilt fur alle Nullstellenz, dass|z| ≤√⁴

20. Das lasst sich aber verbessern, wenn man wahlt f(z) =z⁵, g(z) = −4z+2 und γ=∂B⁺_5/3(0). Fur z mit |z| = ⁵₃ gelten namlich |f(z)| = ³¹²⁵₂₄₃ und |g(z)| ≤ ²⁶₃. Also liegt eine Nullstelle von pin B₁(0) und vier Nullstellen liegen in RG(0,⁵₃, 1).

42

13 Isolierte Singularit¨ aten

13.1 Definition. z₀ heit isolierte Singularitat vonf, wenn es ein > 0 gibt, so dassf holomorph in B(z₀)\ {z₀} ist.

13.2 Bemerkung. (a) f(z) = ¹_z und g(z) =e^1/z besitzen in 0 eine isolierte Singula- ritat.

(b) Sei z₀ eine isolierte Singularitat von f. Dann gibt es ein > 0, so dass f in RG(z₀, , 0) eine Laurentreihe

f(z) = X∞ n=−∞

an(z−z0)ⁿ (13.1)

besitzt.

13.3 Definition. Eine isolierte Singularitat heit

(a) hebbar, wenn in (13.1) alle Laurentkoefzienten zu negativen Exponenten ver- schwinden,

(b) Pol der Ordnung m∈N, wenn a_n=0 fur alle n < −m und a_−m 6=0, (c) wesentlich in allen anderen Fallen.

13.4 Beispiel. (a) f(z) = ^sin_z^(z) besitzt in0 eine hebbare Singularitat, denn ^sinz^(z) = P_∞

n=0(−1)ⁿ_(2n+1)!^z2n .

(b) f(z) = ^sin_z5^(z) besitzt in0einen Pol4-ter Ordnung, denn ^sin_z^5(z) =P_∞

n=0(−1)^{n z}_(2n+1)!²ⁿ⁻⁴ . (c) e^1/z besitzt in 0 eine wesentliche Singularitat, denne^1/z =P0

n=−∞ zⁿ (−n)!.

13.5 Bemerkung. (a) Sei m ∈N. Eine holomorphe Funktion f in RG(z₀, r, 0) hat genau dann inz₀ einen Pol der Ordnungm, wenn es eine in B_r(z₀) holomorphe Funktion h gibt mit f(z) = (z−z₀)^−mh(z) und h(z₀)6=0.

(b) Wenn f in z₀ ein Nullstelle der Ordnung m besitzt, dann besitzt ¹_f in z₀ einen Pol der Ordnung m und umgekehrt.

13.6 Satz (Riemannscher Hebbarkeitssatz). z0 ist genau dann eine hebbare Singu- laritat von f, wenn es r > 0 gibt, so dass f in RG(z0, r, 0) beschrankt ist.

13 Isolierte Singularitaten

13.7 Satz. Eine in RG(z₀, r, 0) holomorphe Funktion f besitzt genau dann in z₀ einen Pol der Ordnung m, wenn es δ, C > 0 gibt, so dass fur alle z∈RG(z₀, δ, 0) gilt _C¹|z−z₀|^−m ≤ |f(z)| ≤C|z−z₀|^−m.

Definition. Eine TeilmengeAeines metrischen RaumsXheit dicht inX, wennA=X, wenn es also zu jedem x∈X eine Folge in Agibt, die gegen x konvergiert.

13.8 Satz (Casorati-Weierstra). z₀ sei eine wesentliche Singularitat von f, und f sei holomorph in U=RG(z₀, r, 0). Dann ist f(U) dicht in C.

13.9 Beispiel. f(z) = e^1/z. Sei w ∈ C\ {0}. Dann existiert λ ∈ C mit e^λ = w. Fur z_n = _λ+2πin¹ gelten limn→∞z_n =0 und f(z_n) =w.

Den folgenden Satz gebe ich nur zur Abrundung an. Einen Beweis ndet man in Remmert und Schumacher, Band 2, Kapitel 10, x4.

13.10 Satz (Groer Satz von Picard). Sei z₀ eine wesentliche Singularitat von f. Dann nimmt f in jeder Umgebung von z₀ jeden Wert mit hochstens einer Aus- nahme unendlich oft an.

44