Traglast und optimale Bemessung von Platten

Research Collection

Working Paper

Traglast und optimale Bemessung von Platten

Author(s):

Wolfensberger, Rudolf Publication Date:

1964

Permanent Link:

https://doi.org/10.3929/ethz-a-000747192

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more

information please consult the Terms of use.

Traglast

und optimale ^Bemessung

von

Platten

R.

Wolfensberger

/ bk

Archivexemplar:

Bild und Grafik, ^{Standort E 36.1}

Zürich 1964

Bericht Nr. 2

Traglast

und optimale Bemessung

von Platten

von

R. WOLFENSBERGER, ^Dt.

^techn.

Technische Forschungs- ^und Beratungsstelle ¹⁹⁶⁴

der Schweizerischen Zementindustrie, Wildegg

Leer

Vide

Empty

Vorwort

Die üblichen Methoden

Berechnung

Stahlbetonplatten ^basieren

auf der Elastizitätstheorie. Für einfache Fälle liegen analytische ^Metho¬

den

Im allgemeinen ^müssen jedoch numerische Verfahren oder

Modellmessungen angewendet ^{werden. Neben den} Schwierigkeiten

dieser Methoden stellt sich im weiteren die Frage ^ihrer Zweckmäßigkeit.

Es scheint wenig ^{sinnvoll, das} Tragvermögen ^einer Stahlbetonplatte ^auf

Grund einer nominellen Spannungsspitze

^{oft rein} lokaler Bedeu¬

tung ^beurteilen

^müssen.

Daher sind Methoden entwickelt worden, ^die das unelastische Material¬

verhalten in der Bestimmung ^der Tragfähigkeit

berücksichtigen

suchen. Die Plastizitätstheorie hat gezeigt, ^{daß das} vornehmlich intuitiv

hergeleitete Bruchlinien-Verfahren obere Grenzwerte der Traglast ^liefert

und somit

einer Überschätzung ^der Tragfähigkeit führen kann. Bisher ist noch keine allgemeine Methode bekannt geworden,

für Platten

untere

Grenzwerte der Traglast

^bestimmen.

In der vorliegenden Arbeit wird eine solche Methode hergeleitet. ^Das

Problem ist

formuliert worden, daß die mathematische Methode der linearen Programmierung

Lösung herangezogen werden kann.

Letztere wird heute bereits umfassend auf dem Gebiete des «Operation

Research» angewendet ^und

^allem

Lösung

Wirtschaftspro¬

blemen herangezogen. ^In der Technik und im speziellen ⁱⁿ der Baustatik hat sie bisher wenig Bedeutung gefunden. ^{Es ist aber}

erwarten, daß sie in vermehrtem Maße

Behandlung der Probleme über die Traglast

und die optimale Bemessung herangezogen werden muß.

Institut für Baustatik (Abteilung ^Massivbau) Eidgenössische ^Technische Hochschule, ^Zürich

1. Juni ¹⁹⁶⁴ Prof. Dr. Bruno Thürlimann

Die vorliegende Arbeit wurde

Verfasser

Institut für Baustatik

(Abteilung Massivbau) ausgearbeitet und als Dissertation eingereicht.

An dieser Stelle möchte

dem Referenten, ^{Herrn Prof.} Dr. B. Thürli¬

mann, für seine wertvollen Ratschläge bestens danken. Herrn Prof. Dr.

H. Ziegler ^dankt

^{für die Übernahme des} Korreferats, ^{sowie für seine} ständige Anteilnahme

Fortgang ^der Abhandlung. Der «Technischen

Forschungs- ^und Beratungsstelle ⁱⁿ Wildegg» ^{und der} «Stiftung ^für systematische wissenschaftliche Forschungen ^auf dem Gebiete des Betons und des Eisenbetons» ist

für die Drucklegung dieser Arbeit

Dank verpflichtet.

R. Wolfensberger

Inhaltsverzeichnis

/.

Einleitung ⁷

2.

Grundlagen ⁹

2.1 Voraussetzungen ⁹

2.2 Grenzwertsätze 12

2.3 Übersicht der bestehenden Arbeiten 14

3. Generelle Gedanken

Vorgeben ¹⁶

3.1 Bestimmung ^der Traglast ¹⁶

3.2 Bestimmung ^der optimalen Armierung ²⁴

3.3 Zusammenfassung ³³

4.

Plastizitätsbedingungen ³⁴

4.1 Plastifizierung ^eines Plattenbereichs 34

4.2 Orthogonale Armierung ³⁴

4.2.1 Plastizitätsbedingungen ³⁴

4.2.2 Lineare Plastizitätsbedingungen ⁵⁰

4.2.3

Graphische Darstellung ^der Plastizitätsbedingungen ⁵²

4.3 Armierung

beliebiger Richtung ⁵⁸

4.3.1 Plastizitätsbedingungen

4.3.2 Allgemeine ^lineare Plastizitätsbedingungen ⁶⁷

5.

Gleichgewichtszustände für ^{Platten 68}

5.1 Gleichgewichtsbedingungen ⁶⁸

5.2 Randbedingungen ⁷²

5.2.1 Freier Rand 72

5.2.2 Einfach gelagerter ^Rand

5.2.3 Eingespannter ^{Rand 75}

5.3 Gleichgewichtszustände ^für spezielle Belastungsverteilung ⁷⁶

5.3.1 Voraussetzungen ⁷⁶

5.3.2

Endlichfach

System

5.3.3 Näherung des Momentenverlaufes 78

6.

Erfüllen ^der Plastizitätsbedingungen ⁸⁰

7.

Traglast

^Platte (Analysis) ⁸²

7.1 Lösungsweg

7.2

Fehlerbetrachtungen ⁸³

7.3 Beispiel ⁸⁵

8.

Minimalarmierung

^Platte (Bemessung) ⁹⁹

8.1 Lösungsweg ⁹⁹

8.2 Fehlerbetrachtungen ¹⁰²

9. Zusammenstellung ^der berechneten Beispiele ¹⁰³

10. Scblußbemerkmg ¹¹⁰

//.

Anhang ¹¹²

11.1 Einschreiben und Umschreiben der Momentenfläche 112 11.2 Lösung ^{des linearen} Programms

Hilfe eines speziellen

Maschinenprogramms ¹¹³

11.3 Genauigkeit ^der Lösung ^{eines linearen} Programms ¹¹⁵

1. Einleitung

Die meisten der heute bekannten Lösungen

Berechnung ^der Trag¬

fähigkeit ^einer Stahlbetonplatte ^{beruhen auf} der Bruchlinientheorie. Die

erste

wichtige ^Arbeit darüber hat Johansen [1; ^S. 277] ^im Jahre ¹⁹³²

veröffentlicht. Drucker, Greenberg, Prager, Hodge [2, 3,4] ^{und Hill} [5]

gelang ^{es, die beiden} fundamentalen Grenzwertsätze der Plastizitäts¬

theorie aufzustellen und

beweisen. Anhand dieser Sätze kann gezeigt werden, daß alle auf der Bruchlinientheorie aufgebauten Lösungen ^eine Belastung ergeben, ^die größer ^oder gleich ^der Traglast ^{ist und daher im} allgemeinen ^die Traglast überschätzt.

Zur Berechnung ^der Traglast ^ist

notwendig, die tatsächlich auftretende

Bruchlinienkonfiguration

^{finden. Fast alle}

^{Arbeiten beschäf¬}

tigen sich mit dieser Aufgabe. Es hat sich gezeigt, ^{daß dies in einfachen}

Fällen schwierig ^{und in} komplizierten ^Fällen praktisch unmöglich ^ist.

In den meisten Veröffentlichungen ^sind

^stark vereinfachte Bruch¬

linienbilder angegeben. ^{So findet}

^{z.B. für die} Traglast einer total

eingespannten Quadratplatte mit oben und

in

und y-Richtung gleicher Armierung ^mit Bruchlinien

längs ^der Diagonalen ^{eine Be-}

48 mp

lastung

Dagegen ^hat neulich Wood [6; ^S. 177] ^{für eine}

/2

37,7 Mp

Brachlinienkonfiguration ^eine Belastung

angegeben. ^Der

/2 Unterschied der beiden Belastungen beträgt 27,5%.

Die vorliegende ^{Arbeit hat}

Ziel, ^eine Berechnungsmethode ^für

Platten

entwickeln mit Resultaten, ^{die in} bezug ^{auf die} Traglast ^auf

der sicheren Seite liegen. ^{Wird eine} grobe Berechnung durchgeführt,

erhält

ein Resultat, ^{das relativ weit}

^der Traglast ^{entfernt ist,}

aber sie dennoch unterschätzt. Mit einer Verfeinerung ^der Berechnungs¬

methode kann

beliebig genau die exakte Lösung ^annähern.

Als zweites wird gezeigt, daß durch kleine Umformungen ^der aufgestell¬

ten

Methode die minimale Armierung einer Platte für eine gegebene ^Be¬

lastung gefunden werden kann. Die gegebene Belastung liegt ^nicht

höher als die Traglast ^{der Platte mit der} gefundenen Armierung. ^Die

Lösung liegt demnach ebenfalls auf der sicheren Seite.

2. Grundlagen

2.1 Voraussetzungen

Die wichtigsten Voraussetzungen

Ermittlung ^der Traglast ^{nach der}

einfachen Plastizitätstheorie sind:

a) ^Die Deformationen (vor ^dem Kollaps) ^sollen

^{klein sein, daß die} Gleichgewichtsbedingungen

undeformierten System befriedigt

werden können (wie bei elastischer Behandlung).

b) ^Es dürfen keine Instabilitäten

Erreichen der Traglast ^auftreten (wie bei elastischer Behandlung).

c) Die Einflüsse

Quer- und Normalkräften werden vernachlässigt.

d) ^Es

^statische Beanspruchungen ^auf (keine Wechselbean¬

spruchungen).

e) ^{Die Lasten müssen im} allgemeinen proportional ^zunehmen.

f) ^Das Material muß plastisch verformbar sein (Rotationsfähigkeit).

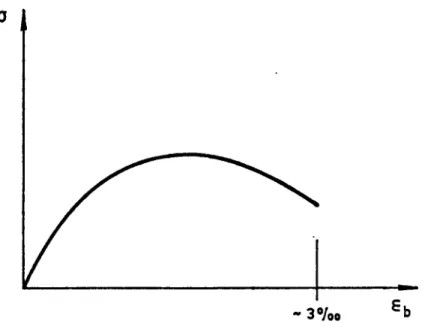
of-

Abb. 2.1 Spannungs-Dehnungs-Diagramm ^eines naturharten Armierungsstahles

(außerhalb ^der Einschnürungszone)

Abb. 2.2 Spannungs-Dehnungs-Diagramm

^Beton

^einer Biegebeanspru¬

chung

Im folgenden soll noch näher auf den Punkt f eingegangen werden. Den

Betrachtungen ^{werden die} Spannungs-Dehnungs-Diagramme ^für

harten Armierungsstahl ^{und Beton} (Abb. ^{2.1 und} 2.2) zugrundegelegt.

In Abb. 2.3 ist das M-0 -Diagramm für einen normal armierten Stahl¬

betonquerschnitt dargestellt.

I ^Normales

'¦• t/h

Abb. 2.3 M-0-Diagramm ^eines Stahlbetonquerschnittes

Es zeigt ^{die Relation} zwischen Moment und Krümmung. ^{Bei Vernach¬}

lässigung ^des Verfestigungsbereiches ^und

^{der Annahme, daß der}

Hebelarm _r\ h der inneren Kräfte konstant ist, geht ^{das M-0 -Dia¬}

gramm

Abb. 2.3 in dasjenige

^{Abb. 2.4 über. Dies} entspricht gut einer normal armierten Stahlbetonplatte.

m/m,

1.o jf/jrfp

Abb. 2.4 Ideal-elastisch-plastisches ^M-

-Diagramm

Das M- ₀ -Diagramm in Abb. 2.4 stellt ein elastisch-ideal-plastisches ^Ver¬

halten dar. Durch Vernachlässigung der elastischen gegenüber ^den pla¬

stischen Verformungen ^erhält

^ein starr-ideal-plastisches ^Verhalten (Abb. 2.5).

Die Gültigkeit der Plastizitätstheorie

ein ideal-plastisches ^Verhalten

der Materialien

Dies trifft sowohl für elastisch-ideal-plastisches

wie für starr-ideal-plastisches ^Material

^In normalen Fällen genügt

jedoch,

die maximale Krümmung ^{0 ein} Vielfaches der Vergleichs¬

krümmung 0P erreicht (Abb. 2.3). ^Im Stahlbau wird das Verhältnis

0J0p durch Instabilität beschränkt [7]. ^Im Stahlbetonbau tritt bei

m/m,

1 ^-

t/h

Abb. 2.5 Starr-ideal-plastisches M-0-Diagramm

stark armierten Querschnitten frühzeitig ein Stauchen der Betondruck¬

zone

ein. Durch Begrenzen ^des Armierungsgehaltes fimax kann dies

hindert werden. Ein schlagartiger Bruch kann durch einen minimalen

Armierungsgehalt /*»» vermieden werden.

Ein solches Versagen ^{kann eintreten,}

das Rißmoment des homo¬

genen Betonquerschnittes ^bei Einrechnung ^der Zugfahigkeit ^{des Betons} größer ^{ist als das} plastische ^{Moment des} gerissenen Stahlbetonquer¬

schnittes.

2.2 Gren%rvertsäti?e ^der Plastizitätstheorie

Die strenge Lösung ^eines Plattenproblems ^{nach der} Plastizitätstheorie ist im allgemeinen ^kaum möglich. Nur in ganz speziellen ^Fällen gelingt ^es,

die statischen und die kinematischen Bedingungen ^über den ganzen

Plattenbereich

erfüllen. Aus diesem Grund kommt den beiden Grenzwertsätzen eine große praktische Bedeutung

Mit ihrer Anwen¬

dung gelingt ^{es, die} Traglast ^eines Systems

beiden Seiten her einzu¬

schränken. Fallen die beiden Schranken _zusammen,

kennt

^die exakte Lösung.

Die beiden Grenzwertsätze lauten nach [8], [9]:

1. Grenzwertsatz (unterer Grenzwert)

Jede Belastung, %u der sich ein stabiler, ^statisch zulässiger Spannungszustand

geben läßt, liegt nicht hoher als die Traglast.

Eine solche Belastung stellt also eine

Schranke für die Traglast dar; ^sie liegt ^noch innerhalb bzw.

der Grenze der Tragfähigkeit ^des Systems.

2. Grenzwertsatz (oberer Grenzwert)

Jede Belastung, zj* der sich ^ein instabiler, kinematisch zulässiger Bewegungszu¬

stand angeben läßt, liegt ^nicht tiefer ^{als die} Traglast.

Eine solche Belastung stellt also eine obere Schranke für die Traglast dar; ^sie liegt außerhalb bzw.

der Grenze der Tragfähigkeit ^des Sy¬

stems.

Die

emgeführten Begriffe sollen noch kurz beschrieben werden.

Eine ausführliche Erklärung ^{ist in} [8] ^und [9]

^finden.

Ein Spannungszustand wird als statisch zulässig bezeichnet,

^einer Gruppe

äußeren und inneren Kräften jeder Teil des betrachteten

Systems ^im Gleichgewicht ^{ist. Ein solcher} Spannungszustand wird stabil genannt,

^{keinem Ort die} Plastizitätsbedingungen ^verletzt

den.

Ein Bewegungszustandwird als kinematisch zulässig bezeichnet,

^mit

den Bindungen ^des Tragwerkes verträglich ^{ist. Ein solcher} Bewegungs¬

zustand wird instabil genannt,

^die Leistung der äußeren Lasten

gleich (oder größer) ^{ist als die} Dissipationsleistung.

In dieser Arbeit werden ausschließlich

Grenzwerte der Traglast gesucht. ^Demnach benötigt

^{den 1.} Grenzwertsatz. Dieser kann in einer anschaulicheren Form folgendermaßen angeschrieben ^werden:

1. Grenzwertsatz (unterer Grenzwert)

Jede Belastung, zf* der sich ^ein möglicher Gleichgewichtszustandfinden läßt, ^dessen Schnittkräfte ^die Plastizitätsbedingungen

keinem Punkt verletzen, ^{ist kleiner}

oder höchstens gleich ^der Traglast.

2.3 Übersicht der bestehenden Arbeiten

Um die Traglast ^{einer Platte}

^bestimmen, existieren heute schon

schiedene Berechnungsmethoden. ^{Es würde}

^{weit fuhren, auf alle}

diese verschiedenen Verfahren einzugehen. ^{Im Buch}

^{Wood [6] fin¬}

det

darüber sehr ausführliche Hinweise mit nützlichen Vergleichen

und Diskussionen.

In Tafel I wird versucht, die verschiedenen Theorien schematisch

ordnen. Darin sind die bis heute bekannten Verfahren mager ^umrandet.

Die Lösungsmethoden ^{mit linearem} Programm, die erstmals in dieser

Arbeit behandelt werden, besitzen eine fette Umrandung.

I Elastizitätstheorie Fließbedingungen

Plastizitätsbedingungen

Lösungen

Programm Bemessung; Bestimmung

optimalen Armierung

PlastizitätstheoriefürPlatten

Strenge Lösungen Näherungen

Lösungen

geschlossener

Gerade

Bruchlinien,

Analysis; Bestimmung

Traglast

Kreisförmige

Beliebige

Bruchlinientheorie

(Johansen)

Bruchlinien,

3. Generelle Gedanken

Vorgehen

Das Ziel dieser Arbeit ist, Lösungen auf der sicheren Seite, ^d.h.

Grenzwerte der Traglast

bestimmen. Nach dem 1. Grenzwertsatz

(unterer Grenzwert) ^der Plastizitätstheorie muß dafür ein möglicher Gleichgewichtszustand gefunden ^werden, dessen Schnittkräfte

kei¬

nem

Punkt die Plastizitätsbedingungen verletzen. Die maximale Bela¬

stung

^allen möglichen Lösungen ^{ist die} Traglast. ^Das Vorgehen

soll

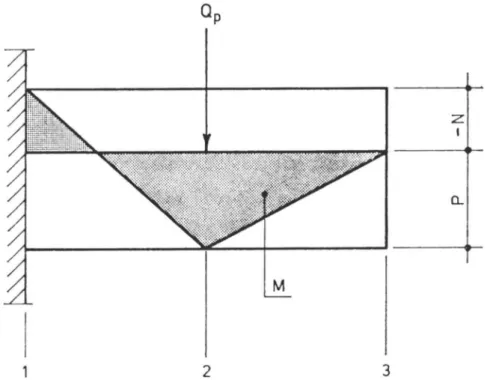
einem einfachen Beispiel erläutert werden. Gegeben ^{sei ein Balken}

mit konstanter Höhe, ^der

^{einem Ende frei} aufliegt ^und

^anderen eingespannt ^{ist. Er} wird in der Mitte mit einer Einzellast Q ^belastet (Abb. 3.1).

1 2

3

Abb. 3.1 Einführungsbeispiel: Bestimmung ^der Traglast

3.1 Bestimmung ^der Traglast

Als

soll bei gegebener Armierung die maximale Belastung Q ge¬

sucht werden,

^{der ein} möglicher Gleichgewichtszustand ^{existiert, des-}

sen

Schnittkräfte

keinem Punkt die Plastizitätsbedingungen ^verletzen.

Diese Belastung ^ist gleich ^der Traglast ^Qp>

^{alle möglichen Gleich¬}

gewichtszustände ^{untersucht werden. In diesem Beispiel handelt}

^sich

um

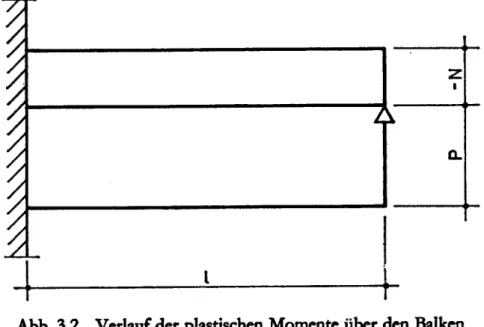
einen Stahlbetonbalken mit einer konstanten Armierung ^{über die}

ganze Länge. ^Das positive plastische ^{Moment (unten} Zug) ^{ist P; das} negative plastische ^{Moment ist}

^N (oben Zug). ^{Beide sind konstant}

über die Balkenlänge (Abb. 3.2).

X

Abb. 3.2 Verlauf ^der plastischen Momente über den Balken

Als

wählt

als statisch bestimmtes Grundsystem den einfachen Balken und führt als überzählige Größe X das Einspannmoment

linken Auflager ^ein (Abb. 3.3).

Abb. 3.3 Grundsystem ^mit überzähliger ^{Größe X}

Das Moment M erhält

durch Superposition des Momentes Q ^M0 infolge der äußeren Belastung Q und des Momentes X Mx infolge ^der überzähligen ^{Größe X}

Grundsystem (einfacher Balken). ^{Darin ist}

Mx das Moment

Grundsystem infolge ^X

^{1, und M0 das Moment}

am

Grundsystem infolge Q

^1.

M

QM0 ^{+ XMX} (3.1)

Somit ist der Ausdruck für M linear in X und Q ^und ergibt ^{für die}

Punkte 1, 2, ³ (Abb. 3.4)

Momentenfläche

Abb. 3.4

Darstellung

zulässigen Momentenfläche,

Plastizitätsbedingungen

Mx

X

M2=y ₊ x±-

"w4 2

M3

0

(3.2)

Diese Momente mit den zugehörigen Auflagerreaktionen und der äuße¬

ren

Belastung Q stellen für jeden ^Wert

Q und X einen möglichen Gleichgewichtszustand ^dar.

Die Forderung, ^{daß die} Plastizitätsbedingungen

keinem Punkt

letzt werden sollen, ^lautet:

-N^Mi^P (3.3)

Sie ist graphisch ^{in Abb. 3.4} dargestellt.

Beachtet _man, daß das Moment zwischen den Punkten 1,2 ^{und 3} gerad¬

linig verläuft,

genügt ^{es, die} Bedingung (3.3)

den Punkten 1, ^{2 und 3}

formulieren.

Diese lauten:

in Punkt 1: X < ^P

-X<N in Punkt 2:

+ X± _< P

Ä4

Ä4

(3.4)

und in Punkt 3:

-N<0<P

In Punkt 3 sind die Ungleichungen trivial. Alle Bedingungen ^{sind in X,} Q,P und N linear.

Gesucht ist natürlich die größtmögliche Belastung Q. ^Im vorliegenden Beispiel ^{ist sie} gleich ^der Traglast QPy ^{weil alle} möglichen Gleichgewichts¬

zustände durch Variation

XuticlQ berücksichtigt ^werden.

Mathematisch kann die Aufgabe folgendermaßen formuliert werden:

Gesucht ist Qmax,

^{daß die} Ungleichungen (3.4), die linear in den freien Variablen -X"undj2 sind, erfüllt werden.

Eine solche Aufgabe ist ein lineares Programm ^{und kann} gelöst ^werden.

Ein allgemeines ^lineares Programm [10], [11] ^ist gegeben ^durch

^lineare

Funktionen

ji

J]

^{+ bi i= 1,2,3}

^(3.5)

mit

Variablen _xi>

und eine Objektfunktion

n

Z

£«ixi ^{+ * (3.6)}

A ⁼l

Durch geeignete ^{Wahl der}

^kann

^Z minimal oder maximal

chen, ^{doch müssen die} j,- und ein Teil der Variablen

positiv ^sein.

Die Nebenbedingungen ^{lauten also:}

ein Teil

> ⁰ (3.7)

ein Teil

ohne Bedingungen

Das lineare Programm ^wird in einem Schema mit transponierter ^Be¬

schriftung dargestellt:

jy

z

-XA <*ik

ajA

bi

Durch kleine Umformungen ^{können die} Bedingungen ^des Beispiels ^auf

die selbe Form wie die Funktionen (3.5), (3.6) ^und (3.7) gebracht ^werden.

Die Ungleichungen (3.4) gehen ^{in die} Gleichungen (3.8) ^{mit den Neben¬}

bedingungen (3.9) ^über.

ji

-X + ^P

j,2=+X ^{+ N}

l X

J4

+£ _j +

+ ^N 2

X

T

Ji > 0; _ja > 0; _ja > 0; _j4 > ⁰

(3.8)

(3.9)

Die Objektfunktion ^{Z hat} folgendes ^Aussehen:

Z

£± (3.10)

Sie muß maximiertwerden. Es ist gleichgültig, ^{ob Q oder Q— maximiert}

wird.

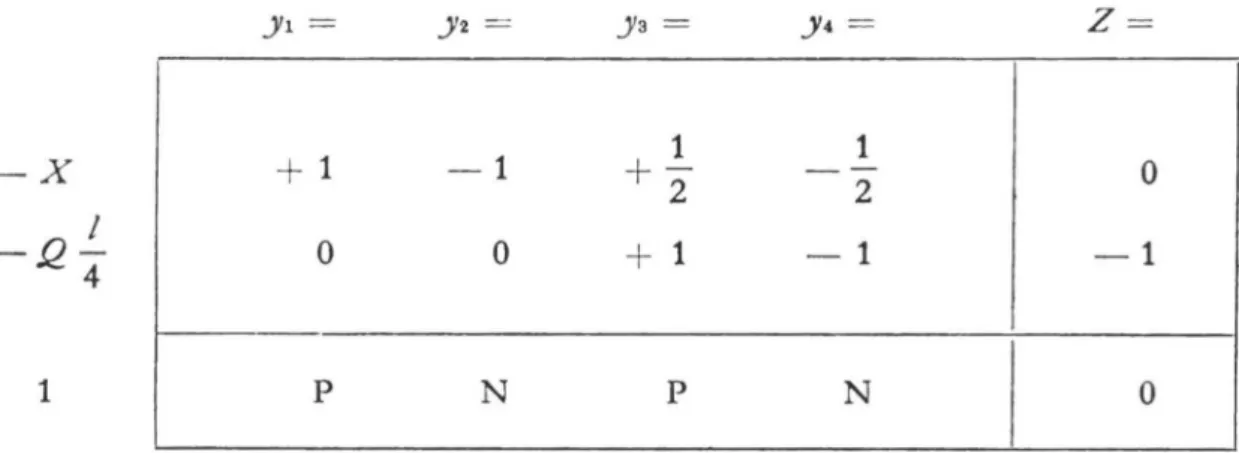
Durch Protokollieren der Funktionen (3.8) ^und (3.10) ^mit transponierter

Beschriftung ^erhält

^{das Schema} des linearen Programms.

X

-a

Jl ⁼ yt ⁼ J3 ⁼ j« ^{= Z =}

+1

X

0 0 + 1 ^— 1 ^— 1

p N p N 0

Zur Veranschaulichung soll dieses lineare Programm, das zwei unab¬

hängige Variable X und Q besitzt, graphisch gelöst ^werden (Abb. 3.5).

Für die analytische Lösung ^{sei auf} [10] ^und [11] ^verwiesen.

QI

A

B

Abb.3.5

Graphische Lösung

Programms

In der Ebene, gebildet ^{durch die} rechtwinkligen Koordinaten X und

Q—, istji

^{0, d.h. X}

^{P eine Gerade, die in der} Figur eingezeichnet

und _{mit ji} bezeichnet wurde. Soll

im Punkt (X, Q-A

^Be¬

dingung ji > ^{0 erfüllt} werden,

muß dieser Punkt in der Halbebene

liegen, die durch diese Gerade begrenzt ^{wird und den} Nullpunkt

hält (der Nullpunkt erfüllt diese Ungleichung). Analog ergeben ^{die Be¬}

dingungen j2 > 0, J3 > 0, j4 > ⁰ drei weitere Halbebenen. Ein Punkt

(Xy Q-Ay der alle vier Nebenbedingungen ^{erfüllt, muß in dem Gebiet} liegen, ^{das diese vier Halbebenen} gemeinsam haben. Dies ist das in der

Figur schraffierte Parallelogramm. ^Nur die Punkte im Innern und auf dem Rand dieses Parallelogramms sind in diesem Problem zulässig. ^Die

Funktion Z ist proportional

^Abstand des Punktes (XyQ-A

^der

Geraden jg—

^{0. Man erkennt dies, indem}

einige Niveaulinien Z

=

konstant dieser Funktion zeichnet. Sie verlaufen parallel der Geraden

Q—

^{0. Die} Extremalzüfgafoe läßt sich also folgendermaßen geome¬

trisch interpretieren:

Unter allen Punkten im Innern oder auf dem Rand des Parallelogramms

ist derjenige gesucht, ^{der den} größten ^Abstand

^{der Geraden} j2—

⁰

hat. Die Anschauung gibt ^{die Ecke A als} Lösung,

^für Q ^eine positive ^Kraft annimmt. Ist Q negativ, also aufwärts gerichtet, ^erhält

man

die Ecke B.

Die Koordinaten

A

X=-N;£±=P + ^ ^(3.11)

sowie die Koordinaten

B

(3.12)

sind die Lösungen des linearen Programms. ^{Für eine nach}

gerich¬

tete

Belastung ^tritt

^der Einspannstelle ^ein negatives ^{und in der Feld¬}

mitte ein positives plastisches ^{Moment auf.}

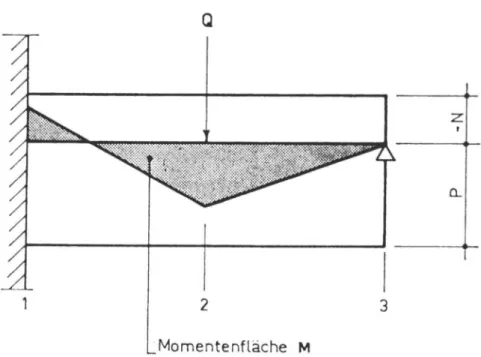
Die Traglast erreicht den Wert

Qp

^{(AP +} IN)

(3.13)

Die Momentenfläche und der Verlauf des plastischen Momentes sind

aus

Abb. 3.6 ersichtlich.

Qr

1 2 3

Abb. 3.6 Verlaufder Momentenfläche

infolge Qp

3.2 Bestimmung ^der optimalen Armierung

Als zweite Aufgabe soll die Größe und die Anordnung der minimalen

Armierung ^{für eine} gegebene Belastung gesucht ^werden. Für die gege¬

bene Belastung ^wird

^allen möglichen Gleichgewichtszuständen ^der-

jenige gesucht, ^für den das kleinste Armierungsvolumen bzw. Armie¬

rungsgewicht genügt,

jedem ^{Punkt die} Plastizitätsbedingungen

zu

erfüllen. Die gegebene Belastung ^{ist dann} gleich ^der Traglast ^{des Bal¬}

kens mit der gefundenen Armierung.

Als erstes soll die Abhängigkeit ^des plastischen ^Momentes

^{der Ar¬}

mierung angegeben ^werden.

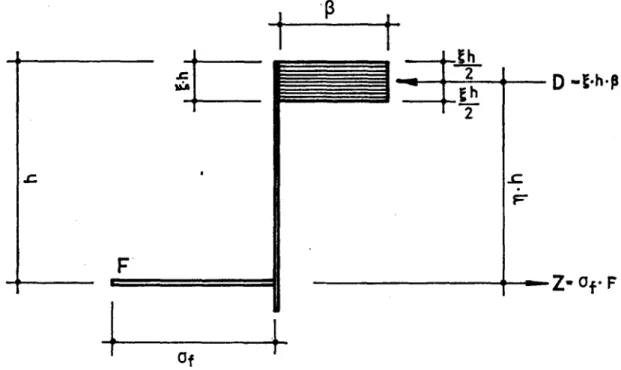
ß

i-IlL .iÜ

2

D -g-h-ß

¦Z-Of

Of

Abb. 3.7 Spannungsverteilung ^{in einem} plastifizierten Stahlbetonquerschnitt infolge Mp

^b o/ ^F

Mit der in Abb. 3.7 dargestellten Spannungsverteilung ^{in einem} plastifi¬

zierten Stahlbetonquerschnitt ^erhält

^das positive ^{und das} negative plastische ^Moment

P

h

(3.14)

Mit der Annahme, ^daß rf

rf'

rj konstant, ^d.h. unabhängig

dem Armierungsgehalt ist,

bei kleinem Armierungsgehalt ^annä¬

hernd zutrifft, ^erhält

^{nach kleiner} Umformung:

FP

ha/

F"-d ^N

(3.15)

h _oj 1

wobei

konstant ist. Da bei einem Tragwerk ^meistens

^eine

V

Armierungsstahlsorte verwendet wird und _{somit af}

konstant ist, gehen ^die Gleichungen (3.15) ^{über in}

P

1

N FP

(3.16)

F"=C2

wobei

rjo/

konstant ist. Für stückweise konstantes h,

ⁱⁿ

Zukunft immer angenommen wird, ^erhält

^{für ein} Teilstück die einfache Beziehung

FP

P

(3.17)

wobei

1 r\ Ofh

FN

iV

konstant ist.

ASi-1

ASi+1

Abb. 3.8 Verlaufvon —N und P

Stabachse

Das Gesamtvolumen ^Kder theoretischen Armierung beträgt:

Tragnrk

V= f _{(FP + FN)} ds (3.18)

Für die Bedingung, daß P und N stückweise linear sind (Abb. 3.8) geht Gleichung (3.18) ^{über in}

Tragmerk

v= i S* ^{<+ Ni+Ni+i + Pi+p'+oJj/ <3-19)}

Wie im vorhergehenden Beispiel ^wählt

den einfachen Balken wieder als statisch bestimmtes Grundsystem ^{und führt als} überzählige ^{Größe X}

das Einspannmoment

^linken Auflager ^ein.

12 3

Abb. 3.9 Einführungsbeispiel ^{für die Bestimmung} der minimalen Armierung

Die Momente

den vier Intervallgrenzen (Abb. 3.9) ^{lauten demnach:}

Mi-.

X

Mz

^ ⁺ xT

M*. -¦fi?+4

Mi

0

(3.20)

(3.22)

Die Forderung, ^daß

keinem Punkt die Plastizitätsbedingungen

letzt sind, ^ist:

-Ni^Mi^Pt (3.21)

Es wird

die Bedingung gestellt, ^{daß P und}

^iV stückweise linear sind (Abb. 3.8).

Damit genügt ^{es, die} Plastizitätsbedingungen

^den Intervallgren¬

zen

anzuschreiben,

^die Plastizitätsbedingungen ^{auch dazwischen}

erfüllen. Somit erhalt

in Punkt 1: Pi > ^X Ni^-X

in Punkt 2: P2 > Q^ + x\

o 4

Nn>-&f-X±

in Punkt 3: P, > X ₊ X-\

N9>-£j-X±

in Punkt 4: Na > ⁰ P4 >0

mit den Nebenbedingungen, daß die freien Variablen Pi, Nit P%y Na, Ps, iVs, ^{Pa und} Na^O ^{sein müssen. Diese} Bedingungen gehen

^der

Definition

P und N hervor.

Für jeden Verlauf der plastischen ^{Momente P und Ny der}

^mit

einem frei gewählten Einspannmoment ^{X die} Ungleichungen (3.22) ^be¬

friedigt, ^{ist die} Traglast ^{des Systems nicht} kleiner als die gegebene ^Be¬

lastung Q.

Gesucht ist das kleinstmögliche Gesamtvolumen der Armierung. ^Das

Gesamtvolumen der Armierung ^{ist nach} Gleichung (3.19)

V=±a |i/(+M ^{+ iW-f Pi + Pa)}

+ | ^/ (+ ^{Ni + N9 + Pt +} P8)

+ ² i _/ (+ iVs + Na + Ps + ^4)} ^(3.23)

wobei V minimiert werden soll.

Mathematisch kann die Aufgabe folgendermaßen formuliert werden:

Gesucht ist Vmn,

^{daß die} Ungleichungen (3.22), ^{die linear} in den freien Variablen Xy Pi, Pa, Ps, Pa» Ni, Nt, N3 ^und Na sind, erfüllt sind.

Eine solche Aufgabe ^ist wiederum ein lineares Programm.

Durch kleine Umformungen ^{können die} Bedingungen ^dieses Beispiels

auf die selbe Form wie die Funktionen des allgemeinen ^{linearen Pro¬}

gramms (3.5), (3.6) ^und (3.7) gebracht ^werden.

Die Ungleichungen (3.22) gehen ^{in die} Gleichungen (3.24) ^{mit den} Nebenbedingungen (3.25) ^über.

yi= -X+Pi

j2= +X + Ni

j8= -a{-x\ ^{+ Pi} j4=+j2^+^f ^+Ni j>=-ü{-x\ ^{+ p*}

J*=+£j ⁺ Xj+N9

J7

+ ^Pa js

-\- Na

(3.24)

Ji > 0, _ja > 0, _j3 > 0, _j4 ^ 0, j5 ^ 0, je > 0, _j7 ^ 0, _j8 ^ ⁰

Pi>0,P2>0,P3>0,P4^0,A/1>0,iV2>0,A73>0,iV4>0 (3.25)

J£" ist eine freie Variable, ^die positiv ^oder negativ ^{sein kann.}

Die Objektfunktion ^{Z hat} folgendes ^Aussehen:

Z

+ Ni

2Nz + Pi + 2P2 + 3iV3 + 3P3 + 2Na + ^2P4 (3.26)

Z muß minimiert werden. Es spielt ^{keine Rolle,} ob die Funktion V oder ihr Vielfaches minimiert wird.

Durch Protokollieren der Funktionen (3.24) ^und (3.26) ^mit transponier¬

ter

Beschriftung ^erhält

das Schema des linearen Programms.

—

X

—

P»

-N, -P.

-Nt

—

Pt -Na

—

Pi -Na

4

Jl ⁼ J» ⁼

J»

J«

4

3

0 0 0

— 1

0

0 0 0 0 0

1

0 ^—

1 0

0 0

0

1

0

0

0

0 0 0

0 0

0

0 0

0 0

0

1 0 0

0

0

0

1

0

0 0

0

0

0 0 0

0

0 0

1 1

0

Ein solches Programm kann nicht mehr graphisch gelöst ^{werden. Der}

zulässige Lösungsbereich, ^{der im}

Beispiel ^ein Parallelogramm

war, ist

ein neundimensionales Gebilde. ^Es gibt jedoch analytische

Methoden [10], [11] ^und insbesondere fertige Bibliotheksprogramme

für elektronische Rechenmaschinen,

^lineare Programme

^lösen.

Es wird hier verzichtet, ^{auf die} verschiedenen Methoden einzugehen.

Es sei

die Lösung dieses Problems angegeben:

4

^24

Pi ⁼⁰ Pi ⁼⁰

p>=4£w

Pa ⁼⁰

/ (3.27)

Ni

⁰ JV3

⁰ Na

⁰

Daß P4 und Na den Wert 0 annehmen, ^hätte

^den Plastizitäts¬

bedingungen ^{in Punkt 4} (3.22) ^{und der} Optimalbedingung, ^{V muß ein}

Minimum sein, ^direkt sagen können. Die letzten zwei Gleichungen

(3.24) ^{wären dann} weggefallen.

Aus der Gleichung (3.27) ^erhält

^{für die totale} Armierung

/* / 1 V

Q

12 \rihof

In Abb. 3.10 ist die Momentenfläche und der Verlauf der erforderUchen

plastischen ^Momente dargestellt.

Den Verlauf und die Größe der minimalen Armierung ^bekommt

sofort

den Gleichungen (3.17). Sie lauten:

Fp

N F" =c3P

G)

\ 1 ^Q

i

x^v

r

(O

¦,

x

t-

/ >ijv -y^X^ ¹

/,

/ M

/

12 3 4

Abb.3.10

Momentenfläche

Verlauf

erforderlichen plastischen

Im vorhergehenden Beispiel ^wird vorausgesetzt, ^{daß P und N stück¬}

weise ^linear sind (Abb. 3.8). Selbstverständlich können auch andere ^Vor¬

aussetzungen gemacht ^{werden, z.B. die Armierung und demzufolge}

P bzw. N soll über einem Bereich konstant verlaufen oder sie soll einen

gewissen ^{Wert nicht} überschreiten. Diese Grenze kann durch konstruk¬

tive Überlegungen ^{oder durch die Bedingung, daß kein spröder Bruch}

eintreten soll, also durch die Forderung fi ^ /umax gegeben ^{sein. Manch¬}

mal ist

konstruktiven Gründen oder _wegen Schwind- und Tempe¬

raturwirkungen ^{erwünscht, eine Armierung} einzulegen. ^{Daß kein} schlagartiger ^{Bruch auftritt, kann durch} Bedingungen, ^wie

^

gedrückt werden. Alle diese zusätzlichen Forderungen ^{können in Form}

von

Ungleichungen angeschrieben ^{werden. Das} Suchen einer optimalen Armierung ^mit den oben erwähnten Bedingungen ^{stellt immer noch ein}

lineares Programm ^{dar. Es} unterscheidet sich generell ^nicht

^den

vorher behandelten ^Fällen.

3.3 Zusammenfassung

Für Stabtragwerke ^sind durch Erfüllen der Plastizitätsbedingungen ^{in ein¬}

zelnen Punkten die Plastizitätsbedingungen über dem ganzen Tragwerk

erfüllt. Da die Schnittkräfte in einem Punkt lineare Funktionen der

bekannten überzähligen Größen und der äußeren Belastung ^{sind, erhält}

man

für das Moment in einem Punkt eine lineare Funktion der unab¬

hängigen Variablen. Die plastischen ^{Momente P/ und Ni} sind bei der

Bestimmung ^der optimalen Armierung unabhängige Variable und bei der Bestimmung ^der Traglast ^Konstante. Durch Formulieren der Plasti¬

zitätsbedingungen Pi ^ Mi ^ —Ni ^{in den einzelnen Punkten} ergeben

sich lineare Ungleichungen ^{in den} unabhängigen Variablen. Diese Un¬

gleichungen ^{mit der} Forderung, daß eine lineare Funktion (Belastung

oder Armierungsvolumen) optimiert ^{werden soll,} bilden ein lineares

Programm.

Indem

das obige Vorgehen auf Platten ausdehnt, ^erhält

^fol¬

gende Forderungen:

Die Plastizitätsbedingungen ^müssen in den Schnittkräften und den pla¬

stischen Momenten linear sein (Kapitel 4).

Die Platte muß auf ein endlichfach statisch unbestimmtes Tragwerk

einfacht werden, ^{damit die} Schnittkräfte lineare Funktionen der über¬

zähligen ^Größen und der äußeren Belastung, ^{d.h. der} unabhängigen

Variablen sind (Kapitel 5.3).

Durch Erfüllen der Plastizitätsbedingungen ⁱⁿ einzelnen Punkten müssen sie über dem ganzen Plattenbereich erfüllt werden (Kapitel 6).

Mit diesen Forderungen ^erhält

durch Formulieren der Plastizitäts¬

bedingungen ^{in den} einzelnen Punkten lineare Ungleichungen ^{in den} unabhängigen ^Variablen.

Diese Ungleichungen ^{mit der} Bedingung, ^{daß eine} lineare Funktion

Belastung (Kapitel 7) ^oder Armierungsvolumen (Kapitel 8)

optimiert

werden soll, ergeben wieder ein lineares Programm.

4. Plastizitätsbedingungen

4.1 Plastifizierung ^eines Plattenbereiches

Alle

eingeführten Bezeichnungen ^sind

Abb. 4.1 und Abb. 4.16 ersichtlich.

Die Plastifizierung eines Plattenbereiches ist durch folgende ^Merkmale gekennzeichnet:

Es existiert mindestens ein Schnitt, ^{dessen Normale}

mit der x-Achse den Winkel _tp einschließt und der

fließende obere oder

Zug¬

eisen schneidet. In einem plastifizierten Bereich reißt die Platte bis

Druckzone auf und öffnet sich. Nur die Stahleinlagen ^{und die Druck¬}

zone

können

diesen Stellen Kräfte übertragen. ^Die Zugkräfte ^{der ein¬}

zelnen Stahleinlagen wirken in deren ursprünglichen Achsrichtung.

Diese Annahme ist konservativ. Sie vernachlässigt ^die sogenannten ^Ver-

dübelungskräfte.

4.2 Orthogonale Armierung

Die beiden Armierungsrichtungen ^{verlaufen in}

^und j-Richtung.

4.2.1 Plastizitätsbedingungen

Um die Plastizitätsbedingungen herzuleiten, ^{wird die Platte in} plastifi-

zierte (aufgerissene) ^{und in elastische} (nicht aufgerissene) Bereiche auf¬

geteilt.

Im elastischen Bereich ist für jeden beliebigen, ^senkrecht

^Platten¬

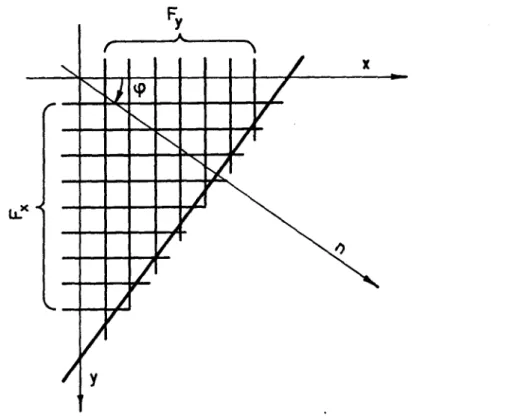
mittelebene geführten Schnitt das Biegemoment kleiner als das plastische

Fy

\

r >

/

V ¦i ⁹

(

^

\

* -<

U."

\)

's,

¦

y

1

Abb. 4.1 Bezeichnungen ^bei orthogonaler Armierung ⁱⁿ

jf-Richtung

Moment. Demzufolge ^{kann die Platte nicht auf-, sondern höchstens}

reißen. Dieser nicht aufgerissene ^{Bereich ist} fähig, ^{durch die} Verzahnung

der Betonkörner Schubspannungen ^und demzufolge ^auch Drillungs¬

momente zu

übertragen.

Daraus ergibt ^sich, daß in einem beliebig geführten ^{Schnitt mit der}

Normalen

(Abb. 4.1) ^das Biegemoment

kleiner als das positive plastische ^{Moment P„ und} größer ^{als das} negative plastische ^Moment

-Akist.

Ein plastifizierter Bereich erstreckt sich entlang eines Risses. Seine Breite ist normalerweise beschränkt. Sie ist sicher kleiner als der Rißabstand.

Fließt in einem aufgerissenen ^{Bereich z.B. die}

Zugarmierung,

beträgt ^das entsprechende positive plastische ^{Moment für einen Schnitt} parallel ^der j-Achse

P*

_*/ K < ^h (4.1.1)

wobei F* die Fläche der

Armierung ^{in der} x-Richtung ^und

t£ h die Distanz zwischen der Zug- ^und der Druckresultierenden dar¬

stellen (Abb. 3.7).

In diesem Schnitt ist die Zugkomponente ^{der fließenden} Armierung ⁱⁿ

der j-Richtung null und daher auch das zugehörige plastische Drillungs¬

moment.

P*,

⁰ (4.1.2)

Daraus folgt, ^{daß in} diesem Bereich die Momente in der

und j-

Richtung Hauptmomente ^sind.

Analog ^erhält

^{für einen Schnitt} parallel der x-Achse das entspre¬

chende positive plastische ^Moment

Py

ofF* rjfh ^(4.1.3)

und das plastische Drillungsmoment

Pyx

⁰ (4.1.4)

Für das Fließen der oberen Armierung ^wird

K

_of ^F» rjN ^h (4.1.5)

NXJ

⁰ (4.1.6)

beziehungsweise

Ny

Of Pf rff ^{h (4.1.7)}

Ny*

⁰ (4.1.8)

Die maximalen und minimalen Biegemomente ^{sowie die} zugehörigen Drillungsmomente ^im plastifizierten ^Bereich, genannt plastische ^Mo¬

mente, erhält

für einen beliebigen ^Schnitt tp (Abb. 4.1) ^{nach den}

Transformationsformeln [12].

Die Momente in

und j-Richtung ^muß

^{durch die} entsprechenden plastischen ^Momente

^Die plastischen Drillungsmomente ^sind gleich ^Null.

P„

Px _cosny + Py ^sin2 tp

P„v

|(P, -Px)sin29>

(-N„)

(-Nx) ^cos2 cp + ( -Ny) ^sin2 tp

N„v

^± {(-Ny)

(-Nx)) ^sin2tp

(4.2)

In der Druckzone des plastifizierten Bereiches existiert ein Spannungs¬

zustand, ^{bei dem die} Spannungen ⁱⁿ

^und j-Richtung ^ebenfalls Hauptspannungen ^{sind. Die} Drillungsmomente ⁱⁿ den Schnitten parallel

der

und j-Achsen ^{sind null,} und daher sind auch die horizontalen

Schubspannungen %xy null. Bei der Berechnung ^der plastischen ^Momente

in

und j-Richtung wird nach Abb. 3.7 angenommen, daß die

größte Betondruckspannung gleich ^der Prismendruckfestigkeit ß ^ist.

Die beiden Hauptspannungen

^und o> sind demnach höchstens gleich ß. ^Das Entstehen eines Risses verhindert, ^{daß die} Normalspannungen

kleiner als null werden. Ein solcher Spannungszustand ^{verletzt die} Bruchhypothese

Mohr nicht und ist demnach auch ein stabiler

Spannungszustand.

Beim Betrachten des ganzen Plattenbereiches ^ist in den elastischen Be¬

reichen für alle Richtungen

-Nn <mn<Pn

mn

ist das Biegemoment ^für den Schnitt in Richtung tp.

Erreicht

P» oder

Nn und _m„9

PH<p ^bzw.

N«? ^{wird der}

Querschnitt plastifiziert.

In diesem Bereich besteht ein zulässiger Gleichgewichtszustand, ^der

weder die Plastizitätsbedingungen ^des Armierungsstahles

X± a/ noch die Bruchhypothesen

Mohr für den Beton verletzt. Der Gleich¬

gewichtszustand ^eines plastifizierten ^{und des} anschließenden elastischen Bereiches ist für den Fall, ^{daß die}

Stahleinlagen ^{fließen, in}

Abb. 4.2 dargestellt. Beim Fließen der oberen Stahleinlagen ^{werden die}

P durch N

Abb. 4.2

Gleichgewichtszustand

plastifiziertem

bei

orthogonaler Armierung

j-Richtung

Für die vollständigen Plastizitätsbedingungen ^{ist also}

fordern, ^daß

für alle Richtungen <p gilt:

-N„ <

P„ (4.3.1)

und für

—Nn

Nnp

(4.3.2)

m» ⁼ Jr» :

mnrp

Jrntp

Nun werden die Bedingungen aufgestellt,

^{welchen —Nn} <

< ^P*

ist und nachträglich gezeigt, ^{daß die erhaltenen} Bedingungen ^{auch die} folgenden Forderungen ^{erfüllen. Bei}

^{P* ist auch mH<p}

^P»?

und bei

—Nn auch _mn<p

Nuq>.

Die plastischen Momente für die Richtung tp sind nach Gleichungen (4.2)

P„

Px cos2 tp

Py sin2 tp

Pnq>

|- ^(P,

^{Px) sin 2 9?}

( -iV„)

( -Nx) ^cos2 y + ( -Ny) ^sin2 ?

(4'2)

Nmp =±((-Ny)-(-Nx))sin2tp

Die Biegemomente

^{und die} Drillungsmomente mnq> erhält

als Funktion

mx, m3 und _mx, nach den Transformationsformeln [12]:

mn ⁼ mx

cos2 9p + /», sin2 _9? -|- mxy sin 2 _9?

mn<p

{my

n*x) ^{sin 2} 9p -f _mxy

_{2 9?}

Eingesetzt ^{in die} Bedingung (4.3.1) ^{—Nn <}

^{< P» erhält}

(4.4)

(

Ak) ^cos2 97 + (

Ny) sin2 9? <

^cos2 9? + my sin2 _9? + % sin 2 _9?

< ^{Px cos2} _9? + Py sin2 9? (4.5)

Nx, Ny, ^{Px und} P^ ^sind positive ^Werte.

Die obige Ungleichung ^wird

^{in zwei einfache} Ungleichungen ^auf¬

geteilt, ^{wobei die}

^{durch die} positiven plastischen ^Momente (untere

Armierung) ^{und die zweite durch die} negativen plastischen ^Momente

(obere Armierung) begrenzt ^wird.

Px cos2 tp + Py ^sin2 tp^m* ^cos2 9? + my sin2 _tp + z*xy sin 2 _9? (4.5.1) (—Nx) ^cos2 9? -f ( -Ny) ^sin2 99 <

^cos2 ₉₇ + «ty sin2 _tp + «fxy sin 2 9? (4.5.2)

Als

soll die Ungleichung (4.5.1) untersucht werden. Nach kurzer

Umformung ^erhält

(Px

mx) ^cos2 9? + (Py

my) ^sin2 tp > mx, sin _{2 9?}

_{2 /*xj>} sin _9?

9?

(4.6)

Für den Fall A, bei dem sin 2 _tp ^ ⁰ und demnach auch tg tp > ⁰ ist, ^ist

der Gültigkeitsbereich

tp in Abb. 4.3 dargestellt, ^wobei tp im Uhr¬

zeigersinn abgetragen ^ist.

Abb. 4.3 Gültigkeitsbereich

^F (cp) im Fall <cA»

Mit diesen Voraussetzungen ^{kann die} Beziehung (4.6) weiter in die Un¬

gleichung (4.7) umgeformt ^werden

(Px-mx) ¹ (P, ⁺ *,)

^ ,,_

H

=

Äx ^und

Ry ^erhält

2 tg<p

Mit den Abkürzungen (A

—mx)

2

Px 1

tg<p ^X Pytg<p> mxy (4.8)

Für den Fall B, ^{bei dem sin 2} tp < ⁰ und demnach auch tg tp < ⁰ ist, ^wird der Gültigkeitsbereich

tp in Abb. 4.4 dargestellt, ^wobei tp im Uhr¬

zeigersinn abzutragen ^ist.

Abb. 4.4 Gültigkeitsbereich

^F (cp) ^{im Fall «B»}

Unter diesen Voraussetzungen ^{und den} obigen Abkürzungen ^erhält

Px

tgy ⁺ Rytgtp ^mxy (4.9)

Diskussion der Funktion F (cp):

Durch Ableiten der Funktion

ergibt ^sich

F(tp)

^Rx + Rytgtp

8F(<p) ^-Rx

dtp ⁺

Ry

sin2 _cp cos2 9?

(4.10)

(4.11)

Durch Nullsetzen der 1. Ableitung ^erhält

^{den Ort} der horizontalen

Tangente

—Px R»

+

⁰

sin2 _cp cos2 cp

(4.12.1)

oder

Ry

=

tg295 (4.12.2)

und indem

wieder einsetzt Px

Py

my

=

tg29? (4.13)

Für den Fall A (tg tp > 0) gibt

folgende Möglichkeiten ^{für die Vor¬}

zeichen

Px ^und Ry\

») ^{Px^O}

Rj >0

Für diese Bedingung ^{ist der} qualitative Verlauf der Funktion F (tp) ⁱⁿ

Abb. 4.5 dargestellt. Diese Funktion besitzt zwei Minima. Es ist sofort

ersichtlich, ^daß durch Erfüllen der Ungleichung (4.8)

^den Stellen der Minima die Ungleichung ^für jedes tp erfüllt ist.

F«p)

TC TC

2

TC 2

<P

TC

b)

Abb. 4.5 Qualitativer ^Verlauf

^F (<p)

^Fall

^{und Rx}

0, Ry ^{>: 0}

Px<0 Ry >0

Abb. 4.6 zeigt ^den qualitativen Verlauf der Funktion F (tp). ^Diese

Funktion besitzt kein Minimum; ^sie geht

^minus Unendlich nach

plus ^{Unendlich. Die} Ungleichung (4.8) ^{kann daher nicht für} jedes tp erfüllt werden. Die Möglichkeit ^Rx < ^{0 und} Ry > ^{0 ist nicht} zulässig.

Tt TC

2

TC

Abb. 4.6 Qualitativer ^Verlauf

^F (<p) ^{im Fall «A» und Rx}

0,Rj ^{Eür 0}

c) ^Px>0

Ry <0

Für diese Bedingung ^{ist der} qualitative ^Verlauf der Funktion F (tp) ⁱⁿ

Abb. 4.7 dargestellt. Die Funktion besitzt kein Minimum. Sie geht

<P

TC TC

2

TC

Abb. 4.7 Qualitativer ^Verlauf

^F (cp) für Fall «A» und Rx

0, Ry

⁰

plus Unendlich nach minus Unendlich. Die Ungleichung (4.8) ^kann

nicht erfüllt werden für jedes tp. Die Möglichkeit ^Px > ^{0 und} Ry < ^{0 ist} nicht zulässig.

d) Px<0

Der qualitative Verlauf der Funktion F (tp) ^{ist in Abb.} (4.8) dargestellt.

Diese Funktion besitzt zwei Maxima, ^und

^{ist sofort} ersichtlich, ^daß

die Ungleichung (4.8) ^{nicht für} jedes 99 erfüllt werden kann.

"W

TC TC

2

-<P

TC

Abb. 4.8 Qualitativer ^Verlauf

^F (cp) für Fall «A» und Rx

0, R,

⁰

Zusammenfassend ^kann gesagt werden, daß für t%tp^0 ^{Rx ^ 0 und} Ry > ⁰ sein müssen, ^{damit die} Ungleichung (4.8) für jedes tp erfüllt ^{werden kann. Dies}

wird erreicht, ^indem

^die Ungleichung

den beiden Minima der Funk¬

tion F (tp) erfüllt.

Für den Fall B, ^{bei dem} _{tg tp} < ⁰ ist, ^{kann nach} analoger Diskussion der verschiedenen Möglichkeiten der Vorzeichen

Px und Ry folgendes

ausgesagt ^werden: