Hochtemperaturentwicklung f¨ ur Spinketten
und
effektive Spinmodelle f¨ ur Spin-Peierls-Systeme
Diplomarbeit Alexander B¨ uhler
Institut f¨ ur Theoretische Physik Universit¨ at zu K¨ oln
Juni 1999
INHALTSVERZEICHNIS i
Inhaltsverzeichnis
1 Einleitung 1
2 Modell 4
3 Hochtemperaturentwicklung der Suszeptibilit¨ at 5
3.1 Methode . . . . 7
3.1.1 Lanczos-Algorithmus und Ergebnisse . . . . 10
3.1.2 Implementierung . . . . 12
3.1.3 Momente-Algorithmus . . . . 15
3.1.4 Implementierung . . . . 16
3.2 Finite-size Korrekturen . . . . 19
4 Bestimmung der spezifischen W¨ arme und der Entropie 23 5 Verbesserte Darstellungen und Vergleiche 24 5.1 Kettenbruch-Darstellung . . . . 25
5.2 Ber¨ ucksichtigung des Tieftemperaturverhaltens . . . . 36
5.3 Vergleich mit Bethe-Ansatz . . . . 44
5.4 Vergleich mit DMRG . . . . 47
6 Darstellungen mit Hilfe der Dispersion 51 7 Effektive Spinmodelle 59 7.1 Grundlagen der Flußgleichungen . . . . 59
7.2 Spin-Peierls-Phase . . . . 63
7.3 Nichtadiabatische Beschreibung der Spin-Phonon-Kopplung . . . 64
7.4 Vergleich mit DMRG . . . . 70
8 Fazit und Ausblick 76
A Matrix des Heisenbergoperators 78
B Daten nach linked-cluster-Methode 80
C Suszeptibilit¨ aten 80
D Zustandssummen 82
E Differentialgleichungen f¨ ur effektives Spinmodell 83
1
1 Einleitung
Die vorliegende Arbeit gliedert sich in zwei Teile. Beide Teile besch¨ aftigen sich mit eindimensionalen Spinmodellen. Diese dienen in vielf¨ altiger Weise der theo- retischen Beschreibung von Festk¨ orpern. Motiviert wird dieser Zugang durch Messungen an verschiedenen Substanzen, die sich aufgrund ihrer quasi eindi- mensionalen Struktur in erster N¨ aherung mit Hilfe von Spinketten modellieren lassen. Nur wenige dieser eindimensionalen Systeme sind exakt l¨ osbar. Sehr oft ist man auf st¨ orungstheoretische Ans¨ atze angewiesen, die einen kleinen Para- meter ben¨ otigen, nach dem entwickelt wird.
Der erste Teil der vorliegenden Arbeit besch¨ aftigt sich mit der Hochtemperatur- entwicklung, d.h. der Entwicklung nach dem kleinen Parameter β = 1/k
BT , von frustrierten isotropen S = 1/2-Ketten. Das Ziel ist die Bestimmung von tempe- raturabh¨ angigen Gr¨ oßen wie die Suszeptibilit¨ at und spezifische W¨ arme. Diese Gr¨ oßen sind im allgemeinen experimentell sehr gut zug¨ anglich, so daß generell die theoretischen Resultate mit dem Experiment verglichen werden k¨ onnen.
In der vorliegenden Arbeit handelt es sich um einen neuentwickelten Zugang zur Hochtemperaturentwicklung. Dabei werden Systeme betrachtet, in de- nen nur N¨ achstnachbar-Wechselwirkung und ¨ Ubern¨ achstnachbar-Wechselwir- kung ber¨ ucksichtigt werden. Letztere bezeichnet man als frustriert. Als Aus- gangspunkt f¨ ur die Modellierung des Systems dient das Heisenbergmodell. Das Heisenbergmodell beschreibt die Wechselwirkung lokaler magnetischer Momente und bildet die Grundlage zur Beschreibung kollektiver magnetischer Ph¨ anomene.
Ein erstes Ziel ist die Berechnung der Suszeptibilit¨ at bei verschwindendem Ma- gnetfeld, dargestellt durch ein Polynom in β und im Fall der frustrierten S = 1/2- Kette dargestellt durch ein Polynom in β und der relativen ¨ Ubern¨ achstnachbar- Kopplung α. Somit steht f¨ ur die Suszeptibilit¨ at ein analytischer Ausdruck zur Verf¨ ugung.
Die Berechnung der Suszeptibilit¨ at erfordert die Bestimmung der großkanoni- schen Zustandssumme f¨ ur das betreffende System. Mit Hilfe der Zustandssum- me kann man weitere thermodynamische Gr¨ oßen ableiten. In der vorliegenden Arbeit wird dabei zus¨ atzlich auf die Berechnung bzw. Entwicklung der spezifi- schen W¨ arme und der Entropie eingegangen.
Zur Durchf¨ uhrung der 1/T -Entwicklung werden verschiedene Methoden ver- wendet, zum einen ein Lanczos-Algorithmus und zum anderen ein sogenannter Momente-Algorithmus. Der Lanczos-Algorithmus zeichnet sich dadurch aus, daß er die Hochdimensionalit¨ at des vorliegenden Problems auf ein niedrigdimen- sionales zur¨ uckf¨ uhrt, wodurch die Berechnungen vereinfacht werden. Jedoch ist die Implementierung der computergest¨ utzten Rechnungen immens speicherauf- wendig. Der Momente-Algorithmus nutzt die M¨ oglichkeiten der Optimierungen f¨ ur das vorliegende Problem effektiver aus. ¨ Uber den Momente-Algorithmus werden die Erwartungswerte von Potenzen des Hamiltonoperators bez¨ uglich aus- gezeichneter Zust¨ ande berechnet.
Da zur Berechnung der physikalischen Gr¨ oßen kein unendlich großes System be-
trachtet werden kann, das den thermodynamischen Limes beschreibt, wird die durch den Speicher der zur Verf¨ ugung stehenden Computer begrenzte System- gr¨ oße maximal ausgenutzt. Dadurch kommt es zu finite-size-Effekten, die im weiteren eingehend untersucht bzw. bestimmt werden m¨ ussen.
Zur besseren Ausnutzung der gewonnenen Informationen, werden die berechne- ten Polynome in einer Pad´ e-Approximation gen¨ ahert. Es handelt sich hierbei um Kettenbruchdarstellungen, die vern¨ unftige Aussagen f¨ ur die berechneten Ergeb- nisse zu tieferen Temperaturen hin erlauben, als dies f¨ ur die Polynome m¨ oglich ist. Zur weiteren Verbesserung der Darstellungen werden im n¨ achsten Schritt Informationen ¨ uber den Tieftemperaturbereich miteingebunden. Es handelt sich hierbei um allgemeine Eigenschaften der jeweiligen physikalischen Gr¨ oße im Tief- temperaturbereich. Die so gewonnenen Ausdr¨ ucke liefern eine bessere Beschrei- bung der jeweiligen Gr¨ oße.
In einem Vergleich der unfrustrierten S = 1/2-Kette zum einen mit exakten Ergebnissen aus dem Bethe-Ansatz und zum anderen mit Resultaten, die mit Hilfe des Theorems zusammenh¨ angender Cluster bestimmt wurden, werden die gewonnen Ergebnisse vorgestellt und diskutiert. Da der Bethe-Ansatz f¨ ur die frustrierte S = 1/2-Kette nicht m¨ oglich ist, werden die Ergebnisse in diesem Fall mit numerischen Resultaten aus DMRG-Rechnungen verglichen.
Ein eigener Abschnitt der Arbeit besch¨ aftigt sich mit Darstellungen der Sus- zeptibilit¨ at der unfrustrierten S = 1/2-Kette mit Hilfe von Dispersionsdaten. Es handelt sich dabei um eine Darstellung der Suszeptibilit¨ at ¨ uber die Dispersion, die f¨ ur die dimerisierte, frustrierte S = 1/2-Kette bestimmt wurde. In der vor- liegenden Arbeit soll diese Darstellung zur Bestimmung der Suszeptibilit¨ at der unfrustrierten Kette erweitert werden. Dies stellt den ung¨ unstigsten Fall dar, und zwar der Darstellung f¨ ur eine unfrustrierte Kette. Da die Dispersion f¨ ur die unfrustrierte Kette bekannt ist, werden durch diesen Zugang Informationen
¨
uber den Tieftemperaturbereich miteingebunden. Durch die Darstellung ¨ uber ei- ne verallgemeinerte T -Variable, die beide Grenzwerte T
→0 und β
→0 korrekt erfaßt, erh¨ alt man schon mit wenigen Informationen einen gute Beschreibung der Suszeptibilit¨ at.
Der zweite Teil der Arbeit besch¨ aftigt sich mit S = 1/2-Ketten gekoppelt an Gitterschwingungen (Phononen). Gerade durch die Ankopplung an Phononen entstehen interessante physikalische Effekte. Ein Beispiel hierf¨ ur ist der Spin- Peierls- ¨ Ubergang, der z.B. in CuGeO
3[1] zu beobachten ist. Andere Substanzen wie α
0− NaV
2O
5[2] zeigen ebenfalls Anzeichen f¨ ur einen Spin-Peierls- ¨ Uber- gang. Bisherige Beschreibungen dieses Phasen¨ ubergangs gehen zumeist von einer adiabatischen Behandlung der Phononen aus. Experimentelle Daten zu CuGeO
3widersprechen jedoch der Voraussetzung der adiabatischen N¨ aherung.
In der vorliegenden Arbeit wird ein effektives Spinmodell mit Hilfe der Fluß-
gleichungen hergeleitet. Die Methode der Flußgleichungen basiert auf kontinu-
ierlichen unit¨ aren Transformationen, die einen gegebenen Hamiltonoperator in
eine einfachere Gestalt ¨ uberf¨ uhren, im g¨ unstigsten Fall in Diagonalgestalt. Das
3
Ziel des zweiten Teils der Arbeit ist es, ein effektives Spinmodell abzuleiten, das implizit die Ankopplung an Gitterschwingungen enth¨ alt. Motiviert wird dieser Zugang durch die anorganische Spin-Peierls-Substanz CuGeO
3. Es handelt sich um eine nichtadiabatische Beschreibung der Phononen. Mit Hilfe der Flußglei- chungen soll das magnetische Subsystem von dem Subsystem der Phononen entkoppelt werden.
Erste Ergebnisse zeigen, daß die Kopplung an Phononen zus¨ atzliche langreich- weitige Spinwechselwirkungen erzeugt, und daß die Spinkopplungen eine Tem- peraturabh¨ angigkeit aufweisen. Das Fernziel dieser Berechnungen soll sein, die aus dem zweiten Teil der Arbeit gewonnenen Informationen zu verwenden, die Darstellung der Suszeptibilit¨ at und anderer physikalischen Gr¨ oßen aus dem er- sten Teil der vorliegenden Arbeit z.B. bez¨ uglich der Spinkopplungen soweit zu verbessern, daß sie genutzt werden k¨ onnen, um die Modellparameter durch den Vergleich mit experimentellen Daten genauer bestimmen zu k¨ onnen.
Die vorliegende Arbeit gliedert sich in acht Abschnitte. Im folgenden Abschnitt wird das Modell zur Beschreibung der S = 1/2-Kette behandelt und motiviert.
Der daran anschließende Abschnitt befaßt sich ausf¨ uhrlich mit den angewand- ten Methoden und deren Implementierung in einem Computerprogramm. Am Ende dieses Abschnittes werden die ben¨ otigten finite-size-Korrekturen genauer untersucht. Die Bestimmung der spezifischen W¨ arme und der Entropie aus den Ergebnissen der vorangegangenen Rechnungen wird in Abschnitt 4 abgeleitet.
Im 5. Abschnitt werden verbesserte Darstellungen der bisherigen Ergebnisse und
deren Vergleich zum Teil mit exakten Resultaten und zum Teil mit numerischen
Ergebnissen vorgestellt. Abschnitt 6 befaßt sich mit verschiedenen Darstel-
lungen der Suszeptibilit¨ at mit Hilfe der Dispersion. Der 7. Abschnitt hat die
Beschreibung der Methode der Flußgleichungen und deren Anwendung auf ein
an Phononen gekoppeltes Spinsystem zum Thema. Der letzte Abschnitt faßt
die Ergebnisse zusammen und gibt einen Ausblick auf m¨ ogliche Erweiterungen.
2 Modell
Da gerade in den letzten Jahren verschiedene experimentelle Substanzen wie CuGeO
3[1], α
0− NaV
2O
5[2], SrCu
2O
3[3], KCuF
3[4], ( VO )
2P
2O
7[5] synthe- tisiert wurden, die man in erster N¨ aherung als quasi eindimensionale frustrierte Heisenbergketten beschreiben kann, ist man sehr an den Eigenschaften solcher Ketten interessiert. Ein besonderer Schwerpunkt liegt in der vorliegenden Ar- beit auf CuGeO
3. Viele Ergebnisse werden mit den f¨ ur CuGeO
3entsprechenden Parametern dargestellt.
c
O O O
Cu Cu
Abbildung 2.1:
Am Beispiel von CuGeO3sind die N¨achstnachbar-Kopplung (Superaus- tausch) entlang durchgezogener Linien und die ¨Ubern¨achstnachbar-Kopplung entlang gestrichelter Linien dargestellt.In der vorliegenden Arbeit wird das Modell der frustrierten S = 1/2 Heisen- bergkette untersucht. Der Hamiltonoperator f¨ ur eine Kette mit N Pl¨ atzen mit N¨ achstnachbar- und ¨ Ubern¨ achstnachbar-Kopplung lautet
H
=
XNi=1
( J
SiSi+1+ αJ
SiSi+2− h S ^
zi) , (2.1)
wobei α das Verh¨ altnis zwischen ¨ Ubern¨ achstnachbar- und N¨ achstnachbar-Kopp- lung beschreibt und h gleich gµ
BH ist mit dem Magnetfeld H. Beim letzten Term handelt es sich um den Beitrag der Zeemann-Energie. Damit die Trans- lationsinvarianz im endlichen System erhalten bleibt, gelten periodische Rand- bedingungen N + i = i. Diese sind im weiteren Verlauf der vorliegenden Arbeit wichtig.
F¨ ur den Fall α = 0 und S = 1/2 sind exakte Ergebnisse vorhanden (Grundzu- stand: Bethe 1931 [6]), ebenso f¨ ur die Suszeptibilit¨ at, die gleichfalls mit Hilfe des Bethe-Ansatzes berechnet wurde [7]. Jedoch ist es nicht m¨ oglich, ¨ uber den Bethe-Ansatz eine exakte L¨ osung f¨ ur die frustrierte Kette anzugeben. Eine Ausnahme bildet der sogenannte Majumdar-Ghosh-Punkt α = 1/2, f¨ ur den der Grundzustand bekannt ist [8, 9]. Hier liegt ein perfekter Singulettproduktzu- stand mit kurzreichweitigen N¨ achstnachbar-Korrelationen vor.
Ein anderer besonderer Fall ist α
≈0.241167. F¨ ur α-Werte oberhalb dieses
kritischen Wertes ¨ offnet sich in der Dispersionsrelation eine L¨ ucke, so daß f¨ ur
angeregte Zust¨ ande ω ( 0 ) > 0 gilt [10, 11]. Es liegt eine spontane Symme-
triebrechung der Translationssymmetrie vor [12]. Im Grundzustand binden sich
benachbarte Paare von Spins bevorzugt zu einem Singulett. Es handelt sich um
5
einen zweifach entarteten Grundzustand mit einem alternierenden Erwartungs- wert
hSiSi+1i.
Bei antiferromagnetischer Kopplung J > 0 werden aufgrund der ¨ Ubern¨ achst- nachbar-Wechselwirkung die Ne´ el-artigen Zust¨ ande geschw¨ acht. Um diesen Sachverhalt zu verdeutlichen, betrachtet man die unfrustrierte Kette im klassi- schen Limes, in der man die Spinoperatoren
Sials klassische Vektoren darstellt.
Bei antiferromagnetischer Kopplung ist die antiparallele Ausrichtung der Spins zueinander die energetisch g¨ unstigste. Diesen Zustand nennt man Ne´ elzustand.
Er stellt im klassischen System den Grundzustand dar. In Abbildung 2.2 ist der
αJ ? αJ
J J
Abbildung 2.2:
Effekt der Frustration (Darstellung der z-Komponente des Spins)Effekt der Frustration illustriert. Dabei sind hier zur Veranschaulichung des Pro- blems die N¨ achstnachbar-Kopplung zickzackf¨ ormig und die ¨ Ubern¨ achstnachbar- Kopplung entlang der Holme dargestellt. Frustration ist also ein Effekt, der erst durch die Hinzunahme der ¨ Ubern¨ achstnachbar-Kopplung entsteht. Dieser Effekt ist nur in eindimensionalen Systemen zu beobachten. Im N´ eelzustand stellt die endliche Untergittermagnetisierung eine langreichweitige Ordnung dar, die die Symmetrie der Spinrotation bricht [13]. Es sei erw¨ ahnt, daß im Quantensystem der N´ eelzustand kein Grundzustand mehr der unfrustrierten bzw. frustrierten Heisenbergkette ist.
3 Hochtemperaturentwicklung der Suszeptibilit¨ at
Bei der konventionellen Hochtemperaturentwicklung wird eine thermodynami- sche Dichte wie z.B. die freie Energie pro Platz f ( β = 1/k
BT ) um β = 0 ent- wickelt. Es handelt sich um eine St¨ orungsrechnung, derren kleiner Parameter β ist. Dabei f¨ uhrt die Hochtemperaturentwicklung z.B. auf die Berechnung von Kumulanten oder die Bestimmung zusammenh¨ angender Cluster. Einen guten Uberblick der bisher verwendeten Methoden zur Hochtemperaturentwicklung im ¨ Heisenbergmodells gibt Ref. [14]. In Anhang B ist das Ergebnis einer Hochtem- peraturentwicklung mittels des Theorems zusammenh¨ angender Cluster [15] auf- gef¨ uhrt.
Im Rahmen der vorliegenden Arbeit wird ein alternativer Zugang f¨ ur die rech-
nergest¨ utzte Hochtemperaturentwicklung zun¨ achst der Suszeptibilit¨ at gew¨ ahlt.
Im weiteren Verlauf der Arbeit werden auch andere Gr¨ oßen wie die spezifische W¨ arme und die Entropie in dieser Weise entwickelt.
Der wesentliche Unterschied zu den konventionellen Verfahren besteht darin, daß Z¨ ahler und Nenner der Suszeptibilit¨ at χ ( T ) mit
χ ( T ) = β N
Sp ( M
2e
-H)
Sp (e
-H) (3.1)
getrennt voneinander entwickelt werden. Im Vergleich zu den konventionellen Verfahren werden hier die zusammenh¨ angenden Cluster mittels endlicher Sy- steme bestimmt. Das Theorem zusammenh¨ angender Cluster [15] gew¨ ahrleistet Ergebnisse im thermodynamischen Limes.
Die Gr¨ oßen in Z¨ ahler und Nenner sind f¨ ur sich genommen noch nicht unabh¨ angig von der Systemgr¨ oße. Das Ziel ist es, eine systemgr¨ oßenunabh¨ angige Funktion zu bestimmen. Um die Abh¨ angigkeiten von der Systemgr¨ oße zu beseitigen, wird die gebrochen rationale Funktion 3.1 wiederum um β = 0 entwickelt, so daß man am Ende einen analytischen Ausdruck, ein Polynom in β, erh¨ alt.
Bei der letzten Entwicklung heben sich die verschiedenen Abh¨ angigkeiten von der Systemgr¨ oße Term f¨ ur Term auf. Eine andere M¨ oglichkeit gibt es auch nicht, da die berechnete Gr¨ oße keine Systemgr¨ oßenabh¨ angigkeiten aufweist. Die Koeffizienten des Polynoms f¨ ur χ sind rationale Zahlen, so daß die Ergebnisse bis zu der berechneten Ordnung absolut exakt sind.
h
S
|M
2e
-H|S
i hS|e-H|Si=0
=0
=0
Polynom (3.2)
Da bei den Berechnungen nur endliche Systeme betrachtet werden k¨ onnen, m¨ ussen auftretende finite-size Effekte besonders beachtet werden. Die Ent- wicklung nach Potenzen von β entspricht einer Entwicklung nach Potenzen von
H, wie man aus der Entwicklung der Expotentialfunktion erkennen kann.
Betrachtet man den Hamiltonoperator 2.1, so besteht dieser aus einer Summe aus ” lokalen“ Termen, die auf n¨ achste Nachbarn bzw. ¨ ubern¨ achste Nachbarn der unfrustrierten bzw. frustrierten Kette wirken. Die Anwendung des Hamil- tonoperators bildet somit lokale Cluster, die man durch den bond zwischen den beteiligten Pl¨ atzen darstellen kann. ¨ Uber das Theorem zusammenh¨ angender Cluster [15] k¨ onnen Entwicklungen physikalischer Gr¨ oßen ¨ uber die Bestimmung der entstehenden Cluster berechnet werden. Dabei werden die entstehenden Cluster jeweils mit einem Gewicht versehen aufsummiert. Viele Cluster ha- ben das gleiche Gewicht, da sie aus Symmetriegr¨ unden gleiche Beitr¨ age liefern.
Durch die Translationssymmetrie entstehen z.B. viele Cluster der gleichen Art.
Das Theorem besagt unter anderem, daß man nur die zusammenh¨ angenden Clu-
ster betrachten muß, da alle unzusammenh¨ angenden Cluster ein Gewicht von
Null haben. F¨ ur die vorliegende Arbeit gibt dieser Sachverhalt einen Anhalts-
punkt bis zu welcher Ordnung von
Hman eine endliche Kette entwickeln darf.
3.1 Methode 7
Das gr¨ oßte zusammenh¨ angende Cluster muß noch vollst¨ andig erfaßt sein, um korrekte Ergebnisse zu erhalten.
Betrachtet man die unfrustrierte Kette, so kommt durch jede Anwendung des Hamiltonoperators ein bond mehr zum jeweils gr¨ oßten zusammenh¨ angenden Cluster hinzu. Da eine Kette mit N Pl¨ atzen N − 1 bonds besitzt, kann man bis H
N-1entwickeln, da dann gerade noch der gr¨ oßte zusammenh¨ angende Cluster richtig beschrieben wird. In der vorliegenden Arbeit wird jedoch aus technischen Gr¨ unden bis H
Nentwickelt, so daß finite-size Effekte auftreten, die in Abschnitt 3.2 genauer untersucht werden.
Ein erster Anhaltspunkt f¨ ur die nachfolgenden Berechnungen der Suszeptibilit¨ at ist die 1/T -Abh¨ angigkeit des f¨ uhrenden Terms der Entwicklung unabh¨ angig von der Kopplungskonstanten (Curie-Gesetz). Dieser Term zeigt, daß f¨ ur parama- gnetische Systeme die thermische Unordnung der Ausrichtung der
” permanenten Momente“ durch das angelegte Feld entgegenwirkt. Dies ist eine charakteristi- sche Gr¨ oße f¨ ur den Hochtemperaturbereich (k
BT
J), in dem die Spins als unabh¨ angig voneinander betrachtet werden k¨ onnen, da keine Korrelationen zwi- schen verschiedenen Spins bestehen
1. Der n¨ achst h¨ ohere Term der Entwicklung, 1/T
2, wird durch das Curie-Weiss-Gesetz beschrieben. F¨ ur ferromagnetische Kopplung ist das Vorzeichen dieses Termes positiv und f¨ ur antiferromagnetische Kopplung negativ. Formal k¨ onnen die ersten beiden Terme der Entwicklung f¨ ur die S = 1/2-Kette als
χ ( T ) = 1 4T
1 − 1
2 J T
(3.3) geschrieben werden.
3.1 Methode
Zur Bestimmung von thermodynamischen Gr¨ oßen des Quantenspinsystems ist man gezwungen, die Spur von Operatoren auszuwerten. Es ist nur in wenigen F¨ allen m¨ oglich, einen geschlossen l¨ osbaren Ausdruck abzuleiten. Die Berech- nung der Spur ist meist sehr aufwendig, da hier bez¨ uglich aller m¨ oglichen Basis- zust¨ ande des physikalischen Systems Erwartungswerte der jeweiligen Operatoren bestimmt werden m¨ ussen. Daher wurde nach einer einfacheren M¨ oglichkeit ge- sucht, die Spursumme f¨ ur einen Operator A ^ zu berechnen. Die vorliegende Methode ist auf das hier betrachtete System der Spin-1/2 Kette zugeschnitten, l¨ aßt sich aber auch problemlos auf Spins beliebiger Gr¨ oße ¨ ubertragen.
Die Methode ist durch zwei einfache Schritte gekennzeichnet i. Platzverdopplung, Erweiterung des Hilbertraumes ii. Einf¨ uhren eines Singulettproduktzustandes
1Formal ist e-J
P
:::=kBT −!1zum einen der Hochtemperaturlimes, als auch der Limes verschwindender AustauschwechselwirkungJ, daJ=kB
Tder relevante Parameter ist.
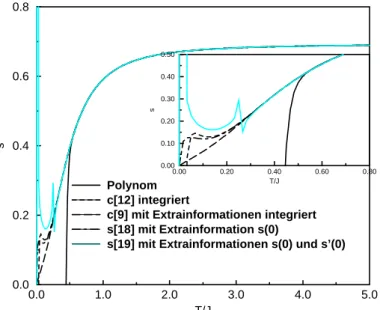
Im ersten Schritt wird neben die eigentliche Kette eine zweite virtuelle Kette gelegt, so daß jeder Platz auf der realen Kette ein Gegen¨ uber auf der virtuellen Kette besitzt. Dies ist eine rein formale Konstruktion. Das Interesse besteht
αJ J
virtuell
real
Abbildung 3.1:
Schematische Darstellung der Methode der Platzverdoppelung und der Wirkung vonHweiterhin an der isotropen Heisenbergkette und nicht in einem Leitersystem.
Der n¨ achste Schritt besteht in der Einf¨ uhrung eines Singulettproduktzustandes
|Si
mit:
|
S
i=
YN
i=1
√
1
2 (|
↑r↓vi−
|↓r↑vi)i
, (3.4)
wobei der Index r f¨ ur die reale Kette und v f¨ ur die virtuelle Kette steht. Ge- gen¨ uberliegende Pl¨ atze auf realer und virtueller Kette bilden also jeweils ein Singulett.
F¨ ur allgemeinen Spin erweitert sich der Zustand eines Singuletts zu
|Siallg:
= 1
√
2S + 1
X2Si=0
(−1)
i|(S− i)
r, (i − S)
vi. (3.5) Mit diesem allgemeinen Ausdruck l¨ aßt sich die Methode der Platzverdoppelung durch Bildung des Produktzustandes auf Spins beliebiger Gr¨ oße anwenden.
Mit der Platzverdoppelung ist eine Erweiterung des Hilbertraumes verbunden.
Daher k¨ onnen die urspr¨ unglichen Operatoren nicht mehr weiterverwendet wer- den, da diese nur in dem kleineren Hilbertraum der realen Kette operieren. Man muß die Wirkung der Operatoren aus dem urspr¨ unglichen System ( A) im erwei- ^ terten System ( A ^
erw) bestimmen. Dies soll eine m¨ oglichst einfache Erweiterung sein. Die Operatoren A ^
erwsollen auf die reale Kette wie die urspr¨ unglichen Ope- ratoren A ^ wirken und auf die virtuelle Kette wie die Identit¨ at. Somit ergibt sich der Hilbertraum F
Aerw^des erweiterten Systems aus dem Urspr¨ unglichen und der Identit¨ at
F
Aerw^= F
r^ A⊗
F
vid. (3.6)
Mit der Operatordefinition A ^
→A ^
erwist auch gew¨ ahrleistet, daß weiterhin nur
das urspr¨ ungliche Problem betrachtet wird. In Abbildung 3.1 ist die Methode
der Platzverdopplung und der Wirkung von
Hschematisch dargestellt.
3.1 Methode 9
Durch diese Konstruktion l¨ aßt sich die Spursumme eines Operators A ^ im ur- spr¨ unglichen System im erweiterten System als einfacher Erwartungswert A ^
erwbez¨ uglich des Singulettproduktzustandes 3.4 darstellen. F¨ ur einen einzelnen Spin ist dieser Zusammenhang direkt ersichtlich
Sp A ^ =
h↑|A ^
|↑i+
h↓|A ^
| ↓i=
h↑r↓v |A ^
erw|↑r↓vi+
h↓r↑v |A ^
erw|↓r↑vi=
hS|A ^
erw|Si, (3.7)
und l¨ aßt sich auf Ketten beliebiger L¨ angen ¨ ubertragen
hS|A ^
erw|Si=
Yi;j
(h↑
r↓v |−
h↓r↑v |)iA ^
erw(|
↑r↓vi−
|↓r↑vi)j=
Yi
h↑r↓v |i
A ^
erw|↑r↓vii+
h↓r↑v |iA ^
erw|↓r↑vii=
Yi
X
";#
h·|i
A ^
|·ii= Sp A ^
. (3.8)
Damit kann im vorliegenden Fall die Spur der Spinoperatoren, die auf der Hei- senbergkette operieren, mit Hilfe einfacher Erwartungswerte dargestellt werden.
Wie man erkennt, leistet der Triplettzustand mit S
z= 0 das Gleiche.
Mit dem Hamiltonoperator
Haus Gleichung 2.1 kann man nun die Suszeptibi- lit¨ at χ(T) f¨ ur verschwindendes Magnetfeld bestimmen
χ ( T ) = 1 N
∂M
∂h
h=0
= 1
N β ( < M
2> − < M >
2)|
h=0= 1
N β < M
2>
|h=0= 1
N β Sp (M
2e
-H) Sp ( e
-H)
h=0
= 1
N β
hS
|(Me
-HerwM )| S
i hS|(e-Herw)|Si
h=0
, (3.9)
wobei h das Magnetfeld in Einheiten von gµ
Bund M =
PN i=1S
zi
die Magneti- sierung ist. Da [H , M ] = 0 gilt, ist die Reihenfolge von
Hund M in Gleichung 3.9 irrelevant.
In der weiteren Arbeit werden die Operatoren aus dem erweiterten Hilbertraum
wie die Urspr¨ unglichen benannt. In Anhang A ist die Matrix des Hamiltonopera-
tors 2.1 aus dem erweiterten Hilbertraum explizit f¨ ur nur N¨ achstnachbar-Kopp-
lung und verschwindendes Magnetfeld aufgef¨ uhrt. ¨ Ubern¨ achstnachbar-Terme
ergeben die gleichen Ergebnisse mit der entsprechenden Ersetzung der Indizes.
Es wurden zwei Methoden zur Berechnung von χ ( T ) verwendet. Zum einen ein Lanczos-Algorithmus und zum anderen der Momente-Algorithmus, mit dem die Koeffizienten in der Entwicklung der Exponentialfunktion in Gleichung 3.9 direkt berechnet werden.
Der Lanczos-Algorithmus zeichnet sich dadurch aus, daß er die Hochdimensio- nalit¨ at von F
Hstark reduziert. Allgemein dient der Lanczos-Algorithmus dazu, Matrizen in Tridiagonalgestalt zu ¨ uberf¨ uhren. Dadurch sind die Berechnungen nach Durchf¨ uhren dieses Algorithmus weniger aufwendig als im urspr¨ unglichen Problem.
Die zweite Methode der direkten Berechnung der Koeffizienten, bei der keine Verringerung der Dimensionalit¨ at des Hilbertraumes herbeigef¨ uhrt wird, erweist sich als vorteilhafter bez¨ uglich Laufzeit und Speicherbedarf, da letztendlich nur Polynome und keine rationalen Funktionen auftreten.
3.1.1 Lanczos-Algorithmus und Ergebnisse
Ziel des Lanczos-Algorithmus ist es, ¨ uber das aus der Linearen Algebra be- kannte Gram-Schmidtsche Orthogonalisierungverfahren das hochdimensionale Eigenwertproblem f¨ ur
Hauf ein niedrigdimensionales zur¨ uckzuf¨ uhren, das mit Standardroutinen gel¨ ost werden kann. Will man das System exakt l¨ osen, so
¨ andert sich die Dimensionalit¨ at nicht. Dies soll hier aber nicht das Ziel sein.
Hier soll versucht werden
H¨ uber den Lanczos-Algorithmus bis zur ben¨ otigten Ordnung in eine m¨ oglichst einfache Gestalt zu ¨ uberf¨ uhren, um die weiteren Berechnungen zu erleichtern. Der Algorithmus ist durch eine dreigliedrige Re- kursionsvorschrift gekennzeichnet, mit deren Hilfe n Vektoren
|q
ii(i = 1 . . . n) der Dimension m sukzessiv konstruiert werden
2. Sei
|q
0ider Nullvektor, b
1= 1 und
|q1iein Startvektor, der ein Zufallsvektor, aber kein Eigenvektor von
Hsein darf. Dann lautet die Konstruktionsvorschrift f¨ ur den Vektor
|q
i+1i, sowie f¨ ur die Skalare a
iund b
i+1a
i=
hq
i|H|q
ii, b
2i+1=
hq
i+1|q
i+1ihqi|qii
, q
i+1=
Hq
i− a
ih
q
i|q
iiq
i− b
2iq
i-1. (3.10) Die auf diese Weise konstruierten Vektoren
|qiisind paarweise orthogonal, wie man mit vollst¨ andiger Induktion zeigen kann. Sie bilden eine Orthogonalba- sis des Krylovraumes K
n(| q
1i,
H)zum Startvektor
|q
1i, der von den Vektoren
{|q1i,H|q1i,H2|q1i, . . . ,Hn-1|q1i}aufgespannt wird. Das Verfahren bricht ab, wenn f¨ ur einen Index j die Gleichung b
j= 0 erf¨ ullt ist.
2Im weiteren wird hier die Bezeichnung aus der Linearen Algebra ¨ubernommen. Dies kann man mit der Analogie Vektorraum - Hilbertraum rechtfertigen.
3.1 Methode 11
Der Algorithmus produziert die Matrixeintr¨ age a
iund b
ieiner reellen, symme- trischen n
×n Matrix
Tmit Tridiagonalgestalt, die gerade die Matrix
Hin der neuen normierten (!) Basis darstellt
T
=
a
1b
2b
2a
2b
30 b
3a
3b
4b
4a
4. ..
0 . . . ...
. (3.11)
Somit wurde die Dimensionalit¨ at von
Hstark reduziert. Geht man vom Hei- senbergoperator 2.1 mit nur N¨ achstnachbar-Wechselwirkung aus, der auf eine Kette mit N Pl¨ atzen wirkt, so kann man korrekte Ergebnisse bis zur N − 1- ten Ordnung erreichen, da dann gerade das gr¨ oßte zusammenh¨ angende Cluster noch enthalten ist. Dies entspricht N Rekursionsschritten. Dadurch wird die urspr¨ ungliche Dimension von 2
2Nauf die Dimension N verringert. F¨ ur eine Bei- spielkette mit 10 Pl¨ atzen wird die Dimension bei der Berechnung der 9. Ordnung um einen Faktor 10
5verringert.
Um diesen Algorithmus auf das vorliegende Problem anwenden zu k¨ onnen, muß man geeignete Startvektoren bzw. Startzust¨ ande w¨ ahlen, jeweils f¨ ur den Nenner und f¨ ur den Z¨ ahler aus Gleichung 3.9. F¨ ur den Nenner ist das der Singulettpro- duktzustand
|S
iund f¨ ur den Z¨ ahler der Zustand M
|S
i=
PNi=1Szi|
S
i. Dies ist f¨ ur den Z¨ ahler m¨ oglich, da man M an e
-Hvorbeiziehen darf mit
hS
|M
2e
-H|S
i=
hS|Me-HM|Si, weil
PNi=1
[S
jSj+1,
Szi] = 0 gilt (Diese Kommutatorrelation bleibt nat¨ urlich auch f¨ ur den ¨ ubern¨ achsten Nachbar-Term
SjSj+2g¨ ultig, da solche Skalarprodukte mit jeder Spinkomponente vertauschen).
Dadurch kann man den Nenner in Gleichung 3.9 Sp (e
-H) =
hS|e-H|Si=
he
-Ti
1;1
(3.12)
= 1 − β
T1;1+ 1 2! β
2hT2i
1;1
− 1 3! β
3hT3i
1;1
+ O( β
4) mit Hilfe der Matrix
Taus Gleichung 3.11 darstellen. Es ist klar, daß man nur den [ 1, 1 ] -Eintrag ben¨ otigt, da dieser gerade dem Erwartungswert bez¨ uglich des
” ersten“ Einheitsvektors in der neuen Basis entspricht. Der Einheitsvektor ist
gerade der entsprechende Startzustand, im vorliegenden Fall also der normierte
Singulettproduktzustand. F¨ ur den Z¨ ahler ist die Entwicklung analog, wobei
noch der Startzustand M|Si normiert werden muß.
3.1.2 Implementierung
Wie l¨ aßt sich nun dieser Algorithmus am effizientesten in einem Computerpro- gramm implementieren? Dazu ist es wichtig, sich dar¨ uber klar zu werden, welche Strukturen man ben¨ otigt, und wie man diese kodiert. Die Hauptstruktur sind in erster Linie die Basiszust¨ ande des physikalischen Systems. Da man davon aus- gehen kann, daß man sehr viele davon ben¨ otigt, sollten diese im Speicherbedarf m¨ oglichst effizient behandelt werden.
Auf der anderen Seite werden mit diesen Basiszust¨ anden alle Rechnungen durch- gef¨ uhrt, so daß der Zugriff darauf m¨ oglichst schnell sein sollte. Am besten daf¨ ur geeignet sind
integer-Variablen, da diese sehr systemnah und die Rechnungendamit sehr schnell sind. Das Hauptproblem besteht in der Kodierung der Basis- zust¨ ande. Jeder Kettenplatz kann durch die Platzverdoppelung vier Zust¨ ande annehmen, den Singulettzustand und die drei Triplettzust¨ ande. Diese Bezeich- nung ist jedoch nur formal, da die Zust¨ ande Kombinationen von Spins aus der realen Kette und aus der virtuellen Kette sind. In Anhang A ist die Wirkung des Hamiltonoperators auf benachbarte Kettenpl¨ atze in einer Matrix zusam- mengefaßt. Die Wirkung auf die ¨ ubern¨ achsten Nachbarn ist analog. Bei einer bitweisen Kodierung f¨ ur eine Kette mit N Pl¨ atzen ben¨ otigt man daf¨ ur 2N Bits, d.h. f¨ ur jedes Platzpaar 2 Bits. Schon bei einer Kette mit nur 16 Pl¨ atzen ge- langt man an die Grenze der nat¨ urlichen Wortl¨ ange der benutzten Rechner von 4 Byte.
Die unfrustrierte Kette l¨ aßt sich damit bis in die 15. Ordnung korrekt entwickeln.
Schließt man jedoch Frustration mit ein, so reicht es nur noch bis zur 7. Ord- nung, da durch die ¨ Ubern¨ achstnachbar-Wechselwirkung Cluster der doppelten L¨ ange im Vergleich zu N¨ achstnachbar-Wechselwirkung entstehen. Zur korrekten Beschreibung darf das gr¨ oßte zusammenh¨ angende Cluster nicht gr¨ oßer als die Kettenl¨ ange sein. In der vorliegenden Arbeit sollen Ergebnisse f¨ ur die unfrustrier- te Kette bis zur 16. Ordnung und f¨ ur die frustrierte Kette bis zur 10. Ordnung erreicht werden. Dies bedeutet f¨ ur die frustrierte Kette, daß man mindestens 20 Pl¨ atze ben¨ otigt, um bis auf finite-size Effekte korrekte Ergebnisse zu berechnen.
Auf den verwendeten Unix Plattformen gibt es die
”
long long“ Variablenty-pen, wodurch ein
long long int8 Byte groß ist. Diese sind ausreichend f¨ ur
die Kodierung der Zust¨ ande einer Kette mit 32 Pl¨ atzen, was f¨ ur die Zwecke der
vorliegenden Arbeit ausreicht. Zur Kodierung der Zust¨ ande
|q
iiaus Gleichung
3.10 wurde eine einfach verkettete Liste angelegt, wobei die einzelnen Listenele-
mente die Basiszust¨ ande des entstehenden Krylovraumes darstellen. Die einzel-
nen Listenelemente werden durch die Struktur
Basiszustanddargestellt (siehe
Abbildung 3.2). F¨ ur den Vorfaktor sind ebenfalls
long long int-Variablenn¨ otig, da diese Zahlen im Laufe der Anwendung von
Hsehr schnell die 4 Byte-
Gr¨ oße ¨ ubersteigen. Es handelt sich um rationale Vorfaktoren, so daß Z¨ ahler und
Nenner getrennt gespeichert werden m¨ ussen. Um die Vorfaktoren so klein wie
m¨ oglich zu halten, werden sie durch einen Euklid-Algorithmus immer wieder so
weit wie m¨ oglich gek¨ urzt.
3.1 Methode 13
struct Basiszustand {
long long int vorfaktor z long long int vorfaktor n unsigned long long int vektor
Basiszustand* right
}
Abbildung 3.2:
Struktur der Basiszust¨andeDie Implementierung des Lanczos-Algorithmus erfordert, daß man immer zwei Zust¨ ande im Speicher beh¨ alt (
|qiiund
|qi-1i), w¨ ahrend der neue Zustand (
|q
i+1i) erzeugt wird, wie aus Gleichung 3.10 ersichtlich ist. Der Hauptteil des Programms ist die Implementierung der Wirkung des Hamiltonoperators, d.h. der Wirkung eines Spinproduktes
SiSi+1auf einen Basiszustand. Dabei handelt es sich um eine einfache Matrix-Vektor-Multiplikation, wobei die Ma- trix in diesem Fall sehr d¨ unn besetzt ist. Die Anwendung des Hamiltonoperators auf diese Basiszust¨ ande erfolgt durch
switch-Anweisungen, in denen an eineneue Liste neue Basiszust¨ ande angeh¨ angt und an diesen entsprechende Bit- manipulationen vorgenommen werden, um die neu entstehenden Basiszust¨ ande darzustellen. Die
switch-Anweisung ist sehr schnell und steht im Innern einerSchleife, in der alle Basiszust¨ ande abgearbeitet werden.
Der Lanczos-Algorithmus erfordert f¨ ur jeden Rekursionsschritt drei Vektor-Vektor- Multiplikationen (Skalarprodukte) und eine Matrix-Vektor-Multiplikation, die durch die verwendeten Algorithmen und Kodierungen recht schnell sind. Das Hauptproblem liegt im Speicherbedarf der entstehenden Zust¨ ande. Da sich die Anzahl der Basiszust¨ ande pro generiertem Zustand
|q
iianfangs ungef¨ ahr um den Faktor 3N erh¨ oht und sich bei den hier benutzten Kettenl¨ angen bei h¨ oheren Ordnungen ungef¨ ahr bei einem Faktor 5 pro Rekursionsschritt einpen- delt, m¨ ussen sehr viele Basiszust¨ ande im Speicher gehalten werden. Es sind also st¨ andig drei Listen, die den drei Zust¨ anden
|q
i-1i,
|q
iiund
|q
i+1iaus Gleichung 3.10 entsprechen, im Speicher zu halten.
Eine einfache Rechnung zeigt den Speicherbedarf zur Berechnung der 8. Ord- nung f¨ ur eine Kette mit N = 16 Pl¨ atzen. Ausgehend von einem Startzustand, der nur aus einem Basiszustand besteht und in einer Struktur mit 28 Byte ko- diert ist, ben¨ otigt man ca. 250 MB RAM, um den zuletzt entwickelten Zustand im Speicher zu halten. Bei diesen Gr¨ oßenordnungen ben¨ otigen auch die Berech- nungen mehr Zeit, da viele Basiszust¨ ande abgearbeitet werden m¨ ussen. Diese Uberschlagsrechnung gilt f¨ ¨ ur die Berechnung des Nenners in Gleichung 3.9. Bei der Berechnung des Z¨ ahlers in dieser Gleichung startet man mit dem Zustand M|Si, der durch die Anwendung von M auf
|Siaus N Basiszust¨ anden besteht.
Somit vervielfacht sich noch einmal der Speicherbedarf gegen¨ uber dem Nenner.
Diese ¨ Uberlegungen zeigen den enormen Speicherbedarf, den man schon f¨ ur niedrige Ordnungen ben¨ otigt, um die Suszeptibilit¨ at der unfrustrierten Kette zu bestimmen. Will man nun noch Frustration ( ¨ Ubern¨ achstnachbar-Kopplung) mit hinzunehmen, so verdoppelt sich der Rechenaufwand, da nun die Hauptroutine mit der Anwendung der Spinprodukte auf Basiszust¨ ande zweimal durchgef¨ uhrt werden muß. Der Speicheraufwand steigt auch immens an, da man in den Strukturen die Vorfaktoren aus rationalen Zahlen durch rationale Funktionen in α ersetzen muß, weil der Frustrationsparameter α in allen Potenzen bis zur entwickelten Ordnung in β auftreten kann (Gleichung 3.10). Ein Vergleich mit der ¨ Uberschlagsrechnung zeigt, daß man mit dieser Methode sehr schnell an die Grenzen der zur Verf¨ ugung stehenden Rechner st¨ oßt. Ein anderes wichtiges Merkmal dieser Methode ist, daß der Lanczos-Algorithmus Matrixeintr¨ age a
iund b
iaus Gleichung 3.10 produziert, die in ihrer Primfaktorzerlegung sehr große Primzahlen aufweisen und somit nicht mehr gek¨ urzt werden k¨ onnen. Dabei besteht die Gefahr, daß diese Zahlen den zul¨ assigen Wertebereich eines
long long intschon bei niedrigen Ordnungen ¨ ubersteigen.
Diese Probleme f¨ uhren zu der einfacheren Methode des Momente-Algorithmus.
Hier werden die Koeffizienten der Entwicklung der Exponentialfunktion direkt berechnet. Diese Methode ist an das vorliegende Problem besser angepaßt.
Der Speicherbedarf ist geringer, die Gr¨ oße der entstehenden Faktoren l¨ aßt sich im voraus absch¨ atzen, so daß ein
” Uberlaufen“ der entstehenden Zahlen nicht ¨ m¨ oglich ist und die Vorfaktoren bei den Berechnungen der frustrierten Kette sind keine rationalen Funktionen, sondern Polynome in α.
Um die Ergebnisse aus beiden Methoden vergleichen zu k¨ onnen, wird hier die h¨ ochste erreichte Ordnung der Suszeptibilit¨ at angegeben. Mit Hilfe des Lanczos- Algorithmus war eine Auswertung der Suszeptibilit¨ at bis zur 9. Ordnung m¨ oglich.
Dabei sind die Konstanten J und k
Baus Gr¨ unden der besseren Lesbarkeit hier und im weiteren auf eins gesetzt.
Suszeptibilit¨ at bis zur 9. Ordnung (unfrustriert)
¨ uber Lanczos-Algorithmus
χ(T ) = 1 4
1 T − 1
8 1 T
2+ 1
96 1 T
4+ 5
1536 1 T
5− 7
5120 1
T
6− 133 122880
1 T
7+ 1
16128 1
T
8+ 1269 4587520
1
T
9(3.13)
Durch Berechnungen mit verschiedenen Ordnungen und Kettenl¨ angen kann man
zeigen, daß die Ergebnisse wirklich unabh¨ angig von der betrachteten System-
gr¨ oße sind. Die Koeffizienten des Polynoms f¨ ur die Suszeptibilit¨ at ¨ andern sich
nicht mehr f¨ ur Berechnungen mit unterschiedlichen Kettenl¨ angen. Ein Vergleich
mit Anhang B zeigt die exakte ¨ Ubereinstimmung der Koeffizienten der Entwick-
lung der Suszeptibilit¨ at, die mit Hilfe des Theorems zusammenh¨ angender Cluster
3.1 Methode 15
berechnet wurde. Diese Ergebnisse belegen die sehr gute Funktionsweise unseres Modells.
3.1.3 Momente-Algorithmus
Die nachfolgend beschriebene Methode ist auf das vorliegende Problem der Hochtemperaturentwicklung zugeschnitten, so daß damit die Berechnungen ef- fizienter als mit dem Lanczos-Algorithmus durchgef¨ uhrt werden k¨ onnen. Es liegen Ergebnisse sowohl f¨ ur die unfrustrierte als auch f¨ ur die frustrierte Kette vor.
Die Methode der direkten Berechnung der Koeffizienten beinhaltet die Taylor- entwicklung der Exponentialfunktion. Es entstehen Potenzen des Hamilton- operators, f¨ ur die die Erwartungswerte bez¨ uglich des Startzustandes bestimmt werden m¨ ussen. Der Startzustand ist
|Sif¨ ur den Nenner und
|MSif¨ ur den Z¨ ahler in Gleichung 3.9:
he-Hi
=
X1n=0
1
n!
h(−βH)ni= 1 −
hHi1 1 !
1
T +
hH2i1 2 !
1
T
2−
hH3i1 3 !
1
T
3+
· · ·(3.14) Die Basiszust¨ ande und die Wirkung des Hamiltonoperators werden wie beim Lanczos-Algorithmus implementiert. Hier bestehen die Listen nun aus den Ba- siszust¨ anden, die durch die Wirkung von
H,
H2,. . . entstehen. Um die Erwar- tungswerte von
H2nund
H2n+1(n
∈N) bestimmen zu k¨ onnen, ben¨ otigt man die zwei Zust¨ ande,
Hn|Siund
Hn+1|Sih
S
|H2n|S
i= (H
n|S
i)2 hS
|H2n+1|S
i= (H
n|S
i)·Hn+1|
S
i. (3.15)
Die Erwartungswerte bez¨ uglich M|Si werden in gleicher Weise berechnet. Hier
wird die Hermitizit¨ at von
Hausgenutzt. Um also die 2n-te Ordnung der Ent-
wicklung bestimmen zu k¨ onnen, reicht es aus,
Hn|S
izu berechnen. Durch diese
Art der Berechnung gen¨ ugt es hier, nur zwei Zust¨ ande, kodiert in zwei Listen,
im Speicher zu halten. Im Vergleich dazu ben¨ otigt der Lanczos-Algorithmus
drei Zust¨ ande bzw. Listen. Ein weiterer Vorteil dieser Methode besteht darin,
daß man pro Entwicklungsschritt nur noch eine Matrix-Vektor-Multiplikation
und eine Vektor-Vektor-Multiplikation durchf¨ uhren muß. Dies bedeutet im Ver-
gleich zum Lanczos-Algorithmus erheblich weniger Laufzeit und auch weniger
Manipulationen an den Listen. Auch hat man hier bei den Berechnungen zur fru-
strierten Kette keine rationalen Funktionen als Vorfaktoren der Basiszust¨ ande,
sondern Polynome in α. Sowohl die Koeffizienten dieser Polynome, als auch
die Koeffizienten der Entwicklung der unfrustrierten Kette lassen sich in ihrer
Gr¨ oße besser absch¨ atzen. Diese erreichen nicht so hohe Zahlen wie dies beim
Lanczos-Algorithmus der Fall ist.
3.1.4 Implementierung
Aus der ¨ Ahnlichkeit der neuen Algorithmusstruktur und der Struktur des Lanczos- Algorithmus ist es recht einfach, das Problem auf dem Rechner zu implemen- tieren. Hier wurde mit der Programmiersprache
” C++“ gearbeitet. Mit dieser Sprache ist es m¨ oglich, Operatoren wie
*(Multiplikation) oder
+(Addition) neu zu definieren, so daß w¨ ahrend der Laufzeit des Programms erkannt wird, welche Operationen konkret f¨ ur die verkn¨ upften Variablen durchgef¨ uhrt werden m¨ ussen. Es ist somit der gleiche Operator, der
integer-Variablen wie auchz.B. Polynome verkn¨ upft. Man nennt diese Eigenschaft das ¨ Uberladen von Operatoren.
Somit konnte mit einigen Unterprogrammen aus dem Lanczos-Algorithmus nach kleinen Modifikationen weitergearbeitet werden. Es wird haupts¨ achlich die Pro- grammstrukur zur Berechnung der frustrierten Kette vorgestellt, da hier die Hauptprobleme in Laufzeit und Speicherbedarf liegen.
Zwei Klassen sind entscheidend. Zum einen die Klasse der Basiszust¨ ande (Ab- bildung 3.3) und zum anderen die Klasse der Vorfaktoren (Abbildung 3.4). Zur
class Basiszustand {
Polynom* vorfaktor
unsigned long long int vektor
Basiszustand* right
}
Abbildung 3.3:
Klasse der Basiszust¨andeBerechnung der frustrierten Kette muß man die ¨ Ubern¨ achstnachbar-Wechselwir- kung getrennt von der N¨ achstnachbar-Wechselwirkung berechnen und abspei- chern. Dazu reicht es nicht mehr aus, Br¨ uche als Vorfaktoren zu verwenden, sondern man ben¨ otigt Polynome in α nach Gleichung 2.1. Da die Polynome vom Grad der berechneten Ordnung in β sind und die Koeffizienten ¨ ahnlich wie beim Lanczos-Algorithmus sehr schnell sehr groß werden, d.h. im Z¨ ahler und im Nenner stehen große Zahlen, ist der Speicherbedarf sehr viel gr¨ oßer als bei der Berechnung der unfrustrierten Kette.
Um den Speicherbedarf soweit wie m¨ oglich einzuschr¨ anken, wurde an einigen
Stellen optimiert. Da bei jeder Anwendung von
Hder Faktor 1/4 hinzukommt,
kann dieser auch nachtr¨ aglich in die Berechnungen eingef¨ ugt werden, und man
ben¨ otigt nur noch ganze Zahlen als Koeffizienten der Polynome. Leider hat dies
auch einen Nachteil, da nun Zweierpotenzen nicht mehr gek¨ urzt werden k¨ onnen,
so daß die Koeffizienten sehr groß werden. Der Variablentyp
long long int(Darstellung bis ca. 10
19) reichte jedoch aus, um die unfrustrierte Kette bis zur
16. Ordnung zu berechnen. Um noch h¨ ohere Ordnungen zu erreichen, m¨ ußte
man sich einen anderen Variablentyp ¨ uberlegen, der folglich auch mehr Speicher
ben¨ otigen w¨ urde und somit das Problem des Speicherbedarfs zus¨ atzlich zur
3.1 Methode 17
class Polynom {
int ord
long long int* coef }
Abbildung 3.4:
Klasse der Vorfaktoren (Polynome)h¨ oheren Ordnung nochmals vervielfachen w¨ urde. Es war leider nicht m¨ oglich, auf bereits existierende Klassen-Pakete zur Darstellung beliebig großer
integer-Zahlen zur¨ uckzugreifen, da diese zuviel Speicher ben¨ otigten.
Um unabh¨ angig von der berechneten Ordnung die Klasse
Polynomals Vorfakto- ren verwenden zu k¨ onnen, haben diese eine dynamische, anpassbare Ordnung.
Dadurch wird gleichzeitig der Speicheraufwand optimiert. Ist der Koeffizient der h¨ ochsten Ordnung Null, so wird das Polynom um einen Grad erniedrigt, und man spart sich den Speicher dieses Koeffizienten. Um die Anzahl der Basiszust¨ ande auf ein Minimum zu reduzieren, werden gleiche Basiszust¨ ande zusammengefaßt und diejenigen mit Vorfaktor Null gel¨ oscht. Dazu wird unter anderem der
quicksort-Algorithmus verwendet, um die Basiszust¨ande zu sor- tieren. Dies verk¨ urzt auch die Berechnung der Skalarprodukte von einer Laufzeit
∝
N
2zu
∝N (N Anzahl Listenelemente). Aus Speichergr¨ unden muß man beim Generieren des neuen Zustandes alle 10
6generierte Basiszust¨ ande sortieren, zu- sammenfassen und gegebenenfalls l¨ oschen. Damit wird zum einen nicht zuviel Speicher auf einmal allokiert und zum anderen kann freigewordener Speicher wieder genutzt werden. Dadurch wird die Laufzeit des
quicksort-Algorithmusan seine obere Grenze von
∝N
2f¨ ur das Sortieren von fast sortierten Listen gebracht. Dies ist leider unumg¨ anglich. Eine weitere Optimierung w¨ urde hier der
heapsort-Algorithmus liefern.Mit diesen Optimierungen kann die Suszeptibilit¨ at f¨ ur die unfrustrierte Kette problemlos berechnet werden. Das Gleiche gilt f¨ ur den Nenner in Gleichung 3.9 der frustrierten Kette. Das einzige Problem besteht nun noch im Speicherbe- darf der Berechnung des Z¨ ahlers in Gleichung 3.9 f¨ ur die frustrierte Kette. Im Vergleich zur Berechnung des Nenners bildet man f¨ ur den Z¨ ahler Erwartungs- werte bez¨ uglich eines Zustandes, der nicht mehr nur aus einem Basiszustand, sondern durch die Anwendung der Magnetisierung M aus N (Anzahl der Ket- tenpl¨ atze) Basiszust¨ anden besteht. Im aufwendigsten Fall ben¨ otigt man N mal soviel Speicher wie bei der Berechnung des Nenners.
Das Speicherproblem wird bei der Berechnung der h¨ ochsten Ordnung relevant.
Um dieses Problem zu vermeiden, wurde auch ein anderer Weg eingeschlagen,
die Erwartungswerte zu berechnen. Aufgrund der Translationsinvarianz der Ope-
ratoren im vorliegenden Problem gilt
hM
2Hni= N
hSz1XN i=1
SziHni
. (3.16) Dadurch erspart man sich die Berechnung der Doppelsumme. Da man in der Spur die Operatoren zyklisch vertauschen darf, wurde zuerst der Hamiltonope- rator auf den Singulettproduktzustand angewandt und erst danach die Magne- tisierung miteingebaut. Dadurch sieht die Rechnung f¨ ur einen Erwartungswert aus der Entwicklung wie folgt aus
h
S
|M
H2nM
|S
i= (h S
|HnSz1)
· XNi=1
SziHn|
S
i!
. (3.17)
Analog lassen sich nat¨ urlich die Erwartungswerte f¨ ur ungerade Potenzen von
Hberechnen. Der Vorteil besteht darin, daß man nicht die Listen mit
Hnangewandt auf M
|S
i, sondern nur angewandt auf
|S
i, im Speicher behalten muß.
Dies entspricht dem Speicheraufwand zur Berechnung des Nenners in Gleichung 3.9. Um nun die Magnetisierung einzubauen, speichert man die Listen
Hnund
Hn+1auf Festplatte ab, wendet ^ S
z1
bzw.
PN i=1S ^
zi
auf diese Listen an und bildet die Skalarprodukte. Am Ende l¨ oscht man die ver¨ anderten Listen und l¨ adt die auf Festplatte gespeicherten Listen wieder in den Arbeitsspeicher. Nun kann man zur n¨ achsten Ordnung gehen, indem man wieder
Hauf diese Listen anwendet.
Um den Festplattenplatz so gering wie m¨ oglich zu halten und dadurch auch die Zugriffszeit so kurz wie m¨ oglich, wurden die Listenelemete bin¨ ar abgespeichert.
Diese Methode der Berechnung des Z¨ ahlers erlaubt vorteilhafterweise Z¨ ahler und Nenner in einem Programm berechnen zu lassen, was die Gesamtlaufzeit in etwa halbiert, da die Listen nur einmal generiert werden m¨ ussen.
Die Berechnungen wurden alle auf einer
SUN Ultra Enterprise 10000am Regionalen Rechenzentrum K¨ oln durchgef¨ uhrt. Diese Plattform stellt pro Pro- zeß 3840 MB Arbeitspeicher zur Verf¨ ugung. Dieser wurde f¨ ur die Berechnungen der h¨ ochsten Ordnung der frustrierten Kette auch vollst¨ andig ausgenutzt bei ei- ner Laufzeit von ungef¨ ahr 10 Tagen. In der h¨ ochsten entwickelten Ordnung ben¨ otigt man rund 60 Millionen Basiszust¨ ande um den entsprechenden Zustand darzustellen. Veranschlagt man im Schnitt 50 bytes pro Listenelement, das einen Basiszustand mit Vorfaktor repr¨ asentiert, so gelangt man schon auf einen Speicherbedarf von 3 GB.
Die Richtigkeit der Koeffizienten wird durch den Vergleich mit den Daten aus Anhang B bzw. selbstkonsistent gepr¨ uft. Der Vergleich mit DMRG (Dichte- matrix-Renormierungsgruppe) zeigt, wie weit man mit Hilfe der berechneten Koeffizienten physikalische Gr¨ oßen darstellen kann.
F¨ ur die unfrustrierte Kette liegen Ergebnisse bis einschließlich 16. Ordnung in β
vor, d.h. 17 Koeffizienten. Da f¨ ur die frustrierte Kette kein direkter Vergleich
3.2 Finite-size Korrekturen 19
mit vorhandenen Ergebnissen m¨ oglich war, konnte die Richtigkeit nur selbst- konsistent ¨ uberpr¨ uft werden. Ein erster Test ist nat¨ urlich der Limes α = 0, bei dem die Ergebnisse der frustrierten Kette in die Ergebnisse der unfrustrierten Kette ¨ ubergehen m¨ ussen. Ein weiterer Test ist die ¨ Ubereinstimmung des Abso- lutterms und des Terms der h¨ ochsten Ordnung in α f¨ ur jede Ordnung in β. Die Berechnung der h¨ ochsten α-Ordnung f¨ ur jede Ordnung in β, d.h. der Koeffi- zient von α
nβ
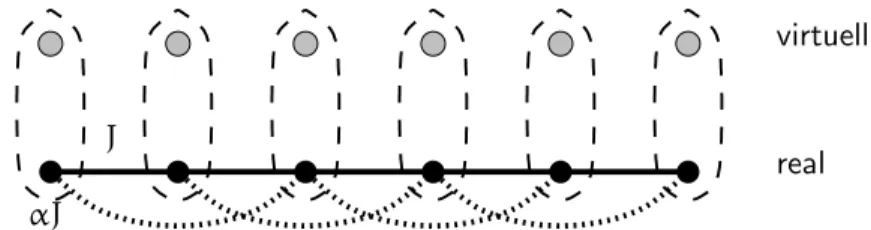
n, enspricht dem Fall, daß keine N¨ achstnachbar-Wechselwirkung in diesem Koeffizienten vorkommt. Es wird ein Term berechnet, der nur aus Ubern¨ ¨ achstnachbar-Kopplungen besteht. Dies enspricht zwei entkoppelter Ket- ten, die nur N¨ achstnachbar-Kopplung besitzen (Abbildung 3.5).
αJ
?
αJ αJ
αJ
Abbildung 3.5:
Bestimmung von Termen der Art αnβn, bei welchen nur Ubern¨¨ achstnachbar-Wechselwirkung vorliegt→Betrachtung zweier entkoppelter Ket- tenDa die Suszeptibilit¨ at pro Platz ausgerechnet wird, m¨ ussen die Ergebnisse ¨ uber- einstimmen. Bei der frustrierten Kette gelang die Berechnung der Suszeptibilit¨ at bis zur 10. Ordnung in β. Die beiden Ergebnisse (Anhang C) wurden in der h¨ ochsten Ordnung korrigiert, da die Kettenl¨ ange der h¨ ochsten berechneten Ord- nung entsprach und somit finite-size Korrekturen n¨ otig waren (Abschnitt 3.2).
Allgemein sei festgehalten, daß die berechneten Gr¨ oßen tats¨ achlich unabh¨ angig von der betrachteten Systemgr¨ oße sind. Durch Rechnungen mit verschiedenen Kettenl¨ angen konnte gezeigt werden, daß die entstehenden Polynome exakt
¨
ubereinstimmen. Dies stellt einerseits eine ¨ Uberpr¨ ufung der Rechnungen und andererseits eine Best¨ atigung des Theorems zusammenh¨ angender Cluster [15]
dar.
3.2 Finite-size Korrekturen
Bei den Berechnungen von Z¨ ahler und Nenner in Gleichung 3.9 kommt es darauf
an, den Speicher optimal zu nutzen. Um keine finite-size-Effekte zu erhalten,
sollte das betrachtete System, d.h. die Kettenl¨ ange m¨ oglichst groß sein. Dabei
bedeuten finite-size Effekte hier, daß aufgrund der periodischen Randbedingun-
gen in hohen Ordnungen der Entwicklung Erwartungswerte berechnet werden,
die in dieser Ordnung eigentlich nicht auftreten d¨ urfen. Bei einer Verl¨ ange-
rung der Kette verschwinden diese Effekte wieder. Da eine Verl¨ angerung der
Kette bei den Berechnungen f¨ ur die h¨ ochsten Ordnungen der Entwicklung aus Speichergr¨ unden nicht m¨ oglich war, mußten finite-size Effekte in Kauf genom- men werden, die nachtr¨ aglich explizit behoben wurden. Bei der Anwendung des Hamiltonoperators 2.1 mit nur N¨ achstnachbar-Wechselwirkung auf den Singu- lettproduktzustand sind jeweils benachbarte Kettenpl¨ atze betroffen, so daß Ba- siszust¨ ande entstehen, bei denen die gr¨ oßten entstehenden zusammenh¨ angenden Cluster aus einem bond bestehen. Durch weiteres Anwenden des Hamiltonope- rators kommt jeweils ein bond zum gr¨ oßten zusammenh¨ angenden Cluster hinzu, d.h. alle Kettenpl¨ atze an diesen bonds sind der Wirkung von
Hausgesetzt bzw.
ausgesetzt worden.
Bei einer Kette mit N Pl¨ atzen gibt es N − 1 bonds, wenn man die periodischen Randbedingungen nicht beachtet. Das bedeutet, daß man nur bis zur Ordnung N − 1 entwickeln darf, ohne finite-size Effekte zu erhalten. Ein typischer finite- size Effekt ist das Umlaufen des gr¨ oßten zusammenh¨ angenden Clusters aufgrund der periodischen Randbedingungen.
N
1
typischer finite-size Effekt
Entwickelt man nun bis zur N-ten Ordnung, so sind die gr¨ oßten entstehenden Cluster aufgrund der periodischen Randbedingungen in dieser Ordnung der Ent- wicklung nicht korrekt erfaßt. Im weiteren wird von einer Kette mit N Pl¨ atzen ausgegangen, die in der N-ten Ordnung entwickelt wird. Es werden die finite-size Effekte f¨ ur den Z¨ ahler und den Nenner aus Gleichung 3.9 getrennt berechnet.
Dabei wird zuerst nur die unfrustrierte Kette betrachtet, und danach werden die Ergebnisse auf die frustrierte Kette ¨ ubertragen.
N − 1
N − 2 N 1 2 3
Abbildung 3.6: Ursache des finite-size-Effektes im Nenner von Gleichung 3.9 F¨ ur den Nenner in Gleichung 3.9 bedeutet dies, daß Erwartungswerte bzw. Spu- ren der Art
hHNi
=
· · ·+
h(S1S2) (S
2S3)
· · ·(S
NS1)i
=
· · ·+
hS21S22· · ·S2Ni(3.18) bei den Berechnungen miteingehen, obwohl diese nicht realisiert sind (sche- amtische Darstellung in Abbildung 3.6). Dabei treten Spinprodukte der Art
^ S
S ^
0mit σ
∈( x, y, z ) auf. Nur Beitr¨ age mit σ = σ
0liefern Werte un- gleich Null, da f¨ ur Spinprodukte mit σ
6=σ
0die Erwartungswerte verschwinden (
h· · ·S ^
i
S ^
0i · · · i
= 0). Es sind Terme mit S ^
2= 1/4, die f¨ ur eine Kette mit N Pl¨ atzen durch die drei Komponenten von σ einen Beitrag von 3
14
N
liefern.
Durch N! M¨ oglichkeiten der Anordnung der Faktoren
SiSi+1kommt man auf einen Faktor N !
·3
1N, der im Nenner in der N-ten Ordnung zuviel berechnet
3.2 Finite-size Korrekturen 21
wurde. Alle anderen Terme, die aus Clustern einer kleineren Gr¨ oße bestehen, sind korrekt erfaßt.
Die finite-size Effekte beim Z¨ ahler von Gleichung 3.9 sind nicht ganz so offen- sichtlich. Auch hier sind nur die gr¨ oßten entstehenden zusammenh¨ angenden Cluster in der N-ten Ordnung f¨ ur die Effekte verantwortlich. Es ergeben sich durch die Magnetisierung M drei Anteile, die betrachtet werden m¨ ussen. Als erstes ist es der Anteil der Art
h
S ^
z1HNS ^
z1i=
· · ·+
hS ^
z1(S
1S2) (S
2S3)
· · ·(S
NS1) ^ S
z1i, (3.19) der zuviel berechnet wird und einen Faktor von N!3
14N+1
produziert. Dabei ist die Begr¨ undung die gleiche wie f¨ ur die finite-size Effekte des Z¨ ahlers. Daf¨ ur fehlen Terme der Art
h
S ^
z1(S
1S2) (S
2S3)
· · ·(S
NSN+1) ^ S
zN+1i, (3.20) die nur f¨ ur die z-Komponenten der Spins einen Beitrag liefern, da der Erwar- tungswert
h
S ^
z1· · ·
X
0
S ^
01
S ^
02
· · · X
S ^
N
^ S
N+1
!
· · ·
^ S
zN+1i
(3.21) f¨ ur σ, σ
0 6=z verschwindet. Durch Abz¨ ahlen der Anordnungen der Spinprodukt- terme
SiSi+1und durch Vertauschen der Indizes der ¨ außersten z-Komponenten der Spins aus der Magnetisierung M ist dies insgesamt ein Beitrag von 2N !
14N+1
, der in den Berechnungen fehlt.
Die periodischen Randbedingungen liefern noch weitere Terme, die in Abbildung 3.7 veranschaulicht sind. Es sind Terme, bei denen ein Kettenplatz in den Spinpro-
N − 1
N − 2 N 1 2 3
Sz
Abbildung 3.7:
Anordnungen der^Szim Z¨ahler von Gleichung 3.9, die finite-size Effekte bewirken.dukten dreifach auftritt. Multipliziert man die Spinproduktterme
SiSi+1f¨ ur diesen Fall aus, ergeben sich Beitr¨ age
S ^
z1
S ^
x1
S ^
y1 ·
S ^
xi
S ^
yi
S ^
zi
, (3.22)
wobei S ^
z1
und S ^
zi
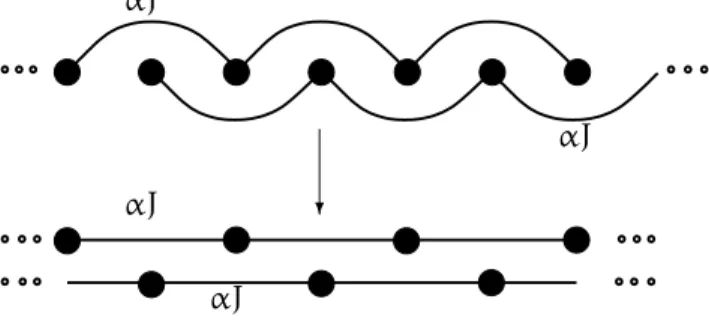
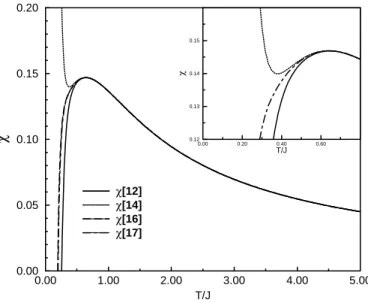
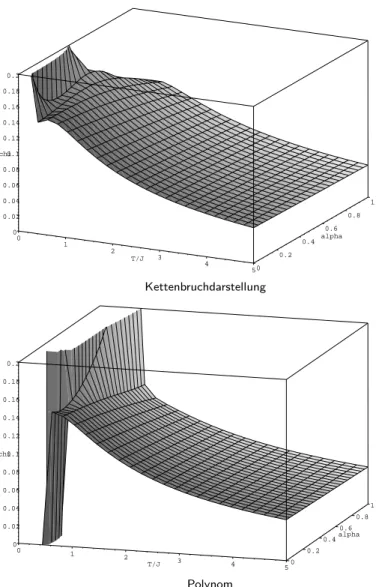
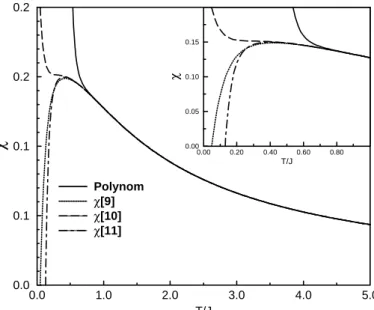
![Abbildung 5.1: Verschiedene Ordnungen der Polynome der unfrustrierten Suszeptibi- Suszeptibi-lit¨ at χ (durchgezogene Linie) und der entsprechenden χ [ n + 1 ]-Kettenbruchdarstellungen (gestrichelte Linie) gegen¨ uber T/J](https://thumb-eu.123doks.com/thumbv2/1library_info/3904649.1525135/32.892.196.756.291.925/verschiedene-unfrustrierten-suszeptibi-suszeptibi-durchgezogene-entsprechenden-kettenbruchdarstellungen-gestrichelte.webp)

![Abbildung 5.7: Verschiedene Darstellungen der spezifischen W¨ arme der frustrierten Kette mit α = 0.35 0.0 1.0 2.0 3.0 4.0 5.0 T/J0.00.10.20.30.40.50.60.70.8s Polynoms[10]s[11] c[10] integriert0.00.10.20.3 0.4 0.5 0.6T/J 0.00.10.20.30.40.5 s](https://thumb-eu.123doks.com/thumbv2/1library_info/3904649.1525135/39.892.217.594.245.555/abbildung-verschiedene-darstellungen-spezifischen-frustrierten-kette-polynoms-integriert.webp)