Statik starrer Körper

Statik starrer Körper

Gleichgewichtsbedingungen (GGB) 0

0 0

ix iy i

F F M

=

=

=

∑ ∑

∑

Lagerreaktionen

à statische und kinematische Bestimmtheit

3 0

a+ − ⋅ =z n

mit a = Summe der Auflagerbindungen z = Summe der Zwischenbindungen

mit z_i = ⋅2 (m_i−1)

mi =Anzahl der SK am Gelenk i n = Anzahl der starren Körper

Schnittgrößen

²

²

dQ dM d M

q Q q

dx = − dx = dx = − Haftung und Reibung

R≤µ0⋅N mit µ₀ =tanα₀ =Haftreibungskoeffizient Schwerpunkt

Fläche _{S S}

xdA ydA

x y

dA dA

=

∫

∫

∫ ∫

bzw. bei bekannten Schwerpunkten von Teilflächen

i i i i

S S

i i

x A y A

x y

A A

⋅ ⋅

=

∑

∑

∑ ∑

Linie _{S S}

xds yds

x y

ds ds

=

∫

∫

∫ ∫

bzw.

i i i i

S S

i i

x l y l

x y

l l

⋅ ⋅

=

∑

∑

∑ ∑

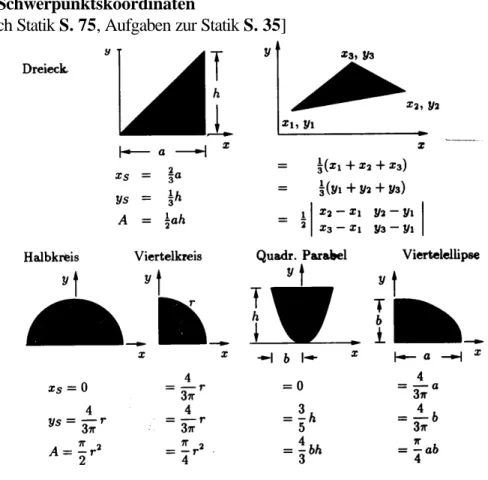
Tabelle von Schwerpunktskoordinaten

[vgl. auch Buch Statik S. 75, Aufgaben zur Statik S. 35]

Flächenträgheitsmomente

²

²

²

y A z

A

yz zy

A

P y z

A

I z dA I y dA

I I z ydA

I I I r dA

=

=

= = − ⋅

= + =

∫

∫

∫

∫

Satz von Steiner

²

²

y y S

z z S

yz yz S S

I I z A

I I y A

I I z y A

= + ⋅

= + ⋅

= − ⋅ ⋅

mit z_S, y_S = Abstand zur jeweiligen Schwerachse

Transformationsformeln

cos(2 ) sin(2 )

2 2

cos(2 ) sin(2 )

2 2

sin(2 ) cos(2 )

2

y z y z

yz

y z y z

yz

y z

yz

I I I I

I I

I I I I

I I

I I

I I

η

ξ

ηξ

α α

α α

α α

+ −

= + ⋅ + ⋅

+ −

= − ⋅ − ⋅

= − − ⋅ + ⋅

Hauptträgheitsmomente

2 2

1,2 2 2

y z y z

yz

I I I I

I +  −  I

= ±   +

 

Hauptachsenrichtung tan(2 _H) 2 ^yz

y z

I I I

α ⋅

= −

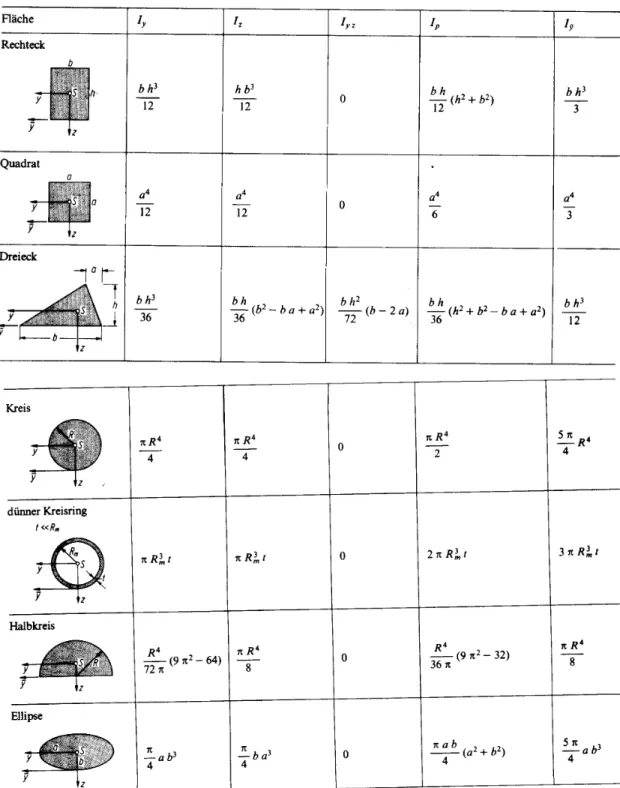
Tabelle von Flächenträgheitsmomenten

[vgl. auch Statik-Aufgaben S. 193, Elastostatik S. 84]

Elastostatik

Spannungen

Normalspannung: ^dN

σ = dA

Schubspannung: ^dQ

τ = dA

Schnittgrößen-Spannungsbeziehungen (SSB)

A

A

A

N dA

Q dA

M z dA

σ τ

σ

=

=

= ⋅

∫

∫

∫

Stab

Spannung ( )

( ) ( )

x N x σ = A x

Dehnung ^{l du}

l dx ε= ∆ = Verlängerung

0^l ( ) l ε x dx

∆ =

∫

Hooke σ = ⋅E ε à l ^{F l}

E A

∆ = ⋅

⋅ Wärmedehnung ε_th = ⋅ ∆α T à _{εges =εel+εth} Wärmespannung σth = − ⋅ ⋅ ∆α E T à σ_ges =σ_el+σ_th

Ebener Spannungszustand

es gilt: τ_xy =τ_yx, τ_{x y} ⊥τ_yx

à bei Schnitt: GGB anwenden, wobei Spannungen jeweils mit zugehöriger Fläche zu multiplizieren (Schnittfläche = dA, Seitenflächen jeweils sin/cos dA)

Transformationsformeln

cos(2 ) sin(2 )

2 2

cos(2 ) sin(2 )

2 2

sin(2 ) cos(2 )

2

x y x y

xy

x y x y

xy

x y

xy ξ

η

ξη

σ σ σ σ

σ α τ α

σ σ σ σ

σ α τ α

τ σ σ α τ α

+ −

= + ⋅ + ⋅

+ −

= − ⋅ − ⋅

= − − ⋅ + ⋅

Hauptspannungen (extremale Normalspannungen)

2 2

1,2 2 2

x y x y

xy

σ σ σ σ

σ = + ±  −  +τ

 

Hauptspannungsrichtungen

* 1

tan(2 ) 2 ^xy

x y

ϕ τ

σ σ

= ⋅

− Richtungen stehen senkrecht à ϕ^*2 =ϕ1^* ±π2 maximale Schubspannungen

2 2

max 2

x y

xy

σ σ τ =  −  +τ

  à ϕ^**=ϕ^*±π4

Mohrscher Spannungskreis

à siehe auch Aufgaben zur Elastostatik, S. 11

Mittelpunkt ^{σm = 12}

(

)

Radius

2 2

2

x y

r σ σ xy

− τ

 

=   +

 

Verzerrungen ( , ) ( , )

( , ) ( , )

x

y

xy

u x y x v x y

y

u x y v x y

y x

ε ε γ

=∂

∂ ∂

= ∂

∂ ∂

= +

∂ ∂

Biegung

Normalspannung ( ) M

z z

σ = I ⋅

max

M

σ = W mit

max

W I

= z

Biegelinie ( ) M x^{( )}

w x′′ = − E J

⋅ (linearisierte DGL der Biegelinie) ( )x w x( )

ϕ = − ′

à Integrationskonstanten aus Randbedingungen

à bei mehreren Bereichen Übergangsbedingungen beachten (keine Sprünge, gleich Biegung)

Überlagerungsmethode à w_max à Myosotis-Formeln

max max

, ²

3 2

F l F l

w E I⋅ ϕ E I⋅

= =

⋅ ⋅ ⋅ ⋅

(auf alle Anteile achten! à vgl. Vorlesungsmitschrift S. 91)

Energiemethoden

Elastische Energie der Bauteile

à Zug/Druck ¹₂

0

²( )

l Z

U N x dx

= E A

∫

0

²( )

l B

M x

U dx

= E I

∫

0

²( )

l Q

U Q x dx

E A κ

= ⋅

∫

6 5 10

9

Rechteck Kreis κ

κ

=

= à Torsion

2 1 2 0

( )

l T

T

P

M x

U dx

= G I

∫

Arbeitssatz W =U

Castigliano

( , ) ( , )

i i , i i

i i

i i

U F M U F M

u = ∂ F ϕ =∂ M

∂ ∂ partielle Ableitung

à Achtung bei Koordiante ϕ à Integral über r dϕ⋅ , nicht _dϕ !!!!

mit Hilfskraft

à an Arbeitsstelle einführen, weiterrechnen wie mit eingeprägter Kraft à nach partieller Ableitung in der weiteren Rechung zu "0" setzen statisch unbestimmte Probleme

à Lagerreaktion durch Hilfskraft ersetzen à Verschiebung zu "0" setzen (da festes Lager) Satz von Meambrea

à statisch unbestimmte Xi stellen sie genau so ein, dass die gesamte im System gespeicherte Energie minimal wird

!

0

i

U

∂ =X

∂ (in U =U F M X( ,_{i i, i})keine Lagerkräfte !!!) Torsion

Kreisquerschnitt

T P

M = ⋅ ⋅G ϑ I mit _P ²

A

I =

∫

Schubspannung _x ^T

P

M r

ϕ I

τ = ⋅ mit _{T x}

A

M =

∫

l

ϑ =∆ϕ ^T

P

M l ϕ ϕ G I⋅

∆ = =

⋅ (vgl. FLEA) Kreisringquerschnitt

4 4

2( )

P a i

I =^π r −r

2

T x

m

M

ϕ A h τ =

⋅ ⋅ Am = umschlossene Fläche

h = Dicke Schubfluß

t= ⋅h τx_ϕ

2

T m

t M

= A

⋅ "1. Bredtsche Formel"

Verformung bei dünnwandigen, geschlossenen Profilen

4 2

T T

m T

M ds M

A G h G I

ϑ = =

⋅ ⋅

Ñ ∫

mit

4 _m2 T

I A

ds h

= ⋅

Ñ ∫

à bei Zweigstegen über einzelne Profile Summieren dünnwandige offene Profile

3 3

1 1

3 3

1

.

n

T T i i

i

I l h bzw I l h

=

= ⋅ ⋅ =

∑

Verdrillung ^T

T

M ϑ =G I

⋅

Schubspannung _i,max ^T _i

T

M h τ = I ⋅

Querschnittskennwerte bei Torsion [vgl. auch Elastostatik S. 108]

Kinematik und Kinetik

Bahn rr r=r t( )

Geschwindigkeit

lim0 t

r dr

v r

t dt

∆ →

= ∆ = =

∆

r r

r r& "Momentangeschwindigkeit"

vrimmer tangentiell zur Bahn à Tangenteneinheitsvektor _t dr er = drr r à vr r r= ⋅ = ⋅v e_t v er_t Beschleunigung a ^dv v r

= dtr = = r r r& &&

Kinematik des Massenpunkts kartesische Koordinaten

x y z

x y z

x y z

r x e y e z e v x e y e z e a x e y e z e

= ⋅ + ⋅ + ⋅

= ⋅ + ⋅ + ⋅

= ⋅ + ⋅ + ⋅

r r r

r r r

& & &

r r r

&& && &&

2 2 2

2 2 2

v x y z ds dt

a x y z s

= + + =

= + + ≠

r & & &

r && && && &&

Polarkoordinaten

( ²) ( 2 )

r z

r z

r z

r r e z e

v r e r e z e

a r r e r r e z e

ϕ

ϕ

ϕ

ϕ ϕ ϕ

= ⋅ + ⋅

= ⋅ + ⋅ + ⋅

= − ⋅ + + ⋅ + ⋅

r r

r r r

& & &

r r r

&& & && & & &&

mit (r&&−rϕ&²)⋅er_r Radialbeschleunigung (rϕ&&+2r& &ϕ)⋅er_ϕ Querbeschleunigung

z e⋅rz

&& Axialbeschleunigung

ebene Bewegung à z = 0 ( )

( )

( ) ( ²) ( 2 )

r r

r

r t r e

v t r e r e

a t r r e r r e

ϕ

ϕ

ϕ

ϕ ϕ ϕ

= ⋅

= ⋅ + ⋅ ⋅

= − ⋅ ⋅ + ⋅ + ⋅ ⋅ ⋅

r r

r & r & r

r && & r && & & r

Kreisbewegung à r = const.

2

( ) ( ) ( )

r

r

r t r e v t r e

a t r e r e

ϕ

ϕ

ϕ

ϕ ϕ

= ⋅

= ⋅

= − ⋅ + ⋅

r r

r & r

r & r && r

mit Winkelgeschwindigkeit ω ϕ= &

à ^{( )} ₂

( ) _r

v t r e

a t r e r e

ϕ

ϕ

ω

ω ω

= ⋅

= − ⋅ + ⋅

r r

r r & r

wobei a_t = ⋅r ω& "Bahnbeschleunigung"

² ²

n

a v r

r ω

= = ⋅ "Zentripetalbeschleunigung"

ebene Bewegung in Polarkoordinaten Radialgeschwindigkeit v_r =r&

Zirkulargeschwindigkeit v_ϕ = ⋅r ω Radialbeschleunigung a_r = − ⋅r&& r ω² Zirkularbeschleunigung a_ϕ = ⋅ + ⋅ ⋅r ω& 2 r& ω

"Zentralbewegung" à a_ϕ =0

à Flächensatz a_ϕ =rω&+2r&ω=¹_r( ²r ⋅ω)&= ⇒ ⋅ =0 r² ω konst. (Ortsvektor überstreicht in gleichen Zeiten gleiche Flächen) Kinetik des Massenpunkts

Bewegungsgesetz

( )

d m v

p F

dt⋅ = =& à mit F =

∑

F m v m a r = ⋅ = ⋅ r & r

x y

m x F

m y F

⋅ =

⋅ =

∑ ∑

&&

&&

Impulssatz (Impuls: p oder J)

0

0 t

m v m v⋅ − ⋅ =

∫

(0)

dL (0)

dt =M L⁽⁰⁾ = ×r p Drehimpuls (Drall) bzgl. Punkt 0 M(0) = ×r F Moment bzgl. Punkt 0

Kinematik der ebenen Bewegung starrer Körper

à SK-Bedingung: "Geschwindigkeitsvektoren von je 2 Punkten haben stets gleiche Komponenten in Richtung ihrer Verbindungs-Geraden."

Grundformel (Euler-Gleichung)

p AP

AP AP

p AP

v v r

r r

v v r

ω ω

= +

→ = ×

⇒ = + ×

r r r&

r& r r

r r r r

Winkelgeschwindigkeitsvektor ist unabhängig vom Bezugspunkt Beschleunigung

P A AP ² AP

ar =ar + ×ωr r& r −ω ⋅rr

"ebene Drehung" à Richtung von ω = konst à ⊥ − −x y Ebene ⇒ = ⋅ω ωr er_z

( )

( ) ²

P A z AP

P A z AP AP

v v e r

a a e r r

ω

ω ω

= + ⋅ ×

= + ⋅ × − ⋅

r r r r

r r & r r r

Momentenpol G

à v_G =0 (à Momentanbewegung = Rotation mit ω um Pol)

²

A G

r r ω v ω

= + r r×

r r

im Komponenten

A

G A

A

G A

x x y y y x

ω ω

= −

= −

&

&

à momentane Geschwindigkeitsverteilung so, als ob Drehpol G fester Punkt um den Scheibe rotiert

à vP = ⋅ω rGP

Impulssatz in integraler Form

2

1

2 1 2 1

( ) ( )

t

F t

S^r =

∫

Drallerhaltungssatz) Lr(0) = × = × ⋅rr r rp r m vr

à Zeitintegration

2

( 0 ) ( 0 )

1

(0) 2 1

t M

t

S^r =

∫

mit Sr_M =

Stoßmoment

Arbeitssatz

(1. Integration der KGG über den Weg) dA=dT "differentielle Form"

mit T = ¹₂m v⋅ ² = kinetische Energie des Massenpunkts kinetische Energie

1 2 1

2 2 ²

k S S

E = m v⋅ + Θ ⋅ω reine Translation E_k = ¹₂m v⋅ ²_S reine Rotation E_k = Θ ⋅¹_{2 S} ω² Übersicht

Einzelmasse (MP) Massenpunktsystem (MPS) starrer Körper (SK) Schwerpunkt

rr rS =r i i

S

r m r m

=

∑

r _m

S

rdm rr =

∫

pr = ⋅m vr pr = ⋅m vrS

(1. Schwerpunktssatz)

pr= ⋅m vrS

i S

R^r=

∑

Fr = ⋅m ar für

0 0

Fr = ⇒ = ⇒ =pr& pr konst

i S

F = ⋅m a

∑

für

i 0

R^r=

∑

Lr(0) = × = × ⋅rr r rp r m vr Lr⁽⁰⁾ = × + Θ ⋅rr r^S p ^S ωr

"starres MPS"

(0) S S

M r p ω

⇒ r = × + Θ ⋅r r& r

L^r(0) =

∫

(0) ( )s S

M r p ω

⇒ r =r × + Θ ⋅r& r

nur angewandt auf raumfesten Bezugspunkt oder Schwerpunkt !

kinetische Energie

1

2 ²

T = m v⋅

1

2 ² _S ²

T = m v⋅ + Θ ⋅ω mit Θ =S

∑

1

2 ² _S ²

T = m v⋅ + Θ ⋅ω mit Θ =_S

∫

Stoßvorgänge

à Impulserhaltung m v₁⋅ + ⋅ = ⋅ + ⋅₁ m v_{2 2} m v_{1 1}^* m v₂ ^*₂ à Energieerhaltung (Π +T)_vor = Π +( T)_nach

Stoßhypothese (Newton)

* *

2 1 1 2

(v −v )= ⋅k (v−v )

mit "Stoßzahl k"

1

k = à vollelastischer Stoß 0

k= à vollplastischer Stoß 0< <k 1 à teilplastischer Stoß Energieverlust

1

2 2

2 2 * *

1 1 1 1

1 2 2 1 1 2 2

2 2 2 2

( ) ( )

V vor nach

T =T −T = m v + m v − m v + m v

à _{1 2} ^{1 2}

1 2

1 ²

( )²

V 2

k m m

T v v

m m

− ⋅

= − ⋅

+