1. ¨ Ubungsblatt f¨ ur den 4. 3. 2008 1. Ubungsbeispiele ¨
(1) Die Gerade g sei durch die Gleichung 2x − y = 3 gegeben. Bestimmen sie Gleichungen der beiden Geraden, die parallel zu g sind und den Abstand 2 von g haben.
Bestimmen sie alle Punkte, die von den beiden Geraden g
1und g
1gegeben durch die Gleichungen g
1: 2x − y = 0 und g
2: x + y = 2 jeweils den Abstand 1 haben.
(2) Gegeben sind die komplexen Zahlen z
1= 2 + 3ı und z
2= 2 − ı. Berechnen sie z
1z
2,
z12
, z
22z
1und
zz21
in der komplexen Standardform a + ib und in komplexen Polarkoordinaten r e
iϕmit r ≥ 0 und ϕ ∈ [0, 2π).
(3) E sei die Menge aller komplexen Zahlen mit Betrag 1, das heißt E = {a + ıb : a, b ∈ R mit a
2+ b
2= 1}. Zeigen sie: Falls z ∈ E dann gilt auch −z ∈ E, z ∈ E und
1z∈ E. Falls y ∈ E und z ∈ E, dann gilt auch yz ∈ E.
(4) Skizzieren sie die folgenden Mengen in der komplexen Ebene
M
1= {z ∈ C : |z − 1| = 1}, M
2= {w ∈ C : ww > 1}, M
3= {u ∈ C : <(iu) > 0}.
(5) Zeigen sie, dass f¨ ur jede beliebige Komplexe Zahl z 6= 0 sich eine reelle Zahl a finden l¨ aßt so dass
1z= az. (Das heißt, 0, z und
1zliegen auf einer Geraden.)
2. Trainingsbeispiele zur Selbstkontrolle T1. Berechnen sie z + w, |z| und |w| f¨ ur z = −ı + 3, w = −2 + 4ı.
T2. Berechnen sie den Cosinus des Winkels zwischen den Vektoren v
1= (1, 2, 1)
tund v
2= (2, 0, 2)
t. F¨ ur welche Winkel wird dieser Wert der Cosinusfunktion angenommen?
T3. Bestimmen sie eine Gleichung welche die Kreislinie mit Mittelpunkt (1, −2) und Radius 2 in
der (x, y)-Ebene definiert.
H ¨ OHERE MATHEMATIK 2, ¨ Ubungen, Sommersemester 2008 2. ¨ Ubungsblatt f¨ ur den 11. 3. 2008
1. Ubungsbeispiele ¨
(6) Die drei komplexen Zahlen z
1= 1 + ı, z
2= 2 + 3ı und z
3= −1 + 2ı sind Eckpunkte eines Dreieckes in der komplexen Ebene. Berechnen sie die Innenwinkel und die Seitenl¨ angen des Dreieckes. F¨ ur die beiden komplexen Zahlen u = ı und v = 1 + ı seien 4
uund 4
vdie Dreiecke mit den Ecken (uz
1, uz
2, uz
3) bzw. (vz
1, vz
2, vz
3). Berechnen sie die Seitenl¨ angen und Innenwinkel der Dreiecke 4
uund 4
v. Berechnen sie die Winkel zwischen z
kund uz
kund zwischen z
kund vz
kf¨ ur k = 1, 2, 3. Fertigen sie eine Skizze mit der drei Dreiecke in der komplexen Ebene an.
(7) Berechnen sie die beiden komplexen Wurzeln von v = 2 + 3ı (d.h. die beiden L¨ osungen von z
2= 2 + 3ı in C ). Skizzieren sie v und die beiden Wurzeln in der komplexen Ebene.
(8) L¨ osen sie die quadratische Gleichung z
2+ (2 + ı)z + 1 = 0 in C .
(9) Beweisen sie: Falls die Zahl z ∈ C \ R L¨ osung der quadratischen Gleichung aw
2+ bw + c = 0 mit a, b, c ∈ R ist, dann ist auch die konjugiert komplexe Zahl z eine L¨ osung der quadratischen Gleichung.
(10) Stellen sie den Ausdruck cos
4(θ) als Linearkombination von Winkelfunktionen mit Vielfachen des Winkels θ im Argument der Winkelfunktionen dar. Das heißt, finden sie eine Darstellung
cos
4(θ) =
?
X
k=0
α
ksin(kθ) + β
kcos(kθ).
Verwenden sie zur Herleitung die Eulersche Darstellung der Cosinusfunktion durch komplexe Exponentialfunktionen.
(11) Es sei l eine Gerade in der komplexen Ebene, die mit der (positiv orientierten) reellen Achse den Winkel ϕ einschließt. Ein beliebiger Punkt z ∈ l auf der Geraden wird ausgew¨ ahlt. Mit d bezeichnen wir den Normalabstand des Koordinatenursprungs von der Geraden. Zeigen sie dass die Formel
d =
Im(e
−ıϕz) gilt.
(12) Skizzieren sie die Menge M =
z ∈ C : Re (1 − 2ı)z
= 0 in der komplexen Ebene. Geben sie eine geometrische Charakterisierung der Punktmenge M an.
2. Trainingsbeispiele zur Selbstkontrolle
T4. Berechnen sie die Polarkoordinatendarstellungen der folgenden komplexen Zahlen: √ −1 − ı, 3 − ı, 3 − 2ı.
T5. Berechnen sie die (kartesische) Standardform a + ıb der Zahlen e
iπ, 2e
iπ4, −e
−ıπ3.
1
3. ¨ Ubungsblatt f¨ ur den 1. 4. 2008 1. Ubungsbeispiele ¨
(13) Bestimmen sie alle L¨ osungen z ∈ C (z = re
ıϕ) der folgenden Gleichungen:
(a) z
3= 1 + ı, (b) ı z
5= 1, (c) z
3= −1.
Skizzieren sie die Lage der L¨ osungen in der komplexen Ebene.
(14) Geben sie alle L¨ osungen z ∈ C der Gleichung z
5− z
2= 0 an. Skizzieren sie die Lage der L¨ osungen in der komplexen Ebene.
(15) Bestimmen sie drei verschiedene L¨ osungen z ∈ C der Gleichung e
z= 3 + 2ı in der komplexen Standardform z = a + ıb. K¨ onnen sie eine L¨ osung mit ganzzahligem Real- und Immagin¨ arteil finden?
(16) Es sei A = ı
ı. Schreiben sie A in der Form A = a + ıb. (Hinweis: x
y= e
ylnx.) (17) L¨ osen sie die folgenden linearen Gleichungssysteme ¨ uber C :
(a) 3x + 6y = 1
2x + 3y = 0 , (b) ıx + y = 0
x + (1 + ı)y = 2ı , (c) (3 + 4ı)x + ıy = 1
(3ı − 4)x − y = 1 , (d) ıx + 2y = 4
2ıx + 4y = 8 .
H ¨ OHERE MATHEMATIK 2, ¨ Ubungen, Sommersemester 2008 4. ¨ Ubungsblatt f¨ ur den 8. 4. 2008
1. Ubungsbeispiele ¨
(18) Schreiben sie f(z) := 3z
2+ 1 in der Form f (x + iy) = u(x, y) + iv(x, y) und zeigen sie, dass u und v die Cauchy-Riemannschen Differentialgleichungen erf¨ ullen. Berechnen sie die komplexe Ableitung f
0(2 + i3) gem¨ aß Definition als f
0(z) = lim
h→0 f(z+h)−f(z)h
.
(19) Schreiben sie f (z) := e
zin der Form f(x + iy) = u(x, y) + iv(x, y) und zeigen sie, dass u und v die Cauchy-Riemannschen Differentialgleichungen erf¨ ullen. Berechnen sie lim
zn→z ezn−ezzn−z
, indem sie f¨ ur z
neine gegen z konvergierende Folge von komplexen Zahlen w¨ ahlen, die auf einer durch z gehenden Geraden geeigneter Neigung liegen. Warum ist es nach obigem erlaubt zu sagen, dass der auf diese spezielle Weise erhaltene Grenzwert die Ableitung von e
zist?
(20) Es seien ~a =
3 4 1 0
, ~b =
i2 i 0 1
, ~c =
2 2 1 1
∈ C
4.
(a) Bestimmen sie ~ x ∈ C
4, so dass 3~ x + 2~a − ~b = 6~ x + 4~c.
(b) Bestimmen sie (falls m¨ oglich) s, t ∈ R , so dass s~a + t~c =
3 2 1 1
.
(21) (a) Entnehmen sie durch m¨ oglichst genaue Konstruktion und Messung aus der Zeich- nung
a b
u
v
z
die Zahlen u
1, u
2, v
1, v
2, z
1, z
2, z
10, z
20in den Darstellungen
~
u = u
1~a + u
2~b, ~v = v
1~a + v
2~b, ~z = z
1~a + z
2~b, ~z = z
01~ u + z
20~ v.
(b) Berechnen sie die Zahlen z
1, z
2aus den gemessenen Zahlen u
1, u
2, v
1, v
2, z
10, z
02und ver- gleichen sie ihr Messergebnis mit dem Rechenergebnis. Zeichnung auf Overheadfolie!.
(22) Es sei V ein Vektorraum ¨ uber einem K¨ orper K und ~a,~b, ~c ∈ V \ {~ o}. Ferner seien r, s, t ∈ K mit r + s + t 6= 0 und r~a + s~b + t~c = ~ o. Zeigen sie, dass sich dann mindestens einer der Vektoren ~a,~b, ~c als Linearkombination der restlichen beiden darstellen l¨ aßt. Gibt es r, s, t ∈ K mit r + s + t 6= 0 und r~a + s~b + t~c = ~ o, so dass sich nur genau einer der drei Vektoren als Linearkombination der beiden restlichen darstellen l¨ aßt?
1
5. ¨ Ubungsblatt f¨ ur den 15. 4. 2008 1. Ubungsbeispiele ¨
Im folgenden seien ~ e
1, ~ e
2, ~ e
3) eine Basis aus drei paarweise zueinander orthogonalen Einheitsvek- toren, die ein Rechtssystem bilden.
(23) Es sei (~ e
1, ~ e
2) eine Basis von R
2aus zwei zueinander orthogonalen Einheitsvektoren und
~
n = n
1~ e
1+ n
2~ e
2= (cos ϕ)~ e
1+ (sin ϕ)~ e
2ein weiterer Einheitsvektor. Ferner sei S : R
2→ R
2die Spiegelung an der durch den Ursprung gehenden Geraden g, die senkrecht auf ~ n steht.
(a) Welche geometrische Abbildung wird durch ~ x 7→ ~ x − 2h~ x, ~ ni~ n beschrieben?
b) Bestimmen sie die Matrix S der Spiegelung bzgl. der Basis (~ e
1, ~ e
2), indem sie die Matrix- elemente durch n
1= cos ϕ, n
2= sin ϕ ausdr¨ ucken.
(c) Zeigen sie, dass die Hintereinanderausf¨ uhrung zweier Spiegelungen S, S
0an Geraden g, g
0durch den Ursprung eine Drehung ergibt, indem sie das Produkt zweier Spiegelmatrizen bil- den und dieses als Drehmatrix erkennen. Sind g, g
0zwei durch ~ o gehende Geraden, dann ist der Winkel zwischen g und g
0der kleinste auftretende Winkel α ∈ [0,
π2] zwischen allen m¨ oglichen Richtungsvektoren von g und g
0. Wie h¨ angt der Winkel zwischen den Spiegelgera- den mit dem Drehwinkel der beiden m¨ oglichen Hintereinanderausf¨ uhrungen S ◦ S
0und S
0◦ S zusammen?
(d) Zeigen sie, dass jede Spiegelung selbstinvers ist. Gibt es auch selbstinverse Drehungen von R
2?
(24) (a) Zeigen sie, dass f¨ ur alle linearen Drehungen D
1, D
2: R
2→ R
2die Gleichung D
1◦ D
2= D
2◦ D
1gilt. D.h. die Drehungen der Ebene mit Drehpunkt ~ o kommutieren. TIPP: Verwenden sie die Matrizen der beiden Drehungen bzgl. einer Orthonormalbasis (~ e
1, ~ e
2) von R
2.
Verwenden sie die Abk¨ urzungen s := sin α, c := cos α, s
0:= sin β, c
0:= cos β.
(b) Zeigen sie, dass die Drehungen D
1, D
2: R
3→ R
3mit
D
1(~ e
1) = ~ e
1, D
1(~ e
2) = ~ e
3, D
1(~ e
3) = −~ e
2und D
2(~ e
1) = ~ e
2, D
2(~ e
2) = −~ e
1, D
2(~ e
3) = ~ e
3nicht kommutieren. Geben sie die Matrizen von D
1und D
2bzgl. (~ e
1, ~ e
2, ~ e
3) an.
(25) Bestimmen sie, falls m¨ oglich, die Winkelmaßzahlen α und β so, dass die Drehmatrizen D
1=
cos α − sin α 0 sin α cos α 0
0 0 1
und D
2=
1 0 0
0 cos β − sin β 0 sin β cos β
kommutieren.
Verwenden sie die Abk¨ urzungen s := sin α, c := cos α, s
0:= sin β, c
0:= cos β.
(26) Es sei D : R
3→ R
3eine Drehung mit ~ e
1000:= D(~ e
1), ~ e
2000:= D(~ e
2), ~ e
3000:= D(~ e
3).
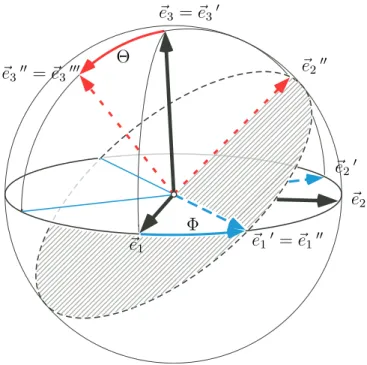
(a) Bestimmen sie eine Rechtsdrehung D
1um die ~ e
3-Achse, so dass D
1(~ e
2) in der Ebene von
~ e
3und ~ e
3000liegt. Setze ~ e
10:= D
1(~ e
1), ~ e
20:= D
1(~ e
2), ~ e
30:= D
1(~ e
3). Geben sie die Matrix D
1von D
1bzgl. (~ e
1, ~ e
2, ~ e
3) an. Bezeichnen sie dabei den Drehwinkel mit Φ.
(b) Bestimmen sie eine Rechtsdrehung D
2um die ~ e
10-Achse, so dass D
2(~ e
30) = ~ e
3000. Setze
~ e
100:= D
2(~ e
10), ~ e
200:= D
2(~ e
20), ~ e
300:= D
2(~ e
30) = ~ e
3000. Geben sie die Matrix D
2von D
2bzgl.
(~ e
10, ~ e
20, ~ e
30) an. Bezeichnen sie dabei den Drehwinkel mit Θ.
(c) Bestimmen sie eine Rechtsdrehung D
3um die ~ e
3000-Achse, so dass D
3(~ e
100) = ~ e
1000und mithin automatisch D
3(~ e
200) = ~ e
2000ist. Jetzt ist ~ e
1000= D
3(~ e
100), ~ e
2000= D
2(~ e
200), ~ e
3000= D
2(~ e
300). Geben sie die Matrix D
3von D
3bzgl. (~ e
100, ~ e
200, ~ e
300) an. Bezeichnen sie dabei den Drehwinkel mit Ψ.
(d) Wie l¨ aßt sich die Matrix D der Drehung D bzgl. (~ e
1, ~ e
2, ~ e
3) durch die drei Drehmatrizen
Φ Θ
~ e
1~ e
2~ e
3= ~ e
30~ e
10= ~ e
100~ e
20~ e
200~
e
300= ~ e
3000Abbildung 1. Die beiden Drehungen D
1, D
2und die Eulerwinkel Φ und Θ
D
1, D
2, D
3darstellen? Die Drehwinkelmaßzahlen Φ, Θ, Ψ in den drei Matrizen heißen Eu- lersche Winkel der Drehung D bzgl. (~ e
1, ~ e
2, ~ e
3).
(e) Dr¨ ucken sie die Matrixelemente von D durch die Eulerschen Winkel aus. Es sollte sich D =
cos Ψ cos Φ − cos Θ sin Φ sin Ψ − sin Ψ cos Φ − cos Θ sin Φ cos Ψ sin Θ sin Φ cos Ψ sin Φ + cos Θ cos Φ sin Ψ − sin Ψ sin Φ + cos Θ cos Φ cos Ψ − sin Θ cos Φ
sin Ψ sin Θ cos Ψ sin Θ cos Θ
ergeben. Durch geeignete Wahl von Φ, Ψ, Θ ∈ R l¨ aßt sich jede 3 × 3-Drehmatrix darstel-
len. D.h. die Gruppe der Drehungen um Achsen, die durch den Ursprung gehen, ist eine
dreiparametrige Gruppe. In der Physik ben¨ otigt man meist die Matrix T der Koordinaten-
transformation von den ungestrichenen zu den dreifach gestrichenen Koordinaten. Sie ist die
zu D inverse Matrix, die sich durch Transponieren von D ergibt, d.h. T = D
>. Warum
ist die Inverse von D gleich der Transponierten von D? ( Herbert Goldstein : Klassische
Mechanik, Seite 118 - 121)
6. ¨ Ubungsblatt f¨ ur den 22. 4. 2008 1. Ubungsbeispiele ¨
(27) (a) Gegeben ist der Vektor v =
√15 21
. Berechnen sie die Matrix M = v v
T=
15 21(
2 1) indem sie das Produkt der 2 × 1 Matrix mit der 1 × 2 nach den Matrixrechenregeln berechnen. Bestimmen sie das Bild der linearen Abbildung, die durch M definiert wird, das heißt, charakterisieren sie M( R
2) = {y = M x : x ∈ R
2}. Berechnen sie (x − Mx) · v f¨ ur einen beliebigen Vektor x ∈ R
2. (b) Berechnen sie A = I − M und das Bild von A. Berechnen sie Ax · v f¨ ur einen beliebigen Vektor x ∈ R
2. Fertigen sie eine Skizze an, die die geometrischen Eigenschaften der Abbilungen M und A veranschaulicht.
(c) Versuchen sie, die obigen Berechnungen auf eine allgemeinere Situation zu ¨ ubertragen. Welche Eigenschaften muss ein Vektor v ∈ R
2haben, damit die Abbildungen M = v v
Tund A = I −M die gleichen geometrischen Eigenschaften haben, wie in der obigen speziellen Situation? Was passiert, wenn sie vom zweidimensionalen Raum in den dreidimensionalen ¨ ubergehen?
(28) Begr¨ unden sie, dass die Menge von Vektoren n
100
,
3−2 0
,
−527
o
linear unabh¨ angig ist. Welche Bedingung muss erf¨ ullt sein, damit die Vektoren
a1,1
00
.. .
0
,
a1,2
a2,2
0
.. .
0
,
a1,3
a2,3
a3,3
.. .
0
, · · · ,
a1,n
a2,n
a3,n
.. .
an,n
eine Menge von linear unabh¨ angigen Vektoren im R
nbilden?
Erkl¨ arung: Betrachten sie die zwei linearen Gleichungen f¨ ur die zwei Unbekannten x, y:
a
1x + b
1y = r
1(1)
a
2x + b
2y = r
2. (2)
Wenn wir nicht wissen, welche der Koeffizienten a
1, a
2, b
1, b
2, r
1, r
2ungleich Null sind, m¨ ussen wir so lange wie m¨ oglich Divisionen beim Eliminieren von Unbekannten vermeiden. Um x zu eliminieren multiplizieren wir (1) mit −a
2, (2) mit a
1und addieren die so erhaltenen Gleichungen. Dies liefert (a
1b
2− a
2b
1)y = a
1r
2− a
2r
1. Wenn wir jetzt wissen (oder voraussetzen), dass a
1b
2− a
2b
16= 0 ist, dann k¨ onnen wir die L¨ osung y durch die Koeffizienten ausdr¨ ucken y =
aa1r2−a2r11b2−a2b1
.
(29) Dr¨ ucken sie auch x durch die Koeffizienten von (1) und (2) aus. Was f¨ allt dabei auf? Mit der Bezeichnung
a1 b1
a2 b2
:= a
1b
2− a
2b
1schreibt sich die CRAMERsche REGEL wie folgt
x =
r1 b1
r2 b2
a1 b1
a2 b2
, y = |
aa12 rr12|
a1 b1
a2 b2
, falls
a1b1
a2b2
6= 0.
(30) Gehen sie bei dem System
a
1x + b
1y + c
1z = r
1(3)
a
2x + b
2y + c
2z = r
2. (4)
a
3x + b
3y + c
3z = r
3. (5)
wie im Bsp. 29 vor und dr¨ ucken sie die Unbekannten, falls m¨ oglich wieder durch die Koeffizienten aus. Wie l¨ aßt sich x mit Hilfe von
a1 b1 c1
a2 b2 c2
a3 b3 c3
:= a
1ab2 c2
3 c3
− a
2b1c3
b3c1
+ a
3b1 c2
b2 c1
schreiben?
(31) Determinante und lineare Unabh¨ angigkeit. Zeigen Sie:
(a) (
aa12) ,
b1b2
sind linear unabh¨ angig genau dann, wenn
a1 b1
a2 b2
6= 0.
(b)
a1a2
a3
,
b1b2
b3
,
c1c2
c3
sind linear unabh¨ angig genau dann, wenn
a1b1c1
a2b2c2
a3b3c3
6= 0.
(32) L¨ osbarkeit und Unl¨ osbarkeit von Systemen linearer Gleichungen.
(a) Geben Sie eine einzige Gleichung mit 100 Unbekannten an, die unl¨ osbar ist.
(b) Zeigen Sie: Wenn eine einzige lineare Gleichung mit 100 Unbekannten eine spezielle L¨ osung besitzt, so besitzt sie unendlich viel weitere L¨ osungen.
(c) Geben Sie ein System von 100 linearen Gleichungen f¨ ur eine Unbekannte an, das l¨ osbar ist.
(d) Zeigen Sie, dass die wichtige FAUSTREGEL “Jedes System von n Gleichungen mit n Unbe-
kannten ist eindeutig l¨ osbar” falsch ist.
7. ¨ Ubungsblatt f¨ ur den 29. 4. 2008 1. Ubungsbeispiele ¨
(33) Sei {a, b, c} eine Menge linear unabh¨ angiger Vektoren in R
n(mit n ≥ 3). Zeigen sie:
(a) Die Menge der Vektoren {a + 5b, a + b + 3c, 6c} ist ebenfalls linear unabh¨ angig.
(b) Die Menge der Vektoren {a + b + c, 2a + 4b + c, 2a + 6b} ist ebenfalls linear unabh¨ angig.
(34) Es sei A eine n × n Matrix ¨ uber R . Beweisen sie:
(a) L = {x ∈ R
n: Ax = 0} ist ein Unterraum des R
n, das heißt, u, v ∈ L ⇒ u + v ∈ L und λ ∈ R , v ∈ L ⇒ λv ∈ L.
(b) Die lineare Abbildung x 7→ Ax ist genau dann bijektiv wenn L = {0}.
(35) Es sei
A =
3 2 3 4 2 4 2 2 3 2 1 1 1 1 1 1 0 1 0 1
.
(a) Bestimmen sie die gr¨ oßte Anzahl linear unabh¨ angiger Spalten von A.
(b) Geben sie f¨ ur ϕ : R
5→ R
4mit ϕ(x) = Ax die Menge Im(ϕ) = {ϕ(x) : x ∈ R
5} in der Form Im(ϕ) = L(v
1, v
2, . . . , v
k) an, wobei die Anzahl k der ben¨ otigten Vektoren so klein wie m¨ oglich (minimal) sein soll,
(36) L¨ osen sie das inhomogene lineare Gleichungssystem Ax = b mit A =
3 2 1 4 6 2 4 0 3 1 5 6 1 7 7
und b =
4 1 5
.
(37) Bestimmen sie L
1= {x ∈ R
3: 2x
1+x
2= 0, x
1+x
2+x
3= 0}, L
2= {x ∈ R
3: x
1+6x
2= 0},
L
3= {x ∈ R
4: x
1+ x
2+ x
3+ x
4= 0} und L
4= {x ∈ R
5: 3x
1− 6x
2+ 2x
5= 0} indem
sie L
k(f¨ ur k = 1, 2, 3, 4) als Linearkombination der Form L
k= L(v
1k, v
k2, . . .) darstellen. Die
Anzahl der ben¨ otigten Vektoren soll jeweils minimal sein.
H ¨ OHERE MATHEMATIK 2, ¨ Ubungen, Sommersemester 2008 8. ¨ Ubungsblatt f¨ ur den 6. 5. 2008
1. Ubungsbeispiele ¨
(38) L¨ aßt sich der Vektor v = (4, 6, 3, −1)
Tals Linearkombination der Vektoren a
1= (2, 3, 0, 2)
T, a
2= (1, −2, −2, 1)
Tund a
3= (9, 3, −3, 4)
Tdarstellen? Wenn ja, geben sie die Koeffizienten einer solchen Linearkombination an.
(39) Finden sie alle Linearkombinationen der Vektoren a
1a
2, a
3und v aus Beispiel 38 die den Vektor (3, 1, −2, 3)
Tergeben.
(40) Bestimmen sie einen Vektor x ∈ R
4, der orthogonal zu den Vektoren v
1= (1, 1, 0, 1)
T, v
2= (2, 1, −1, −1)
Tund v
3= (1, −1, 1, 0)
Tist. Wie viele solcher Vektoren gibt es?
(41) Betrachten sie die lineare Abbildung x 7→ A · x auf R
3mit A = 1
15
16 2 9
−8 −1 18
−5 −10 0
.
Gibt es einen Vektor x 6= 0, der sein eigener Bildvektor unter der linearen Abbildung ist, d.h.
f¨ ur den x = Ax gilt. Wenn ja, bestimmen sie einen solchen Vektor. Gibt es auch einen Vektor y 6= 0, der die H¨ alfte seines Bildvektors ist, das heißt f¨ ur den 2y = Ay gilt?
(42) Gegeben ist die Matrix
M =
1 0 2 −2
2 3 0 1
−2 1 0 1
−1 2 3 0
und der Vektor y =
−9 4 0
−10
.
Finden sie x ∈ R
4so dass y der Bildvektor von x unter der linearen Abbildung f : R
4→ R
4mit f (z) = M z ist. Seien m
1, m
2, m
3und m
4die Spalten der Matrix M . Finden sie einen Vektor w ∈ R
4so dass w· m
i= y
if¨ ur i = 1, 2, 3, 4 gilt, wobei y
idie Komponenten des Vektors y bezeichnen.
(43) Bestimmen sie die inverse Matrix B
−1von B =
1 −2 1
0 2 1
1 1 1
.
1
9. ¨ Ubungsblatt f¨ ur den 20. 5. 2008 1. Ubungsbeispiele ¨
(45) Sei A eine obere Dreiecksmatrix mit n ≥ 1 Zeilen und Spalten. Zeigen sie det A = a
1,1a
2,2· . . . · a
n,n.
TIPP: Entwickeln sie die Determinante nach den Elementen der ersten Spalte von A.
(46) Es sei A eine k × k-Matrix, B eine m × m-Matrix und C :=
A 0 0 B
die Blockdiagonalmatrix, die links oben als Teilmatrix A, rechts daneben eine k × m- Nullmatrix, unterhalb von A eine m × k-Nullmatrix und rechts daneben als Teilmatrix B enth¨ alt. Zeigen sie
det C = det A · det B.
TIPP: Entwickeln sie die Determinante von C nach der ersten Spalte von C.
(47) (a) Zeigen sie: Wenn in einer n × n-Matrix A die ersten beiden Zeilen ¨ ubereinstimmen, dann ist det A = 0.
TIPP: Entwickeln sie die Determinante auf zwei Arten: einmal nach der ersten Zeile und einmal nach der zweiten Zeile.
(b) Seien c ∈ R , A =
a
1,1, . . . , a
1,na
2,1, . . . , a
2,n.. . .. . a
n,1, . . . , a
n,n
und ˜ A :=
a
1,1+ ca
2,1, . . . , a
1,n+ ca
2,na
2,1, . . . , a
2,n.. . .. .
a
n,1, . . . , a
n,n
.
Zeigen sie det A = det ˜ A.
(48) Berechnen sie die Determinante von
2 1 0 −3 6
3 −1 0 3 −6
8 1 0 −3
2 3
0 5 −2 1 7
−2 −1 1 0 1
, indem sie die Erkenntnis aus dem vorigen Beispiel n¨ utzen.
(49) Zeigen sie: Die Spalten
a
1a
2a
3
und
b
1b
2b
3
sind genau dann linear unabh¨ angig, wenn
a
2b
3− a
3b
2a
3b
1− a
1b
3a
1b
2− a
2b
1
6=
0 0 0
.
Ohne geometrische Argumentation, rein algebraisch!
H ¨ OHERE MATHEMATIK 2, ¨ Ubungen, Sommersemester 2008 10. ¨ Ubungsblatt f¨ ur den 27. 5. 2008
1. Ubungsbeispiele ¨
(50) Sei P = {a
0+ a
1x + a
2x
2+ a
3x
3| a
i∈ R } der Vektorraum aller Polynome vom Grad kleiner gleich 3 ¨ uber R .
(a) Zeigen sie: B = {3, 1 + x, x + x
2, 2x
3} ist eine Basis von P .
(b) Berechnen sie die Koordinaten des Vektors v = 1 + x + x
2+ x
3∈ P bez¨ uglich der Basis B. Warum bezeichnen wir das Polynom v als
” Vektor“?
(51) Es sei
A =
1 1 2 2 1 0 3 1 1
.
(a) Berechnen sie det(A) und geben sie ein Argument an, das belegt, dass die inverse Matrix zu A existiert. Berechnen sie A
−1.
(b) Berechnen sie mit Hilfe von A
−1die L¨ osung des linearen Gleichungssystems A · x =
6 3
−10
.
(c) Bestimmen sie eine 3 × 3-Matrix C die die Gleichung C · A = 4A
2+ A erf¨ ullt.
(52) Es seien a =
1 0 2
, b =
2
−1 1
, c =
0 0 1
. Von einem Vektor x sind die Orthogonalprojek- tionen auf die Vektoren a, b und c bekannt:
D x, a
kak E a
kak = 1
√ 5 a kak , D
x, b kbk
E b
kbk = − 1
√ 6 b kbk , D
x, c kck
E c kck = o.
Bestimmen sie alle Vektoren x, falls es mehrere geben sollte, die obige Eigenschaft haben.
(53) Zeigen sie:
B = (
2 1 1 1
,
1 0 0 1
,
1 2 0 1
,
0 0 0 1
)
ist eine Basis des Vektorraums R
4und bestimmen sie die Koordinaten (α
1, α
2, α
3, α
4) des Vektors (4, 2, 1, 1)
Tbez¨ uglich B.
Sei nun b ein beliebiger Vektor in R
4. Geben sie den Koordinatenvektor β = (β
1, β
2, β
3, β
4)
Tdes Vektors b bez¨ uglich der Basis B in der Form β = A · b mit einer geeigneten Matrix A an.
1
11. ¨ Ubungsblatt f¨ ur den 3. 6. 2008 1. Ubungsbeispiele ¨
(54) Berechnen sie die Eigenwerte und zugeh¨ orige Eigenvektoren der Matrizen
A
1=
5 10 4 −1
, A
2= 1 2
0 3
, A
3=
1, 4 −1, 0 0, 5 −0, 1
, A
4=
1 −1 1 1
,
A
5=
cos ϕ − sin ϕ sin ϕ cos ϕ
, A
6=
1, 4 0, 5
−1, 0 −0, 1
, A
7=
2 −2 3
−2 −1 6
1 2 0
,
A
8=
3 1 4 0 2 6 0 0 5
, A
9=
−2 1 0
1 −2 1
0 1 −2
, A
10= 1 3
2 1 2
−2 2 1 1 2 −2
.
(55) Geben sie die L¨ osung des Anfangswertproblems
m x
00+ kx = 0; x(0) = 0, 05 [m], x
0(0) = −0, 1 [m/sec]
an, wobei die Masse m = 0, 4[kg] und die Federkonstante k = 12[N/m] gegeben sind.
(56) Angenommen, in der Kraftbilanz, die zur Gleichung des harmonischen Oszillators f¨ uhrt, wird ausser der Federkraft und der Beschleunigungskraft noch eine Reibungskraft ber¨ ucksichtigt.
Wir nehmen an, die Reibungkraft wirkt der Bewegungsrichtung entgeben (das heißt entgegen- gesetzt zum Geschwindigkeitsvektor). Wir nehmen weiters an, die St¨ arke der Reibungskraft ist direkt proportional zum Betrag der Geschwindigkeit, mit einem Proportionalit¨ atsfaktor c > 0. Finden sie eine Differentialgleichung zweiter Ordnung, welche die Bewegung eines solchen (durch Reibung) ged¨ ampften Oszillators beschreibt.
(57) L¨ osen sie das Anfangswertproblem
mx
00+ cx
0+ kx = 0; x(0) = x
0; x
0(0) = 0;
f¨ ur einen beliebigen Anfangswert x
0∈ R . Die Konstanten m und k seien wie in Beispiel 55. Berechnen sie die L¨ osung f¨ ur c = 1 [N sec/m] und f¨ ur c = 20 [N sec/m]. Schreiben sie dazu die Differentialgleichung in ein 2 × 2 Differentialgleichungssystem um. (Setzen sie dazu x = (
xx12) = (
xx0)). Entkoppeln sie das System indem sie die Eigenwerte und Eigenvektoren der Systemmatrix berechnen und den Anfangswert als Linearkombination der Eigenvektoren darstellen. Gehen sie weiter, wie in der Vorlesung besprochen, vor.
Verwenden sie MatLab um die L¨ osungskurven in der (x
1, x
2)-Ebene f¨ ur die beiden M¨ og- lichkeiten von c zu skizzieren. W¨ ahlen sie als Anfangswert x
0=
0,10. (58) Betrachten sie die folgende Anordnung von Federn und Massen.
l
l/3 l/3
m m
Die beiden Massen m sind gleich groß und alle drei Federkonstanten seien gleich k. Stellen sie ein Differentialgleichungssystem vierter Ordnung auf, das die Bewegung der beiden schwin- genden Massen beschreibt. Verwenden sie als Koordinaten die Auslenkungen der Massen aus den jeweiligen Ruhelagen und die Geschwindigkeiten der beiden Massen.
Verwenden sie Matlab um die Eigenwerte und Eigenvektoren der Systemmatrix zu be- stimmen. F¨ ur die konkrete Berechung k¨ onnen sie die Masse und Federkonstante aus Beispiel 55 verwenden. Geben sie die L¨ osungskurven des Differentialgleichungssystems an, wenn der Anfangsvektor Real- bzw. Immagin¨ arteil eines Eigenvektors ist. Verwenden sie MatLab um die Projektionen der L¨ osungskurven auf die (x
1, x
2)-Ebene bzw. auf die (x
3, x
4)-Ebene zu zeichnen.
(59) Skizzieren sie die L¨ osungskurven eines 2 × 2-Differentialgleichungssystems x
0= Ax in der (x
1, x
2) Ebene, wenn sie wissen, dass v
1= (2, 1)
Tund v
2= (−1, −1)
TEigenvektoren der Matrix A zu den Eigenwerten λ
1= −2 und λ
2= 2 sind. Wie sieht die Skizze aus, wenn λ
2= −1 gesetzt wird, und sonst alles gleich bleibt?
(60) Skizzieren sie die L¨ osungskurven eines 2 × 2-Differentialgleichungssystems x
0= Ax in der
(x
1, x
2) Ebene, wenn sie wissen, dass a = (2, 1)
Tund b = (−1, −1)
TReal- und Immagin¨ arteil
eines Eigenvektors der Matrix A zum Eigenwert λ = −1 − i sind. Wie sieht die Skizze aus,
wenn λ = 1 + i gesetzt wird, und sonst alles gleich bleibt?
12. ¨ Ubungsblatt f¨ ur den 18. 6. 2008 1. Ubungsbeispiele ¨
(61) Zeigen Sie, dass die durch a
n:=
2n+13n+2definierte Folge (a
n)
n∈Nmonoton, beschr¨ ankt und konvergent gegen
23ist.
(62) F¨ ur welche a, b, c > 0 ist die durch f
n:=
a·n+bc·ndefinierte Folge (f
n)
n∈Nstreng monoton fallend?
(63) (i) Es sei a ≥ 1. Zeigen Sie, dass lim
n→∞ n√ a = 1 ist.
TIPP: a − 1 = ( √
na)
n− 1
nund x
n+ y
n= (x − y)(x
n−1+ . . . + y
n−1).
(ii) Zeigen Sie mit Hilfe von (i), dass auch f¨ ur 0 < a < 1 die Gleichung lim
n→∞ n√ a = 1 gilt.
(64) Welche der folgenden Behauptungen sind wahr, welche falsch?
(i) Die Summe divergenter Folgen ist divergent.
(ii) Die Summe divergenter Folgen kann konvergent sein.
(iii) Das Produkt divergenter Folgen ist divergent.
(iv) Es gibt divergente Folgen, deren Produktfolge konvergiert.
Belegen Sie die Ihre Antworten durch Beispiele oder Gegenbeispiele.
(65) Berechnen Sie:
n→∞
lim
3 · 5
n+ 2 · 6
n7 · 10
n, lim
n→∞
−8n
3+ 6n
2+ 1 2n
3+ 12n ,
∞
X
j=3
5 · 3 4
j,
∞
X
j=2
1 2
4j,
n→∞