Der Übergangsproblematik Schule-Hochschule im Fach Mathematik begegnen. Das Kooperationsprojekt „Überpro“.
Volltext
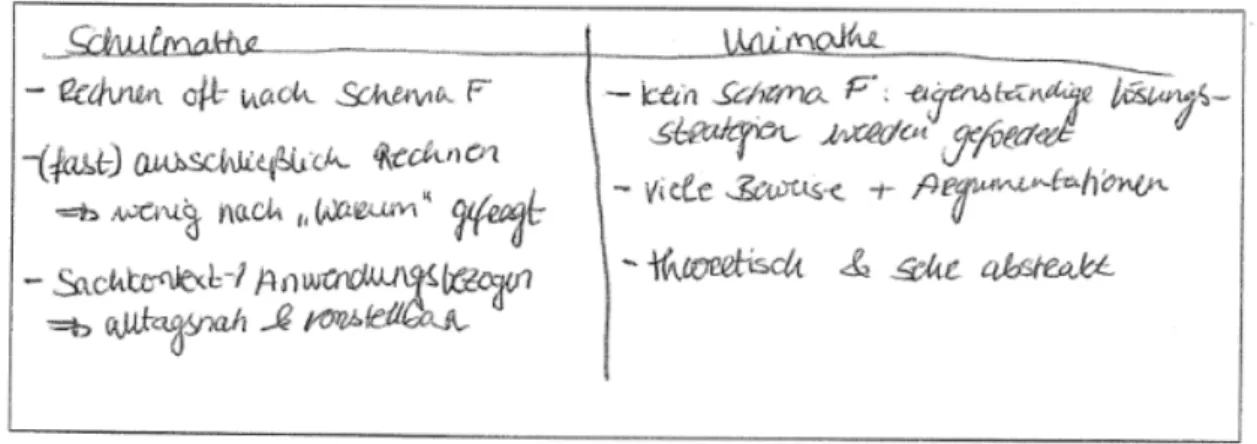
Abbildung
ÄHNLICHE DOKUMENTE
▪ Ladung zum Kolloquium innerhalb von drei Monaten, Nichtbestehen =
Da auch die Dispersaldistanzen ja lange nicht für die meisten Tierarten bekannt sind und wahrscheinlich oft unterschätzt werden (Kap. 2.7.2), sollten auch hier eher ein
Diese Flächen sind für eine wirtschaftliche Windenergienutzung geeignet und werden deshalb weiter untersucht.. Durch Überlage- rung von den maßgeblichen Kriterien für
"Ich kann mitgestalten" im Rahmen schüleraktiver Un- terrichtsphasen weisen jedoch darauf hin, dass die Schüler bestehende Freiheitsgrade auch als solche wahrnehmen, und dies
legenheit, viele der armenischen Kirchenlieder zuhören, welche theils durch ihre Eigenthiimlichlkeit mich anzogen , theils aber besonders dadurch mein Interesse errcgien , dass sie
Eine individuelle Rückmeldung ist jederzeit möglich, direkt im Anschluss an den Beitrag oder – nach Anfertigen entsprechender Notizen – allgemein für die gesamte Klasse, etwa
Sommersemester 2013 Universität Bielefeld. Klausurergebnisse Funktionen
Klausurergebnisse Mathematik f¨ ur Biologen