Numerik f¨ur Ingenieure

Numerik f¨ ur Ingenieure

Steffen B¨ orm

Stand 17. April 2020

Alle Rechte beim Autor.

Inhaltsverzeichnis

1 Einleitung 5

1.1 Beispiel: Sortieren . . . . 6

1.2 Beispiel: Schnelle Fourier-Transformation . . . . 11

2 Lineare Gleichungssysteme 15

2.1 Beispiel: Differentialgleichung . . . . 15

2.2 Allgemeine Aufgabenstellung . . . . 17

2.3 Dreiecksmatrizen . . . . 17

2.4 LR-Zerlegung . . . . 20

2.5 Fehlerverst¨ arkung . . . . 27

2.6 QR-Zerlegung . . . . 33

2.7 Ausgleichsprobleme . . . . 42

3 Nichtlineare Gleichungssysteme 47

3.1 Beispiel: Lagrange-Punkte im Gravitationsfeld . . . . 47

3.2 Bisektionsverfahren . . . . 49

3.3 Allgemeine Fixpunktiterationen . . . . 51

3.4 Newton-Verfahren . . . . 56

4 Eigenwertprobleme 63

4.1 Beispiel: Schwingende Saite . . . . 63

4.2 Vektoriteration . . . . 64

4.3 Inverse Iteration . . . . 69

4.4 Orthogonale Iteration . . . . 73

4.5 QR-Iteration . . . . 79

4.6 Praktische QR-Iteration

. . . . 82

5 Approximation von Funktionen 85

5.1 Beispiel: Computergrafik . . . . 85

5.2 Polynominterpolation . . . . 86

5.3 Auswertung per Neville-Aitken-Verfahren . . . . 87

5.4 Auswertung mit Newtons dividierten Differenzen . . . . 89

5.5 Approximation von Funktionen . . . . 93

6 Numerische Integration 97

6.1 Beispiel: Wahrscheinlichkeiten . . . . 97

6.2 Quadraturformeln . . . . 98

6.3 Fehleranalyse . . . . 103

7 Gew¨ohnliche Differentialgleichungen 111

7.1 Beispiel: Numerische Simulationen . . . . 111

7.2 Integralgleichung . . . . 112

7.3 Zeitschrittverfahren . . . . 114

7.4 Verfeinerungen und Variationen

. . . . 119

Literaturverzeichnis 125

1 Einleitung

Viele Gesetzm¨ aßigkeiten in den Natur-, Ingenieur- und auch Wirtschaftswissenschaften werden mit Hilfe mathematischer Gleichungen beschrieben: Die auf Newton zur¨ uckge- henden Axiome der klassischen Mechanik werden in der Regel mit Hilfe von Differen- tialgleichungen ausgedr¨ uckt, das Verhalten einfacher Schaltungen mit Hilfe der Kirch- hoff’schen Gesetze, w¨ ahrend bei der Modellierung des zu erwartenden Gewinns eines Aktienpakets Integrale zum Einsatz kommen.

In einfachen F¨ allen lassen sich diese Gleichungen per Hand l¨ osen, in der Praxis ist es jedoch wesentlich h¨ aufiger nicht m¨ oglich: Entweder l¨ asst sich die L¨ osung nicht in der

¨

ublichen Weise in geschlossener Form darstellen, oder es sind schlicht zu viele Variablen im Spiel.

Die numerische Mathematik (oder kurz Numerik ) besch¨ aftigt sich mit der Frage, wie derartige Probleme m¨ oglichst schnell gel¨ ost werden k¨ onnen. Dabei ist die Wahl des rich- tigen Verfahrens von entscheidender Bedeutung: Ein lineares Gleichungssystem mit der Cramer’schen Regel aufzul¨ osen ist zwar theoretisch machbar, f¨ uhrt in der Praxis aber schon bei relativ kleinen Problemen zu einem inakzeptablen Zeitaufwand. Das Gauß’sche Eliminationsverfahren dagegen ist wesentlich effizienter und kann auf modernen Com- putern auch noch Systeme mit 10 000 Unbekannten in vertretbarer Zeit behandeln.

Ein weiterer wichtiger Gesichtspunkt ist die Genauigkeit der Berechnung: Bei Be- rechnungen auf Grundlage von Messdaten treten immer auch Messfehler auf, die das Ergebnis der Berechnung verf¨ alschen. Bei der Modellierung eines physikalischen Prozes- ses wird man in der Regel von vereinfachenden Annahmen ausgehen und so einen Mo- dellfehler einf¨ uhren, der ebenfalls das Ergebnis ver¨ andert. Schließlich kommen bei der Durchf¨ uhrung der Berechnung auf einem Computer auch noch Rundungsfehler hinzu.

Um die Qualit¨ at des Ergebnisses beurteilen zu k¨ onnen, m¨ ussen wir also auch untersu- chen, welche Genauigkeit wir ¨ uberhaupt erwarten d¨ urfen.

Viele numerische Verfahren bieten die M¨ oglichkeit, einen Kompromiss zwischen Ge- schwindigkeit und Genauigkeit einzugehen: Falls wir wissen, dass unsere Messfehler oh- nehin nur eine Genauigkeit von 3% des Ergebnisses zulassen, ist es unkritisch, auch die Berechnung so weit zu vereinfachen, dass sie einen zus¨ atzlichen Fehler von h¨ ochstens 1%

hinzuf¨ ugt, daf¨ ur aber wesentlich schneller ausgef¨ uhrt werden kann. Deshalb werden viele der im Rahmen dieser Vorlesung vorgestellten Verfahren N¨ aherungsverfahren sein, bei denen wir sowohl Zeitbedarf als auch Genauigkeit analysieren.

In diesem Kapitel werden wir zun¨ achst einige einfache Algorithmen kennen lernen,

mit deren Hilfe sich Aufgaben, die auf den ersten Blick sehr rechenintensiv sind, sehr

elegant und schnell l¨ osen lassen.

1.1 Beispiel: Sortieren

Als Beispiel daf¨ ur, welchen Einfluss die Wahl des Algorithmus auf den Aufwand f¨ ur das L¨ osen eines Problems hat, untersuchen wir die einfache Aufgabe, n Zahlen a

, a

, . . . , a

∈

zu sortieren. Es soll also ein sortierter Vektor

b

a =











ˆ a

ˆ a

.. . ˆ a











, ˆ a

≤ ˆ a

≤ . . . ≤ ˆ a

konstruiert werden, der dieselben Eintr¨ age wie der urspr¨ ungliche Vektor enth¨ alt, f¨ ur den also

{a

, . . . , a

} = {ˆ a

, . . . , a ˆ

}

gilt. Ein einfacher Algorithmus f¨ ur die Behandlung dieser Aufgabe ist das Sortieren durch Einf¨ ugen: Wir gehen davon aus, dass die ersten k Eintr¨ age bereits sortiert sind, dass also a

≤ a

≤ . . . ≤ a

gilt. Nun m¨ ochten wir a

in diesem Teilvektor an die richtige Stelle bringen. Dazu vergleichen wir a

zun¨ achst mit dessen gr¨ oßtem Element a

. Falls a

≤ a

gilt, sind wir fertig. Ansonsten muss a

vor a

eingef¨ ugt werden.

Also pr¨ ufen wir, ob a

≤ a

gilt. Falls ja, geh¨ ort a

zwischen a

und a

. Falls nein, muss a

auch vor a

eingef¨ ugt werden. Im ung¨ unstigsten Fall, n¨ amlich wenn a

< a

gilt, ben¨ otigen wir k Vergleiche, um die richtige Position f¨ ur a

zu finden.

Auf dieser Grundidee k¨ onnen wir nun aufbauen: Wir beginnen mit dem Teilvektor a

, der trivial

” sortiert“ ist. Dann f¨ ugen wir nach und nach a

, a

, . . . , a

mit der beschrie- benen Technik ein. Um den Arbeitsaufwand m¨ oglichst gering zu halten, speichern wir das gerade einzuf¨ ugende Element in einer Hilfsvariablen y und schaffen Platz im bereits sortierten Vektor, indem wir dessen Eintr¨ age nach rechts verschieben, solange die richti- ge Position nicht gefunden ist. Der resultierende Algorithmus nimmt die folgende Form an:

procedure insertionsort(n, var a);

for k = 1 to n − 1 do begin y ← a

; i ← k;

while i ≥ 1 and a

> y do begin a

← a

; i ← i − 1

end;

a

← y end

Die Funktion wird mit dem Vektor a = (a

, . . . , a

) aufgerufen und ¨ uberschreibt ihn mit dem aufsteigend sortierten Vektor

a = (ˆ a

, . . . , ˆ a

).

Es stellt sich die Frage nach dem Arbeitsaufwand, den dieser Sortieralgorithmus mit

sich bringt. Ein sinnvolles Maß f¨ ur den Aufwand ist die Anzahl der Vergleiche, die der

Algorithmus im ung¨ unstigsten Fall ben¨ otigt. Im schlimmsten Fall wird die innere Schleife

1.1 Beispiel: Sortieren

k Vergleiche ben¨ otigen, so dass insgesamt

n−1

X

k=1

k = n(n − 1) 2

Vergleiche anfallen. F¨ ur große Vektoren erwarten wir also einen Aufwand von ungef¨ ahr n

/2 Vergleichsoperationen.

Ein weiterer einfacher Sortieralgorithmus ist das bubblesort -Verfahren: F¨ ur jedes i ∈ {1, . . . , n − 1} wird a

mit a

verglichen, und falls a

> a

gelten sollte, werden die beiden Eintr¨ age getauscht. Dieses Vorgehen wird wiederholt, bis alle Eintr¨ age in der richtigen Reihenfolge vorliegen.

procedure bubblesort(n, var a);

repeat σ ← 0;

for i = 1 to n − 1 do if a

> a

then begin

h ← a

; a

← a

; a

← h;

σ ← σ + 1 end

until σ = 0

Nach dem ersten Durchgang der inneren Schleife ist sicher gestellt, dass das gr¨ oßte Element im letzten Eintrag des Vektors angekommen ist, nach dem zweiten ist auch das zweitgr¨ oßte an seinem Ort angekommen, nach dem k-ten Durchgang stehen die k gr¨ oßten Elemente sortiert am Ende des Vektors, so dass nach n − 1 Durchg¨ angen der Vektor vollst¨ andig sortiert ist. Die Anzahl der Vergleiche bel¨ auft sich also auf h¨ ochstens (n − 1)

. Wir k¨ onnen den Algorithmus so modifizieren, dass die innere Schleife im k-ten Durchgang nur noch bis n − k l¨ auft, da die letzten k − 1 Eintr¨ age ja bereits sortiert sind.

Dann gen¨ ugen wie beim Sortieren durch Einf¨ ugen

n−1

X

k=1

(n − k) = n(n − 1) 2

Vergleichsoperationen, um den Vektor vollst¨ andig zu sortieren.

Beide Algorithmen sind zwar einfach, allerdings aufgrund des quadratisch mit dem Datenvolumen wachsenden Arbeitsaufwands f¨ ur große Vektoren zu langsam. Deshalb suchen wir nach einer schnelleren Variante.

Erfolgreich in diesem Bereich sind “divide and conquer”-Verfahren (lateinisch “divide et impera”, deutsch “teile und herrsche”), die auf der Idee beruhen, ein Problem in kleine Teilproblem zu zerlegen, die sich einfacher l¨ osen lassen, um dann aus den L¨ osungen der Teilprobleme eine L¨ osung des Gesamtproblems zu rekonstruieren.

Als Beispiel soll hier das mergesort -Verfahren vorgestellt werden. Zur Vereinfachung

der Darstellung beschr¨ anken wir uns auf den Fall, dass die L¨ ange der Vektoren eine

Zweierpotenz ist, dass also n = 2

f¨ ur ein p ∈

gilt. Den zu sortierenden Vektor a k¨ onnen wir in zwei H¨ alften

b =











b

b

.. . b











:=











a

a

.. . a











, c =











c

c

.. . c











:=











a

a

.. . a











zerlegen. Wir gehen davon aus, dass wir die kleineren Teilvektoren b und c sortieren, dass wir also sortierte Vektoren

b

=











ˆ b

ˆ b

.. . ˆ b











, ˆ b

≤ ˆ b

≤ . . . ≤ ˆ b

,

c =











ˆ c

ˆ c

.. . ˆ c











, ˆ c

≤ ˆ c

≤ . . . ≤ ˆ c

praktisch konstruieren k¨ onnen. Sobald uns diese Vektoren zur Verf¨ ugung stehen, l¨ asst sich einfach der kleinste Eintrag des Vektors a berechnen, denn es gilt

min{a

, . . . , a

} = min{b

, . . . , b

, c

, . . . , c

}

= min{ ˆ b

, . . . , ˆ b

, ˆ c

, . . . , c ˆ

} = min{ ˆ b

, c ˆ

}.

Wir m¨ ussen lediglich pr¨ ufen, ob ˆ b

kleiner oder gr¨ oßer als ˆ c

ist. Im ersten Fall ist ˆ b

der erste Eintrag ˆ a

des gesuchten sortierten Vektors

a, im zweiten Fall ist es ˆ c

. F¨ ur die Berechnung des zweitkleinsten Eintrags bietet es sich an, den bereits berechneten kleinsten Eintrag aus unserer Menge zu entfernen und erneut nach dem Minimum zu suchen. Entsprechend k¨ onnen wir auch die folgenden Eintr¨ age des Ergebnisvektors

a auf den Vergleich von jeweils nur zwei Zahlen zur¨ uckf¨ uhren.

procedure mergesort(n, var a);

if n ≥ 2 then begin

m

← n/2; m

← n − m

; for i ∈ {1, . . . , m

} do b

← a

; for i ∈ {1, . . . , m

} do c

← a

; mergesort(m

, b);

mergesort(m

, c);

k ← 1; ` ← 1;

for i = 1 to n do

if ` > m

do begin a

← b

; k ← k + 1 end else if k > m

do begin a

← c

; ` ← ` + 1 end else if b

≤ c

do begin a

← b

; k ← k + 1 end else begin a

← c

; ` ← ` + 1 end

end

1.1 Beispiel: Sortieren

7 3 8 4 5 8 9 1 6

7 3 8 4 5 8 9 1 6

3 4 7 8 1 5 6 8 9

1 3 4 5 6 7 8 8 9

Zerlegen

Teilprobleme sortieren

Zusammensetzen

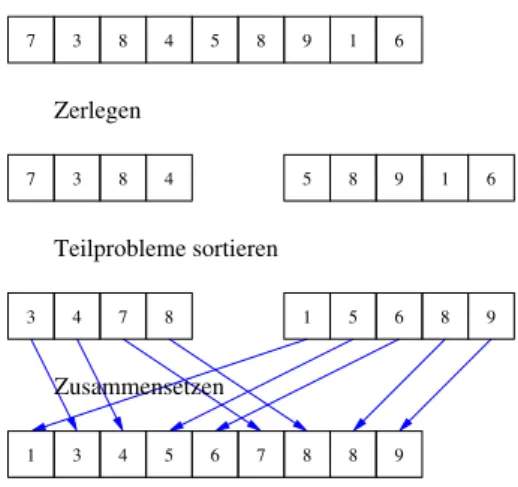
Abbildung 1.1: Prinzip des Mergesort-Algorithmus

Anschaulich gehen wir so vor, dass wir jeweils die ersten Eintr¨ age der beiden sortierten Teilvektoren

b und

c vergleichen, den kleineren der beiden in das Ergebnis ¨ ubernehmen und aus dem urspr¨ unglichen Vektor streichen, bis

a vollst¨ andig gef¨ ullt ist. Dabei gibt k jeweils den ersten noch g¨ ultigen Eintrag in dem Vektor b

an, w¨ ahrend ` dieselbe Rolle f¨ ur den Vektor

c spielt und i den n¨ achsten zu bestimmenden Eintrag des Ergebnisvektors

a festlegt. Wir pr¨ ufen zun¨ achst, ob einer der beiden Vektoren bereits leer ist. In diesem Fall ¨ ubernehmen wir einfach den Rest des anderen Vektors. Ansonsten vergleichen wir die kleinsten Eintr¨ age der beiden Vektoren und kopieren den kleineren.

Ist dieser Algorithmus nun schneller als der vorige? Zur Beantwortung dieser Frage bezeichnen wir die Anzahl der Vergleichsoperationen, die f¨ ur einen Vektor der L¨ ange n erforderlich sind, mit R

. Da unser Algorithmus f¨ ur n = 1 nichts tut, gilt

R

= 0.

F¨ ur n > 1 werden zun¨ achst die Teilvektoren sortiert, daf¨ ur sind R

und R

Ver- gleichsoperationen erforderlich. Um die beiden Teilvektoren zusammenzusetzen sind n Vergleiche erforderlich (Vergleiche der Laufvariablen z¨ ahlen wir nicht). Insgesamt erhal- ten wir die Formel

R

= R

+ R

+ n.

Unsere Aufgabe besteht nun darin, diese Rekurrenzgleichung zu l¨ osen. Dazu beschr¨ anken wir uns zun¨ achst auf den Fall, dass n eine Zweierpotenz ist, dass also n = 2

mit p ∈

gilt, und erhalten

R

= 2R

+ 2 = 2 = 2 · 1,

R

= 2R

+ 4 = 8 = 4 · 2,

R

= 2R

+ 8 = 24 = 8 · 3,

R

= 2R

+ 16 = 64 = 16 · 4,

R

= 2R

+ 32 = 160 = 32 · 5.

Diese Folge legt nahe, dass R

= n log

(n) gilt, und diese Gleichung l¨ asst sich in der Tat f¨ ur Zweierpotenzen auch direkt beweisen.

F¨ ur allgemeine n ∈

k¨ onnen wir immerhin noch eine Absch¨ atzung erhalten, indem wir geeignet auf- und abrunden. Dazu verwenden wir die Gauß-Klammern, die durch

bxc := max{n ∈

: n ≤ x}, dxe := min{n ∈

: x ≤ n} f¨ ur alle x ∈

definiert sind.

Lemma 1.1 (Rekurrenzabsch¨ atzung) Die durch R

:= 0,

R

:= R

+ R

+ n mit m := bn/2c f¨ ur alle n ∈

definierten Gr¨ oßen erf¨ ullen die Absch¨ atzung

R

≤ ndlog

(n)e (1.1)

f¨ ur alle n ∈

.

Beweis. Wir f¨ uhren den Beweis per abschnittsweiser Induktion.

Induktionsanfang. F¨ ur n = 1 gilt R

= 0 = 1 · 0 = 1dlog

(1)e.

Induktionsvoraussetzung. Sei N ∈

so gegeben, dass (1.1) f¨ ur alle n ∈ [1 : N ] gilt.

Induktionsschritt. Sei n := N + 1. Falls n eine gerade Zahl ist, also n = 2m gilt, d¨ urfen wir die Induktionsvoraussetzung wegen m ≤ N anwenden, um

R

= R

+ R

+ n = 2R

+ n ≤ 2mdlog

(n/2)e + n

= ndlog

(n) − 1e + n = ndlog

(n)e

zu erhalten. Falls n hingegen ungerade ist, m¨ ussen wir einen etwas genaueren Blick auf den Logarithmus werfen: Sei p := dlog

(n)e, es gelte also p − 1 < log

(n) ≤ p und damit auch 2

< n ≤ 2

. Wegen n = N + 1 ≥ 2 muss p ≥ 1 gelten, also ist 2

gerade. Da n ungerade ist, folgt n < 2

, also 2

< n + 1 ≤ 2

und somit dlog

(n + 1)e = dlog

(n)e, so dass wir

dlog

(m)e = dlog

((n − 1)/2)e = dlog

(n − 1)e − 1 ≤ dlog

(n)e − 1, dlog

(n − m)e = dlog

((n + 1)/2)e = dlog

(n + 1)e − 1 = dlog

(n)e − 1

erhalten. Wir haben m = (n−1)/2 = N/2 ≤ N, d¨ urfen also die Induktionsvoraussetzung auf R

anwenden. Da n = N +1 ≥ 2 gilt, also m ≥ 1, haben wir auch n−m ≤ n−1 = N , so dass wir die Induktionsvoraussetzung auch auf R

anwenden k¨ onnen und

R

= R

+ R

+ n ≤ mdlog

(m)e + (n − m)dlog

(n − m)e + n

≤ n(dlog

(n)e − 1) + n = ndlog

(n)e erhalten. Damit ist der Beweis vollst¨ andig.

Unser neuer Algorithmus ben¨ otigt also lediglich eine zu n log

n proportionale Anzahl

von Operationen anstelle einer zur n

proportionalen, so dass beispielsweise das Sortieren

von n = 2

≈ 1 000 000 Zahlen mit 2

· 20 ≈ 20 000 000 Vergleichsoperationen erfolgen

kann statt mit

≈ 500 000 000 000. In diesem Fall ist mergesort um einen Faktor

von ungef¨ ahr 25 000 schneller.

1.2 Beispiel: Schnelle Fourier-Transformation

1.2 Beispiel: Schnelle Fourier-Transformation

Wir untersuchen die Berechnung der Fourier-Transformation eines Vektors x ∈

mit geradem n ∈

. Sie ist gegeben durch

x =











x

x

.. . x











, x ˆ

:=

n−1

X

j=0

x

e

,

x :=











ˆ x

ˆ x

.. . ˆ x











Wenn wir die n Werte des Vektors

x in dieser Weise berechnen, m¨ ussen f¨ ur jeden minde- stens n Multiplikationen durchgef¨ uhrt werden, so dass mindestens n

Rechenoperationen erforderlich werden. Die Berechnung l¨ asst sich wesentlich schneller durchf¨ uhren, wenn wir die Struktur der in der Formel auftretenden Koeffizienten ausnutzen: Wir setzen m := n/2 und zerlegen die Summe in eine Summe ¨ uber gerade Indizes j = 2k und eine Summe ¨ uber ungerade Indizes j = 2k + 1 und erhalten

ˆ x

=

n−1

X

j=0

x

e

=

m−1

X

k=0

x

e

+

m−1

X

k=0

x

e

=

m−1

X

k=0

x

e

+ e

m−1

X

k=0

x

e

. (1.2) Falls ν ∈ {0, . . . , m − 1} gelten sollte, stellen wir fest, dass die erste Summe gerade die Fourier-Transformierte des Vektors der geraden Indizes ist,

y :=











x

x

.. . x











, y ˆ

:=

m−1

X

k=0

y

e

,

y :=











ˆ y

ˆ y

.. . ˆ y











,

w¨ ahrend sich die zweite Summe als Fourier-Transformierte des Vektors der ungeraden Indizes entpuppt, also als

z :=











x

x

.. . x











, z ˆ

:=

m−1

X

k=0

z

e

,

z :=











ˆ z

ˆ z

.. . ˆ z











.

In diesem Fall k¨ onnen wir also statt einer Fouriertransformation f¨ ur einen Vektor der L¨ ange n zwei Fouriertransformationen f¨ ur Vektoren der L¨ ange m = n/2 durchf¨ uhren und anschließend die Ergebnisse kombinieren, um das Ergebnis zu berechnen: Gem¨ aß (1.2) gilt die Gleichung

ˆ

x

= ˆ y

+ e

z ˆ

f¨ ur alle ν ∈ {0, . . . , m − 1}.

Falls dagegen ν ∈ {m, . . . , n − 1} gilt, k¨ onnen wir die Periodizit¨ at der komplexen Expo- nentialfunktion ausnutzen: Es gelten

e

= e

, e

= −e

, und wir k¨ onnen (1.2) in der Form

ˆ x

=

m−1

X

k=0

y

e

+ e

m−1

X

k=0

z

e

=

m−1

X

k=0

y

e

− e

X

k=0

z

e

= ˆ y

− e

ˆ

z

f¨ ur alle ν ∈ {m, . . . , n − 1}

schreiben und so ebenfalls auf Grundlage der Hilfsvektoren

y und

z berechnen.

Falls wir voraussetzen, dass auch n/2, n/4 und so weiter gerade sind, falls also n = 2

f¨ ur ein p ∈

gilt, k¨ onnen wir diese Rechenvorschrift rekursiv anwenden, um den besonders schnellen Algorithmus von Cooley und Tukey f¨ ur die Berechnung der Fourier- Transformation zu erhalten:

procedure fft(n, x, var

x) if n = 1 then

ˆ x

= x

else begin

m ← n/2;

for k ∈ {0, . . . , m − 1} do begin y

← x

; z

← x

end;

fft(m, y,

y);

fft(m, z,

z);

γ ← 1; ω ← e

;

for ν = 0 to m − 1 do begin ˆ

x

← y ˆ

+ γ z ˆ

; x ˆ

← y ˆ

− γ z ˆ

; γ ← γω

end end

Hier werden die Werte e

mit Hilfe der n-ten Einheitswurzel ω = e

berechnet, um m¨ oglichst selten die aufwendige Berechnung der komplexen Exponentialfunktion zu ben¨ otigen. Es gilt ω

= (e

)

= e

, und diese Koeffizienten werden der Reihe nach f¨ ur ν = 0, . . . , m in der Variablen γ bereit gestellt.

Wir haben bereits gezeigt, dass der Algorithmus das richtige Ergebnis berechnet, wir

k¨ onnen aber auch zeigen, dass er das schneller als der urspr¨ ungliche Ansatz tut: Dazu be-

zeichnen wir mit R

die Anzahl der arithmetischen Operationen, die f¨ ur eine Vektorl¨ ange

von n ∈

ben¨ otigt wird. F¨ ur n = 1 ben¨ otigt unser Algorithmus keine arithmetischen

1.2 Beispiel: Schnelle Fourier-Transformation Operationen (Kopiervorg¨ ange z¨ ahlen wir nicht mit), es gilt also R

= 0. F¨ ur ein gerades n ∈

fallen zwei rekursive Aufrufe f¨ ur Vektoren der L¨ ange n/2 an, also ein Aufwand von 2R

. Die Berechnung der Einheitswurzel ω z¨ ahlen wir als eine Operation. In der Schleife f¨ ur ν m¨ ussen jeweils zwei Multiplikationen, eine Addition und eine Subtraktion ausgef¨ uhrt werden, um ˆ x

und ˆ x

zu bestimmen. Insgesamt fallen also

R

= 2R

+ 4n/2 + 1 = 2R

+ 2n + 1

arithmetische Operationen an. Ausgehend von R

= 0 k¨ onnen wir diese Gleichung aufl¨ osen: Wir verwenden den Ansatz R

= 2n log

n + n − 1. Falls die Gleichung f¨ ur n/2 gilt, folgt

R

= 2R

+ 2n + 1 = 2(2(n/2) log

(n/2) + (n/2) − 1) + 2n + 1

= 2n(log

(n) − 1) + n − 2 + 2n + 1 = 2n log

(n) + n − 1.

Der Rechenaufwand w¨ achst also fast linear mit der Dimension des Vektors.

2 Lineare Gleichungssysteme

2.1 Beispiel: Differentialgleichung

F¨ ur eine gegebene Funktion f ∈ C[0, 1] m¨ ochten wir eine Funktion u ∈ C

[0, 1] finden, die die Differentialgleichung

−u

(t) = f (t) f¨ ur alle t ∈ (0, 1) (2.1) mit den Randbedingungen

u(0) = 0, u(1) = 0

erf¨ ullt. Da die L¨ osung aus einem unendlich-dimensionalen Funktionenraum stammt und sich deshalb nicht in der endlichen Speichermenge, die einem Computer zur Verf¨ ugung steht, darstellen l¨ asst, gehen wir zu einer N¨ aherungsl¨ osung ¨ uber: F¨ ur ein n ∈

ersetzen wir das kontinuierliche Intervall [0, 1] durch die durch

t

:= hi, h := 1

n + 1 f¨ ur alle i ∈ {0, . . . , n + 1}

gegebene diskrete Punktmenge {t

, . . . , t

}. Wir sind nur noch daran interessiert, die Werte der L¨ osung in diesen Punkten zu berechnen, also

x

:= u(t

) f¨ ur alle i ∈ {0, . . . , n + 1}.

Die Werte x

und x

brauchen wir nicht zu berechnen, weil sie bereits durch die Randbedingungen

x

= u(t

) = u(0) = 0, x

= u(t

) = u(1) = 0 festgelegt sind

Um ein praktisch l¨ osbares Problem zu erhalten, m¨ ussen wir die Ableitung in der Differentialgleichung durch etwas ersetzen, das sich mit Hilfe der Werte x

, . . . , x

berechnen l¨ asst. Nach Definition der Ableitung gelten u

(t

) ≈ u(t

) − u(t

)

h , u

(t

) ≈ u(t

) − u(t

)

h ,

und indem wir die erste Approximation in die zweite einsetzen folgt u

(t

) ≈ u(t

) − 2u(t

) + u(t

)

h

. (2.2)

Durch Einsetzen in unsere Differentialgleichung erhalten wir

−x

+ 2x

− x

h

≈ −u

(t

) = f (t

) f¨ ur alle i ∈ {1, . . . , n}.

Wir k¨ onnen also N¨ aherungen der Werte x

berechnen, indem wir das lineare Gleichungs- system

−˜ x

+ 2˜ x

− x ˜

h

= f (t

) f¨ ur alle i ∈ {1, . . . , n}

mit n Gleichungen und den n Unbekannten ˜ x

, . . . , x ˜

aufl¨ osen. Damit folgt u(t

) = x

≈

˜

x

, wir haben also eine N¨ aherung der L¨ osung in den Punkten t

, . . . , t

gefunden, die sich ohne explizite Kenntnis der Funktion u berechnen l¨ asst.

Zur Vereinfachung fassen wir die Unbekannten und die rechte Seite zu Vektoren zu- sammen und stellen das Gleichungssystem durch eine Matrix dar:

A := 1 h













2 −1

−1 . .. ...

. .. ... −1

−1 2













, x :=











˜ x

˜ x

.. .

˜ x











, b :=











f (t

) f (t

)

.. . f(t

)











. (2.3)

Damit haben wir eine Matrix A ∈

und einen Vektor b ∈

und suchen einen Vektor x ∈

, der die Gleichung

Ax = b

l¨ ost. Die L¨ osung der Gleichung k¨ onnen wir dann als N¨ aherung der L¨ osung der Diffe- rentialgleichung interpretieren. Da sie die kontinuierliche Punktmenge [0, 1] durch die diskrete Punktmenge {t

, t

, . . . , t

} ersetzt, bezeichnet man sie als Diskretisierung der Differentialgleichung (2.1).

Bemerkung 2.1 (Genauigkeit) Falls u viermal stetig differenzierbar ist, k¨ onnen wir die Taylor-Entwicklung um t

in Kombination mit dem Zwischenwertsatz verwenden, um

u(t

) − 2u(t

) + u(t

)

h

= u

(t

) + h

12 u

(η)

mit einem Punkt η ∈ [t

, t

] zu beweisen. Unsere N¨ aherung der zweiten Ableitung sollte unter diesen Bedingungen also relativ genau sein, falls das Quadrat der Schrittweite h klein im Verh¨ altnis zu der vierten Ableitung ist.

Bemerkung 2.2 (Verallgemeinerung) Differenzenquotienten der Form (2.2) lassen

sich erheblich verallgemeinern, um partielle Differentialgleichungen aus vielen verschie-

denen Anwendungsgebieten (Elektrostatik und -dynamik, Str¨ omungsdynamik, Struktur-

mechanik) zu behandeln. Besonders erfolgreich ist die Methode der finiten Elemente, die

sich besonders gut f¨ ur die Behandlung komplizierter Geometrien eignet.

2.2 Allgemeine Aufgabenstellung

2.2 Allgemeine Aufgabenstellung

Wir interessieren uns f¨ ur Verfahren, mit denen sich allgemeine lineare Gleichungssysteme der Form

a

x

+ a

x

+ . . . + a

x

= b

, a

x

+ a

x

+ . . . + a

x

= b

,

.. .

a

x

+ a

x

+ . . . + a

x

= b

l¨ osen lassen. Wie zuvor verwenden wir die Matrix A ∈

und die Vektoren x, b ∈

, gegeben durch

A =











a

a

. . . a

a

a

. . . a

.. . .. . . .. .. . a

a

. . . a











, x =











x

x

.. . x











, b =











b

b

.. . b











,

um die Gleichung in der kompakten Schreibweise

Ax = b (2.4)

darstellen zu k¨ onnen. Im Folgenden werden wir Matrizen immer mit Großbuchstaben A, L, . . . bezeichnen, w¨ ahrend wir f¨ ur ihre Eintr¨ age die entsprechenden Kleinbuchstaben a

, `

, . . . verwenden.

2.3 Dreiecksmatrizen

Bevor wir uns allgemeinen linearen Gleichungssystemen zuwenden, untersuchen wir zun¨ achst zwei wichtige Spezialf¨ alle:

Definition 2.3 (Dreiecksmatrizen) Seien L, R ∈

. Falls

`

= 0 f¨ ur alle i < j gilt, nennen wir L eine untere Dreiecksmatrix. Falls

r

= 0 f¨ ur alle i > j gilt, nennen wir R eine obere Dreiecksmatrix.

Ob eine Dreiecksmatrix regul¨ ar ist, l¨ asst sich besonders einfach nachpr¨ ufen: Eine be-

liebige quadratische Matrix ist genau dann regul¨ ar, wenn ihre Determinante ungleich

null ist, und die Determinante einer Dreiecksmatrix ist gerade das Produkt ihrer Diago- nalelemente: F¨ ur eine untere Dreiecksmatrix L ∈

und eine obere Dreiecksmatrix R ∈

gelten

det(L) =

n

Y

i=1

`

, det(R) =

n

Y

i=1

r

,

also sind beide Matrizen genau dann regul¨ ar, wenn alle Diagonalelemente ungleich null sind.

Lineare Gleichungssysteme mit regul¨ aren Dreiecksmatrizen lassen sich besonders ein- fach aufl¨ osen. F¨ ur die Herleitung der entsprechenden Algorithmen zerlegen wir die Auf- gabe wieder in kleinere Teilaufgaben: Wir f¨ uhren Teilmatrizen

L

=







`

.. . . ..

`

. . . `







, L

=







`

.. .

`







und Teilvektoren

x

=







x

.. . x







, b

=







b

.. . b







ein und schreiben das zu l¨ osende Gleichungssystem Lx = b in Blockform:

`

L

L

x

x

= Lx = b = b

b

.

Durch Einsetzen der Teilvektoren und -matrizen sieht man leicht, dass beide Gleichungen

¨ aquivalent sind. Blockmatrizen und -vektoren lassen sich genau wie

” normale“ Matrizen und Vektoren multiplizieren, so dass wir aus der Blockform der Gleichung die Beziehung

b

b

= `

L

L

x

x

=

`

x

L

x

+ L

x

erhalten. Komponentenweise gesehen ergeben sich die Gleichungen

`

x

= b

, L

x

+ L

x

= b

,

von denen sich die erste einfach aufl¨ osen l¨ asst: Da L als regul¨ ar vorausgesetzt ist, gilt

`

6= 0, so dass wir die Gleichung

x

= b

`

erhalten. Da wir x

nun kennen, k¨ onnen wir die zweite Gleichung in die Form

L

x

= b

− L

x

2.3 Dreiecksmatrizen bringen und stellen fest, dass wir wieder ein lineares Gleichungssystem mit einer unteren Dreiecksmatrix erhalten haben, allerdings diesmal mit lediglich n−1 Unbekannten. Falls n > 1 gelten sollte, k¨ onnen wir die beiden Schritte (Division durch das Diagonalelement, Subtraktion einer Spalte von der rechten Seite b) auf immer kleiner werdende Matrizen anwenden, bis x

berechnet ist. Wir erhalten den folgenden Algorithmus:

procedure forward subst(n, L, var b, x);

for j = 1 to n do begin x

← b

/`

;

for i ∈ {j + 1, . . . , n} do b

← b

− `

x

end

Wie man sieht wird zun¨ achst x

berechnet, dann wird von b

der Vektor L

x

sub- trahiert und anschließend zu dem durch L

definierten Teilproblem ¨ ubergegangen. Die Variable j gibt dabei jeweils den Index des linken oberen Elements der gerade behan- delten Teilmatrix an.

In praktischen Implementierungen wird man in der Regel auf den zus¨ atzlichen Vek- tor x verzichten und den Vektor b im Zuge des Verfahrens mit den Komponenten des L¨ osungsvektors ¨ uberschreiben.

Aus naheliegenden Gr¨ unden bezeichnet man dieses Verfahren mit dem Namen Vorw¨ artseinsetzen.

F¨ ur obere Dreiecksmatrizen k¨ onnen wir ¨ ahnlich vorgehen. Wir verwenden die Zerle- gung

R

R

r

x

x

= Rx = b = b

b

mit passend definierten Teilvektoren und -matrizen und erhalten die Gleichungen r

x

= b

, R

x

+ R

x

= b

,

die wir in die Form

x

= b

/r

, R

x

= b

− R

x

bringen k¨ onnen, die sich ¨ ahnlich wie zuvor direkt in einen Algorithmus ¨ ubersetzen l¨ asst:

procedure backward subst(n, R, var b, x);

for j = n downto 1 do begin x

← b

/r

;

for i ∈ {1, . . . , j − 1} do b

← b

− r

x

end

In diesem Fall gibt j jeweils den Index des rechten unteren Elements der gerade behan-

delten Teilmatrix an. Auch hier l¨ asst sich der zus¨ atzliche Vektor x einsparen, wenn man

die Eintr¨ age des Vektors b mit dem Ergebnis ¨ uberschreibt. Es ¨ uberrascht nicht, dass dieser Algorithmus unter dem Namen R¨ uckw¨ artseinsetzen bekannt ist.

Nat¨ urlich m¨ ussen wir uns auch in diesem Fall wieder die Frage stellen, wie groß der Rechenaufwand unserer Algorithmen ist. Traditionell werden dabei lediglich die arith- metischen Operationen mit reellen Zahlen gez¨ ahlt und nicht Kopiervorg¨ ange oder Ma- nipulationen der Indizes. In diesem Sinne ben¨ otigt das Vorw¨ artseinsetzen

n

X

j=1

(1 + 2(n − j)) = n + 2

n

X

j=1

(n − j) = n + 2

n−1

X

j=0

j = n + 2 n(n − 1) 2 = n

Operationen, und dasselbe Ergebnis erhalten wir auch f¨ ur das strukturell sehr ¨ ahnliche R¨ uckw¨ artseinsetzen. Da bei beiden Operationen jeweils

n

X

i=1

i = n(n + 1) 2 > n

2

Matrixeintr¨ age verarbeitet werden m¨ ussen, ist dieser Rechenaufwand kaum weiter zu reduzieren, der Algorithmus darf also als effizient angesehen werden.

2.4 LR-Zerlegung

Unser Ziel ist es nun, das L¨ osen des allgemeinen linearen Gleichungssystems (2.4) auf das L¨ osen unterer und oberer Dreiecksmatrizen zur¨ uckzuf¨ uhren, denn diese Aufgaben lassen sich mit den bereits diskutierten Verfahren einfach l¨ osen. Die Idee besteht darin, die Matrix als ein Produkt aus einer unteren und einer oberen Dreiecksmatrix darzustellen:

Definition 2.4 (LR-Zerlegung) Sei A ∈

eine Matrix. Sei L ∈

eine untere und R ∈

eine obere Dreiecksmatrix. Falls

A = LR (2.5)

gilt, bezeichnen wir das Paar (L, R) als eine LR-Zerlegung der Matrix A.

Falls uns eine LR-Zerlegung zur Verf¨ ugung steht, k¨ onnen wir das Gleichungssystem in der Form

b = Ax = LRx

schreiben und mit dem Hilfsvektor y = Rx auf die Gleichungen

b = Ly, y = Rx

zur¨ uckf¨ uhren, die sich durch Vorw¨ arts- und R¨ uckw¨ artseinsetzen einfach aufl¨ osen lassen.

Also wenden wir uns der Aufgabe zu, zu einer gegebenen Matrix A eine LR-Zerlegung zu konstruieren. Dazu zerlegen wir die beteiligten Matrizen wieder in Teilmatrizen

A

=







a

. . . a

.. . . .. .. . a

. . . a







, A

=







a

.. . a







, A

= a

. . . a

,

2.4 LR-Zerlegung

L

=







`

.. . . ..

`

. . . `







, L

=







`

.. .

`







,

R

=







r

. . . r

. .. .. . r







, R

= r

. . . r

und stellen die definierende Gleichung (2.5) in der Form a

A

A

A

= A = LR = `

L

L

r

R

R

dar. Komponentenweise gelesen ergeben sich aus dieser Gleichung die Beziehungen

a

= `

r

, (2.6a)

A

= L

r

, (2.6b)

A

= `

R

, (2.6c)

A

= L

R

+ L

R

, (2.6d) die wir der Reihe nach aufl¨ osen k¨ onnen. Wir gehen dazu f¨ ur den Augenblick davon aus, dass a

6= 0 gilt, und stellen fest, dass `

= 1 und r

= a

die erste Gleichung (2.6a) erf¨ ullen. Da wir diese beiden Zahlen nun kennen, k¨ onnen wir die Gleichungen (2.6b) und (2.6c) aufl¨ osen:

L

= A

/r

, R

= A

. Mit diesen Vektoren bringen wir die vierte Gleichung (2.6d) in die Form

A

− L

R

= L

R

und stellen fest, dass es uns wieder gelungen ist, ein Problem der Dimension n auf ein gleichartiges Problem der Dimension n − 1 zu reduzieren: Die Matrizen L

und R

ergeben sich aus der LR-Zerlegung der Matrix A

− L

R

.

Bei der praktischen Umsetzung dieser Konstruktion ist es wichtig, den zur Verf¨ ugung stehenden Speicher m¨ oglichst geschickt auszunutzen. Da wir in der Regel die Matrix A nicht mehr ben¨ otigen, sobald wir ihre Zerlegung kennen, k¨ onnen wir den von ihr benutz- ten Speicher mit den Daten der Zerlegung ¨ uberschreiben: Die erste Zeile k¨ onnen wir mit R

uberschreiben, die erste Spalte kann ¨ L

aufnehmen, der Koeffizient `

muss nicht gespeichert werden, weil er nach Definition immer gleich eins ist. Entsprechend k¨ onnen wir A

mit der Matrix A

− L

R

¨ uberschreiben und erhalten als Zwischenergebnis











r

r

. . . r

`

a

− `

r

. . . a

− `

r

.. . .. . . .. .. .

`

a

− `

r

. . . a

− `

r











.

Mit der rechten unteren Teilmatrix k¨ onnen wir nun in derselben Weise verfahren, um die n¨ achsten Zeilen und Spalten der Faktoren L und R zu konstruieren, bis wir schließlich das Ergebnis













r

r

. . . r

`

r

. .. .. . .. . . .. . .. r

`

. . . `

r













, (2.7)

konstruiert haben, das die vollst¨ andige LR-Zerlegung in sehr kompakter Form beschreibt.

Man k¨ onnte diesen Algorithmus rekursiv umsetzen, so wie wir es bei dem mergesort - Algorithmus und der schnellen Fourier-Transformation getan haben, aber in diesem Fall ist es einfacher und effizienter, eine Variable k einzuf¨ uhren, die angibt, welche Zeile und Spalte der Matrizen L und R als n¨ achstes zu berechnen ist. Dann erhalten wir die folgende Rechenvorschrift:

procedure lr decomp(n, var A);

for k = 1 to n do begin for i ∈ {k + 1, . . . , n} do

a

← a

/a

; { `

← a

/r

} for i, j ∈ {k + 1, . . . , n} do

a

← a

− a

a

{ a

← a

− `

r

} end

Nat¨ urlich m¨ ussen wir auch in diesem Fall untersuchen, wie hoch der Rechenaufwand ist.

Indem wir z¨ ahlen, wieviele Rechenoperationen in den Schleifen auftreten und wie oft sie durchlaufen werden, erhalten wir

n

X

k=1

(n − k) + 2(n − k)

=

n−1

X

k=0

k + 2

n−1

X

k=0

k

= n(n − 1)

2 + 2 n(n − 1)(2n − 1) 6

= 3n(n − 1) + 2n(n − 1)(2n − 1)

6 = n(n − 1)(4n + 1)

6

= n(4n

− 4n + n − 1)

6 < 2

3 n

Operationen. Der kubische Rechenaufwand wird dadurch relativiert, dass wir ihn nur einmal f¨ ur jede Matrix betreiben m¨ ussen: Sobald die LR-Zerlegung vorliegt, erfordert das L¨ osen f¨ ur eine beliebige rechte Seite nur noch quadratischen Aufwand.

Der Aufwand l¨ asst sich weiter reduzieren, wenn wir besondere Eigenschaften der Ma-

trix ausnutzen k¨ onnen. Ein Beispiel ist die Tridiagonalmatrix, die wir in unserem Bei-

spiel (2.3) kennen gelernt haben: Da a

= a

= . . . = a

= 0 und a

= a

= . . . =

a

= 0 gelten, m¨ ussen wir in unserem Algorithmus diese Werte nicht ber¨ ucksichtigen

und k¨ onnen den ersten Schritt mit nur drei Rechenoperationen ausf¨ uhren. Da auch die

verbleibende Teilmatrix tridiagonal ist, stellen wir fest, dass insgesamt nicht mehr als

3n Operationen erforderlich sind. Entsprechend k¨ onnen wir auch das Vorw¨ arts- und

2.4 LR-Zerlegung R¨ uckw¨ artseinsetzen mit jeweils nicht mehr als 3n Operationen durchf¨ uhren, erhalten also einen L¨ osungsalgorithmus, dessen Rechenaufwand linear mit der Matrixdimension w¨ achst. Viel effizienter kann ein Algorithmus nicht sein, der n Koeffizienten des Ergeb- nisvektors x berechnet.

Jetzt k¨ onnen wir uns einem Punkt widmen, den wir bisher vernachl¨ assigt haben:

Unsere Konstruktion ist nur durchf¨ uhrbar, falls a

6= 0 gilt, denn bei der Berechnung von L

wird durch r

= a

dividiert. Da der Algorithmus auch auf Teilmatrizen angewendet wird, muss sicher gestellt sein, dass auch bei allen auftretenden Teilmatrizen diese Bedingung erf¨ ullt ist.

In diesem Zusammenhang wird h¨ aufig der Fehler begangen, nicht zwischen den Dia- gonalelementen der Matrix A und den Diagonalelementen der Matrizen A

zu unter- scheiden. Diese Unterscheidung ist allerdings wichtig: Wenn wir die Beispiele

B = 1 2

2 4

, C =

1 2 2 0

untersuchen, stellen wir fest, dass nach dem ersten Schritt unseres Algorithmus B

= 0 und C

= −4 gelten. Im ersten Fall besitzt also B

eine Null auf der Diagonalen, obwohl B das nicht tut. Im zweiten Fall besitzt zwar C eine Null auf der Diagonalen, aber C

nicht.

In der Praxis sind wir nat¨ urlich daran interessiert, ein Verfahren zu benutzen, das f¨ ur alle regul¨ aren Matrizen A funktioniert. Beispielsweise ist das System

0 2 1 0

x

x

= 2

1

problemlos l¨ osbar und die Matrix auch regul¨ ar, aber da der linke obere Eintrag gleich null ist, k¨ onnen wir keine LR-Zerlegung finden. Es gibt allerdings einen einfachen Ausweg:

Wir tauschen die erste und zweite Zeile des Systems, um 1 0

0 2 x

x

= 1

2

zu erhalten. Die in diesem System auftretende Matrix besitzt eine LR-Zerlegung. Wir d¨ urfen also hoffen, dass wir durch das Umordnen der Zeilen der Matrix zu einem allge- mein einsetzbaren Verfahren kommen.

Definition 2.5 (Permutationsmatrix) Sei P ∈

. Falls in jeder Zeile von P genau ein Eintrag gleich eins und alle anderen gleich null sind und falls dasselbe auch f¨ ur jede Spalte gilt, heißt P Permutationsmatrix.

Bemerkung 2.6 (Permutation) Unter einer Permutation versteht man eine Abbil- dung π : {1, . . . , n} → {1, . . . , n}, die bijektiv ist, also lediglich eine Umordnung der Zahlen von 1 bis n beschreibt.

Wenn P eine Permutationsmatrix ist, k¨ onnen wir

π(j) = i f¨ ur alle i, j ∈ {1, . . . , n} mit p

= 1

definieren. Da jede Spalte der Matrix P nur genau eine Eins enth¨ alt, ist π wohldefi- niert. Da jede Zeile nur genau eine Eins enth¨ alt, ist π auch injektiv und damit eine Permutation. F¨ ur einen beliebigen Vektor x ∈

gilt

Px =







x

.. . x







,

also beschreibt die Matrix P gerade die Umordnung der Zeilen des Vektors entsprechend der zugeh¨ origen Permutation π.

Lemma 2.7 (Permutationsmatrizen) Seien P, Q ∈

Permutationsmatrizen.

Dann ist auch ihr Produkt PQ eine Permutationsmatrix.

Beweis. Sei i ∈ {1, . . . , n}. Da P eine Permutationsmatrix ist, existiert genau ein ˆ j ∈ {1, . . . , n} mit p

= 1. Da Q ebenfalls eine Permutationsmatrix ist, existiert genau ein ˆ k ∈ {1, . . . , n} mit q

= 1, und wir erhalten

(PQ)

=

n

X

j=1

p

q

= q

=

(

1 falls k = ˆ k,

0 ansonsten f¨ ur alle k ∈ {1, . . . , n}, also enth¨ alt die i-te Zeile des Produkts nur genau eine Eins und ist ansonsten gleich null.

Entsprechend k¨ onnen wir mit den Spalten verfahren.

Unser Ziel ist es nun, mit Hilfe einer geeigneten Permutation LR-Zerlegungen f¨ ur beliebige regul¨ are Matrizen zu konstruieren. Man spricht von einer LR-Zerlegung mit Pivotsuche oder einer pivotisierten LR-Zerlegung.

Satz 2.8 (LR-Zerlegung mit Pivotsuche) Sei A eine regul¨ are Matrix. Dann exi- stiert eine Permutationsmatrix P ∈

so, dass die Matrix PA eine LR-Zerlegung (L, R) besitzt, dass also

PA = LR

mit einer unteren Dreiecksmatrix L und einer oberen Dreiecksmatrix R gilt.

Beweis. Wir f¨ uhren den Beweis per Induktion ¨ uber n ∈

. F¨ ur n = 1 setzen wir p

= 1,

`

= 1 und r

= a

und sind fertig.

Sei nun n ∈

so gegeben, dass die Behauptung f¨ ur alle Matrizen A ∈

gilt. Sei A ∈

regul¨ ar. Um den bereits bekannten Zugang anwenden zu k¨ onnen, m¨ ussen wir daf¨ ur sorgen, dass der Eintrag a

nicht gleich null ist. Dieses Ziel erreichen wir, indem wir ein i

∈ {1, . . . , n} mit

|a

| ≥ |a

| f¨ ur alle i ∈ {1, . . . , n}

2.4 LR-Zerlegung w¨ ahlen und mit Hilfe einer Permutationsmatrix die i

-te Zeile mit der ersten Zeile ver- tauschen. Dazu verwenden wir P

∈

mit

ˆ p

=







1 falls i = j, i 6∈ {1, i

},

1 falls i = 1, j = i

oder i = i

, j = 1, 0 ansonsten

f¨ ur alle i, j ∈ {1, . . . , n},

denn diese Matrix leistet genau das Geforderte. Nun untersuchen wir die Matrix A

:= PA.

Da ˆ a

= a

das betragsgr¨ oßte Element der ersten Spalte ist, kann es nur gleich null sein, wenn die gesamte Spalte gleich null ist. Das w¨ are aber ein Widerspruch zu der Regularit¨ at von A, also muss ˆ a

6= 0 gelten. Somit k¨ onnen wir wie zuvor verfahren, indem wir

A

=

ˆ a

A

A

A

, L

=

`

L

L

, R

=

r

R

R

einf¨ uhren, wieder

`

:= 1, r

:= ˆ a

= a

, L

:= A

/ˆ a

, R

:= A

setzen und nach einer LR-Zerlegung der Teilmatrix

B := A

− L

R

∈

suchen. Im Allgemeinen braucht eine derartige Zerlegung nicht zu existieren, aber falls wir zeigen k¨ onnen, dass B regul¨ ar ist, k¨ onnten wir uns auf die Induktionsvoraussetzung berufen, um immerhin eine pivotisierte LR-Zerlegung zu finden.

Da A und P

regul¨ ar sind, gilt dasselbe auch f¨ ur PA

= A

=

ˆ a

A

A

A

= `

L

I

r

R

B

, also muss der rechte Faktor

r

R

B

regul¨ ar sein, also insbesondere surjektiv. Damit muss auch B surjektiv sein, also regul¨ ar.

Nun d¨ urfen wir die Induktionsvoraussetzung anwenden, die die Existenz einer Permu- tationsmatrix P

∈

und einer LR-Zerlegung (L

, R

) mit

P

B = L

R

garantiert. Mit Hilfe dieser Matrizen k¨ onnen wir nun die gesuchte Zerlegung konstruieren:

Wir setzen P :=

1 P

P,

L :=

`

P

L

L

, R :=

r

R

R