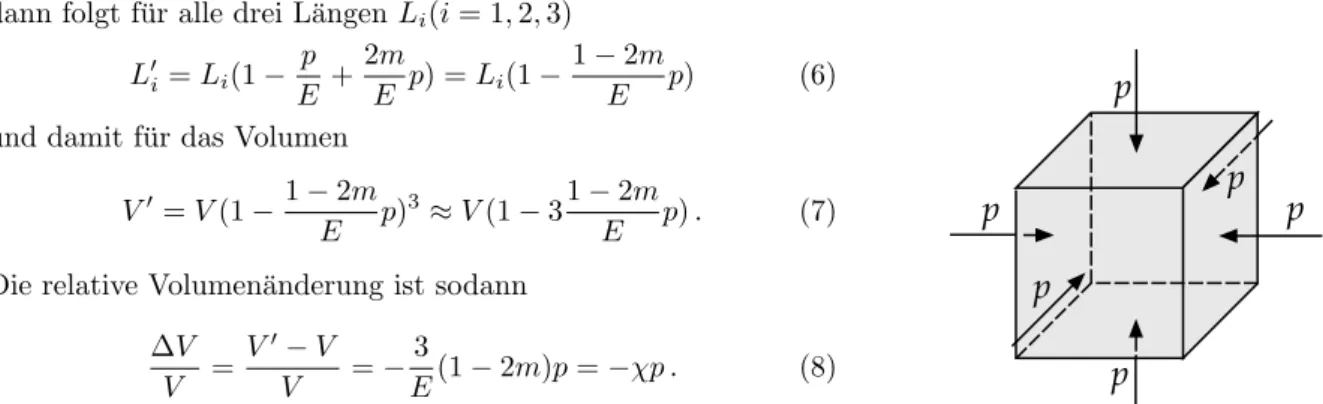1. Interatomare Kr¨ afte

Elastizit¨ at und Festigkeitslehre

In den fr¨uheren Abschnitten der Mechanik haben wir uns mit starren K¨orpern besch¨aftigt, d.h. mit Ob- jekten, bei denen die Abst¨ande und Winkel im K¨orperinnern unver¨andert bleiben. Die Zahl der Freiheits- grade war dann auff = 6 begrenzt. Wir nahmen stillschweigend an, dass innere Kr¨afte Deformationen des K¨orpers verhindern, ganz gleichg¨ultig, wie gross die ¨ausseren Kr¨afte waren. Bei festen K¨orpern ist dies n¨aherungsweise erf¨ullt, wenigstens solange die dazu erforderlichen inneren Kr¨afte nicht allzu gross werden.

Bei genauer Beobachtung lassen sich aber immer Deformationen (Dehnung, Biegung etc.) feststellen, die bei zu grosser Beanspruchung irreversibel sind oder zum Bruch f¨uhren k¨onnen.

Abbildung 1:Die Natur als Modell f¨ur technische Konstruktionen.

Aufgabe der Festigkeitslehre ist es, den Zusammenhang zwischen den ¨ausseren, an einem K¨orper angrei- fenden Kr¨aften und den dadurch im Innern entstehenden Kr¨aften (oder Spannungen) und damit ver- kn¨upften Deformationen zu finden. Technische Bauwerke (H¨auser, T¨urme, Br¨ucken, Bahnen) m¨ussen so dimensioniert werden, dass (bei gleichzeitig m¨oglichst geringem Materialaufwand) bei gegebener ¨ausserer Beanspruchung an keiner Stelle im Innern die maximal zul¨assige Spannung, wie sie durch das Materi- al vorgegeben ist, ¨uberschritten wird. In der Natur ist diese Aufgabe z.B. beim Aufbau von Knochen und Gelenken in Verbindung mit Muskeln meistens optimal gel¨ost (Abbildung 1). In der Geschichte der Menschheit wurden die optimalen L¨osungen (beispielsweise im Br¨uckenbau, siehe Abbildung 2) schon lange vor der Entwicklung der mathematischen und physikalischen Methoden zu ihrer Berechnung ge- funden. Wir k¨onnen also nur nachvollziehen, was unseren Vorfahren bereits empirisch gelungen ist. Auch m¨ussen wir uns auf ein paar wenige, einfache F¨alle beschr¨anken.

Abbildung 2:Links: Pont du Gard, im 1. Jh. v. Chr. von R¨omern erbautes Aqu¨adukt in S¨udfrankreich.

Rechts: Coalbrookdale-Br¨ucke, die 1728 in England erbaute erste Eisenbr¨ucke.

1. Interatomare Kr¨ afte

Derstarre K¨orperist eine Fiktion. Alle Stoffe (nicht nur Gase und Fl¨ussigkeiten) sind mehr oder weniger deformierbar, d.h. unter dem Einfluss ¨ausserer Kr¨afte ¨andert sich ihre Gestalt.

Die Ursache liegt in den interatomaren Kr¨aften, die zwischen den Atomen des Stoffes bestehen. Diese Kr¨afte sind am st¨arksten in festen Stoffen, deren Atome am dichtesten gepackt sind. Ihrer Natur nach sind es elektrische Kr¨afte; Gravitations- oder Kernkr¨afte spielen in diesem Zusammenhang gar keine Rolle.

Werden die einzelnen Atome aus ihrer urspr¨unglichen Lage verschoben, so treten innere Kr¨afte auf, bis sich, im statischen Fall, ein Gleichgewicht zwischen den inneren und ¨ausseren Kr¨aften einstellt.

Wir betrachten zwei Atome. F~ sei die vom Atom 1 auf das Atom 2 ausge¨ubte Kraft. Bei sehr kleinem AbstandristF >0, die Atome stossen sich ab infolge der gleichen Ladung der Kerne und der ¨Uberlap-

1 2

r -

-

−F~ F~ pung ihrer Elektronenwolken. Bei gen¨ugend grossem Abstand verur- sachen die elektrischen Van-der-Waals-Kr¨afte eine Anziehung (F <

0).

r V(r)

F(r)

V_o r_o

absto`end Gleichgewicht

anziehend

Somit gibt es einen Gleichgewichtsabstandr=r◦, f¨ur denF= 0 gilt. F¨ur kleinerk¨onnen wirF also in eine Taylorreihe um r₀entwickeln:

F(r) =F(r₀+ (r−r₀))

=F(r0)

| {z }

=0

+ dF

dr

r=r₀

·(r−r0) +1 2

d²F dr²

r=r₀

·(r−r0)²+. . . .

Unter der Annahme, dass der quadratische und alle h¨oheren Terme in der N¨ahe der Gleichgewichtslage vernachl¨assigbar klein sind, k¨onnen wirF f¨ur jenen Bereich nun in der linearen Form

F(r) =−k(r−r◦) (1)

schreiben. k > 0 hat dabei die Bedeutung einer Federkonstanten¹. Mit F = −dV /dr lautet dann die potentielle Energie des Atomes 2 im Kraftfeld des Atomes 1: V(r) = −V◦+ ^k₂(r−r_◦)², wie bei einer Feder² (Parabelform). Im Gleichgewichtsabstandr₀ ist die potentielle Energie minimal (V(r₀) =−V₀).

Angesichts dieser Verh¨altnisse erkl¨art man sich den festen, kristallinen K¨orper in folgender Weise: Die gegenseitigen Kr¨afte zwingen die Atome in feste Lagen, f¨uhren zu regul¨aren Lagen der Ketten von Atomen mit hoher Symmetrie. Abbildung 3 zeigt als Beispiel die regelm¨assige Anordnung der Natrium- und Chlor- Atome im Kochsalzkristall; ebenfalls zeigt sie die Anordnung der Atome in einem Eisenkristall.

Abbildung 3:Im Caesiumchlorid-Kristall (CsCl, links) ist jedes helle (Cs) Atom von acht dunklen (Cl) Atomen um- geben und umgekehrt. Wenn helle und dunkle Atome identisch sind, entsteht eines der h¨aufigsten Me- tallgitter, das

”kubisch raumzentrierte“. Eisen hat z.B. diese Struktur. Im Kochsalz-Kristall (NaCl, rechts) besetzen sowohl die hellen (Na) als auch die dunklen (Cl) Atome die Ecken eines W¨urfels.

Jedes helle Atom ist oktaedrisch von sechs dunklen umgeben und umgekehrt. Sind helle und dunkle Atome identisch, so ergibt sich ein einfaches kubisches Gitter.

1Zur Federkonstante: vgl. Kap.7-5 im Halliday (

”Von einer Federkraft verrichtete Arbeit“).

2Das Federpotential wird in der noch ausstehenden Vorlesung zum harmonischen Oszillator nochmals aufgegriffen werden.

In der N¨aherung, dass wir die interatomaren Kr¨afte wirk- lich durch Federkr¨afte ersetzen, wie nebenstehend gezeigt, k¨onnen wir auch anschaulich verstehen, wie ein K¨orper auf

¨aussere Belastungen reagiert. Bei Zugbelastung tritt in Zug- richtung eine Verl¨angerung auf, die ohne Zug wieder ver- schwindet. Beim Eisen (vgl. Abb.3) m¨ussten wir das Bild noch mit zus¨atzlichen diagonalen Federn erg¨anzen. Diese er- zeugen in der Richtung quer zum Zug ein Zusammenziehen.

Allgemein ist der Zusammenhang zwischen den ¨ausseren und den inneren Kr¨aften kompliziert. Er h¨angt von der geometrischen Form des K¨orpers und der St¨arke und Ri- chung der ¨ausseren Kr¨afte ab; insbesondere vom Winkel zwischen der Wirkungslinie der Kraft und den Kristallach- sen. Deshalb m¨ussen wir deren Lage kennen - die Kenntnis der Struktur ist also unabdingbar, um pr¨azise Aussagen machen zu k¨onnen.

DehnungStauchungScherungDrillungBiegung Abbildung 4:Die Grundtypen der Deformationen eines star- ren K¨orpers: Verl¨angerung (Dehnung) eines Zylin- ders unter Zug (links) mit gleichzeitiger Verringe- rung des Umfangs, Verk¨urzung unter Druck (Stau- chung) mit Vergr¨osserung des Umfangs, Verschie- bung der Zylinderachse (Scherung) unter Schub (Mitte), Verdrehung der Mantelfl¨ache (Drillung) unter Torsionsbelastung (Mitte rechts) und Ver- biegung (rechts).

Zus¨atzlich zu den in der obigen Abbildung gezeigten Deformations-Varianten sei noch die hydrostatische Kompression erw¨ahnt, die einen K¨orper in allen Richtungen gleichm¨assig zusammengedr¨uckt und dabei sein Volumen verkleinert.

Zwei weitere Eintr¨age in der Rubrik der Begriffe: Wenn es bei einem Material durch die innere Struktur bestimmte, ausgezeichnete Richtungen gibt, dann wird dieses anisotrop genannt. Wir k¨onnen uns hier z.B. an die unterschiedliche Bruchfestigkeit von Holz entlang oder quer zur Maserung erinnern. Beim isotropen K¨orper hingegen spielt die Richtung der Kraft f¨ur die Deformation keine Rolle. Dies kann bei kristallinen Substanzen der Fall sein, wenn das Objekt aus vielen kleinen, beliebig orientierten Kristallen besteht.

2. Elastizit¨ at und Plastizit¨ at

Um qualitative Aussagen bez¨uglich der Deformierbarkeit eines K¨orpers machen zu k¨onnen, unterscheiden wir modellhaft(!) zwei Extremf¨alle: vollkommen elastische versus vollkommen plastische K¨orper.

• Elastische K¨orper: Die Deformation ist hier eine eindeutige Funktion der ¨ausseren Kr¨afte, un- abh¨angig von der Vorgeschichte. Nimmt man die ¨ausseren Kr¨afte weg, so verschwindet sie voll- st¨andig. Beim Anbringen der Kr¨afte wird die geleistete Deformationsarbeit vollst¨andig in potentielle Energie (Deformationsenergie) umgewandelt.

• Plastische K¨orper: Die durch die ¨ausseren Kr¨afte bewirkte Deformation bleibt nach Wegnahme der Kr¨afte vollst¨andig bestehen; die Deformationsarbeit geht vollst¨andig in W¨arme ¨uber (z.B. Knet- masse).

Reale feste K¨orper liegen immer zwischen diesen beiden Grenzf¨allen: F¨ur kleine Kr¨afte sind sie fast v¨ollig elastisch, f¨ur grosse Kr¨afte fast vollkommen plastisch. F¨ur die Federn in unserem Modell bedeutet dies:

Sobald wir sie ¨uberdehnen, kommen wir in den plastischen Bereich, wo alte Form nicht mehr zur¨uckkehrt.

Wann dies der Fall ist, h¨angt vom Material ab; innerhalb gewisser, f¨ur Gl¨aser z. B. recht engen, Grenzen sind alle Materialien elastisch. Um ein numerisches Beispiel zu geben: Ein 1 m langer, zylindrischer Stahlstab von 1 cm Durchmesser verl¨angert sich bei einer Last, die dem Gewicht von 1 t entspricht, um 0.5 mm. Bei 2 t Last verl¨angert er sich permanent um 1.2 mm. Wir sprechen dann von plastischer Verformung. Bei 3 t Last ist die Verl¨angerung 2 mm, und der Stab bricht in der Regel.

Anmerkung: Wir beschr¨anken uns im Folgenden auf den statischen Fall, die K¨orper sind in Ruhe, die Kr¨afte sind zeitunabh¨angig. Dynamische Beanspruchungen durch zeitabh¨angige, z. B. oszillierende Kr¨afte, wie sie in der Praxis fast immer vorliegen, sind wesentlich schwieriger zu behandeln. Dies beruht u.a.

darauf, dass sich dabei Materialeigenschaften im Laufe der Zeit ver¨andern k¨onnen (Erm¨udungsbruch).

3. Spannungen

Da wir nicht weiter mit Kr¨aften zwischen einzelnen Atomen rechnen wollen, und eine eher makroskopische Beschreibung anstreben, ist es zweckm¨assig, statt der Kr¨afte (mechanische) Spannungen einzuf¨uhren.

Spannungen sind definiert als Kr¨afte pro Fl¨acheneinheit im Innern eines K¨orpers. Man f¨uhrt sie ein, indem man in Gedanken in einem Punkt P im Innern einen Schnitt der Fl¨achedAmacht.

Es ist ¨ublich, diese Kr¨afte in ihre Normal- und Tangentialkomponenten bez¨uglich der Schnittfl¨achen zu zerlegen, d ~F = d ~FN +d ~FT, und zu defi- nieren:

Normalspannung : σ=dFN

dA Schubspannung :³ τ =dFT

dA Als Einheit wird meist 1 Pascal (Pa) = 1 Newton/m² verwendet. Istσ >0 so spricht man umgangssprachlich von Zug, istσ <0 von Druck.

r P

6

A A A A A A K

d ~FT

d ~FN

d ~F

dA

Man beachte, dass der Druck in einem Fluid (Gase oder Fl¨ussigkeiten) zwar ebenso definiert wird. In einem Fluid ist der Druck aber stets unabh¨angig von der Richtung der Schnittfl¨ache, w¨ahrend die Spannungen in einem Festk¨orper von der Richtung der Fl¨ache abh¨angen. Da Spannungen keine Vektoren sind, ist ¨uberdies keine Vektoraddition m¨oglich. Nur wenn alle Spannungen auf dasgleicheFl¨achenelement bezogen werden, darf man die zugeh¨origen Kr¨afte wie Vektoren addieren.

Im Allgemeinen ist es ein ¨ausserst kompliziertes Unterfangen, den vollst¨andigen Spannungszustand f¨ur eine spezifische Situation anzugeben. Wir beschr¨anken uns im Folgenden auf einige wenige Spezialf¨alle und diskutieren die empirisch gefundenen Zusammenh¨ange zwischen Spannung und Deformation f¨ur elastische K¨orper.

4. Die elastischen Konstanten isotroper K¨ orper

Solange wir innerhalb des linearen Bereichs bleiben, sind Spannung und Deformation zueinander pro- portional, wobei verschiedene Proportionalit¨atskonstanten (= elastische Konstanten) definiert werden k¨onnen.

3Achtung: Die Schubspannungτ ist nicht mit dem ebenfalls mitτ (meist jedoch mitτ◦o.¨a.) bezeichneten Drehmoment zu verwechseln.

4.1 Das Hooke’sche Gesetz

Wir schneiden aus einem isotropen K¨orper einen Quader mit den Kantenl¨angen L1, L2 und L3 her- aus. Dieser Quader wird zun¨achst nur in Richtung vonL1mit einer konstanten Normalspannungσ1be- lastet (σ2 =σ3 = 0). Die Spannung verl¨angert den Quader um ∆L1. Als Dehnung bezeichnen wir die die relative L¨angen¨anderung ∆L/Lund finden, dass sie im linearen Bereich proportional zur Spannungσ ist:

₁=∆L1

L₁ ∝σ₁. _L

1

L'₃ L₂>L'₂

L₃>L'₃

L1<L'₁ m1

m₁

L₃

L₂ L'₁

L'₂

L'₃

Diese Beobachtung ist unter dem Namen Hooke’sches Gesetz bekannt. Etwas allgemeiner formuliert lautet es, f¨ur ein Objekt der L¨ange ` mit Querschnitt A, an dem eine Kraft F zieht, und daher eine Normalspannungσ=F/Awirkt:

=∆`

` = σ

E. (2)

Die Proportionalit¨atskonstante E [Dimension = Kraft pro Fl¨ache] heisst Elastizit¨atsmodul und ist ab- h¨angig vom Material sowie in kleinerem Masse von dessen Vorbehandlung. Das Hooke’sche Gesetz

m

¡ mP

mB

gilt nur f¨ur kleine Dehnungen bis zur sogenannten Proportionalit¨atsgrenzeσp

der Spannung. Wird sie ¨uberschritten, so tritt plastische Verformung auf, die oft mit einer Erh¨ohung der Proportionalit¨atsgrenze und der BruchfestigkeitσB

verbunden ist.⁴ Bei noch gr¨osserer Belastung beginnt das Material zu fliessen und schliesslich bricht es. Die Gr¨osse der verschiedenen Bereiche h¨angt wieder sehr stark vom Material (hart – weich, spr¨ode – z¨ah) und seiner Vorbehandlung ab (siehe Tabelle 1).

4.2 Poisson-Zahl und Kompressibilit¨at

Wir haben oben schon erkannt, dass mit der L¨angendehnung immer auch ein Zusammenziehen in Quer- richtung verkn¨upft ist. F¨ur die relative Querkontraktion qfinden wir

q= |∆L2| L2

= |∆L3| L3

=m=mσ

E. (3)

Die Poisson-Zahlmist dimensionslos und ebenfalls materialabh¨angig: 0.5≥m >0. Die Querkontraktion ist also mindestens um die H¨alfte kleiner als die Dehnung.

Wird der Quader nicht nur in einer, sondern in allen drei Richtungen durch die Normalspannungen σ1, σ2undσ3beansprucht, so wird die Kantenl¨angeL1infolge der Spannungσ1 gedehnt um den Faktor (1 +1). Die Spannungenσ2 undσ3 sind senkrecht aufL1und bewirken Querkontraktionen um (1−q2) und (1−q3). Die neue Kantenl¨angeL⁰₁ ergibt sich daher zu

L⁰₁=L₁(1 +₁)(1−q₂)(1−q₃)≈L₁(1 +₁−q₂−q₃). (4) Da die Dehnungen und Kontraktionen klein sind (₁, q₂, q₃<<1), konnten die Terme zweiter und dritter Ordnung in undq vernachl¨assigt werden. Mit unseren obigen Beziehungen erhalten wir dann

L⁰₁=L1(1 + σ1

E −m

E(σ2+σ3)). (5)

Entsprechende Beziehungen gelten f¨ur L⁰₂undL⁰₃.

Sind speziell alle Spannungen gleich gross, σ1=σ2 =σ3=:σ, wie man dies beispielsweise beim hydro- statischen Spannungszustand in Fl¨ussigkeiten antrifft, und gilt ferner−p=σ <0 (p= Druck),

4Zur Orientierung: Im Halliday wird die Proportionalit¨atsgrenze mit (

”Zug-/Druckfestigkeit“)Rmbezeichnet, die Bruch- festigkeit mit (

”Streckgrenze“)Re).

dann folgt f¨ur alle drei L¨angen Li(i= 1,2,3) L⁰_i=Li(1− p

E +2m

E p) =Li(1−1−2m

E p) (6)

und damit f¨ur das Volumen V⁰=V(1−1−2m

E p)³≈V(1−31−2m

E p). (7) Die relative Volumen¨anderung ist sodann

∆V

V = V⁰−V V =−3

E(1−2m)p=−χp . (8)

p

p

p p

p p

Die Gr¨osse χ heisst Kompressibilit¨at. Da bei allseitigem Druck das Volumen jedes K¨orpers verkleinert wird, ist sicherχ >0, d.h. 2m <1, m <0.5, wie oben erw¨ahnt wurde.

4.3 Scherung und Schubspannung

Um den Einfluss von Schubspannungen zu erfassen, w¨ahlen wir als Mo- dellobjekt einen W¨urfel, an dem tangential zu einer der W¨urfelfl¨achen A eine Scher- oder Schubkraft F angreift, der also durch eine Schubspan- nungτ=F/Abeansprucht wird. Dies kippt alle zuAsenkrechten Kanten des W¨urfels um den sogenannten Schubwinkelα, der f¨ur gen¨ugend kleine Schubspannungen propotional zuτ ist:

α= 1

Gτ mit G= E

2(1 +m). (9)

F

l _

Die Materialgr¨osseGheisst Schubmodul.

In Tabelle 1 sind typische Werte verschiedener soeben besprochener Gr¨ossen aufgef¨uhrt. Die Bruchfes- tigkeit ist diejenige Spannung, bei der das Material bricht. Die zul¨assige Spannung liegt dann jeweils um einen (je nach Anwendung unterschiedlich ausfallenden) Sicherheitsfaktor tiefer. Da Holz und Knochen stark anisotrop sind, werden daf¨ur zwei Werte, parallel und senkrecht zur Faser, angegeben. Extrem grosse Festigkeiten werden erreicht in hochreinen Einkristallen, wie sie in Form von F¨aden (

”Whiskers“) gez¨uchtet werden k¨onnen. So sind in Graphit, Al203 und SiC ZugfestigkeitenσB bis zu 2×10¹⁰ N/m² gemessen worden.

Material Elastizit¨atsmodul Bruchfestigkeit Bruchdehnung

E σB B

[10⁹N/m²] [10⁷N/m²] [%]

Al rein, weich 72 1.3 50

α−Eisen 218 10 50

CrV-Federstahl 212 155 5

Beton 40 5

H¨olzerk(⊥) Maserung 15 (1.5) 5–20 (0.3–1) Knochen kompakt (spongi¨os) 18 (0.08) 12 (0.22)

Knochenk(⊥) 16 8.5 (1) 0.6 (0.2)

Sehnen (Bandscheiben) 0.7 6.5 (1.1)

Menschenhaar 3.6

Tabelle 1: Elastische Konstanten f¨ur verschiedene Materialien.

Aus Tabelle 1 kann man entnehmen, dass Knochen elastischer sind als Beton und dass letzterer auch eher bricht. Dies erm¨oglicht Karatek¨ampfern ihre spektakul¨aren Durchschlagskraft-Demonstrationen.

Ein Bruch kann sowohl bei Dehnung als auch bei Stauchung auftreten. Bei isotropem Aufbau der K¨orper sind Elastizit¨atsmodul und Bruchfestigkeit f¨ur alle Kraftrichtungen gleich gross. F¨ur die meisten biologi- schen Materialien ist dies allerdings nicht der Fall.

5. Beispiele

5.1. Belastung eines einseitig eingespannten Balkens Ein homogener Balken der L¨ange L mit dem rechteckigen Querschnitt A = BH = 2Bh sei an einer Seite fest ein- gespannt und am anderen Ende durch eine vertikale Kraft F >> G belastet. Das Eigengewicht des Balkens wird ver- nachl¨assigt und die auftretenden Deformationen sind klein.

Die Belastung f¨uhrt zu einem Drehmoment bez¨uglich der Ein- spannstelle. Diese bewirkt eine Biegung des Balkens. Bei einer solchen Biegung wird das obere Ende des Balkens gedehnt, das untere gestaucht. Zwischen dem unteren und dem obe- ren Ende muss also eine Schicht liegen, die weder gestaucht noch gedehnt wird, d.h. ihre urspr¨ungliche L¨ange beibeh¨alt.

Diese Schicht wird neutrale Faser genannt. Man kann sich ihre Existenz verdeutlichen, indem man in Gedanken den Balken durch eine Gliederkette mit elastischen Kopplungs- st¨ucken ersetzt. Die Verl¨angerung der Federn im oberen Teil und die Verk¨urzung im unteren Teil l¨asst uns die Richtung der Normalspannungen ablesen. Sie ziehen im oberen Teil und dr¨ucken im unteren Teil, in der Mitte verschwinden sie. Es ist plausibel, folgenden Ansatz zu machen:

σ(x, y, z) = ˜σ(x)z .⁵

Die Normalspannung ist proportional zu z und nicht von y abh¨angig. z = 0 entspricht dann σ(x,0) = 0, d.h. der span- nungslosen, neutralen Faser.

NF F x=L

x=0 x y

z

x m z

o

z F

y

o dA B h₁ H

h₂

A=B·H

Wir vermuten nat¨urlich, dass z = 0 auch der Mitte des Balkens entspricht, wegen der Symmetrie des Balkens bez¨uglich seiner Mittelebene, aber wir wollen dies nicht voraussetzen, sondern aus den Gleichge- wichtsbedingungen beweisen.

Beim Gliederkettenmodell beobachten wir ¨uberdies, dass die Schnittebenen senkrecht zur neutralen Faser auch bei Belastung senkrecht zu dieser bleiben. Wir wollen ferner annehmen, dass sie bei den kleinen Belastungen und Verschiebungen im elastischen Bereich, mit denen wir uns befassen, ihre Form nicht

¨andern. Dies kann nur dann der Fall sein, wenn die Schubspannungen entlang der Schnittebene konstant sind:

τ(x, y, z) =τ(x)

(τ = τ(y) w¨urde z.B. das Rechteck zu einem Parallelogramm verformen). Nun k¨onnen wir die stati- schen Gleichgewichtsbedingungen anwenden und die Spannungen explizit berechnen. Wir ben¨utzen drei Bedingungen, n¨amlich:

1. Die Kr¨aftesumme in der z−Richtung bezogen auf das Balkenst¨uck vonx= 0 bisxsoll null sein.

2. Die Kr¨aftesumme in der x−Richtung soll null sein.

3. Die Kr¨afte m¨ussen bez¨uglich dem Zentrum der Schnittfl¨ache entsprechend dem Hebelgesetz im Gleichgewicht sein (eigentlich: deren Drehmoment muss verschwinden).

5Die Proportionalit¨atskonstante ˜σhat demnach nicht die Dimension vonσ.

Mathematisch ausgedr¨uckt haben die drei Bedingungen folgende Form und Bedeutung:

(1) PF_z= 0 =−F+R

Aτ(x, y, z)dA=−F+τ(x)R

dxdy=−F+τ(x)A ⇒ τ(x) = ^F_A

τ(x) ist damit offensichtlich nicht vonxabh¨angig, sondern konstant. Die Schubspannungen entlang jeder Schnittebene senkrecht zur neutralen Faser sind gleich, und zwar gleich der ¨ausseren Last dividiert durch die Querschnittsfl¨ache des Balkens.

(2) PFx= 0 =R

Aσ(x, y, z)dA=R

Aσ(x)zdydz˜ = ˜σ(x)R dyRh2

h₁ zdz =Bσ(x)(h˜ ²₁−h²₂)/2

Hieraus folgth²₁=h²₂ undh1=h2=H/2 =h– die neutrale Faser liegt in der Tat genau in der Mitte.

(3) Hebelgesetz : x·F =R

Az·σdA, mit σ= ˜σ(x)·z wird x·F = ˜σ(x)R

Az²dA . Die Gr¨osseR

Az²dAwird Fl¨achentr¨agheitsmomentIz der Schnittfl¨acheAgenannt. Damit ergibt sich

˜

σ(x) = F x

I_z ⇒ σ(x, z) = F xz

I_z . (10)

Die Normalspannungen nehmen mit dem Abstand von der neutralen Faser sowie vom Balkenende linear zu. Sie erreichen ihre gr¨ossten Werte am oberen und unteren Rand des Schnittes (z=±h), und an der Einspannstellexmax=L:σmax=F Lh/IzDer Stab wird dort brechen, wenn bei zunehmender Belastung F die Spannungσmaxdie ZugfestigkeitσB ¨uberschreitet.

F¨ur unseren rechteckigen Balken l¨asst sich das Fl¨achentr¨agheitsmoment ausrechnen:

I_z= Z +h

−h

z²dA= Z

dy Z h

−h

z²dz=2

3Bh³= BH³

12 = AH²

12 . (11)

Die H¨ohe des Balkens geht mit der dritten Potenz ein, die Breite nur linear, und es ist σ(x, z) =12F xz

AH² . (12)

Analysieren wir dieses Resultat etwas n¨aher:

• Wo wird die Spannung am gr¨ossten?

a) z= maximal =±H/2 : σ_max=±_BH^{6F x}2 =±^{6F x}_AH

Die maximale Zug(Druck)spannung tritt, wie bereits erkannt, an der oberen (unteren) Seite des Balkens auf. Sie ist bei vorgegebener Fl¨ache umgekehrt proportional zur H¨ohe des Balkens. Man kann also bei gleichem Material die Spannungen durch die Wahl eines schmalen und hohen statt eines breiten und flachen Balkens erniedrigen. Das Gleiche gilt auch f¨ur die Durchbiegung von zweiseitig eingespannten (oder aufgelegten) Balken unter Last.

b) x= maximal =L: σ_max=±^{6F L}_AH

Bei zu grosser Belastung wird der Balken also an der Einspannstelle (Skischuh!) brechen.

• Wo wird die Spannung am kleinsten?

Da in der Schnittmitte in der N¨ahe der neutralen Faser beiz= 0 nur kleine Spannungen auftreten, kann dort Material weggenommen werden. Daher werden f¨ur Schienen und Tr¨ager im H¨auserbau I-Profile verwendet. Falls die Belastung alle m¨oglichen Richtungen annimmt, ist die Rohrform optimal (R¨ohrenknochen, Federn). Auch hier kann man die Spannungen und Durchbiegungen re- duzieren, wenn man das Fl¨achentr¨agheitsmoment vergr¨ossert, d. h. einen gr¨osseren Radius w¨ahlt.

Material kann in der Mitte eingespart werden, d.h. grosse Rohre mit d¨unnen W¨anden sind kleinen Rundst¨aben gleicher Masse vorzuziehen.

• Wie kann man die maximale Spannung f¨ur allex(i.e. entlang der L¨ange des Balkens) konstant halten?

Man variiert die Balkenh¨ohe:H=H(x).

σmax= 6F x BH²

= konst.! = 6F L

BH(L)² ⇒ H(x) =H(L) rx

L

x H(x)

L

• Was bringen Verstrebungen?

Die maximale Spannung bei dieser Art von Belastung (Biegebelastung) ist um ca. einen Faktor L/h gr¨osser als bei Zugbelastung σ_zug =F/Amit der gleichen Kraft. Durch Verstrebungen oder Seilz¨uge (siehe Abb.5) kann die Biegebelastung in eine Druckbelastung des Balkens (σ_zug negativ) und eine Zugbelastung des Seils verwandelt und damit die Tragkraft wesentlich gesteigert werden.

Im Skelett sind es die Muskeln, welche zum Teil diese Funktion aus¨uben.

F

F F_zug

F_zug Abbildung 5: Seile in der Technik und Mus-

keln im menschlichen K¨orper verwandeln Druck- in Zug- belastungen und steigern so die Tragkraft.

• Wie verl¨auft die Raumkurve der neutralen Faser?

Ein Mass f¨ur die Biegung der Stabachse im SchnittA(x) ist der Kr¨ummungsradiusρ(x). Sind A₁ und A₂ Querschnitte in der Nachbarschaft von x, die im undeformierten Zustand im Abstand s parallel zueinander stehen, so schneiden sich deren Symmetrieachsen im Kr¨ummungsmittelpunkt M der Stabachse (neutralen Faser). Nach dem Strahlensatz gilt dann

M ρ

s

s+ ∆s h1

HH

N F ρ+h₁

ρ =s+ ∆s(h₁)

s , d.h. 1 + h₁

ρ = 1 +∆s(h₁) s , also h₁

ρ = ∆s(h₁)

s =ε(h₁) = σ(h₁)

E =σ(x)h˜ ₁ E , und mit Gl.(10) ist 1

ρ= F x

I_zE . (13)

Wir suchen jetzt die Gleichung der BiegekurvezN F(x), wobei xund zN F die Koordinaten eines Achsenpunktes sind (z_{N F} = 0 bezeichne die Lage der neutralen Faser ohne Belastung (F= 0)).

x

zN F

ds≈ dx

ρ

α)

dϕ x

x+dx Zun¨achst m¨ussen wir den zugeh¨origen Kr¨ummungsradius ρ mit zN F(x) verkn¨upfen. F¨ur zwei benachbarte Achsenpunkte gilt

dϕ=α_x+dx−α_x≈dα

dxdx=dα. (14) Andererseits gilt dϕ≈ dx

ρ und dz_{N F}

dx = tanα≈α (f¨ur|α| 1).

Wir haben also dα=dϕ= dx

ρ =d²zN F

dx² dx, und es folgt aus Gl.(13): d²zN F

dx² = 1 ρ= F x

I_zE .

Aus dieser Differentialgleichung erh¨alt man durch zweimaliges Integrieren zN F(x) = F

I_zE x³

6 +C1x+C2

.

Die Integrationskonstanten lassen sich aus den Randbedingungen bestimmen: Aus ^dz_dx^{N F}

_x=L = 0 (horizontale Tangente an der Einspannstelle) erh¨alt manC1= ^L₂², und auszN F(L) = 0 (Nullpunkt) C2= ^L₃³. Damit wird die Gleichung der neutralen Faser zu

z_{N F}(x) = F L³ 6EI_z

(x

L)³−3(x L) + 2

. (15)

Die Durchbiegung ist erwartungsgem¨ass proportional zu F, umgekehrt proportional zum Elasti- zit¨atsmodul Eund am gr¨ossten am Ende des Balkens beix= 0:

a b

D

h H

d/2 R

r

z_{N F}(x= 0) = F L³

3EI_z =: ˜z(0). (16)

Diese maximale Durchbiegung kann klein gehalten werden, indem ein gros- ses Fl¨achentr¨agheitsmomentI_zgew¨ahlt wird. Werfen wir mit diesem Wissen einen Blick auf die Fl¨achentr¨agheitsmomente

– eines Rechtecks:I_z= ₁₂¹ba³,

– eines Doppel-T-Tr¨agers (I-Profil):I_z= ₁₂¹(DH³−dh³), – eines Rohres:Iz= ^π₄(R⁴−r⁴),

so zeigt sich unsere fr¨uhere Intuition best¨atigt: Zur Vermeidung einer ¨Uber- beanspruchung eignen sich besonders I-Profile sowie d¨unnwandige, grosse Rohre.

Wird der gleiche Balken zweiseitig eingespannt oder aufgelegt, so ist die maximale Durchbiegung in Einheiten von ˜z(0) durch einen rationalen Faktor angebbar. Das Gleiche gilt f¨ur die maximale Spannung, die sich ebenfalls um einen rationalen Faktor von derjenigen f¨ur den einseitig eingespannten Balken unterscheidet. ¨Ahnliches gilt schliesslich auch, wenn die Last gleichm¨assig auf den Balken verteilt ist.

F D m_max

F

Durchbiegung

[(FL³)/(3EI_z)] Spannung [(FLH)/(2I_z)]

1 1

3/8 1/2

1/16 1/4

5/128 1/8

1/64 1/8

1/128 1/12

Abbildung 6:Durchbiegung und maximale Spannung f¨ur verschiedenartige Auflagen und Be- lastungen desselben Balkens.

5.2. Belastung der Wirbels¨aule

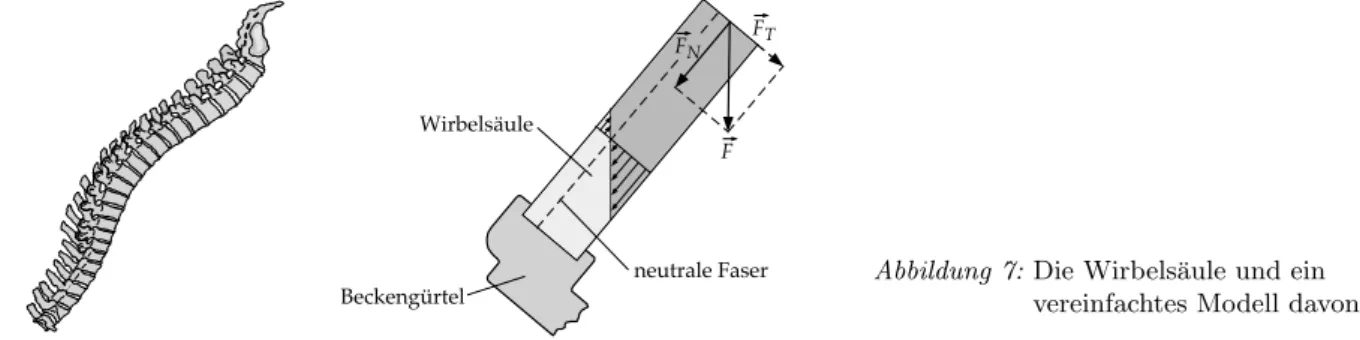
Die Wirbels¨aule bildet die bewegliche Achse des menschlichen K¨orpers. Sie wird sowohl Druck-, Zug-, Biege-, als auch Torsionsbelastungen ausgesetzt. Ein zentrales Element der Wirbels¨aule sind die Band- scheiben, welche die elastischen Verbindungen zwischen zwei starren Wirbeln darstellen. Der Elasti- zit¨atsmodul der Bandscheiben (E '5 MPa) ist viel kleiner als derjenige vieler anderer Materialien, aber ca. 5 mal gr¨osser als derjenige von Gummi (E '1 MPa). Uns interessiert der Spannungsverlauf in der auf Biegung beanspruchten Wirbels¨aule. In einem vereinfachten Modell betrachten wir die Wirbels¨aule als homogenen, elastischen Balken wie in Abbildung 7 skizziert.

Wirbelsäule

Beckengürtel

neutrale Faser F_T

F F_N

Abbildung 7: Die Wirbels¨aule und ein vereinfachtes Modell davon.

Der Balken (Wirbels¨aule) ist am unteren Ende fest eingespannt (Beckeng¨urtel) und am oberen Ende mit einer senkrecht nach unten gerichteten Kraft F~ (Heben einer schweren Last) belastet. Wir zerlegen die Kraft F~ in eine Komponente normal (F~N) und eine Komponente tangential (F~T) zur Querschnittsfl¨ache der Wirbels¨aule.F~_N ruft eine Stauchung der Wirbels¨aule hervor, was zu einer homogenen Normalspan- nung in einem Querschnitt f¨uhrt. Die KraftF~_T hingegen bewirkt ein Biegemoment, und somit in einem Querschnitt denselben Verlauf der Normalspannung wie beim einseitig eingespannten Balken. Auf der dorsalen Seite tritt eine Dehnung und auf der ventralen Seite eine Stauchung der Wirbels¨aule auf. Durch die zus¨atzliche konstante Normalspannung vonF~N wird die neutrale Faser zur dorsalen Seite hin verscho- ben. Der Verlauf der totalen Normalspannung in einem Querschnitt ist in der Abbildung eingezeichnet.

Die Belastung mit der KraftF~ erzeugt haupts¨achlich eine Druckspannung in der Wirbels¨aule, gegen¨uber welcher die Bandscheiben sehr widerstandsf¨ahig sind. Auf der dorsalen Seite bleibt aber bei geneigter Wirbels¨aule immer eine Zugbelastung der Bandscheibe bestehen, die sich nachteilig auf diese auswirkt.

Bei extremer Biegebelastung k¨onnen aufgrund der hohen Zugbelastung der Bandscheiben gravierende Sch¨aden auftreten (Bandscheibenbruch).

5.3. Torsion eines zylindrischen Stabes

Ein zylinderischer Stab mit L¨ange`und RadiusRwerde einseitig eingespannt und am freien Ende durch ein axiales Drehmomentτ`beansprucht. Im Gleichgewicht istτ`=τ_◦= 2F R. Infolge der Beanspruchung werden die Querschnitte verdreht.

x

A(x) R

F

o

o

Eine gerade Mantellinie geht in eine Schraubenlinie ¨uber.

Um die Spannungen im SchnittA(x) zu bestimmen, denkt man sich den Stab wiederum durchgeschnitten und die Spannungen so angebracht, dass Gleichgewicht herrscht und die Schnitte nur verdreht werden. Dies ist der Fall, wenn azimutale Schubspannungen wirken. Es ist zun¨achst aus geometrischen Gr¨unden rϕ=δx.

r

b q

x

o

o

Bei kleinen Verdrillungen ist der Torsionswinkel δ einer Schub- spannungτ proportional:

δ= τ

G. Also wird τ=δG=Grϕ x.

Die Gleichtgewichtsbedingung verlangt dann

τ_◦=

R

Z

r=0

τ2πrdrr= 2πϕG x

R

Z

0

r³dr=πϕGR⁴

2x . Somit wird τ =Grϕ x = 2τ_◦

πR⁴r. (17) Die Schubspannungen sind also unabh¨angig vonx. Sie werden maximal f¨urr=R:

τmax= 2τ◦

πR³.

Diese Ergebnisse kann man benutzen, um mit Hilfe eines TorsionspendelsSchubmodule zu messen. Der verdrehte Draht ¨ubt ein r¨ucktreibendes Drehmomentτϕaus, das durch obige Gleichung (17) gegeben ist.

Der Drehimpulssatz f¨ur ebene Bewegungen liefert (mit dem Tr¨agheitsmomentI_◦) die Bewegungsgleichung

  2R

`

I◦

d²ϕ

dt² =τ◦=−πR⁴G 2` ϕ mit der L¨osung ϕ(t) =ϕ◦cos(ωt−δ),

wobei ω=R² r πG

2`J_◦.

Diese L¨osung hat nat¨urlich nur im G¨ultigkeitsbereich des Hoo- ke’schen Gesetzes einen Sinn.