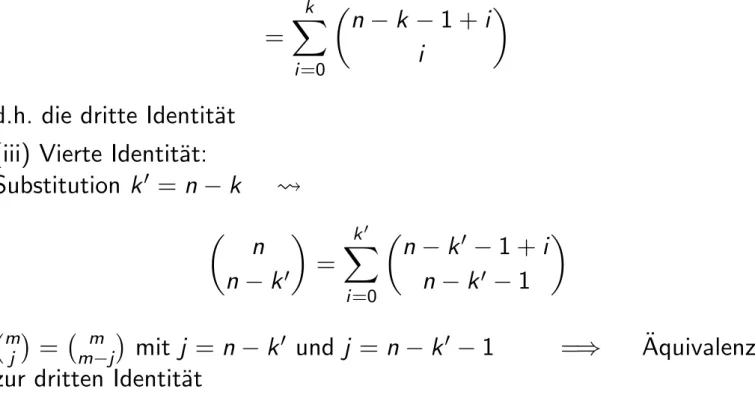” wahr“) bzw. f (

Aussage

Unter einer Aussage versteht man einen sprachlichen Ausdruck, dem man eindeutig einen der beiden Wahrheitswerte w (

” wahr“) bzw. f (

” falsch“) zuordnen kann.

Aussagen werden mit Großbuchstaben bezeichnet, A : Beschreibung ,

und k¨ onnen mit logischen Operationen verkn¨ upft werden. Grundlegende mathematische Aussagen, die nicht aus anderen Aussagen abgeleitet werden k¨ onnen, nennt man Axiome.

1 / 1

Beispiel

Verschiedene Aussagen Wahre Aussage

A: Jede nat¨ urliche Zahl ist ein Produkt von Primzahlen.

Falsche Aussage

B : Jede Primzahl ist ungerade (2 ist eine gerade Primzahl)

Unbewiesene Vermutung (wahr oder falsch, d.h. eine Aussage, bei der der Wahrheitswert noch nicht entschieden werden konnte)

C : Es gibt unendlich viele Primzahlzwillinge gr¨ oßter bisher bekannter Primzahlzwilling (Stand 19.4.2006):

16869987339975 · 2 ¹⁷¹⁹⁶⁰ ± 1

Logische Operationen

Logische Aussagen k¨ onnen durch die in der folgenden Tabelle angegebenen Operationen verkn¨ upft werden.

Bezeichnung Schreibweise (Sprechweise) wahr, genau dann wenn

Negation ¬A (nicht A) A falsch ist

Konjunktion A ∧ B (A und B ) A und B wahr sind

Disjunktion A ∨ B (A oder B ) A oder B wahr ist Antivalenz A 6≡ B (entweder A oder B ) A und B verschiedene

Wahrheitswerte haben Implikation A = ⇒ B

B ⇐ = A

(aus A folgt B )

(B folgt aus A) A falsch oder B wahr ist Aquivalenz ¨ A ⇐⇒ B (A ist ¨ aquivalent zu B ) A und B den gleichen

Wahrheitswert haben

3 / 1

Um in logischen Ausdr¨ ucken Klammern zu sparen, wird festgelegt, dass ¬ st¨ arker bindet als ∧ sowie ∨ und diese wiederum st¨ arker als = ⇒, ⇐⇒

sowie 6≡.

Bei der Implikation ist zu beachten, dass B nur dann wahr sein muss, wenn A wahr ist. Aus falschen Voraussetzungen k¨ onnen sowohl richtige, als auch falsche Schl¨ usse gezogen werden.

F¨ ur die Oder-Verkn¨ upfung wird auch das

” +“-Symbol verwendet und f¨ ur die Und-Verkn¨ upfung das

” ·“-Symbol. Verwendet man dann 0 f¨ ur den Wert ” falsch“ und interpretiert jeden anderen Wert als

” wahr“, k¨ onnen die logischen Verkn¨ upfungen durch Rechnen mit nat¨ urlichen Zahlen

durchgef¨ uhrt werden.

In der folgenden Tabelle sind die Wahrheitswerte der vorgestellten Verkn¨ upfungen angegeben. Dabei steht w f¨ ur wahr und f f¨ ur falsch.

A B ¬A A ∧ B A ∨ B A 6≡ B A = ⇒ B A ⇐⇒ B

w w f w w f w w

w f f f w w f f

f w w f w w w f

f f w f f f w w

5 / 1

Beispiel

Darstellung der Verkn¨ upfung von Aussagen mit Hilfe von Schaltern (geschlossen ⇐⇒ wahre Aussage, ge¨ offnet ⇐⇒ falsche Aussage) Und-Verkn¨ upfung (seriell) Oder-Verkn¨ upfung (parallel)

negierte Aussage: Schalter der bei falscher Aussage geschlossen ist

Antivalenz: A 6≡ B bzw. (A ∧ ¬B ) ∨ (¬A ∧ B )

Aquivalenz: ¨ A ⇐⇒ B bzw. (A ∧ B ) ∨ (¬A ∧ ¬B )

7 / 1

Implikation: A = ⇒ B bzw. ¬A ∨ B

DIN 40900 Symbole f¨ ur Schaltungen

Konjunktion Disjunktion Antivalenz

Negation Implikation Aquivalenz ¨

wahr: 1, falsch: 0, Negation: Kreis

9 / 1

Identit¨ aten und Regeln f¨ ur logische Operationen F¨ ur logische Operationen gelten die folgenden Identit¨ aten.

Assoziativgesetze:

(A ∧ B ) ∧ C = A ∧ (B ∧ C ) (A ∨ B ) ∨ C = A ∨ (B ∨ C ) Kommutativgesetze:

A ∧ B = B ∧ A A ∨ B = B ∨ A De Morgansche Regeln:

¬(A ∧ B ) = (¬A) ∨ (¬B )

Distributivgesetze:

(A ∧ B ) ∨ C = (A ∨ C ) ∧ (B ∨ C ) (A ∨ B ) ∧ C = (A ∧ C ) ∨ (B ∧ C ) Sonstige:

¬(¬A) = A A ∧ A = A A ∨ A = A Alternative Darstellungen:

Implikation: A = ⇒ B = ¬A ∨ B = ¬A ⇐ = ¬B Aquivalenz: ¨ A ⇐⇒ B = (A ∧ B ) ∨ (¬A ∧ ¬B )

Antivalenz: A 6≡ B = (A ∧ ¬B ) ∨ (¬A ∧ B )

11 / 1

Die alternativen Formulierungen werden oft in Beweisen benutzt.

Ein logischer Ausdruck, der unabh¨ angig vom Wahrheitswert der auftretenden Aussagen immer wahr bzw. immer falsch ist, wird als

Tautologie bzw. Kontradiktion bezeichnet. Ein solcher Ausdruck kann bei einer Umformung durch w (oder 1) bzw. f (oder 0) ersetzt werden.

Insbesondere gelten die Identit¨ aten:

A ∨ ¬A = w bzw. A ∧ ¬A = f , A ∨ w = w bzw. A ∧ w = A ,

A ∨ f = A bzw. A ∧ f = f .

Beweis

Untersuchung aller M¨ oglichkeiten f¨ ur die Wahrheitswerte der Aussagen Tabelle f¨ ur die erste De Morgansche Regel

¬(A ∧ B ) = (¬A) ∨ (¬B )

A B A ∧ B ¬A ¬B ¬(A ∧ B ), (¬A) ∨ (¬B )

w w w f f f

w f f f w w

f w f w f w

f f f w w w

analoge Argumentation f¨ ur andere Regeln

13 / 1

Beispiel

Umformung der Aussage

|x − 1| > 1

| {z }

A

= ⇒ (x < 0) ∨ (x > 2)

| {z }

B

De Morgansche Regel ¬(C ∨ D ) = ¬C ∧ ¬D = ⇒

¬B = ¬(x < 0) ∧ ¬(x > 2) = (x ≥ 0) ∧ (x ≤ 2) = 0 ≤ x ≤ 2 (A = ⇒ B ) ⇐⇒ (¬B = ⇒ ¬A), d.h.

0 ≤ x ≤ 2 = ⇒ |x − 1| ≤ 1 = w

Alternative: benutze Definition der Implikation

Quantoren

Als Abk¨ urzung f¨ ur die Formulierungen

” es gibt . . . “,

” f¨ ur alle . . . “

werden der Existenzquantor ∃ und der Allquantor ∀ verwendet. Diese Quantoren werden h¨ aufig in Verbindung mit Aussagen A(p) benutzt, die von einem Parameter p aus einer Menge P abh¨ angen.

Schreibweise Bedeutung

∃ p ∈ P : A(p) es gibt mindestens ein p aus P , f¨ ur das A(p) wahr ist

∀ p ∈ P : A(p) f¨ ur alle p aus P ist A(p) wahr

15 / 1

Bei der Negation der beiden Aussagentypen vertauschen sich die Quantoren:

¬ ∃ p ∈ P : A(p)

= ∀ p ∈ P : ¬A(p)

¬ ∀ p ∈ P : A(p)

= ∃ p ∈ P : ¬A(p)

Gebr¨ auchlich ist ebenfalls die Schreibweise ∃! f¨ ur die Formulierung

” es gibt

genau ein . . . “.

Beispiel

Negation des Kriteriums f¨ ur die Konvergenz einer Folge a ₁ , a ₂ , . . . gegen 0:

∀ ε > 0 ∃ n _ε ∀ n ∈ N : n > n _ε = ⇒ |a _n | < ε

Negation durch Negieren der Kernaussage und Ersetzen der Quantoren,

∃ ↔ ∀

Ersetzen der Implikation (A = ⇒ B = ¬A ∨ B ) und Anwendung der De Morganschen Regel (¬(A ∨ B ) = ¬A ∧ ¬B )

¬(n > n _ε = ⇒ |a _n | < ε) = ¬(n ≤ n _ε ∨ |a _n | < ε) = n > n _ε ∧ |a _n | ≥ ε negierte Aussage:

∃ ε > 0 ∀ n _ε ∃ n ∈ N : n > n _ε ∧ |a _n | ≥ ε Vereinfachung: ∃ ε > 0 : |a _n | ≥ ε f¨ ur unendlich viele n ∈ N

17 / 1

Direkter Beweis

Eine Behauptung B kann bewiesen werden, indem sie aus bekannten wahren Aussagen A hergeleitet oder auf solche zur¨ uckgef¨ uhrt wird:

A = ⇒ B .

Die Aussagen A k¨ onnen dabei auch Voraussetzungen beinhalten, die f¨ ur

die G¨ ultigkeit der Behauptung B notwendig sind.

Beispiel

Satz des Pythagoras:

a ² + b ² = c ²

mit a, b den L¨ angen der Katheten und c der L¨ ange der Hypothenuse eines rechtwinkligen Dreiecks

Direkter Beweis:

benutze als bekannt: ¨ Ahnliche Dreiecke, d.h.

Dreiecke mit gleichen Winkeln, haben die gleichen Seitenverh¨ altnisse.

Anwendung auf ∆(A, B , C ) ∼ ∆(A, C , M ) = ⇒

|AC | : |AB| = |AM | : |AC |, d.h. |AC | ² = |AB | · |AM | analog:

|BC | ² = |AB | · |BM |

19 / 1

Addition der letzten beiden Gleichungen unter Ber¨ ucksichtigung von

|AM | + |BM | = |AB | = ⇒

a ² + b ² = |BC | ² + |AC | ² = |AB | |BM | + |AB | |AM | = |AB | ² = c ²

Indirekter Beweis

Um zu zeigen, dass aus Voraussetzungen V eine Behauptung B folgt

(V = ⇒ B ), kann man die Annahme, dass die Aussage B bei G¨ ultigkeit der Voraussetzungen V falsch ist, zu einem Widerspruch f¨ uhren:

V ∧ (¬B ) = ⇒ F ,

mit einer falschen Aussage F , insbesondere F = ¬V oder F = B . Speziell gilt

B = (¬B = ⇒ F ) ,

falls keine Voraussetzungen getroffen sind, d.h. die Aussage B ist wahr, wenn aus der Annahme, dass B falsch ist, die G¨ ultigkeit einer falschen Aussage F gefolgert werden kann.

21 / 1

Beweis

(i) Beweismethode durch Widerspruch:

V ∧ (¬B ) = ⇒ F

Umformung mit der Darstellung der Implikation als Disjunktion, C = ⇒ D = ¬C ∨ D , und der De Morganschen Regel,

¬(C ∧ D ) = ¬C ∨ ¬D

¬(V ∧ (¬B )) ∨ F = (¬V ) ∨ B ∨ F , d.h. die

” Widerspruchsimplikation“ ist wahr g.d.w. B wahr ist, denn ¬V und F sind falsch

(ii) ¨ Aquivalente Darstellung von B :

¬B = ⇒ F = B ∨ F = B ,

Beispiel

Indirekter Beweis der Irrationalit¨ at von √ 2

Annahme, dass die Behauptung B falsch ist, d.h. es gilt (bzw. wahr ist)

¬B : √

2 = p

q mit p, q ∈ N ∧ ggT(p, q ) = 1 (gek¨ urzter Bruch p/q) und ggT dem gr¨ oßten gemeinsamen Teiler

Quadrieren und Multiplikation mit q ² 2q ² = p ²

= ⇒ p ² und p gerade: p = 2r q ² = 2r ² = ⇒ q gerade

Widerspruch zu ggT(p, q ) = 1, d.h.

(¬B ) = ⇒ F , eine falsche Aussage ; also ist B wahr

23 / 1

Vollst¨ andige Induktion

Aussageformen mit nat¨ urlichen Zahlen als Parametern kann man mit vollst¨ andiger Induktion beweisen. Ist A(n) eine von n ∈ N abh¨ angige

Aussage, so sind dazu die folgenden beiden Beweisschritte durchzuf¨ uhren.

Induktionsanfang: Man zeigt, dass A(1) richtig ist.

Induktionsschluss: Man zeigt, dass aus der Annahme, dass A(n)

richtig ist (Induktionsvoraussetzung), folgt, dass auch A(n + 1) richtig ist, d.h.

A(n) = ⇒ A(n + 1) .

Beispiel

Beweis der Formel f¨ ur die Summe der Quadratzahlen, A(n) :

n

X

k=1

k ² = 1 ² + 2 ² + · · · + n ² = 1

6 n(n + 1)(2n + 1) , mit vollst¨ andiger Induktion

Induktionsanfang, ¨ Uberpr¨ ufung von A(1):

1

X

k=1

k ² = 1 ² = 1 · 2 · 3

6 X

25 / 1

Induktionsschluss, A(n) = ⇒ A(n + 1):

n+1

X

k =1

k ² =

n

X

k=1

k ² + (n + 1) ² = n(n + 1)(2n + 1) 6

| {z }

A(n)

+(n + 1) ²

= (n + 1)

n(2n + 1) + 6(n + 1)

6 = (n + 1)(n + 2)(2n + 3) 6

Verwendung der Induktionsvoraussetzung bei der zweiten Gleichheit

Beispiel

Anzahl der Spiele bei einem Tennis-Turnier (K.O.-System) mit 2 ⁿ Teilnehmern:

2 ⁿ − 1 (n = 7 bei einem Grand-Slam)

(i) Beweis mit vollst¨ andiger Induktion:

Induktionsanfang (n = 1):

2 = 2 ¹ Teilnehmer 1 = 2 ¹ − 1 Spiele X Induktionsschluss (n → n + 1):

2 ⁿ⁺¹ Teilnehmer zwei Gruppen mit je 2 ⁿ Teilnehmern

Induktionsvoraussetzung = ⇒ [2 ⁿ − 1] Spiele in jeder Gruppe zus¨ atzliches letztes Spiel f¨ ur die Sieger der beiden Gruppen

2 · [2 ⁿ − 1] + 1 = 2 ⁿ⁺¹ − 1 Spiele bei 2 ⁿ⁺¹ Teilnehmern

27 / 1

(ii) Einfachere Argumentation ohne vollst¨ andige Induktion:

Beim K.O.-System verliert bis auf den Gewinner jeder Teilnehmer genau einmal; jedes Spiel hat genau einen Verlierer.

ein Spiel weniger als die Teilnehmerzahl

Alternativbeweis auch bei Teilnehmerfeldern beliebiger Gr¨ oße anwendbar

(z.B. bei Freilosen)

letzte 3 Runden des Wimbledon-Turniers von 1985

29 / 1

Beispiel

Paradox:

” Alle M¨ ause sind grau“

Beweis mit vollst¨ andiger Induktion Induktionsschluss (n → n + 1):

n + 1 M¨ ause: M ₁ , . . . , M _n+1

M ₁ , . . . , M _n und M ₂ , . . . , M _n+1 jeweils grau nach Induktionsvoraussetzung

= ⇒ n + 1 M¨ ause grau

Grund f¨ ur den Widerspruch: fehlender Induktionsanfang

fehlerhafter Beweis (offensichtlich gibt es ebenfalls weiße M¨ ause)

Menge

Eine Menge A besteht aus verschiedenen Elementen a ₁ , a ₂ , . . .:

A = {a ₁ , a ₂ , . . .} .

Werden die Elemente durch eine Eigenschaft E charakterisiert, so schreibt man

A = {a : a besitzt die Eigenschaft E } . Die Reihenfolge der Elemente ist dabei unerheblich.

Schreibweise Bedeutung

a ∈ A a ist Element von A

a ∈ / A a ist nicht Element von A A ⊆ B A ist Teilmenge von B

A 6⊆ B A ist keine Teilmenge von B A ⊂ B A ist echte Teilmenge von B

|A| Anzahl der Elemente in A

∅ leere Menge

31 / 1

Gilt |A| < ∞ bzw. |A| = ∞, so spricht man von einer endlichen bzw.

unendlichen Menge. Mengen heißen gleichm¨ achtig, wenn es eine bijektive Abbildung zwischen ihren Elementen gibt (|A| = |B | f¨ ur endliche Mengen).

Die Menge P(A) aller Teilmengen von A wird als Potenzmenge bezeichnet, d.h.

P (A) = {B : B ⊆ A} .

Dabei gilt ∅ ∈ P (A), A ∈ P (A) und, f¨ ur eine endliche Menge,

|P(A)| = 2 ^|A| .

Zahlenmengen

F¨ ur folgende Zahlenmengen benutzt man Standardbezeichnungen.

nat¨ urliche Zahlen: N = {1, 2, . . .}

ganze Zahlen: Z = {. . . , −1, 0, 1, . . .}

rationale Zahlen: Q = {p/q : p ∈ Z , q ∈ N , ggT(p, q) = 1}

reelle Zahlen: R = {x : x = lim _n→∞ q _n , q _n ∈ Q } komplexe Zahlen: C = {x + iy : x , y ∈ R , i ² = −1}

Gebr¨ auchlich sind ebenfalls die Schreibweisen N ⁰ = N ∪ {0} und

R ⁺ = {x ∈ R : x > 0} und dazu entsprechend Z ⁻ , Z ⁻ 0 , Q ⁺ , Q ⁺ 0 , Q ⁻ , Q ⁻ 0

R ⁺ 0 , R ⁻ , R ⁻ 0 .

33 / 1

Mengenoperationen

F¨ ur zwei Mengen A und B sind die folgenden Operationen definiert.

Vereinigung:

A ∪ B = {x : x ∈ A ∨ x ∈ B } Durchschnitt:

A ∩ B = {x : x ∈ A ∧ x ∈ B } Differenz, Komplement¨ armenge:

A \ B = {x : x ∈ A ∧ x ∈ / B } symmetrische Differenz:

A∆B = (A \ B ) ∪ (B \ A) = (A ∪ B ) \ (A ∩ B )

In der Abbildung sind die Mengenoperationen mit Hilfe sogenannter Venn-Diagramme illustriert.

A B A ∪ B

A ∩ B A \ B A∆B

35 / 1

Ist B ⊂ A, fallen einige der Diagramme zusammen:

A = A ∪ B B = A ∩ B A \ B = A∆B

Regeln f¨ ur Mengenoperationen

F¨ ur Mengenoperationen gelten die folgenden Identit¨ aten.

Assoziativgesetze:

(A ∩ B ) ∩ C = A ∩ (B ∩ C ) (A ∪ B ) ∪ C = A ∪ (B ∪ C ) Kommutativgesetze:

A ∩ B = B ∩ A A ∪ B = B ∪ A De Morgansche Regeln:

C \(A ∩ B ) = (C \A) ∪ (C \B ) C \(A ∪ B ) = (C \A) ∩ (C \B )

37 / 1

Distributivgesetze:

(A ∩ B ) ∪ C = (A ∪ C ) ∩ (B ∪ C ) (A ∪ B ) ∩ C = (A ∩ C ) ∪ (B ∩ C )

Diese Regeln entsprechen den Gesetzen f¨ ur logische Operationen, wenn

man die Operatoren ∪, ∩ durch ∧, ∨ ersetzt und C \ durch ¬.

Beweis

zeige die erste De Morgansche Regel:

C \(A ∩ B ) = (C \A) ∪ (C \B ) linke Menge

x ∈ C \(A ∩ B ) ⇐⇒ x ∈ C ∧ x ∈ / (A ∩ B )

⇐⇒ x ∈ C ∧ (x ∈ / A ∨ x ∈ / B ) Distributivgesetz f¨ ur logische Operationen,

U ∧ (V ∨ W ) = (U ∧ V ) ∨ (U ∧ W ) ,

¨ aquivalente Darstellung

(x ∈ C ∧ x ∈ / A) ∨ (x ∈ C ∧ x ∈ / B ) ⇐⇒ x ∈ (C \A ∪ C \B ) x in rechter Menge

analoge Argumentation f¨ ur die anderen Gesetze

39 / 1

Mandelbrot-Menge

Die Mandelbrot-Menge M besteht aus allen Punkten c = a + ib =(a, b b) der komplexen Ebene, f¨ ur die die durch

z _n+1 = z _n ² + c , z ₀ = 0 , definierte Folge beschr¨ ankt bleibt.

In der Abbildung wurde die Geschwindigkeit, mit der die Folge divergiert,

zur Definition der Farbwerte verwendet. Dadurch wird insbesondere der

fraktale Rand hervorgehoben.

-2 -1 0 1 -1.5

-1 -0.5 0 0.5 1 1.5

20 40 60 80 100

41 / 1

Matlab -Skript zur Generierung des Pixelbildes

>> N = 100; % maximale Iterationszahl

>> R = 1000; % Radius f¨ ur Divergenz

>> d = 0.1; % Abstand der Bildpunkte

>> xmin=-2.5; xmax=1; ymin=-1.5; ymax=1.5; % Bildausschnitt

>> % Initialisierung der Parameter, Startwerte und Farbindizes

>> [x,y] = meshgrid([xmin:dxmax],[ymin:d:ymax]); c = x+i*y;

>> z = zeros(size(c)); f = zeros(size(c));

>>

>> % Iteration

>> for n=1:N

>> z = z.^2 + c; f = f+(abs(z)<R);

>> end

>> % Konvertierung in ein Pixelbild

Kartesisches Produkt

Das kartesische Produkt zweier Mengen A und B ist die Menge aller geordneten Paare von Elementen der beiden Mengen:

A × B = {(a, b) : a ∈ A ∧ b ∈ B } . Es gilt

(a, b) = (a ⁰ , b ⁰ ) ⇐⇒ (a = a ⁰ ∧ b = b ⁰ ) ,

d.h. im Gegensatz zu der Gleichheit von Mengen ({a, b} = {b, a}) ist die Reihenfolge wesentlich.

F¨ ur endliche Mengen gilt |A × B | = |A| · |B |.

Entsprechend definiert man das n-fache kartesische Produkt A ₁ × · · · × A _n

als die Menge aller geordneten Tupel (a ₁ , . . . , a _n ) mit a _k ∈ A _k . Sind die Mengen gleich, so schreibt man A ⁿ = A × · · · × A.

43 / 1

Relation

Stehen Elemente einer Menge A in Beziehung zu Elementen aus einer Menge B , so kann dies mit Hilfe einer Relation ausgedr¨ uckt werden. Diese besteht aus geordneten Paaren (a, b) der Elemente, die durch die

Beziehung verkn¨ upft sind. Eine Relation R ist also eine Teilmenge des kartesischen Produkts von A und B . Man sagt a steht in Relation zu b und schreibt a R b:

a R b ⇐⇒ (a, b) ∈ R ⊆ A × B .

Beispiel

Relationale Datenbank: Zuordnung von Eigenschaften

Carl Friedrich Gauß

Nummerierung der Namen und Fachgebiete Beschreibung der Relation R als Teilmenge von {1, . . . , 7} × {1, 2, 3}:

R ∼ {(1, 2), (2, 3), (3, 3), (4, 1), (4, 3),

(5, 2), (5, 3), (6, 2), (6, 3), (7, 1), (7, 2), (7, 3)}

45 / 1

Eigenschaften von Relationen

Eine Relation R auf einer Menge A (R ⊆ A × A) heißt

reflexiv, wenn jedes Element in Relation zu sich selbst steht:

∀a ∈ A : a R a

symmetrisch, wenn die Reihenfolge der Elemente keine Rolle spielt:

a R b = ⇒ b R a

antisymmetrisch, wenn aus der Symmetrie die Identit¨ at folgt:

a R b ∧ b R a = ⇒ a = b

transitiv, wenn aus einer Kette das mittlere Element entfernt werden kann: a R b ∧ b R c = ⇒ a R c

total, wenn je zwei Elemente in mindestens einer Richtung in Relation

stehen: ∀a, b ∈ A : a R b ∨ b R a

Ist eine Relation reflexiv, symmetrisch und transitiv, so wird sie

Aquivalenzrelation genannt. Es wird dann meist ¨ a ∼ b statt a R b oder (a, b) ∈ R geschrieben. Eine ¨ Aquivalenzrelation unterteilt die Menge A in disjunkte Teilmengen (¨ Aquivalenzklassen), wobei zwei Elemente einer Teilmenge zueinander in Relation stehen (¨ aquivalent sind), w¨ ahrend zwei Elemente aus unterschiedlichen Teilmengen dies nicht tun.

Ist eine Relation reflexiv, antisymmetrisch und transitiv, so ist sie eine Halbordnung und man schreibt meist a ≤ b statt a R b oder (a, b) ∈ R . Ist eine Halbordnung zus¨ atzlich total, heißt sie (totale) Ordnung und A heißt durch ≤ geordnet.

47 / 1

Beispiel

Halbordnung und ¨ Aquivalenzrelation auf der Potenzmenge P(M ), der Menge aller Teilmengen einer Menge M

(i) Mengeninklusion ⊆:

Halbordnung in P (M ), denn A ⊆ A reflexiv

A ⊆ B ∧ B ⊆ A = ⇒ A = B antisymmetrisch

A ⊆ B ⊆ C ⇒ A ⊆ C transitiv

(ii) ” hat gleich viele Elemente wie“:

Aquivalenzrelation in ¨ P (M ) f¨ ur eine endliche Menge M , denn

|A| = |A| reflexiv

|A| = |B | = ⇒ |B | = |A| symmetrisch

|A| = |B | = |C | ⇒ |A| = |C | transitiv

49 / 1

Abbildung

Unter einer Abbildung f von einer Menge A in eine Menge B versteht man eine Vorschrift, die jedem a ∈ A eindeutig ein bestimmtes b = f (a) ∈ B zuordnet:

f : A −→ B .

F¨ ur die Elementzuordnung verwendet man die Schreibweise a 7→ b = f (a)

und bezeichnet b als das Bild von a, bzw. a als ein Urbild von b.

Ist U ⊆ A, so heißt f (U ) = {f (a) : a ∈ U } ⊆ B das Bild von U und f¨ ur V ⊆ B heißt f ⁻¹ (V ) = {a : f (a) ∈ V } ⊆ A das Urbild von V unter der Abbildung f .

Die Menge f (A) heißt Wertebereich und A Definitionsbereich der

Eine Abbildung kann man folgendermaßen illustrieren.

Wie aus dem Bild ersichtlich ist, m¨ ussen nicht alle Elemente aus B als Bild eines Elementes aus A auftreten und ein Element aus B darf auch Bild mehrerer Elemente aus A sein, d.h. Elemente aus der Bildmenge k¨ onnen mehrere Urbilder haben. Es muss allerdings f¨ ur jedes Element aus A ein eindeutiges Bild geben, das heißt von jedem a muss genau ein Pfeil ausgehen.

Statt Abbildung verwendet man auch den Begriff Funktion, insbesondere in der reellen und komplexen Analysis.

51 / 1

Eigenschaften von Abbildungen Eine Abbildung

f : A −→ B zwischen zwei Mengen A und B heißt

injektiv, falls f (a) 6= f (a ⁰ ) f¨ ur alle a, a ⁰ ∈ A mit a 6= a ⁰

surjektiv, falls es f¨ ur jedes b ∈ B ein a ∈ A gibt mit f (a) = b bijektiv, falls f sowohl injektiv als auch surjektiv ist.

Diese Begriffe lassen sich anhand von Mengendiagrammen illustrieren:

Beispiel

Abbildungen zwischen den nat¨ urlichen Zahlen f : N −→ N

(i) Bijektiv:

f (n) = n − (−1) ⁿ vertauscht benachbarte Zahlen

1 7→ 1 − (−1) ¹ = 1 + 1 = 2 2 7→ 2 − (−1) ² = 2 − 1 = 1 3 7→ 4

4 7→ 3

· · ·

53 / 1

(ii) Surjektiv:

n 7→ Anzahl der Dezimalziffern zu jeder Ziffernzahl f (n) gibt es ein Urbild n.

(iii) Injektiv:

f (n) = n ² f¨ ur n, n ⁰ ∈ N gilt: n 6= n ⁰ = ⇒ n ² 6= n ⁰² (iv) Weder surjektiv noch injektiv:

n 7→ n¨ achstgr¨ oßere Primzahl

nicht surjektiv, da nur Primzahlen als Bilder auftreten

nicht injektiv, da z.B. f (14) = 17 = f (15)

Verkn¨ upfung von Abbildungen Die Verkn¨ upfung oder Komposition zweier Abbildungen f : A → B und g : B → C ist durch

a 7→ (g ◦ f )(a) = g (f (a)), a ∈ A , definiert und in dem Diagramm ver- anschaulicht.

Die Verkn¨ upfung ◦ ist assoziativ, d.h.

(h ◦ g ) ◦ f = h ◦ (g ◦ f )

aber nicht kommutativ, denn im Allgemeinen ist f ◦ g 6= g ◦ f .

55 / 1

Beispiel

Verkn¨ upfungen der Abbildungen

f (D ) = D ∩ [0, 2), g (D ) = D ∪ [0, 3), h(D ) = D \ [2, 3) auf der Menge der Teilmengen von R

(i) f ◦ g 6= g ◦ f (nicht kommutativ):

Gegenbeispiel f¨ ur die Menge [1, 4)

(ii) (h ◦ g ) ◦ f = h ◦ (g ◦ f ) (assoziativ):

(h ◦ g )(D ⁰ ) = h(D ⁰ ∪ [0, 3)) = D ⁰ ∪ [0, 2) D ⁰ = f (D )

(h ◦ g ) ◦ f (D ) = (D ∩ [0, 2)) ∪ [0, 2)) = [0, 2) gleiches Resultat bei anderer Klammerung

(g ◦ f )(D ) = g (D ∩ [0, 2)) = (D ∩ [0, 2)) ∪ [0, 3) = [0, 3)

= ⇒ h ◦ (g ◦ f )(D ) = [0, 3) \ [2, 3) = [0, 2)

57 / 1

Inverse Abbildung

F¨ ur eine bijektive Abbildung f : A → B ist durch

b = f (a) ⇔ a = f ⁻¹ (b)

die inverse Abbildung f ⁻¹ : B → A definiert.

Insbesondere ist a = f ⁻¹ (f (a)), d.h. f ⁻¹ ◦ f ist die identische Abbildung.

Bei Funktionen ist bei der Schreibweise zu beachten, dass keine

Verwechslung mit dem Kehrwert entsteht: f ⁻¹ (x ) 6= f (x ) ⁻¹ . Fehlt das

Argument x , so muss aus dem Kontext ersichtlich sein, was gemeint ist.

Fakult¨ at

Das Produkt der ersten n nat¨ urlichen Zahlen wird mit n! = 1 · 2 · · · n

bezeichnet (lies: n Fakult¨ at). Konsistent mit der Definition des leeren Produktes setzt man 0! = 1.

Die Zahl n! entspricht der Anzahl der verschiedenen M¨ oglichkeiten n unterschiedliche Objekte anzuordnen, d.h. der Anzahl der Permutationen von n Elementen.

F¨ ur großes n kann das asymptotische Verhalten von n! mit Hilfe der Stirlingschen Formel,

n! = √

2πn (n/e) ⁿ (1 + O(1/n)) , approximiert werden.

59 / 1

Binomialkoeffizient Der Binomialkoeffizient

n k

= n!

(n − k )!k ! = n(n − 1) · · · (n − k + 1)

1 · · · (k − 1)k , n, k ∈ N ⁰ , n ≥ k , gibt die Anzahl der k -elementigen Teilmengen einer Menge mit n

Elementen an.

Insbesondere gilt aufgrund der Konvention 0! = 1

Beispiel

2-elementige Teilmengen der Menge {a, b, c , d , e }

5 M¨ oglichkeiten f¨ ur das erste Element, 4 M¨ oglichkeiten f¨ ur das zweite Element (keine gleichen Elemente)

5 · 4 m¨ ogliche Paare

Irrelevanz der Reihenfolge der Elemente von Mengen ({u, v } = {v , u})

= ⇒ Division durch 2, d.h.

5 · 4

2 = 5!/3!

2! = 5

2

= 10 M¨ oglichkeiten Teilmengen

{a, b}, {a, c }, {a, d }, {a, e }, {b, c }, {b, d }, {b, e }, {c , d }, {c , e }, {d , e }

61 / 1

Pascalsches Dreieck

Die Binomialkoeffizienten ⁿ _k

= _(n−k)! ^n! _k! lassen sich mit Hilfe der Rekursion

n + 1 k

=

n k − 1

+

n k

in einem Dreiecksschema, dem sogenannten Pascalschen Dreieck, berechnen.

0 k

1

1 k

1 1

2 k

1 2 1

& + . & + .

3 k

1 3 3 1

.. . .. . .. .

Beweis

zu zeigende Rekursion:

n + 1 k

=

n k − 1

+

n k

,

d.h. (n + 1)!

(n + 1 − k )! k ! = n!

(n − k + 1)! (k − 1)! + n!

(n − k )! k ! Division durch n! und Multiplikation mit (n − k + 1)! k !

n + 1 = k + (n + 1 − k ) X

63 / 1

Binomische Formel

Mit der binomischen Formel lassen sich Potenzen einer Summe von zwei Variablen berechnen. F¨ ur alle n ∈ N ⁰ gilt

(a + b) ⁿ = a ⁿ + n

1

a ⁿ⁻¹ b + · · · +

n n − 1

ab ⁿ⁻¹ + b ⁿ

=

n

X

k=0

n k

a ^n−k b ^k .

Beweis

vollst¨ andige Induktion

Induktionsanfang (n = 0):

0

X

k=0

0 k

a ^0−k b ^k = 0

0

a ⁰ b ⁰ = 1 = (a + b) ⁰ Induktionsschluss (n → n + 1):

Induktionsvoraussetzung = ⇒

(a + b) ⁿ⁺¹ = (a + b) (a + b) ⁿ = (a + b)

n

X

k =0

n k

a ^n−k b ^k

Indexverschiebung (k ← k − 1) im zweiten Summand b P . . .

n

X

k=0

n k

a ^n−k+1 b ^k +

n+1

X

k=1

n k − 1

a ^n−k+1 b ^k

65 / 1

Konvention _n+1 ⁿ

= 0 = ₋₁ ⁿ

Summation jeweils von 0 bis n + 1

Rekursion f¨ ur Binomialkoeffizienten n

k

+

n k − 1

=

n + 1 k

Formel f¨ ur (a + b) ⁿ⁺¹

n+1

X

k=0

n + 1 k

a ^n+1−k b ^k

Identit¨ aten f¨ ur Binomialkoeffizienten

F¨ ur Binomialkoeffizienten gelten folgende Identit¨ aten:

2 ⁿ =

n

X

k =0

n k

,

0 =

n

X

k =0

n k

(−1) ^k , n ≥ 1 , n

k

=

k

X

i=0

n − k − 1 + i i

, k < n ,

n k

=

n−k

X

i=0

k − 1 + i k − 1

, k > 0 .

67 / 1

Beweis

(i) Erste und zweite Identit¨ at:

Folgerungen aus dem Binomischen Lehrsatz, (a + b) ⁿ =

n

X

k=0

n k

a ^n−k b ^k ,

mit a = b = 1 bzw. a = −b = 1 (ii) Dritte Identit¨ at:

wiederholte Anwendung der Rekursionsformel

Ersetzen des letzten Binomialkoeffizienten ^n−k ₀

durch ^n−k−1 ₀

=

k

X

i =0

n − k − 1 + i i

d.h. die dritte Identit¨ at (iii) Vierte Identit¨ at:

Substitution k ⁰ = n − k n

n − k ⁰

=

k

X

i=0

n − k ⁰ − 1 + i n − k ⁰ − 1

m j

= _m−j ^m

mit j = n − k ⁰ und j = n − k ⁰ − 1 = ⇒ Aquivalenz ¨ zur dritten Identit¨ at

69 / 1

Illustration der letzten beiden Identit¨ aten als Summationswege im Pascalschen Dreieck

dritte Identit¨ at: 1 + 2 + 3 + 4 = 10

vierte Identit¨ at: 1 + 3 + 6 = 10

Kombinatorik von Mengen

Die folgende Tabelle gibt die Anzahl der M¨ oglichkeiten an, aus einer Menge mit n verschiedenen Elementen k Elemente auszuw¨ ahlen, wobei unterschieden werden muß, ob die Reihenfolge eine Rolle spielt (nicht sortiert) und Wiederholungen zugelassen sind.

nicht sortiert sortiert ohne Wiederholungen n(n − 1) · · · (n − k + 1)

n k

mit Wiederholungen n ^k

n + k − 1 k

71 / 1

Beweis

(i) Auswahl ohne Wiederholungen:

Ber¨ ucksichtigung der Reihenfolge n M¨ oglichkeiten f¨ ur das erste,

(n − 1) M¨ oglichkeiten f¨ ur das zweite, . . .

(n − k + 1) M¨ oglichkeiten f¨ ur das k -te Element Gesamtzahl der M¨ oglichkeiten:

n(n − 1) · · · (n − k + 1)

(ii) Auswahl mit Wiederholungen:

Ber¨ ucksichtigung der Reihenfolge

n M¨ oglichkeiten f¨ ur jedes Element, insgesamt n ^k

Ohne Ber¨ ucksichtigung der Reihenfolge

Plazierung von n − 1 Markierungen zwischen n + k Punkten

• — • — • — • — • — • — • — •

M M M M

um 1 verminderte Anzahl der Punkte zwischen der (i − 1)-ten und i -ten Markierung − b Anzahl der Wiederholungen des i -ten Elements nach (i)

n + k − 1 n − 1

m¨ ogliche Markierungen

73 / 1

Beispiel

Anzahl der M¨ oglichkeiten bei zweimaligem Ziehen aus einer Urne mit einer roten, einer gr¨ unen und einer blauen Kugel (n = 3, k = 2)

nicht sortiert sortiert ohne Wiederholungen

(ohne Zur¨ ucklegen) n · · · (n − k + 1) = 3 · 2 = 6 ⁿ _k

= ³ ₂

= 3

mit Wiederholungen

(mit Zur¨ ucklegen) n ^k = 3 ² = 9 ^n+k−1 _k

= ⁴ ₂

= 6

Beispiel

Deutsches Autokennzeichen:

Kombination von ≤ 3 Buchstaben f¨ ur den Landkreis oder die Stadt,

≤ 2 weiteren Buchstaben und einer bis zu vierstelligen Zahl

26 ⁿ m¨ ogliche Kombinationen aus n Buchstaben

(26 + 26 ² + 26 ³ ) · (26 + 26 ² ) · 9999 = 1.28 · 10 ¹¹ m¨ ogliche Kennzeichen

75 / 1

Komplexe Zahlen

Um auch Wurzeln aus negativen Zahlen bilden zu k¨ onnen, f¨ uhrt man eine imagin¨ are Einheit i als eine der L¨ osungen von

i ² = −1 ein und bezeichnet

C = {z = x + iy : x , y ∈ R }

als die Menge der komplexen Zahlen. Dabei werden x und y Real- bzw.

Imagin¨ arteil genannt:

x = Re z , y = Im z .

Beispiel

Addition und Multiplikation komplexer Zahlen (i) Addition:

(2 + 3i) + (4 − 5i) = (2 + 4) + (3 + (−5))i

= 6 − 2i (ii) Multiplikation:

(2 + 3i) · (4 − 5i) = 8 − 10i + 12i − 15i ²

|{z}

=−15

= 23 + 2i (i ² = −1)

77 / 1

Komplexe Konjugation

F¨ ur eine komplexe Zahl z = x + iy definiert man die konjugiert komplexe Zahl

¯

z = x − iy .

Geometrisch bedeutet die komplexe Konjugation eine Spiegelung an der x -Achse: (x , y ) → (x , −y ).

Die komplexe Konjugation ist mit den arithmetischen Operationen vertr¨ aglich:

z ₁ ◦ z ₂ = ¯ z ₁ ◦ z ¯ ₂

f¨ ur ◦ = +, −, ∗, /.

Beispiel

Vertr¨ aglichkeit von komplexer Konjugation mit dem Bilden von Summe und Produkt der komplexen Zahlen z = 2 − i, w = 1 + 3i

(i) Addition:

z + w = (2 + i) + (1 − 3i) = 3 − 2i z + w = (2 − i) + (1 + 3i) = 3 + 2i Ubereinstimmung ¨

(ii) Multiplikation:

z w = (2 + i)(1 − 3i) = (2 + 3) + (1 − 6)i = 5 − 5i zw = (2 − i)(1 + 3i) = (2 + 3) + (−1 + 6)i = 5 + 5i gleiches Resultat 5 − 5i

79 / 1

Betrag einer komplexen Zahl

Der Betrag einer komplexen Zahl z = x + iy ist als

|z | = p

x ² + y ² = √ z ¯ z definiert.

F¨ ur z ∈ R ist diese Definition konsistent mit der Definition der

Betragsfunktion f¨ ur reelle Zahlen und besitzt analoge Eigenschaften.

Positivit¨ at:

|z | ≥ 0, |z | = 0 ⇐⇒ z = 0

Beweis

(i) Positivit¨ at X (ii) Multiplikativit¨ at:

Produkt:

|z ₁ z ₂ | ² = |(x ₁ + iy ₁ )(x ₂ + iy ₂ )| ² = |(x ₁ x ₂ − y ₁ y ₂ ) + i(x ₁ y ₂ + x ₂ y ₁ )| ²

= x ₁ ² x ₂ ² + y ₁ ² y ₂ ² + x ₁ ² y ₂ ² + x ₂ ² y ₁ ² , da die Terme ±2x ₁ x ₂ y ₁ y ₂ sich aufheben

Ubereinstimmung mit ¨

|z ₁ | ² |z ₂ | ² = (x ₁ ² + y ₁ ² )(x ₂ ² + y ₂ ² ) Quotient:

Anwendung der bewiesenen Identit¨ at f¨ ur das Produkt von Betr¨ agen

|(z ₁ /z ₂ )||z ₂ | = | (z ₁ /z ₂ )z ₂

| {z }

z

| ⇐⇒ |z ₁ /z ₂ | = |z ₁ |/|z ₂ |

81 / 1

(iii) Dreiecksungleichung:

Quadrieren der Ungleichungskette und Subtraktion von |z ₁ | ² + |z ₂ | ²

−2|z ₁ ||z ₂ | ≤ z ₁ ¯ z ₂ + ¯ z ₁ z ₂ ≤ 2|z ₁ ||z ₂ |

Re z = (z + ¯ z )/2, u v ¯ = ¯ u v ¨ aquivalente Ungleichung

|Re(z 1 z ¯ ₂ )| ≤ |z 1 ||z 2 |

bzw., da z ₁ z ¯ ₂ = (x ₁ + iy ₁ )(x ₂ − iy ₂ ) = (x ₁ x ₂ + y ₁ y ₂ ) + (. . .)i,

|x ₁ x ₂ + y ₁ y ₂ | ≤ q

x ₁ ² + y ₁ ² q

x ₂ ² + y ₂ ² erneutes Quadrieren und Subtraktion von x ₁ ² x ₂ ² , y ₁ ² y ₂ ²

2x ₁ x ₂ y ₁ y ₂ ≤ x ₁ ² y ₂ ² + x ₂ ² y ₁ ²

Beispiel

Illustration der Eigenschaften des Betrags f¨ ur z ₁ = −1 + 2i, z ₂ = 3 − 4i (i) Berechnung des Betrags (alternative Methoden):

|x + iy | = p

x ² + y ²

|z ₁ | = q

(−1) ² + 2 ² = √ 5

|z | ² = z ¯ z , dritte binomische Formel

|z ₂ | = p

(3 − 4i)(3 + 4i) = p

9 − 16i ² =

i

=−1

√ 25

(ii) Multiplikativit¨ at:

z ₁ z ₂ = (−1 + 2i)(3 − 4i) = (−3 − 8i ² + 6i + 4i) = 5 + 10i = ⇒

|z ₁ z ₂ | = √

25 + 100 = √

125 = 5 √

5 = |z ₂ | |z ₁ |

83 / 1

(iii) Dreiecksungleichung:

z ₁ + z ₂ = 2 − 2i = ⇒

||z ₁ | − |z ₂ || = 5 − √

5 = 2.7639 ≤

|z ₁ + z ₂ | = √

8 = 2.8284 ≤ |z ₁ | + |z ₂ | = √

5 + 5 = 7.2361

Formel von Euler-Moivre

Die Exponentialfunktion mit imagin¨ arem Argument l¨ asst sich mit Hilfe der trigonometrischen Funktionen ausdr¨ ucken:

exp(iϕ) = cos ϕ + i sin ϕ

f¨ ur ϕ ∈ R . Der Kosinus und der Sinus entsprechen also dem Real- und Imagin¨ arteil komplexer Zahlen mit Betrag 1 (| exp(iϕ)| = 1).

Invertiert man die obige Formel, so folgt cos ϕ = Re e ^iϕ = 1

2 e ^iϕ + e ^−iϕ sin ϕ = Im e ^iϕ = 1

2i e ^iϕ − e ^−iϕ .

Die Identit¨ aten zwischen exp, cos und sin gehen auf Euler und Moivre zur¨ uck. Sie bilden die Grundlage f¨ ur die geometrische Interpretation

komplexer Zahlen und spielen in der Fourier-Analysis eine wichtige Rolle.

85 / 1

Beispiel

Berechnung trigonometrischer Funktionen f¨ ur

ϕ _k = π/2 ^k , k = 1, 2, . . .

definiere

x _k = Re exp(iϕ _k )

| {z }

z

= cos ϕ _k

Andere trigonometrische Funktionen k¨ onnen algebraisch durch die Kosinus-Funktion ausgedr¨ uckt werden:

sin ϕ _k = q

1 − x _k ² , tan ϕ _k = sin ϕ _k cos ϕ _k =

q

1 − x _k ²

x _k .

z ₃ auf der Diagonale des Par- allelogramms mit Eckpunkten 0, 1, z ₂ +1, z ₂ , |z ₃ | = 1 = ⇒

z ₃ = z ₂ + 1

|z ₂ + 1|

Re (z ₂ + 1) = x ₂ + 1, Im (z ₂ + 1) = Im z ₂ = q

1 − x ₂ ² = ⇒ x ₃ = Re z ₃ = x ₂ + 1

q

(x ₂ + 1) ² + 1 − x ₂ ²

= x ₂ + 1

√ 2x ₂ + 2 =

√ 2x ₂ + 2 2 Einsetzen von x ₂ = Re z ₂ = √

2/2 x ₃ = p√

2 + 2/2 allgemeine Rekursion x _{k +1} = √

2x _k + 2/2 cos(π/16) = x ₄ =

r q √

2 + 2 + 2/2, usw.

87 / 1

Gaußsche Zahlenebene

Komplexe Zahlen z = x + iy lassen sich mit den Punkten der Ebene

identifizieren. Der Betrag entspricht dem Abstand vom Ursprung, Real-

und Imagin¨ arteil sind die Projektionen auf die reelle bzw. imagin¨ are Achse,

und die konjugiert komplexe Zahl ¯ z = x − iy ergibt sich durch Spiegelung

an der reellen Achse.

In Polarkoordinaten erh¨ alt man aus der Formel von Euler-Moivre die Darstellung

z = x + iy = r (cos ϕ + i sin ϕ) = r exp(iϕ)

mit r = |z |. Der Winkel ϕ ist nur bis auf Vielfache von 2π bestimmt und wird als Argument von z bezeichnet:

ϕ = arg z .

Als Standardbereich (Hauptwert) wird das Intervall (−π, π] vereinbart.

Es gilt

tan ϕ = Im z

Re z = y x .

Das Argument arg z kann also mit Hilfe der Arcustangens-Funktion aus dem Quotienten y /x bestimmt werden. Dabei ist der richtige Zweig zu w¨ ahlen, d.h. falls x = Re z < 0 muß je nach Vorzeichen von x und y π oder −π zum Wert der Umkehrfunktion addiert werden.

89 / 1

Bezeichnet ϕ _H = arctan(y /x ) ∈ [−π/2, π/2], (x , y ) 6= (0, 0), den Winkel des Hauptzweigs des Arkustangens, so ist

ϕ = arg z =







ϕ _H , x ≥ 0

ϕ _H + π, x < 0 ∧ y ≥ 0 ϕ _H − π, x < 0 ∧ y < 0

F¨ ur x = y = 0 ist ϕ beliebig und wird im allgemeinen null gesetzt.

Die Polardarstellung einiger komplexer Zahlen ist in der folgenden Tabelle angegeben.

z 1 −1 ±i 1 ± i −1 ± i √

3 ± i 1 ± √ 3i

r 1 1 1 √

2 √

2 2 2

ϕ 0 π ±π/2 ±π/4 ±3π/4 ±π/6 ±π/3

Beispiel

Umwandlung in Polar- und Standardform (i) Umwandlung von z = 1 + √

3i in Polarform:

r = |z | = √

1 + 3 = 2, ϕ _H = arctan( √

3/1) = π/3 wegen x = Re z = 1 ≥ 0 keine Korrektur des Winkels:

ϕ = arg z = ϕ _H = π/3 Formel von Euler-Moivre

z = 2 exp(i π/3)

= 2 (cos(π/3) + i sin(π/3)) Kontrolle:

cos(π/3) = 1/2, sin(π/3) = √

3/2 X

91 / 1

(ii) Umwandlung von z = −1 + i in Polarform:

r = |z | = √

1 + 1 = √

2, ϕ _H = arctan(1/(−1)) = −π/4 wegen x = Re z = −1 < 0 Korrektur des Winkels:

y = Im z = 1 ≥ 0 = ⇒

ϕ = arg z = ϕ _H + π = −π/4 + π = 3π/4 Formel von Euler-Moivre

z = √

2 exp(i (3π/4))

Multiplikation komplexer Zahlen

Das Produkt zweier komplexer Zahlen z _k = x _k + iy _k = r _k exp(iϕ _k ), k = 1, 2 ist

z ₁ z ₂ = (x ₁ x ₂ − y ₁ y ₂ ) + (x ₁ y ₂ + x ₂ y ₁ )i = r ₁ r ₂ exp(i(ϕ ₁ + ϕ ₂ )) .

Geometrisch entspricht die Multipli- kation mit einer komplexen Zahl z = re ^iϕ einer Streckung um den Faktor r und einer Drehung um den Winkel ϕ wie in der Abbildung f¨ ur z = z ₂ (r = r ₂ , ϕ = ϕ ₂ ) illustriert ist.

93 / 1

Beispiel

Multiplikation und Quadrat komplexer Zahlen (i) Produkt von 1 + i = √

2 exp(i π/4) und √

3 + 3i = 2 √

3 exp(i π/3) Verwendung der Standardform:

(1 + i)( √

3 + 3i) = √

3 − 3 + √

3 + 3 i Verwendung der Polarform:

√

2 exp(i π/4) · 2 √

3 exp(i π/3) = 2 √

6 exp(i 7π/12) (ii) Quadrat von z = 3 + √

3i = 2 √

3 exp(i π/6)

√ √

Division komplexer Zahlen

Der Quotient zweier komplexer Zahlen,

z _k = x _k + iy _k = r _k exp(iϕ _k ), k = 1, 2 ist

z ₁ /z ₂ = x ₁ x ₂ + y ₁ y ₂

x ₂ ² + y ₂ ² + x ₂ y ₁ − x ₁ y ₂

x ₂ ² + y ₂ ² i = r ₁

r ₂ exp(i(ϕ ₁ − ϕ ₂ )) . Speziell ist

1

z = 1

r ² ¯ z = 1

r exp(−iϕ) = x

r ² − y r ² i .

Geometrisch l¨ asst sich der Kehrwert einer komplexen Zahl durch Spiegelung am Einheitskreis konstruieren, wie in der Abbildung veranschaulicht ist.

95 / 1

Bezeichnet w den Fußpunkt der

H¨ ohe auf der Hypothenuse des

rechtwinkligen Dreiecks, das durch

die Tangente von z an den Einheits-

kreis gebildet wird, dann erh¨ alt man

1/z durch Spiegelung an der reellen

Achse: 1/z = ¯ w .

Beweis

(i) Quotient zweier komplexer Zahlen:

z _k = x _k + iy _k = r _k exp(i ϕ _k ), k = 1, 2 Standardform

z ₁

z ₂ = x ₁ + iy ₁

x ₂ + iy ₂ = (x ₁ + iy ₁ )(x ₂ − iy ₂ ) (x ₂ + iy ₂ )(x ₂ − iy ₂ )

= (x ₁ x ₂ + y ₁ y ₂ ) + (x ₂ y ₁ − x ₁ y ₂ )i x ₂ ² + y ₂ ²

Polarform

z ₁

z ₂ = r ₁ exp(iϕ ₁ )

r ₂ exp(iϕ ₂ ) = r ₁

r ₂ exp(iϕ ₁ − iϕ ₂ )

97 / 1

(ii) Kehrwert:

1

z = 1

x + iy = x − iy

(x + iy )(x − iy ) = ¯ z

x ² + y ² = z ¯

r ² = 1

r exp(−iϕ) (iii) Geometrische Konstruktion mit Hilfe des Satzes von Pythagoras:

Quadrat der L¨ ange der Kathete = Produkt der L¨ ange der Hypothenuse und der L¨ ange des entsprechenden Hypothenusenabschnitts = ⇒

1 ² = |z | |w | , d.h. korrekter Betrag von ¯ w = 1/z ^! :

| w ¯ | = |w | = 1/|z | = |1/z |

Spiegelung an der reellen Achse Anderung des Vorzeichen des ¨

Arguments:

Beispiel

Berechnung von (1 + √

3i) + 2 exp(−iπ/6) exp(iπ/2)(1 − i)

Summe im Z¨ ahler in Standardform:

(1 + √

3i) + 2 √

3/2 − i/2

= (1 + √

3) + ( √

3 − 1)i Produkt im Nenner in Polarform:

exp(iπ/2) · √

2 exp(−iπ/4) = √

2 exp(iπ/4) = 1 + i Quotient, erweitert mit (1 − i)

((1 + √

3) + ( √

3 − 1)i)(1 − i)

(1 + i)(1 − i) = 2 √

3 − 2i

2 = 2 exp(−iπ/6) bzw. in Standardform

2(cos(π/6) − i sin(π/6)) = √ 3 − i

99 / 1

Beispiel

Analyse eines Schaltkreises mit komplexer Darstellung von Spannung und Stromst¨ arke:

U (t ) = U ₀ e ^{i(ωt +ϕ)} , I (t ) = I ₀ e ^{i(ωt +ψ)} zeitunabh¨ angiger komplexer Widerstand Z = U (t )/I (t ) Schaltelemente

Widerstand R Spule L Kondensator C

Addition der komplexen Widerst¨ ande bei Serienschaltung:

Z _gesamt = Z ₁ + Z ₂

Addition der Kehrwerte der komplexen Widerst¨ ande bei Parallelschaltung:

1

Z _gesamt = 1

Z ₁ + 1

Z ₂ = ⇒ Z _gesamt = Z ₁ Z ₂ Z ₁ + Z ₂

Re Z : Wirkwiderstand, Im Z : Blindwiderstand, |Z |: Scheinwiderstand oder Impedanz

101 / 1

Gesamtwiderstand

Z _gesamt = iωL + R (iωC ) ⁻¹

R + (iωC ) ⁻¹ = 100iΩ + 300Ω(−200iΩ) 300Ω − 200iΩ

=

i − 6i 3 − 2i

· 100Ω = 2 − 3i

3 − 2i · 100Ω = (2 − 3i)(3 + 2i)

13 · 100Ω

= 1200 − 500i

13 Ω ≈ (92.31 − 38.46i)Ω Impedanz

|Z _gesamt | = 100 p

12 ² + 5 ² /13Ω = 100Ω Wechselspannung U _effektiv = 220V Effektivstrom

I _effektiv = U _effektiv

|Z _gesamt | = 220V

100Ω = 2.2A

Einheitswurzeln

Die Gleichung z ⁿ = 1 hat in C genau n L¨ osungen

z _k = w _n ^k , w _n = exp(2π i/n), k = 0, . . . , n − 1 , die als Einheitswurzeln bezeichnet werden.

Wie in der Abbildung veranschau- licht ist, bilden die Einheitswurzeln ein dem Einheitskreis einbeschriebenes re- gelm¨ aßiges n-Eck.

103 / 1

Beispiel

Kubische und quartische Einheitswurzeln

alternativ: Berechnung von

z _k = exp(2πik /3), k = 0, 1, 2 mit der Formel von Euler-Moivre

z ₀ = exp(0) = 1

z ₁ = exp(2πi/3) = cos(2π/3) + i sin(2π/3) = −1/2 + i √ 3/2 z ₂ = exp(4πi/3) = cos(4π/3) + i sin(4π/3) = −1/2 − i √

3/2 mehrdeutige Wurzel: 3 verschiedene Werte f¨ ur z ^1/3

105 / 1

Beispiel

L¨ osen der Gleichung z ³ + 3z ² i − 3z + 7i = 0 Raten der Nullstelle z ₁ = i:

i ³ + 3i ² i − 3i + 7i = −i − 3i − 3i + 7i = 0 X Polynomdivision

( z ³ + 3z ² i − 3z + 7i ) : ( z − i ) = z ² + 4z i − 7 z ³ − z ² i

4z ² i − 3z 4z ² i + 4z

− 7z + 7i

− 7z + 7i 0

L¨ osungsformel f¨ ur quadratische Gleichungen

Alternative Methode

binomische Formel ¨ aquivalente Gleichung (z + i) ³ = −8i Darstellung komplexer Einheitswurzeln

(−8i) ^1/3 = (2i)1 ^1/3 = (2i) exp(2πik /3), k = 0, 1, 2 und

z _k = −i + (2i) exp(2πik /3), k = 0, 1, 2

107 / 1

Potenzen einer komplexen Zahl

Um Potenzen komplexer Zahlen zu bilden, verwendet man am geeignetsten die Polarform z = r e ^iϕ . F¨ ur m ∈ Z ist

z ^m = r ^m e ^imϕ .

Die gleiche Formel bleibt auch f¨ ur rationale Exponenten m = p/q ∈ Q

richtig, allerdings ist das Ergebnis aufgrund der Mehrdeutigkeit der q-ten

Einheitswurzel nicht eindeutig. Da die Gleichung w ^q = 1 die q L¨ osungen

Beispiel

Berechnung der m¨ oglichen Werte f¨ ur

z = (−1 + i) ^2/3 Polarform: r = √

1 + 1 = √

2, ϕ = arctan(1/(−1)) + π = 3π/4

√

2 exp(3π i/4) 2/3

= √

2 exp(πi/2)w ₃ ^2k , k = 0, 1, 2 , mit w ₃ = exp(2πi/3)

exp(π i/2) = i, Formel von Euler-Moivre m¨ ogliche Werte:

z ₀ = √

2 i z ₁ = √

2 i exp(4π i/3) = √

2 i (cos(4π/3) + i sin(4π/3))

= √

2 (− sin(4π/3) + i cos(4π/3)) = √

2( √

3/2 − i/2) z ₂ = √

2 i exp(8π i/3) = √

2(− √

3/2 − i/2)

109 / 1

Probe

z ₁ ³ = √

2 i exp(4πi/3) 3

= 2i ³ exp(4π i)

| {z }

=1

= −2 i = (−1 + i) ²

d.h. z ₁ = (−1 + i) ^2/3

analoge Probe f¨ ur z ₀ und z ₂

Beispiel

Mehrdeutigkeit von Potenzen f¨ ur irrationale oder imagin¨ are Exponenten benutze:

exp(2πk i) = 1 = ⇒ z ^s = (z · 1) ^s = z ^s exp(2π ks i) f¨ ur k ∈ Z

unendlich viele L¨ osungen auf dem Einheitskreis:

i ^π = exp((π/2 + 2πk )i) ^π

= exp i(π ² /2 + 2π ² k )

, k ∈ Z unendlich viele L¨ osungen auf einer Halbgeraden:

π ⁱ = exp(ln π + 2πk i) ⁱ = exp(i ln π − 2πk )

= exp(−2πk ) exp(i ln π), k ∈ Z

unendlich viele L¨ osungen auf der positiven reellen Achse:

i ⁱ = exp((π/2 + 2π k )i) ⁱ

= exp(−π/2 − 2π k ), k ∈ Z

111 / 1

Geraden und Kreise in der Gaußschen Zahlenebene Die Gleichung

|z − a| = s |z − b|, s 6= 1 ,

beschreibt einen Kreis mit Mittel- punkt

w = 1

1 − s ² a − s ² 1 − s ² b und Radius

r = s

|1 − s ² | |b − a|

Beweis

(i) Koordinatenform der Kreisgleichung:

setze

z = x + iy , a = a ₁ + ia ₂ , b = b ₁ + ib ₂ Quadrieren der Gleichung |z − a| = s|z − b|

(x − a ₁ ) ² + (y − a ₂ ) ² = s ² (x − b ₁ ) ² + (y − b ₂ ) ² bzw. nach Umformung

(1 − s ² )(x ² + y ² ) + c ₁ x + c ₂ y = d Division durch 1 − s ² und quadratische Erg¨ anzung

(x − p) ² + (y − q) ² = σr ² mit σ ∈ {−1, 1}

Existenz von L¨ osungen = ⇒ σ = 1 (Kreisgleichung)

113 / 1

(ii) Mittelpunkt und Radius:

Einsetzen von z = a + t (b − a) in |z − a| = s |z − b|

|t | = s |t − 1| ⇐⇒ t ₁ = −s

1 − s , t ₂ = s 1 + s

zwei Schnittpunkte des Kreises mit der Geraden durch die Punkte a und b

z ₁ = 1

1 − s a − s

1 − s b, z ₂ = 1

1 + s a + s 1 + s b Mittelpunkt des Kreises

w = 1

2 (z ₁ + z ₂ ) = 1

1 − s ² a − s ² 1 − s ² b Radius

r = 1

|z −z | =

(1 + s ) − (1 − s )

a − s(1 + s) + s (1 − s ) b

= s

|b−a|

Alternative Methode

Geometrischer Beweis mit Hilfe des Kreises des Apollonius (200 v. Chr.)

|z − a| = s |z − b|

⇐⇒ festes Verh¨ altnis der Abst¨ ande der Punkte Z zu zwei gegeben Punk- ten A und B :

|AZ | / |ZB | = s

Zum Beweis sei o.B.d.A. s < 1, d.h. A liegt innerhalb des Kreises.

Punkte Z _i und Z _a auf der Geraden durch AB , definiert durch

|AZ _i | / |Z _i B | = s , |AZ a | / |Z a B | = s

Schneiden der Geraden durch Z und Z _i sowie der Geraden durch Z und Z _a mit der Geraden durch A parallel zu ZB Punkte S _i und S _a

115 / 1

gleiche Seitenverh¨ altnisse (Strahlens¨ atze) f¨ ur die ¨ ahnlichen Dreiecke

∆(A, Z _i , S _i ) ∼ ∆(B , Z _i , Z ) und ∆(A, Z _a , S _a ) ∼ ∆(B , Z _a , Z ) = ⇒

|AS _i |

|BZ | = |AZ _i |

|Z _i B | = s , |AS _a |

|BZ | = |Z _a A|

|Z _a B | = s

|AZ | / |BZ | = s = ⇒ |AZ | = |AS _i | = |AS _a |

Addition der Winkel in den zwei gleichschenkligen Dreiecken ∆(A, S _i , Z ) und ∆(A, S _a , Z ),

2 ^ (A, Z , S _i ) + 2 ^ (A, Z , S _a ) + ^ (Z , A, S _i ) + ^ (Z , A, S _a ) = 360 ^◦

Beispiel

Bestimmung von Mittelpunkt und Radius f¨ ur den Kreis C : |z | = 1

2 |z − 3i|

(i) Mittelpunkt und Radius gem¨ aß der allgemeinen Formeln:

w = 1

1 − s ² a − s ²

1 − s ² b = 1

1 − 1/4 0 − 1/4

1 − 1/4 (3i) = −i

r = s

|1 − s ² | |b − a| = 1/2

1 − 1/4 |3i| = 2 (a = 0, b = 3i, s = 1/2)

117 / 1

(ii) Bestimmung der Koordinatenform (z = x + iy ):

Quadrieren der Gleichung |(x , y )| = |(x , y − 3)|/2 x ² + y ² = 1

4 (x ² + y ² − 6y + 9) Umformungen

3x ² + 3y ² = −6y + 9

⇐⇒ x ² + y ² + 2y = 3

quadratische Erg¨ anzung y ² + 2y = (y + 1) ² − 1 Standardform x ² + (y + 1) ² = 2 ²

Mittelpunkt: (0, −1), Radius: 2