Double Parton Distributions in the Nucleon on the Lattice Dissertation
Volltext
Abbildung
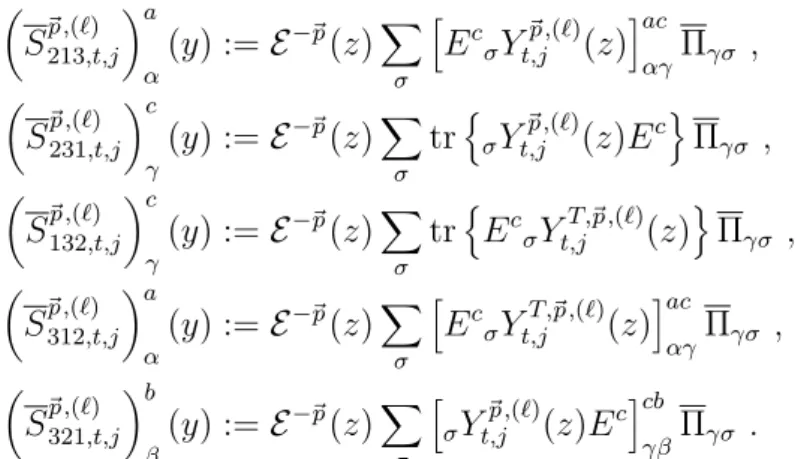
ÄHNLICHE DOKUMENTE
In this paper, we carry out the first direct lattice calculation for the valence quark distribution of the pion using the LaMET approach.. Our results are comparable quantitatively
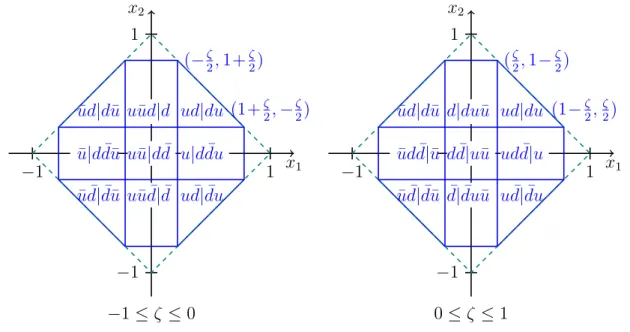
APPENDIX B: OPERATOR RELATIONS FOR LEADING-TWIST DISTRIBUTION AMPLITUDES In the following we give the relations between the operators whose matrix elements dene moments of the
The nucleon distribution amplitude can be inferred from matrix elements of local three-quark operators, and a central issue in our approach is the renormalization these operators..
ner (formed from the sar by prefixing J „the 60th part"), the word would be Assyrian and mean ,,r yoke", while the Accadian representative was su¬. tu 1 or sudun. The ner
The tree-level production modes of a vector boson in association with jets
quantum chromodynamics (QCD), while providing constraints on the quark distributions in a similar way to inclusive production of a vector boson. The PDF fit is performed at NNLO
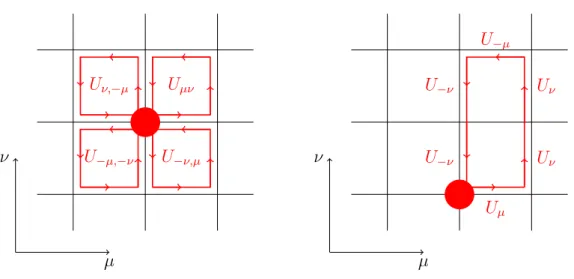
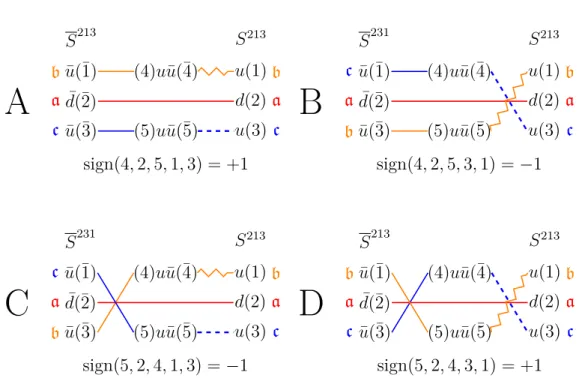
Combining the different lattice graphs to physical amplitudes in an isospin basis, we can compare our lattice results with the computation in chiral perturbation theory performed
LHCb VELO data event 2d projection, top half 37 Daniel Saunders, iCSC 2016 - Data Reconstruction in Modern Particle Physics Lecture 1/2... Tracking - Pattern recognition Tracking