Heinz Junek Vorlesung im SS 2009
Institut f¨ ur Mathematik Universit¨ at Potsdam
e-mail: junek@rz.uni-potsdam.de
July 20, 2009
Contents
1 Einf¨ uhrung und Beispiele 2
1.1 Differentialgleichungen als mathematische Modelle . . . . 2
1.2 Isoklinenmethode . . . . 7
1.3 Ein Einzigkeitssatz . . . . 8
2 Elementare L¨ osungsmethoden 11 2.1 Differentialgleichungen mit getrennten Variablen . . . . 11
2.2 Differentialgleichungen mit homogenen Variablen . . . . 13
2.3 Lineare Differentialgleichungen . . . . 14
2.4 Exakte Differentialgleichungen und integrierender Faktor . . . . 17
2.5 Anwendungsaufgaben und Prozessmodellierung . . . . 21
3 Existenzs¨ atze 24 3.1 Vollst¨ andige metrische R¨ aume . . . . 24
3.2 Der Banachsche Fixpunktsatz . . . . 26
3.3 Existenzs¨ atze . . . . 27
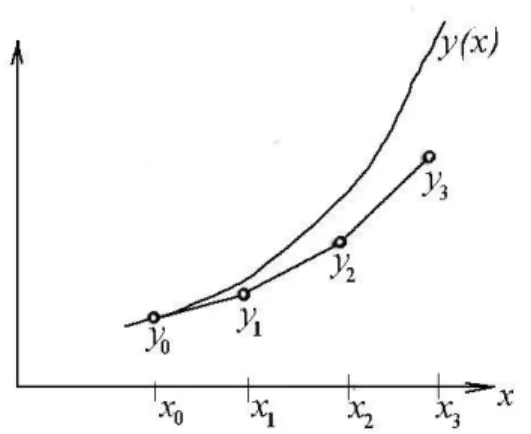
4 Numerische Verfahren 36 4.1 Das Eulersche Polygonzugverfahren . . . . 36
4.2 Verbessertes Euler-Verfahren, Heun-Verfahren . . . . 38
4.3 Das Runge–Kutta–Verfahren . . . . 39
5 Lineare Systeme und lineare DGL n-ter Ordnung 42 5.1 Picard-Lindel¨ of f¨ ur Systeme . . . . 42
5.2 Lineare Systeme und Fundamentalsysteme . . . . 43
5.3 Die Reduktionsmethode . . . . 48
5.4 Lineare Systeme mit konstanten Koeffizienten . . . . 51
5.5 Differentialgleichungen n–ter Ordnung . . . . 59
5.6 Partikul¨ are L¨ osungen und Faltungen . . . . 61
5.7 Die Schwingungsgleichung . . . . 65
5.8 Die Wellengleichung und die Besselsche Differentialgleichung . . . . 70
5.9 Ber¨ uhmte Differentialgleichungen 2. Ordnung . . . . 73
6 Qualitative Theorie und dynamische Systeme 76
6.1 Autonome Systeme und Phasenraum . . . . 76
6.2 Invariante Mengen und Klassifizierung kritischer Punkte . . . . 81
6.3 Stabilit¨ atsanalyse . . . . 83
6.4 Stabilit¨ atsanalyse mittels Ljapunov-Funktion . . . . 87
6.5 Grenzzyklen und chaotische Attraktoren . . . . 90
7 Randwertprobleme zweiter Ordnung 93 7.1 Einf¨ uhrende Beispiele . . . . 93
7.2 Wer braucht Randwertprobleme? . . . . 94
7.3 Der inhomogene harmonische Oszillator als Testmodell . . . . 95
7.4 Das Sturmsche Randwertproblem . . . . 98
7.5 Reduktion des allgemeinen RWP auf ein S-RWP . . . 101
7.6 Eigenwertprobleme . . . 104
7.7 Sturmsche Eigenwertprobleme . . . 105
7.8 Sturm-Liouvillesche EWP und Orthogonalsysteme . . . 108
7.9 Spektraldarstellung symm. Integraloperatoren in L
2[a, b] . . . 112
8 Literatur 117
1. Was ist eine gew¨ ohnliche Differentialgleichung, was ist ein Anfangswertproblem?
2. Erl¨ autern Sie die Isoklinenmethode. Welche Hypothese ¨ uber das L¨ osungs verhalten der Differentialgleichungen kann man damit gewinnen?
3. Welche Eindeutigkeitsaussagen lassen sich f¨ ur Anfangswertprobleme machen?
4. Erl¨ autern Sie elementare L¨ osungsmethoden und wenden Sie diese auf Beispiele an!
5. Machen Sie Aussagen ¨ uber das L¨ osungsverhalten linearer Differentialgleichungen! Wie erh¨ alt man spezielle L¨ osungen f¨ ur eine inhomogene lineare Differentialgleichung?
6. Was sind Inhalte und Beweis des Existenz- und Eindeutigkeitssatzes von
Picard-Lindel¨of? 7. (Erl¨ autern Sie numerische Verfahren zur L¨ osung von Anfangswertproblemen!)
8. Was ist ein lineares Differentialgleichungssystem? Welche Eigenschaften besitzt der L¨ osungsraum eines homogenen linearen Differentialgleichungssystem?
Was versteht man unter einem Fundamentalsystem?
Wie erh¨ alt man die L¨ osungen eines inhomogenen Systems?
9. Wozu dient die
Wronski-Determinante?
10. Welche Beziehungen bestehen zwischen linearen Differentialgleichungen n-ter Ordnung und linearen Systemen 1. Ordnung?
11. Wozu dient das Reduktionsverfahren?
12. Welche L¨ osungsverfahren gibt es f¨ ur lineare Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten? Man erl¨ autere dies am Beispiel von Differentialgleichungen 2.
Ordnung.
13. Was versteht man unter dem Phasenraum und dem Phasenportr¨ at? Wie bestimmt man die Orbits?
14. Was versteht man unter kritischen Punkten eines Differentialgleichungssystems bzw. einer Differentialgleichung n-ter Ordnung?
15. Wann heißt ein kritischer Punkt stabil bzw. asymptotisch stabil? Welche Kriterien?
16. Was sind Ljapunov- Funktionen? Wozu dienen sie?
17. Was sind lineare Randwertprobleme 2. Ordnung?
18. Wozu dient die Greensche Funktion? Wie wird sie gewonnen?
19. Was ist ein Sturm-Liouvillesches Eigenwertproblem? Was weiß man ¨ uber die Existenz und Eigenschaften von Eigenwerten und Eigenfunktionen?
20. Wie kann das Sturmsche RWP unter Verwendung von Entwicklungen nach Eigenfunktio- nen gel¨ ost werden?
Halten Sie zu allen Themen geeignete einfache Beispiele bereit!
1 Einf¨ uhrung und Beispiele
1.1 Differentialgleichungen als mathematische Modelle
Die mathematische Modellierung von Prozessen aller Art vollzieht sich prinzipiell nach folgendem Schema
Experiment bzw. empirische Befunde
↓
Auffinden der wesentlichen Parameter
↓
Aufstellen des mathematischen Modells
(z.B. lineares Gleichungssystem, Differentialgleichungen, Gleichungen in anderen mathematischen Strukturen)
↓
Mathematische Bearbeitung - Existenz von L¨ osungen
- Eindeutigkeit und Mehrdeutigkeit - Konstruktive Ermittlung der L¨ osungen
↓
Interpretation der L¨ osung und Verbesserung des Modells
F¨ ur die Beschreibung von Prozessen, insbesondere von dynamischen Zusammenh¨ angen, sind Differentialgleichungen h¨ aufig das geeignete Instrument.
Unter einer Differentialgleichung versteht man grob gesprochen eine Gleichung, in der Funktio- nen und ihre Ableitungen vorkommen. H¨ angen die gesuchten Funktionen nur von einer Gr¨ oße, z.B. der Zeit, ab, so f¨ uhrt das zu gew¨ ohnlichen Differentialgleichungen. Ein einfaches aber wichtiges Beispiel ist durch die Gleichung
y
0= ky
des radioaktiven Zerfalls einer Probe der Masse y = y(t) gegeben. H¨ angen die Funktionen von mehreren Variablen, z.B. von Orts– und Zeitkoordinaten ab, so sind geeignete Modelle durch partielle Differentialgleichungen gegeben. Ein Beispiel hierf¨ ur ist die W¨ armeausbreitung in einem Stab. Bezeichnet u = u(x, t) die Temperatur am Ort x zum Zeitpunkt t, so ist die Anderung dieser Funktion durch die W¨ ¨ armeleitungsgleichung
∂
2u
∂x
2− ∂u
∂t = 0 gegeben.
Historisch werden gew¨ ohnliche Differentialgleichungen bereits von den Begr¨ undern der Differential-
Integralrechnung
Newtonund
Leibnizzur Beschreibung physikalischer Prozesse, insbesondere
mechanischer Bewegungen eingesetzt. Intensiv weiterentwickelt und durch trickreiche Tech-
niken erg¨ anzt wurde die Theorie durch die Gebr¨ uder
Bernoulli, durch
Jacobiund
Euler. In
der theoretischen Mechanik wurden partielle Differentialgleichungen erstmals durch
Lagrange,
Cauchyund sp¨ ater
Hamiltoneingesetzt. Die Grundgleichungen der Elektrodynamik wurden
von
Maxwellaufgestellt, in der Thermodynamik ist
Nernstzu nennen. Die Grundgleichun- gen der allgemeinen Relativit¨ atstheorie, ebenfalls formuliert als partielle Differentialgleichungen, stammen von
Einstein. In der Quantenmechanik ist insbesondere die
Schr¨odinger–Gleichung zur Beschreibung der Elektronenzust¨ ande zu nennen. Wir definieren nun genauer unseren Un- tersuchungsgegenstand unseres Lehrgebietes:
Definition 1.1 (Differentialgleichungen und Anfangswertprobleme) .
1. Eine explizite, gew¨ ohnliche Differentialgleichung 1. Ordnung (kurz Dgl) ist eine Gleichung der Form
y
0= F (x, y). (1)
Dabei ist F : (a, b) × (c, d) →
Reine vorgegebene Funktion.
2. Eine L¨ osung der Dgl (1) ist eine differenzierbare Funktion y = y(x), die wenigstens auf einem Teilintervall von (a, b) die folgende Gleichung erf¨ ullt:
y
0(x) = F x, y(x) .
3. Ein Anfangswertproblem (kurz (AWP)) ist eine Dgl zusammen mit einem Anfangswert (x
0, y
0), also
y
0= F (x, y) mit y(x
0=)y
0. (2)
4. Eine L¨ osung eines AWP (2) ist eine Funktion y = y(x), die in einer Umgebung von x
0die Differentialgleichung sowie die Anfangsbedingung y(x
0) = y
0erf¨ ullt.
Wir betrachten einige Beispiele:
Beispiel 1.2 (Evolutionsgleichung: Radioaktiver Zerfall und Bakterienwachstum) Be- zeichnet y = y(x) die zum Zeitpunkt x vorhandene Menge einer radioaktiven Substanz, so ist die in dem Zeitabschnitt ∆x zerfallene Menge ∆y durch die Formel
∆y = k · y(x) · ∆x
gegeben. Dabei ist k ein negativer Proportionalit¨ atsfaktor, der f¨ ur die jeweilige Substanz charakteristisch ist. F¨ ur ein Bakterienwachstum ergibt sich unter der Voraussetzung eines unbeschr¨ ankten Lebensraumes dieselbe Gleichung mit einer positiven Konstanten k. Division durch ∆x und Grenz¨ ubergang ∆t → 0 f¨ uhrt zur Differentialgleichung
y
0= ky, (3)
der sogenannten Evolutionsgleichung oder Wachstums/Zerfallsgleichung. Hierbei sind oft nur die L¨ osungen gesucht, die zum Anfangszeitpunkt x = x
0eine Anfangsbedingung
y(x
0) = y
0(4)
erf¨ ullen. Die beiden Bedingungen (3) und (4) zusammen bilden dann das Anfangswertproblem
im oben definierten Sinn.
Wie die Probe zeigt, ist die Funktion
y(x) = c · e
k(x−x0)f¨ ur jedes c ∈
Reine L¨ osung der Evolutionsgleichung auf ganz
R, undy(x) = y
0· e
k(x−x0)l¨ ost das zugeh¨ orige AWP zum Anfangsweert (x
0, y
0).
Es bleibt die Frage, ob es außer dieser L¨ osung weitere L¨ osungen gibt. Wir nehmen dazu an, dass y
1= y
1(x) eine weitere L¨ osung der Differentialgleichung w¨ are. Dann erf¨ ullt die Hilfsfunktion
h(t) = y
1(x) e
kxdie Gleichung
h
0(x) = y
10· e
kx− y
1e
kxk
e
2kx= y
10− ky
1e
kx= 0 f¨ ur alle x,
also ist h(x) = konstant. Mithin ist y
1(x) = ce
kx. Insbesondere ist das Anfangswertproblem eindeutig l¨ osbar.
Beispiel 1.3 (Begrenztes Wachstum, Kondensatoraufladung) F¨ ur ein Wachstum mit be- grenzten Ressourcen ist eine L¨ osung mit y(x) → ∞ f¨ ur x → ∞ sicher unm¨ oglich.
Diese Prozesse k¨ onnen also sicherlich nicht durch eine Differentialgleichung y
0= ky beschrieben werden. Ein m¨ ogliches Modell w¨ are aber die Gleichung
y
0= ky + l(y
∞− y) = A − By,
wobei y
∞ein m¨ oglicher S¨ attigungswert f¨ ur x → ∞ ist. Insgesamt ergibt sich also mit neuen Konstanten c
1, c
2die Differentialgleichung
y
0= c
1y + c
2.
Eine entsprechende Gleichung ergibt sich zum Beispiel auch f¨ ur die Aufladung eines Konden- sators gem¨ aß Stromlaufplan in Figur
1.Figure 1: Kondensatoraufladung
Bezeichnet Q = Q(x) die Ladung der Kapazit¨ at C zum Zeitpunkt x, so gilt unter Verwendung des Ohmschen Gesetzes U
R= R · I, der Kondensatorformel Q = C · U
Cund wegen Q
0= I die Gleichung
Q
0= I = U
RR = 1
R
U
e− U
C= 1 R
U
e− Q C
, also Q
0= U
eR − 1
C Q
als Spezialfall obiger Gleichung.
Beispiel 1.4 (Logistische Gleichung) Laufen Wachstums- und Verdr¨ angungsprozesse in einer Population y(t) gleichzeitig ab, so ist ein Ansatz
y
0= cy(y
∞− y) = αy − βy
2mit einer S¨ attigungskonstanten y
∞plausibel. Diese Differentialgleichung wurde 1838 zur Mod- ellierung von
Verhulstvorgeschlagen und von ihm als logistische Differentialgleichung bezeich- net. Die L¨ osungsfunktion zeigte gute ¨ Ubereinstimmung mit der empirisch ermittelten Bev¨ olkerungs- entwicklung. F¨ ur die L¨ osung verweisen wir auf Beispiel
2.3.Beispiel 1.5 (Chemische Reaktionen) Die Anzahl der Ausgangsstoffe f¨ uhrt zu einer Klas- sifikation der chemischen Reaktionen und bestimmt wesentlich die Art der Differentialgleichung.
Man unterscheidet z.B.:
Reaktion 1. Ordnung : A X, X
0= k(A − X) (s.2.20), Reaktion 2. Ordnung : A + B X, X
0= k(A − X)(B − X) (s.2.21).
Beispiel 1.6 (Harmonischer Oszillator) Schwingungsvorg¨ ange f¨ uhren, da Kr¨ afte und Beschle- unigungen zu ber¨ ucksichtigen sind, immer auf Differentialgleichungen 2. Ordnung. Betrachten wir einen Federschwinger nach Abbildung
2(links).Figure 2: Federschwinger
Es sei y = y(x) die Position der Masse m zum Zeitpunkt x. Die y-Skala sei dabei so positioniert, dass die Ruhelage der Masse bei 0 liegt. Die Bilanz aus Tr¨ agheitskraft F = m·y
00und Hookescher Federkraft F = −ky ergibt die Gleichung
my
00= −ky oder my
00+ ky = 0.
Man erkennt, dass y
1(x) = sin
qkm
x und y
2(x) = cos
qkm
x zwei L¨ osungen der Differentialglei- chung sind. Offenbar ist auch jede Linearkombination
y(x) = c
1sin
rk
m x + c
2cos
rk
m x
eine L¨ osung. Es bleibt wiederum die Frage, ob außerdem weitere L¨ osungen existieren. Wir
wollen dieser Frage zun¨ achst nicht weiter nachgehen, sondern auf einen Zusammenhang zwischen
Differentialgleichungen h¨ oherer Ordnung und Systemen von Differentialgleichungen 1. Ordnung
hinweisen. Betrachtet man neben der Ortsvariablen y = y(x) die Geschwindigkeit v = v(x) =
y
0(x) als zus¨ atzliche Variable, so ist die Gleichung my
00+ ky = 0 ¨ aquivalent zu dem System
y
0(x) = v(x) v
0(x) = − k
m y (t)
Diese Methode l¨ asst sich verallgemeinern: Jede Differentialgleichung n-ter Ordnung ist zu einem System von n Differentialgleichungen von 1. Ordnung ¨ aquivalent. In der Tat liefert jede L¨ osung einer Differentialgleichung
y
(n)= f (x, y, y
0, . . . , y
(n−1)) (∗) einen L¨ osungsvektor (y, y
0, . . . , y
(n−1)) des folgenden Differentialgleichungssystems
y
0= y
1y
10= y
2.. .
y
0n−1= f (x, y, y
1, . . . , y
n−1)
Ist umgekehrt (y, y
1, . . . , y
n−1) eine L¨ osung dieses Differentialgleichungssystems, so erf¨ ullt y wegen y
(n)= y
n−10die Differentialgleichung (∗). Daher gen¨ ugt es prinzipiell, sich bei Existenz–
und Eindeutigkeitsfragen auf Systeme 1. Ordnung zu beschr¨ anken.
In vielen Lehrb¨ uchern wird f¨ ur Federschwinger die Abbildung 2(rechts), als Lageskizze verwen- det. Der Leser m¨ oge die Differentialgleichung unter Ber¨ ucksichtigung der Schwerkraft angeben.
Welche L¨ osungen hat diese Gleichung? (Siehe auch Abschnitt
2.3)Beispiel 1.7 (R¨ auber-Beute-Modelle) Differentialgleichungssysteme treten aber auch selbst¨ andig als Modelle auf. Sie sind das geeignete Werkzeug, wenn mehrere sich gegenseitig beeinflussende Gr¨ oßen in ihrer zeitlichen Entwicklung zu untersuchen sind. Beispiel f¨ ur ein solches dynamisches System ist das von
Volterraintensiv untersuchte R¨ auber–Beute–Modell. Es bezeichne y
1(x) eine Population von Hasen und y
2(x) eine Population von F¨ uchsen, die auf dem gleichen Terri- torium leben. Wir nehmen nun an, dass die Hasen die einzige Nahrungsquelle der F¨ uchse sind.
G¨ abe es keine Kopplung zwischen den Populationen, so w¨ urden sie sich nach den Gleichungen
y
01= α
1y
1y
02= −α
2y
2mit gewissen Konstanten α
1, α
2> 0 entwickeln. Ber¨ ucksichtigen wir nun die Wechselwirkung der Populationen, so ist die Dezimierung der Hasen durch die F¨ uchse in der Zeiteinheit ∆x proportional zu y
1· y
2, und ebenso ist die Zunahme der Fuchspopulation zu y
1· y
2proportional.
Das f¨ uhrt auf das Gleichungssystem
y
10= α
1y
1− β
1y
1y
2y
20= −α
2y
2+ β
2y
1y
2mit positiven Konstanten α
1, α
2, β
1, β
2, das als R¨ auber–Beute–Modell bezeichnet wird.
1.2 Isoklinenmethode
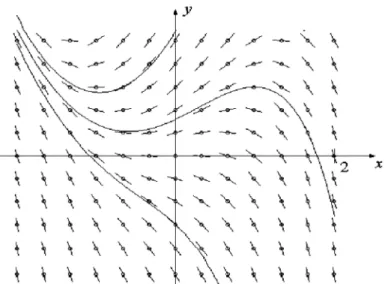
Wir versuchen zun¨ achst graphisch, uns einen Einblick in die L¨ osungsmannigfaltigkeit von Dif- ferentialgleichungen 1. Ordnung zu verschaffen. Dazu benutzen wir die folgende Definition, die wir dann am Beispiel der Differentialgleichung
y
0= y − x
2sogleich graphisch umsetzen werden. Es sei y
0= F (x, y) mit D(F ) ⊆
R2eine Differentialglei- chung. Die Zahlentripel
(x, y, y
0) =
x, y, F (x, y)
heißen Richtungselemente der Differential gleichung, sie werden durch eine kleine Strecke durch den Punkt (x, y) mit gegebenem Anstieg F (x, y) veranschaulicht. Die Menge aller Richtungse- lemente heißt Richtungsfeld der Differentialgleichung. Zur Arbeitser-leichterung bestimmt man die Kurven gleichen Anstiegs, Isoklinen genannt, als Punkt-mengen {(x, y) : F(x, y) = c} f¨ ur jeweils festes c ∈
R. F¨ ur die Differentialgleichung y
0= y − x
2ist die Isokline zur Steigung c durch die Gleichung y − x
2= c, also durch y = x
2+ c gegeben. Tr¨ agt man nun auf den Isokli- nen die entsprechenden Richtungselemente ein, so ergibt sich das Richtungsfeld nach Abbildung
3. H¨atte man nun eine L¨ osungskurve y = y(x), so m¨ ussten die Richtungselemente jeweils die Tangentenrichtung angeben. Umgekehrt m¨ usste sich durch ”Mitschwimmen” im Richtungsfeld eine L¨ osung ergeben (Str¨ omungslinien). Das f¨ uhrt zu den folgenden
Hypothesen zum L¨ osungsverhalten:
b) Man erh¨ alt L¨ osungen als Str¨ omungslinien im Richtungsfeld (vgl. Existenzsatz von Peano und Eulersches Polygonzugverfahren).
b) Durch jeden Anfangspunkt (x
0, y
0), gibt es eine L¨ osung.
c) L¨ osungen k¨ onnen sich nicht schneiden (unter einem positiven Schnittwinkel), Tangieren w¨ are jedoch denkbar.
d) Im gegebenen Beispiel gibt es zu jedem Anfangspunkt genau eine L¨ osung.
Es wird das Anliegen der nachfolgenden Abschnitte sein, geeignete Voraussetzungen f¨ ur die G¨ ultigkeit dieser Hypothesen zu finden.
F¨ ur das oben betrachtete Beispiel ist es aber bereits jetzt m¨ oglich, L¨ osungen auch analytisch zu gewinnen. Die graphisch gewonnenen L¨ osungen lassen vermuten, dass unter anderem auch Parabeln als L¨ osungen auftreten. Ein Ansatz
y = ax
2+ bx + c
mit unbestimmten Koeffizienten f¨ uhrt nach dem Einsetzen in die Differentialgleichung auf 2ax + b = ax
2+ bx + c − x
2. Der Koeffizientenvergleich ergibt als einzige L¨ osung a = 1, b = 2, c = 2.
Also ist y = x
2+ 2x + 2 eine L¨ osung der Differentialgleichung. Um zu weiteren L¨ osungen zu kommen, betrachten wir y
0= y − x
2als eine durch den Term −x
2gest¨ orte Gleichung y
0= y, deren allgemeine L¨ osung ja y = ce
xwar. Nun ist leicht zu sehen, dass eine additive ¨ Uberlagerung beider L¨ osungen zu einer L¨ osungsschar
y = (x
2+ 2x + 2) + ce
xmit c ∈
Rder Gleichung y
0= y − x
2f¨ uhrt. Diese Technik wird im Abschnitt
2.3allgemein untersucht
werden. Zusammen mit dem im n¨ achsten Abschnitt zu beweisenden Einzigkeitssatz hat man
mit obiger Darstellung dann aber bereits alle L¨ osungen gewonnen.
Figure 3: Richtungsfeld der Differentialgleichung y
0= y − x
21.3 Ein Einzigkeitssatz
Definition 1.8 (Lipschitzbedingung) Es seien I und J zwei Intervalle in
Rund es sei F : I × J →
Reine Funktion auf dem Rechteck I × J . Man sagt, dass F auf I × J eine Lipschitzbedingung bzgl. y erf¨ ullt, wenn es eine Konstante L derart gibt, dass
|F (x, y
1) − F (x, y
2)| ≤ L|y
1− y
2|
f¨ ur alle x ∈ I und alle Paare y
1, y
2∈ J gilt. Jede Konstante L mit dieser Eigenschaft heißt eine Lipschitz–Konstante.
Ein handliches Kriterium zur ¨ Uberpr¨ ufung der Lipschitzbedingung ist f¨ ur partiell differenzier- bare Funktionen durch den folgenden Satz gegeben:
Satz 1.9 Ist
∂F∂y(x,y)auf I × J beschr¨ ankt, so erf¨ ullt F auf I × J eine Lipschitz- Bedingung.
Beweis. Die Anwendung des Mittelwertsatzes der Differentialrechnung bez¨ uglich der Variablen y ergibt zusammen mit der vorausgesetzten Beschr¨ anktheit der partiellen Ableitung eine Ab- sch¨ atzung
F (x, y
1) − F (x, y
2) y
1− y
2
=
∂F (x, η)
∂x
≤ L, woraus sich durch Umstellen die gew¨ unschte Ungleichung ergibt.
Der Beweis des Einzigkeitssatzes st¨ utzt sich auf den folgenden Hilfssatz, der ein Spezialfall des sp¨ ater zu behandelnden
Gronwall-Lemmas ist:
Satz 1.10 Es sei ϕ(x) eine auf [0, b] stetig differenzierbare Funktion mit ϕ(0) = 0. Außerdem g¨ abe es eine Zahl L ≥ 0 mit
|ϕ
0(x)| ≤ L · |ϕ(x)| f¨ ur alle x ∈ [0, b].
Dann ist ϕ(x) = 0 f¨ ur alle x ∈ [0, b].
Beweis. Wir w¨ ahlen eine Zahl 0 < h ≤ b mit L · h < 1. Wir wollen zeigen, dass ϕ auf dem Intervall [0, h] verschwindet. Angenommen, dies w¨ are nicht der Fall. Dann g¨ abe es ein x
0∈ [0, h]
mit |ϕ(x
0)| = max
|ϕ(x)| : x ∈ [0, h] > 0. Aus dem Mittelwertsatz der Differentialrechnung und unseren Voraussetzungen folgt die Existenz einer Zahl x
1∈ [0, h] mit
|ϕ(x
0)| = |ϕ(x
0) − ϕ(0)| = |x
0· ϕ
0(x
1)| ≤ h · |ϕ
0(x
1)| ≤ h · L · |ϕ(x
1)| ≤ h · L · |ϕ(x
0)|.
Das ist wegen h · L < 1 aber nicht m¨ oglich. Also gilt ϕ(x) = 0 auf [0, h]. Das Verfahren wird nun f¨ ur das Intervall [h, 2h] wiederholt und solange fortgesetzt, bis b erreicht ist.
Satz 1.11 (Einzigkeitssatz) Erf¨ ullt die Funktion F : I × J →
Reine Lipschitz-Bedingung bzgl. y auf I × J , so existiert zu jedem Punkt (x
0, y
0) im Innern von I × J h¨ ochstens eine L¨ osung y = y(x) des Anfangswertproblems
y
0= F(x, y) mit y(x
0) = y
0.
Beweis. Es seien y
1(x) und y
2(x) zwei L¨ osungen auf einer Umgebung [x
0− h, x
0+ h] von x
0. Wir setzen ϕ(s) = y
1(x
0+ s) − y
2(x
0+ s) f¨ ur s ∈ [0, h]. Wegen
|y
10(x) − y
20(x)| = |F (x, y
1(x)) − F(x, y
2(x))| ≤ L|y
1(x) − y
2(x)| und y
1(x
0) − y
2(x
0) = 0 folgen
|ϕ
0(s)| ≤ L|ϕ(s)| f¨ ur 0 ≤ s ≤ h und ϕ(0) = 0.
Aus Satz (3) folgt ϕ(s) = 0 f¨ ur alle 0 ≤ s ≤ h, und das zeigt y
1(x) = y
2(x) f¨ ur alle x
0≤ x ≤ x
0+ h. Entsprechend zeigt man y
1(x) = y
2(x) f¨ ur x
0− h ≤ x ≤ x
0.
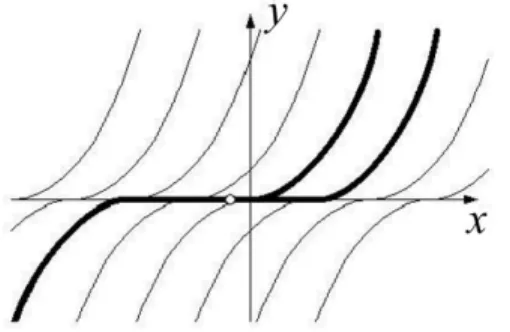
Beispiel 1.12 (
Clairautsche Differentialgleichung) Wir werden zeigen, dass die
Clairautsche Differentialgleichung y
0=
p|y| (s.a. Beispiel
1.13) ein Beispiel daf¨ur ist, dass nicht jedes Anfangswertproblem eindeutig l¨ osbar ist. Ohne Lipschitz-Bedingung kann die Einzigkeit also verloren gehen:
F¨ ur jedes α ∈
Rsind die folgenden Funktionen in der Form y(x) =
+
14(x − α)
2f¨ ur x ≥ α
−
14(x − α)
2f¨ ur x < α , x ∈
R,L¨ osungen der Differentialgleichung, wie die Probe leicht ergibt (s. Abbildung
4).Weitere L¨ osungen ergeben sich nun durch Zusammensetzung dieser Parabel¨ aste mit St¨ ucken der x-Achse. Das bedeutet, dass jedes Anfangswertproblem mit einem Anfangswert auf der x-Achse Verzweigungen der L¨ osung zul¨ asst. Nat¨ urlich kann die Funktion F(x, y) =
p|y| auf keinem Rechteck, das die x-Achse schneidet, eine Lipschitz-Bedingung erf¨ ullen (direkter Nachweis?).
Beispiel 1.13 (Der leckende Wassereimer) Man k¨ onnte meinen, dass das Ph¨ anomen aus
Beispiel
1.12eine rein mathematische Spitzfindigkeit ist. Dem ist aber nicht so! Vielmehr tritt
dieser Effekt durchaus bei realen Systemen auf, und die genannten Verzweigungsm¨ oglichkeiten
der L¨ osung haben die Konsequenz der nicht eindeutigen Vorhersagbarkeit der Zukunft oder der
Figure 4: L¨ osungskurven der Differentialgleichung y
0= − p
|y|, leckender Wassereimer.
Unm¨ oglichkeit der Rekonstruktion der Vergangenheit. Folgendes Beispiel steht hierf¨ ur stell- vertretend. Wir stellen uns einen zylinderf¨ ormigen Eimer vor, der im Boden ein kleines Loch hat. Es seien
x die Zeit und y = y(x) die F¨ ullh¨ ohe des Eimers zum Zeitpunkt x.
Dann ist die ¨ Anderung ∆y der Wasserstandsh¨ ohe gegeben durch:
∆y = v · ∆x · a mit v = Auslaufgeschwindigkeit, a = Lochfl¨ ache.
Also ist y
0= v · a. Die Energiebilanz (kinetische Energie=potentielle Energie) ergibt 1
2 ∆m · v
2= ∆m · g · y.
Hieraus folgt
v
22 = gy, v = −
p2gy.
Das Minuszeichen deswegen, weil v der y-Achse entgegengerichtet ist. Einsetzen liefert schließlich eine Variante der Clairautschen Dgl:
y
0= −
p2a
2g √
y.
Die L¨ osungschar ergibt sich aus Abbildung
4durch Spiegelung an der y-Achse (Zeitumkehr!).
Aufgaben zu Abschnitt
11. Der radioaktive Zerfall und die Halbwertszeit: Unter der Halbwertszeit λ eines radioaktiven Materials versteht man die Zeit, nach der die H¨ alfte des Materials zerfallen ist. Diese Werte findet man in Tabellenb¨ uchern. F¨ ur Kobalt60 betr¨ agt sie λ = 5.26 Jahre.
Wieviel Prozent einer gegebenen Menge Kobalt60 sind nach einem bzw. nach zwei Jahren zerfallen?
2. Richtungsfelder:
(a) Zeichnen Sie das Richtungsfeld zur Differentialgleichung y
0= − x y . (b) Zeichnen Sie drei L¨ osungskurven ein.
(c) Treffen Sie eine Vermutung zur analytischen Darstellung der L¨ osungen und f¨ uhren Sie die Probe aus.
3. Richtungsfelder: Es sei y
0= y(1 − y). Skizzieren Sie das Richtungsfeld! Zeichnen Sie
L¨ osungskurven zu den Anfangswerten y(0) = 1.5, y(0) = 0.3, y(0) = 0.7, y(0) = −0.5 ein!
2 Elementare L¨ osungsmethoden
Dank des Eindeutigkeitssatzes aus dem vorstehenden Abschnitt gewinnen Probierverfahren oder geschickte Ans¨ atze zur L¨ osung von Differentialgleichungen an Berechtigung, da man nicht bef¨ urchten muss, durch spezielle Ans¨ atze L¨ osungen zu verlieren. Obwohl die wenigsten Differ- entialgleichungen mit elementaren Methoden l¨ osbar sind, gibt es jedoch eine Reihe wichtiger Typen, die eine elementare Behandlung zulassen.
2.1 Differentialgleichungen mit getrennten Variablen
Gleichungen der Form
y
0= f (x) · g(y)
heißen Differentialgleichungen mit getrennten Variablen. F¨ ur diese Differentialgleichungen gilt der folgende Satz:
Satz 2.1 Es seien I, J ⊆
Rzwei offene Intervalle und es seien f : I →
Rund g : J →
Rstetige Funktionen. Zu jedem Anfangswert (x
0, y
0) ∈ I × J mit g(y
0) 6= 0 existiert eine Umgebung U ⊆ I von x
0derart, dass das Anfangswertproblem
y
0= f(x)g(y) mit y(x
0) = y
0auf U genau eine L¨ osung y = y(x) besitzt. Diese L¨ osung ergibt sich durch Aufl¨ osung der nach- folgenden Gleichung nach y:
y
Z
y0
dη g(η) =
x
Z
x0
f (ξ)dξ (5)
Im Fall g(y
0) = 0 ist y(x) = y
0eine L¨ osung des Anfangswertproblems, es kann aber weitere L¨ osungen geben.
Beweis. Wegen g(y
0) 6= 0 k¨ onnen wir ohne Beschr¨ ankung der Allgemeinheit den Fall g(y
0) > 0 annehmen. Da g stetig ist, existiert ein offenes Intervall V von y
0mit g(y) > 0 f¨ ur alle y ∈ V . Nehmen wir zun¨ achst die Existenz einer L¨ osung y = y(x) auf einer gewissen Umgebung U = U (x
0) an. F¨ ur x ∈ U gilt dann
y
0(x) = f (x)g(y(x)), also auch y
0(x)
g(y(x)) = f (x).
Die Integration nach x und die Anwendung der Substitutionsregel ergibt dann
x
Z
x0
y
0(ξ) g(y(ξ)) dξ =
x
Z
x0
f(ξ) dξ,
und mit der Substitution η = y(x) folgt daraus die Formel (5).
Umgekehrt l¨ ost jede Funktion y = y(x), die (5) erf¨ ullt, offenbar auch das Anfangswertproblem.
Es bleibt daher f¨ ur die Existenz und Einzigkeit der L¨ osung y = y(x) nur zu zeigen, dass die
Gleichung (5) auf einem geeigneten Rechteck U × V eine eindeutige Aufl¨ osung nach y = y(x) zul¨ asst. Dies l¨ sst sich aus dem Satz ¨ uber implizite Funktionen herleiten, wir geben aber einen direkten Beweis:
Die Funktion
G(y) =
y
Z
y0
1 g(η) dη
ist wegen g(y) > 0 auf V streng monoton wachsend und daher invertierbar auf dem offenen Intervall G(V ). Wegen G(y
0) = 0 ist 0 ein innerer Punkt von G(V ). Die Funktion
F (x) =
x
Z
x0
f (ξ) dξ
ist stetig und erf¨ ullt F (x
0) = 0. Daher existiert ein offenes Intervall U = U (x
0) mit F (U ) ⊆ G(V ).
Folglich kann auf U durch die Gleichung y = G
−1F(x), x ∈ U, eine stetig differenzierbare Funk- tion y = y(x) definiert werden, die die Gleichung G(y) = F(x), also Formel (5), erf¨ ullt.
Beispiel 2.2 Als erstes Beispiel betrachten wir das Anfangswertproblem y
0= yx mit y(1) = 2. Die in Satz
2.1beschriebene Methode ergibt
dy
dx = yx,
y
Z
2
dη
η =
x
Z
1
ξdξ,
ln |η|
y
2
= ξ
22
x 1
, ln y − ln 2 = x
2− 1
2 , y = 2e
x2−1
2
.
Beispiel 2.3 (Logistische Differentialgleichung) F¨ ur die in Beispiel
1.4angegebene logis- tische Differentialgleichung zum Anfangswert (x
0, y
0) mit y
06= 0 und y
06=
αβergibt die Methode der getrennten Variablen die folgende L¨ osung:
y
0= αy − βy
2,
y
Z
y0
dη
αη − βη
2=
Zxx0
dξ.
Mit 1
η(α − βη) = 1/α
η + β/α α − βη folgt weiter nach der Integration
1
α ln y
α − βy = x + c .
Die Aufl¨ osung nach y ergibt schließlich
y = α
β + c
1e
−αxmit einer Konstanten c
1> 0. Interessant ist das Langzeitverhalten der L¨ osung, es gilt n¨ amlich
x→∞
lim y(x) = α/β. Die L¨ osung hat also den stabilen Grenzwert α/β. Die konstante Funktion y ≡ α/β ist selbst eine L¨ osung, die wegen y
0≡ 0 eine station¨ are L¨ osung heißt.
Bemerkung 2.4 Als Erg¨ anzung zum Satz
2.1bemerken wir, dass f¨ ur das Anfangswertproblem y
0= f (x)g(y) mit g(y
0) = 0 immer die L¨ osung y ≡ 0 vorliegt. Die Clairautsche Differential- gleichung y
0= 1 ·
p|y| aus Beispiel
1.12mit Anfangswert y(1) = 0 zeigt aber, dass durchaus mehrere L¨ osungen existieren k¨ onnen.
2.2 Differentialgleichungen mit homogenen Variablen
Differentialgleichungen der Form
y
0= H y x
heißen Differentialgleichungen mit homogenen Variablen. Hier ist ein Beispiel:
y
0= 9x
2+ 3y
22xy = 9 + 3(
yx)
22
yx. Satz 2.5 Die Differentialgleichung y
0= H y
x
wird durch die Substitution z = y
x in die Dif- ferentialgleichung z
0= H(z) − z
x mit getrennten Variablen ¨ uberf¨ uhrt.
Beweis. Aus z = y x folgt
z
0= xy
0− y
x
2= xH (z) − y
x
2= H(z) − y/x
x = H(z) − z
x .
F¨ ur das oben genannte Beispiel ist H(z) = 9 + 3 z
22z , und f¨ ur z ergibt sich damit die Differen- tialgleichung
z
0= H(z) − z
x = (9 + z
2)/2z
x .
Trennung der Variablen f¨ uhrt auf
Z
2z
9 + z
2dz =
Z1
x dx , und mit der Substitution u = 9 + z
2, du = 2z dz folgt
Z
du u =
Z
dx
x , also u = c · x . Somit ist 9 + z
2= c · x, also 9 + y
2/x
2= c · x, und schließlich y = ± √
cx
3− 9x
2mit c ∈
R.2.3 Lineare Differentialgleichungen
Differentialgleichungen der Form
y
0+ a(x)y = b(x)
mit stetigen Funktionen a(x) und b(x) heißen lineare Differentialgleichungen. Ist b ≡ 0, so spricht man von einer homogenen linearen Differentialgleichung. Da lineare Differentialgleichun- gen offensichtlich in einer geeigneten Umgebung jedes Punktes (x
0, y
0) eine Lipschitz–Bedingung erf¨ ullen, sind alle derartigen Anfangswertprobleme eindeutig l¨ osbar.
Satz 2.6 Das Anfangswertproblem f¨ ur die homogene Differentialgleichung y
0+ a(x)y = 0 mit y(x
0) = y
0hat die L¨ osung
y = y
0e
−
x
R
x0
a(t)dt
.
Insbesondere ist jede L¨ osung auf dem Definitionsbereich von a(x) definiert.
Beweis. Die genannte Differentialgleichung hat getrennte Variable, und die dort entwickelten Methoden sind anwendbar.
Wie bei allen linearen Gleichungen in der Mathematik gibt es auch hier einen engen Zusammen- hang zwischen der homogenen und der inhomogenen Gleichung:
Satz 2.7 Es sei L
homdie Menge aller L¨ osungen der homogenen Dgl y
0+ a(x)y = 0, und es sei y
∗eine beliebige spezielle L¨ osung der inhomogenen Dgl y
0+ a(x)y = b(x). Dann gilt f¨ ur L¨ osungsmenge L
inhder inhomogenen Gleichung die Formel
L
inh= y
∗+ L
hom.
Beweis. Es ist die Gleichheit beider Mengen nachzuweisen. Wir haben zun¨ achst zu zeigen, dass f¨ ur jede homogene L¨ osung y
h∈ L
homdie Funktion y = y
∗+ y
hzu L
inhgeh¨ ort. In der Tat gilt
(y
∗+ y
h)
0+ a(x)(y
∗+ y
h) = y
∗0+ y
0h+ a(x)y
∗+ a(x)y
h= y
∗0+ a(x)y
∗+ y
h0+ a(x)y
h= b(x) .
Es sei umgekehrt eine beliebige L¨ osung y ∈ L
inhgegeben. Dann erf¨ ullt die Funktion ˜ y = y − y
∗wegen
˜
y
0+ a(x)˜ y = y
0− y
∗0+ a(x)(y − y
∗) = b(x) − b(x) = 0 die homogene Differentialgleichung. Also gilt auch
L
inh− y
∗⊆ L
hom.
Zur Ermittlung der L¨ osungsgesamtheit der inhomogenen Differentialgleichung fehlt wegen obige3r S¨ atze nur noch ein effektives Verfahren zur Gewinnung spezieller L¨ osungen der inhomogenen Differentialgleichung. Hierzu verwendet man folgende Verfahren:
a) Variation der Konstanten
b) Produktansatz y(x) = u(x) · v(x) von
Euler(s. Aufgabe
2)c) Geschickter Ansatz
d) Faltungskalk¨ ul (s. Abschnitt
5.6)Satz 2.8 (Variation der Konstanten) Ist y
h(x) eine nichttriviale L¨ osung der homogenen Differentialgleichung y
0+ a(x)y = 0, so kann durch den
Bernoulli-Ansatz
y(x) = c(x) · y
h(x)
eine partikul¨ are L¨ osung der inhomogenen Differentialgleichung ermittelt werden. Als allgemeine L¨ osung der inhomogenen Differentialgleichung y
0+ a(x)y = b(x) ergibt sich dann
y
inh(x) = c · e
−Ra(x)dx+
Zb(x)e
Ra(x)dxdx
· e
−Ra(x)dxmit c ∈
R.
Beweis. Setzt man y(x) = c(x) · y
h(x) in die inhomogene Differentialgleichung ein, so ergibt die linke Seite
y
0+ a(x)y = c
0· y
h+ cy
h0+ a(x)c · y
h(x) = c
0y
h+ c · (y
h0+ a(x) · y
h) = c
0y
h+ 0 = c
0y
h. Falls die Funktion c = c(x) so gew¨ ahlt wird, dass c
0y
h= b(x) gilt, so w¨ are y(x) eine L¨ osung.
Dies liefert f¨ ur c = c(x) die Bedingung
c
0(x) = b(x) · y
−1h(x) = b(x) · e
Ra(x)dx. Eine L¨ osung dieser Gleichung ist
c(x) =
Zb(x)e
Ra(x)dx
dx,
woraus mit y(x) = c(x) · y
heine partielle L¨ osung y
∗(x) =
Zb(x)e
Ra(x)dxdx
· e
−Ra(x)dxentsteht. Der Satz
2.7liefert dann die oben angegebene allgemeine L¨ osung der inhomogenen Gleichung.
Das in (3) angegebene Verfahren zur Konstruktion partikul¨ arer L¨ osungen hat den Vorteil der
Universalit¨ at. F¨ ur spezielle Inhomogenit¨ aten kann man jedoch oft viel schneller zu einer par-
tikul¨ aren L¨ osung kommen. Wir haben eine solche Methode bereits in Abschnitt
1.2bei der
Behandlung des Beispiels angewandt. Hier ist eine allgemein Formulierung:
Satz 2.9 (Geschickter Ansatz) Ist in der Differentialgleichung y
0= ay + P(x)
a 6= 0 eine Konstante und ist P (x) ein Polynom vom Grad n, so existiert eine partikul¨ are L¨ osung, die ebenfalls ein Polynom vom Grad n ist.
Beweis. Es sei P (x) =
n
P
j=0
a
jx
j. Der Ansatz
y =
n
X
j=0
b
jx
jf¨ uhrt beim Einsetzen in die Differentialgleichung auf
n
X
j=1
jb
jx
j−1=
n
X
j=0
ab
jx
j+
n
X
j=0
a
jx
j.
Der Koeffizientenvergleich ergibt das folgende eindeutig l¨ osbare lineare Gleichungssystem zur Bestimmung der b
j:
0 = ab
n+ a
njb
j= ab
j−1+ a
j−1; 1 ≤ j ≤ n .
Bemerkung 2.10 Das Verfahren ist auch f¨ ur andere Inhomogenit¨ aten gut geeignet. F¨ ur die Gleichung
y
0= ay + P (x)e
bxf¨ uhrt der Ansatz y = Q(x)e
bxmit einem Polynom Q(x) zum Ziel. F¨ ur a 6= b w¨ ahlt man dabei Q(x) vom gleichen Grad wie P (x), f¨ ur a = b w¨ ahlt man den Grad um eins h¨ oher. F¨ ur die Gleichung
y
0= ay + P (x) sin x
liefert der Ansatz y = Q
1(x) sin x + Q
2(x) cos x mit zwei Polynomen Q
1(x) und Q
2(x) eine L¨ osung.
Aufgaben zu den Abschnitten
2.1-2.31. Man zeige, dass lineare Differentialgleichungen invariant sind bez¨ uglich linearer Transfor- mationen z = α(x)y + β(x).
2. Man zeige, dass der Produktansatz y(x) = u(x) · v(x) ebenfalls zur Bestimmung einer partikul¨ aren L¨ osung geeignet ist (sogenannter Euler- Ansatz).
3. Man finde die allgemeine L¨ osung der Differentialgleichung y
0= 2xy + x
2.
4. Bestimmen Sie die allgemeine L”osung und die L”osung zum jeweils angegebenen An- fangswert:
a) (2 Pkte) y
0= y e
x1 + e
x, y(1) = −1, b) (3 Pkte) y
0= 2xy
x
2− y
2, y(2) = 1 , c) (2 Pkte) y
0− y = 2x
2, y(0) = 1, d) (2 Pkte) y
0+ 2y
x = x
3, y(1) = 1.
5. (3 Pkte) Bestimmen Sie die L”osung zur logistischen Differentialgleichung y
0= y − y
2, y(0) = 0.1
und skizzieren Sie diese L”osung.
6. Es sei T > 0 und es seien a(t), b(t) stetige, T -periodische Funktionen auf
R, d.h. a(t+T ) = a(t) und b(t + T ) = b(t) f¨ ur alle t ∈ R. Es sei
y
0= a(t)y + b(t). (6)
Beweisen Sie folgende Behauptungen:
a) Ist y L¨ osung von (6) und ist z(t) = y(t + T ) f¨ ur alle t ∈ R, dann ist z auch eine L¨ osung von (6).
b) Eine L¨ osung y von (6) ist T –periodisch genau dann, wenn y(0) = y(T ) ist.
c) Ist b(t) ≡ 0 und ist
T
R
0
a(s)ds = 0, dann ist jede L¨ osung von (6) T –periodisch.
d) Ist a(t) ≡ 0 und ist
T
R
0
b(s)ds = 0, dann ist jede L¨ osung von (6) T –periodisch.
e) Ist b(t) ≡ 0 und
RT 0a(s)ds < 0, dann gilt f¨ ur jede L¨ osung y von (6): lim
t→∞
y(t) = 0.
f) Ist
T
R
0
a(s)ds 6= 0, dann hat (6) genau eine T –periodische L¨ osung.
7. Die Bernoullische Differentialgleichung hat die Gestalt y
0= P (x)y + Q(x)y
αmit α ∈ R.
(Name nach
Jakob Bernoulli). F¨ ur α = 0 oder α = 1 ist die Differentialgleichung linear, und die L¨ osungen sind uns schon bekannt. Es sei nun α / ∈ {0, 1}.
Zeigen Sie: Sind die Funktionen P(x), Q(x) auf einem offenen Intervall I stetig, so besitzt die Bernoullische Anfangswertaufgabe
y
0= P (x)y + Q(x)y
αmit x
0∈ I, y(x
0) = y
0> 0 und α / ∈ {0, 1}
genau eine L¨ osung auf einem x
0enthaltenden Teilintervall von I. Man erh¨ alt sie, indem man die Bernoullische DGL durch die Substitution z = y
1−αin eine lineare Differential- gleichung ¨ uberf¨ uhrt.
2.4 Exakte Differentialgleichungen und integrierender Faktor
Definition 2.11 Eine Differentialgleichung der Form
P (x, y) + Q(x, y)y
0= 0 bzw. P (x, y) dx + Q(x, y) dy = 0
mit stetig partiell differenzierbaren Funktionen P und Q heißt exakt auf dem offenen Rechteck I × J , falls folgende Bedingung erf¨ ullt ist:
∂P
∂y = ∂Q
∂x (Integrabilit¨ atsbedingung)
Satz 2.12 Eine Differentialgleichung P + Q y
0= 0 ist genau dann exakt auf I × J , wenn es eine zweimal stetig partiell differenzierbare Funktion
Φ : I × J →
Rmit grad Φ = ∂Φ
∂x , ∂Φ
∂y
= (P, Q) auf I × J gibt. Eine solche Funktion Φ kann nach folgender Gleichung bestimmt werden:
Φ(x, y) =
x
Z
x0
P (ξ, y) dξ +
y
Z
y0
Q(x
0, η) dη f¨ ur beliebiges (x
0, y
0). (7)
Jede zweimal stetig partiell differenzierbare Funktion Φ mit gradΦ = (P, Q) heißt eine Poten- tialfunktion zur zugeh¨ origen Dgl.
Beweis. (⇐) Es sei Φ eine Funktion mit grad Φ = (P, Q). Dann folgt aus dem Satz von Schwarz
∂P
∂y = ∂
2Φ
∂x∂y = ∂
2Φ
∂y∂x = ∂Q
∂x .
(⇒) Wir definieren Φ mit obiger Formel und zeigen grad Φ = (P, Q). Es sind
∂Φ(x, y)
∂x = P (x, y) und
∂Φ(x, y)
∂y = ∂
∂y
x
Z
x0
P (ξ, y) dξ + Q(x
0, y)
=
x
Z
x0
∂P (ξ, y)
∂y dξ + Q(x
0, y) =
x
Z
x0
∂Q(ξ, y)
∂ξ dξ + Q(x
0, y)
= Q(x, y) − Q(x
0, y) + Q(x
0, y) = Q(x, y).
Das zeigt grad Φ = (P, Q).
Satz 2.13 Ist Φ(x, y) eine Potentialfunktion zu P + Q y
0= 0, so sind die ”Potentiallinien”
y = y(x) mit Φ x, y(x)
= const L¨ osungen der Gleichung P + Q y
0= 0.
Beweis. Ist y = y(x) die Gleichung einer Potentiallinie von Φ, so gilt Φ(x, y(x)) = c f¨ ur alle x in einem Intervall I
0. Aus der verallgemeinerten Kettenregel folgt dann
0 = d
dx Φ(x, y(x)) = ∂Φ
∂x · dx dx + ∂Φ
∂y · dy
dx = P (x, y(x)) + Q(x, y(x))y
0, was zu beweisen war.
Folgerung 2.14 Exakte Differentialgleichungen sind (modulo des Satzes ¨ uber implizite Funk-
tionen) explizit l¨ osbar.
Beweis. Nach obigen S¨ atzen gibt es zu exakten Differentialgleichungen passende Potentialfunk- tionen, und deren Potentiallinien sind L¨ osungen.
Wir demonstrieren das Verfahren an einigen Beispielen.
Beispiel 2.15 Wir betrachten die Dgl
2x dx + 2y dy = 0.
Sie ist offenbar exakt, und mittels Probe sehen wir, dass die Funktion Φ(x, y) = x
2+ y
2auf
R2\ {(x, 0) : x ∈
R} eine Potentialfunktion ist. Daher sind die Potentiallinien
Φ(x, y) = c f¨ ur c > 0
L¨ osungen der Dgl. Die explizite Gleichung dieser Potentiallinien ist y(x) = ±
pc − x
2mit |x| < c.
Beispiel 2.16 Wir betrachten die Gleichung
(3x
2+ y
2) + 2xyy
0= 0.
Schritt 1: Pr¨ ufung auf Exaktheit:
∂
∂y (3x
2+ y
2) = 2y, ∂
∂x (2xy) = 2y.
Schritt 2: Ermittlung einer Potentialfunktion Φ mittels Formel (7) und (x
0, y
0) = (0, 0):
Φ(x, y) =
Zx0
P (ξ, y) dξ +
y
Z
0
Q(0, η) dη =
Zx0
(3ξ
2+ y
2) dξ + 0 = x
3+ xy
2.
Schritt 3: Bestimmung von Potentiallinien: Wir l¨ osen die Gleichung Φ(x, y) = x
3+ xy
2= c f¨ ur beliebige Parameter c nach y auf. Das ergibt
y(x) = ±
r
c − x
3x mit c ∈
R,
und dies ist auf geeigneten Definitionsbereichen eine L¨ osungsschar der urspr¨ unglichen Differen- tialgleichung.
2.17 (Methode des integrierenden Faktors) Falls die Differentialgleichung
P + Qy
0= 0 (8)
noch nicht exakt ist, so kann sie eventuell durch Multiplikation mit einem geeigneten Faktor M (x, y) in eine exakte Differentialgleichung
P · M + Q · M · y
0= 0 (9)
¨
uberf¨ uhrt werden. In diesem Fall heißt M(x, y) ein integrierender Faktor. In den Punkten M (x, y) 6= 0 ist offenbar jede L¨ osung y(x) der Differentialgleichung (8) eine L¨ osung von (6) und umgekehrt. Das Ziel muss also darin bestehen, einen integrierenden Faktor zu finden. Hier bedient man sich der Methode, Ans¨ atze der Form
M (x, y) = M(x) oder M(x, y) = M (y)
zu machen und M durch L¨ osen einer passenden Differentialgleichung zu bestimmen. Wir demon- strieren das an einem Beispiel:
Beispiel 2.18 Es sei
4x + 3y
2+ 2xy · y
0= 0.
Dann ist
∂P∂y= 6y 6=
∂Q∂x= 2y, die Differentialgleichung ist also nicht exakt. Wir versuchen einen Ansatz M (x, y) = M(x) und erhalten:
∂P M
∂y = ∂P
∂y · M + P · 0 =
!∂QM
∂x = ∂Q
∂x · M + Q ∂M
∂x , also
6yM = 2yM
!+ 2xyM
0. Die Division durch y ergibt die Differentialgleichung
M
0= 2
x M bzw. dM
M = 2 dx x , also ist M(x) = x
2ein integrierender Faktor. Somit ist
(4x + 3y
2) · x
2+ 2xy · x
2· y
0= 0 exakt und besitzt ein Potential.
Aufgaben zum Abschnitt
2.41. Pr¨ ufen Sie auf Exaktheit und ermitteln Sie ggf. Potentialfunktionen:
(a) (2 Pkt.) xy
2+ y − xy
0= 0 ,
(b) (4 Pkt.) (2xe
y− 1) + (x
2e
y+ 1)y
0= 0 ,
2. (3 Pkt.) Bestimmen Sie ein Potential zu der folgenden Differentialgleichung aus Euler’s Publikation ”De integratione aequationum differentialum”, St. Petersburg 1760:
2axy − y
3+ (ax
2− 3xy
2)y
0= 0 .
3. (5 Pkt.) Finden Sie zu der folgenden Differentialgleichung einen integrierenden Faktor der Form M = M (x), bestimmen Sie ein Potential und die L¨ osungsschar:
(x + y
2) dx − 2xy dy = 0.
2.5 Anwendungsaufgaben und Prozessmodellierung
Bereits im Abschnitt
1.1hatten wir in die Modellierung von Prozessen durch Differentialgle- ichungen eingef¨ uhrt. Hier geben wir weitere Beispiele f¨ ur die drei dort schon genannten Wachs- tumsmodelle.
2.19 (Evolutionsgleichung, Wachstum ohne Grenzen) Die zugeh¨ orige Gleichung ist y
0= c · y(t) mit c ∈
R.
Beispiele solcher Prozesse sind der radioaktive Zerfall, die kontinuierliche Verzinsung eines Kap- itals, die bakterielle Vermehrung aber auch die sogenannte barometrische H¨ ohenformel. Das letztgenannte Beispiel soll etwas ausf¨ uhrlicher diskutiert werden. Gesucht ist dabei der Zusam- menhang zwischen dem Luftdruck p und der H¨ ohe h uber der Erdoberfl¨ ¨ ache unter der ideal- isierten Voraussetzung, dass die Temperatur in allen H¨ ohen gleich ist. Der Druckunterschied
∆p bei der H¨ ohenver¨ anderung ∆h ist gegeben durch
∆p = g ∆m
A , (∗)
wobei g die Erdbeschleunigung und ∆m die Masse der Lufts¨ aule der H¨ ohe ∆h mit Querschnitt A ist. Da nach der Gasgleichung
p · ∆V = ∆m · R · T,
also ∆m
A = p∆V
A · R · T = p · ∆h R · T ist, folgt aus (∗) die Gleichung
∆p = − g
RT p · ∆h . Mithin ist
dp
dh = − g RT p.
Bestimmen Sie die L¨ osung dieser Gleichung an!
2.20 (S¨ attigungsprozesse und Diffusion) In
1.3haben wir als Beispiel eines S¨ attigungs- prozesses die Aufladung eines Kondensators betrachtet und die Gleichung
y
0= k(y
∞− y(t)) mit k ≥ 0 und y
∞∈
Rerhalten.
Weitere Beispiele f¨ ur diese Differentialgleichung sind die folgenden:
a) Diffusionsprozesse: In einem Beh¨ alter m¨ ogen sich in zwei Kammern unterschiedlich konzen- trierte Salzl¨ osungen befinden. Wir setzen voraus, dass die Kammer mit der hochkonzentrierten L¨ osung ein sehr viel gr¨ oßeres Volumen als die andere Kammer hat. Dann wird die Konzentra- tion c(t) der Salzl¨ osung in der kleinen Kammer nach Entfernung der Zwischenwand durch die stattfindenden Diffusionsprozesse durch die Gleichung
c
0(t) = α(c
∞− c(t))
beschrieben. Hier ist c
∞die Konzentration in der großen Kammer.
b) Abk¨ uhlungsgesetz: Ein erhitzter K¨ orper gibt an seine Umgebung W¨ arme ab, seine Temperatur T (t) ¨ andert sich dabei nach dem Gesetz (Newton!)
T
0(t) = α(T
U− T(t)) . Hierbei ist T
Udie Umgebungstemperatur.
c) Mitscherlich–Gesetz: Der Hektarertrag E(x) einer Getreidesorte h¨ angt von der D¨ ungergabe x nach dem Gesetz
E
0(x) = α(E
∞− E(x))
ab. Dieser Zusammenhang wurde experimentell von
Mitscherlichin guter N¨ aherung best¨ atigt.
d) Chemische Reaktionen 1. Ordnung wurden bereits in Beispiel
1.5betrachtet.
e) Die Lernfunktion.
f) Ratensparen oder die Tilgung eines Kredits gen¨ ugen bei der Idealisierung stetiger Verzinsung der Gleichung y
0= αy + β mit α, β ≥ 0. Die Spiegelung der Zeitachse t → −t ¨ uberf¨ uhrt die Gleichung in obige Form.
2.21 (Logistisches Wachstum, Verhulst-Gleichung) Zur Modellierung des Bev¨ olke-rungswachstums y = y(x) unter Beachtung von Verdr¨ angungsprozessen kann unter Vorbehalten die logistische
Differentialgleichung
y
0(x) = γy(x) · (y
∞− y(x)) = αy − βy
2mit γ, y
∞, α, β ∈
R,
verwendet werden. Dies wurde erstmalig von dem Versicherungsmathematiker
Verhulst(∗1804–
†1849, belgischer Mathematiker) vorgeschlagen. Die Gleichung wurde bereits in Beispiel
2.3gel¨ ost, es ergab sich
y = α
β + c · e
−αx.
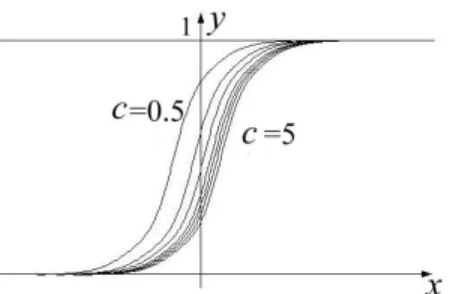
In Figur
5sind einige L¨ osungskurven f¨ ur α = β = 1 und verschiedene c > 0 dargestellt. Weitere Beispiele logistischen Wachstums sind die chemischen Reaktionen 2. Ordnung (s.
1.5), dieVerbreitung einer Epidemie ohne medizinische Behandlung oder Isolierung der Erkrankten oder auch die Verbreitung von Ger¨ uchten durch Mund–zu–Mund Propaganda.
Figure 5: Einige L¨ osungen der Verhulst-Gleichung
Zahlreiche weitere Prozesse, die sich durch obige Differentialgleichungen beschreiben lassen, findet man bei
H. Heuser, Gew¨ ohnliche Differentialgleichungen, und bei
H. Braun, Differen- tialgleichungen und Anwendungen.
Aufgaben zum Abschnitt
2.51. Ausbreitung eines Ger¨ uchtes: Potsdam hat 150000 Einwohner. Jede Person hat t¨ aglich ca. 2, 5 Kontakte mit anderen. Von einer Person geht ein Ger¨ ucht aus.
(a) (2 Pkt.) Stellen Sie eine Differentialgleichung zur mathematischen Beschreibung der Informationsausbreitung auf.
(b) (1 Pkt.) Nach welcher Zeit sind 90% aller Einwohner informiert?
3 Existenzs¨ atze
In diesem Abschnitt werden wir einen Existenz– und Eindeutigkeitssatz f¨ ur Anfangswertprob- leme mit Lipschitz–Bedingung beweisen. Dabei wird die L¨ osung als Grenzwert einer iterativ zu gewinnenden Funktionenfolge konstruiert werden. Als Werkzeug benutzen wir das Banach- sche Fixpunktverfahren, das ein universell einsetzbares Hilfsmittel zum L¨ osen von Gleichungen der verschiedensten Art, nicht nur von Differentialgleichungen, ist. Wir stellen das Verfahren zun¨ achst in seiner abstrakten Form ohne Bezug zu Differentialgleichungen dar.
3.1 Vollst¨ andige metrische R¨ aume
Definition 3.1 (metrische R¨ aume) Unter einem metrischen Raum versteht man ein Paar (E, d), wobei E eine nichtleere Menge und d : E × E →
Reine reellwertige Funktion, genannt Metrik bzw. Distanzfunktion, mit folgenden Eigenschaften ist:
a) Stets gilt d(x, y) ≥ 0, und es gilt d(x, y) = 0 genau dann, wenn x = y ist.
b) Stets gilt d(x, y) = d(y, x).
c) Stets gilt d(x, z) ≤ d(x, y) + d(y, z).
Der n–dimensionale Raum
Rnmit der euklidischen Abstandsfunktion d(x, y) =
v u u t
n
X
i=1
(x
i− y
i)
2f¨ ur x, y ∈
Rnist ein gut bekanntes Beispiel eines metrischen Raumes. F¨ ur unsere sp¨ ateren Anwendungen wird aber der wesentlich kompliziertere, unendlichdimensionale Raum wichtig sein:
Satz 3.2 Der Raum C[a, b] =
n
f : [a, b] →
R
f ist stetig auf [a, b]
o
mit d(f, g) = max
a≤t≤b
|f(t) − g(t)|, der sog. Tschebyscheff–Metrik, ist ein metrischer Raum.
Beweis. Wegen des Satzes vom Maximum ist die Abstandsfunktion d wohldefiniert, der Nach- weis der Eigenschaften a)-c) ist sehr einfach.
In metrischen R¨ aumen kann wie ¨ ublich eine Konvergenz von Folgen eingef¨ uhrt werden:
Definition 3.3 Es sei (E, d) ein metrischer Raum. Eine Folge (x
n) von Elementen x
n∈ E heißt konvergent gegen x ∈ E, wenn d(x
n, x) eine Nullfolge ist. Es gilt also
x = lim
n→∞
x
n⇐⇒ lim
n→∞