Praktikumsvorbereitung 212 Zähigkeit von Flüssigkeiten 231 Polarisiertes Licht

UNIVERSITÄT HEIDELBERG Physikalisches Praktikum für Naturwissenschaftler II B

Praktikumsvorbereitung 212 Zähigkeit von Flüssigkeiten 231 Polarisiertes Licht

241 Wechselstromeigenschaften von RCL-Gliedern (2-Tages-Versuch) 242 Spannungsverstärkung

246 Elektrolytischer Trog Erläuterungen zur Dosimetrie

Grundlagen zu den Versuchen der Radioaktivität 251/252 Statistik / Halbwertszeit

253 Absorption von E- und J-Strahlung

254 Absorption und Dosimetrie von Röntgenstrahlen 255 Röntgenspektrometer

Die Versuche werden in der Reihenfolge der Versuchsnummern durchgeführt.

Ausgabe 102007/20

I Vorbemerkung

Dieses Praktikum verfolgt haupts¨ achlich drei Ziele:

1. Sie lernen den Umgang mit physikalischen Messger¨ aten und Messappara- turen.

2. Kenntnisse, die Sie bereits erworben haben (oder noch erwerben werden) sollen durch die ¨ Uberpr¨ ufung im Experiment gesichert werden.

3. Das F¨ uhren eines Protokolls.

Zu diesem Zweck enth¨ alt das Praktikum Versuche mit ¨ uberschaubarer Theo- rie und einfachen Messapparaturen, deren Funktionsweise leicht einzusehen ist.

Nat¨ urlich ist damit nicht die Messgenauigkeit aufwendiger Apparaturen, wie sie in der Forschung verwendet werden, erreichbar. Das Ziel des Praktikums sind weniger pr¨ azise Ergebnisse, sondern Sie sollen lernen, die Einfl¨ usse, die die Messgenauigkeit begrenzen, zu erkennen und einzusch¨ atzen. Aus diesem Grund sollen bei der Auswertung die Ergebnisse stets mit einer Fehlerabsch¨ atzung an- gegeben werden.

Lesen Sie bei der Versuchsvorbereitung die Versuchsanleitung genau durch und uberlegen Sie, was bei der Versuchsdurchf¨ ¨ uhrung und Auswertung gemacht werden soll, welche Messwerte Sie brauchen, usw. Nur so k¨ onnen Sie z¨ ugig messen und vermeiden unn¨ otige Mehrarbeit durch Fehler beim Auswerten.

Gestalten Sie die Auswertung ¨ ubersichtlich und kennzeichnen Sie alle Anga- ben so, dass man sofort erkennen kann, worum es sich handelt (z.B.:

” aus der Zeichnung abgelesen:“,

” Literaturwert:“,

” Mittelwert der Messreihe:“). End- ergebnisse werden stets zusammen mit ihrem Fehler angegeben und besonders kenntlich gemacht, z.B. durch doppeltes Unterstreichen. Es ist unsinnig, den Fehler mit mehr als zwei Stellen anzugeben; das Ergebnis soll bis auf maximal zwei ungenaue Stellen angegeben werden (s.u.).

Bei graphischen Darstellungen von Messwerten ist folgendes zu beachten:

•

Die graphische Darstellung erfolgt grunds¨ atzlich auf Millimeterpapier bzw.

Logarithmenpapier.

•

Richtige Gr¨ oße w¨ ahlen. Nutzen Sie wenn m¨ oglich den vollen Bereich des mm-Papiers bzw. Logarithmenpapier.

•

Bei jeder Achse Messgr¨ oße und Maßeinheit angeben (Bsp.: T in

^◦

C, T [

^◦

C], T/

^◦

C).

•

Um sich das Eintragen der Messpunkte zu erleichtern, empfiehlt es sich eine sinnvolle Achseneinteilung zu w¨ ahlen (z.B. 1

^◦

C=0,5 cm oder 1 cm oder 2 cm zu w¨ ahlen und nicht 1

^◦

C=0,4 cm oder 2,5 cm)

•

Verbinden Sie beim Zeichnen von Kurven nicht einfach die Punkte mit- einander (

” Malen nach Zahlen“), sondern versuchen Sie die Streuung der Messwerte auszugleichen.

•

Befinden sich mehrere Kurven in einem Diagramm, so sind die einzelnen Kurven und Messwerte zu kennzeichnen (Legende hinzuf¨ ugen).

•

Jede Zeichnung, Tabelle und Diagramm muss mit einer Text- ¨ Uberschrift versehen werden.

II Vorbereitung

Um das Praktikum effizient durchzuf¨ uhren, ist eine gr¨ undliche Vorbereitung notwendig. Es ist nicht in Ihrem Interesse die Versuche

” starr“ nach Anleitung abzuarbeiten, ohne zu verstehen was Sie ¨ uberhaupt praktizieren. Die erfolgrei- che Teilnahme am Praktikum setzt voraus, dass Sie ein entsprechendes Kennt- nisniveau der mit den Versuchen verkn¨ upften Physik besitzen. Ob diese Kennt- nisse aus Ihrem Fundus oder aus Ihrer Vorbereitung stammen, ist nat¨ urlich belanglos. Informieren Sie sich vor Beginn der Versuchsdurchf¨ uhrung, ¨ uber die Stichpunkte, die bei den jeweiligen Versuchen unter dem Kapitel

” Vorberei- tung“ aufgelistet sind. Dabei reicht das alleinige Studium der Praktikumsan- leitung keinesfalls aus.

Die Praktikumsanleitung ist kein Lehrbuch!

Zu jedem Versuch sind daher zus¨ atzlich Literaturempfehlungen angegeben. Bei den meisten Versuchen ist es vollkommen ausreichend, wenn Sie sich mit Hilfe der Standardwerke (Walcher, Gerthsen, Bergmann-Sch¨ afer, etc.) auf die Versuche vorbereiten.

Um Ihnen die Vorbereitung zu erleichtern, sind neben den Stichpunkten zus¨ atz- lich noch Fragen in der Praktikumsanleitung aufgelistet.

Eine Versuchsdurchf¨ uhrung ohne ausreichende Vorbereitung ist klarerweise oh- ne Lerneffekt und nicht sinnvoll. Die Praktikantin oder der Praktikant muss in diesem Fall damit rechnen, nach Hause geschickt zu werden und den Versuch zu einem sp¨ ateren Zeitpunkt zu wiederholen.

Die folgenden Punkte fassen das Basiswissen zusammen, ¨ uber das Sie bei den

Versuchen verf¨ ugen sollten:

1. Mathematische Voraussetzungen - elementare Funktionen: Polynome, tri- gonometrische Funktionen, Logarithmus- und Exponential-Funktion - ele- mentares Differenzieren und Integrieren - gew¨ ohnliche Differentialgleichun- gen: Schwingungsgleichung/Kraftgesetz, Gleichung des nat¨ urlichen Wachs- tums.

2. Statistik und Fehler - Mittelwert, Standardabweichung, statistische und systematische Fehler, Fehler des Mittelwertes, Fehlerfortpflanzung, Gauß- verteilung.

3. Die 7 Basiseinheiten des SI-Systems : m, kg, s, A, K, mol, Cd.

4. Mechanik - Newtonschen Gesetze; Kr¨ afteparallelogramm - Erhaltungss¨ atze f¨ ur Translation und Rotation (Energie, Impuls, Drehimpuls) - Drehmo- ment, Tr¨ agheitsmoment u. Steinerscher Satz - Hooksches Gesetz, Elasti- sche Konstanten - Resonanzkurve - F¨ ur Studierende mit Hauptfach Phy- sik: Differentialgleichung des ged¨ ampften harmonischen Oszillators und typische L¨ osungen - Schallgeschwindigkeit, longitudinale und transversale Schwingungen.

5. Elektrizit¨ atslehre - Elementarladung und Ladungserhaltung; Faraday- Konstante, Avogadrokonstante, Stoffmenge - Ohmsches Gesetz, Kirch- hoffsche Regeln, spezifischer Widerstand - Messbereichserweiterung von Messinstrumenten - Kondensator, Kapazit¨ at. F¨ ur Studierende mit Haupt- fach Physik: Herleitung Kondensatorentladung, Bewegung einer Ladung im elektrischen Feld.

6. Optik - Reflexions- und Brechungsgesetz - Abbildung mit Linsen (geo- metrische Bildkonstruktion, Linsengleichung, Abbildungsmaßstab) - kon- tinuierliche und Linienspektren (qualitatives Verst¨ andnis) - Aufl¨ osungs- verm¨ ogen optischer Instrumente.

7. W¨ armelehre - W¨ arme, Zustandsgr¨ oßen (Temperatur, innere Energie,...), Zustandsgleichung des idealen Gases - 1. und 2. Hauptsatz, W¨ armebilanz, spezifische W¨ arme, Phasendiagramm, Dampfdruck - F¨ ur Studierende mit Hauptfach Physik: Van-der-Waals-Gleichung realer Gase, Verlauf der Iso- thermen im

p(V

)-Diagramm, Gesetz von Dulong-Petit, Freiheitsgrade und Gleichverteilungssatz, Clausius-Clapeyron Gleichung.

Die Kenntnis dieses Basiswissens erspart nat¨ urlich nicht das sorgf¨ altige Durch- arbeiten der Anleitung und die Vorbereitung der anderen Kapitel im Skript.

Insbesondere sollten Sie sich bei der Vorbereitung auch schon ¨ uber die Versuchs- durchf¨ uhrung, die Messmethoden und ¨ uber die Auswertung Gedanken machen.

Machen Sie sich bewusst, was und wie Sie messen werden und sch¨ atzen Sie ab, welchen Einfluss die Fehler der Einzelmessungen auf den Gesamtfehler haben (Bsp.: eine quadratische Gr¨ oße geht mit doppeltem Gewicht ein, als eine linea- re).

III Durchf¨ uhrung der Versuche

Sehen Sie sich die Apparatur gr¨ undlich an und machen Sie sich mit der Funk- tion aller Einzelteile vertraut. Spielen Sie die Messprozedur nach M¨ oglichkeit zun¨ achst qualitativ durch. Wenn Sie eine elektrische Schaltung herzustellen haben, kontrollieren Sie zun¨ achst selbst sorgf¨ altig, ob Sie keine Schaltfehler gemacht haben.

Vor Anlegen der Spannung muss die Schaltung vom Assistenten abgenommen werden.

Das Protokoll wird auch w¨ ahrend der Messungen l¨ uckenlos gef¨ uhrt, d.h. man soll keine großen Zwischenr¨ aume f¨ ur sp¨ atere Eintragungen lassen. Lassen Sie sich Zeit zum F¨ uhren eines ordentlichen Protokolls.

Ein Protokoll ist eine dokumentarische Darstellung des gesamten Versuchsab- laufs: Versuchsaufbau, Versuchsdurchf¨ uhrung, Erfassung und Auswertung von Messdaten, Diskussion der Ergebnisse. Die Qualit¨ at der bei einem Prakti- kumsversuch erzielten Ergebnisse h¨ angt nicht nur vom Messverfahren und der Genauigkeit der Messger¨ ate ab, sondern auch vom exakten experimentellen Arbeiten und der korrekten Protokollf¨ uhrung. Im Einzelnen soll das Protokoll enthalten:

1. ¨ Uberschrift und Versuchsnummer.

2. Einleitung: Formulierung der theoretischen Grundlagen, sowie physikali- scher Begriffe und Gesetze, die zum Verst¨ andnis des Versuchs erforderlich sind.

3. Das Protokoll muss so ausgelegt sein, dass Formeln, die f¨ ur den Versuch

ben¨ otigt werden, und zwar zun¨ achst in der Form, in der man sie als allge-

mein bekannt voraussetzen kann, dann die f¨ ur den Versuch n¨ otigen Um-

formungen. Damit man den Einfluss der Fehler der gemessenen Gr¨ oßen

auf das Versuchsergebnis leichter ¨ ubersehen kann, ist es zweckm¨ aßig, die

Formeln auf die Form

Versuchsergebnis = Funktion der direkt gemessenen Gr¨oßen

zu bringen. Alle Abk¨ urzungen, die in den Formeln vorkommen, m¨ ussen erkl¨ art sein, evtl. mit Hilfe der Skizze der Apparatur. Diesen Teil des Pro- tokolls schreiben Sie am besten schon zu Hause bei der Vorbereitung.

4. Skizze und Beschreibung der Versuchsanordnung (schematisch, Schaltplan bei elektrischen Schaltungen).

5. Knappe aber vollst¨ andige Angaben ¨ uber das Messverfahren, soweit dies nicht v¨ ollig selbstverst¨ andlich ist. Das Protokoll muss selbsterkl¨ arend sein!

6. Pr¨ asentieren Sie Ihre Messergebnisse in Form von Tabellen und Diagram- men, die klar und ausreichend beschriftet sein m¨ ussen. Kommentieren Sie diese mit einigen einleitenden S¨ atzen.

7. F¨ uhren Sie nach M¨ oglichkeit eine vorl¨ aufige Auswertung unmittelbar nach der Messung durch.

8. Bei der Auswertung m¨ ussen alle Zwischenrechnungen im Protokollheft aus- gef¨ uhrt werden. Vergleichen Sie, soweit vorhanden, Ihre Messergebnisse mit Literaturwerten. Bei der Fehlerabsch¨ atzung ber¨ ucksichtigen Sie nur die Faktoren, die Sie quantitativ kennen, also im allgemeinen die zuf¨ alli- gen Fehler und die mutmaßliche Genauigkeit der Eichung der Instrumente.

Es gen¨ugt vollst¨andig, sich auf die Faktoren zu beschr¨anken, die die Messgenauigkeit haupts¨achlich begrenzen.

Wenn Sie glauben, dass bei dem Versuch systematische Fehler auftreten, die Sie nicht quanti- tativ erfassen k¨ onnen, machen Sie hier¨ uber eine kurze Bemerkung. Achten Sie darauf, dass Sie alle zur Auswertung n¨ otigen Angaben aufgeschrieben haben (z.B. Barometerstand, Zimmertemperatur, etc.).

9. Zusammenfassung und kritische Diskussion. Fassen Sie am Schluss der Auswertung den gesamten Versuch mit einigen kurzen S¨ atzen zusammen.

Gehen Sie dabei auf die physikalische Fragestellung ein, das Messprinzip, die Messergebnisse und Fehler. Setzen Sie sich kritisch mit dem Versuch auseinander. Gibt es M¨ oglichkeiten den Versuchsaufbau oder das Mess- prinzip zu verbessern? Gibt es M¨ oglichkeiten die Fehler zu minimieren?

IV Messgenauigkeit und Fehlerabsch¨ atzung

Jede Messung kann nur mit einer begrenzten Genauigkeit durchgef¨ uhrt werden.

Zwei unabh¨ angige Messungen werden daher unterschiedliche Ergebnisse liefern.

Damit das Resultat einer Messung aussagekr¨ aftig ist, reicht es nicht aus nur den Zahlenwert des Messergebnisses anzugeben, sondern es muss auch eine Aussage

¨ uber die Messgenauigkeit gemacht werden. Dies geschieht z.B durch die Angabe eines Intervalls [x

−

∆x, x + ∆x] bzw.

x±

∆x, (1)

innerhalb dessen der

” wahre Wert“ mit einer bestimmten, anzugebenen Wahr- scheinlichkeit liegt.

Beispiel:

Die Bestimmung der Erdbeschleunigung mit einem Fadenpendel ergab folgen- des Resultat:

g

= (9, 81

±

0, 03) m/s

².

(2)

Die erste Zahlenangabe entspricht der besten Sch¨ atzung des

” wahren Wertes“.

Die zweite Zahl ist die Messgenauigkeit, die man h¨ aufig auch den

” Fehler“ des Messergebnisses nennt. Das Wort

” Fehler“ darf nicht falsch interpretiert wer- den. Diese Angabe gibt nicht etwa den Betrag an, um den das Messergeb- nis falsch ist, sondern stellt ein Unsicherheitsbereich dar, in dem der

” wahre Wert“ mit einer bestimmten Wahrscheinlichkeit liegt. Wie groß diese Wahr- scheinlichkeit ist, werden wir an sp¨ aterer Stelle diskutieren. Das Resultat der Messung ist dann wie folgt zu interpretieren:

Als beste Sch¨atzung f¨ur die Erdbeschleunigung wurde ein Wert von

9, 81

m/s²bestimmt. Der wahre Wert liegt mit einer bestimmten Wahr- scheinlichkeit im Intervall 9,78 m/s² ... 9,84 m/s²

.

Beachten Sie, dass es bei der Angabe des Messergebnisses und der Mess- unsicherheit keinen Sinn macht beliebig viele Nachkommastellen anzugeben (Taschenrechnerergebnis). Die Angabe

g

= (9, 8114587

±

0, 0298682) m/s

²

(3) ist sinnlos. Die Messgenauigkeit soll auf eine oder h¨ ochstens zwei signifikante Stellen gerundet werden und die letzte signifikante Stelle des Messergebnisses soll der selben Gr¨ oßenordnung entsprechen wie die Messgenauigkeit:

g

= (9, 81

±

0, 03) m/s

².

(4)

IV.1 Systematische und Statistische Fehler

Bei einer Messung k¨ onnen zwei Arten von Fehlern auftreten: Systematische Fehler und statistische (zuf¨ allige) Fehler. Systematische Fehler f¨ uhren dazu, dass das Messergebnis einseitig vom wahren Wert abweicht. Eine Wiederholung der Messung zeigt immer die gleiche Abweichung. Der Messwert ist entweder immer gr¨ oßer oder immer kleiner als der

” wahre Wert“. Im Gegensatz dazu schwanken bei zugrundeliegenden statistischen Fehlern, die Messwerte zuf¨ allig.

Mal sind sie gr¨ oßer, das andere mal kleiner als der

” wahre Wert“.

IV.1.1 Systematische Fehler

Systematische Fehler werden zun¨ achst durch die begrenzte Genauigkeit der Eichung der Instrumente verursacht. Bei Maßst¨ aben und Skaleneinteilungen ist die absolute Genauigkeit in der Regel etwas besser als die Ablesegenauigkeit.

An vielen Analogmessinstrumenten ist zus¨ atzlich noch eine Genauigkeitsklasse angegeben. Diese gibt den relativen Fehler des Messbereichsendwertes an. Wird z.B. mit einem Voltmeter der Klasse 1,5 innerhalb eines Messbereiches von 200 V eine Messung durchgef¨ uhrt, so betr¨ agt der Fehler 1,5% von 200 V, d.h.

3 V. Bei digitalen Instrumenten wird der Fehler in der Regel durch zwei Gr¨ oßen angegeben. Einen prozentualen Fehler, der sich entweder auf dem Messwert (Angabe

v.M. = vom Messwert

) oder auf den Messbereich (Angabe

v.E. = vom Endwert

) bezieht, sowie eine Fehlerangabe in der Form:

±

x Digits. Die letztere Angabe bedeutet, dass der Messwert um

±

x Einheiten der hintersten Stelle der Anzeige schwanken kann.

Beispiel: Mit einem digitalen Voltmeter mit der Genauigkeitsangabe

±

1, 5% v.M.,

±

3 Digits

wird ein Spannung von 12,00 V gemessen. Der absolute Fehler berechnet sich aus 1,5% vom Messwert sowie drei Einheiten der letzten Stelle: 1,5% von 12,00 V und 3

×

10 mV = 180 mV + 30 mV = 210 mV.

Desweiteren k¨ onnen systematische Fehler auch durch Umwelteinfl¨ usse wie Tem- peraturdriften, Einkopplung elektrischer Felder (z.B. Netzbrummen) etc. oder aber auch durch grunds¨ atzliche M¨ angel des Messverfahrens verursacht wer- den. Z.B. muss bei der Messung an einer hochohmigen Spannungsquelle der Innenwiderstand des Voltmeters ber¨ ucksichtigt werden (wichtig in Versuch 41

Temperaturmessung

). Geschieht dies nicht, treten systematische Abweichungen auf.

Nr.

x

[V] Nr.

x

[V] Nr.

x

[V] Nr.

x

[V]

1 5,070 6 5,039 11 5,053 16 5,038 2 5,073 7 5,043 12 5,054 17 5,058 3 5,031 8 5,034 13 5,078 18 5,040 4 5,024 9 5,034 14 5,071 19 5,071 5 5,034 10 5,079 15 5,050 20 5,051 Tabelle 1:

Ergebnisse einer 20-maligen Spannungsmessung.

F¨ ur die Absch¨ atzung von systematischen Fehlern lassen sich keine allgemeinen Regeln aufstellen. Es kommt im Einzelfall auf den Scharfsinn und die physika- lischen Kenntnisse des Experimentators an. Allerdings k¨ onnen systematische Fehler auch noch nach einer Messung ber¨ ucksichtigt werden. Sind die Ursachen bekannt, kann das Messergebnis entsprechend korrigiert werden.

IV.1.2 Statistische Fehler

Statistische Fehler entstehen durch zuf¨ allige Prozesse w¨ ahrend des Messprozes- ses. Ursachen hierf¨ ur sind z.B. das Rauschen eines Sensors oder thermodyna- mische Prozesse. Auch der Experimentator selbst kann eine statistische Fehler- quelle darstellen, da dieser stets die Messwerte aufnehmen, ablesen und inter- pretieren muss. All dies kann statistischen Schwankungen unterliegen. Z.B. wird man bei einer mehrmaligen Zeitmesung mit einer Stoppuhr aufgrund schwan- kender Reaktionszeiten verschiedene Ergebnisse erhalten.

Statistische Fehler haben die Eigenschaft, dass die Messergebnisse zuf¨ allig um den ” wahren Wert“ schwanken. Falls es m¨ oglich ist eine Messung mehrmals zu wiederholen, k¨ onnen solche Fehler mit Mitteln der Statistik aus der Streuung der Messwerte ermittelt werden.

Tabelle 1 zeigt ein Beispiel, bei dem eine elektrische Spannung

x

20-mal ge- messen wurde. Die Messwerte sind in Abbildung 1 eingetragen.

Gesucht ist ein Wert der die beste Sch¨ atzung des wahren Wertes darstellt. Mit

Hilfe statistischer ¨ Uberlegungen l¨ asst sich zeigen, dass dieser Bestwert dem

arithmetischen Mittelwert entspricht:

0 2 4 6 8 10 12 14 16 18 20 4,96

4,98 5,00 5,02 5,04 5,06 5,08 5,10 5,12 5,14

Einzelmessung Mittelwert

Messung

S p annung x [V]

Abbildung 1:

Darstellung von 20 unabh¨angigen Messungen einer elektrischen Spannung x. Die waagrechte Linie entspricht dem Mittelwert.

¯

x

= 1

N N i=1

x_i.

(6)

Dieser Wert ist in Abbildung 1 als waagrechte Linie eingezeichnet.

Neben der besten Sch¨ atzung des

” wahren Werts“ (Mittelwert) m¨ ussen wir zus¨ atzlich noch eine Aussage ¨ uber die Genauigkeit der Messung machen. Dazu wiederholen wir die Messung nicht nur 20-mal sondern viele Male mehr. In Abbildung 2 sind z.B. 3500 Einzelmessungen aufgetragen. Hier ist noch deut- licher zu erkennen, dass die Messwerte symmetrisch um einen mittleren Wert streuen. Die meisten Messwerte liegen in der N¨ ahe des Mittelwertes. Aber es gibt auch einzelne

” Ausreißer“, die weiter weg vom Mittelwert liegen. Um dies

0 500 1000 1500 2000 2500 3000 3500

4,96 4,98 5,00 5,02 5,04 5,06 5,08 5,10 5,12 5,14 5,16

Messung

S p annung x [V]

Abbildung 2:

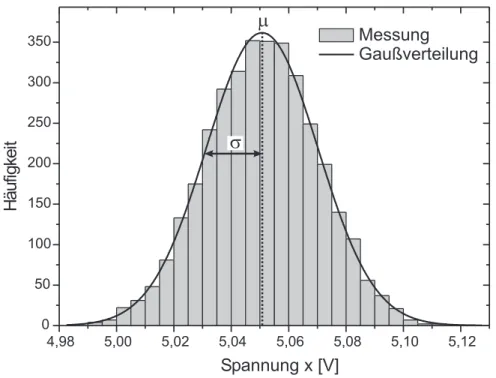
Darstellung von 3500 Messungen.

zu quantifizieren empfiehlt sich eine andere grafische Darstellung der Messwer- te in Form eines Histogramms. Dabei wird gez¨ ahlt, wieviele Einzelmessungen innerhalb eines bestimmten Intervalls aufgetreten sind und die entsprechende H¨ aufigkeit in Form eines S¨ aulendiagramms dargestellt. Solch ein Histogramm ist in Abbildung 3 dargestellt. F¨ ur sehr viele Messungen, streng genommen f¨ ur unendlich viele, n¨ ahert sich das Histogramm einer bekannten Verteilung, die als Normal- bzw. Gaußverteilung bezeichnet wird und durch

P(x) =

1

√

2π σ exp

−

(µ

−x)²

2σ

²

(7)

dargestellt wird. Die Gaußverteilung beschreibt eine Wahrscheinlichkeitsdichte,

4,98 5,00 5,02 5,04 5,06 5,08 5,10 5,12 0

50 100 150 200 250 300

350

Messung

Gaußverteilung

H äuf ig kei t

Spannung x [V]

s m

Abbildung 3:

Histogramm von 3500 Einzelmessungen. Die durchgezogene Linie zeigt die dazugeh¨orige Gaußverteilung mit den Parametern µ und σ.

Die Gaußverteilung ist hier nicht auf Eins normiert, sondern auf die Fl¨ache des Histogramms.

d.h.

_b

a

P(x)dx

(8)

gibt die Wahrscheinlichkeit an, dass ein Wert

x_i

gemessen wird, der im Intervall

a≤x_i≤b

liegt. Durch den Vorfaktor 1/

√

2π σ ist die Verteilung normiert, d.h.

_∞

−∞

P(x)dx

= 1. (9)

Dies ist sofort einsichtig, da mit 100%-iger Wahrscheinlichkeit irgendein Wert gemessen wird.

Eine Gaußverteilung besitzt zwei Parameter. Die Lage des Maximums der Ver- teilung wird durch die Gr¨ oße

µ

bestimmt und entspricht dem wahrscheinlich- sten Wert. Die Breite der Verteilung ist durch die Gr¨ oße

σ

(Abbildung 3) gegeben.

Falls die Messwerte tats¨ achlich gaußverteilt sind - und das ist sehr h¨ aufig der Fall - k¨ onnen wir annehmen, dass wir das Messergebnis einer großen Anzahl von Einzelmessungen, ebenfalls durch die Parameter

µ

und

σ

beschreiben k¨ onnen.

Wie sich zeigen l¨ asst, konvergiert der arithmetische Mittelwert ¯

x

f¨ ur eine große Anzahl von Einzelmessungen, gegen den wahrscheinlichsten Wert

µ

N→∞

lim

x

¯ = lim

N→∞

1

N

N i=1

x_i

=

µ.

(10)

Der Mittelwert stellt somit, wie wir bereits zuvor erw¨ ahnt haben, die beste Sch¨ atzung des

” wahren Werts“ dar.

Die Breite der Gaußverteilung wird durch

σ

bestimmt. Je gr¨ oßer

σ, desto brei-

ter ist die Verteilung und umso gr¨ oßer ist die Streuung der Messwerte um den wahrscheinlichsten Wert

µ. Wir k¨

onnen daher

σ

als ein Maß f¨ ur die Messge- nauigkeit interpretieren.

F¨ ur eine große Anzahl von Einzelmessungen l¨ asst sich zeigen, dass die Reihe (Wurzel aus der mittleren quadratischen Abweichung vom Mittelwert)

S_E

=

1

N N i=1

(¯

x−x_i

)

²,

(11)

gegen

σ

konvergiert:

N→∞

lim

S_E

=

σ.

(12)

S_E

wird als

Standardbweichung

einer Messreihe bezeichnet. Allerdings ist hier Vorsicht geboten.

S_E

ist nur dann ein guter Sch¨ atzwert f¨ ur die Streuung der Messwerte, wenn viele Einzelmessungen durchgef¨ uhrt werden. Bei nur wenigen Messungen wird die Streuung um den Mittelwert ¨ ubersch¨ atzt. Eine genauere Uberlegung zeigt, dass es besser ist als Maß f¨ ¨ ur die Streuung die Gr¨ oße

S_E

=

1

N−

1

N i=1

(¯

x−x_i

)

²,

(13)

zu verwenden.

S_E

wird auch als der

mittlere Fehler einer Einzelmessung

bezeichnet.

Intervall

±σ ±

2σ

±

3σ Wahrscheinlichkeit 68,3% 95,5% 99,7%

Tabelle 2:

Wahrscheinlichkeiten f¨ur unterschiedliche Werte von σ.

Wird eine Messung viele male wiederholt und als beste Sch¨ atzung des

” wahren Wertes“ der Mittelwert ¯

x

angegeben, so ist dieser nat¨ urlich genauer als der Messwert einer Einzelmessung und zwar um den Faktor 1/

√

N

:

S_M

=

1

N(N−

1)

N i=1

(¯

x−x_i

)

².

(14)

S_M

wird auch als

mittlerer Fehler des Mittelwerts

oder einfach als

Stan- dardfehler

bezeichnet.

Mit Hilfe von Gleichung (8) l¨ asst sich berechnen, mit welcher Wahrscheinlich- keit ein Messwert

x_i

im Bereich von

±σ

um den wahrscheinlichsten Wert

µ

schwankt:

_µ+σ

µ−σ

P(x)dx

= 68, 3 %. (15)

Die Wahrscheinlichkeit, dass bei einer Messung ein Wert im Bereich [µ

−σ, µ+σ]

auftritt betr¨ agt 68,3 %. Analog lassen sich auch die Wahrscheinlichkeiten f¨ ur den 2σ bzw. 3σ-Bereich bestimmen.

F¨ ur das Endergebnis einer Messung gibt man in der Regel den 1σ-Fehler

S_E

bzw.

S_M

an. Wird ein gr¨ oßerer Fehlerbereich angegeben (z.B. 3σ-Fehler) ist dies gesondert zu vermerken.

Beispiel:

F¨ ur die in Tabelle 1 angegebenen Messdaten errechnen sich die Ergebnisse wie folgt:

Mittelwert:

x

¯ = 1 20

20 i=1

x_i

= 5, 070 V +

...

+ 5, 051 V

20 = 5, 051 V. (16)

Fehler einer Einzelmessung:

S_E

=

1

19

20 i=1

(¯

x−x_i

)

²

= 0, 0173 V. (17)

Fehler des Mittelwerts:

S_M

=

1

20

·

19

20 i=1

(¯

x−x_i

)

²

= 0, 0039 V. (18) Das Endergebnis wird in der Form

¯

x±S_M

bzw.

x

¯

±

∆x (19)

angegeben. Anstatt

S_M

schreibt man auch h¨ aufig f¨ ur den Fehler einfach ∆x.

In unserem Beispiel erhalten wir

x

= (5, 051

±

0, 004) V. (20)

IV.2 Fehlerfortpflanzung

Bei vielen Praktikumsversuchen reicht es nicht aus nur eine physikalisch Gr¨ oße zu messen und dessen Fehler abzusch¨ atzen. In der Regel sollen aus dem Mess- ergebnis weitere Gr¨ oßen und dessen Genauigkeiten bestimmt werden.

Beispiel:

Es soll die Verlustleistung

P

eines ohmschen Widerstands

R, an dem die Span-

nung

U

anliegt, bestimmt werden. Dazu wird der Widerstand

R

und die Span- nung

U

gemessen und gem¨ aß

P

=

U²

R

(21)

die Verlustleistung berechnet. Da sowohl

R

als auch

U

nur mit einer bestimmten Genauigkeit bestimmt wurden, besitzt auch die daraus abgeleitete Gr¨ oße

P

eine endliche Genauigkeit.

Die Bestimmung dieser Genauigkeit geschieht mit Hilfe der Differentialrech- nung.

Wenn die direkt gemessenen Gr¨ oßen

x

und

y

um kleine Betr¨ age

dx

und

dy

ge¨ andert werden, ver¨ andert sich der Wert einer Funktion

f

=

f

(x, y) um

df

=

∂f

∂xdx

+

∂f

∂ydy

(vollst¨ andiges Differential) (22)

Hier bedeutet

∂f /∂x

die partielle Differentation der Funktion

f

nach

x, d.h.

die Ableitung von

f

nach

x, wobei die Variabley

als Konstante behandelt wird.

Wenn wir in dieser Gleichung die Differentiale

dx

und

dy

durch die Feh- ler ∆x und ∆y der direkt gemessenen Gr¨ oßen ersetzen wollen, m¨ ussen wir ber¨ ucksichtigen, dass sich die Fehler im Mittel teilweise kompensieren werden, wenn sie voneinander unabh¨ angig sind. Daher berechnet man den mittleren Fehler ∆f durch

” quadratische Addition“ nach dem Gaußschen Fehlerfortpflanzungsgesetz:

∆f =

∂f

∂x

∆x

₂

+

∂f

∂y

∆y

₂

(23) Hier und im Folgenden wird unter ∆x bei zuf¨ alligen Fehlern, der mittlere Feh- ler

S_M

nach Gleichung (14), bei systematischen Fehlern die oben diskutierten Uberlegungen verstanden. ¨

F¨ ur das oben angef¨ uhrte Beispiel (21) berechnet sich der Fehler wie folgt:

P

=

P(U, R)

(24)

∆P =

∂P

∂U

∆U

₂

+

∂P

∂R

∆R

₂

(25)

=

2

U R

∆U

₂

+

−U² R²

∆R

₂

(26) Die funktionale Abh¨ angigkeit der zu ermittelnden Gr¨ oße von den direkt gemes- senen hat h¨ aufig eine einfache Form. Es lohnt sich, die folgenden Formeln zu merken, die aus der allgemeinen Gleichung (23) folgen:

f

=

ax

∆f =a∆x (27)

f

=

x

+

y

∆f = (∆x)

²

+ (∆y)

²

(28)

f

=

xy, f

=

x/y

∆f

f

=

∆x

x

₂

+

∆y

y

₂

(29)

f

=

x^±b

∆f

f

=

|b|

∆x

x , b

= const. (30)

Merken Sie sich:

Farbe Frequenz [THz]

U_S

[V] ∆U

_S

[V]

gelb 518,7 -0,59 0,05

gr¨ un 549,0 -0,72 0,05

blau 687,9 -1,28 0,05

UV 821,3 -1,88 0,05

Tabelle 3:

Messdaten aus dem Versuch Fotoeffekt.

1. ” Der absolute Fehler einer Summe oder Differenz zweier Gr¨ oßen ist gleich der quadratischen Summe der absoluten Fehler der Summanden“.

2. ” Der relative Fehler des Produkts oder des Quotienten zweier Gr¨ oßen ist gleich der quadratischen Summe der einzelnen relativen Fehler“.

F¨ ur eine Fehlerabsch¨ atzung kann man statt den Gleichungen (28) und (29) auch die einfacheren Formeln ∆f = ∆x + ∆y bzw. ∆f /f = ∆x/x + ∆y/y verwenden.

Bevor man mit der Messung beginnt, sollte man sich mit Hilfe der Gleichun- gen (27) bis (30) ¨ uberlegen, durch welche Fehler die Genauigkeit der Messung haupts¨ achlich begrenzt wird. Man kann dann versuchen, die empfindlich in das Resultat eingehenden Fehler klein zu halten.

V Ausgleichsrechnung

Bei vielen Praktikumsversuchen kommt es h¨ aufig vor, dass die Steigung

m

einer linearen Funktion bestimmt werden muss. Hier im Praktikum k¨ onnen Sie dies auf zwei verschiedene Arten machen. Eine grafische Methode die hier erl¨ autert werden soll und eine rechnerische Methode die im n¨ achsten Abschnitt

Lineare Regression

diskutiert wird.

Wir wollen die Bestimmung einer Geradensteigung anhand eines Beispiels mit

Daten des Versuchs 35,

Fotoeffekt

erl¨ autern. Bei diesem Versuch wird mit Hil-

fe einer Fotozelle das Planck’sche Wirkungsquantum bestimmt werden. Da-

zu wird die Fotozelle mit Licht unterschiedlicher Frequenz (Farbe) beleuchtet

und gemessen, bei welcher Sperrspannung

U_S

der Fotostrom verschwindet. Die

Messdaten sind in Tabelle 3 zusammengefasst und in Abbildung 4 dargestellt.

500 550 600 650 700 750 800 850 -2,0

-1,8 -1,6 -1,4 -1,2 -1,0 -0,8 -0,6 -0,4

DU_S= -1,21 V DU_S= -1,37 V

Df = 323,8 THz

Fehlergerade

S per rs pannung U

S

[V ]

Frequenz [THz]

Df = 266,6 THz

Ausgleichsgerade

Abbildung 4:

Bestimmung der Steigung und dessen Fehler mit Hilfe einer Ausgleichsgerade (durchgezogen) und Fehlergerade (punktiert).

Das Planck’sche Wirkungsquantum l¨ asst sich aus der Steigung ∆U

_S/∆f

des Graphen gem¨ aß

h

=

e

∆U

_S

∆f

,

(31)

bestimmen, wobei

e

die Elementarladung darstellt. Um die Steigung zu be- rechnen legen wir zun¨ achst durch alle Messpunkte unter Ber¨ ucksichtigung der Messfehler eine Ausgleichsgerade. Dabei soll die Gerade so platziert werden, dass die Abweichung der einzelnen Messpunkte von der Gerade im Mittel mi- nimal wird.

F¨ ur das Planck’sche Wirkungsquantum berechnen wir:

h

=

e

∆U

_S

∆f =

e

1, 37 V

323, 8 THz = 6, 78

×

10

⁻³⁴

Js. (32) Um den Messfehler abzusch¨ atzen, legen wir durch die Messwerte eine zweite Gerade (Fehlergerade). Diese sollte maximal steil (oder maximal flach) sein aber noch innerhalb der Fehler der einzelnen Messungen liegen. Hieraus erhalten wir:

h

=

e

∆U

_S

∆f =

e

1, 21 V

266, 6 THz = 7, 27

×

10

⁻³⁴

Js. (33) Den Fehler sch¨ atzen wir aus der Differenz der beiden Steigungen ab. Somit lautet das Ergebnis dieser Messung:

h

= (6, 8

±

0, 5)

×

10

⁻³⁴

Js. (34)

VI Lineare Regression

Sofern bei einer Messung keine systematischen Fehler auftreten und die Messda- ten normalverteilt sind, gilt f¨ ur die Wahrscheinlichkeit, f¨ ur

x_i

den Wert

y_i

zu messen:

P_i

= 1

2π∆y

_i²

exp

−

1 2

y_i−f(x_i

)

∆y

_i

₂

,

(35)

wobei ∆y

_i

den Fehler von

y_i

bezeichnet. Die Gesamtwahrscheinlichkeit

P

alle

N

Messwerte zu messen, berechnet sich aus dem Produkt der Einzelwahrschein- lichkeiten

P_i

:

P

=

i

P_i

(36)

=

i

1 2π∆y

²_i

exp

−

1 2

i

y_i−f

(x

_i

)

∆y

_i

₂

.

(37)

Gesucht werden nun die Funktionsparameter von

f(x), f¨

ur die die Wahrschein-

lichkeit

P

maximal wird. Der erste Term in (37) stellt eine Konstante dar, die

nicht von den Funktionsparametern abh¨ angt. Somit wird die Wahrscheinlich-

keit maximal, wenn die Summe in der Exponentialfunktion minimal wird. Diese

Summe wird auch als

χ²

-Summe bezeichnet.

χ²≡

i

y_i−f

(x

_i

)

∆y

_{i 2}

.

(38)

Wir wollen uns im Folgenden auf lineare Funktionen beschr¨ anken, d.h.

f

(x) =

mx

+

n.

(39)

F¨ ur die Berechnung der Parameter

m

und

n

folgt dann:

χ²

(m, n) =

i

y_i−

(mx

_i

+

n)

∆y

_i

₂

= Minimum (40)

Durch diese Methode wird eine Gerade mit den Parametern

m

und

n

bestimmt, f¨ ur die die quadratischen Abst¨ ande der Messwerte

y_i

von der Geraden minimal wird. Durch den Faktor 1/∆y

²_i

werden zus¨ atzlich Messwerte mit einem kleinen Fehler ∆y

_i

st¨ arker gewichtet als Messwerte mit einem großen Fehler (Methode der kleinsten Fehlerquadrate, engl.: least square method).

F¨ ur die Berechnung von

m

und

n

m¨ ussen wir die Nullstellen der partiellen Ableitungen bestimmen:

∂χ²

∂m

=

−

2

i

x_iy_i−

(mx

_i

+

n)

∆y

²_i

= 0 (41)

∂χ²

∂n

=

−

2

i

y_i−

(mx

_i

+

n)

∆y

_i²

= 0. (42)

Au߬ osen nach den Funktionsparametern liefert:

m

= 1

ξ

1

∆y

_i²

x_iy_i

∆y

_i² − x_i

∆y

_i² y_i

∆y

_i²

(43)

n

= 1

ξ

x²_i

∆y

_i² y_i

∆y

_i² − x_i

∆y

_i²

x_iy_i

∆y

_i²

,

(44)

mit

ξ

= 1

∆y

²_i

x²_i

∆y

²_i − x_i

∆y

²_{i 2}

.

(45)

F¨ ur den Fall, dass alle Fehler gleich groß sind, d.h. ∆y

_i≡

∆y, vereinfachen sich diese Gleichungen:

m

=

xy−x¯

¯

y

x²−x²

(46)

n

=

x²y

¯

−x xy

¯

x²−x² .

(47)

Da die Messwerte

y_i

fehlerbehaftet sind, besitzen auch die Funktionsparameter einen Fehler den wir mit ∆m bzw. mit ∆n bezeichnen. Die Fehler berechnen sich nach der Gauss’schen Fehlerfortplanzung:

∆m

²

=

i

∂m

∂y_{i 2}

∆y

²_i

(48)

∆n

²

=

i

∂n

∂y_{i 2}

∆y

²_i.

(49)

Mit Hilfe von Gleichung (43) und (44) erhalten wir:

∆m

²

= 1

ξ

i

1

∆y

_i²

(50)

∆n

²

= 1

ξ

i

x²_i

∆y

_i²,

(51)

wobei

ξ

in Gleichung (45) definiert wurde. Sind wiederum alle ∆y

_i≡

∆y gleich groß, so vereinfachen sich diese Berechnungen zu

∆m

²

= ∆y

² N

1

x²−x²,

(52)

∆n

²

= ∆y

² N

x²

x²−x².

(53)

Die hier ausgef¨ uhrten ¨ Uberlegungen gelten nicht nur f¨ ur lineare Funktionen, sondern lassen sich auch auf andere Funktionen ¨ ubertragen.

Wir wollen wieder eine Beispielrechnung mit den Daten des Versuchs Fotoeffekt

(Tabelle 3) durchf¨ uhren. Hier entspricht

x

=Frequenz,

U_S

=

y

und ∆U

_S

= ∆y.

Da die Fehler der einzelnen Messungen alle gleich groß sind, m¨ ussen wir nur die Mittelwerte in Gleichung (46) berechnen:

¯

x

= 6, 442

×

10

¹⁴

Hz (54)

¯

y

=

−

1, 118 V (55)

xy

=

−

7, 815

×

10

¹⁴

VHz (56)

x²

= 4, 295

×

10

²⁹

Hz

²

(57)

x²

= 4, 150

×

10

²⁹

Hz

²

(58) F¨ ur die Steigung folgt:

m

=

xy−x¯

¯

y

x²−x²

=

−

4, 238

×

10

⁻¹⁵

V Hz. (59) Das Plank’sche Wirkungsquantum erhalten wir durch Multiplikation mit der Elementarladung:

h

= 1, 602

×

10

⁻¹⁹

C

·

4, 238

×

10

⁻¹⁵

V Hz = 6, 79

×

10

⁻³⁴

Js. (60) Den Fehler berechnen wir mit Hilfe von Gleichung (52):

∆m

²

= ∆y

²

N

(x

²−x²

)

,

(61)

wobei nach Tabelle 3 f¨ ur ∆y = 0, 05 V und f¨ ur

N

= 4 zu w¨ ahlen ist. Wir erhalten f¨ ur den Fehler von

h:

∆h =

e

∆m = 0, 33

×

10

⁻³⁴

Js. (62) Das Messergebnis lautet somit

h

= (6, 8

±

0, 3)

×

10

⁻³⁴

Js. (63)

Versuch 212

Z¨ ahigkeit von Fl¨ ussigkeiten

Abbildung 1:

Kugelfallviskosimeter und Kapillarviskosimeter.

I Messaufbau

•

Messzylinder aus Hartglas mit Messskaler, gef¨ ullt mit Polyethylengly- kol. Am unteren Teil des Zylinders befindet sich eine Pr¨ azisionskapillare (L¨ ange: 100 mm

±

0,5 mm , Kapillardurchmesser 1,5 mm

±

0,01 mm).

•

Kugeln aus

” Hostaform C“ mit folgenden Durchmessern: 2r = 2,0 / 3,0 / 4,0 / 5,0 / 6,0 / 7,144 / 8,0 / 9,0 mm (

±

1%). Die Dichte der Kugeln und die Dichte von Polyethylenglykol ist im Anhang angegeben.

•

Thermometer

•

Pinzetten, Bechergl¨ aser

•

Maßstab

•

Stoppuhren

II Literatur

•

Standardwerke der Physik: Gerthsen, Bergmann-Sch¨ afer, Tipler.

•

Demtr¨ oder,

Experimentalphysik 1, Springer Verlag.

•

W. Walcher,

Praktikum der Physik, B.G.Teubner Stuttgart.

•

Die Ableitung des Gesetz von Stokes finden Sie in W. Nolting,

Grundkurs:

Theoretische Physik, Band 1.

•

Homepage des Praktikums (http://www.physikpraktika.uni-hd.de).

III Vorbereitung

Bereiten Sie sich auf die Beantwortung von Fragen zu folgenden Themen vor: Reale Fl¨ ussigkeiten, innere Reibung, Z¨ ahigkeit (Viskosit¨ at), Temperatur- abh¨ angigkeit der Z¨ ahigkeit, laminare Str¨ omung, Stokes’sches Gesetz, Gesetz von Hagen-Poiseuille, Reynold’sches ¨ Ahnlichkeitsgesetz, Reynoldszahl, Turbu- lenz.

F¨ur Mathematiker und Physiker:

Berechnen Sie die Zeitabh¨ angigkeit

der Geschwindigkeit

v(t) einer in eine Fl¨

ussigkeit fallende Kugel. Stellen Sie

dazu mit Hilfe den an der Kugel angreifenden Kr¨ aften eine Differentialglei- chung auf und l¨ osen Sie diese unter Ber¨ ucksichtigung der Anfangsbedingung

v(0) = 0. Nach welcher Zeit ist die Geschwindigkeit der Kugel nahezu konstant?

Verst¨ andnisfragen:

1. Welche Kr¨ afte wirken auf eine fallende Kugel in einer Fl¨ ussigkeit und wie lautet die Differentialgleichung?

2. Wann erreicht die fallende Kugel ihre Endgeschwindigkeit?

3. Erl¨ autern Sie den Unterschied zwischen laminarer und turbulenter Str¨ omung.

4. Was besagt die Reynoldszahl? Wie groß ist die kritische Reynoldszahl f¨ ur eine Kugel die in einer Fl¨ ussigkeit f¨ allt und wie groß ist sie bei einer Rohr- str¨ omung?

5. Welche Kraft wirkt, wenn zwei parallele Platten, zwischen denen sich eine Fl¨ ussigkeit befindet, gegeneinander verschoben wird?

6. Was besagt das Gesetz von Hagen-Poiseuille?

7. Wie erh¨ oht sich der Fluss, wenn der Rohrdurchmesser bei konstanten Druck verdoppelt wird?

IV Aufgaben

1. Bestimmen Sie die Viskosit¨ at von Polyethylenglykol nach Stokes mit einem Kugelfallviskosimeter. Zus¨ atzlich ist die G¨ ultigkeitsgrenze des Stokes’schen Gesetzes zu ¨ uberpr¨ ufen, indem der ¨ Ubergang von laminarer zu turbulenter Umstr¨ omung der Kugel (Wirbelabl¨ osung) ermittelt wird.

2. Bestimmen Sie die Z¨ ahigkeit von Polyethylenglykol nach Hagen-Poiseuille mit dem Kapillarviskosimeter.

3. Vergleichen Sie die unter 1. und 2. gewonnenen Werte miteinander.

V Grundlagen

Bewegt sich ein K¨ orper mit

konstanter Geschwindigkeit

in einem fluiden oder gasf¨ ormigen Medium, so ist trotz der gleichf¨ ormigen Bewegung eine Kraft notwendig, um die Bewegung aufrecht zu erhalten. Dies scheint zun¨ achst wi- derspr¨ uchlich zum zweiten Newtonschen Gesetz zu sein, nach dem ein K¨ orper beschleunigt wird wenn auf ihn eine Kraft wirkt. Allerdings gilt dies nur im Va- kuum. Bei der Bewegung in einem Medium wirken zus¨ atzlich Reibungskr¨ afte, die dazu f¨ uhren, dass bei einer konstanten ¨ außeren Kraft, die Nettokraft ver- schwindet und sich der K¨ orper mit konstanter Geschwindigkeit bewegt.

Die Reibung wird bei Fl¨ ussigkeiten durch zwischenmolekulare Kr¨ afte verur- sacht. Diese f¨ uhrt dazu, dass bei der Bewegung eines K¨ orpers durch eine Fl¨ ussigkeit,

das Medium teilweise mitbewegt wird. Sie alle haben dies

schon beim morgendliche Fr¨ uhst¨ uck erlebt. Taucht man einen L¨ offel in ein Honigglas und zieht diesen dann senkrecht nach oben heraus, so bleibt auf- grund der Adh¨ asion eine d¨ unne Honigschicht am L¨ offel haften. Diese Schicht wechselwirkt mit benachbarten Molek¨ ulen, so dass beim Herausziehen ein gan- zer Honigklumpen mitbewegt wird. Die Reibungskr¨ afte lassen sich auch beim Umr¨ uhren von Honig oder Marmelade beobachten. Sie m¨ ussen eine deutliche Kraft aufwenden um den L¨ offel im Glas zu bewegen. Beim Umr¨ uhren von Kaf- fee ist dieser Effekt kaum wahrzunehmen. Offenbar h¨ angt die Reibungskraft von der

” Z¨ ahigkeit“ der Fl¨ ussigkeit ab.

F v

z

v´

Abbildung 2:

Gedankenexperi- ment zur Bestimmung der inne- ren Reibung. Die Fl¨ussigkeit soll sich schichtweise in Richtung der Kraft bewegen.

Um die Reibungskr¨ afte eines K¨ orpers in einer Fl¨ ussigkeit zu quantifizieren, betrachten wir die Anordnung nach Abbildung 2. Bei diesem (Gedanken)- Experiment befindet sich zwischen zwei gleich großen Platten, die im Abstand

z

parallel zueinander ausgerichtet sind, eine Fl¨ ussigkeit. Die untere Platte ruht.

Auf die obere Platte wird eine Kraft ausge¨ ubt, so dass sie sich mit konstanter

Geschwindigkeit

v

bewegt. Da an der oberen Platte aufgrund der Adh¨ asion ein Fl¨ ussigkeitsfilm haftet, bewegt sich dieser mit der Geschwindigkeit der Platte mit. Andererseits betr¨ agt die Geschwindigkeit des Fl¨ ussigkeitsfilms die an der unteren, ruhenden Platte haftet, Null. Aus Stetigkeitsgr¨ unden m¨ ussen daher die dazwischen liegenden Fl¨ ussigkeitsschichten mit unterschiedlichen Geschwindig- keiten aneinander vorbeigleiten. Die oberste Fl¨ ussigkeitschicht, die sich mit der Platte mitbewegt, ¨ ubt auf die darunter liegende Schicht eine Tangentialkraft aus und beschleunigt diese auf eine Geschwindigkeit

v

. So beschleunigt jede Schicht die darunterliegende und wird gleichzeitig von dieser nach dem Reak- tionsprinzip gebremst.

Experimentell zeigt sich, dass die Kraft

F

, die notwendig ist um die obe- re Platte zu bewegen, proportional zur Fl¨ ache

A

und zur Geschwindigkeit

v

und umgekehrt proportional zum Abstand

z

ist. Bewegt sich die obere Platte gleichf¨ ormig, so verschwindet die Nettokraft, d.h. die Reibungskraft

F_r

ist vom Betrag her gleich groß wie die auf die obere Platte ausge¨ ubte Kraft

F

. F¨ ur die (Newtonsche) Reibungskraft gilt dann:

F_r

=

η A v

z.

(1)

F¨ ur den allgemeinen Fall dr¨ uckt man diese Gleichung besser durch den Ge- schwindigkeitsgradienten

dv/dz

aus:

F_r

=

η A dv

dz.

(2)

Die Proportionalit¨ atskonstante

η

ist eine fl¨ ussigkeitsspezifische Gr¨ oße und wird als dynamische Viskosit¨ at, Z¨ ahigkeit oder meist auch nur als Viskosit¨ at bezeich- net. F¨ ur die Maßeinheit gilt nach Gleichung (1): [η]=Pa s.

¹

Das Newtonsche Reibungsgesetz gilt nat¨ urlich auch f¨ ur andere K¨ orpergeome- trien. Gleiten die einzelnen Fl¨ ussigkeitschichten aneinader ab ohne sich zu ver- mischen, spricht man von einer Schichtstr¨ omung oder von einer

laminaren Str¨omung. Bei großen Geschwindigkeiten und bei speziellen K¨

orpergeometri- en, ist dies nicht mehr der Fall. In der Fl¨ ussigkeit kommt es dann zur Bildung von Wirbeln, die die Schichten vermischen. Bei diesen

turbulenten Str¨omun- gen

ist der Sr¨ omungswiderstand viel gr¨ oßer als bei einer laminaren Str¨ omung, so dass das Newtonsche Reibungsgesetz seine G¨ ultigkeit (Abbildung 3) verliert.

Reynoldszahl

1In manchen Lehrb¨uchern findet man auch noch die Einheit Poise: 10 Poise=1 Pa s.

Abbildung 3:

Bewegung einer Kugel durch eine Fl¨ussigkeit. Links: Laminare Str¨omung bei der die Fl¨ussigkeit den K¨orper symmetrisch umfließt. Die einzel- nen Schichten gleiten aneinander ab ohne sich zu vermischen. Rechts: Turbu- lente Str¨omung bei hohen Geschwindigkeiten. In Folge der Wirbelbildung kommt es zu einer Vermischung der Fl¨ussigkeit.

Ob sich eine Fl¨ ussigkeit laminar oder turbulent verh¨ alt, l¨ asst sich mit Hilfe der dimensionslosen Reynoldszahl

absch¨atzen. Die Reynoldszahl ist

eine semiempirische Gr¨ oße, die das Verh¨ altnis der (doppelten) kinetischen Energie eines Volumenelements der Fl¨ ussigkeit, zu den Reibungsverlusten beschreibt:

Re

= 2E

_kin

W_Reibung.

(3)

Je gr¨ oßer die kinetische Energie der Fl¨ ussigkeit, desto instabiler wird die Str¨ omung. Andererseits wirkt die innere Reibung der Fl¨ ussigkeit d¨ ampfend und somit stabilisierend auf die Str¨ omungsbewegung. Bei kleinen Reynolds- zahlen ist

E_kin≤W_Reibung

und die Fl¨ ussigkeit str¨ omt laminar. Oberhalb eines kritischen Wertes

Re_kr

tritt dagegen eine turbulente Str¨ omung auf. In diesem Fall gilt:

E_kinW_Reibung

.

F¨ uhrt man eine charakteristische L¨ ange

L

ein, die die Geometrie des Str¨ omungssystems beschreibt, so l¨ asst sich die Reynoldszahl auch wie folgt darstellen:

Re

=

ρvL

η ,

(4)

wobei

v

die mittlere Str¨ omungsgeschwindigkeit und

ρ

die Dichte der Fl¨ ussigkeit beschreibt. Bei einer Rohrstr¨ omung ist f¨ ur

L

der Rohrdurchmesser einzusetzen.

Bei der Bewegung einer Kugel durch eine Fl¨ ussigkeit beschreibt

L

den Durch-

messer der Kugel.

Die kritische Reynoldszahl h¨ angt vom jeweiligen Experiment ab. Beispiels- weise zeigt sich experimentell, dass bei der Str¨ omung einer Fl¨ ussigkeit durch ein Rohr, der ¨ Ubergang von laminarer zur turbulenter Str¨ omung bei einer Reynoldszahl von

Re_kr

=2300 erfolgt. Nat¨ urlich ist der ¨ Ubergang nicht scharf, so dass auch bei der kritischen oder h¨ oheren Werten der Reynoldszahl noch ein laminarer Fluss m¨ oglich ist. Allerdings reicht ab der kritischen Reynoldszahl bereits eine kleine St¨ orung aus, um die Str¨ omung in eine turbulente umschlagen zu lassen. Bei der Bewegung einer Kugel durch eine Fl¨ ussigkeit, erfolgt der Ubergang von laminarer zu turbulenter Str¨ ¨ omung bereits bei viel kleineren Reynoldszahlen. Experimentell zeigt sich, dass hier die kritische Reynoldszahl ungef¨ ahr Eins betr¨ agt:

Re_kr≈

1

Bestimmung der Viskosit¨at mit einem Kugelfallviskosimeter nach Stokes

Bewegt sich eine Kugel mit dem Radius

r

mit konstanter Geschwindig- keit

v

durch eine Fl¨ ussigkeit, so wirkt auf sie die Reibungskraft:

F_r

= 6πηrv. (5)

Diese Gleichung wird als das Gesetz von Stokes bezeichnet. Die Herleitung folgt aus dem Newtonschen Reibungsgesetz (1) und findet sich in den meisten Lehrb¨ uchern der theoretischen Mechanik. Zu beachten ist, dass das Stokes’sche Gesetz eine N¨ aherung f¨ ur laminare Str¨ omungen mit

Re <1 ist und nur f¨

ur unendlich ausgedehnte Fl¨ ussigkeiten g¨ ultig ist. Wir werden an sp¨ aterer Stelle daher noch Korrekturen anbringen m¨ ussen.

Unter Ausnutzung des Stokes’sche Gesetz l¨ asst sich die Viskosit¨ at

η

einer Fl¨ ussigkeit bestimmen. Beim Kugelfallviskosimeter wird eine Kugel mit dem Radius

r

in die Fl¨ ussigkeit, dessen Viskosit¨ at bestimmt werden soll, fallen gelas- sen. Nach einer Beschleunigungsphase bewegt sich die Kugel mit einer konstan- ten Sinkgeschwindigkeit

v_s

. In diesem Fall verschwinden alle an die Kugel an- greifende Kr¨ afte, d.h. Gewichtskraft

F_g

=

ρ_kV_kg, AuftriebskraftF_a

=

−ρ_fV_kg

und Reibungskraft

F_r

=

−

6πηrv

_s

heben sich auf:

F_g

+

F_a

+

F_r

= 0. (6)

Dabei beziehen sich die mit

k

indizierten Gr¨ oßen auf die Kugel und die mit

f

indizierten, auf die Fl¨ ussigkeit. Einsetzen der einzelnen Kr¨ afte und Aufl¨ osen

F

r

F

_a

F

_g

Messbeginn

Messende

Thermometer

L t

v

_s

L

=

t

Abbildung 4:

Bestimmung der Visko- sit¨at einer Fl¨ussigkeit mit einem Kugel- fallviskosimeter. Bewegt sich die Kugel mit konstanter Geschwindigkeit, heben sich alle angreifenden Kr¨afte auf.

nach

η

liefert f¨ ur die Viskosit¨ at der Fl¨ ussigkeit:

η

= 2

9

g

(ρ

_k−ρ_f

)

v_s r².

(7)

Durch Messung der Sinkgeschwindigkeit

v_s

kann so die Viskosit¨ at bestimmt werden.

Bestimmung der Viskosit¨at nach Hagen-Poiseuille: Laminare Rohrstr¨omung

Eine andere Methode die Viskosit¨ at einer Fl¨ ussigkeit zu bestimmen, ist die Mes-

sung des Volumenstroms einer laminaren Rohrstr¨ omung. Betrachten wir dazu

ein Rohr der L¨ ange

L

und Radius

R

(Abbildung 5). Damit eine Str¨ omung ¨ uber-

haupt m¨ oglich ist, muss an den Stirnfl¨ achen eine Druckdifferenz ∆p =

p₁−p₂

vorhanden sein. Im Fall einer laminaren Str¨ omung kann die Bewegung der

Fl¨ ussigkeit wieder als Schichtstr¨ omung interpretiert werden, wobei bei einem

Rohr mit kreisf¨ ormigen Querschnitt, einzelne Zylinderm¨ antel aneinander ab-

gleiten. Auf einen koaxialen Teilzylinder in der Fl¨ ussigkeit mit dem Radius

p

₁

p

₂

L

2R

Abbildung 5:

Laminare Rohrstr¨omung. Unter dem Einfluss der Druckdifferenz p₁−p₂ str¨omt die Fl¨ussigkeit in einem zylindrischen Rohr mit einem para- belf¨ormigen Geschwindigkeitsprofil.

r < R, wirkt aufgrund der Druckdifferenz eine Kraft

F_p

=

πr²

(p

₁−p₂

). (8) Andererseits wirkt auch die Newtonsche Reibungskraft

F_r

=

−

2πrLη

dv

dr.

(9)

Bei einer station¨ aren Str¨ omung, bei der sich die einzelnen Schichten mit konstanter Geschwindigkeit bewegen, muss die Nettokraft verschwinden, d.h.

F_p

=

F_r

:

−

2πrLη

dv

dr

=

πr²

(p

₁−p₂

). (10) Hieraus folgt f¨ ur den Geschwindigkeitsgradienten

dv

dr

=

p₁−p₂

2ηL

r.

(11)

Integration ¨ uber

r

unter Ber¨ ucksichtigung der Randbedingung

v(R) = 0, liefert

f¨ ur die Geschwindigkeitsverteilung in der Fl¨ ussigkeit

v(r) =p₁−p₂

4ηL (R

²−r²

). (12)

Diese Gleichung stellt ein Rotationsparaboloid dar. Die Fl¨ ussigkeit besitzt dem- nach das in Abbildung 5 gezeigte parabolische Geschwindigkeitsprofil.

Um den Volumenstrom, d.h. die Fl¨ ussigkeitsmenge, die pro Zeiteinheit durch die Querschnittsfl¨ ache des Rohres str¨ omt, zu bestimmen, m¨ ussen wir ¨ uber die

gesamte Querschnitts߬ ache integrieren:

dV dt

=

R

0

2πrv(r)dr =

π(p₁−p₂

)R

⁴

8ηL

.

(13)

Beachten Sie die Abh¨ angigkeit von

R⁴

. Eine Verdopplung des Rohrradius ver- sechzehnfacht den Volumenstrom!

Gleichung (13) wird nach dem deutschen Wasserbau-Ingenieur Gotthilf Hein- rich Ludwig Hagen und nach dem franz¨ osischen Arzt und Physiologen Poiseuil- le, auch als das Gesetz von Hagen-Poiseuille bezeichnet.

Sind L¨ ange und Radius des Rohres und die Druckdifferenz bekannt, so kann durch Messung des Volumenstroms die Viskosit¨ at bestimmt werden.

VI Durchf¨ uhrung des Versuchs

1. Bestimmung der Viskosit¨at nach Stokes mit einem Kugelfallvis- kosimeter

Bei dem Versuch wird die Fallzeit ∆t der Kugel zwischen zwei im Ab- stand ∆s angebrachten Markierungen gemessen. Die Messungen sind entweder mit steigendem oder mit fallendem Kugelradius durchzuf¨ uhren. Notieren Sie sich die Temperaturen der Fl¨ ussigkeiten w¨ ahrend der Messung mit den kleinsten Kugeln.

Legen Sie die Fallstrecke der Kugeln fest und notieren Sie diesen Wert. Der Abstand der ersten Messmarke von der Fl¨ ussigkeitsoberfl¨ ache ist so zu w¨ ahlen, dass sich die Kugel beim Durchlaufen der ersten Messmarke, mit konstanter Geschwindigkeit bewegt. Lassen Sie von jedem Durchmesser 5 Kugeln die Fall- strecke m¨ oglichst in der Rohrachse durchfallen. Zur Bestimmung der Fallzeit dienen die zahlreich beigegebenen Handstoppuhren. Bei den kleinsten Durch- messern empfiehlt sich eine Simultanmessung von mehreren Kugeln durch- zuf¨ uhren. Damit sich die Messzeiten bei den kleinen Kugeln nicht ¨ uber einen zu langen Zeitraum erstrecken, k¨ onnen Sie hier eine k¨ urzere Fallstrecke verwen- den. Der Innendurchmesser des Kugelfallgef¨ aßes ist am Viskosimeter angege- ben. Vergessen Sie nicht diesen Wert in Ihr Protokoll aufzunehmen.

Sie m¨ ussen bei der Durchf¨ uhrung des Experiments unbedingt darauf achten,

dass an den Kugeln keine Luftbl¨ aschen haften. Sortieren Sie daher vor dem

Einbringen der Kugeln in das Fallgef¨ aß, zun¨ achst einige Kugeln des jeweiligen

Durchmessers in ein Becherglas und geben Sie etwas Fl¨ ussigkeit mit hinein.

Schwenken Sie das Becherglas vorsichtig um, so dass die Kugeln vollst¨ andig benetzt sind und keinerlei Luftbl¨ aschen mehr daran zu erkennen sind. Mit der Pinzette werden dann die mit der Fl¨ ussigkeit benetzten Kugeln in das Fallgef¨ aß gegeben.

2. Bestimmung der Viskosit¨at nach Hagen-Poiseuille mit einem Kapillarviskosimeter

Stellen Sie unter den Ausfluss der Kapillare ein Becherglas und ¨ offnen Sie den Hahn, indem Sie ihn parallel zur Kapillare drehen. Warten Sie nach dem ¨ Offnen so lange ab, bis sich die Str¨ omungsverh¨ altnisse stabilisiert haben und eine gleichm¨ aßige Tropfenfolge zu beobachten ist. Sobald dies der Fall ist, stellen Sie einen leeren Messzylinder unter den Ausfluss, star- ten die Stoppuhr und notieren die Anfangsh¨ ohe

h_A

der Fl¨ ussigkeitss¨ aule.

F¨ uhren Sie dies am besten gemeinsam mit Ihrem Partner durch, indem einer die H¨ ohe des Fl¨ ussigkeitspiegels abliest und der andere gleichzeitig den Messzylinder unterstellt und die Stoppuhr startet. Messen Sie f¨ ur das Gemisch 1 die Ausstr¨ omzeit von ca. 20 cm

³

bis 25 cm

³

der Fl¨ ussigkeit.

Nachdem diese Mengen ausgestr¨ omt sind, schließen Sie den Hahn und messen erneut die H¨ ohe des Fl¨ ussigkeitsspiegels

h_E

. Notieren Sie die Raumtemperatur.

Achtung: Da eine Wiederholung der Messung relativ lange dauert, bei einer einmaligen Messung aber die M¨ oglichkeit eines Irrtums besteht, m¨ ussen zur Kontrolle Zwischenwerte des Volumens aufgenommen werden. Notieren Sie daher bei laufender Stoppuhr die Ausflusszeit bei 5, 10, 15, 20, 25 cm

³

.

Achten Sie unbedingt nach Beendigung dieser Messung, dass der Hahn der Kapillare geschlossen ist.

VII Auswertung

Zu 1)

•

Nach Gleichung (7) ergibt sich f¨ ur die Sinkgeschwindigkeit

v_lam

einer Kugel unter dem Einfluss Stokes’scher Reibung bei laminarer Str¨ omung:

v_lam

= 2

9

g ρ_k−ρ_f

η r².

(14)

Tr¨ agt man den Mittelwert der Sinkgeschwindigkeit gegen das Quadrat des Radius auf, so ergibt sich im G¨ ultigkeitsbereich des Stokes’schen Gesetz ei- ne Gerade. Da allerdings die Dichte der Kugeln etwas vom Radius abh¨ angt, ist es besser das Verh¨ altnis ¯

v/(ρ_k−ρ_f

) gegen

r²

aufzutragen, wobei ¯

v

den Mittelwert ihrer gemessenen Sinkgeschwindigkeit bei den jeweiligen Radi- en bezeichnet.

•

Das Stokes’sche Gesetz ist nur f¨ ur eine unendlich ausgedehnte Fl¨ ussigkeit g¨ ultig. Wegen des endlichen Durchmessers des Fallrohres, wird die Sink- geschwindigkeit verf¨ alscht und systematisch zu klein gemessen, wobei der Fehler mit wachsendem Kugelradius zunimmt. Dies l¨ asst sich durch die Ladenburg’sche Korrektur

λ

im Stokes’schen Gesetz ber¨ ucksichtigen:

F_r

= 6πηrvλ (15)

mit

λ

=

1 + 2, 1

r R

,

(16)

wobei

R

den Radius des Fallrohres beschreibt. Bei der Korrektur m¨ ussen daher die Sinkgeschwindigkeiten mit dem Faktor

λ

multipliziert werden.

Uberlegen Sie sich, ob im Rahmen der Messgenauigkeit der Sinkgeschwin- ¨ digkeiten der einzelnen Kugeln, eine Korrektur sinnvoll ist und tragen Sie diese gegebenenfalls in das gleiche Diagramm mit ein.

•

Legen Sie durch den linearen Bereich eine Gerade die durch den Ursprung geht und bestimmen Sie aus der Steigung die Viskosit¨ at. Berechnen Sie mit diesem Viskosit¨ atswert f¨ ur jeden Kugelradius nach Gleichung (14) den zu jedem Messwert

v

geh¨ orenden theoretischen Wert

v_lam

, d.h. die Werte, die auf der extrapolierten Anfangsgeraden liegen. Zus¨ atzlich ist f¨ ur jeden Kugelradius (Durchmesser

d) die Reynoldszahl

Re

=

ρ_fv d

η

(17)

zu berechnen. Dabei beschreibt

v

die bei dem jeweiligen Kugelradius ge- messene Sinkgeschwindigkeit.

Tragen Sie das Verh¨ altnis

v/v_lam

gegen log

Re

auf (einfach logarithmisches

Papier mit drei Dekaden) und bestimmen Sie die Stelle, an denen ein Knick

in der Kurve auftritt. An dieser Stelle verliert das Stokes’sche Gesetz seine

G¨ ultigkeit und die laminare Str¨ omung schl¨ agt in eine turbulente Str¨ omung

um. Sch¨ atzen Sie den Zahlenwert f¨ ur die kritische Reynoldszahl ab.

Zu 2)

•

Berechnen Sie die Z¨ ahigkeit nach Hagen-Poiseuille. Beachten Sie, dass der Druck in der Kapillare durch die H¨ ohe der Fl¨ ussigkeitss¨ aule bestimmt wird. W¨ ahrend des Abfließens der Fl¨ ussigkeit ¨ andert sich in der S¨ aule die Fl¨ ussigkeitsh¨ ohe und damit die Druckdifferenz in der Kapillare. F¨ ur die Berechnung der Druckdifferenz ist daher der Mittelwert von Anfangs- und Endh¨ ohe

h_A, h_E

zu benutzen.

•

Berechnen Sie die Reynoldszahl der Kapillare und ¨ uberzeugen Sie sich, dass laminare Str¨ omung vorlag.

•

Vergleichen Sie die gemessenen Viskosit¨ aten nach Hagen-Poiseuille mit den Werten nach Stokes (Fehlergrenzen absch¨ atzen!). Achten Sie darauf, dass die Temperaturen u.U. verschieden sind.

VIII Anhang

Dichte der Kugeln:

∅

2 mm bis 7,144 mm 1,375 g/cm

³< ρ <1,380 g/cm³

∅

8 mm 1,355 g/cm

³< ρ <1,360 g/cm³

∅

9 mm 1,360 g/cm

³< ρ <1,365 g/cm³

(Bitte die Werte mit den Angaben auf dem Kugelsortierkasten vergleichen.)

17 18 19 20 21 22 23 24 25 26

1,144

1,146

1,148

1,150

1,152

1,154

Dic hte [g/c

3

m ]

T emperatur [°C]

Dichte von Polyethylenglykol

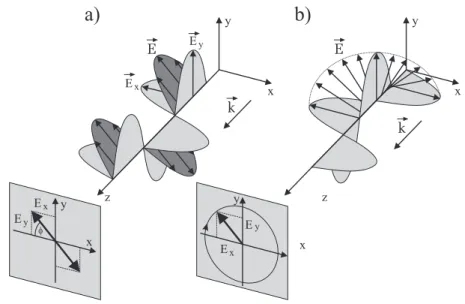
Versuch 231 Polarisiertes Licht

Abbildung 1: Versuchsaufbau.

I Messaufbau

•

Drehtisch mit Winkeleinteilung und drei Halterungen

•

Diodenlaser (

λ

= 670

nm

)

•

Detektor (Fotoelement BPY 63) mit Verst¨ arker

•

Linearanalysator,

λ/

4-Pl¨ attchen sowie zwei planparallele Glasplatten (BK7 oder SF6 mit den Brechungsindizees n

_BK7

= 1,514 und n

_SF6

=1,796 f¨ ur

λ

=670 nm.

II Literatur

•

W. Walcher, Praktikum der Physik, B.G.Teubner Stuttgart.

•

Bergmann-Sch¨ afer, Experimentalphysik, Band III,

•

Homepage des Praktikums (http://www.physikpraktika.uni-hd.de).

III Vorbereitung

Bereiten Sie sich auf die Beantwortung von Fragen zu folgenden Themen vor: Grundlagen der geometrischen Optik (Brechung, Reflexion), Wellenoptik (Eigenschaften von elektromagnetischen Wellen, Huygen’sches Prinzip), linear, zirkular und elliptisch polarisiertes Licht, Polarisation durch Reflexion (Fres- nel’sche Formeln, Gesetz von Brewster), Polarisation durch Doppelbrechung (

λ

/4-Pl¨ attchen).

Verst¨ andnisfragen:

1. Warum kommt bei senkrecht zueinanderstehenden Linearpolarisationsfil- tern kein Licht durch?

2. Was passiert bei drei aufeinanderfolgenden Polarisationsfiltern mit den Po- larisationsrichtungen 0

^◦

-45

^◦

-90

^◦

, wenn unpolarisiertes Licht einf¨ allt? Wie viel Licht kommt ungef¨ ahr durch?

3. Wozu verwendet man ein

λ

/4-Pl¨ attchen? Worauf beruht das Funktions- prinzip solch eines Pl¨ attchens?

4. Zwei Polfilter stehen senkrecht zueinander. Wie muss ein

λ

/4-Pl¨ attchen zwischen die zwei Polfilter eingef¨ ugt werden, damit die durchgelassene Lichtintensit¨ at maximal wird?

5. Wie ist der Brewsterwinkel definiert? Welche Eigenschaften hat im Brew- sterwinkel reflektiertes und transmittiertes Licht?

IV Aufgaben

1. ¨ Uberpr¨ ufen Sie mittels Brewster’scher Reflexion die Markierung der Schwingungsebene am Laser.

2. Messen Sie die Intensit¨ at des an einer Glasscheibe reflektierten und trans-

mittierten Lichts in Abh¨ angigkeit des Einfallswinkels und der Polarisati-

onsrichtung.