Grundlagen der Informationsverarbeitung

Strukturwissenschaft

Grundlagen der Informationsverarbeitung

früher: Grundlagen der Informationstechnik I

Grundlagen der Informationstechnik II à heute: Grdlgn. der Informationsübertragung Vorlesung basiert auf Lehrbuch

S. Wendt – „Nichtphysikalische Grundlagen der Informationstechnik“

Technik à stellt Produkte (Erzeugnisse) bereit

Produkt Zweckbestimmung,

Arbeitsweise

materiell-energetische Erscheinung (Form)

Funktion Rolle in einem Prozess

Rolle an einem Prozess (Vorgang) an dem der

Nutzer beteiligt ist

Prozess, der dem Menschen dient materiell-energetisch

z.B. ernähren, kleiden, wohnen, reisen

informationell z.B. unterhalten, belehren, warnen, berechnen, steuern

Informationstechnik Übertragungstechnik

z.B. Telefon, Fernehen

Verarbeitungstechnik z.B. Computer, Robotersteuerung

physikalisch: materiell-energetisch, auch Chemie, Biologie nicht physikalisch: mathematisch

logisch

erkenntnistheoretisch (philosophisch)

Bei einem informationsverarbeitenden technischen Gebilde (Produkt, Gerät, Apparat, Schaltung, System) kann die Verbindung zwischen seiner Erscheinung (materielle- energetische Struktur) und seiner Funktion (Rolle, Zweck) nur durch Interpretation (Zuordnung von Bedeutung zur Form à Signal) hergestellt werden.

Materiell-energetische Sachverhalte werden als Ausdruck informationeller Sachverhalte interpretiert.

Pilosophisch

}

Informationsverarbeitungsaufgabe

zugrundeliegender Formalismus

Produkt der Inf.-Verarbeitung (technisches Gerät) Bsp.: w = 25

Formalismus: w als Summe von Zweierpotenzen darstellbar

4 3 2 1 0

16 8 1 1 2 1 2 0 2 0 2 1 2 w= + + = ⋅ + ⋅ + ⋅ + ⋅ + ⋅ Koeffizienten zu Binärvokabel (Tupel) zusammengefasst:

w = 11001(2)

à ' ' ' ' ' (Implementierung) (hell bedeutet 1 ; dunkel bedeutet 0)

a) Der Informationsbegriff und sein Umfeld

[Was ist Information, Symbol, Signal, Interpretation, Nachricht, Datum]

Information: Wissen, Wissbares

„Was können wir wissen ?“ (Fragestellung der Erkenntnistheorie) 1.1 Erkenntnistheoretische Betrachtungen

1.1.1 Wahrnehmung

Ausgangspunkt: menschliche Erfahrungen Was man

• über seine Sinnesorgane zufließend erlebt

• als aus dem eigenen Inneren kommend erlebt Wir denken in Ursache -Wirkungszusammenhängen:

à Was sind Ursachen unserer Erfahrungen ? à (Sinnes-) Reize aus der Außenwelt

à innere Reize, sogar von Erfahrungen stammend Niedrigste Stufe: reine Empfindung

später direkte Verarbeitung Interpretation

Realisierung

Empfindungen Erkanntes Bedeutungen

wahrnehmen

empfinden erkennen interpretieren

Reize

auslösen Erfahrungen

Ergebnis des Empfindens: unstrukturiertes Erlebnis

Ergebnis des Erkennens: Erfahrung einer strukturierten Welt von Objekten in Raum und Zeit

Objekte sind die elementaren Komponenten der Struktur, die der Erkennungsvorgang als Erfahrung liefert

à Individuen, voneinander unterscheidbar, zählbar

Objekte Û Zählbares ⇒ die natürlichen Zahlen: Begriff (abstraktes Objekt der nat. Zahl) Objekte erkennen und unterscheiden können bedeutet auch sie zählen können

zählbar heißt nicht durch beliebig kleine Änderungen in etwas anderes (anderes Objekt) überführbar

à diskrete Welt von Objekten Den Objekten lassen sich Attribute zuordnen

Ø falls Wert aus einem Kontinuum à Eigenschaft Ø falls anders (z.B. „ledig“) à Attribut

Erfahrung von Objekteigenschaften (Größe, Farbe, Gewicht, Alter, Dauer, ...) à vermitteln kontinuierlichen Aspekt der Welt

à reelle Zahlen als Formalismus Begriff des Kontinuums

Eigenschaften: Messbares

beliebig kleine Änderungen: andere Eigenschaft

Man erfährt auch, daß Beziehungen zwischen Objekten bestehen können

Zwei Objekte stehen entweder in einer bestimmten Beziehung zueinander oder sie tun es nicht: das ist entscheidbar

Objektbeziehungen Û Entscheidbares (ja/nein; wahr/falsch à 2 elementiger Wertevorrat)

Objekte

in der Außenwelt über Sinnesorgan zufließend

erlebt und erkannt

in der Innenwelt

aus eigenem Inneren zufließend erlebt, z.B.: Träume, Gedanken, Begriffe konkretes Objekt

mit Eigenschaften aus der kontinuierlichen Welt behaftet

abstrakte Objekte (Begriffe) weder zeitlich noch räumlich ausgedehnt

Gegenstände räumlich ausgedehnt

und strukturiert

Prozesse (Vorgänge) zeitlich ausgedehnt

und strukturiert

Beziehung zwischen Gegenständen: Bestandteilsbeziehungen Beziehungen zwischen Gegenständen und Prozessen: Mitwirkungsbeziehung

„Gegenstand A wirkt am Prozeß B mit“

Mit Prozessen verbunden: Ereignisse: Anfang, Ende, ....

(Vorgänge, Geschehen) Glockenschläge, Signalflanken, Impulse Ereignisse geschehen zu einem Zeitpunkt

Festlegung des Zeitpunkts willkürlich, auf Vereinbarung beruhend 1.1.2 Abstraktion und Identifikation

Abstraktion: Begriffsbildung: Gewinnung abstrakter Objekte durch Verdichtung unserer Erfahrungen

Identifikation: Hinlenkung der Aufmerksamkeit auf ein best. Objekt Abstraktion von à Klassenbildung

à Findung

Klassenbildung à Verdichtung einer Vielzahl von Objekten zu einem Typ

Objekt ---- Zugehörigkeit ---- Klasse ("Menge" von Objekten gleichen Typs) :

: :

Typ à Satz von Merkmalen, der das Wesen einer Klasse erfasst

à Satz von Merkmalen, die ein Objekt besitzt um zu der betreffenden Klasse gerechnet zu werden

Bsp: "Dackel Waldi" à Waldi ist ein Dackel

Das konkrete Objekt (Gegenstand) gehört zur Objekt ist Mitglied der Objekt ist Element der

Klasse der Dackel oder:

... ist ein Objekt (Exemplar) vom Typ Dackel à Typ ist ein abstraktes Objekt

Repräsentant

à konkretes Objekt, das als "typisch" zur Klassenbildung herangezogen wird Bei Klassenbildung durch Verdichtung zum Typ entstehen unscharfe Begriffe

à von manchen Objekten läßt sich die Zugehörgkeit zur Klasse nicht immer zweifelsfrei (eindeutig) entscheiden

[Beispiel: Farbe ....]

à Wahrscheinlichkeit der Zugehörigkeit angeben à "fuzzy logic"

"fuzzy sets"

Klassifikation eines bestimmten Objekts

à durch Zeigen (Aufmerksamkeit darauf lenken) à durch Umschreiben

à durch Benennen

Benennen: Namen für konkrete Objekte

à Benennungen für abstrakte Begriffe (Objekte)

materiell-energetisches Muster, das wahrgenommen wird und als Hinweis auf das gemeinte Objekt interpretiert wird:

à Symbol für das gemeinte Objekt (stellvertretend für das Objekt benutzt)

1.1.3 Information in Menschen und Maschinen Information:

Wissbares; etwas, das man wissen kann Materielle-energetische Objekte kann man

Speichern Transportieren Verarbeiten

Ebenso Information

im Gedächtnis mitteilen z.B. bei Begriffbildung

Wahrnehmen à wahrgenommene Information

Interpretieren à mitgeteilte Information empfangene Information Verarbeiten à hergeleitete Information

Vergessen à verlorene Information

Mitgeteilte Information, die in materiell-energetischen Mustern symbolisiert ist, wird bezeichnet

• als Daten, wenn Verfügbarkeit des Musters vom Interesse ist (Interpretierbarkeit zu jedem beliebigen Zeitpunkt) à gespeicherte Information

• als Nachrichten, wenn auf den Vorgang des Sendens, Empfangens und Interpretierens von Symbolen (mitgeteilte Information) Wert gelegt wird

1.2 Mengenlehre Klassenbildung:

à Zuordnung von Objekten zu einer Klasse durch Verdichtung zu einem Typ, der (als Satz von Merkmalen) das "Wesen" einer Klasse wiedergibt

Mengendefinition von Georg Cantar (1845-1918)

"Unter einer Menge verstehen wir eine Zusammenfassung von bestimmten,

wohlunterschiedenen Objekten (Dingen) unserer Anschauung und unseres Denkens zu einem Ganzen."

Es können beliebige, willkürlich ausgewählte Objekte (ohne gemeinsame Merkmale) zusammengefasst werden zu einer Menge (kein Typ erforderlich).

Typ Schärfe Mächtigkeit

Klasse muß sein kann sein kann angebbar sein Menge kann sein muß sein muß angebbar sein Bildung von Mengen

a) Durch Aufzählung der zugehörigen Objekte (nur bei endlichen Mengen möglich) z.B.: M = {1, 2, 3, 4}

b) über definierte Bedingung

z.B.: G={ | (x x∈¥)∧(x restlosteilbardurch− 2)}

à Typ

{ | ( ) ( )}

T = ∩ =R S x x∈ ∧ ∈R x S à kein Typmerkmal

x∈R à Objekt x ist ein Element (Mitglied) der Menge R oder: x gehört zu R

u∉R à u gehört nicht zu R (kein Element von R)

Teilmengen

S ist eine Teilmenge (Untermenge, Subset) von M à S⊆M Û jedes Element von S gehört auch zu M

• unechte Teilmenge von M à M ⊆M;∅ ={}⊆M

• eine echte Teilmenge S ist à nicht leer und

à es gibt mindestens ein Element von M, das nicht zu S gehört à ∅ ⊂ ⊂S M (Definition der echten Teilmenge von M) z.B.:

{ , }

M = a b P M( ) = ∅{ ,{ },{ },{ , }}a b a b

echte Teilmengen von M

Überdeckung (cover) t einer Menge

eine Menge von nichtleeren Teilmengen von M (Blöcke), die sich zu M vereinigen

1 2

(M) {C C, ,....,C_N}

τ =

mit ∅ ⊂C_i ⊆Mund _{1 2}

1

...

N

i N

i

C C C C M

=

= ∪ ∪ ∪ =

U

à Jedes Element von M gehört zu mindestens einem Block Ci

Bsp: M ={ , , , }a b c d

1 2

( ) {{ , },{ , },{ , , }}

( ) {{ , },{ },{ , }}

M a b b c a c d

M a c b a d

τ τ

=

=

Partition von M

Überdeckung mit der zusätzlichen Bedingung, daß ihre Blöcke paarweise disjunkt sind

i j

C ∩C = ∅ wenn i≠ j Bsp: M ={1,2,3,4}

(M) {{1,3},{2,4}}

Π =

à gröbste Partition: Π_gröbst(M) ={{1,2,3,4}}={M} |Π_gröbst| 1= à feinste Partition: Π_feinst(M) ={{1},{2},{3},{4}} |Π_feinst| |= M|

à alle anderen Partitionen sind gröber als die Feinste und feiner als die Gröbste 1 |< andere Part. | |< M| Kartesisches Produkt zweier Mengen A und B

(A ={1;3} , B = {c,d,e}) ist die Menge aller geordneten Paare (a,b) mit a ÎA, b ÎB

{( , ) | }

A B× = a b a∈A und b∈B Bsp.:

{(1, ),(1, ),(1, ),(3, ),(3, ),(3, )}

A B c d e c d e

A B B A

× =

× ≠ ×

à nicht kommutativ Mehrfaches Kartesisches Produkt

1 2 1 2 1 1 2 2

1 1 1 2 2 2

... { , ,..., | , ,..., }

( ) ( ) {( , , ),( , , ),....,( , , )}

n n n n

n m r

A A A a a a a A a A a A

A B C A B C A B C a b c a b c a b c

× × × = ∈ ∈ ∈

× × = × × = × × = à assotiativ

[(A B× ×) C bedeutet nicht ((( , ), ),....)a b_{1 1} c₁ ]

Darstellung des n-fachen karthesischen Produkts durch n-dimensionale Matrizen:

Bsp: n = 2

A ={1;3}; B = {c,d,e}

B

c d e

1 (1,c) (1,d) (1,e) A

3 (3,c) (3,d) (3,e)

|A B× × × =... Z| |A| |⋅ B| ....|⋅ ⋅ Z|

1.2.2 Relationen und Strukturen

Relationen à Bezeichnungen zwischen Objekten

Strukturen à durch Bezeichnung gegliederte Objekte (relationale Struktur) rein formal: Jede Relation ist die Teilmenge einer kartesischen Produkts

inhaltlich: bestimmt durch eine Aussageform, mit der die Objekte in die gemeinte Beziehung gesetzt werden

z.B.: x ist kleiner als y

x,y: Variablennamen; Wertevorräte dazu: x∈X y; ∈Y z.B.: x y, ∈¡ Kart. Produkt: ¡ ¡×

Relation: {( , ) |x y x< y}⊆ ס ¡

à Wertepaar, das die Aussageform zu einer wahren Aussage macht ----

p lebt in s

p: Person Î Personenkreis P; P = {Anton, Erich, Karl, Theo}

s: Stadt Î Menge von Städten S; S = {London, Paris, Rom}

S

London Paris Rom

Anton X

Erich

Karl X

P

Theo X

Relation: {(Anton.Paris), (Karl,London),(Theo,Paris)}

p lebt in Jahr t in s à 3 stellige Relation

Wer lebt wann wo ?

Mehrstellige Relationen lassen sich auf eine Menge zweistelliger Relationen zurückführen Zweistellige Relationen (auch Abbildungen [mappings])

Teilmengen von A B×

Bsp: A={0;1};B= ∅{ ,{0},{1},{0;1}}=P A( )

Welches Element von A kommt in welchen Teilmengen von A (Elemente von B = P(A)) vor?

Aussageform:

a Î A gehört zu S Î B Einträge in die Relationsmatrix

W – T – 1 – ja – X F – F – 0 – nein –

B

∅ {0} {1} {0;1}

0 0 1 0 1

A 1 0 0 1 1

Als Teilmenge des kart. Produkts A B×

{(0,{0}), (0,{0;1}), (1,{0}), (1,{0,1})} à Graph der Relation à 0 Î {0}

A

(Quellmenge)

B

(Zielmenge)

Relation

0 Æ

{0}

1 {1}

{0,1}

formale Eigenschaften zweistelliger Relationen

• links vollständig à Jedes Element von A steht mit mindestens einem Element von B in der betreffenden Beziehung (hier: a ÎS)

• links unvollständig à Gegenteil

• rechts vollständig à zu jedem b ÎB steht mindestens ein a ÎA in Beziehung

• rechts unvollständig à (hier: zu Æ steht kein a ÎA in der Beziehung a ÎÆ) von A auf B: links- und rechtsvollständig

von A in B: linksvollständig, rechtsunvollständig aus A auf B: linksunvollständig, rechtsvollständig

Abbildung {

• links eindeutig à Jedem Element a Î A wird höchstens ein Element b Î B zugeordnet

• links mehrdeutig à Gegenteil

• rechts eindeutig à Jedes Element b Î B steht zu höchstens einem Element a Î A in Beziehung

• rechts mehrdeutig à Gegenteil

von A in B à vollständige Funktion Funktion: links eindeutige Abbildung

{

Relationen zwischen den Elementen ein- und derselben Menge

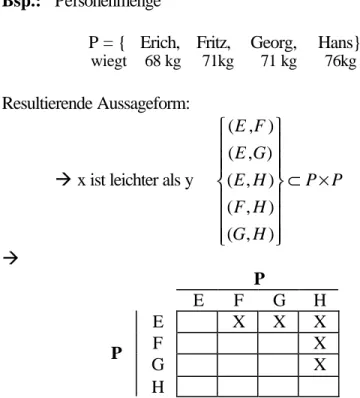
² R⊆ × =A A A Bsp.: Personenmenge

P = { Erich, Fritz, Georg, Hans}

wiegt 68 kg 71kg 71 kg 76kg Resultierende Aussageform:

à x ist leichter als y

( , ) ( , ) ( , ) ( , ) ( , ) E F E G

P P E H

F H G H

 

 

 

  ⊂ ×

 

 

 

 

 

à

P

E F G H

E X X X

F X

G X

P H

andere Aussageform: "x ist nicht schwerer als y"

"x ist so schwer wie y"

Relation zwischen der selben Menge A

= Relation über A (Relation auf A)

= "quadratische" Relation (wegen Gestalt der Relationsmatrix bzw. des quadrat.

kartesischen Produkts R⊂ × =A A A²) Eigenschaften

• Reflexivität

• Symmetrie

• Transitivität à Reflexivität

à Steht ein Element zu sich selbst in der Beziehung R ?

• Jedes a ÎA steht zu sich selbst in der Beziehung R à R ist reflexiv [In Matrix: Hauptdiagonale mit Einsen]

• Kein a Î A steht zu sich selbst in der Beziehung R à R ist antireflexiv

P

E

F G

H

P

E

F G

H

P

E

F G

H

• Mindestens ein Element steht zu sich in der Beziehung R und mindestens ein Element steht nicht zu sich selbst in der Beziehung R à R ist weder reflexiv, noch antireflexiv à Symmetrie (a ¹ b)

• aus (a,b) Î R folgt (b,a) Î R à R ist symmetrisch [symmetrische Matrix]

• aus (a,b) Î R folgt (b,a) Ï R à R ist antisymmetrisch

• ansonsten: weder symmetrisch noch antisymmetrisch

à Transitivität

• aus (a,b) Î R und (b,c) Î R folgt (a,c) Î R à R ist transitiv

• aus (a,b) Î R und (b,c) Î R folgt (a,c) Ï R à R ist antitransitiv

• ansonsten: weder noch

Einteilung der Relationen Äquivalenzrelation

R ist reflexiv, symmetrisch und transitiv (z.B.: x ist so schwer wie y):

R heißt Äquivalenzrelation

R teilt die Menge A in ihre Äquivalenzklassen ein

à R erzeugt die Partition von A in die Äquivalenz-Klasse (Klasse: alle Element des betr. Typs)

i.Bsp.: P(P) = {{E}, {F,G}, {H}}

Verträglichkeitsrelation

a kennt b, b kennt c, aber a kennt c nicht

Die Relation "x kennt y" ist reflexiv und symmetrisch, sie ist aber nicht notwendigerweise transitiv

à Verträglichkeitsrelation (compatibility relation)

à reflexiv, symmetrisch, Transitivitätseigenschaftem irrelevant transitive Verträglichkeitsrelation ist eine Äquivalenzrelation Symbol: a:b a und b sind verträglich

b :c b und c sind unverträglich

Ordnungsrelationen 1. Art (reflexive OR)

à reflexiv, antisymmetrisch, transitiv Bsp.:

à ≤ zwischen Zahlenwerten [M ={1,2,3}; ]≤

1 2 3

1 1 1 1

2 0 1 1

3 0 0 1

"lineare Ordnung 1. Art " à Vollordnung à [ ({ , }); ]P a b ⊆

weder { }a ⊆{ }b noch { }b ⊆{ }a à a∪b

∩

à a, b sind inkommensurabel (unvergleichbar, nebengeordnet)

"Partial- oder Halbordnung"

2. Art (antireflexive OR) Typ: ,< ⊂, ( )Ø

1 2 3

reflektierende Kanten

{a}

{ } {a,b}

{b}

übergreifende Kante

1 2 3

{a}

{ } {a,b}

{b}

bei mehreren Elementen:

à übersichtlichere Darstellung durch Hasse-Diagramm

• Pfeile: von unten nach oben

• reflektierende und übergreifende Kanten werden weggelassen (Angabe ob vorhanden oder nicht)

Bsp.: [ ({ , , }; ]P a b c ⊆

auch vollst. Graph des antireflexiven, antitransitiven Kerns der reflexiven OR

reflexiv, symmetrisch, transitiv Äquivalenz-Relation

reflexiv, weder symmetr. noch antisymmetr., transitiv Quasi-Ordnungsrelation

reflexiv, antisymmetrisch, transitiv reflexive Ordnungsrelation (1. Art) z.B.: "x ist nicht schwerer als y"

à sondern: leichter oder gleich schwer (höchstens so schwer wie y)

Aus x≤ ∧ ≥y x y folgt x = y à Antisymmetrie

{a,b} {b,c}

{a} {c}

{a,b,c}

{a,c}

{b}

{ }

H (76)

F (71)

E (68)

G

(71) gleichgeordnet à

{H}

- {F,G}

-

{E}

Bsp: für antireflexive OR [{{ , },{ , },{ },{ },a b a c b a { }}, ]⊂

{a,b} {a,c} à maximale Elemente der OR

[keinem anderen vorgeordnet]

{a} {b}

antireflexive Halbordnung

[Folgengeflechte, partially ordert set

à poset] ( à minimale Elemente der OR

[keinem anderen nachgeordnet] )

{ } à minimales Element: kleinstes El.

[allen anderen vorgeordnet]

OR: antisymmetrisch transitiv

Schichtungen: antireflexiv antisymmetrisch Schichtungen

Relationsgraph à vgl. Buch S. 35

Buch: Schichtordnung nach maximalem Abstand von den minimalen Elementen auch möglich: desgleichen nach maximalem Abstand von den maximalen Elementen

1.3 Signale, Symbole, Sprachen

Erscheinungsformen empfangener Information

à materiell-energetische Sachverhalte, die unsere Sinnesorgane reizen und den Informationsempfang auslösen

Erscheinungsformen wahrgenommener Information

Erscheinungsformen mitgeteilter Information

Signale Sprachgebilde

auf der Basis von Informationen

1.3.1 Signale

à Erscheinungsformen wahrgenommener Information

à physikalische Sachverhalte und Strukturen in Raum und Zeit

1 2

( , , , ) ( , , , )

...

( , , , )

n

s x y z t s x y z t S

s x y z t

 

 

 

= 

 

 

 

die si: Werte aus einem Eigenschaftskontinuum

oder: Element einer diskreten Menge, die durch Intervalleinteilung eines Eigenschaftenkontinuums gewonnen wurden

Skalares Signal:

( , , , ) s=s x y z t

Extremformen

raumunabh. Signale : S = s(t) zeitunabh. Signale : S = s(x,y,z)

durch Aufzeichnen bzw.

Abspielen 1-, 2- oder 3-dimensionale Muster

1.3.2 Symbole

(leicht produzierbares) Signal als Stellvertreter eines zu identifizierenden Objekts. Das gemeinte Objekt ist die Interpretation des Signals

: elementares Symbol für den Planeten Jupiter

"Jupiter": zusammengesetztes Symbol für diesen Planeten

==

9 : elementares Symbol für die natürliche Zahl neun

"neun": zusammengesetztes Symbol für die natürliche Zahl neun

==

1984 : kein Symbol für eine natürliche Zahl

| | | |

à Symbole für natürliche Zahlen à Umschreibung für eine natürliche Zahl

1 0

1 10³ 9 10² 8 10 4 10 n= ⋅ + ⋅ + ⋅ + ⋅

Bausteine strukturierter Symbole (à interpretierbar) : Zeichen (à nicht interpretierbar) Bausteinmenge, linear geordnet à Alphabet

2. Grund für strukturierte Symbole:

1:1-Abbildungen zwischen Symbolmengen

z.B.: 1:1-Abbildung zw. gesprochener und geschriebener Sprache

durch verschiedene Symbolerzeugungsapparate erzeugt Bsp: für technischen Symbolerzeugungsapparat

"Morsen mit Taschenlampe"

g g g AS à strukturiertes Symbol für ein Zeichen

g g g− à Morsesymbol

1000110 à ASCII-Symbol für das Zeichen "f"

à Problem: Wörter gegeneinander abgrenzen Lösungen:

• eigenes Zeichen für Abgrenzung

• Wörter fester Länge

• Wortbildung so, daß Abgrenzung erkennbar (kein Wort darf Anfangsstück eines anderen sein) à Fanø-Code

Binärsignale

Zweiwertige Signale: Durch Intervalleinteilung eines Eigenschaftskontinuums gewonnen z.B. einer Spannung

à 2 Schwellenwerte

1.3.3 Sprachen Aspekte:

• Syntax: formale Regeln zur Erstellung interpretierbarer Sprachgebilde; aus Bausteinen

• Semantik: Regeln zur Interpretation der Sprachgebilde

• Pragmatik: Regeln zum Umgang mit der Sprache zu bestimmten Zwecken, Stilfragen

1.3.3.1 Zweck der Sprache

Identifikation von Objekten/Strukturen durch Umschreibungen à (Zeigen)

à (Benennen) à Umschreiben

à direkte Umschreibung: Angabe eines Weges, Algorithmus nach dem sich das Gewünschte ermitteln lässt

à indirekte Umschreibung: Angabe eines Satzes von Bedingungen, die das Gewünschte erfüllen muss

Wissensvermittlung (durch Aussagen) Zwecke

Aufforderung zur Identifikation: Fragen Aufforderung zum Handeln (Anweisung) Aussagenlogik

à handelt von elementaren und zusammengesetzten Aussagen und ihren Wahrheitswerten ({wahr, falsch})

A und B à Aussageform

[Heute ist Donnerstag] und [Der Hahn kräht auf dem Mist] à Aussage Weder ist heute nicht Donnerstag noch kräht der Hahn nicht auf dem Mist

Transformation von Aussagen best. Form in anders geformte, über inhaltgleiche (interpretationsäquivalente) Aussagen à formale Regeln zur Transformation von Aussageformen in interpretationsähnliche Formen

Aspekte

Kalkül zur Berechnung des Wahrheitswertes zusammengesetzter Aussagen aus den Wahrheitswerten der elementaren Aussagen und der Form ihrer Zusammensetzung

Aussagen werden mit Junktoren (verbundene Sprachelemente) zusammengesetzt [vgl. Buch S. 76 und Ergänzungsblatt]

nicht A A und B

A oder B (inklusives ODER)

entweder A oder B (exklusives ODER) wenn A dann B (Implikation)

A dann und nur dann, wenn B (genau dann, wenn) weder A noch B

nicht (A und B zugleich) (A und B schließen einander aus)

Variable in Aussageformen

Aussage: "Die Haare von Kaiser Augustus waren schwarz."

"Die Handschuhe von Kaiser Nero waren rot."

A) Zwei Aussagen der gleichen Form

Aussagevariable variieren z.B. a' à Variable, Werte: z.B.: oben Aussagevariable

B) Individuenvariablen

statt "Kaiser Augustus", "Kaiser Nero", "Ottonormalverbraucher", ….

Aussageform:

Die Haare von X waren schwarz

C) "Die Handschuhe von Kaiser Augustus waren schwarz"

Funktionsvariable f (...) [f(Kaiser Augustus) = die Haare von (Kaiser Augustus)]

à eindeutige Zuordnung zu einem Argumentenwert hier: dem Kaiser Augustus wurden seine Haare zugeordnet

f (Kaiser Augustus) waren schwarz à f (x) waren schwarz D) "waren schwarz" ordnet den Haaren von Kaiser Augustus eine Farbe zu

verallgemeinert: eine Eigenschaft, ein Attribut, ein Prädikat zu z.B. auch: "waren rot", "waren schüttern", "waren frisch gewaschen", ....

Prädikatvariable: P (die Haare von Kaiser Augustus) = ... waren schwarz P [ f (x) ]

Quantoren

∀ : "alle" ("für alle", "für jeden", "von jedem", "von allen", ….)

¬∀ : "nicht alle" ("einige")

∃ : "mindestens eins" ("es gibt mindestens eine ...") [∃1 : "eins und nur eins" ("genau eins")

¬∃ : "kein, keines, ..." ("Es gibt keine ...")

"Alle Menschen sind klug"

à ist Aussage der Form ∀x: P x( ) x ∈ Menge (Klasse) aller Menschen

⇔ "Kein Mensch ist nicht klug"

: ( )

x P x

¬∃ ¬

⇔ ¬∃x: Q x( ) mit Q(x): x ist dumm [Q x( )⇔ ¬P x( )]

"Kein Mensch ist dumm"

: ( ) x P x

¬∀ : "Nicht alle Menschen sind klug"

⇔ ∃x: ¬P x( ) : "Mindestens ein Mensch ist nicht klug"

⇔ ∃x: Q x( ) : "Mindestens ein Mensch ist dumm"

: ( ) x P x

∃ : "Es gibt mindestens einen klugen Menschen"

⇔ ¬∀x: ¬P x( ) : "Nicht alle Menschen sind nicht klug"

⇔ ¬∀x: Q x( ) : "Nicht alle Menschen sind dumm"

: ( ) x P x

¬∃ : "Kein Mensch ist klug"

⇔ ∀x: ¬P x( ) : "Alle Menschen sind nicht klug"

⇔ ∀x: Q x( ) : "Alle Menschen sind dumm"

=====

"Zu jedem Schloss gibt es (mindestens) einen passenden Schlüssel"

hat die Form: ∀ ∃x: y: P x y( , ) x ∈ Menge aller Schlüssel y ∈ Menge aller Schlösser P(x,y) = zu Schloss x passt Schlüssel y Vertauscht: ∃ ∀y: x: P x y( , )

"Es gibt (mindestens) einen Schlüssel, der zu jedem Schloss passt"

à ist nicht interpretationsäquivalent zur ersten Aussageform

: : ( , ) : : ( , )

x y P x y y x P x y

∀ ∃ ⇔ ∃ ∀

: : ( , ) x y P x y

∀ ∃ : "Zu jedem Schloss gibt es einen passenden Schlüssel"

: : ( , )

x y P x y

¬∃ ¬∃ : "Zu keinem Schloss gibt es keinen Schlüssel, der zum Schloss passt"

: : ( , )

x y P x y

¬∃ ∀ ¬ : "Es gibt kein Schloss, zu dem alle Schlüssel nicht passen"

: : ( , )

x y P x y

∀ ¬∀ ¬ : "Für jedes Schloss gilt, dass nicht alle Schlüssel nicht passen"

Wenn nur über Individuenvariable qualifiziert wird:

Prädikatenlogik erster Stufe; Individuenvariable: Variable 1. Stufe

: 1( ) 2( )

x P x P x

∀ ⇒

2. Stufe: Quantifiziert wird auch über Funktions- und Prädikatenvariable, deren Argumente Individuen sind, also Belegungen von Variablen erster Stufe sind.

. . . .

m-te Stufe: Quantifiziert wird über Variable, von deren Argumenten mindestens eines die Belegung einer Variablen (m-1)-ter Stufe ist

Bsp.:

: ( 1[" ( , )"] 2[" ( , )"] 3[" ( , )"]) 4[" ( , )]

p P p x y P p x y P p x y P p x y

∀ ∧ ∧ ⇒

Quantifiziert wird nur über eine Variable der 2. Stufe: p(x,y) à Aussageform gehört zur Prädikatenlogik 2. Stufe x, y, z: Objekte aus der selben Menge

p(x,y): x steht zu y in der Relation p P1: p ist symmetrisch

, : ( , ) ( , )

x y p x y p y x

∀ ↔

P2: p ist transitiv

, , : [ ( , ) ( , )] ( , ) x y z p x y p y z p x z

∀ ∧ ⇒

P3: p ist linksvollständig

: : ( , )

x y p x y

∀ ∃

P4: p ist reflexiv : ( , ) x p x y

∀