18. November 2005

(1)

Ingenieure

Othmar Marti

Abteilung Experimentelle Physik Universität Ulm

18. November 2005

(2)

(3)

I. Vorbemerkungen 9

1. Übungsblätter und Folien 13

2. Einleitung 17

2.1. Allgemeines zur Physik . . . 17

2.2. Einheitensysteme . . . 19

2.3. Fehler . . . 21

2.4. Dimensionsanalyse . . . 22

2.5. Literatur . . . 23

II. Mechanik starrer Körper 27

3. Kinematik 29 3.1. Bewegung in einer Dimension . . . 29

3.1.1. Momentangeschwindigkeit und Beschleunigung . . . 30

3.2. Bewegung in zwei und drei Dimensionen . . . 33

3.2.1. Vektoren und Vektorrechnung . . . 33

3.2.2. Bsp: Wurfbewegung. . . 36

3.2.3. Gleichförmige Kreisbewegung (mit vektorieller Darstellung). 38 3.2.4. Nichtkommutativität endlicher Drehungen . . . 39

4. Dynamik, die Newtonschen Axiome 43 4.1. Trägheitsgesetz: Erstes Newtonsches Axiom . . . 43

4.2. Kraft, Masse,Impuls: Zweites Newtonsches Axiom . . . 44

4.2.1. Masse (m) . . . 44

4.2.2. Kraft (F) . . . 45

4.2.3. Arten von Kräften . . . 46

4.2.4. Beispiele zur Lösung von Bewegungsproblemen. . . 47

4.3. Anwendungen der Newtonschen Axiome . . . 50

4.3.1. Reibung . . . 50

4.3.2. d'Alembert'sches Prinzip . . . 54

4.3.3. Bewegung mehrerer miteinander verbundener Körper . . . . 55

4.3.4. Kräfte in bewegten Bezugssystemen . . . 57

(4)

4.3.5. Numerische Methoden . . . 60

4.4. Arbeit,Energie,Leistung . . . 61

4.4.1. Arbeit und Energie bei konstanter Kraft, kinetische Energie 61 4.4.2. Arbeit und Energie bei veränderlicher Kraft . . . 63

4.4.3. Allgemeine Formulierung der Arbeit bei 3 Dimensionen . . . 65

4.4.4. Potentielle Energie . . . 67

4.4.5. Energieerhaltungssatz . . . 74

4.4.6. Verallgemeinerter Energiesatz . . . 77

4.4.7. Leistung . . . 77

4.5. Teilchensysteme und Impulserhaltung . . . 79

4.5.1. Massenmittelpunkt . . . 79

4.5.2. Impulserhaltung. . . 81

4.5.3. Massenmittelpunkt als Bezugssystem . . . 82

4.5.4. Kinetische Energie eines Teilchensystems . . . 83

4.5.5. Stösse in einer Dimension . . . 84

4.5.6. Stösse in drei Dimensionen . . . 86

4.5.7. Kraftstoss . . . 88

4.5.8. Rückstossantriebe . . . 89

4.6. Drehbewegungen . . . 90

4.6.1. Winkel, Winkelgeschwindigkeit und Winkelbeschleunigung . 90 4.6.2. Drehmoment und Trägheitsmoment . . . 91

4.6.3. Kinetische Energie der Drehbewegung. . . 94

4.6.4. Berechnung der Trägheitsmomente . . . 94

4.6.5. Drehimpuls und Drehimpulserhaltung . . . 96

4.6.6. Rollende Körper . . . 98

4.6.7. Vektorcharakter von Drehgrössen . . . 101

4.6.8. Drehungen um beliebige Achsen: Trägheitstensor . . . 104

4.6.9. Kreiselbewegung . . . 105

4.7. Statische Gleichgewichte von starren Körpern . . . 107

4.7.1. Schwerpunkt. . . 107

4.7.2. Kräftepaare . . . 109

4.7.3. Stabilität des Gleichgewichts . . . 110

4.8. Schwerkraft oder Gravitation . . . 111

4.8.1. Keplersche Gesetze . . . 111

4.8.2. Newtonsches Gravitationsgesetz . . . 112

4.8.3. Schwere und träge Masse . . . 117

4.8.4. Raumfahrt . . . 118

4.8.5. Potentielle Energie, Gesamtenergie und Umlaufbahnen . . . 118

III. Mechanik deformierbarer fester Körper 121

(5)

5. Skalare Elastomechanik 125

5.1. Dehnung und Kompression . . . 125

5.2. Scherung . . . 126

5.3. Verdrillung eines Drahtes . . . 127

5.4. Biegung . . . 128

5.5. Beziehung zwischen den elastischen Konstanten . . . 131

5.6. Anelastisches Verhalten . . . 132

5.7. Elastomechanik anisotroper Körper . . . 133

IV. Spezielle Relativitätstheorie 137

6. Bezugssysteme 141 6.1. Michelson-Versuch . . . 141

6.2. Die Einsteinschen Postulate . . . 142

6.3. Punktereignisse . . . 143

6.4. Rückdatierung . . . 144

7. Relativistische Mechanik 147 7.1. Relativität der Gleichzeitigkeit . . . 147

7.1.1. Massstabsvergleich . . . 150

7.1.2. Uhrenvergleich . . . 151

7.1.3. Der transversale relativistische Dopplereekt . . . 153

7.1.4. Addition der Geschwindigkeiten . . . 154

7.1.5. Messung der Beschleunigung . . . 156

7.1.6. Bewegte Masse . . . 157

7.1.7. Masse-Energie-Äquivalenz . . . 160

7.2. Lorentz-Transformation. . . 167

7.2.1. Vergleich der Lorentz-Transformation mit der Galilei-Transformation169

V. Schwingungen und Wellen 171

8. Schwingungen 173 8.1. Harmonische Schwingungen . . . 173

8.1.1. Harmonische Schwingungen und Kreisbewegung . . . 175

8.1.2. Energiebilanz bei harmonischen Schwingungen . . . 176

8.1.3. Feder-Masse-System im Schwerefeld . . . 177

8.1.4. Pendel im Schwerefeld . . . 179

8.1.5. Bewegung in der Nähe von Gleichgewichtspunkten . . . 182

8.2. Gedämpfte Schwingung . . . 183

8.2.1. Güte des schwingungsfähigen Systems. . . 184

8.3. Erzwungene (gedämpfte) Schwingung und Resonanz . . . 185

8.4. Überlagerung von Schwingungen . . . 188

8.4.1. Schwingungen in unterschiedliche Richtungen . . . 189

(6)

8.4.2. Schwingungen gleicher Richtung und Frequenz, aber unter-

schiedlicher Amplitude . . . 189

8.4.3. Schwingungen gleicher Richtung, aber leicht unterschiedli- cher Frequenz . . . 190

8.4.4. Fouriertransformation . . . 191

8.5. Gekoppelte Schwingungen . . . 194

8.6. Verallgemeinerung: Fundamental- oder Eigenschwingungen . . . 198

9. Wellen 201 9.1. Wellen in 1 Dimension . . . 201

9.1.1. Wellenberge . . . 201

9.1.2. Ausbreitungsgeschwindigkeit . . . 205

9.1.3. Harmonische Wellen . . . 206

9.1.4. Energieübertrag bei Wellen . . . 207

9.1.5. Superposition und Interferenz harmonischer Wellen . . . 208

9.2. Wellen in 2 und mehr Dimensionen . . . 210

9.2.1. Ebene Wellen . . . 210

9.2.2. Kugelwellen . . . 211

9.2.3. Interferenz am Beispiel von Wasserwellen . . . 212

9.2.4. Beugung am Beispiel von Wasserwellen . . . 216

10.Optische Phänomene 221 10.1. Polarisation . . . 221

10.1.1. Polarisation durch Absorption . . . 221

10.1.2. Polarisation durch Streuung . . . 223

10.1.3. Polarisation durch Reexion . . . 223

10.2. Beugung . . . 225

10.3. Absorption, Dispersion und Streuung . . . 225

10.3.1. Absorption . . . 225

10.3.2. Dispersion und Kommunikation . . . 226

10.3.3. Streuung . . . 229

10.4. Welle-Teilchen-Dualismus . . . 231

VI. Geometrische Optik 235

11.Reexion und Brechung 239 11.1. Lichtstrahlen . . . 239

11.2. Reexion . . . 239

11.3. Brechung . . . 241

11.4. Totalreexion und optische Kommunikation . . . 242

11.5. Prismen . . . 242

(7)

12.Optische Instrumente 245

12.1. Spiegel . . . 245

12.2. Linsen . . . 247

12.2.1. Brechung an Kugelächen . . . 247

12.2.2. Abbildungsmassstab . . . 248

12.2.3. Dünne Linsen . . . 248

12.2.4. Dicke Linsen. . . 249

12.3. Lupe . . . 250

12.4. Mikroskop . . . 250

12.5. Kollimationsoptik für Laserdioden . . . 251

12.6. Beamer . . . 251

VII.Anhang 253

13.Dierentiation und Integration 255 13.1. Dierentiationsregeln . . . 255

13.2. Dierentiation einfacher Funktionen . . . 256

13.3. Taylorreihe und Reihen . . . 257

13.4. Einige Reihen . . . 258

14.Rechnen mit Integralen 259 14.1. Unbestimmte Integrale . . . 260

15.Berechnungen in ebenen schiefwinkligen Dreiecken 263 16.Simulation von Photonenstatistiken 265 16.1. Delphi-Programm . . . 265

16.2. Maple 7 -Programm . . . 266

17.Korrekturen 269

Index 269

(8)

(9)

Vorbemerkungen

(10)

(11)

Mitteilungen

• Prüfungen sind, gemäss Studienordnungen, studienbegleitend. Nach Semes- terende wird eine Klausur geschrieben. Diese zählt zur Vordiplomsnote.

• Am 19. Dezember 2001 wird während der Vorlesungszeit eine unverbindli- che Probeklausur geschrieben. Themen der Probeklausur werden die Teile I bis III sein. Diese Probeklausur soll Ihnen helfen, sich an Klausuren zu gewöhnen.

• Während den Übungsstunden werden Aufgaben unter Aufsicht und Anlei- tung des Assistenten gelöst.

• Zusätzlich gibt es Hausaufgaben, die von Assistenten korrigiert werden.

• Die Zulassung zur Klausur wird erteilt, wenn Sie an mindestens 13 Übungs- stunden teilgenommen haben und wenn Sie mindestens 80% der Hausauf- gaben (vollständig oder teilweise gelöst) abgegeben haben. Diese Zahlen re- duzieren sich, wenn Sie aus Gründen, die Sie nicht zu vertreten haben (mit Nachweis!), nicht in der Lage waren die geforderten Leistungen zu erbringen.

• Am 12.2. 2002 gibt es eine Faschingsvorlesung.

• Klausur zur Vorlesung statt.

Fragestunde zur Klausur: 25. 2. 2002, 10:00 H2 (voraussichtlich) Fragestunde zur Klausur: 4. 3. 2002, 10:00 H2 (voraussichtlich) Datum: 7. 3. 2002

Uhrzeit: 9:00 bis 11:00 Ort: 43.2.101/104

Hilfsmittel: Taschenrechner Anmeldung: bis 28. 2. 2002

Aufgabenblatt und Lösungen (HTML)¹ oder(PDF)² Resultate³

Aufgabenblatt und Lösungen der Nachklausur(HTML)⁴ oder(PDF)⁵ Resultate der Nachklausur⁶

• Kontakte:

1Ueb/klausur/index.html

2Ueb/klausur/klausur.pdf

3resultat.htm

4Ueb/nklausur/index.html

5Ueb/nklausur/nachklausur.pdf

6resultatnk.htm

(12)

Vorlesung Prof. Dr. sc. nat/ETH Zürich Othmar Marti, N25,541, othmar.marti@physik.uni-ulm.de⁷, Tel. 23011

Vorlesungsassistenz Prof. Dr. Martin Pietralla, martin.pietralla@physik.uni-ulm.de⁸

Übungsgruppen Manuel Gonçalves, manuel.goncalves@physik.uni-ulm.de⁹

Charly Imhof, charly.imhof@physik.uni-ulm.de¹⁰

Holger Schieferdecker, holger.schieferdecker@physik.uni-ulm.de¹¹

7mailto:othmar.marti@phys ik.uni-ulm.de

8mailto:martin.pietra lla@physik.uni-ulm.de

9mailto:manuel.goncal ves@physik.uni-ulm.de

10mailto:charly.imhof@phys ik.uni-ulm.de

11mailto:holger.s chieferdecker@physik.uni-ulm.de

(13)

Übungsblätter

• Übungsblatt 1 vom 16. 10. 2001 (HTML oderPDF)

• Probeklausur vom 19. 12. 2001 (HTML)¹ oder(PDF)²

• Übungsblatt 11 vom 8. 1. 2002 (HTML oder PDF)

• Übungsblatt 15 vom 5. 2. 2002 (HTML oder PDF)

• Klausur vom 7. 3. 2002(HTML)³ oder(PDF)⁴

• Nachklausur vom 12. 4. 2002 (HTML)⁵ oder (PDF)⁶

1Ueb/ue0/index.html

2Ueb/ue0/uebungsblatt0.pdf

3Ueb/klausur/index.html

4Ueb/klausur/klausur.pdf

5Ueb/nklausur/index.html

6Ueb/nklausur/nachklausur.pdf

(14)

Folien

• Folien zur Vorlesung am 16. 10. 2001 PDF

(15)

Übungsblätter und Folien werden in der Regel am Vortrag der Vorlesung zu- gänglich gemacht_.

(16)

(17)

Eine wunderbare Website zum Aufarbeiten Ihres Wissens ist Hyperphysics¹ von R. Nave. Ergänzend gibt es vom gleichen Autor auch Hypermath².

2.1. Allgemeines zur Physik

Dieser Sto wurde am 16.10.2001 behandelt Materialien:

Beziehungen zwischen den Naturwissenschaften

• Messbare und berechenbare Grössen

• Kräfte, Energien

• Quantenphänomene (Laserdiode, Transistor)

1http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html

2http://hyperphysics.phy-astr.gsu.edu/hbase/hmat.html#hmath

(18)

Grössenordnungen: Siehe auch Film: Grössenordnungen

Strecke m

Protonenradius 10⁻¹⁵

Atomradius 10⁻¹⁰

Virusdurchmesser, Gate-Dimension eines Transistors 10⁻⁷ Riesenamöbe, kleinste Si-Release-Strukturen 10⁻⁴

Walnuss 10⁻²

Mensch 10⁰

Höchster Berg 10⁴

Erddurchmesser 10⁷

Sonnendurchmesser 10⁹

Abstand Erde-Sonne 10¹¹

Durchmesser Sonnensystem 10¹³

Abstand von α-Centauri 10¹⁶

Durchmesser Milchstrasse 10²¹

Durchmesser sichtbares Universum 10²⁶

Masse kg

Elektron 10⁻³⁰

Proton 10⁻²⁷

Aminosäure 10⁻²⁵ Hämoglobin 10⁻²² Grippevirus 10⁻¹⁹ Riesenamöbe 10⁻⁸ Regentropfen 10⁻⁶

Ameise 10⁻²

Mensch 10²

Re 6/6 oder E101 10⁵

Pyramide 10¹⁰

Erde 10²⁴

Sonne 10³⁰

Milchstrasse 10⁴¹ Universum 10⁵²

(19)

Zeitintervall s

Licht durchquert einen Atomkern 10⁻²³

Elementarprozesse einer chemischen Reaktion 10⁻¹⁶ Schwingungsperiode des sichtbaren Lichtes, kürzeste Pulse 10⁻¹⁵ Schwingungsperiode von Mikrowellen 10⁻¹⁰

Halbwertszeit Myon 10⁻⁶

Schwingungsperiode höchster hörbarer Töne 10⁻⁴

Zeit zwischen zwei Herzschlägen 10⁰

Halbwertszeit des freien Neutrons, Unterrichtsstunde 10³

Dauer der Erdumdrehung 10⁵

Umlaufszeit der Erde um die Sonne 10⁷

Lebensdauer Mensch 10⁹

Halbwertszeit²³⁹-Plutonium 10¹²

Lebensdauer einer Gebirgskette 10¹⁵

Halbwertszeit Uran 10¹⁶

Alter der Erde 10¹⁷

Alter des Universums 10¹⁸

2.2. Einheitensysteme

Dieser Sto wurde am 16.10.2001 behandelt (Siehe Tipler, Physik[Tip94, 1]) (Siehe Gerthsen, Physik[GV95, 1])

Wir rechnen in unserer Vorlesung ausschliesslich mit dem gesetzlichen Einhei- tensystem: SI.

s Sekunde, Zeiteinheit. Deniert mit der Frequenz des Überganges zwischen zwei Hyperfeinniveaus des¹³³Cäsium-Isotops. Diese Frequenz ist9⁰192⁰631⁰770Hz. m Meter, Längeneinheit. Abgeleitete Grundeinheit, deniert mit der Sekunde

und der Lichtgeschwindigkeit im Vakuum c= 299⁰729⁰458 ^m_s.

kg Kilogramm, Masse-Einheit (nicht Gewicht). Deniert mit dem Urkilogramm in Sèvres. Dies ist die am schlechtesten bekannte Grundeinheit.

K Kelvin, Temperatur A Ampère, Stromstärke mol Mol, Stomenge cd Candela, Lichtstärke

(20)

Faktor Vorsilbe Abkürzung Faktor Vorsilbe Abkürzung

10¹⁸ Exa E 10⁻¹⁸ Atto a

10¹⁵ Peta P 10⁻¹⁵ Femto f

10¹² Tera T 10⁻¹² Piko p

10⁹ Giga G 10⁻⁹ Nano n

10⁶ Mega M 10⁻⁶ Mikro µ

10³ Kilo k 10⁻³ Milli m

10² Hekto h 10⁻² Zenti c

10¹ Deka da 10⁻¹ Dezi d

Grösse SI-Einheit Symbol

Länge Meter m

Zeit Sekunde s

Masse Kilogramm kg

Fläche Quadratmeter m²

Volumen Kubikmeter m³

Frequenz Hertz Hz =s⁻¹ =f rac1s

Geschwindigkeit Meter/Sekunde m s⁻¹ = ^m_s Beschleunigung Meter / Quadratse-

kunde m s⁻² = ^m_s2

Kraft Newton N =kg m s⁻² = ^{m kg}_s2

Energie, Arbeit,

Wärmemenge Joule J =N m=kg m² s⁻²^{kg m}_s2 ²

Druck, Ener-

giedichte oder

Joule/Kubikmeter Pascal P a=N m⁻² =J m⁻³ = ^kg_ms²

Leistung Watt W =J s⁻¹ = ^{kg m}_s3 ²

Dichte Kilogramm / Kubik-

meter kg m⁻³ = _m^kg3

Temperatur Kelvin K

Stromstärke Ampère A

Ladung Coulomb C=A s

Stromdichte Ampère / Quadrat-

meter A m⁻² = _m^A2

Spannung Volt V =J C⁻¹ = ^{kg m}_s3A²

Widerstand Ohm Ω =V A⁻¹ = ^{kg m}_s3A²²

Kapazität Farad F =C V⁻¹ = _{kg s}^s⁴^a²2

elektrische Feldstär-

ke Volt/Meter V m⁻¹ = ^{kg m}_s3A

magnetische Feld-

stärke Ampère/Meter A m⁻¹

magnetische Induk-

tion Tesla T =V s m⁻² = _{A s}^kg2

Induktivität Henry H =V s A⁻¹ = ^{kg m}_s2A²²

Lichtstärke Candela cd

Energiedosis Gray Gy =J kg⁻¹ = ^m_s2²

Aktivität Becquerel Bq=s⁻¹ = ¹_s

Stomenge Mol mol

(21)

2.3. Fehler

Dieser Sto wurde am 16.10.2001 behandelt (Siehe Tipler, Physik[Tip94, 3])

Jede Messung ist fehlerbehaftet

Beispiel in Vorlesung: Messung der Geschwindigkeit Es gibt drei Fehlertypen:

Grobe Fehler Entstehen durch Unachtsamkeit, mangelnde Kenntnis, usw.

Systematische Fehler Können prinzipiell bestimmt und auch nachträglich, bei korrekt geführtem Laborjournal, korrigiert werden. Sie treten immer in gleicher Weise auf.

Beispiel: Voltmeter mit abgelaufener Kalibrierfrist.

Zufällige Fehler Sie sind bei jeder Wiederholung einer Messung anders. Zu den zufälligen Fehlern gehören auch die Rundungsfehler bei digitalen Messgerä- ten.

Arithmetisches Mittel hxi= 1 n

Xn

i=1

x_i = 1

n(x₁+x₂+. . .+x_i+. . .+x_n) (2.1) Standardabweichung

sx = vu ut 1

n−1 Xn

i=1

(xi− hxi)² (2.2) Zufällige Fehler löschen sich teilweise aus, also ist

s_hxi= s_x

√n = vu ut 1

(n−1)n Xn

i=1

(x_i− hxi)² (2.3) Besteht ein Experiment aus mehreren Teilmessungen, muss das Fehlerfort- panzungsgesetz nach Gauss angewandt werden. Sei

Y =Y (X₁, X −2, . . . , X_m) (2.4) Dann ist der resultierende Fehler

s_Y = vu ut

Xm

j=1

µ ∂V

∂X_js_X_j

¶₂

(2.5) Beispielsweise ist der Druck bei einem zylinderförmigen Kolben durch p = _πr^F2

gegeben. Der fehler ist also

(22)

s_p =

sµ 1 πr²s_F

¶₂ +

µ−2F πr³ s_r

¶₂

(2.6)

2.4. Dimensionsanalyse

Die Dimension zeigt, wie eine Grösse von den Basisgrössen, z.B. Länge, Zeit und Masse abhängt. Wie man nicht Äpfel mit Birnen verrechnen kann, müssen bei einer physikalischen Gleichung die Dimensionen auf beiden Seiten übereinstimmen.

Die Dimensionsanalyse ist ein mächtiges Werkzeug, um zu testen, ob man richtig gerechnet haben könnte³.

Beispiel

x=x0+v0t+ 1

2a0t² (2.7)

Gleichung (2.7) ist richtig, wenn man wie unten für die Länge L und für die Zeit T einsetzt.

L= [X] =L= [x₀] = L

TT = [v₀t] = L

T²T² = [1

2a₀t²] (2.8) Beispiel: Schwingungsdauer eines Pendels

Die Schwingungsdauer t hängt von der Länge `, der Masse m und der Erdbe- schleunigung g ab. Also ist

t ≈m^αl^βg^γ (2.9)

oder

T¹ =M^αL^β µ L

T²

¶_γ

=L^β+γM^αT^−2γ (2.10) Der Exponentenvergleich ergibt α = 0, γ = −¹₂ und damit β = ¹₂. Wir erraten, dass die Schwingungsdauer eines Pendels wie

t≈ s

l

g (2.11)

ist, das korrekte Resultat, wenn man von Vorfaktoren absieht.

3Man kann damit beweisen, dass man einen Fehler gemacht hat, nicht aber dass man richtig gerechnet hat. Dies ist analog zur Neunerprobe

(23)

2.5. Literatur

Die Vorlesung orientiert sich an den Werken von Tipler[Tip94], Physik, und Gerthsen/Vogel[GV95], Physik. Zum Aufarbeiten des gelernten Stoes (nicht als Einsteigerliteratur) kann

auch Kneubühls[Kne74] Repetitorium der Physik empfohlen werden. Mathema- tische Probleme und Formeln sind sehr schön im Bronstein[BSMM00] zusammen- gefasst. Diese Datei gibt es auch als PDF-Datei⁴ und als Web-Site⁵.

4PhyIng1.pdf

5http://wwwex.physik.uni-ulm.de/lehre/PhysIng1/

(24)

(25)

[BSMM00] I.N. Bron²tein, K.A. Semendjajew, G. Musiol, and H. Mühlig. Ta- schenbuch der Mathematik. Verlag Harri Deutsch, 2000.

[GV95] Ch. Gerthsen and H. Vogel. Physik. Springer Verlag, 18. auage edi- tion, 1995.

[Kne74] F. Kneubühl. Repetitorium der Physik. Teubner Verlag, 1974.

[Tip94] Paul A. Tipler. Physik. Spektrum Verlag, 1994.

(26)

(27)

Mechanik starrer Körper

(28)

(29)

Die Kinematik befasst sich mit der Frage nach dem Wie einer Bewegung, nicht nach dem Warum.

3.1. Bewegung in einer Dimension

Dieser Sto wurde am 16.10.2001 behandelt

(Siehe Tipler, Physik[Tip94, 19]) (Siehe Gerthsen, Physik[GV95, 3]) Begrie:

Geschwindig- keit, Durch- schnittsge- schwindigkeit Aus dem Alltagsleben:

Durchschnittsgeschwindigkeit= Gesamtstrecke

Gesamtweg (3.1)

Physik: Mathematische Formulierung Gesamtweg:

∆x=x₂−x₁ (3.2)

Gesamtzeit:

∆t=t₂−t₁ (3.3)

Wir schreiben für die Durchschnittsgeschwindigkeit

< v >= ∆x

∆t = x₂−x₁

t₂−t₁ (3.4)

Was ist die Durchschnittsgeschwindigkeit bei drei Strecken(x₂−x₁),(x₃−x₂),(x₄− x3)hintereinander, die in den Zeiten(t2−t1),(t3−t2),(t4−t3)durchfahren werden?

< v >= ∆x

∆t = (x2−x1) + (x3−x2) + (x4−x3)

(t₂−t₁) + (t₃−t₂) + (t₄−t₃) = x4−x1

t₄−t₁ (3.5) Dieser Sto wurde am 17.10.2001 behandelt

Materialien:

(30)

Was bedeutet das, wenn wir (18. Jahrhundert) von Ulm nach Buchhorn (103 km, Durlesbach (-36 km (wir wandern zurück) , 9h) wandern?

Ulm, Durlesbach und Buchhorn liegen auf einem Kreissegment, also auf einer Linie. Also ist die Durchschnittsgeschwindigkeit

< v >= 103km−36km

35h+ 9h = 67km

44h ≈1.5km

h (3.6)

Der Sprachgebrauch im Alltag sagt:

< v >= 103km+ 36km

35h+ 9h = 139km

44h ≈3.2km

h (3.7)

Es wurde mit den Beträgen gerechnet.

Wir verwenden ausschliesslich die physikalische Denition nach Gleichung (3.5) und Gleichung (3.6) !

Graphische Darstellung einer linearen Bewegung

3.1.1. Momentangeschwindigkeit und Beschleunigung

Dieser Sto wurde am 17.10.2001 behandelt (Siehe Tipler, Physik[Tip94, 19]) (Siehe Gerthsen, Physik[GV95, 10]) Momentan-

geschwindig-

keit Momentangeschwindigkeit ⇔ Tangente ⇔ Ableitung v = lim

∆t→0

∆x

∆v = dv

dt = ˙x (3.8)

(31)

Graphische Darstellung einer linearen Bewegung Beispiel

Sei x(t) = Atⁿ+Bt^m. Dann ist v(t) = dx

dt = d

dt(Atⁿ+Bt^m) = nAtⁿ⁻¹+mBt^m−1 (3.9)

Beschleunigung ⇐⇒ Änderung der Momentangeschwindigkeit Beschleunigung Mittlere Beschleunigung

< a >= ∆v

∆t (3.10)

Momentanbeschleunigung

a(t) = lim

∆t→0

∆v

∆t = dv(t)

dt (3.11)

Beschleunigung und Ort

a(t) = dv(t)

dt = d^dx(t)_dt

dt = d²x(t)

dt² = ¨x (3.12)

Wie kommt man von einer bekannten Beschleunigung zum Ort?=⇒Integration Integration

Graphische Darstellung einer Geschwindigkeit und Integration

(32)

dv

dt =a (3.13)

Wir multiplizieren die obige Gleichung mitdt

dv=adt (3.14)

Nun integrieren wir auf beiden Seiten von der Zeit t= 0¹ bis t Zt

0

dv = Zt

0

adt (3.15)

und erhalten

v(t)−v(0) = a×t|^t₀ =a×t (3.16) oder mitv(0) =v₀

v(t) =v0+a×t (3.17) Dabei ist die Anfangsbedingung mit eingerechnet.

Weg:

dv

dt =v =v₀ +a×t (3.18)

Wir integrieren auf beiden Seiten Zt

0

dx= Zt

0

(v₀+a×t)dt (3.19)

und erhalten

x(t)−x(0) = (v₀×t+ 1

2a×t²)

¯¯

t

0

=v₀×t+ 1

2a×t² (3.20) oder mitx(0) =x₀

x(t) =x₀ +v₀×t+1

2a×t² (3.21)

Schauen Sie in einem Mathematikbuch oder (Siehe Tipler, Physik[Tip94, 30]) nach, wie die Integration durchgeführt wird

Materialien

• Bremsweg bei konstanter Beschleunigung²

1Sollte der Zeitwert für den Anfangswert des Integrationsintervalls nicht null sein, verschieben wir die Zeitskala um den entsprechenden Wert

2http://webphysics.ph.msstate.edu/jc/library/2-6/index.html

(33)

Gleichung (3.18) kann verstanden werden, in dem man realisiert, dass die Ge- schwindigkeit sich vonv₀ nachv₀+atändert, so dass< v >= ^v⁰^+(v₂⁰^+at) =v₀+¹₂at² ist.Gleichungen bei konstanter Beschleunigung

v = v₀+at x = x0+v0t+ 1

2at² (3.22)

Durchschnittsgeschwindigkeit

< v >= ∆x

∆t = (x₀+v₀t+ ¹₂at²)−x₀

t = 1

2(v₀ +v) (3.23) Wenn die Endgeschwindigkeit v_e = v₀ +at ist, erhält man aus ∆x = x(t) = v0t+ ¹₂at² mit t = ^v^e^−v_a ⁰

∆x=v0ve−v0

a + 1 2a

µve−v0

a

¶₂

= v0ve

a − v²₀ 2 + v²_e

2a − vev0

a + v₀² a

v_e² =v²₀ + 2a∆x (3.24)

3.2. Bewegung in zwei und drei Dimensionen

3.2.1. Vektoren und Vektorrechnung

(Siehe Tipler, Physik[Tip94, 47]) Vektoren

Materialien

• Graphische Vektoraddition³ Graphische Addition

Vektoraddition

3http://webphysics.ph.msstate.edu/jc/library/3-2a/index.html

(34)

Dieser Sto wurde am 23.10.2001 behandelt Materialien

Folien zur Vorlesung am 23. 10. 2001 PDF

Übungsblatt 2 vom 23. 10. 2001 (HTML oder PDF) Komponentenschreibweise

A= (A₁,A₂) = µ A₁

A₂

¶

(3.25) Länge

A= q

A²₁+A²₂ (3.26)

Winkel mit der x-Achse

cos(Θ) = A_x

A (3.27)

Einheitsvektoren ex in x-Richtung,ey in y-Richtung, ez-in z-Richtung.

A =A=Axex+Ayey+Azez (3.28) Addition

A+B = (A_xe_x+A_ye_y +A_ze_z) + (B_xe_x+B_ye_y+B_ze_z)

= (A_x+B_x)e_x+ (A_y+B_y)e_y + (A_z+B_z)e_z (3.29) Geschwindig-

keiten Geschwindigkeitsvektor

r =xe_x+ye_y+ze_z (3.30)

Mittlere Geschwindigkeit

(35)

<v >= ∆r

∆t (3.31)

Momentangeschwindigkeit

v= lim

∆t→0

∆r

∆t = dr

dt = ˙r (3.32)

Ableitung in Komponenten

v = lim

∆t→0

∆r

∆t = lim

∆t→0

∆xe_x+ ∆ye_y+ ∆ze_z

∆t

= lim

∆t→0

∆x

∆te_x+ lim

∆t→0

∆y

∆te_y+ lim

∆t→0

∆z

∆te_z (3.33)

also

v= dx

dtex+ dy

dtey+ dz

dtez (3.34)

Analog zur obigen Rechnung erhält man die Beschleunigung aus der Geschwin- digkeit.

Mittlere Beschleunigung

<a>= ∆v

∆t (3.35)

Momentanbeschleunigung

a = lim

∆t→0

∆v

∆t = dv

dt = ˙v = ¨r (3.36)

oder auch

a = dvx

dt e_x+ dvy

dt e_y +dvz

dt e_z (3.37)

Relativgeschwindigkeit

(36)

vM ensch gegen Erde =vBus gegen Erde+vM ensch gegen Bus (3.38)

Materialien

• Relativbewegungen⁴

• Kombination von Drehbewegung und Translation⁵

3.2.2. Bsp: Wurfbewegung

(Siehe Tipler, Physik[Tip94, 53])

Wurfbewegungen sind zusammengesetzte Bewegungen (Beispiel aus (Siehe Tipler, Physik[Tip94, 53]) )

Siehe auchSimulation von Walter Fendt⁶ Uni Heidelberg⁷ oderUni Würzburg⁸.

6http://home.a-city.de/walter.fendt/phd/wurf.htm

7http://physik1.physik.uni-heidelberg.de/vrlsg/data/detail/2-2-6.htm

8http://didaktik.physik.uni-wuerzburg.de/ pkrahmer/home/java1.html

(37)

Bild aus (Siehe Tipler, Physik[Tip94, 55]) . Rot ist die horizontale, grün die vertikale Position markiert. Die horizontalen Abstände sind, innerhalb meiner Zeichengenauigkeit, gleich, deuten also auf eine konstante Geschwindigkeit hin.

Beschleunigungen

Sei x(t= 0) = 0,y(t= 0) = 0, vx(t = 0) =vx,0 und vy(t= 0) =vy,0

a_y(t) = −g

a_x(t) = 0 (3.39)

Geschwindigkeiten

vy(t) = −g∗t+vy,0

vx(t) = vx,0 (3.40)

Ort

y(t) = −1

2g∗t²+vy,0∗t

x(t) = v_x,0∗t (3.41)

Diese Bewegung ist parabelförmig, wie man leicht sieht, wenn man x(t) nach t auöst und einsetzt.

y(x) =−1 2d

µ x v_x,0

¶₂ + v_y,0

v_x,0x (3.42)

(38)

3.2.3. Gleichförmige Kreisbewegung (mit vektorieller Darstellung)

Dieser Sto wurde am 23.10.2001 behandelt (Siehe Tipler, Physik[Tip94, 61]) (Siehe Gerthsen, Physik[GV95, 16]) Siehe auch Uni Würzburg⁹ oder vonWalter Fendt¹⁰.

Kreisförmige Bewegungen gibt es

• Fahrt durch eine Kurve mit Fahrrad, Auto, Schlittschuhen ...

• Zentrifuge

• Satelliten

Schematische Darstellung eines Satelliten

Der Satellit |v| = v bewegt sich im Kreis mit dem Radius r. In kleinen Zeiten t bewegt er sich um vt in der ursprünglichen Richtung weiter. Er fällt um h. Der Satz des Pythagoras angewandt auf das rechtwinklige Dreieck ergibt

r²+ (vt)² = (r+h)² =r²+ 2rh+h² (3.43) Kleine Zeiten bedeutet, dass h¿r ist. Also kann

F allgesetz, W eg und Beschleunigung (vt)² ≈2rh =⇒ h= ¹₂^v_r²t²

z }| {

= 1

2at² (3.44)

geschrieben werden.

Zentripetal- beschleuni-

gung Vergleich

9http://didaktik.physik.uni-wuerzburg.de/ pkrahmer/home/gravrot.html#rot

10http://home.a-city.de/walter.fendt/phd/karussell.htm

(39)

a_z = v²

r (3.45)

Wennr(t) = (rcos(ωt),rsin(ωt),0)ist ( ω heisst Kreisfrequenz und wird benö- tigt, um aus der Zeit eine als Argument der Winkelfunktion benötigte dimensions- lose Grösse zu erzeugen), dann ist

v(t) = d

dtr(t) = (−rωsin(ωt), rωcos(ωt),0) (3.46) und

a_z(t) = d

dtv(t) = d²

dt²r(t) = (−rω²cos(ωt),−rω²sin(ωt),0) =−ω²r(t) (3.47)

Zentripetalbewegung. Die durchr1,r2 und durchv1,v2aufgespannten Dreiecke sind ähnlich

Materialien

• Masse auf Kreisbahn mit Gegengewicht¹¹

3.2.4. Nichtkommutativität endlicher Drehungen

Materialien

(40)

Beispiel für die Nichtvertauschbarkeit endlicher Drehungen

Die mathematische Darstellung eine Drehung um die z-Achse kann wie folgt hergeleitet werden:

Jeder Vektor A =



 Ax

A_y A_z



 kann als A = Axex +Ayey +Azez geschrieben

werden. Dabei ist e_x =



 1 0 0



,e_y =



 0 1 0



, und e_z =



 0 0 1



. Die Funktion R_z(A, α) soll den VektorA um die z-Achse drehen.

Wenn der Vektor Aum die z-Achse gedreht wird, dann ist der gedrehte Vektor Rz(A, α) = A⁰ =



 f(A_x,A_y, α) g(Ax,Ay, α)

A_z



. Die z-Komponente wird dabei nicht verän- dert, die x- und die y-Komponenten sind Funktionen der ursprünglichen x- und y-Komponenten sowie des Winkels.

In der Abbildung links wird gezeigt, wie e_x transformiert wird. Rechts wirde_y transformiert.

Wir erhalten: R_z(e_x,α) = R_z







 1 0 0



,α



=



 cosα sinα

0



.

Rz(ey,α) = Rz







 0 1 0



,α



=



 −sinα cosα

0



.

R_z(e_x,α) =R_z







 0 0 1



,α



=



 0 0 1



.

Mit R_z(A,α) = R_z(A_xe_x +A_ye_y + A_ze_z,α) = A_xR_z(e_x,α) + A_yR_z(e_y, α) +

(41)

AzRz(ez, α) =  A_xcosα−A_ysinα Axsinα+Aycosα

A_z

. Diese letztere Gleichung kann als

R_z(A,α) =A⁰ =



 Axcosα−Aysinα A_xsinα+A_ycosα

A_z



=



 cosα −sinα 0 sinα cosα 0

0 0 1







 Ax

A_y A_z





(3.48) Damit kann eine Drehung um die Z-Achse kann als Matrix

D_z(α) =



 cos(α) −sin(α) 0 sin(α) cos(α) 0

0 0 1



 (3.49)

Durch formales Rotieren der Koordinaten z →y,y →x und x→z bekommt man die Drehmatrix für eine Drehung um die y-Achse

D_y(α) =



 cos(α) 0 sin(α)

0 1 0

−sin(α) 0 cos(α)



 (3.50)

Weiteres formales Rotieren der Koordinaten z → y, y →x und x → z liefert die Drehmatrix für eine Drehung um die x-Achse

D_x(α) =



 1 0 0 0 cos(α) −sin(α) 0 sin(α) cos(α)



 (3.51)

Die Drehung um die y-Achse um −π/2 (=90^◦) und dann um die x-Achse um

−π/2 wird mit Matrizen als

r⁰ = D_x(−π/2)D_y(−π/2)r

=



 1 0 0 0 0 1 0 −1 0







 0 0 −1 0 1 0 1 0 0







 1 0 0





=



 0 0 −1

1 0 0

0 −1 0







 1 0 0





=



 0 1 0



 (3.52)

Werden die Drehungen in umgekehrter Reihenfolge durchgeführt, so ist

(42)

r⁰ = D_x(−π/2)D_y(−π/2)r

=



 0 0 −1 0 1 0 1 0 0







 1 0 0 0 0 1 0 −1 0







 1 0 0





=



 0 −1 0 0 0 1 1 0 0







 1 0 0





=



 0 0 1



 (3.53)

Grosse Drehungen können nicht vertauscht werden. Es gibt viele

Eigenschaften in der Physik, die nicht kommutativ sind

(43)

Axiome

4.1. Trägheitsgesetz: Erstes Newtonsches Axiom

Alltägliche Beobachtung: alle Bewegung stoppt ⇒ Aristoteles nimmt dies als Naturgesetz an.

Newton argumentiert: Reibungskräfte stoppen die Bewegung. Wenn es keine Reibungskräfte gäbe würde sich der Bewegungszustand nicht ändern.

Erstes Newtonsches Axiom:

Wenn F = P

i

F

_i

= 0 ist, ändert ein Körper seinen Bewe- gungszustand nicht, d.h. er bleibt in Ruhe oder bewegt sich mit konstanter Geschwindigkeit.

1. Newtonsches Axiom , Trägheitsgesetz

Bsp: Galileis Gesetz (Siehe Tipler, Physik[Tip94, 72])

Bezugssystem Wir wählen einen Koordinatenursprung0und ein Koordinatensys- tem und schreiben alle Gleichungen in Bezug auf dieses Koordinatensystem auf.

Bezugssysteme können

• x in Bezug zur Erde sein

• x in Bezug zu einem Gefährt sein (Bus, Zug, Flugzeug,. . .)

• x in Bezug zur Milchstrasse sein

• . . .

Ein Bezugssystem, in dem das erste Newtonsche Axiom gilt, heisstInertialsys- tem.Gibt es Inertialsysteme?

(44)

4.2. Kraft, Masse,Impuls: Zweites Newtonsches Axiom

das zweite Newtonsche Axiom beantwortet die Frage: Was ist die Ursache der Bewegung?

Newtons Formulierung:

Die Änderung des Impulses (P = mv) eines Körpers ist gleich der auf den Körper wirkenden Kraft

F = dp

dt = d(mv)

dt (4.1)

Bernoullis Formulierung

^a

Die Beschleunigung eines Körpers ist umgekehrt proportional zu seiner Masse und proportional zur resultierenden Kraft a =

F m

aDiese Formulierung ist ein Spezialfall!

Das zweite Newtonsche Axiom wird auch Aktionsgesetzgenannt.

Bernoulli m muss konstant sein (analog zur Durchschnittsgeschwindigkeit) Newton analog zur Momentangeschwindigkeitmit

m =const

F = ^d(mv)_dt = ^dm_dtv+m^dv_dt = m^dv_dt =ma

Einheit der Kraft: 1N = 1

^mkg_s2

Materialien

• Experiment mit Luftkissenbahn und Fallgewicht¹

4.2.1. Masse ( m )

Dieser Sto wurde am 24.10.2001 behandelt Die Masse im zweiten Newtonschen Axiom ist die träge Masse.

Massenbestimmung mit dem 2. Newtonschen Axiom

(45)

• gleiche Kraft auf zwei Massen m1 und m2

• F =m₁a₁ =m₂a₂ ⇒ ^m_m¹

2 = ^a_a²

1

Masse: Einheit kg, deniert mit Urkilogramm in Sèvres ⇒ Sekundärnormale, Eichung!

4.2.2. Kraft ( F )

Dieser Sto wurde am 24.10.2001 behandelt Einheit der Kraft:N = ^{m kg}_s2 Name: Newton

Kraft und Bahnkurve r(t)bei konstanter Masse F =ma =mdv

dt =md²r

dt² (4.2)

d.h. die Kraft hängt von der Krümmung der Bahnkurve r(t)ab.

Impuls: Denition:p=mv Einheit ^mkg_s =Ns

Die Weiterentwicklung der Physik nach Newton (u.a. Quantenmechanik) hat gezeigt, dass der Begri des Impulses p universell verwendbar ist, nicht aber m und v.

Beantworten Sie die Fragen in (Siehe Tipler, Physik[Tip94, 78]) . 4.2.2.1. Drittes Newtonsches Axiom

Drittes Newtonsches Axiom:

Kräfte treten immer paarweise auf. Wenn vom Körper A aus auf den Körper B die Kraft F ausgeübt wird, so wird vom Körper B die Kraft −F auf den Körper A ausgeübt.

Diese Reaktionskraft ist also gleich gross wie die ursprüngliche Kraft, aber entge-

gengesetzt gerichtet.

Beispiele: Gewicht auf Tisch

(46)

Während das erste wie auch das zweite Newtonsche Axiom auch in der Quanten- mechanik und in der Relativitätstheorie gelten, versagt in diesen moderneren physi-

kalischen Theorien das dritte Newtonsche Axiom.

Bsp: Wirkt die Kraft instantan?

4.2.2.2. Kraft durch Gewicht und schwere Masse

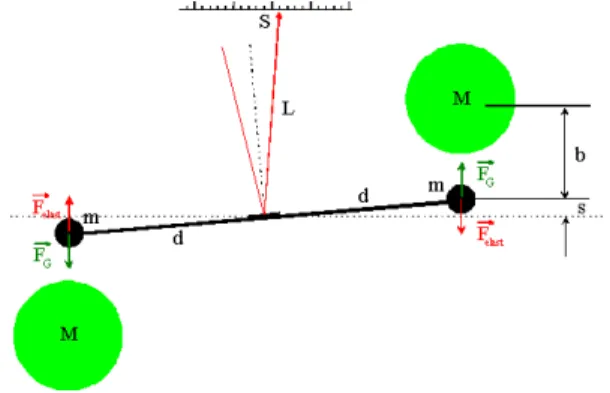
Dieser Sto wurde am 24.10.2001 behandelt (Siehe Tipler, Physik[Tip94, 78]) (Siehe Gerthsen, Physik[GV95, 46]) Jede Masse wird von jeder anderen Masse angezogen (Gravitation).

Die Erdanziehung auf eine Masse m ist

FG=mg (4.3)

|g|=g = 9.81^m_s2^s ist die Fallbeschleunigung auf Meereshöhe. ms ist die schwere Masse.

Anwendung: Massenbestimmung durch Kraftvergleich.

Wenn an einem Ort Fg,1 =Fg,2 ist, so ist auch m1 =m2. Wenn an einem Ort F_g,1 =αF_g,2 ist, so ist auch m₁ =αm₂.

4.2.3. Arten von Kräften

Materialien

Übungsblatt 3 vom 30. 10. 2001 (HTML oder PDF) Fundamentale Kräfte

1. Gravitationswechselwirkung

2. elektromagnetische Wechselwirkung

3. starke Wechselwirkung (Kräfte zwischen Kernbausteinen wie Protonen oder Neutronen

4. Schwache Wechselwirkung (Verantwortlich z.B. für den Zerfall der freien Neu- tronen).

Kontaktkräfte

Die Kraft ist proportional zur Auslenkung F =−kx, analog zur Feder. Anwen- dung: Federwaage.

(47)

4.2.4. Beispiele zur Lösung von Bewegungsproblemen

(Siehe Tipler, Physik[Tip94, 86])

FZ, FG und FN sind Kräfte auf den Körper F_Z =ma_x

Reaktionskraft aufFZ: F_Z⁰ =−FZ

3. Newtonsches Axiom: Kraft durch ziehende Hand = - Kraft auf Körper Wenn die Masse des Fadensm_F ist, ist

F −F_Z⁰ =m_fa_x

Masse des Fadens vernachlässigbar: F −F_Z⁰ ≈0

Fadenspannung

Bei vernachlässigbarer Masse ist |F_Z| überall im Faden gleich. F_Z heisst die Zugkraft.

Beispiel: schiefe Ebene

(48)

Schiefe Ebene

F_G,x=F_Gsin Θ =mgcos Θ F_G,y =−F_Gcos Θ =−mgcos Θ In unserem Koordinatensystem ist a_y null.

PF_y =F_N −mgcos Θ = 0 Also: FN =mgcos Θ

Die x-Komponente ist P

x =mgsin Θ =ma_x oder a_x =gsin Θ

Beispiel: Gewicht an einer Schnur

Links: Konstruktion mit Kräfteparallelogramm, rechts vergrösserte Ansicht.

Gegeben ist: F_g, α und β

Mit dem Sinussatz für beliebige Dreiecke (Seitenlänge dividiert durch den Sinus des Gegenwinkels ist konstant)

F_g

sin(α+β) = F₁

sin(π/2−β) = F₂

sin(π/2−α) (4.4) umgeformt

(49)

F1 = Fg cos(β) sin(α+β) F₂ = F_g cos(α)

sin(α+β) (4.5)

Schlussfolgerung: Wenn α und β gegen null gehen, dann werden die Kräfte F₁ und F2 sehr gross. Sie können leicht die maximal zulässige Seilspannung überstei- gen.

Beispiel: Zentrifugalregulator (Erndung von James Watt)

Schematische Darstellung des Wattschen Zentrifugalregulators. Die Masse m wird durch die Gravitation und die Seilspannung beschleunigt. Die resultierende Kraft ist die Zentripetalkraft FZ.

Zentripetalkraft

F_Z =mω²r=F_Zsin Θ (4.6) und

FZcos Θ =mg=FG (4.7) Zusammen

FZsin Θ

F_Zcos Θ = tan Θ = mω²r mg = r

gω² (4.8)

also ist für kleineΘ

ω = rg

r tan Θ≈ rgΘ

r (4.9)

Der Wattsche Regulator ist also ein Drehzahlmesser.

(50)

4.3. Anwendungen der Newtonschen Axiome

Dieser Sto wurde am 30.10.2001 behandelt (Siehe Gerthsen, Physik[GV95, 80])

Wir setzen voraus, dass wir alle Kräfte kennen: dann können wir die Beschleu- nigung und damit auch die bewegung eines Teilchens bestimmen.

4.3.1. Reibung

Erfahrung: wenn man versucht, ein Möbelstück zu verschieben, muss man eine Kraft ausüben.

Reibungskräfte versuchen, Bewegungen zu verhindern oder zu dämpfen

4.3.1.1. Haftreibung

Beobachtung: Wenn ein Körper mit der Kraft FN, der Normalkraft, auf einen anderen Körper gedrückt wird, wird mindestens eine Kraft

F ≥F_H =µ_HF_N (4.10)

benötigt, um den Körper in Bewegung zu setzen.F_H heisst Haftreibungskraft.

µ_H ist der Haftreibungskoezient.

Umgekehrt gilt die Aussage, dass wenn die zur Auageäche parallele Kraft F < F_H ist, bewegt sich der Körper nicht. Die Haftreibungskraft, englisch: stiction, ist eines der grössten Probleme in der Mikrosystemtechnik (englisch Micro-Electro- Mechanical-Systems, MEMS) und in der Festplattenindustrie.

4.3.1.2. Gleitreibung

Wenn ein Körper gleitet, dann gilt die Beziehung

F_G =µ_GF_N (4.11)

wobei F_G dieGleitreibungskraft und µ_G der Gleitreibungskoezient ist.

(51)

Schematische Darstellung der Haft- und Gleitreibungskraft als Funktion der angelegten, parallel zur Auage wirkenden Kraft.

Schematisch verhalten sich Haftreibungskraft und Gleitreibungskraft wie in der Abbildung gezeigt.

4.3.1.2.1. Eigenschaften

• µ_G≤µ_H

• µ_G hängt von der Relativgeschwindigkeit der Oberächen ab.F_G ist im Ge- schwindigkeitsbereich von 1cm/s bis einigen m/s näherungsweise konstant.

Ausserhalb dieses Geschwindigkeitsbereiches nimmt die Gleitreibungskraft zu.

• µ_G und µ_H hängen von der Struktur der Oberächen und ihrer Zusammen- setzung ab, nicht aber von der scheinbaren makroskopischen Kontaktäche A_M ab.

• µ_G und µ_H hängen von der wahren Kontaktäche A_W ¿A_M ab sowie vom Kontaktdruck in dieser Fläche. (Deshalb ist die Reibung zwischen ultraa- chen Endmassen extrem gross.)

4.3.1.2.2. Schlussfolgerung Die Reibung wird von temporären Bindungen zwischen den Atomen der Oberächen der einzelnen Reibpartnern gebildet. Zusätzlich und meistens auch dominierend ist jedoch die zur Abscherung mikroskopischer Er- höhungen (Asperities in englisch) benötigten Kräfte.

(52)

Kräfte auf einen Körper auf einer schiefen Ebene. Die x-Achse sei parallel zur Auage, die y-Achse senkrecht dazu.

XF_y =F_N −mgcosα= 0 (4.12)

XFx=mgsinα−FH = 0 (4.13)

Oder

F_H =mgsinα = F_N

cosαsinα=F_N tanα (4.14) Der Haftreibungskoezient ist gleich dem Tangens des Winkels, bei dem der Körper zu gleiten beginnt.

µH = tanαmax (4.15)

Gleitreibung wird durch Messung der Beschleunigung bestimmt.

F_x =mgsinα−µ_GF_G =ma_x (4.16)

a_x =g(sinα−µ_gcosα) (4.17) oder

µ_g = tanα− a_x

gcosα (4.18)