Festigkeitsberechnung von Kegelschalen mit linear veränderlicher Wandstärke

Research Collection

Doctoral Thesis

Festigkeitsberechnung von Kegelschalen mit linear veränderlicher Wandstärke

Author(s):

Honegger, Emil Publication Date:

1919

Permanent Link:

https://doi.org/10.3929/ethz-a-000098890

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

FESTIGKEITSBERECHNUNG VON KEGELSCHALEN MIT

LINEAR VERÄNDERLICHER

WANDSTÄRKE

VONDER

EIDGENÖSSISCHEN TECHNISCHEN HOCHSCHULE

IN

ZÜRICH

ZURERLANGUNG DER

WÜRDE EINES DOKTORS DER

TECHNISCHEN WISSENSCHAFTEN

GENEHMIGTE

PROMOTIONSARBEIT

VORGELEGT VON

EMIL HONEGGER,

DIPL. MASCH.-ING.

AUS HINWIL

(ZÜRICH)

REFERENT: HERR PROF. DR. E. MEISSNER KORREFERENT: HERR PROF. DR. A. STODOLA

219

LUZERN1919 BUCHDRUCKEREIKELLER & Co.

Leer

^-

Vide

^-

Empty

Meinem Vater

Leer

^-

Vide

^-

Empty

INHALTSVERZEICHNIS.

Seite

Einleitung ⁷

Bezeichnungen 9

I.Abschnitt: Mathematischer Teil.

§ 1. Ableitung ^der Grundgleichungen 12

§ ^2. Spezialfälle, welche eineVereinfachung ^desmathematischen Problems

gestatten 18

§ ^{3. Die} Integration ^der

homogenen Differentialgleichung

^{für den} Kegel

mit linear veränderlicher Wandstärke 21

§ ^{4. Die}partikulären Integrale^{der nicht}

homogenen Differentialgleichungen

³³

II. Abschnitt: Diskussion der praktischen Aufgabe.

§ 5. Die Randbedingungen ³⁹

§ ^{6. Die} elementaren Belastungsfälle 41

§ ^7. Erläuterung ^der Berechnungsweise ^{im Falle} zusammengesetzter ^Be¬

lastung ⁴⁴

§ ^{8. Die} elastischen Verschiebungen 48

III.Abschnitt: Numerische Berechnungen.

§ 9. Nach aussen verstärkter Kegel^{: a = 6°} 50

§ 10. Nach aussen verjüngter Kegel: ^{a = 6°} 59

§ 11. Nach aussen verjungte ebene Scheibe: a ⁼ 0° . . 62

§ 12. Nach aussen verjüngter Kegel: ^{a =} 29° 3' 12" 71

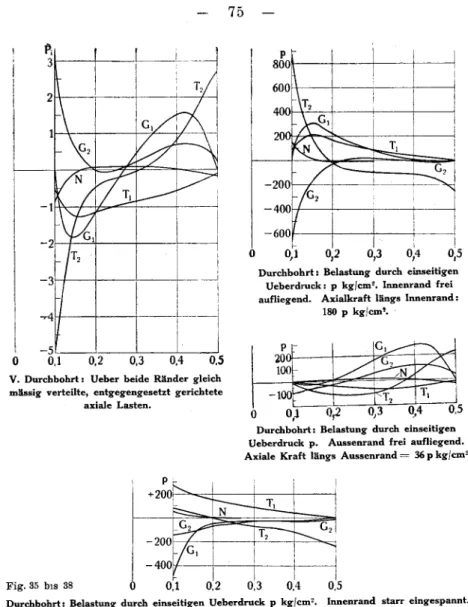
§ ^13. Graphische Integration ^der Grundgleichungen ^{nach der Methode von}

Prof. Meissner 75

§ 14. Besprechung ^{der Resultate und} Vergleich ^mit Kegelschalen ^unver¬

änderlicher Wandstärke 80

A. Kegel ^{von a = 6"} Neigungswinkel ⁸¹ B. Kegel ^{von a =} 29° 3' 12" Neigungswinkel ⁸⁸ C. Vergleich ^{der nach aussen linear} verjüngten Kegelschalen ^von

a — 6° und a = 29° 3' 12" 91

Leer

^-

Vide

^-

Empty

1

EINLEITUNG.

Diese,

^auf

Anregung

^{von Prof.} Meissner vorgenommene Unter¬

suchung

^dertechnisch

wichtigen Kegelschalen

^mit linear veränder¬

licher Wandstärke soll ein relativ

bequemes, praktisch

^verwend¬

bares Verfahren für die

Berechnung

des elastischen Verhaltens dieser Schalen erläutern. ^— Die

erste,

^{von Prof.}

Stodola1)

^an¬

gegebene Lösung

^{beschränkt sich auf}

Kegel

konstanter Wandstärke und erfordert die

Integration

^einer

Difierentialgleichung

^fünfter

Ordnung.

^{Prof. Meissner hat}

gezeigt2),

^{dass die} Difierential¬

gleichung

^vierter

Ordnung,

^{auf deren}

Integration

^das Problem bei

zweckmässiger

^{Wahl der} Unbekannten

hinausläuft,

^{in zwei}

Differentialgleichungen

^zweiter

^Ordnung zerfällt;

^die

Lösungen

dieser beiden

Gleichungen

^sind

konjugiert komplexe

^Grössen.

Für den

Kegel

konstanter Wandstärke hat Dr.

Dubois3)

^die

Verwendbarkeit der Methode ausführlich

dargetan;

^die

Lösung

wird alsdann durch Besselsche Funktionen

gegeben.

^{— Im vor¬}

liegenden Fall,

^{wo die} Wandstärke linear mit dem Abstand von

der

Kegelspitze

^sich

^ändert,

^{führt die}

Festigkeitsuntersuchung

^auf

eine

hypergeometrische Differentialgleichung,

^deren

Integrale

^durch

konvergierende

Reihen berechnet werden können.

Die

gewählten Bezeichnungen

schliessen sich _genau an die von Prof. Meissner verwendeten

an4),

^{denn diese}

verbürgen

^die

grösstmögliche

Einfachheit der

Darstellung.

^{Dazu weisen aber} diese

Bezeichnungen

ⁱⁿ

'

vorliegendem

Fall veränderlicher Wand¬

stärke noch einen

weitern,

wesentlichen Vorteil auf: sie

geben

^die

von einem

Schalenquerschnitt übertragenen

^{Kräfte und. Momente} in ihrer totalen Grösse ^und

zeigen

ⁱⁿ übersichtlicher

Weise,

^wie

') A.Stodola: Die Dampfturbinen ^(vierte Auflage, ^{Seite 597).}

2) E. Meissner:DasElastizitätsproblem^{für dünneSchalen.}Physikal.^Zeitschr.

14.Jahrgang. ^{Seite 343. — Ueber} Elastizität und Festigkeit ^{dünner Schalen} Vierteljahrschrift ^der Naturforschenden Gesellschaft Zürich. 1915, ^{Seite 23.}

s) ^Dubois: Festigkeit ^der

Kegelschale.

^{Diss. Zürich, 1917.}

4) ^In Uebereinstimmung^{mit: Love,} Lehrbuch der Elastizität. Deutschvon A.Timpe.

Leipzig

^1907.

jeder

^{Teil der dünnen Schale}

mittragen

^{hilft. Im}

Gegensatz

^hie-

zu würden die

spezifischen Spannungen,

^{die nicht nur mit den aus¬}

geübten

^{Kräften und}

Momenten,

^{sondern auch} noch mit der ört¬

lichen Schalenstärke veränderlich

sind,

^ein

schwerleserliches,

^un¬

deutliches Bild der Verhältnisse

geben.

Es sei noch

erwähnt,

^dass ein grosser Teil der numerischen

Berechnungen

^{mit einem 50 cm}

langen

Eechenschieber

ausgeführt

wurde. Dies erwies sich als genau genug, in Anbetracht der Ver¬

nachlässigungen,

die in der Theorie dünner Schalen

gemacht

^wer¬

den. ^— Wo grössere

Genauigkeit notwendig

war, wurde mit ^acht¬

stelligen Logarithmen gearbeitet.

Herrn Prof. Meissner bin ich für die

Unterstützung

^{bei der}

Entstehung

^{dieser Arbeit zu} grossem Dank

verpflichtet.

^Auch

Herrn Dr. Dubois möchte ich für manchen

guten

Eat meinen Dank

aussprechen.

BEZEICHNUNGEN.

a

Komplenient

^{zum halben}

Spitzenwinkel

^des

Kegels,

^{auf die}

Mittelfläche

bezogen.

s

Länge

^der

Erzeugenden,

^{von der}

Spitze

aus, in der Mittelfläche gemessen,

h Dicke der

Schale,

^{normal zur} Mittelfläche.

cp Breitenwinkel.

Fig.

^1.

Fig.l

Das Element der

Kegelschale,

auf welches die Grund¬

gleichungen bezogen

^werden

sollen,

^sei

begrenzt

^durch:

die beiden

Kegelmantelflächen,

^{welche die Schale selbst}

begrenzen

;

zwei

Meridianebenen,

^{die um den Winkel}

Hcp

voneinander abstehen_;

zwei

Kegelflächen,

^die die Mittelfläche der untersuchten

Kegelschale

^{im Abstand s und}

(s-f-ds)

^{von der}

Spitze

normal durchsetzen und ^mit ihr koaxial sind.

Durch den

geometrischen Mittelpunkt

dieses Elementes sollein

rechtwinkliges Koordinatensystem

^so

gelegt werden,

^dass: die

-|-

^{x-Achse mit der}

Mittelflächen-Erzeugenden

^zu¬

sammenfällt,

^im Sinne zunehmender s;

die

-\-

z-Acbse normal auf der

Kegelmittelfläche

^{steht und}

nach dem Innern des

Kegels zeigt;

die

-f- y-Achse

^{in die}

^Tangente

^{an den} Parallelkreis fällt und mit den x- und z-Achsen ein

rechtshändiges System

x, y, ^z bildet.

a%

Normalspannung

ⁱⁿ der

Eichtung -|-

x, im Abstände z von

der

Mittelfläche, zusammengesetzt

^aus:

axo Normalspannung

^{in der}

Mittelfläche,

^{von z}

unabhängig.

°xz

^{von z}

abhängiger

^{Teil von}

_ax.

o ⁼ a -4- _a

X xo I _xz

ebenso: a = er 4- _u

y yo ^I yz

r

Schubspannung,

^{wirkend in der koaxialen}

Normalkegelfläche.

Tj Normalkraft,

^auf

eine,

^die

Kegelmittelfläche

^{in einem Parallel¬}

kreis normal durchsetzendeFläche

wirkend,

^{von derim Parallel¬}

kreis _gemessenen

Länge

1 ; also:

Tj

⁼

oxo h.f)

^ebenso

gilt:

T2

^{= a h.} demnach ist:

T2

Normalkraft auf einen

Meridianschnitt,

^{von der} im Meridian gemessenen

Länge

^1.

Gl Biegungsmoment,

^{um die}

_y-Achse

drehend_; Fläche wie für

T,

; also:

Gi

⁼

6hS°«»«

^ebenso

^gilt:

"2 (J

°yz

max

N Eesultierende

Querkraft;

Fläche wie bei

T, (Fig. 2a).

N ⁼

j

^rdz

£ Deformationskomponente

ⁱⁿ

Kichtung -|-

^x.

3

Neigungswinkel

^der

Tangente

^{an die} deformierte

Erzeugende

der Schalenmittelfläche _gegen die x-Achse im undeformierten Zustand.

Fig.

^2.

dx ds

') Eigentlich^: Tj ⁼

I

<rxdz ( \_; aber z darf neben _p vernach-

«-^ ^{\ P /}

lässigt

^werden.

- 11 ^—

exo

Spezifische Dehnung

^{in der}

x-Richtung,

^{in der} Mittelfläche.

sx

Entsprechend,

^{im Abstände z von der} Mittelfläche.

e

Spezifische Dehnung

^{in der}

Mittelfläche,

^und

e _„

„im

^{Abstand z von}

^dieser,

^{in der y-}

Richtung.

Fig.²

X Aeussere

Belastung

pro Flächeneinheit der

Kegelmittelfläche,

in der

-{- ^x-Richtung

^wirkend.

Z

Desgleichen,

^{in der}

-\- z-Richtung.

E Elastizitätsmodul:

2.1X106.

v Poissonsche Konstante: 0<3.

Einheiten:

kg,

cm, ^sec.

Mathematischer Teil.

Eine

Kegelschale,

^deren Wandstärke

beliebig

^{mitdem Abstand}

von der

Spitze

^sich

ändert,

sei in

bezug

^{aufihre Achse}

symmetrisch

belastet. Das

homogene

^und

isotrope

^Material

_gehorche

dem Hookeschen

Gesetz;

^es werde also an keiner Stelle über die

Proportionalitätsgrenze,

^hinaus

beansprucht.

Infolge

^der

vollständigen Symmetrie

^{werden auf} einen Meridian¬

schnitt nur

Normalspannungen

^{wirken und} es werden

Punkte,

^die

vor der Deformation in einer

Meridianebene lagen,

^{auch nach} der Deformation in dieser

liegen.

Wir setzen voraus, ^{dass die}

Schalenstärke

klein sei im Ver¬

hältnis zu ihren

übrigen Abmessungen,

^{und dass} ferner die De¬

formationen klein seien im Verhältnis zu den

Scbalenabmessungen.

Dies erlaubt uns, ^die

Normalspannungen,

^{welche auf der}

_Kegel¬

mittelflächenormal

stehen,

^zu

vernachlässigen

^und

anzunehmen,

^dass eine Normale zur

Kegelmittelfläche

nach der Deformation normal auf der deformierten

Schalenmittelfiäche

stehe.

Im mathematischen Teil wird _vorerst die

Untersuchung

^all¬

gemein

^für

beliebige Veränderlichkeit

der Schalenstärke durch¬

geführt. Nachträglich

^werden

jene Spezialfälle herausgegriffen,

welche sich rechnerisch _besonders einfach

gestalten,

^{und von diesen}

der

Kegel

^mitlinear veränderlicher

Wandstärke eingehend

^behandelt.

§

^1.

Ableitung

^der

Grundgleichungen.

Gleichgewichts-Bedingungen.

Wird ein Element der

Kegelschale

^von dieser

losgetrennt

ge¬

dacht,

^{so kann sein}

Gleichgewicht

dadurch

ungestört

^{erhalten an¬}

genommen

werden,

dass in den

Schnittflächen

die früher wirkenden

Spannungen

^durch

gleich

grosse ^und

gleich gerichtete

äussere Kräfte ersetzt werden.

Gleichzeitig

^{sollen die schon} früher am

Element

angreifenden

äusseren Kräfte

weiterwirken.

— 13 ^—

Das

Kräftesystem,

welches auf ^das betrachtete Schalenelement

wirkt,

^{setzt sich}

folgendermassen

^zusammen:

a)

^Auf

eine,

^{in einem} Meridianschnitt

liegende Begrenzungsfläche

wirken:

1. eine Normalkraft:

dT2

⁼

T2ds

^{= hds}

ajo

^•

2. ein

Biegungsmoment:

dG2

⁼

G2ds

⁼

itfds _oyzmax

b)

^{Auf eine}

Begrenzungsfläche,

^{welche im Abstand s von der}

Kegelspitze

^{normal zur}

Kegelmittelfläche

^{steht und diese}

längs

eines Parallelkreises durchsetzt:

1. eine Normalkraft:

d

T,

⁼

Tj

^s

^ûcp

^{cos« = h s}

^àc/>

oxo ^{. cos«}

2. ein

Biegungsmoment

^:

d

Gx

⁼

Gl

^s

^&<p

^{cos« = -A\%s}

^dcp

oxz max

• cos«

3. eine

Querkraft:

d N ⁼

[j"

^t

dz]

^s

^Açp

^{cos« = N s}

^à.cp

^cos«

c)

^{Die äussere}

Belastung

^des

Kegels

^{sei durch ihre}

beiden,

^auf

dieFlächeneinheitder

Kegelmittelfläche bezogenen Komponenten

nach den 4- x- und 4-

z-Eichtungen gegeben.

^{— Nach Voraus¬}

setzung ^{wird die dritte}

Komponente,

^nach + y, ^zu Null. ^— Alsdann wirken auf das Schalenelement:

Xs cos«

dcp

^{ds Z scos«}

Acp

^ds

Ein

Kräftesystem genügt,

^{falls es im}

Gleichgewicht ist,

^den

6

Gleichgewichtsbedingungen.

^{Von diesen werden bei dem hier}

betrachteten

Kräftesystem

^{3 identisch}

befriedigt, infolge

^{der voraus¬}

gesetzten Symmetrie

^der

Belastung

; ^es sind dies die

Komponenten¬

gleichung

^{nach der}

y-Richtung

^{und die}

Momentengleichungen

^um

die x- und die z-Achsen. ^— Die 3

übrigen Gleichgewichts¬

bedingungen

^nehmen

folgende

^{Gestalt an}

(Fig. 2a):

1.

Koniponentengleichung

^{nach der}

x-Richtung:

0 ⁼ d

(s

^cos«

dcp

^h

oxo)

^{— h ff ds cos«}

^dcp -f-

^{X s cosa}

dcp

^ds

welche,

^{durch ds •}

dtp dividiert,

^auch

geschrieben

^werden

kann:

d

(sTj)

^—

T8 -f-

^{s X = 0. 1}

2.

Komponentengleichung

^{nach der}

z-Richtung:

0 = d

(s

^cos«

dcp N) -f-

^{s cos«}

dcp

^{ds Z}

-j-

^{h ds a}

dcp

^sin«

welche,

^{nach Division} durch

tga>ds<dcp

^auch

geschrieben

werden kann:

^(sN) ^{+ T2 tg« +}

^sZ

3.

Momentengleichung

^{um die}

y-Achse:

0.

d

(y

^{h2 s cos«}

^dcp

oxz max

)

^{^-h2 ds er} m„ cos« dcp 4-

6 yz ^{max ^} i

yz

max

— S COS«

dçp

^{N ds =} 0.

Nach Division mit cosa ^•

dçp

^{• ds}

d

ds

(s Gx)

^_

G2

^{— sN 0.}

— 15 ^—

Deformationszustand.

Die

Formänderung

^{wird in}

jedem

Punkte durch die beiden

Verschiebungskomponenten £

^und

£ gegeben.

Der

Krümmungsradius

g der deformierten

Erzeugenden hängt

mit dem

Neigungswinkel

^{3 der}

Tangente

^an diese durch die Be¬

ziehung

^zusammen:

1 d* däf _s. ^.

P ds ds2 ^{s *}

Die

spezifischen Dehnungen

^der

Kegelmittelfläche

^sind

gegeben

durch:

e ⁼

Ü

= i". ^{f = *}

~ ?**"

xo ds ^{- yo s}

Daraus

ergibt

sich für die

Dehnung

^einer Faser im Abstandz von der Mittelebene:

z

p

[s^COSa -j- Ç^{cosa —} (f

—(-

z) ^{sina — zsintf}cosa] ^— [s^{cosa - z} sina)

y ^S COSa ^— z sina

wo das erste Glied im Zähler den normalen Achsenabstand nach der

Deformation,

^{das zweite vor der}

Deformation, angibt.

^{— Wird}

imNenner dieses Ausdrucks^z

gegenüber

^s

vernachlässigt

^{und sin ^}

durch

tg

^{3" =}

£

^•

ersetzt,

^so

geht

^{er über in:}

e ^_ i ^— ? tgo Lt.— ^{% — i} tgg 1 _3, c

y s s ^* s s

Beziehungen ^zwischen Spannungen ^und Dehnungen.

Für einen ebenen

Spannungszustand ^gelten

^{nach dem Hooke'-}

schen Gesetz die

Beziehungen:

a ⁼ , 5 (ê ^{-1- v e}); ^{a =} , 5 (e -4- v e

)

^•

Da nach

Voraussetzung

^die

Normalspannungen

_az

vernachlässigt werden,

besitzen diese

Gleichungen

^im

vorliegenden

^Falle

Gültig¬

keit und

ergeben

^nach

zweckmässiger ^Umformung:

6

T ^— Eh /c. I _v ^{' -} S ^

• T ^— Eh

I*

^{— ; ^a}_{_I_} «

c.\

Ti ^—

r^i^

^{+ v} —g—)'

i2-r^z^l—s

^{r^ )}

7

Aufstellung ^der

Differentialgleichungen.

Wird aus den beiden

Komponentengleichungen (1)

^und

(2)

^die Kraft

T2 eliminiert,

^so

ergeben

^sie:

(sTj)'

^sin«

-f- (s N)*

^cosa

-f-

^{s X sin«}

-)-

^{s Z cos«= 0.}

Durch die Schreibweise:

F(s)

⁼

) [X

^sin«

-}-

^Z

cos«]

^{s ds A}

0

geht

^diese

Gleichung

in die Form über:

s

Tj

^sin«

-f

^{s N cosa = —}

F(s).

8

Diese

Gleichung sagt,

^{dass die zur} Achse des

Kegels parallelen Kräfte,

^{die an der Schale}

angreifen,

^{falls diese durch} einen den Parallelkreis s enthaltenden

Nonnalkegel abgeschnitten wird,

im

Gleichgewicht

^{sind. — Diese}

Gleichung,

^welche

ebensogut

^direkt

hergeleitet

^werden

kann,

^{kann eine der} beiden

Komponenten¬

gleichungen ersetzen, gegenüber

^{denen sie den}

symmetrischen

^Auf¬

bau als Vorteil aufweist.

Die

vorliegende Aufgabe

^besteht

darin,

^{für eine}

beliebige,

^den

gemachten Voraussetzungen genügende Belastung

^der

Kegelschale

die

Unbekannten;

3 Kräfte:

Tv T2, N,

2 Momente:

Gr„ G2,

2

Deformationskomponenten £

und

£,

als Funktionen des Ortes zu bestimmen. ^— Es ist

leicht,

^bei ge¬

gebener

Deformation der

Schale,

^die

übrigen

⁵

Unbekannten

zu

bestimmen,

^{wie aus den}

Gleichungen (6)

^und

(7)

^{zusammen mit}

(2)

^oder

(8)

ersichtlich ist_;

überhaupt

sind sämtliche Unbekannten

— 17 ^—

eindeutig feststellbar,

sobald zwei als Funktionen von s bekannt sind. Diese beiden Grundvariablen können

beliebig gewählt

^wer¬

den,

^{und die}

grösstmögliche

Einfachheit der

Differentialgleichung gewähren

die Unbekannten:

5 :

ieraus

=

£•;

!

folgt:

B ⁼ sT,

:

h2

Tx

^{= h3B}_s

T2

^{== 2 h h- B}

+

^h=:B"'

+s

^X

N =

F(8)

s cos«

—

s

B

tg«

S ffxo

h B

gemäss (1)

nach

(8)

Die eine

Differentialgleichung

^des Problems kann nun her¬

geleitet werden,

indem in der

Momentengleichung (3)

die Momente als Funktionen von •?> nach

(7) geschrieben werden,

^{und anderseits}

N

gemäss (9)

durch die Unbekannte B ersetzt wird. Die Momenten¬

gleichung

^{nimmt dann}

folgende

^{Gestalt an:}

s *••

+ ^(l + 3S^--f(3S^:-l)^

^|

=

18*5.

(1 _ *) B ⁺

^M-

(i ^_ ,,).

E h ^{v '} 'Eh3 cos« ^{v '}

Die zweite

Differentialgleichung

^wird

gefunden,

^{indem die}

Dehnungen

^{durch die}

Spannungen ausgedrückt

^{werden und dann}

verlangt wird,

^{dass die ersteren den}

Kompatibilitätsbedingungen genügen

^{sollen. — Nach}

(5)

^{ist für z = 0}

£yo

⁼

^{Uz±*&- also:£}

⁼

(£_ eyo

^s)

^cotg«.

f*

⁼

(ew

^-

£yo

^{- S}

V) ^GOtZa

^{= *• 10}

In dieser

Gleichung

^können:

£xo

⁼ _E-£

(Ti

^{- "}

T.)

yo

—

E h

À (T,

^{- -}

Tl}

gesetzt werden,

^{wo dann}

T1

^und

T3

ihrerseits durch die in B aus¬

gedrückten

Werte ersetzt werden. Auf diese Weise

ergibt sich;

II

sB-

+(1 +

³

s£)

^B-

^{+ (s[2 +} ,]hE ⁺ 2s^-l) §

⁼

h cotga |h- ^{v '} h ^{' >} h2 \ Das Problem ist nun

zurückgeführt

^{auf die}

Lösung

^{der beiden}

linearen,

^simultanen

Differentialgleichungen

^zweiter

Ordnung (I)

und

(II),

^{was im}

allgemeinen

dadurch erreicht werden

kann,

^dass

man die aus der Elimination der einen Unbekannten entstandene

Differentialgleichung

^vierter

Ordnung integriert.

§

^2.

Spezialfälle,

welche eine

Vereinfachung

^des

mathematischen Problems

gestatten.

Prof.

Meissner1)

^hat

gezeigt,

^{dass für besondere Formen der}

Kegelschale

^die

Differentialgleichung

^vierter

Ordnung

^{in zwei}

Differentialgleichungen

^zweiter

Ordnung

^zerfällt; diese

Spezialfälle

sollen nun

hergeleitet

werden.

Zur

Vereinfachung

^der Schreibweise seien

folgende

^Abkür¬

zungen

eingeführt:

L

(U)

^{= h}

cotg« [s

^U»

+ (1 +

^{3 s}

~)

^{U- —}

5]

^C

çp ^_ 2 v h*

cotga

j 12 (1 ^—v2)

D ^{*1- E} E

5P2 ⁼

K2 + v)

^h"

+

^{3 s}

h-] cotg« ^

^{= — E}

Die beiden simultanen

Differentialgleichungen (I)

^und

(II)

schreiben sich dadurch:

E h2 sina

L

(B) +

5V ^B=

h *-\S-è ^{(2 +}

^"- ¥

s) + ?

^x

_I cotg"-

') ^{E. Meissner: a. a.0.}

— 19 ^-

Die

vollständigen Integrale

^dieser

Gleichungen

^{setzen sich}

zusammen aus einem

Integral

^der

homogenen Differentialgleichung

und einem additiven

partikulären Integral.

^{Vorerst sollen die}

Integrale

^der

homogenen Differentialgleichung

^ermittelt

werden,

welche

Gültigkeit

^{haben bei}

jeder Belastung,

^abernur im besondern Falle verschwindender

spezifischer Belastungen

X und Z und Be¬

lastungsfunktion

^F

(s)

^{das Problem}

vollständig

^lösen.

Obige

^Glei¬

chungen gehen

^{über in:}

L

(») +

cpx ^{S =}

\

^B

L

(B) +

<p2 ^{B =}

À2

^S

Durch Eliminieren von

B, respektive

^•$:

L L

(3)

^{+ L}

(gp1 3) +

_cp%^L

(S) + (cPl

cp2 ^-

^ À2)

^{5«=0 IVa}

L L

(B) +

^L

(>2B) ⁺

<px^L

(B) + (^

<p2 ^-

lt À2)

^{B=0 2}

Es werde nun die besondere Annahme

gemacht:

L

p) + (c + f/l)

^{3 = 0 3}

worin c eine Konstante

ist,

^{über die noch}

verfügt

werden kann.

Durch

Ausführung

^der

Differenzialoperation

^{L an}

obiger Gleichung geht

diese über in:

L L

(3) -f

^L

(cPl 3) |

^{e L}

(J)

^{= 0 4}

und durchEliminieren von L L

($)

^{und L}

(3)

^{aus den}

Gleichungen (I), (IVa)

^und

(4) folgt:

[- (Vi

^-

^{c) (c} + 90 + {cpx

<pa ^-

Xx À2)]

^{» = 0}

c2

+ (SP!

^-

SPg)

^{c -}

X, \

^{= 0. 5}

Hierin ist alles

übrige konstant,

^{also muss auch} konstant sein:

CP\ ^— 9>2 ^{= 2}

k0

⁼

[3

^{yh* —}

(2 -f ?)

^{h* — 2 s}

h-] cotg«

⁶ C2

+

²

k0

^{c -}

\ \

^{= 0}

Ci

^=-

k0 + VVT^,T c*

^{= -}

ko

^-

iWT\h

⁷

Aus

Gleichung (6) folgt:

—

(1

^—

v)

^{h" — s h" =}

k0 ^tga.

Durch

Integration

^dieser

Gleichung ergibt

^{sich für die Wandstärke}

der

Kegelschale

^{das Gesetz:}

h ⁼ a

-f

^{b s}

+

^{e sv}

falls b ^{= —} jrzz~\ ^{un(i a un(l e}

Integrationskonstanten

^sind.

Gehorcht die Schalendicke dem Gesetz

(III),

^so

geht

^die

Differenzialgleichung

^vierter

Ordnung (I)

^{über in die beiden}

Differentialgleichungen

^zweiter

Ordnung:

L

(3) + (cx + Vx)

^{5 = 0} _|V

L

(*) 4 (c2 + *,)*

^{= °-}

Sind die beiden

vollständigen Integrale

dieser Differential¬

gleichungen

^{ermittelt in der}

;Form

^:

~si

⁼

Kt ^ + K2 32 \

⁼

K, 38 + K4 *4

wo mit K die

verfügbaren Integrationskonstanten

^bezeichnet

sind,

so kann die zweite

abhängige

Grundvariable leicht mit Hülfe der

Beziehungen (IV)

^und

(I') gefunden

^werden:

L

i\) + (cx + *>,) ^

^{= 0}

L

(^ +

cßl

^

⁼

}.t BT

cx

^

^{= -}

),x B,

V ebenso c2

$n

^{= —}

^Kx Bn

Um nun auf den besondern Fall zu

kommen,

bei welchem die Schalenstärke linear mit dem Abstand von der

Kegelspitze

^sich

ändert, genügt

es, im Ausdruck

(III)

^die

Integrationskonstante

e ⁼ 0 _zu setzen:

h ⁼ a

-f

^{b s. Ill'}

Hierdurch treten dann noch

folgende Vereinfachungen

^ein: cpx ^{= 3 v b}

cotg« k0

⁼

(v

^—

1)

^b

cotg«

(p2 ⁼

(2 -|- v)

^b

cotg« (1

^—

v)

^{b — —}

k0 tga

- 21 ^—

Die beiden

Differenzialgleichungen (IV)

^lauten

nunmehr,

ausführlich

geschrieben

^:

h

cotg« [

^{s >~}

^{+ (l +}

^{8 b}

^¥7)) *•-!]+

^IV-

+ I ^{(1 +}

²

^v)

^b

^cotg«

^±

^{^(T—v)^ cotg2^—}

¹²

⁽¹

^—v*

^{) 1}

^3=0.

§

^{3. Die}

Integration

^der

homogenen Differentialgleichung

für den

Eegel

mit linear veränderlicher Wandstärke.

Normalform der hypergeometrischen Differentialgleichung.

In den im

vorhergehenden Paragraphen gefundenen Gleichungen (IV),

^{welche im hier} betrachteten Falle

Gültigkeit besitzen,

^lassen

sich wesentliche

Vereinfachungen

^durch

folgende

^{Variablen-Sub¬}

stitution erzielen:

s ^{= —}

^

^{t h = a}

⁽¹

^—-

^t)

Es werden dadurch:

A

^— _

A A ^

i_

^! di

ds a dt ds2 ^' a2 dt2

Werden dann ferner die

Abkürzungen eingeführt:

o-x ^{= 2 v}

+ y/(i

^-

^vf

^-

^JIb^2 ^tg2«

ffj! ^{= 2 v —}

\/(l

^-

^vf

^-

^{^} (1b7

^v2)

^tg2«

so schreiben sich die beiden

Differentialgleichungen:

O

+ lt=î ⁺ t)

^dt

⁺ U ⁺ °i) Fct^ï)

^=°

d«* , , w , .,.- , ,. , , ^-

=0 IV

dta +

\t

^{—1 "T}

^t)

^{dt "I \t "T}

"2/

t(t-l)'

Dies sind zwei

hypergeometrische Differentialgleichungen,

deren

allgemeinste

Form lautet:

')

1 ^—a ^—a' ^. 1—y^— y'\T7, ^, |-'oo' , r/ , aa,\ ^Y Y"

+ (^^+i^^)Y'

⁺

(=^

⁺

^{^+* x(x-ir}

^:()

]) Felix Klein: „Ueber ^die hypergeometrische Funktion." Autographie.

Leipzig. ^{Teubner. 1906. — Seite 46.}

Durch

Vergleichen entsprechender Koeffizienten,

unter Berück¬

sichtigung

^{der zwischen den}

Exponenten

^der

hypergeometrischen Differentialgleichung geltenden Beziehung1):

«

+

^a'

+ ^/? + /?'+

r

+ ^y'

⁼

^1,

ergeben

sich für diese

folgende

^Werte:

+

¹ y ⁼ 0

ß

⁼

+ }

⁺

y/y-

- 0,

2 ^' V ₄ "i

Diese Werte beziehen sich auf die erte der

Gleichungen (IV);

um die

Exponenten

^{der zweiten}

Gleichung

^zu

erhalten, genügt

es, in den

Beziehungen ß

^und

ß',

a{ ^durch u2 ^zu

ersetzen,

^während

a,

«',

7 und

7'

unverändert bleiben.

« und «' sind die zum

singulären

^{Punkte t = 0}

gehörigen Exponenten

^der

hypergeometrischen Funktion,

^während

ß

^und

/?'

dem Punkte t ^{= °°} und y und

y'

^{dem dritten}

singulären

^Punkt

t ⁼

—|—

¹

zugeordnet sind.2)

Integrale ^{für die} Umgebung ^{von t = o.}

Ein erstes

Integral

^{der ersten}

Differentialgleichung (IVT")

^kann

ohne weiteres

hingeschrieben

^werden:

worin2)

^:

^

^{= t • F}

(a1 bL

c,

t)

a, ⁼

/?+« +

7 ⁼

} ⁺ \/t

^{'- °'i}

Cj ^{= 1 — a — a'— 3}

- °"i

VI

F(a, b,

c,

t)

^{= 1}

+ ^t+ ^{^t«^±i)}

_(c

₊

₁₎ ^f

⁺

l ^a (a

4-

1) (a

+

^{2) b} (b

+

i) (b

+

2) _f3 ,

' 3! c (c + 1) (c

-f

2) ^~T

1) ^F.Klein: a. a. 0. Seite 43.

2) ^Die

folgenden

Kechnungen ^beziehen sich, ^wenn nicht anders vermerkt, immer auf die erste der Gleichungen (IV").

— 23 ^—

Aus der

Symmetrie

^der

Differenzialgleichung folgt,

^dass y und

f gleichberechtigt sind;

^{daher kann das eben}

angeführte Integral

auch in einer andern Schreibweise

gegeben werden,

^{indem in}

obigen

Werten überall _y durch

>''

^{ersetzt wird:}

^

^{= t}

⁽¹

^-

^t)2F (a,' b/ c/ ^t)

^VT

worin

V ^{=/?+« + 7'}

⁼

| ⁺ v/f3^

C ⁼ 3

Das

Integral 3, konvergiert jedenfalls

^{im Innern des Einheits¬}

kreises,

^{d. h für}

|t]

^{< 1. Ob es auf dem} Einheitskreise auch noch

konvergiert,

^{muss erst} untersucht werden. Diese

Frage

^soll

aber hier nicht weiter

verfolgt werden,

weil sie für die

folgenden zahlenmässigen Berechnungen,

^{wo nur rasch}

konvergierende

^Inte¬

grale

verwendet werden ^{und 5} demnach höchstens für

jt|

^{< 0 • 5}

berechnet werden _muss, ohnehin

belanglos

^ist.

Es sei noch

erwähnt,

^{dass das}

gefundene Integral ^

^leicht

auf elementarem

Weg hergeleitet

^werden

kann,

^{indem die Reihe:}

A

+

^Bt

+

^Ct2

+

^{D f}

+

^Et4

-f

^{= 3}

in die

Gleichung (IV") eingesetzt wird,

^woraus sich das bereits bekannte

Koefflzientengesetz

^ohne

Schwierigkeiten ergibt.

Ein

zweites,

^{in der}

^Umgebung

des Punktes t ⁼ 0

gültiges Integral

^kann

gewöhnlich

^{aus dem ersten}

gefunden werden,

^indem in diesem überall ^« und «' miteinander vertauscht werden. Auch das zweite

Integral gestattet

^zwei

gleichwertige Schreibweisen, je

^{nach dem y oder}

y'

^zur

^Berechnung

^der Koeffizienten heran¬

gezogen wird. ^{— Im}

vorliegenden

^Fall würde aber:

C, ⁼ 1

-|-

^{«' — a = — 1}

und es wären daher sämtliche Glieder der

irypergeometrischen

Reihe nach dem zweiten unendlich _gross. ^Die Reihe würde ihre

Bedeutung

^verlieren.

Um ein zweites

Integral

^zu

finden,

^{muss die}

angeführte

^kri¬

tische

Wirkung

^der

ganzzahligen

^Differenz:

a ^— a' ⁼

-f-

²

umgangen

werden,

^was durch einen

Grenzübergang

erreicht wird. ^— Es sei s eine kleine

Zahl,

^die

beliebig

klein werden

soll;

a ^—• «' ⁼⁼ 2

+

^{* 0:' = a -- 2 -- £ : — 1 — e. 1}

Alsdamn werden:

--ß+

^«'

=

/? +

^«'

= l ^-

+

7"

— a ^-

1

—

2 1

~~

2

-«i*

^{= 3}

+

^{£ —= (}

£

=

h

-2 ^—

— 2

£

2

«£

⁼

+ \/|

^—

^ffi

3

\

⁼

-v/4

^{— °"i £}

cî

^{== 1}

+

^{«' — « = — 1 — £ =} ci ^{4 — e.}

Folglich

^:

T^—

t;1-^!-

^, (a,-2--<0(V^8-«). , ("1-2-e)(aj^-1-e){b1-2-

£)(brl

-«)4-

+ ] ^«

Wird nun diese Eeihe

multipliziert

^mit:

v~' '

(aj ^{— 2 —} e) (at^{— 1—}e) (bj ^-2-~<:) (bt ^{— 1 —} £) ^"

und

nachträglich

^{£ = 0}

_gesetzt,

^so

geht

^{sie über in das} erste

Integral 3r

^{— Wird also} die lineare Kombination

gebildet

^:

.* __

|~m

(2, e) *3 ^-

tfj

^ ^-

L

^;

J

£ ⁼ o

soist $* ein zweites

Integral

^der

vorliegenden Differentialgleichung.

Dieses kann auch

geschrieben

^werden:

^n*

[

^{m (2, e)e»92 - i9t «}

_J

£ =r 0.

Hierin hat m

(2, a) 32

^{die Form:}

t ^-1-« 2! (- ^{1 -} «) (-e)

f"

1 ^, (at^-2-e) (bt^-2-e) ^.

]

^.

(a1-2-E)(a1-l-£)(b1-2-£)(b1-l-E)[

^{' (—1 —} *)

J

^'

i

t+1-£fl

^{I (ai-£)(bi-}

f)t

^{i (%-e) (axH-1-e)(a2-g)(a2}

⁺

^1-*)t

2

_i_

lg

"T"

L ³ (1^—e) "T" 3^•4^•(1^—f)(2^—«) ^{"" "''}

J

- 25 ^-

Wird im zweiten Ausdruck ^{6 = 0}

gesetzt,

^so

geht

^er genau in die Form

-5^

^{über. Wird der erste} Ausdruck durch ^s dividiert und wird

nachträglich

^{a = 0}

gesetzt,

^{so lautet er:}

t ^'

(«4^-2) (14^-1) (bi-2)

(bi -~ï) +

(ax^- 1)(bj^- 1)

=

E(^t) Folglich

^hat man, falls der ^erste Ausdruck

(6)

^{nach dem Grenz¬}

übergang

^mit

E-(t),

^{der zweite vor dem}

Grenzübergang

^mit

rI>(s)

bezeichnet wird:

5

v2

â

⁼

[^-fL

^{= o}

^{+ K»}

Wie ohne weiteres

ersichtlich,

^{wird das erste Glied nach dem}

Grenzübergang

^{die Gestalt annehmen:}

- t

Igt

^F

(at b,

ct

t) +

^t

6>'(t).

⁷

Im Ausdruck

(7)

^hat

6>'(t)

^{die Gestalt:}

ö'(t)

⁼

c,'

^t

+ c;

^t2

+ C8'

^t3

+ C4'

^t4

+

⁸

p ^{, __}at (ai

+

1) ^{.. ..} (at+^n-1)bi (bt +1). ^{. .}(bx +^{n-1) ft}

n

—

3-4

(2-f-n)-n!

^«

' 9

.

Y ^,_l

¹

^1_\

Dieses Gesetz lässt sich am einfachsten herleiten durch

logarith¬

mische Differentiation des

allgemeinen

^{Gliedes der} unendlichen Reihe ^<I>

(«):

7 M (at^—e)^-f^1—e)^.,..(at-fn^—1—e)(bt^—e) ^....ibt+^n—1—e) ^, n

^nW— (1 ^- £) (2^— <0 ^{. . . .} (n^— e) ^{• 3 • 4 . . . .} (2+n) Nun ist:

d llg Zn(e)] _

1 d ZD(e)

de Zn(e) ^de

d Zn(e) ₇ ^{, s d} [lg Zn(e)|

—5T- ^{= A.00} de"

Die

Ableitung

^von

lg Za(c)

^{nach £}

^gibt,

^{nachdem e = 0}

^gesetzt

wurde,

die Summe im Ausdruck

(9)

; der ^vor der Summe stehende Faktor ist

Zn(0).

^—

Das zweite Glied im Ausdruck

(5")

^{lässt sich in}

gleicher

Weise berechnen und

ergibt:

[•f]

^{e = 0 = * 0"}

^{W 10}

0"

(t)

⁼

C/'

^t

-f C/' t2+ C3" t'-|-

^{' 11}

12

n ^» _ ai (ai

+

1) (ai

+

^n-l) bt (bt

+

^n—1) ^

3 ^•4 . . . . (2 + n) ^•n!

=q \ 3

+

^v.

Werden nun die

Ergebnisse (7)

^und

(10)

ⁱⁿ

(5") eingesetzt,

so wird:

$*2

^=-

tlgt.F (a, b,

Cl

t) +

^t

02 ^(t)

^-

ï-—ï2__ ⁺

^V||

+

_(ax - 2)

(^njl^-lMbr^7!)

^{* *}

worin:

ß2 (t)

⁼

C,

^t

+ C2

^t2

-J- C8

^t3

+ C4

^t*

+

^Vila

p ^>! f»! | 1) ^{. , . .} (at

-f

^{n -} 1) ht ^{. , , ,} (bt

|

^{n - 1)}

n

—

3 ^. 4 ^. 5 ^. . . . . (3

-f

n) ^n!

V _{f^_}

_+.

JL

^{i i}

'„to ^U+"

"•" 3

+

^v ax

+

^v

( b±

+

Das

vorliegende

^zweite

Integral

^hätte auch in elementarer Weise

hergeleitet

^werden

können,

^{durch Einsetzen} der Funktion:

~\ ^lg

^t

+

_j

+

^A

+

^{B t}

+

^{C t2}

+

^{1) t3}

+

^{E t*}

+

⁼

3,

in die

Differentialgleichung (IV"). Allerdings

^{setzt das die} Kennt¬

nis der

allgemeinen

^{Form von}

32

^voraus.

Das

vollständige Integral

^der

homogenen Differentialgleichung (IV")

lautet somit:

* =

KÏ$1 + K2 V, ^«

wo mit K die aus den

Randbedingungen

^bestimmten

Integrations¬

konstanten bezeichnet sind. Wie schon

erwähnt,

^{hat diese}

Lösung

nur

Gültigkeit

^für

|t|

^<

1,

da sie für

grössere

^Werte des

Arguments

^nicht

konvergiert.