Karlsruher Institut f¨ur Technologie Institut f¨ur Theoretische Festk¨orperphysik Ubungen zur Modernen Theoretischen Physik I¨ SS 14
Prof. Dr. Gerd Sch¨on L¨osungen zu Blatt 1
Andreas Heimes, Dr. Andreas Poenicke 23.04.2014
1. Photoelektrischer Effekt und Gegenfeldmethode (2 Punkte)
(a) (1 Punkt) Der Zusammenhang zwischen kinetischer Energie der Elektronen, Aus- trittsarbeit und Energie der Photonen ist gegeben durch
Ekin =hf −Φ
(b) (1 Punkt) Die Elektronen durchlaufen eine SpannungeU. Stellt man die Spannung entsprechend ein, so dass der Strom durch den Amperemeter gerade verschwindet, entspricht die kinetische Energie der Elektronen gerade
Ekin=eU.
Wir erhalten entsprechend den Zusammenhang h= e(U1−U2)
f1−f2
= 0,42eV
1014Hz = (0,42·1,602·10−19J)10−14s= 6,73·10−34J s.
Der Literaturwert w¨are h= 6.62606957(29)·10−34J s.
2. Delta-Funktion (2 Punkte)
(1 Punkt) Zun¨achst zeigen wir die Normierung der Delta-Folgen (a)-(c).
(a) Z ∞
−∞
dx 1
√2πe−x
2
2 = 1
√π Z ∞
−∞
dye−y2 = 1
√π Z ∞
−∞
dx Z ∞
−∞
dye−x2e−y2 1/2
= 1
√π Z 2π
0
dϕ Z ∞
0
dr r e−r2 1/2
= 1
√π
−πe−r2
∞ r=0
1/2
(b)
Z ∞
−∞
dx 1 π
x2+2 = 1 π
Z ∞
−∞
dy 1
1 +y2 = 1
πatan(y)
∞
y=−∞= 1 (c)
Z /2
−/2
dx1 = 1 (1 Punkt) Es reicht weiterhin zu zeigen, dass lim→0
Rdx δ(x)f(x) =f(0).
Z ∞
−∞
dx δ(x)f(x) = Z ∞
λ
dx δ(x)f(x) + Z −λ
−∞
dx δ(x)f(x) + Z λ
−λ
dx δ(x)f(x)
F¨ur jede der Dirac-Folgen (a)-(c) finden wir eine Nullfolge λ → 0 f¨ur → 0, so dass lim→0Rλ
−λδ(x) = 1. Der Mittelwertsatz der Integralrechnung liefert dann f(ξ1)
Z ∞ λ
dx δ(x) +f(ξ2) Z −λ
−∞
dx δ(x) +f(ξ3) Z λ
−λ
dx δ(x)
mit ξ1 ∈(λ,∞), ξ2 ∈(−∞,−λ), ξ3 ∈[−λ, λ]. Insbesondere gilt f¨urf(x) = 1, nach Vorraussetzung, dass
→0lim Z λ
−λ
δ(x) = 1⇒ lim
→0
Z ∞ λ
dx δ(x) = lim
→0
Z −λ
−∞
dx δ(x) = 0 und damit
→0lim Z ∞
−∞
dx δ(x)f(x) = lim
→0f(ξ3) Z λ
−λ
dx δ(x) =f(0)
Alternativ k¨onnen wir diesen Zusammenhang explizit f¨ur die jeweiligen Dirac-Folge zeigen, z.B. f¨ur den Lorentz:
→0lim Z ∞
−∞
dx 1 π
x2+2f(x) = lim
→0
Z ∞
−∞
dy 1 π
1
1 +y2f(y) =f(0) Z ∞
−∞
dy 1 π
1
1 +y2 =f(0).
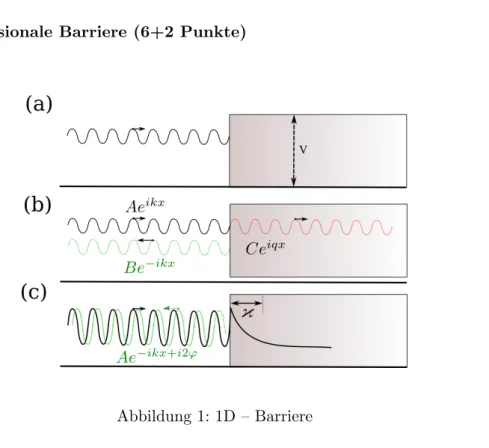
3. Eindimensionale Barriere (6+2 Punkte)
Abbildung 1: 1D – Barriere Gegeben sei die eindimensionale Schr¨odingergleichung
i~∂ψ(x, t)
∂t =−~2 2m
∂2ψ(x, t)
∂x2 +V(x)ψ(x, t) (1)
mit dem Potential
V(x) =
0 , x <0
V , x≥0 . (2)
Weiter sei V reel und positiv.
(a) (2 Punkte)Stetigkeitsbedingungen:
Wir machen den Ansatz ψ(x, t) =φ(x)e−iωt und erhalten
~ωφ(x) =−~2 2m
∂2φ(x)
∂x2 +V(x)φ(x) (3)
Die Integration von (3) ¨uber den IntervallI= (x0−, x0+) liefert Z x0+
x0−
dx~ωφ(x) =−~2 2m
∂φ(x)
∂x
x0+ x=x0−
+ Z x0+
x0−
dx V(x)φ(x).
Sind sowohlφ(x) als auchV(x) beschr¨ankt im IntervallI, so k¨onnen wir die Inte- grale nach oben absch¨atzen,
Z x0+ x0−
dx~ωφ(x)
<2~ωmaxx∈I|φ(x)|
Z x0+ x0−
dx V(x)φ(x)
<2maxx∈I|V(x)φ(x)|
Im Limes →0 gilt
lim→0 2~ωmaxx∈I|φ(x)|= 0 lim→0 2maxx∈I|V(x)φ(x)|= 0 Damit erhalten wir die Stetigkeit der Ableitungen
→0lim
∂φ(x0+)
∂x = lim
→0
∂φ(x0−)
∂x
Aus der Stetikeit der Ableitung in jedem Punktx0 folgt direkt auch die Stetigkeit der Funktionφ(x).
(b) (2 Punkte)Wellenfunktion f¨ur~ω > V: Durch Einsetzen des Ansatzes
φ(x) =
A eikx+B e−ikx x <0
C eiqx x≥0 (4)
in (3) finden wir
~ω= ~2k2
2m ⇔~k=√ 2m~ω
~ω= ~2q2
2m +V ⇔~q =p
2m(~ω−V)
Aus den Stetigkeitsbedingungen lim→0φ(−) = lim→0φ() und lim→0∂φ(−) = lim→0∂φ() folgen die Beziehungen
A+B=C k(A−B) =qC und damit
r = B
A = k−q k+q t= C
A = 2k k+q
Die Stromdichte ergibt sich aus j(x, t) = ~
2mi ψ∗(x, t)∂xψ(x, t)−ψ(x, t)∂xψ∗(x, t)
= Re ~
miψ∗(x, t)∂xψ(x, t)
= Re ~
miφ∗(x)∂xφ(x)
Durch einsetzen von (4) finden wir jL(x, t) = ~k
m(|A|2− |B|2) = ~k m|A|2
(k+q)2
(k+q)2 −(k−q)2 (k+q)2
= ~|A|2 m
4k2q (k+q)2 jR(x, t) = ~q
m|C|2 = ~|A|2 m
4k2q (k+q)2
Damit w¨are die StromerhaltungjL=jR gezeigt.
(c) (2 Punkte)Wellenfunktion f¨ur~ω < V: Da nun ~ω < V ist, finden wir q=ip
2m(V −~ω) und somitκ =p
2m(V −~ω).
Die entsprechende rechtsseitige Wellenfunktion ist also gegeben durch φ(x) =Ce−κx.
Wir finden also eine exponentiell unterdr¨uckte Aufenthaltswahrscheinlichkeit im klassisch verbotenen Bereich. Die charakteristische Eindringtiefe ist gegeben durch
∆x∼1/κ. Der Reflektionskoeffizient ist nun gegeben durch r= B
A = k−iκ
k+iκ = eiϕ
e−iϕ =ei2ϕ
mit tan(ϕ) = −κk. Zun¨achst stellen wir fest, dass |A|2 =|B|2, die Welle wird also totalreflektiert. Desweiteren erh¨alt die reflektierte Welle gegen¨uber der Einfallenden eine zus¨atzliche Phasenverschiebung, wie in Abb. 1(c) angedeutet. Wir finden
ϕ=−atan
p1−~ω/V p
~ω/V
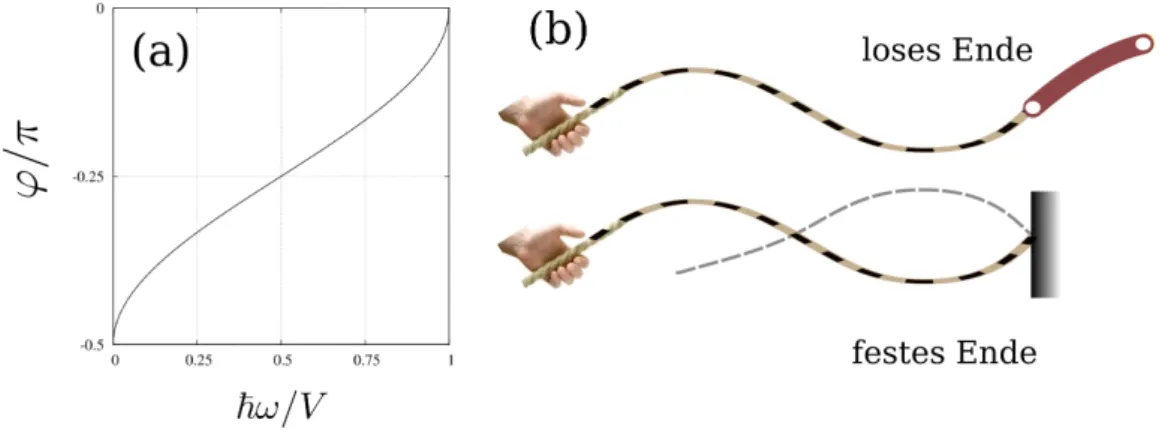
Wie wir Abb. 2(a) entnehmen k¨onnen, variiertϕzwischen −π/2 f¨ur~ω→0 und 0 f¨ur~ω→V. Die beiden Grenzf¨alle entsprechen in der klassischen Mechanik jeweils der Reflektion einer ebenen Welle an einem festen oder losen Ende (siehe Abb. 2 (b)).
Dort geht die Reflektion an einem festen Ende auch mit einer Phasenverschiebung von π einher.
(d) (2 Punkte)Bonus-Aufgabe: Totalreflektiertes Wellenpaket Wir betrachten das reflektierte Wellenpaket
ψref(x, t) = Z
dk g(k)ei[−ω(k)t−kx+2ϕ(k)]
. (5)
Der Integrand liefert den gr¨oßten Beitrag in dem Bereich, in dem der Phasenfaktor θ(k) =−ω(k)t−kx+ 2ϕ(k) station¨ar ist. Aufgrund der speziellen Form von g(k) entwickeln wir diesen in linearer Ordnung ink−k0,
−ω(k)t−kx+ 2ϕ(k) =−ω0t−k0x+ϕ0+ ∂ω
∂kt−x+ 2∂ϕ
∂k
k=k0
(k−k0) +· · ·
Abbildung 2: Totalreflektion
Wir betrachten die Zeitverz¨ogerung an der Barriere. F¨ur x = 0 verschwindet die Klammer, falls
∂ω
∂k k=k0
∆t= 2∂ϕ
∂k k=k0
Hierbei istvg = ∂ω/∂k|k=k
0 die Gruppengeschwindigkeit des Wellenpakets und
∂ϕ
∂k k=k0
=− ∂
∂katan κ
k
k=k0
=− k2 k2+κ2
∂kκ k − κ
k2
k=k0
=− k2 k2+κ2
− 1 κ
− κ k2
k=k0
= 1 κ k=k0
Damit erhalten wir
∆t= 2 1 vgκ
k=k0
(6) Dieses Ergebnis ist einleuchtend: Die Welle dringt ∆x ∼ 1/κ tief in die klassisch verbotene Region ein und hat eine Gruppengeschwindigkeit vg. F¨ur den Hin- und R¨uckweg der L¨ange 2∆x ben¨otigt die Welle also die Zeit ∆t= 2∆x/vg= 2/κvg.