Absence of gravitational contributions to the running Yang-Mills coupling

arXiv:0710.1002v2 [hep-th] 16 Oct 2007

MPP-2007-145 HU-EP-07/49

Absence of gravitational contributions to the running Yang-Mills coupling

Dietmar Ebert ^1,2 , Jan Plefka ² , and Andreas Rodigast ²

1

Max-Planck-Institut f¨ ur Physik (Werner-Heisenberg-Institut) F¨ ohringer Ring 6, D-80805 M¨ unchen, Germany

2

Institut f¨ ur Physik, Humboldt-Universit¨ at zu Berlin, Newtonstraße 15, D-12489 Berlin, Germany debert@mppmu.mpg.de, plefka,rodigast@physik.hu-berlin.de

The question of a modification of the running gauge coupling of (non-) abelian gauge theories by an incorporation of the quantum gravity contribution has recently attracted considerable interest.

In this letter we perform an involved diagrammatical calculation in the full Einstein-Yang-Mills system both in cut-off and dimensional regularization at one loop order. It is found that all gravita- tional quadratic divergencies cancel in cut-off regularization and are trivially absent in dimensional regularization so that there is no alteration to asymptotic freedom at high energies. The logarithmic divergencies give rise to an extended effective Einstein-Yang-Mills Lagrangian with a counterterm of dimension six. In the pure Yang-Mills sector this counterterm can be removed by a nonlin- ear field redefinition of the gauge potential, reproducing a classical result of Deser, Tsao and van Nieuwenhuizen obtained in the background field method with dimensional regularization.

PACS numbers: 12.10.Kt, 04.60.-m, 11.10.Hi

Perturbatively quantized general relativity is well known to be a non-renormalizable theory due to the neg- ative mass dimension of its coupling constant κ [1]. The coupling to matter fields does generically not improve the situation [1, 2, 3], although the possibility of pertur- bative finiteness of the maximally supersymmetric grav- ity theory is still open [4]. Hence, Einstein’s theory of gravity does not constitute a fundamental theory as its non-renormalizability necessitates the inclusion of an in- finite set of higher dimension counterterms in the per- turbative quantization process. Nevertheless, as advo- cated by Donoghue [5], it may be treated as an approx- imation to a fundamental theory of quantum gravity by the methodology of effective field theories in order to de- scribe interactions at scales well below the Planck mass M P ∼ 1/κ ∼ 10 ¹⁹ GeV.

In an interesting recent paper Robinson and Wilczek [6] reported on a calculation in Einstein gravity coupled to Yang-Mills theory, where the quantum gravity con- tributions to the running of the Yang-Mills coupling g were investigated at one-loop order. Interestingly a neg- ative gravitational contribution to the Callan-Symanzik β function, which quantifies the flow of the Yang-Mills coupling with the energy scale E, was found

β g ≡ dg

d ln E = − b 0

(4π) ² g ³ + a 0

(4π) ² E ² κ ² g , (1) with a 0 = − 3/2 in our conventions for the gravitational coupling κ ² , see (2). Irrespective of the non-gravitational value of b 0 this would render any gauge theory assymp- totically free at energies E close to the Planck mass (in- cluding e.g. pure U (1) Maxwell theory). Responsible for this effect were quadratic divergencies in one-loop graphs containing the graviton propagator [7]. As a number of discussed scenarios of physics beyond the standard model contain higher dimensional gravity theories with small gravitational scales, such an effect might be observable at the Large Hadron Collider, as was qualitatively stud- ied in [8].

However, two recent works have cast doubts on the results of [6] by reconsidering this effect in Einstein- Maxwell theory. The authors of [6] used the back- ground field method, which contains subtle dependen- cies on gauge conditions leading to gauge dependent re- sults of the effective action. To our undestanding the essence of the problem in [6] lies in expanding the grav- itational field about flat Minkowski space and the gauge field about a nontrivial solution of the flat space Yang- Mills field equations, which does not constitute a solution of the coupled Einstein-Yang-Mills system. Indeed in [9]

Pietrykowski repeated the analysis of [6] in the abelian theory employing a parameter dependent gauge condition and obtained a gauge dependent result. In a very recent analysis Toms [10] pointed out the aforementioned sub- tleties in the background field approach and studied the problem in Einstein-Maxwell theory employing an elab- orated gauge invariant and gauge condition independent formulation of the background field method due to Vilko- visky and De Witt [11]. Here dimensional regularization was used and a vanishing gravitational contribution to the gauge coupling β –function was found.

In view of these discussions it should be stressed that

the question of one loop divergencies in the Einstein-

Yang-Mills theory was already studied more than 30

years ago in the classical work of Deser, Tsao and van

Nieuwenhuizen [3]. In a background field approach con-

sidering fluctuations about a general gravitational and

gauge field background the necessary one loop countert-

erms were computed by these authors in dimensional

regularization. In the pure Yang-Mills sector only one

dimension–six counterterm of the form Tr[(D µ F ^µν ) ² ]

arose, which moreover must be removed through a non-

linear field redefinition of the gauge field. Hence already

these results were in contradiction with the findings of

[6]. However, one might be worried about the use of

dimensional regularization in all these computations, it

being insensitive to quadratic divergencies which at the

same time give rise to a nonvanishing a 0 in the Callan-

2 Symanzik β –function (1) as reported in [6] using a cutoff

prescription.

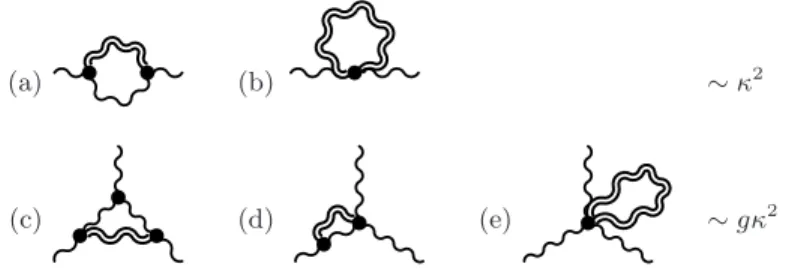
In view of the recent interest in the problem, its poten- tial experimental relevance and the discussed technical controveries we have conducted a conceptually straight- forward but involved diagrammatical calculation in the full Einstein-Yang-Mills system in cut-off and dimen- sional regularization. For this the gravitational contribu- tions to the gluon self-energy and vertex function were evaluated at one loop order. The relevant diagrams are listed in figure 1. We find that all quadratic divergen- cies cancel in cut-off regularization, and they are triv- ially absent in dimensional regularization. The logarith- mic divergent contributions are substracted by precisely the dimension–six countertem found by Deser, Tsao and van Nieuwenhuizen [3] confirming their results and show- ing explicitly the non-renormalizability of the Einstein- Yang-Mills theory. In particular the β –function of the Yang-Mills coupling constant g receives no gravitational contributions at the one loop order, in contradiction to the findings of [6], i.e. a 0 = 0 in (1).

The starting point of our analysis is the Einstein-Yang- Mills theory

L EYM = 2 κ ²

√ − g R − ¹ ₂ √

− g g ^µρ g ^νσ Tr [F µν F ρσ ] , (2) with the Ricci scalar R and the Yang-Mills field strength F µν = ∂ µ A ν − ∂ ν A µ − i g [A µ , A ν ]. In the renormalization process we will be led to add additional dimension–six operators to this theory, as discussed above. The metric tensor is split into a flat Minkowski background η µν = diag(1, − 1, − 1, − 1) and the graviton field h µν

g _µν = η µν + κ h µν . (3) The Einstein-Yang-Mills lagrangian is then expanded up to second order in h µν in order to read off the relevant propagator (modulo gauge fixing) and gluon-graviton vertices occuring in figure 1. We work in Feynman gauge for the gluons and in harmonic (de Donder) gauge for the gravitons with the gauge condition ∂ ^ν h µν = ¹ ₂ ∂ µ h. The resulting graviton propagator reads

αβ p γδ =

i

I ^αβ,γδ − _d−2 ¹ η ^αβ η ^γδ

p ² + i0 . (4)

with I ^µν,αβ ≡ ¹ 2 (η ^µα η ^νβ + η ^µβ η ^να ). As gravitational ghosts do not couple to gluons they do not appear in our one-loop computations. We furthermore note the two gluon–one graviton vertex [15]

p q

µ a ν b

α β = − iκδ ^ab

P ^µν,αβ p · q + η ^µν p ^(α q ^β) + ¹ ₂ η ^αβ p ^ν q ^µ − p ^ν η ^µ(α q ^β)

− q ^µ η ^ν(α p ^β)

(5)

and the two gluon–two graviton vertex

p µ a q

ν b αβ

γδ

= i 2 κ ² δ ^ab

(p ^ν q ^µ − p · q η ^µν )P ^αβ,γδ +p · q(2I ^µν,α(γ η ^δ)β + 2I ^µν,β(γ η ^δ)α

− I ^µν,αβ η ^γδ − I ^µν,γδ η ^αβ ) +2p ^(α q ^β) P ^µν,γδ + 2p ^(γ q ^δ) P ^µν,αβ +

2p ^α η ^ν[µ η ^β](γ q ^δ) +2p ^γ η ^ν[µ η ^δ](α q ^β)

− p ^ν (q ^α P ^µβ,γδ + q ^β P ^αµ,γδ +q ^γ P ^αβ,µδ + q ^δ P ^αβ,γµ ) + { (p, µ) ↔ (q, ν) }

,

(6) where we have defined P ^µν,αβ ≡ ¹ 2 (η ^µα η ^νβ + η ^µβ η ^να − η ^µν η ^αβ ). Using these expressions we have computed the divergent pieces of the two–gluon graphs (a) and (b) of figure 1 with an incoming momentum of q to be

(a) = i

16π ² κ ² (q ² η ^µν − q ^µ q ^ν ) δ ^ab h

− 3 2

Λ ² 0

− q ² 6

log Λ ²

2 ǫ

+ finite i , (b) = i

16π ² κ ² (q ² η ^µν − q ^µ q ^ν ) δ ^ab 3 2

Λ ² 0

, (7)

where we quote both the cut off ( | k ² | < Λ ² ) and di- mensional (d = 4 − ǫ) regularized results. For details of the calculation see [12]. Note the cancellation of the quadratic divergence which already leads to the absence of gravitational corrections to the β function of g in the abelian theory.

For an abelian gauge theory this would be all there is to do, as there are no cubic gauge field vertices. In order to substract the remaining divergence in (7) at a given renormalization point µ we have to augment the Einstein- Yang-Mills lagrangian (2) by novel dimension–six coun- tertems. Taking into account the Bianchi identity there are naively three possible structures

O ¹ ≡ Tr[ (D µ F νρ ) ² ] , O ² ≡ Tr[ (D µ F ^µ ν ) ² ] , O 3 ≡ i Tr[ F µ ν F ν ρ F ρ µ ] . (8) However, it turns out that they are linearly related up to total derivative terms

O 2 = 1

2 O 1 − 2 g O 3 + total derivatives . (9)

We are thus led to add the terms d 1 O ¹ and d 2 O ² to

our lagrangian, where d 1,2 are the corresponding cou-

pling constants. Note that the term d 2 O 2 in the ex-

tended effective lagrangian is proportional to the low-

est order equations of motion D µ F ^µν = 0 and could

be removed by a field redefiniton of the gauge field

A µ → A µ − d 2 D ν F ^ν µ /2 up to higher dimension oper-

ators.

3

(a) (b) ∼ κ

²

(c) (d) (e) ∼ gκ

²

FIG. 1: Graviton loop corrections to the gluon two and three point functions.

The new two gluon vertices of d 1 O 1 and d 2 O 2 are

µ a q ^O

¹

ν b = 2i d 1 δ ^ab q ² (q ² η ^µν − q ^µ q ^ν ) , (10)

µ a q ^O

2

ν b = i d 2 δ ^ab q ² (q ² η ^µν − q ^µ q ^ν ) . (11)

The associated counterterms to these vertices can be used to cancel the logarithmic poles of (a) + (b) in (7). How- ever, due to the identical tensor structure of (10) and (11) these two counterterms are only fixed up to one free parameter.

In order to fix this free parameter we move on to the three–gluon graphs (c), (d) and (e) which probe the non–

abelian sector of the theory. Expanding L EYM to cubic order in gluons and up to quadratic order in gravitons we read off the relevant three gluon–one graviton vertex

p q k

µ a

ν b ρ c

αβ

= − gκf ^abc h

P ^αβ,µν (p − q) ^ρ +η ^µν η ^ρ(α (p − q) ^β) +cycl(µ, p; ν, q; ρ, k) i

(12)

and the involved three gluon-two graviton vertex

p q

k

αβ µ a ν b

ρ c

γδ

= 1

2 gκ ² f ^abc

(p − q) ^ρ (2I ^µν,α(γ η ^δ)β +2I ^µν,β(γ η ^δ)α − I ^µν,αβ η ^γδ

− I ^µν,γδ η ^αβ − η ^µν P ^αβ,γδ ) +2

(η ^µν P ^γδ,ρ(β

+I ^µν,γδ η ^ρ(β )(p − q) ^α) + { (α, β) ↔ (γ, δ) } +cycl(µ, p; ν, q; ρ, k)

.

(13) With these the evaluation of the three–gluon graphs of figure 1 can be performed, and we find the divergent con-

tributions in cut-off and dimensional regularization (c) = 1

16π ² gκ ² f ^abc (

(η ^µν (p ^ρ ( 5 6 p · q + 1

4 q · k)

− q ^ρ ( 5 6 q · p + 1

4 p · k)) + . . . )

− 5

6 (k ^µ k ^ν (p − q) ^ρ + . . . )

− 1

4 (p ^ρ q ^µ k ^ν − p ^ν q ^ρ k ^µ ) )

log Λ ²

2 ǫ

, (14)

(d) = 1

16π ² gκ ² f ^abc (

h (η ^µν (p ^ρ ( − 7 6 p · q − 1

6 p · k − 3 4 q · k)

− q ^ρ ( − 7 6 q · p − 1

6 q · k − 3

4 p · k) + . . . ) + (k ^µ k ^ν (p − q) ^ρ + . . . )

+ 3

4 (p ^ρ q ^µ k ^ν − p ^ν q ^ρ k ^µ ) i log Λ ²

2 ǫ

+ 3

2 (η ^µν (p − q) ^ρ + . . . ) Λ ²

0 )

, (15)

(e) = − 1

16π ² gκ ² f ^abc 3

2 (η ^µν (p − q) ^ρ + . . . ) Λ ²

0

, (16) where the external gluons carry the labels (µ, p; ν, q; ρ, k) and the dots refer to a symmetrization in these labelings.

Summing these contributions up we again observe a can- cellation of the quadratic divergencies arising in cut–off regularization. In order to subtract the remaining log- arithmic divergencies in the three–gluon amplitudes we need to consider the three point vertices of d 1 O 1 and d 2 O 2 emerging from (8)

p q

k

µ a ν b

ρ c

O

₁

= d 1 gf ^abc

η ^µν (p ^ρ (4p · q + 2p · k)

− q ^ρ (4q · p + 2q · k)) + . . .

− 2 (k ^µ k ^ν (p − q) ^ρ + . . . )

, (17)

p q

k

µ a ν b

ρ c

O

₂

= d 2 gf ^abc

η ^µν (p ^ρ (2p · q + p · k + 3q · k)

− q ^ρ (2q · p + q · k + 3p · k)) + . . .

− (k ^µ k ^ν (p − q) ^ρ + . . . )

− 3(p ^ρ q ^µ k ^ν − p ^ν q ^ρ k ^µ ) .

(18)

4 Remarkably it turns out that O ² alone provides the right

tensor structures to remove all the divergences of (14)- (16). Renormalization of the two and three point gluon functions is then performed by considering the extended effective Einstein-Yang-Mills theory augmented by d 2 O ² plus all the associated counter terms. The complete ef- fective lagrangian at the one-loop level is then of the schematic form

L = L ext + L CT ,

L ext = L EYM, ren + d 2 Tr[(D µ F ^µν ) ² ] , L CT =δ 2 (∂A) ² + g δ ^3g ₁ A ² ∂A + δ ₁ ^2d

²

(∂ ² A) ²

+ g δ ₁ ^3d

²

∂ ² A ∂AA + O (A ⁴ ) . (19) The computed divergencies are then substracted at a renormalization scale µ through a choice of renormaliza- tion conditions. This leads to the following κ ² dependen- cies of the dimension–six counterterms

δ ^2d ₁

²

_O(κ

₂

₎ = δ ₁ ^3d

²

_O(κ

₂

₎ = 1 16π ²

1 6 κ ²

( log( ^Λ _µ

²₂

)

2 µ

^−ǫ

ǫ

) , (20) where the first equality δ ^2d ₁

²

| ^O (κ

²

) = δ ₁ ^3d

²

| ^O (κ

²

) arises as a necessary condition on the renormalization of the gluon selfenergy and vertex function and constitutes an inde- pendent consistency check of our results as required by the Slavnov-Taylor-Ward identity. Also note that this countertem is in prescise agreement to the one found by Deser, Tsao and van Nieuwenhuizen [3] with the back- ground field method. In particular the Yang-Mills vertex counterterm δ 1 and wavefunction renormalization δ 2 re- ceive no contributions at order κ ² . The counterterms (20) then lead to the following relations of renormalized g, d 2 to bare g 0 , d 2,0 couplings at one loop order

g g 0

= 1 + 3

2 δ 2 − δ ₁ ^3g , d 2

d 2,0

= 1 + δ 2 − δ ₁ ^2d

²

d 2,0

. (21)

This then provides the following gravitational contribu- tions to the β functions of the gauge coupling g and the novel coupling d 2

β g

_O

(κ

²

) = 0, β d

₂

_O

(κ

²

) = 1 (4π) ²

1

3 κ ² . (22) However, the renormalization of d 2 through gravitational interactions is not of particular relevance as this coupling can be removed through a nonlinear field redefinition as mentioned above.

Let us qualitatively extend our discussion to the gluon four point function. A simple dimensional considera- tion of loop integrals for the gluon four point function yields a new operator structure κ ⁴ Tr(F ⁴ ), which can- not be removed by the above quoted field redefinition.

This is in agreement with the findings of [3], where it was shown that such terms appear as the square of the energy-momentum tensor, (T µν ) ² .

Interesting further extension of this work would be to consider large extra dimension scenarios, where a cut- off prescription appears mandatory, as well as the cou- pling to additional matter fields. The case of gauged N extended supergravities was considered in [13] in the background field method with dimensional regulariza- tion, where a vanishing of the beta function for N > 4 was found.

Acknowledgments

We would like to thank Harald Dorn, Dieter L¨ ust, Kelly Stelle and Stefan Theisen for important discussions. D.E.

expresses his gratitude to Dieter L¨ ust and his colleagues for the kind hospitality at the Max-Planck-Institute for Physics (Werner-Heisenberg-Institute) and for financial support. Our computation made use of the symbolic ma- nipulation system FORM [14].

[1] G. ’t Hooft and M. J. G. Veltman, Annales Poincare Phys.

Theor. A 20 , 69 (1974).

[2] S. Deser and P. van Nieuwenhuizen, Phys. Rev. D10 (1974) 411; Phys. Rev. D10 (1974) 401.

[3] S. Deser, H. S. Tsao and P. van Nieuwenhuizen, Phys. Rev.

D10 (1974) 3337.

[4] E. Cremmer and B. Julia, Phys. Lett. B80 (1978) 48; B. de Wit and H. Nicolai, Nucl. Phys. B208 (1982) 323; Z. Bern, J. J. Carrasco, L. J. Dixon, H. Johansson, D. A. Kosower and R. Roiban, Phys. Rev. Lett. 98 (2007) 161303.

[5] F. Donoghue, Phys. Rev. Lett. 72 (1994) 2996; Phys. Rev.

D50 (1994) 3874.

[6] S.P. Robinson and F. Wilczek, Phys. Rev. Lett. 96 (2006) 231601.

[7] S.P. Robinson, PhD Thesis, M.I.T., 2005.

[8] I. Gogoladze and C.N. Leung, Phys. Lett. B645 (2007) 451;

Q. G. Huang, JHEP 0703 (2007) 053.

[9] A.R. Pietrykowski, Phys. Rev. Lett. 98 (2007) 061801.

[10] D.J. Toms, Phys. Rev. D76 (2007) 045015.

[11] G.A. Vilkovisky, Nucl. Phys. B185 (1981) 189;

B.S. DeWitt, in Quantum Field Theory and Quantum Statistics, Volume 1, Adam Hilger, Bristol, 1987.

[12] A. Rodigast, Diploma thesis, Humboldt University Berlin, 2007; available at http://qft.physik.hu-berlin.de.

[13] S. M. Christensen, M. J. Duff, G. W. Gibbons and M. Rocek, Phys. Rev. Lett. 45 (1980) 161.

[14] J.A.M.Vermaseren ”New features of FORM”, math-ph/0010025.

[15] The brackets [. . .] and (. . .) denote unit weight

anti–symmetrization and symmetrization respectively, i.e.

Λ

[a

1...an]

=

n¹!

(Λ

^a₁^...an

± permutations) and Λ

₍a

1...an)

=

_n¹_!

(Λ

a₁...an

+ permutations).