Untersuchung der elektronischen Struktur von CuO mit resonanter Röntgen-Raman-Streuung

Untersuchung der elektronischen Struktur von CuO mit resonanter

R¨ ontgen-Raman-Streuung

Dissertation

zur Erlangung des Doktorgrades der Naturwissenschaften des Fachbereichs Physik der Universit¨ at Dortmund

vorgelegt von Gordon D¨ oring

September 2001

Zweiter Gutachter: Prof. Dr. M. Tolan

Tag der m¨ undlichen Pr¨ ufung: 26. Oktober 2001

Inhaltsverzeichnis

Einleitung 1

1 Grundlagen der unelastischen R¨ ontgenstreuung 3

1.1 Beschreibung des Streuprozesses . . . . 3

1.2 Der doppelt differentielle Streuquerschnitt . . . . 4

1.3 Resonant unelastische R¨ ontgenstreuung . . . . 9

2 Elektronische Eigenschaften von ¨ Ubergangsmetallverbindungen 17 2.1 Grenzen der Dichtefunktionaltheorie . . . . 17

2.2 Formale Beschreibung korrelierter Systeme . . . . 19

2.3 Die Bandl¨ ucke bei ¨ Ubergangsmetallverbindungen . . . . 21

2.4 Berechnung der elektronischen Struktur . . . . 26

2.4.1 Atomare Multiplettrechnungen . . . . 26

2.4.2 Kristallfeldaufspaltung . . . . 27

2.4.3 Hubbard Modelle . . . . 28

2.4.4 Eine Cluster Rechnung f¨ ur CuO . . . . 30

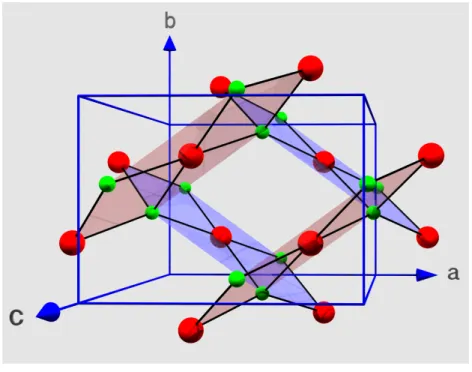
2.5 Die Kristallstruktur von CuO . . . . 35

3 Fluoreszenzspektroskopie an CuO 37 3.1 Das Rowland-Spektrometer am HARWI Messplatz . . . . 37

3.2 Messung der Kupfer K _{α 1} -Fluoreszenz von CuO . . . . 41

3.2.1 Eichung von Monochromator und Spektrometer . . . . 41

3.2.2 Durchf¨ uhrung der Messungen und erste Ergebnisse . . . . . 43

3.2.3 Stabilit¨ at des Monochromators . . . . 45

3.3 Auswertung der Messdaten . . . . 45

3.3.1 Wahl der Fitfunktionen . . . . 46

i

3.3.2 Ergebnisse und Stabilit¨ at der Fitprozedur . . . . 48

3.3.3 Deutung der Ergebnisse . . . . 53

3.4 Die Polarisationsabh¨ angigkeit der Fluoreszenzspektren . . . . 56

3.4.1 Polarisationsabh¨ angigkeit des Dipol- und Quadrupol- Matrixelements . . . . 56

3.4.2 Messung der Polarisationsabh¨ angigkeit . . . . 59

3.4.3 Vergleich und Schlussfolgerungen . . . . 59

4 Elektronische Anregung durch Zwischenzustands-Wechsel- wirkung 65 4.1 St¨ orungstheoretische Behandlung der Zwischenzustands- Wechselwirkung . . . . 65

4.2 Shakeup-Satelliten . . . . 70

4.2.1 Streuwinkelabh¨ angigkeit . . . . 71

4.2.2 Simulation der Polarisationsabh¨ angigkeit . . . . 76

4.2.3 Anregungsenergieabh¨ angigkeit . . . . 80

Zusammenfassung 89

A Die analytische Approximation der Voigtfunktion 93

Abbildungsverzeichnis 101

Einleitung

Seit der Entdeckung von Hochtemperatur supraleitenden Kupraten besteht in der Festk¨ orperphysik ein großes Interesse daran, deren elektronische Struktur auch im normalleitenden Zustand besser zu verstehen. Schon seit langem ist dabei be- kannt, dass sich die Eigenschaften dieser Verbindungen und auch die von ¨ Uber- gangsmetalloxiden wie FeO, CoO, NiO oder CuO nicht auf der Grundlage einer Einteilchen-Bandstruktur erkl¨ aren lassen [Mott 1949]. Grund hierf¨ ur sind star- ke Korrelations- und Austauschwechselwirkungen zwischen den lokalisierten 3d- Elektronen und die ¨ Anderung des Grundzustand-Potentials bei einem ¨ Ubergang in einen angeregten Zustand. Diese Effekte f¨ uhren dazu, dass selbstkonsistente Einteilchen-Bandstrukturrechnungen h¨ aufig ein metallisches Verhalten von ¨ Uber- gangsmetallverbindungen vorhersagen, die jedoch in der Realit¨ at meist Halbleiter oder Isolatoren sind.

Bessere Ergebnisse erzielen dagegen Methoden wie atomare Multiplett-Rechnun- gen oder Cluster Rechnungen, die die Gitterperiodizit¨ at vernachl¨ assigen, daf¨ ur aber lokale Elektron-Elektron Wechselwirkungen im Grundzustand und in ange- regten Zust¨ anden explizit ber¨ ucksichtigen k¨ onnen. Die Werte der ben¨ otigten Mo- dellparameter dieser Ans¨ atze ergeben sich in der Regel aus ab initio Rechnungen oder durch Vergleich mit experimentellen Daten.

Eine der experimentellen Methoden, die zur Bestimmung dieser Parameter einen Beitrag liefern, ist die Photoemissionsspektroskopie. Sie stellt jedoch aufgrund ih- rer hohen Oberfl¨ achensensitivit¨ at extrem hohe Anforderungen an die Qualit¨ at der verwendeten Proben. Zudem ist die Kristallstruktur und die chemische Zusam- mensetzung der Oberfl¨ ache h¨ aufig von der des Volumens verschieden. Dagegen unterliegt die resonante R¨ ontgen-Raman-Streuung wegen der Verwendung von har- ter R¨ ontgenstrahlung als Sonde nicht diesen Einschr¨ ankungen. Als Methode zur Untersuchung der elektronischen Struktur von Festk¨ orpern gewinnt sie durch die rapide Entwicklung der Synchrotronstrahlungsquellen immer mehr an Bedeutung.

In Anwendung auf Systeme, in denen stark korrelierte Elektronen vorliegen, wur- de die resonante R¨ ontgen-Raman-Streuung in j¨ ungerer Zeit unter anderem zur Untersuchung von La 2 CuO 4 [Abbamonte 1999], Ca 2 CuO 2 Cl 2 [Hasan 2000] und Nd ₂ CuO ₄ [H¨ am¨ al¨ ainen 2000] genutzt. Diese Messungen gaben Anlass zu Diskus- sionen ¨ uber die Deutung der teilweise recht unterschiedlichen Ergebnisse.

Vor diesem Hintergrund wird im Rahmen dieser Arbeit mithilfe der resonanten

1

R¨ ontgen-Raman-Streuung die elektronische Struktur von CuO untersucht. Die Be- deutung dieser Substanz liegt in der großen ¨ Ahnlichkeit ihrer kristallinen und elek- tronischen Struktur mit der von Hochtemperatur supraleitenden Kupraten, was CuO aus Sicht der Theorie zu einer idealen Modellsubstanz macht [Ghijsen 1988]

[Eskes 1990]. Ziel der Arbeit ist es, die Besonderheiten der elektronischen Struktur des ¨ Ubergangsmetalloxids CuO herauszustellen und dabei das Potenzial der reso- nanten R¨ ontgen-Raman-Streuung als Untersuchungsmethode aufzuzeigen. Hierzu werden in Kapitel 1 zun¨ achst die Grundlagen der resonant unelastischen R¨ ont- genstreuung erl¨ autert. Nach der Herleitung des doppelt differentiellen Streuquer- schnitts und dessen Diskussion wird demonstriert, wie sich aus der Analyse von R¨ ontgen-Fluoreszenzspektren Informationen ¨ uber die unbesetzte Zustandsdichte in der N¨ ahe der Fermienergie gewinnen lassen. Kapitel 2 besch¨ aftigt sich mit der theoretischen Beschreibung der elektronischen Struktur von ¨ Ubergangsmetallver- bindungen. Es werden sowohl die Probleme selbstkonsistenter Bandstrukturrech- nungen aufgezeigt, als auch einige alternative Ans¨ atze vorgestellt. Einer dieser Ans¨ atze, ein einfaches Modell eines (CuO ₄ ) ⁶⁻ Clusters, wird ausf¨ uhrlicher bespro- chen und es wird dargestellt, wie man mit dessen Hilfe ein Energieniveauschema und damit die Energie lokaler elektronischer Anregungen im CuO bestimmen kann.

In Kapitel 3 wird die Durchf¨ uhrung und die Auswertung von Messungen der Kup-

fer K _{α 1} -Fluoreszenzspektren beschrieben. Hier wird zun¨ achst die Abh¨ angigkeit der

Spektren von der Energie des einfallenden R¨ ontgenstrahls untersucht, um daraus,

wie in Kapitel 1 erl¨ autert, R¨ uckschl¨ usse ¨ uber die unbesetzte Zustandsdichte in der

N¨ ahe der Fermienergie zu ziehen. Weiterhin werden durch die Analyse der Abh¨ an-

gigkeit des Fluoreszenzspektrums von der Richtung des Polarisationsvektors des

einfallenden Strahls Informationen ¨ uber die Symmetrie der unbesetzten Zust¨ ande

gewonnen. Eine Besonderheit der resonanten R¨ ontgen-Raman-Streuung an CuO,

n¨ amlich die Zwischenzustands-Wechselwirkung zwischen dem Core-Loch und den

lokalisierten 3d-Elektronen, wird in Kapitel 4 diskutiert. Nach einer st¨ orungstheo-

retischen Behandlung dieser Wechselwirkung werden Messungen von Energiever-

lustspektren vorgestellt und die Ergebnisse anhand der Theorie interpretiert. Es

wird gezeigt, dass die zu beobachtende Streuwinkelabh¨ angigkeit der Spektren ein

Polarisationseffekt ist und nicht auf eine ¨ Anderung des Impuls¨ ubertrags bei Va-

riation des Streuwinkels zur¨ uckzuf¨ uhren ist. Weiterhin wird im Rahmen einer Mo-

dellrechnungen die Abh¨ angigkeit der Spektren von der Anregungsenergie erkl¨ art,

um daraus weitere R¨ uckschl¨ usse ¨ uber die Art des Zwischenzustands zu ziehen.

Kapitel 1

Grundlagen der unelastischen R¨ ontgenstreuung

In diesem Kapitel werden die theoretischen Grundlagen der unelastischen R¨ ontgen- streuung dargestellt. Zun¨ achst wird eine ¨ Ubersicht ¨ uber die Geometrie des Streu- prozesses gegeben. Es folgt eine Herleitung des doppelt differentiellen Streuquer- schnitts und dessen Diskussion f¨ ur den Fall resonant unelastischer Streuung.

1.1 Beschreibung des Streuprozesses

Bei der unelastischen Photonenstreuung trifft, wie in Abbildung 1.1 dargestellt, ein Photon mit dem Wellenvektor ~k 1 , der Energie ¯ hω ₁ und dem Polarisationsvek- tor ˆ ₁ auf das streuende System. Das gestreute Photon hat den Wellenvektor ~k ₂ ,

k ₁ h ω , ₁ h

φ

, ε ₁ k , 2 ω , ε 2 2

Abbildung 1.1: Schematische Darstellung des unelastischen Streuprozesses.

3

die Energie ¯ hω ₂ und den Polarisationsvektor ˆ ₂ . Auf das System wird folglich die Energie ¯ hω = ¯ h(ω ₁ − ω ₂ ) und der Impuls ~ q = ¯ h(~k ₁ − ~k ₂ ) ¨ ubertragen.

Nimmt man an, dass der Energie¨ ubertrag klein gegen¨ uber der Photonenenergie ist, so ergibt sich

|~ q | ≈ 2¯ h|~k 1 | sin(Φ/2), (1.1) wobei Φ der Streuwinkel ist. Durch Wahl der Parameter ¯ hω 1 , ~k 1 , ˆ 1 und Φ lassen sich durch Analyse der gestreuten Strahlung R¨ uckschl¨ usse auf die Streuprozesse in der Probe ziehen. Die Messgr¨ oße bei einem solchen Experiment ist der sogenann- te doppelt differentielle Streuquerschnitt (DDSQ), auf den im Folgenden n¨ aher eingegangen werden soll.

1.2 Der doppelt differentielle Streuquerschnitt

Der doppelt differentielle Streuquerschnitt ist definiert als:

d ² σ

dΩdω ₂ = 1 N

Anzahl der in [Ω,Ω + dΩ] und [ω ₂ ,ω ₂ + dω ₂ ] gestreuten Photonen

Stromdichte der einfallenden Photonen × dΩ × dω ₂ . (1.2) N ist hierbei die Zahl der streuenden Teilchen in der Probe. Die Anzahl der ge- streuten Photonen errechnet sich aus [Sturm 1987]

N ₂ = N ₁ X

i,f

P _i W _{|i; ~ k}

1 i→|f ; ~ k 2 i n(~k ₂ ) d ³ k ₂ . (1.3) N ₁ ist die Anzahl der einfallenden Photonen und P _i die Wahrscheinlichkeit, das streuende Elektronensystem im Anfangszustand |ii vorzufinden. W _{|i; ~ k}

1 i→|f; ~ k 2 i ist die Wahrscheinlichkeit pro Zeiteinheit eines ¨ Ubergangs vom Anfangszustand |ii des Elektronensystems und dem Wellenvektor ~k 1 des Photons in einen Endzustand

|fi des Elektronensystems und dem Wellenvektor ~k ₂ des Photons. n( ~k ₂ ) d ³ k ₂ ist die Zahl der m¨ oglichen Zust¨ ande im Phasenraumvolumen d ³ k ₂ f¨ ur das gestreute Photon. Es gilt:

n(~k ₂ ) d ³ k ₂ = V _c

(2π) ³ k ² ₂ dk ₂ dΩ = V _c

(2πc) ³ ω ₂ ² dω ₂ dΩ , (1.4) wobei V _c das Quantisierungsvolumen ist. Zusammen mit der Stromdichte der ein- fallenden Photonen

I ₀ = N ₁ c

V _c (1.5)

1.2. Der doppelt differentielle Streuquerschnitt 5

erh¨ alt man damit f¨ ur den DDSQ:

d ² σ

dΩdω ₂ = V _c ² (2π) ³

ω ² ₂ c ⁴

1 N

X

i,f

P _i W _{|i; ~ k}

1 i→|f ; ~ k 2 i . (1.6) Um diese Beziehung auszuwerten, ben¨ otigt man einen Ausdruck f¨ ur die ¨ Uber- gangswahrscheinlichkeit. Dazu betrachtet man zun¨ achst den Hamiltonoperator der Elektronen im elektromagnetischen Feld der Photonen [Blume 1985]:

H = X

j

1 2m

~ p j − e

c

A(~ ~ r j , t) 2

− eV (~ r j )

+ X

~ k,λ

¯ hω _{~ k}

a ^† _~

k,λ a _{~ k,λ} + 1 2

. (1.7)

Hierbei erstreckt sich die erste Summe ¨ uber alle Elektronen im streuenden Sys- tem und die zweite Summe ¨ uber alle Wellenvektoren ~k und die beiden Polarisa- tionsm¨ oglichkeiten λ. A(~ ~ r ) ist der Vektorpotential-Operator des Photonfeldes in Coulomb-Eichung ( ∇ · ~ A ~ = 0), ~ r _j und ~ p _j sind die Orts- und Impulsoperatoren der Elektronen. a ^† und a sind die Erzeuger- und Vernichteroperatoren f¨ ur das quanti- sierte Photonenfeld. Terme, die die Kopplung der Elektronen ¨ uber ihr magnetisches Moment an das Photonenfeld beschreiben, sind in (1.7) nicht enthalten und sollen im Folgenden vernachl¨ assigt werden.

In der Teilchenzahldarstellung erh¨ alt man f¨ ur den Vektorpotential-Operator:

A(~ ~ r , t) = X

~ k,λ

s 2π¯ hc ² V c ω ~ k

~ _{~ k,λ} a _{~ k,λ} e ^{i( ~ k·~ r−ω ~ k t)} + ~ _~ ^∗

k,λ a ^† _~

k,λ e ^{−i( ~ k·~ r−ω ~ k t)}

. (1.8)

~ _{~ k,λ} sind hierbei die Komponenten der Polarisationseinheitsvektoren ˆ _{~ k} der Pho- tonen mit Wellenvektor ~k. Da f¨ ur die betrachteten Streuprozesse die Vernichtung eines Photons |~k ₁ i und die Erzeugung eines Photons |~k ₂ i gefordert wird, ist es not- wendig, dass der Vektorpotential-Operator zweimal auf den Anfangszustand |i; ~k ₁ i wirkt. F¨ ur den Hamiltonoperator (1.7) ist es daher zweckm¨ aßig, die Terme nach Potenzen in A ~ zu ordnen. Man erh¨ alt:

H = H 0 + H rad + H _int ⁰ + H _int ⁰⁰ (1.9) mit

H ₀ = X

j

~ p _j ²

2m − eV ( r ~ _j ) (1.10)

H _rad = X

~ k,λ

¯ hω _{~ k}

a _~ ^†

k,λ a _{~ k,λ} + 1 2

(1.11) H _int ⁰ = − e

mc X

j

A(~ ~ r _j , t) · ~ p _j (1.12)

H _int ⁰⁰ = e ² 2mc ²

X

j

A ~ ² (~ r _j , t) (1.13)

Der in A ~ quadratische Term H _int ⁰⁰ liefert bereits in 1. Ordnung St¨ orungsrechnung einen Beitrag zur ¨ Ubergangsrate. Betrachtet man zun¨ achst nur diesen Beitrag, so ergibt sich nach Fermis goldener Regel:

W ⁽¹⁾

|i; ~ k 1 i→|f; ~ k 2 i = 2π

¯ h

h~k ₂ ; f |H _int ⁰⁰ |i; ~k ₁ i

2

δ (E _f − E _i − ¯ h(ω ₁ − ω ₂ )) . (1.14) Der in A ~ lineare Term H _int ⁰ beschreibt in 1. Ordnung St¨ orungsrechnung wegen des einzelnen Photonen-Erzeuger- bzw. Vernichteroperators Prozesse der Emission oder Absorption eines Photons. Zum DDSQ tr¨ agt H _int ⁰ erst in 2. Ordnung St¨ o- rungsrechnung bei. Die Herleitung dieses Beitrages soll an dieser Stelle ausf¨ uhrlich dargestellt werden, da hierauf aufbauend in einem sp¨ ateren Kapitel auch auf Pro- zesse h¨ oherer Ordnung eingegangen wird.

Zun¨ achst geht man davon aus, dass sich das Elektronensystem vor der Wechselwir- kung mit dem Photon zum Zeitpunkt t = t ₀ in einem Eigenzustand |i, ti von H ₀ befindet. Die Zeitentwicklung ist dann gem¨ aß der zeitabh¨ angigen St¨ orungsrechung durch die Neumann-Reihe gegeben. In der Dirac-Darstellung gilt also:

|Ψ, ti _D = |Ψ, t ₀ i _D + 1 i¯ h

Z t t 0

dt ⁰ H ˜ _int ⁰ (t ⁰ )|Ψ, t ₀ i _D

+ 1

(i¯ h) ² Z t

t 0

dt ⁰ Z t ⁰

t 0

dt ⁰⁰ H ˜ _int ⁰ (t ⁰ ) ˜ H _int ⁰ (t ⁰⁰ )|Ψ, t 0 i D + · · · (1.15)

mit

|Ψ, ti _D = e ^{h ¯ i H 0 t} |Ψ, ti und H ˜ _int ⁰ = e ^{h ¯ i H 0 t} H _int ⁰ e ^{− ¯ h i H 0 t} . (1.16)

Da f¨ ur die ¨ Ubergangswahrscheinlichkeit die Zeitentwicklung der gest¨ orten Zust¨ an-

de f¨ ur große Zeiten entscheidend ist und nicht das Verhalten kurz nach Einsetzen

der St¨ orung, ist es sinnvoll, den Fall t 0 → −∞ zu betrachten. Das Einsetzen der

St¨ orung wird dabei durch Einf¨ ugen eines Faktors e ^t ber¨ ucksichtigt, wobei am Ende

der Rechnung der Grenz¨ ubergang lim →0 durchgef¨ uhrt werden muss.

1.2. Der doppelt differentielle Streuquerschnitt 7

Der Term 2. Ordnung in (1.15) f¨ uhrt dann auf die ¨ Ubergangsamplitude:

hf |Ψi ⁽²⁾ = − 1

¯ h ²

Z t

−∞

dt ⁰ Z t ⁰

−∞

dt ⁰⁰ hf| H ˜ _int ⁰ (t ⁰ )e ^{t 0} H ˜ _int ⁰ (t ⁰⁰ )e ^{t 00} |ii (1.17) Zur Vereinfachung der Schreibweise wurde hierbei die Indizierung der Wellenfunk- tionen in der Dirac-Darstellung weggelassen, ebenso die Wellenvektoren der Pho- tonen im Anfangszustand ~k ₁ und im Endzustand ~k ₂ . Zur weiteren Vereinfachung sollen nur die Photonen-Erzeuger und Vernichter des Vektorpotential-Operators geschrieben werden, die einen nicht verschwindenden Beitrag liefern, also der Ver- nichter a ~ k 1 und der Erzeuger a ^† _~

k 2 . Fasst man die Operatoren mit den zeitunabh¨ an- gigen Vorfaktoren zusammen, erh¨ alt man

H _int ⁰ = c e ^{−iω 1 t} + c ^† e ^{iω 2 t} (1.18) mit

c = s

2π¯ hc ² V _c ω ₁

X

j, λ

~ p _j · ~ _{~ k}

1 ,λ e ^{i~ k 1 ·~ r j} a _{~ k}

1 ,λ , c ^† = s

2π¯ hc ² V _c ω ₂

X

j, λ

~ p _j · ~ _~ ^∗

k 2 ,λ e ^{−i~ k 2 ·~ r j} a ^† _~

k 2 ,λ . (1.19) Hiermit und mit der Zeitentwicklung des Hamiltonoperators (1.16), sowie nach Einf¨ ugen eines vollst¨ andigen Satzes von Eigenfunktionen |ni von H ₀ unter Aus- nutzung der Vollst¨ andigkeitsrelation

X

n

|nihn| = 1 (1.20)

erh¨ alt man ¹ :

hf|Ψi ⁽²⁾ = − 1

¯ h ²

X

n

Z t

−∞

Z t ⁰

−∞

dt ⁰ dt ⁰⁰ hf |e ^{h ¯ i H 0 t 0} c ^† e ^{iω 2 t 0} e ^{− ¯ h i H 0 t 0} |ni

×hn|e ^{h ¯ i H 0 t 00} c e ^{−iω 1 t 00} e ^{− ¯ h i H 0 t 00} |iie ^{t 0} e ^{t 00}

= − 1

¯ h ²

X

n

Z t

−∞

Z t ⁰

−∞

dt ⁰ dt ⁰⁰ hf |c ^† |nihn|c|ii

×e ( ⁺ ¯ h ⁱ (E f −E n +¯ hω 2 ) ) ^{t 0} e ( ⁺ ¯ h ⁱ (E n −E i −¯ hω 1 ) ) ^{t 00} . (1.21)

1 Der Term, bei dem der Erzeuger auf den Anfangszustand und der Vernichter auf den Zwi-

schenzustand wirkt, die Emission also vor der Absorption geschieht, wurde hierbei zun¨ achst

vernachl¨ assigt.

Die Ausf¨ uhrung der Zeitintegrationen ergibt hf |Ψi ⁽²⁾ = − 1

¯ h ²

X

n

hf |c ^† |nihn|c|ii + _{¯ h} ⁱ (E _n − E _i − ¯ hω ₁ )

e ( ⁽²⁺ _{h ¯} ^{i (E} f −E _i −¯ hω) ) ^t

2 + _{¯ h} ⁱ (E _f − E _i − ¯ hω) , (1.22) mit ω = (ω 1 − ω 2 ). Die ¨ Ubergangsrate, also die ¨ Ubergangswahrscheinlichkeit pro Zeiteinheit, erh¨ alt man hieraus ¨ uber:

W ⁽²⁾

|i; ~ k 1 i→|f ; ~ k 2 i = lim

→0

d dt

hf|Ψi ⁽²⁾

2

= lim

→0







X

n

hf |c ^† |nihn|c|ii (E _n − E _i − ¯ hω ₁ ) − i¯ h

2 d dt

e ^4t

(E _f − E _i − ¯ hω) ² + 4¯ h ^{2 2}







= lim

→0







X

n

hf |c ^† |nihn|c|ii (E _n − E _i − ¯ hω ₁ ) − i¯ h

2

4 e ^4t

(E _f − E _i − ¯ hω) ² + 4¯ h ^{2 2}







(1.23) Der Grenz¨ ubergang des rechten Faktors ergibt:

lim →0

4 e ^4t

(E _f − E _i − ¯ hω) ² + 4¯ h ^{2 2} =

0 f¨ ur E f − E i − ¯ hω 6= 0

∞ f¨ ur E _f − E _i − ¯ hω = 0

= 2π

¯

h δ (E f − E i − ¯ hω) (1.24) Der Grenz¨ ubergang des linken Faktors von (1.23) l¨ asst sich zwar mathematisch einfach durchf¨ uhren, es ist jedoch die m¨ ogliche Nullstelle des Nenners zu beachten.

F¨ ur = 0 und den Resonanzfall ¯ hω ₁ = E _n − E _i w¨ urde der Ausdruck divergieren.

Physikalisch w¨ urde dies bedeuten, dass die Energie des sogenannten intermedi¨ aren Zwischenzustandes |ni unendlich scharf, und damit die Lebensdauer unendlich groß ist. Tats¨ achlich aber hat dieser angeregte Zustand nur eine endliche Lebensdauer τ , was aufgrund der Unsch¨ arferelation einer Energieverbreiterung entspricht. Um dies zu ber¨ ucksichtigen ist in (1.23) der Energieeigenwert E n um einen Imagin¨ arteil, der sogenannte Lebensdauerverbreiterung iΓ _n , zu erg¨ anzen. Man erh¨ alt also als Ergebnis:

W _|i; ⁽²⁾ _~

k 1 i→|f ; ~ k 2 i = 2π

¯ h

X

n

hf|c ^† |nihn|c|ii (E _n − E _i − ¯ hω ₁ ) − iΓ _n

2

δ (E f − E i − ¯ hω) (1.25)

1.3. Resonant unelastische R¨ ontgenstreuung 9 Addiert man die ¨ Ubergangsamplituden der 1. und 2. Ordnung St¨ orungsrechnung vor Berechung der ¨ Ubergangsrate und setzt die Definitionen (1.13), (1.8) und (1.19) ein, so erh¨ alt man ¨ uber (1.6) den DDSQ bis zur 2. Ordnung St¨ orungsrechnung:

d ² σ dΩdω ₂ = ¯ h

e ² mc ²

2

ω 2

ω ₁ X

f

(ˆ 1 · ˆ ^∗ ₂ )

* f

X

j

e ^{i( ~ k 1 − ~ k 2 )·~ r j} i

+

+ 1

m X

n

D f

ˆ ^∗ ₂ · P

j ~ p _j e ^{−i~ k 2 ·~ r j} n E D

n ˆ ₁ · P

j ~ p _j e ^{i~ k 1 ·~ r j} i E (E _n − E _i − ¯ hω ₁ ) − iΓ _n

2

δ (E _f − E _i − ¯ hω) (1.26) Hierbei bezeichnet |ii nicht mehr einen beliebigen Anfangszustand des Systems sondern den Grundzustand, den das System vor dem Streuprozess mit der Wahr- scheinlichkeit P = 1 annimmt. F¨ ur den Fall ¯ hω ₁ (E _n − E _i ) ist der Beitrag 2.

Ordnung zu vernachl¨ assigen [Sch¨ ulke 1991].

In der Literatur findet sich h¨ aufig noch ein weiterer Term, der zum DDSQ beitr¨ agt [Sakurai 1967]. In der Schreibweise von Gleichung (1.25) hat er die Form:

W ⁰⁽²⁾

|i; ~ k 1 i→|f ; ~ k 2 i = 2π

¯ h

X

n

hf|c|nihn|c ^† |ii E _n − E _i + ¯ hω ₂

2

δ (E _f − E _i − ¯ hω) (1.27) Dieser Beitrag stammt von den in (1.21) nicht ber¨ ucksichtigten Prozessen, bei de- nen der Photonen-Erzeuger a ^† _~

k 2 auf den Anfangszustand und der Vernichter a _{~ k}

1

auf den intermedi¨ aren Zwischenzustand wirkt. Unter der Annahme, dass der An- fangszustand der Grundzustand ist, kann ein solcher Prozess nie resonant werden, da die Differenz E _n − E _i immer positiv ist. Dies rechtfertigt nachtr¨ aglich das Ver- nachl¨ assigen solcher Prozesse in Gleichung (1.21). Im folgenden Abschnitt sollen die Eigenschaften des DDSQ, insbesondere nahe einer Resonanz ¯ hω 1 ≈ (E n − E i ), betrachtet werden.

1.3 Resonant unelastische R¨ ontgenstreuung

Der Term 1. Ordnung in Gleichung (1.26) dominiert f¨ ur nicht-resonante unelasti- sche Streuprozesse. Dagegen erf¨ ahrt der Term 2. Ordnung eine resonante Verst¨ ar- kung, wenn die einfallende Photonenenergie ann¨ ahernd gleich der Differenz zweier Energieniveaus ist, also

¯

hω ₁ ≈ E _n − E _i . (1.28)

In einem solchen Fall spricht man von resonant unelastischer R¨ ontgenstreuung

(RIXS) oder auch von resonanter R¨ ontgen-Raman-Streuung.

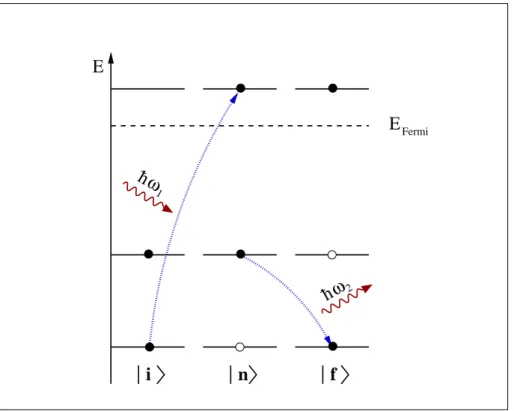
Physikalisch l¨ asst sich der resonante Streuprozess folgendermaßen verstehen: Das einfallende Photon mit der Energie ¯ hω ₁ wird vom System absorbiert, wobei ein Elektron aus einem energetisch tiefliegenden Niveau, im Folgenden allgemein als Core-Niveau bezeichnet, in ein unbesetztes Niveau oberhalb der Fermi-Energie an- geregt wird. Dieser Zwischenzustand besitzt eine endliche Lebensdauer und zerf¨ allt, indem ein Elektron eines h¨ oher liegenden besetzten Niveaus das entstandene Loch im Core-Niveau wieder auff¨ ullt. Die dabei frei werdende Energie wird entweder auf ein weiteres Elektron ¨ ubertragen (Auger-Prozess) oder, wie in Abbildung 1.2 schematisch dargestellt, in Form eines Photons der Energie ¯ hω ₂ abgestrahlt. Das entstehende Emissionsspektrum enth¨ alt also Informationen sowohl ¨ uber die unbe- setzten Zust¨ ande oberhalb der Fermi-Energie als auch ¨ uber die besetzten Zust¨ ande, die an der Emission beteiligt sind.

n

i f

h

1

h 2

E E

ω

ω

Fermi

Abbildung 1.2: Schematische Darstellung der resonant unelastischen Streuung.

Die resonante Verst¨ arkung dieses Streuprozesses als Funktion der einfallenden Pho- tonenenergie ist durch den Lorentzfaktor

L 1 (ω 1 ) = 1

(E _n − E _i − ¯ hω ₁ ) ² + Γ ² _n (1.29) gegeben. Man erkennt, dass die Verst¨ arkung f¨ ur den Fall voller Resonanz mit

¯

hω ₁ = (E _n − E _i ) nur durch die endliche Lebensdauerverbreiterung Γ _n begrenzt

1.3. Resonant unelastische R¨ ontgenstreuung 11 wird. Weiterhin ist es wichtig festzustellen, dass f¨ ur den ersten Schritt, der Ab- sorption eines Photons und den hierdurch induzierten ¨ Ubergang des Elektronen- systems in den intermedi¨ aren Zwischenzustand |ni, die Energieerhaltung nicht er- f¨ ullt sein muss. Prinzipiell tragen alle Zwischenzust¨ ande zum DDSQ bei, erfah- ren jedoch durch (1.29) eine Gewichtung, sodass Beitr¨ age von Zust¨ anden, f¨ ur die

|E _n − E _i − hω ¯ ₁ | Γ _n ist, vernachl¨ assigbar sind. Da Γ _n selbst bei einem Core-Loch Zustand nur wenige eV betr¨ agt, ist die Anzahl der Zwischenzust¨ ande, die einen relevanten Beitrag zum DDSQ liefern, gering.

Um in einem einfachen Modell den Zusammenhang zwischen der elektronischen Struktur des Systems und dem Emissionsspektrum als Funktion von ¯ hω ₂ zu ver- deutlichen, nimmt man zun¨ achst an, dass die beiden Matrixelemente

M ₁ = D

f

ˆ ^∗ ₂ · X

j ~ p _j e ^{−i~ k 2 ·~ r j} n

E

und M ₂ = D

n

ˆ ₁ · X

j ~ p _j e ^{i~ k 1 ·~ r j} i

E

(1.30) unabh¨ angig von ¯ hω 1 und ¯ hω 2 sind. Weiterhin ist zu ber¨ ucksichtigen, dass nicht nur der intermedi¨ are Zwischenzustand |ni, sondern auch der Endzustand |fi eine endliche Lebensdauer besitzt. Analog zur Behandlung des Zwischenzustandes bei der Herleitung von Gleichung (1.25) addiert man in Gleichung (1.23) die imagin¨ are Lebensdauerverbreiterung iΓ _f zur Energie des Endzustands E _f und erh¨ alt dadurch anstatt der Deltafunktion (1.24) einen zweiten Lorentzfaktor

L 2 (ω 1 , ω 2 ) = 1

(E _f − E _i − ¯ h(ω ₁ − ω ₂ )) ² + Γ ² _f . (1.31) Schließlich ersetzt man noch die Summation ¨ uber alle Zwischenzust¨ ande |ni durch eine Energieintegration unter Verwendung der energetischen Zustandsdichte ρ() der unbesetzten Niveaus und erh¨ alt f¨ ur das Emissionsspektrum bei fester Energie der einfallenden Photonen:

I _{ω 1} (ω ₂ ) ∝ Z

ρ() A _n (E _n − E _i − ¯ hω ₁ ) A _f (E _f − E _i − ¯ hω ₁ + ¯ hω ₂ ) d, (1.32) mit den Lorentzfunktionen

A _n,f (E) = 1

E ² + Γ ² _n,f . (1.33)

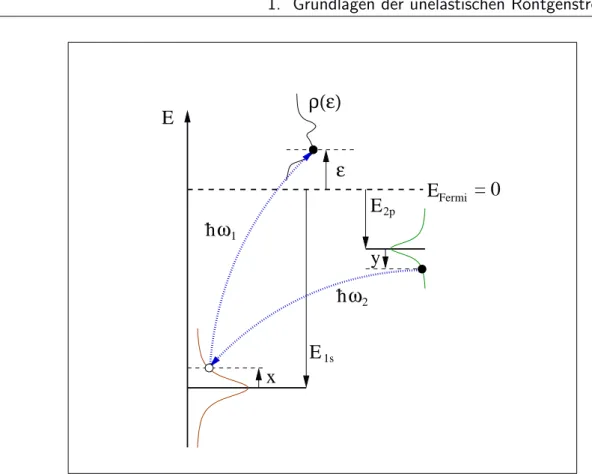
Zur Deutung dieses Ausdrucks ben¨ otigt man noch die Abh¨ angigkeit von E _i , E _f und E _n von der Integrationsvariablen und die Verkn¨ upfung mit den charakteristischen Bindungsenergien des Systems. Diese ergibt sich f¨ ur den konkreten Fall einer K _α - Emission, also einem ¨ Ubergang |2pi → |1si, aus der Abbildung 1.3. Man erh¨ alt:

E _n − E _i = − E _1s

E _f − E _i = − E _2p . (1.34)

ρ(ε)

h ω 2

h ω ₁ E

= 0 ε

x

y

1s

E _2p E _Fermi

E

Abbildung 1.3: Definition der an der K _α -Emission beteiligten Energieniveaus. Die Energieachse wird so gew¨ ahlt, dass E _Fermi = 0 ist. Die Bindungsenergien E _1s und E _2p sind demnach negativ.

Damit entsprechen die Gr¨ oßen

x = − E _1s − ¯ hω ₁

y = − E 2p − ¯ h(ω 1 − ω 2 ) (1.35) den Argumenten der Lorentzfunktionen in Gleichung (1.32), was durch das Ein- zeichnen der entsprechenden Lorentzfunktionen in Abbildung 1.3 angedeutet wer- den soll. Das Emissionsspektrum ist also gegeben durch

I ω 1 (ω 2 ) ∝ Z

ρ() A n ( − E 1s − ¯ hω 1 ) A f ( − E 2p − ¯ hω 1 + ¯ hω 2 ) d. (1.36)

Zur Diskussion dieses Ergebnisses werden im Folgenden zwei Grenzf¨ alle der Zu-

standsdichte ρ() betrachtet.

1.3. Resonant unelastische R¨ ontgenstreuung 13

Fall 1: Anregung in ein scharfes Energieniveau

Nimmt man an, dass es nur einen einzelnen, energetisch scharfen unbesetzten Zu- stand bei E = ₀ gibt, so l¨ asst sich die Zustandsdichte schreiben als

ρ() = δ( − ₀ ) . (1.37)

Man erh¨ alt f¨ ur das Emissionsspektrum

I _{ω 1} (ω ₂ ) ∝ A _n ( ₀ − E _1s − hω ¯ ₁ ) A _f ( ₀ − E _2p − hω ¯ ₁ + ¯ hω ₂ ) . (1.38) Der erste Faktor A _n ist nicht von ω ₂ abh¨ angig. Beim zweiten Faktor A _f handelt sich um eine Lorentzfunktion mit dem Maximum bei

¯

hω ₂ ^max = ¯ hω 1 + E 2p − 0 . (1.39) Die Position des Maximums im Emissionsspektrum ist also abh¨ angig von der Ener- gie der einfallenden Photonen ¯ hω ₁ . Bei ¨ Anderung von ¯ hω ₁ verschiebt sich das Ma- ximum auf der ¯ hω ₂ -Skala linear, was als Raman-Shift bezeichnet wird.

Die Intensit¨ at im Maximum des Emissionsspektrums I _{ω 1} (ω ^max ₂ ) wird durch den Faktor A _n in (1.38) bestimmt. Dieser ist ebenfalls von ¯ hω ₁ abh¨ angig und wird f¨ ur

¯

hω ₁ ^max = E _1s − ₀ maximal.

Fall 2: Anregung in ein Kontinuum

Liegt ein strukturloses Kontiuum von unbesetzten Zust¨ anden vor, welches bei = 0 ≥ E Fermi einsetzt, so schreibt man f¨ ur die Zustandsdichte

ρ() = θ( − ₀ ) , (1.40)

wobei θ(x) die Stufenfunktion ist. F¨ ur das Emissionsspektrum ergibt sich:

I _{ω 1} (ω ₂ ) ∝ Z ∞

−∞

θ( − ₀ ) A _n ( − E _1s − ¯ hω ₁ ) A _f ( − E _2p − ¯ hω ₁ + ¯ hω ₂ ) d

= Z ∞

−∞

θ(E 1s + ¯ hω 1 − 0 − ) ˜ A n (˜ )

| {z } I ₁ (˜ )

A f (E 1s − E 2p + ¯ hω 2 − ˜ )

| {z } I ₂ (¯ hω ₂ − ) ˜

d˜

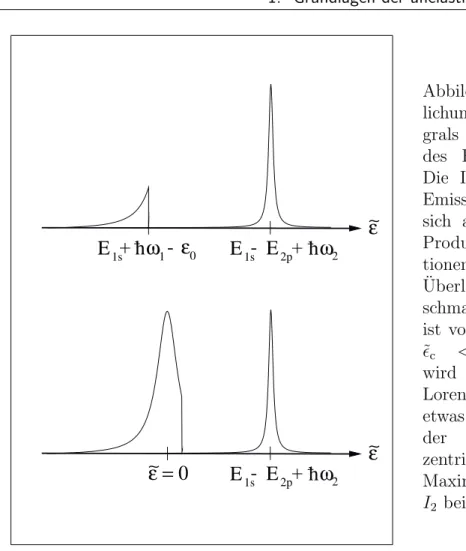
(1.41) Hierbei wurde die Substitution ˜ = E 1s +¯ hω 1 − durchgef¨ uhrt, sowie die Symmetrie A _n (˜ ) = A _n (−˜ ) ausgenutzt. I ₁ (˜ ) ist eine bei ˜ = 0 zentrierte Lorentzfunktion, die durch die Stufenfunktion an der Stelle ˜ _c = E _1s + ¯ hω ₁ − ₀ abgeschnitten wird.

I 2 (¯ hω 2 − ˜ ) ist eine Lorentzfunktion, die an der Stelle ˜ = E 1s − E 2p + ¯ hω 2 zentriert

ist. Das Emissionsspektrum ergibt sich aus der Faltung der beiden Funktionen I ₁

und I ₂ . Zur Veranschaulichung der Gestalt und der Position beider Funktionen sind

ε∼

E _1s + h ω ₁ - ε ₀ E _1s - E _2p + h ω ₂

∼ε = 0 E _1s - E _2p + h ω ₂ ε∼

Abbildung 1.4: Veranschau- lichung des Faltungsinte- grals 1.41 zur Berechnung des Fluoreszenzspektrums.

Die Intensit¨ at I ω 1 (ω 2 ) des Emissionsspektrums ergibt sich aus dem Integral des Produktes beider Funk- tionen, dem sogenannten Uberlapp. Die Position der ¨ schmalen Lorentzfunktion ist von ω ₂ abh¨ angig. Oben:

˜

_c < 0. Der Uberlapp ¨ wird maximal, wenn die Lorentzfunktion I ₂ (rechts) etwas links der Sprungstelle der Funktion I ₁ (links) zentriert ist. Unten: ˜ _c > 0 Maximaler ¨ Uberlapp, wenn I ₂ bei ˜ = 0 zentriert ist.

diese in Abbildung 1.4 f¨ ur die F¨ alle ˜ _c < 0 (oben) und ˜ _c > 0 (unten) dargestellt.

Da die Lebensdauerverbreiterung des 1s-Niveaus deutlich gr¨ oßer ist als die des 2p- Niveaus ² , kann angenommen werden, dass I ₂ wesentlich schmaler ist als I ₁ . Man erh¨ alt f¨ ur die Position des Maximums des Emissionsspektrums:

¯

hω ₂ ^max ≈

E _2p + ¯ hω ₁ − ₀ f¨ ur ¯ hω ₁ ≤ ₀ − E _1s

E _2p − E _1s f¨ ur ¯ hω ₁ > ₀ − E _1s (1.42) F¨ ur einfallende Photonenenergien kleiner als ₀ − E _1s erh¨ alt man ebenfalls eine lineare Raman-Shift. Sobald aber die volle Resonanz erreicht und ¨ uberschritten ist, bleibt die Position des Maximums des Emissionsspektrums konstant.

Die beiden untersuchten Beispiele stellen die Grenzf¨ alle einer realen Zustands- dichte dar, in der weder unendlich scharfe Energieniveaus noch ein strukturloses Kontinuum vorkommt. Prinzipiell l¨ asst sich aber auch im allgemeinen Fall die

2 F¨ ur Kupfer gilt zum Beispiel: Γ _1s = 0.775 eV , Γ _{2p 1/2} = 0.31 eV , Γ _{2p 3/2} = 0.28 eV

[Zschornack 1989]

1.3. Resonant unelastische R¨ ontgenstreuung 15 Zustandsdichte aus den Emissionsspektren gewinnen, sofern die Lebensdauerver- breiterungen und Energieeigenwerte des Zwischenzustands und des Endzustands bekannt sind (siehe zum Beispiel [Wittkop 2000]).

Ein Vorteil dieser Spektroskopiemethode liegt in der hohen Eindringtiefe des hoch- energetischen R¨ ontgenlichts, welche selbst bei Anregungen nahe einer Absorpti- onskante in der Gr¨ oßenordnung mehrerer Mikrometer liegt. Oberfl¨ achenverunrei- nigungen oder mikroskopische Inhomogenit¨ aten in der Probe haben daher nur einen vernachl¨ assigbaren Einfluss auf das Messergebnis. Weiterhin erm¨ oglicht die resonante Streuung durch die Auswahl der Energie der einfallenden Photonen die sogenannte Elementselektivit¨ at, also die gezielte Untersuchung eines bestimmten Elements in einer Umgebung aus Fremdatomen.

Da die resonante R¨ ontgen-Raman-Streuung Photonen als Sonde benutzt, ist es im Gegensatz zu Methoden der Photoemissionsspektroskopie (PES) nicht notwendig, die Gesamtzahl der Elektronen im System zu ¨ andern. Bei der Untersuchung iso- lierender oder halbleitender Materialien kann es nicht zu einer Beeinflussung der Ergebnisse durch die elektrische Aufladung der Probe kommen, was bei der PES h¨ aufig ein Problem darstellt.

Schließlich ist zu betonen, dass bei der RIXS zuvor unbesetzte Zust¨ ande nur als

Folge elektronischer Anregungen besetzt werden. Dies ist besonders bei stark kor-

relierten Systemen von Vorteil, da hier das Einbringen eines zus¨ atzlichen Elektrons

wie bei der inversen Photoemission zu einer grundlegenden ¨ Anderung der elektro-

nischen Struktur durch starke Elektron-Elektron Wechselwirkungen f¨ uhrt. Hierauf

soll im folgenden Kapitel n¨ aher eingegangen werden.

Kapitel 2

Elektronische Eigenschaften von Ubergangsmetallverbindungen ¨

In diesem Kapitel sollen die elektronischen Eigenschaften von ¨ Ubergangsmetall- verbindungen diskutiert, sowie die elektronische und kristalline Struktur von CuO beschrieben werden.

2.1 Grenzen der Dichtefunktionaltheorie

Die Berechnung der elektronischen Struktur eines Systems geh¨ ort zu den wichtig- sten Aufgaben der theoretischen Festk¨ orperphysik. Hierbei spielt die sogenannte Dichtefunktionaltheorie (DFT) eine bedeutenden Rolle. Sie basiert auf dem Theo- rem von Hohenberg und Kohn, welches besagt, dass die Gesamtenergie eines Sy- stems von wechselwirkenden Elektronen in einem ¨ außeren Potential ein Funktional der Elektronendichte ρ(~ r ) ist. Die Elektronendichte des Grundzustands ρ ₀ (~ r ) mi- nimiert die Gesamtenergie [Singh 1994], also

E[ρ] ≥ E 0 = E[ρ 0 ]. (2.1)

Leider ist die Form des Funktionals E[ρ] im Allgemeinen unbekannt und muss gen¨ ahert werden. Zun¨ achst schreibt man jedoch die Elektronendichte als Summe uber die Einteilchendichten ¨

ρ(~ r ) = X

bes.

ϕ ^∗ _i (~ r ) ϕ _i (~ r ) , (2.2)

wobei ¨ uber alle besetzten Zust¨ ande summiert wird. Die ϕ _i (~ r ) sind die sogenannten Kohn-Sham Orbitale und l¨ osen die Kohn-Sham Gleichungen:

T + V _ei (~ r ) + V _H (~ r ) + V _xc (~ r )

ϕ _i (~ r ) = _i ϕ _i (~ r ). (2.3)

17

Dabei ist T die kinetische Energie, V _ei (~ r ) die Coulomb-Energie der Elektronen im Kernpotential und V _H (~ r ) der Hartree Teil der Elektron-Elektron Coulomb- Wechselwirkung

V _H (~ r ) = e ² Z

d~ r ⁰ ρ(~ r ⁰ )

|~ r − ~ r ⁰ | . (2.4)

V _xc (~ r ) ist das unbekannte Austausch-Korrelations-Potential, f¨ ur das eine geeignete N¨ aherung eingesetzt werden muss.

Die Kohn-Sham Gleichungen erm¨ oglichen die iterative Berechnung der elektroni- schen Struktur des Grundzustandes. Dabei l¨ ost man das Gleichungssystem unter Verwendung der Elektronendichte ρ ⁽ⁿ⁻¹⁾ (~ r ), welche aus dem vorhergehenden Ite- rationsschritt (n − 1) bekannt ist. Als Ergebnis erh¨ alt man einen neuen Satz von Einteilchen-Wellenfunktionen ϕ _i (~ r ) mit den zugeh¨ origen Energieeigenwerten _i . Uber Gleichung (2.2) erh¨ ¨ alt man daraus eine neue Elektronendichte ρ ⁽ⁿ⁾ (~ r ) und wiederholt den Zyklus bis zur Selbstkonsistenz, also solange, bis sich keine weiteren Anderungen an der Ladungsdichte ergeben. Als Ergebnis dieses Prozesses erh¨ ¨ alt man die Energieeigenwerte der Wellenfunktionen, die sich in Form der Bandstruk- tur darstellen lassen.

Ein entscheidendes Problem dieser Methode ist die N¨ aherung des nicht-lokalen Austausch-Korrelations-Potentials V _xc (~ r ). H¨ aufig wird dieser Beitrag im Rahmen der local density approximation (LDA) durch das lokale Austauschpotential eines homogenen Elektronengases ersetzt. Obwohl diese N¨ aherung bei schwach korre- lierten Systemen in der Regel zu guten Vorhersagen der Einteilchen-Bandstruktur f¨ uhrt, stimmen die Berechnungen der elektronischen Struktur von stark korrelier- ten Systemen h¨ aufig nicht mit den experimentellen Befunden ¨ uberein. Der Grund hierf¨ ur liegt zum einen in der N¨ aherung der Vielteilchenwechselwirkung durch ein effektives Einteilchen-Potential und zum anderen daran, dass die unbesetzen Zu- st¨ ande keinen Beitrag zu den Iterationen des Selbstkonsistenz-Zyklusses liefern. Bei einem gegebenen Potential werden alle Energieeigenwerte des Hamiltonoperators berechnet und f¨ ur die N niedrigsten Eigenwerte werden die zugeh¨ origen Eigenzu- st¨ ande als besetzt angenommen. N ist dabei die Anzahl der Elektronen im System.

Im n¨ achsten Iterationszyklus tragen somit nur die Wellenfunktionen der besetzten Zust¨ ande zur Elektronendichte und damit zum neuen Potential bei. Bei Erreichen der Selbstkonsistenz sind die unbesetzten Zust¨ ande also L¨ osungen im Potential des Grundzustandes des N-Elektronensystems. Eine ¨ Anderung dieses Potentials bei Entfernen eines Elektrons aus einem besetzten Zustand oder bei Hinzuf¨ ugen eines Elektrons in einen zuvor unbesetzten Zustand wird nicht ber¨ ucksichtigt.

Ein gutes Beispiel f¨ ur das Versagen der DFT bei der Betrachtung hochkorrelierter

Systeme sind ¨ Ubergangsmetallverbindungen, bei denen eine nicht abgeschlosse-

ne d-Schale zu starken d-d Wechselwirkungen f¨ uhrt. Ladungsfluktuationen des

Typs d ^N _i d ^N _j → d ^N−1 _i d ^N+1 _j (N ist hier die mittlere Anzahl von d-Elektronen pro

2.2. Formale Beschreibung korrelierter Systeme 19 Ubergangsmetallatom, i und j sind zwei verschiedene Gitterpl¨ ¨ atze), die bei d- artigen Leitern den Prozess des Ladungstransportes beschreiben, werden durch Zweiteilchen Coulomb-Wechselwirkungen beeinflusst, die die DFT nicht ber¨ uck- sichtigt [Sawatzky 1984]. So ergeben LDA Rechnungen f¨ ur zweiwertiges Kupfer- oxid (CuO) einen d-Leiter [Grioni 1989], w¨ ahrend man experimentell eine Band- l¨ ucke von 1.4 eV findet [Koffyberg 1982]. Alternative Ans¨ atze zur Berechnung der elektronischen Struktur korrelierter Systeme werden in den Abschnitten 2.3 und 2.4.1 diskutiert. Zun¨ achst soll jedoch eine formale Beschreibung solcher Systeme vorgestellt werden, die gleichzeitig die Verkn¨ upfung der elektronischen Struktur mit experimentell zug¨ anglichen Messgr¨ oßen herstellt.

2.2 Formale Beschreibung korrelierter Systeme

Eine fundamentale Gr¨ oße zur Beschreibung der elektronischen Struktur eines Fest- k¨ orpers ist die sogenannte spektrale Dichtefunktion (SDF), die die Wahrscheinlich- keit daf¨ ur angibt, ein Elektron mit dem Wellenvektor ~k in das System einzubringen oder aus diesem zu entfernen, wobei sich die Energie des Systems um ¯ hω ¨ andert.

Die SDF ist definiert als:

A(~k,¯ hω) = X

f

hN _f ⁻ |c _{~ k} |N ₀ i

2 δ(¯ hω + E _f ⁻ − E ₀ )

+ X

f

hN _f ⁺ |c _~ ^†

k |N ₀ i

2

δ(¯ hω − E _f ⁺ + E ₀ ) (2.5)

Hierbei bezeichnet |N 0 i den Grundzustand des N-Elektronensystems mit der Ener- gie E ₀ . |N _f ⁻ i und |N _f ⁺ i sind m¨ ogliche Endzust¨ ande des (N-1)- bzw. (N+1)- Elektronensystems, E _f ⁻ und E _f ⁺ sind die zugeh¨ origen Energien. Die Summation ersteckt sich ¨ uber alle m¨ oglichen Endzust¨ ande. c _~ ^†

k erzeugt ein Elektron mit dem Wellenvektor ~k und c ~ k ist der entsprechende Vernichter. F¨ ur den Fall unkorrelierter Systeme vereinfacht sich (2.5) zu:

A ⁰ (~k,¯ hω) = δ(¯ hω − E _~ ⁰

k ), (2.6)

wobei E _~ ⁰

k die Einteilchenenergie eines Elektrons mit Wellenvektor ~k ist. In diesem Fall entspricht A ⁰ (~k,¯ hω) der Einteilchen-Bandstuktur.

Eine M¨ oglichkeit, die SDF experimentell zu bestimmen, ist die winkelaufgel¨ o-

ste Photoemissionsspektroskopie (Angular Resolved Photoemission Spectroscopy,

ARPES) f¨ ur den Bereich besetzter Zust¨ ande, bzw. die winkelaufgel¨ oste inver- se Photoemissionsspektroskopie (Angular Resolved Inverse Photoemission Spec- troscopy, ARIPES) f¨ ur den Bereich der unbesetzten Zust¨ ande. Nimmt man an, dass die kinetische Energie des ausfallenden (einfallenden) Photoelektrons groß ist, man also dessen Wechselwirkung mit dem ¨ ubrigen System w¨ ahrend und nach dem Photoemissionsprozess vernachl¨ assigen kann (sudden approximation), l¨ asst sich die Einteilchen-Wellenfunktion Φ des Photoelektrons von der Vielteilchen- Wellenfunktion Ψ(N − 1) des ¨ ubrigen Systems abseparieren. Man erh¨ alt in dieser N¨ aherung f¨ ur die Intensit¨ at des Photoemissionsspektrums [H¨ ufner 1995]:

I PES (E) ∝ X

i,f,~ k

|hΦ f,E _kin |~ r |Φ _{i,~ k} i | ² A(~k,E) (2.7)

Φ _{i,~ k} ist die Einteilchen-Wellenfunktion des Photoelektrons mit Wellenvektor ~k vor dem Prozess, Φ _{f,E kin} die Wellenfunktion des freien Photoelektrons mit der kineti- schen Energie E kin nach dem Prozess, wobei ¨ uber alle Wellenvektoren, Anfangs- und Endzust¨ ande summiert wird.

Im Gegensatz zu dieser recht einfachen Beziehung zwischen der SDF und der In- tensit¨ at eines Photoemissionsspektrums besteht bei der unelastischen R¨ ontgen- streuung ein komplexer Zusammenhang zwischen der Messgr¨ oße, dem sogenannten dynamischen Strukturfaktor S(~ q, ω), und der Faltung der SDF des Grundzustan- des A(~k, E) mit der SDF des angeregten Zustandes A(~k + ~ q, E + ¯ hω). Es gilt [Sternemann 2000]:

S(~ q,ω) = − 1

π Im χ(~ q,ω) = − 1

π Im χ ^sc (~ q,ω)

1 − v(q)χ ^sc (~ q,ω) (2.8) und

Im χ ^sc (~ q,ω) = −

Z d~k (2π) ³

Z E F

E F −¯ hω

dE

2π A(~k,E) A(~k + ~ q,E + ¯ hω) (2.9) χ(~ q,ω) ist die Polarisationsfunktion, χ ^sc (~ q,ω) die effektive Polarisationsfunktion und v(q) = ^4πe _{|~ q |} 2 ² die Fouriertransformierte des Coulomb-Potentials. ~ q und ¯ hω sind der Impuls- und der Energie¨ ubertrag.

Die Faltung der beiden SDF berschreibt das Vernichten eines Zustandes mit

E < E _F in Kombination mit dem Erzeugen eines Zustandes mit E > E _F . Im

Unterschied zur winkelaufgel¨ osten Photoemission erh¨ alt man damit auch Zugang

zu Anregungsprozessen, bei denen die Ladungserhaltung im System gilt und welche

f¨ ur viele wichtige Eigenschaften entscheidend sind (z.B. W¨ armeleitung, Leitf¨ ahig-

keit, optische Eigenschaften).

2.3. Die Bandl¨ ucke bei ¨ Ubergangsmetallverbindungen 21

2.3 Die Bandl¨ ucke bei

Ubergangsmetallverbindungen ¨

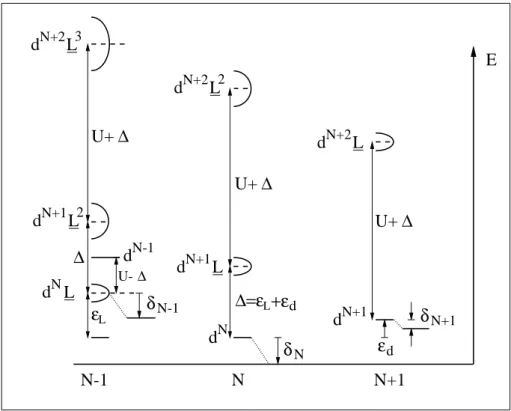
In einem sehr einfachen Modell kann man annehmen, dass der Ladungstrans- port in einem System stark lokalisierter d-Elektronen auf Ladungsfluktuationen des Typs d ^N _i d ^N _j → d ^N−1 _i d ^N+1 _j basiert, wobei effektiv ein Elektron vom Gitterplatz i zum Gitterplatz j transportiert wird. Da hierdurch zwei lokalisierte Ladungen er- zeugt werden ist einsichtig, dass dazu die Coulomb-Energie U aufgebracht werden muss. Nimmt man weiterhin an, dass sich die beiden Ladungen durch Wechsel- wirkung mit den n¨ achsten Nachbaratomen durch den Festk¨ orper bewegen k¨ onnen (d ^N+1 _j d ^N _k → d ^N _j d ^N+1 _k bzw. d ^N−1 _i d ^N _k → d ^N _i d ^N−1 _k ), so erh¨ alt man durch diese Delokalisa- tion zwei schmale Energieb¨ ander der Breite w deren Abstand durch U gegeben ist.

Unterhalb der Fermienergie befindet sich das Band, welches dem Entfernen eines Elektrons (d ^N → d ^N−1 ) entspricht und das als unteres Hubbard Band (UHB) be- zeichnet wird. Analog befindet sich oberhalb der Fermienergie das obere Hubbard Band (OHB), welches das Hinzuf¨ ugen eines Elektrons (d ^N → d ^N+1 ) beschreibt.

Da die oben beschriebene Ladungsfluktuation beide Prozesse kombiniert, l¨ asst sie sich auch als ein direkter ¨ Ubergang vom UHB in das OHB auffassen. Man er- h¨ alt einen d-Leiter, wenn der Abstand U der beiden B¨ ander kleiner ist als ihre Bandbreite w, wenn also gilt

U < 1

2 (w N−1 + w N+1 ) ≈ w. (2.10)

Andernfalls erh¨ alt man einen Halbleiter oder Isolator. Die ¨ Anderung der Band- breite, z.B. durch Variation der Gitterkonstanten durch Temperatur- oder Druck-

¨

anderung, kann somit einen Mottschen Metall-Isolator ¨ Ubergang hervorrufen.

Im Widerspruch zu diesem Modell zeigt sich jedoch, dass Verbindungen der schwe- ren 3d- ¨ Ubergangsmetalle (Co, Ni, Cu) h¨ aufig eine Abh¨ angigkeit der Bandl¨ ucke vom jeweiligen Liganden aufweisen, was nicht durch die Liganden-unabh¨ angige Coulomb-Energie erkl¨ art werden kann [Zaanen 1985]. So besitzt z.B. CuS metal- lischen Charakter, w¨ ahrend CuO, wie bereits erw¨ ahnt, ein Halbleiter mit einer Bandl¨ ucke von 1.4 eV ist. Dieses Verhalten ist ein Hinweis darauf, dass im Bereich unterhalb der Fermienergie neben dem UHB auch Ladungsfluktuationen vom Typ d ^N → d ^N L eine Rolle spielen. Hierbei bezeichnet L ein Loch im Liganden p-Band.

Uberg¨ ¨ ange zwischen diesem Lochband und dem OHB (d ^N → d ^N+1 L) werden als Ladungstransfer bezeichnet. Der Abstand beider B¨ ander ist die Ladungstransfer- energie ∆. Ist die Coulomb-Energie U gr¨ oßer als ∆, wird die Bandl¨ ucke durch die Ladungstransferenergie bestimmt. Die Bedingung f¨ ur einen metallischen Leiter ist dann

∆ < 1

2 (W + w), (2.11)

N

d d ^N+1

w

d d ^N

d ^N d

N N-1

N N

d L E

d s

UHB OHB

∆ W

U ^F

Abbildung 2.1: Die energetische Lage aller relevanten Niveaus f¨ ur den Fall eines Ladungstransfer Halbleiters. Oberes Hubbard Band (OHB) und unteres Hubbard Band (UHB) sind durch die Coulomb-Energie U getrennt. Der Abstand des Ligan- den p-Lochbandes vom OHB ist gleich der Ladungstransferenergie ∆, welche hier die Bandl¨ ucke bestimmt.

wobei W die Breite des Liganden p-Lochbandes ist.

Da die n¨ otige Energie zum Erzeugen eines Lochs im Liganden p-Band stark von der Elektronegativit¨ at des Liganden abh¨ angt, ergeben sich die beobachteten unter- schiedlichen Eigenschaften verschiedener Verbindungen der genannten ¨ Ubergangs- metalle. Abbildung 2.1 zeigt die Lage aller beteiligten Niveaus bez¨ uglich der Fermi- energie f¨ ur den Fall eines Ladungstransfer-Halbleiters. Ebenfalls eingezeichnet ist das unbesetzte Metall s-Band (d ^N → d ^N s), welches aufgrund seiner hohen Energie f¨ ur die betrachteten Prozesse keine Rolle spielt.

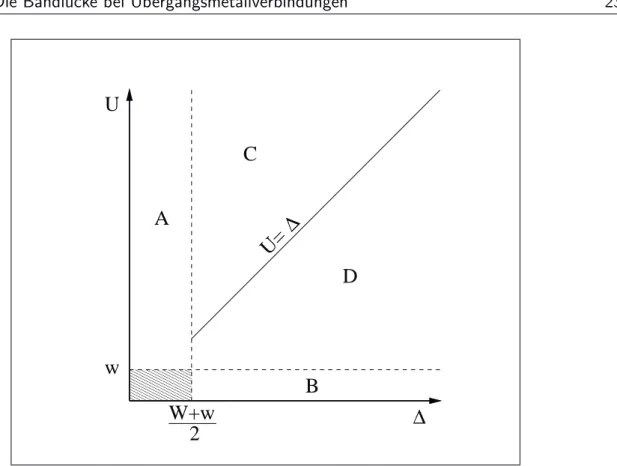
In diesem einfachen Modell entscheidet die Gr¨ oße von U und ∆ im Vergleich zu- einander und im Vergleich zu den Bandbreiten w und W dar¨ uber, ob ein Metall oder ein Isolator vorliegt. Zur Verdeutlichung zeigt Abbildung 2.2 das sogenannte ZSA-Diagramm [Zaanen 1985] (nach Zaanen, Sawatzky und Allen), in dem in der Art eines Phasendiagramms zwischen vier Bereichen unterschieden wird, f¨ ur die sich verschiedene elektronische Eigenschaften ergeben.

• Bereich A (∆ < ^w+W ₂ ): p-Metall; Beispiele: CuS, CuSe und NiSe.

Die Leitung erfolgt im Wesentlichen durch L¨ ocher im Liganden p-Band.

• Bereich B (U < w): d-Metall; Beispiele: TiO und CrO ₂ .

Die Leitf¨ ahigkeit wird hier durch schwere Elektronen und L¨ ocher im Metall

d-Band hervorgerufen.

2.3. Die Bandl¨ ucke bei ¨ Ubergangsmetallverbindungen 23

U=

∆

W+w 2 A

B C

D

∆ U

w

Abbildung 2.2: Das ZSA-Diagramm. Die Bereiche A bis D im Diagramm ent- sprechen unterschiedlichen elektronischen Eigenschaften der dort einzuordnenden Verbindungen (vgl. Text).

• Bereich C ( ^w+W ₂ < ∆ < U ): Ladungstransfer Halbleiter oder Isolatoren;

Beispiele: CuO, CuCl ₂ und CuBr ₂ .

Die Bandl¨ ucke ist n¨ aherungsweise proportional zu ∆.

• Bereich D: (w < U < ∆): Mott-Hubbard Isolatoren; Beispiele: V ₂ O ₃ , Ti ₂ O ₃ , Cr ₂ O ₃ .

Die Bandl¨ ucke ist n¨ aherungsweise proportional zu U .

In der Realit¨ at sind die ¨ Uberg¨ ange zwischen den Bereichen nat¨ urlich fließend und es kommt an den Grenzlinien zu starken Hybridisierungseffekten zwischen allen beteiligten B¨ andern.

Bis hierher ber¨ ucksichtigt man in diesem einfachen Modell nur die Konfigurationen

d ^N+1 eines (N+1)-Elektronensystems, d ^N eines N-Elektronensystems sowie d ^N−1

und d ^N L eines (N-1)-Elektronensystems. Es ergeben sich jedoch weitere Konfigu-

rationen, wenn man auch f¨ ur das N- und (N+1)-Elektronensystem einen Ladungs-

transfer Prozess zul¨ asst und weiterhin die M¨ oglichkeit von mehrfachen Ladungs-

transfer Prozessen, also z.B. d ^N → d ^N+2 L ² , in Betracht zieht. Zur Bestimmung der Bandl¨ ucke E _g berechnet man dann die Grundzustandsenergie E ₀ eines jeden Systems und erh¨ alt auf diese Weise

E _g = (E ₀ ^N−1 − E ₀ ^N ) + (E ₀ ^{N +1} − E ₀ ^N ). (2.12) Zur Veranschaulichung zeigt Abbildung 2.3 die Lage der wichtigsten Konfiguratio- nen der (N-1)-, N- und (N+1)-Elektronenzust¨ ande eines Ladungstransfer Halblei- ters in einem Energieniveau-Diagramm.

Die niedrigste Energie besitzt die d ^N Konfiguration des N-Elektronensystems.

∆

δ

∆

∆

δ

δ d

d

d

d d

∆

∆=ε _L ε _L

d

d d

N-1

N-1 N

N

N+1 N+1

N U- ∆

U+

+ε _d U+

U+

ε _d L ³

L ²

L ²

N+2

N+2

N+2

N+1 N+1

L

L

E

N-1 N N+1

L d

Abbildung 2.3: Energieniveau-Diagramm der wichtigsten Konfigurationen eines Ladungstransfer Halbleiters. Ebenfalls eingezeichnet sind die Hybridisierungsener- gien δ _x der jeweiligen Grundzust¨ ande.

Im Abstand ∆ oberhalb von d ^N befindet sich der Zustand mit einem einfachen Ladungstransfer (d ^N+1 L). Die Bandbreite entspricht der Breite W des Liganden- Lochbandes ¹ . Deutlich zu h¨ oheren Energien hin verschoben befindet sich der Zu- stand mit einem zweifachen Ladungstransfer (d ^N+2 L ² ), der die Bandbreite 2W

1 Zur Vereinfachung der Abbildung wird die Breite des d-Bandes sowie der Hubbard B¨ ander

vernachl¨ assigt.

2.3. Die Bandl¨ ucke bei ¨ Ubergangsmetallverbindungen 25 besitzt. Ausgehend von d ^N+1 L muss hier nicht nur erneut die Ladungstransfer- energie aufgebracht werden, sondern aufgrund der bereits vorhandenen Ladung am d-Metall zus¨ atzlich noch die Coulomb-Energie U .

Der Grundzustand des (N+1)-Elektronensystems ist der d ^N+1 Zustand. Der ener- getische Abstand der Zust¨ ande d ^N und d ^N+1 ist gleich der Elektronenaffinit¨ at _d . Die Konfiguration mit einfachem Ladungstransfer ist um die Summe aus Ladungs- transferenergie und Coulomb-Energie zu h¨ oheren Energien hin verschoben.

Da sich das Energieniveau-Diagramm auf einen Ladungstransfer Halbleiter bezieht, ist die Konfiguration d ^N−1 nicht der Grundzustand des (N-1)-Elektronensystems.

Der Grund hierf¨ ur ist, dass man f¨ ur einen Ladungstransfer zwar die Energie ∆ aufbringen muss, gleichzeitig aber die Coulomb-Energie U durch den Ausgleich der positiven Ladung am Metall gewonnen wird. Da hier ∆ < U ist, erh¨ alt man einen niedrigeren Energiewert f¨ ur die Konfiguration d ^N L, die damit den Grund- zustand dieses Systems bildet. Der Abstand der Konfigurationen d ^N und d ^N L ist gleich der ersten Ionisierungsenergie _L des Liganden. Hieraus ergibt sich, dass die Ladungstransferenergie gegeben ist durch

∆ = _d + _L . (2.13)

Ausgehend von d ^N L erfordert ein weiterer Ladungstransfer das Aufbringen der Energie ∆ und, um einen dritten Ladungstransfer durchzuf¨ uhren und zur Konfi- guration d ^N+2 L ³ zu gelangen, die Energie U + ∆.

Unter Verwendung von Gleichung (2.12) und unter Ber¨ ucksichtigung der unter- schiedlichen Grundzustandshybridisierungsenergien δ _N−1 , δ _N und δ _N+1 erh¨ alt man damit die Bandl¨ ucke

E _g = (δ _N + _L − δ N−1 ) + (δ _N + _d − δ _N+1 )

= ∆ + 2δ _N − δ N−1 − δ _N+1 . (2.14)

Obwohl diese bisher rein ph¨ anomenologische Beschreibung von ¨ Ubergangsmetall- verbindungen eine Erkl¨ arung f¨ ur die unterschiedlichen elektronischen Eigenschaf- ten der einzelnen Verbindungen anhand einiger weniger Parameter liefert, ist noch unklar, wie diese Parameter zu berechnen sind. Weiterhin ist offen, wie die Wech- selwirkung verschiedener Konfigurationen ber¨ ucksichtigt werden kann, also z.B.

die Mischung von d ^N und d ^N+1 L im Grundzustand. Hier stellt der bisherige, rein ionische Ansatz, also die Zuordung eines Elektrons entweder zu einem Metallatom oder zu einem Ligandenatom, sicherlich eine zu grobe N¨ aherung dar.

Im n¨ achsten Abschnitt wird daher ein kurzer ¨ Uberblick ¨ uber Ans¨ atze gegeben, mit

denen eine quantitative Berechnung der elektronischen Struktur einschließlich der

vorhandenen Parameter m¨ oglich ist.

2.4 Berechnung der elektronischen Struktur

2.4.1 Atomare Multiplettrechnungen

Ist eine Schale eines Atoms nicht vollst¨ andig gef¨ ullt, so ergeben sich f¨ ur die N vorhandenen Elektronen verschiedene M¨ oglichkeiten der Kopplung der einzelnen Bahndrehimpulse L _i und Spins S _i zu einem gesamten Bahndrehimpuls L und einem Gesamtspin S. Unter Ber¨ ucksichtigung des Pauli Verbots erh¨ alt man beispielsweise f¨ ur das System d ² 45 m¨ ogliche Kombinationen der beiden d-Orbitale, welche sich zu ^2S+1 L = ¹ S, ³ P, ¹ D, ³ F und ¹ G zusammenfassen lassen ² [de Groot 1991].

Aufgrund unterschiedlicher Coulomb- und Austauschenergien verschiedener Kon- figurationen ergibt sich eine Multiplett Aufspaltung. Um diese zu berech- nen entwickelt man zun¨ achst den 1/r Term der Elektron-Elektron Coulomb- Wechselwirkung in eine Reihe von Legendre Polynomen [Cowan 1981]:

1

|~ r ₁ − ~ r ₂ | = 1 r ₁₂ =

∞

X

k=0

r ^k _<

r ^k+1 _> P _k (cos θ) (2.15)

~ r ₁ und ~ r ₂ sind die Orte der beiden wechselwirkenden Elektronen und θ ist der Winkel zwischen beiden Ortsvektoren. r _< (und analog r _> ) ist definiert als r _< = min (|~ r ₁ |; |~ r ₂ |). P _k ist das Legendre Polynom k-ten Grades.

F¨ ur den Radialteil des Coulomb-Matrixelementes U(a,b,c,d) = hab|2e/r ₁₂ |cdi er- h¨ alt man damit die Summe ¨ uber die sogenannten Slater Integrale R ^k :

R ^k (ab,cd) = Z

r 1

Z

r 2

r ^k _<

r ^k+1 _> R ^∗ _a (r ₁ ) R ^∗ _b (r ₂ ) R _c (r ₁ ) R _d (r ₂ ) dr ₁ dr ₂ (2.16) Hierbei fasst a = (n,l) (und analog b,c und d) die Haupt- und Drehimpuls- quantenzahl des a-ten Elektrons zusammen. R _a (r) ist dessen Radialwellenfunk- tion. Im verallgemeinerten Fall (2.16) wird h¨ aufig zwischen den Coulomb-Termen F ^k (a,b) = R ^k (ab,ab) und den Austausch-Termen G ^k (a,b) = R ^k (ab,ba) unterschie- den.

Weiterhin f¨ uhrt die Winkelintegration des Matrixelements zu Auswahlregeln, so- dass nur wenige der Slater-Integrale tats¨ achlich zur Coulomb-Energie beitragen.

Im Fall einer reinen d-d Wechselwirkung sind dies die drei Coulomb-Terme F ⁰ , F ² und F ⁴ , die in der Literatur h¨ aufig auch durch die sogenannten Racah-Parameter ausgedr¨ uckt werden. Diese sind definiert durch [Cowan 1981]:

A = F ⁰ − F ⁴ /9 (2.17)

2 Die Drehimpulse L=0,1,2,3,... werden hierbei wie ¨ ublich mit S, P, D, F,... bezeichnet

2.4. Berechnung der elektronischen Struktur 27

B = (9F ² − 5F ⁴ )/441 (2.18)

C = 5F ⁴ /63 (2.19)

Als direkte Konsequenz der Elektron-Elektron Coulomb-Wechselwirkung erf¨ ullt die Konfiguration mit der niedrigsten Energie die Hundschen Regeln:

1. S ist maximal.

2. Unter Ber¨ ucksichtigung von Punkt 1 ist L maximal.

3. F¨ ur mehr (weniger) als halb gef¨ ullte Schalen koppeln L und S zum Gesamtdrehimpuls J = L + S (J = |L − S|).

Ubertragen auf das Beispiel eines d ¨ ² Systems bedeutet dies, dass die Konfiguration

2S+1 L _J = ³ F ₂ die niedrigste Energie besitzt und damit den Grundzustand darstellt.

Die Reihenfolge der Energien der anderen Konfigurationen geht allerdings aus den Hundschen Regeln nicht hervor.

2.4.2 Kristallfeldaufspaltung

Befindet sich das betrachtete Atom in einem Kristall, kann die Aufhebung der Entartung durch das Kristallfeld zu einem Grundzustand f¨ uhren kann, der nicht den Hundschen Regeln entspricht. Abbildung 2.4 zeigt die Kristallfeldaufspaltung des Grundzustands eines d ⁸ Systems in verschiedenen Kristallfeldsymmetrien. Dem freien Atom entspricht ein sph¨ arisches Kristallfeld ohne Auszeichnung einer Rich- tung. Der Grundzustand ist der Zustand ³ F, den man bereits f¨ ur das d ² System erhalten hat. Hierbei zeigt sich die Analogie zwischen einem System mit zwei Elek- tronen in einer ansonsten leeren Schale und einem System mit zwei L¨ ochern in einer ansonsten vollen Schale. Ein Unterschied ergibt sich lediglich bei der Kopplung L und S zum Gesamtdrehimpuls J gem¨ aß der dritten Hundschen Regel. In der Ab- bildung erkennt man zwei jeweils f¨ unffach entartete Energieniveaus, die durch die Elektron-Elektron Coulomb-Wechselwirkung aufgespalten sind, wodurch sich ein vollst¨ andig besetztes Spin-up Niveau (Majorit¨ atsspin) und ein zweifach unbesetz- tes Spin-down Niveau (Minorit¨ atsspin) ergibt.

Im kubischen Kristallfeld spaltet jedes dieser Niveaus in ein zweifach entartetes Niveau mit e _g Symmetrie (d _x ² −y ² , d _3z ² −r ² ) und ein dreifach entartetes Niveau mit t 2g Symmetrie (d xy ,d yz , d xz ) auf. Im Grundzustand der Symmetrie ³ A 2g ist das e g

Niveau des Minorit¨ atsspins unbesetzt, das System koppelt also nach wie vor zu

S = 1.