Exercises to Wissenschaftliches Rechnen I/Scientific Computing I (V3E1/F4E1) Winter 2016/17

Exercises to Wissenschaftliches Rechnen I/Scientific Computing I (V3E1/F4E1)

Winter 2016 / 17

Prof. Dr. Martin Rumpf

Alexander Effland — Stefanie Heyden — Stefan Simon — Sascha Tölkes

Problem sheet 8

Please hand in the solutions on Tuesday December20!

Exercise23 4 Points

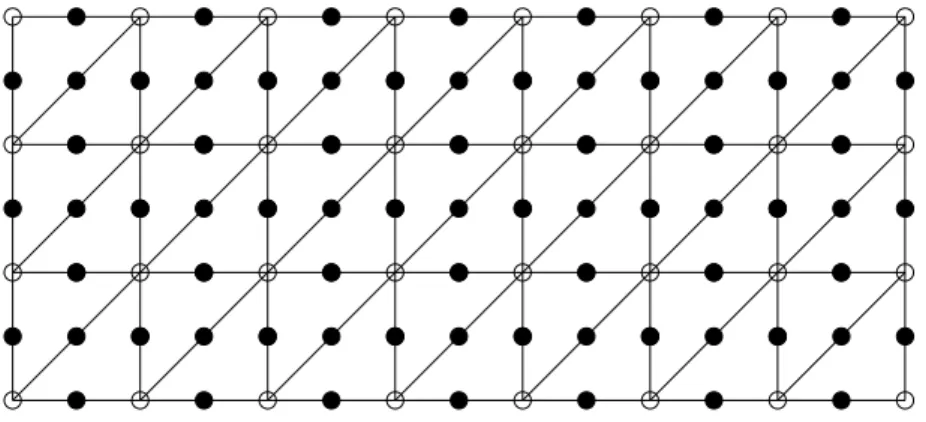
For m,n ≥_{2 let} G = {_{1, . . . ,m}} × {_{1, . . . ,n}} be a rectangular grid. On G, a regular triangular mesh T_h can be constructed by using the points in G as vertices for the triangles as shown in Figure1 (in this example, m =8 andn =4 and the circles ◦ correspond to the elements of G). On the triangular mesh T_h, we consider the

Figure1: Triangular mesh for Crouzeix-Raviart elements.

Crouzeix-Raviart finite element spaceV_h (the degrees of freedom for the Crouzeix- Raviart elements are the filled circles • in Figure1). Derive an explicit formula for the total number of degrees of freedom ofV_h in terms ofm and n. Compare your result with the number of degrees of freedom of theP₁-finite element space onT_h.

Exercise24 4 Points Consider the following triangle T⊂_R²with vertexes x₀, x₁ and x₂:

x₀ x₁

x2

y₂

y₁ y0

Derive an explicit formula for the local stiffness matrix of the Crouzeix-Raviart finite element onT in terms of x0, x1 and x2, where y0, y1 and y2 represent the degrees of freedom located at the midpoints of the edges.

Exercise25 4 Points

Let Ω = (0, 1), T_h be a given triangulation on Ω and f ∈ L²(_Ω). Furthermore, let u∈ H¹(_Ω) be the weak solution of

−u⁰⁰ = f inΩ, u(₀) =u(₁) =_{0 .}

Derive an a posteriori error estimate for the discrete solution u_h ∈ V_h w.r.t. the H¹(_Ω)-seminorm R

Ω|u⁰|²dx¹₂

, whereV_h is the space of P₁-finite elements on T_h. Hint: Follow the proof of Theorem 2.3and use Lagrange interpolation.

Exercise26 4 Points

LetΩ = (0, 1)² and T_h be a given triangulation on Ω. For f ∈ L²(_Ω)consider

−_∆u = f inΩ,

u =0 on ∂Ω. (1)

We denote byu the weak solution of (1) and byu_h the discrete solution on the space ofP₁-finite elements onT_h. Find some f ∈ L²(_Ω) _{such that}u 6=u_h, but ηT =_{0 for} all T ∈ T_h.