Multistep Predictions from Multivariate ARMA-GARCH
Models and their Value for Portfolio Management Jaroslava Hlouskova
Kurt Schmidheiny Martin Wagner
02-12 November 2002
Diskussionsschriften
Universität Bern
Volkswirtschaftliches Institut Gesellschaftstrasse 49 3012 Bern, Switzerland Tel: 41 (0)31 631 45 06
Multistep Predictions from Multivariate ARMA-GARCH Models and their Value for Portfolio Management
∗Jaroslava Hlouskova
Department of Economics and Finance Institute for Advanced Studies
Stumpergasse 56 A-1060 Vienna
Kurt Schmidheiny
Department of Economics University of Bern Gesellschaftsstrasse 49
CH-3012 Bern
Martin Wagner
Department of Economics University of Bern Gesellschaftsstrasse 49
CH-3012 Bern
Abstract
In this paper we derive the closed form solution for multistep predictions of the conditional means and their covariances from multivariate ARMA-GARCH models. These are useful e.g. in mean variance portfolio analysis when the rebalancing frequency is lower than the data frequency. In this situation the conditional mean and covariance matrix of the sum of the higher frequency returns until the next rebalancing period is required as input in the mean variance portfolio problem. The closed form solution for this quantity is derived as well. We assess the empirical value of the result by evaluating and comparing the performance of quarterly and monthly rebalanced portfolios using monthly MSCI index data across a large set of ARMA-GARCH models. The results forcefully demonstrate the substantial value of multistep predictions for portfolio management.
JEL Classification: C32, C61, G11
Keywords: Multivariate ARMA-GARCH models, volatility forecasts, portfolio optimiza- tion, minimum variance portfolio
∗This work has been supported by OLZ and Partners Asset and Liability Management AG.
I Introduction
In this paper we derive the closed form solution for multistep predictions of the conditional means and covariances from multivariate ARMA-GARCH models. These are useful e.g. in mean variance portfolio analysis, when the rebalancing frequency is lower than the data fre- quency. We assess the empirical value of this result by evaluating the performance of quarterly rebalanced portfolios using monthly MSCI index data and compare their performance with the performance of the corresponding monthly rebalanced portfolios. Additionally we also consider the importance of transaction costs.
Multistep prediction in GARCH models has been considered previously in e.g. Baillie and Bollerslev (1992), who derive the minimum mean squared error forecasts for the conditional mean and the conditional variance of univariate ARMA-GARCH processes. We extend their results to the multivariate case and derive closed form representations for the conditional mean and the conditional covariancesh-steps ahead. In addition we derive the explicit formula for the conditional covariance of the sum of the conditional means up to h-steps ahead. This corresponds, when modelling asset returns, to the conditional variance of the cumulative returns over anh-period horizon.
The above result may be useful for mean variance portfolio analysis, when portfolio re- allocations take place at a lower frequency than the data used in estimating the underlying GARCH models. Mean variance portfolio analysis (see Section 2) requires estimates of ex- pected returns and their covariances. If the rebalancing frequency is lower than the data frequency, the expected returns over the rebalancing interval are given by the cumulative ex- pected returns at the higher data frequency. Hence, the need for the conditional variance of cumulative returns. If the portfolio is, as in our empirical application, adjusted quarterly, and one estimates GARCH models using monthly data, one needs predictions for the conditional means and covariances up to 3-months. The empirical part of our study is closely related to Nilsson (2002) and Polasek and Pojarliev (2001a, 2001b), who use 1-step predictions from multivariate GARCH models for portfolio selection using - as we do - MSCI regional indices.
Our study differs in the use of multistep predictions and also our empirical results are based on a larger set of GARCH models.1
1Contrary to Nilsson (2002), we exclude GARCH-in-Mean models, whose multistep predictions are not covered by our result and are a subject of further research. Polasek and Pojarliev (2001a) use a Bayesian approach to GARCH modelling.
The value of the derived multistep predictions for portfolio management is evaluated on monthly data for six regional MSCI indices over the evaluation period January 1992 to December 2001. The empirical investigation is performed from the perspective of a Swiss investor, hence all indices are converted to Swiss Francs.2 For a large number, 66 to be precise, of ARMA-GARCH models the corresponding global minimum variance portfolios are tracked, both for monthly and quarterly rebalancing. In the latter case the quarterly rebalanced portfolioscorrectlybased on multistep predictions andincorrectlybased on 1-step predictions are evaluated. For the quarterly adjusted portfolios based on correct predictions the following results are obtained. The best performing portfolio, in terms of gross return, outperforms the MSCI world index by 2.9 % per annum. A vast majority of ARMA-GARCH based portfolios has higher gross return than the benchmark, the over-performance being on average 1.05 % per annum. Also for net returns after deducting transaction costs the quarterly rebalanced ARMA-GARCH portfolios show favorable performance. It is remarkable to note that a majority of the ARMA-GARCH portfolios result in higher (gross and net) return than the naive portfolio based on the sample mean and covariance. The performance of quarterly rebalanced portfolios that are incorrectly based on 1-step predictions from the ARMA-GARCH models is computed in order to focus on the effect of correct multistep predictions on portfolio performance. It turns out that multistep prediction is of considerable value. For 79 % of the models the portfolios based on the correct prediction outperform the corresponding ”incorrect” portfolio. The average over-performance is 0.34 % gross return per annum. Monthly rebalanced portfolios are evaluated for the same set of models in order to quantify the effect of lower-frequency portfolio rebalancing (based on correct multistep predictions) compared to rebalancing at the data frequency. Surprisingly, even for net returns after deducting transaction costs, the correct and also the incorrect quarterly rebalanced portfolios outperform the monthly rebalanced portfolios. These results forcefully demonstrate the substantial value of multistep predictions for portfolio management.
The paper is organized as follows: In Section 2 the portfolio optimization problem, the ARMA-GARCH models considered as well as the multistep prediction problem are briefly dis- cussed. In Section 3 the data are described and the empirical results are presented. Section 4 briefly summarizes and concludes. In the Appendix we explain in detail the computation of multistep predictions of the conditional means and covariances for multivariate ARMA-
2This feature is e.g. shared by Hamelink (2000).
GARCH models and present detailed results for all implemented models.
II Portfolio Optimization and ARMA-GARCH Models
In this section we introduce the portfolio optimization problem, describe the implemented multivariate GARCH models and discuss the main features of multistep prediction of condi- tional means and covariances from multivariate ARMA-GARCH models.
II.A Portfolio Optimization
This study is performed within the framework of mean-variance (MV) portfolio analysis (Markowitz (1952) and (1956)). MV analysis assumes that the investor’s decision and hence the optimal portfolio only depends on the expected return and the conditional variance of the portfolio return, the latter measuring risk.3 Having a universe ofnrisky assets and investment horizon of one period the investor faces the following decision problem at timet:
M inxt σ2pt+1=
n
i,j=1
xitxjtcov(rit+1, rjt+1|It)
s.t. E(rpt+1|It) =
n
i=1
xitE(rit+1|It) =r,
n
i=1
xit= 1, xit ≥0
whererpt+1 and σpt+12 denote the portfolio return and portfolio variance, respectively. Given a fixed value of the expected return, E(rpt+1|It) = r, the fractions, xit, of wealth invested in an individual asset i are chosen to minimize the risk of the portfolio return. In this study, we additionally assume nonnegativexit, i.e. short sales are prohibited. E(rit+1|It) and cov(rit+1, rjt+1|It) are approximated by predictions (e.g. from GARCH models) of individual asset returns and their covariances over the period from t to t+ 1, given the information set at t denoted by It. The above optimization problem leads, by varying ¯r, to the well- known efficient frontier. The optimal portfolio choice from the set of mean-variance efficient portfolios depends on the investor’s preferences and also on the consideration of a potential risk free asset. Omitting the constraintE(rpt+1|It) =r leads to the global minimum variance portfolio, which is independent of expected returns.
It is well-known that MV optimization is very sensitive to errors in the estimatedE(rpt+1|It) and cov(rit+1, rjt+1|It), see Chopra, Hensel and Turner (1993) or Best and Grauer (1991).
3MV analysis is consistent with von Neumann-Morgenstern utility maximization if either the asset returns are multivariate normally distributed or the investor’s preferences can be described by a quadratic utility function.
Chopra and Ziemba (1997) point out that the asset allocations of efficient portfolios are more sensitive to uncertainty in the expected returns than to uncertainty in their conditional covari- ances. By focusing on the global minimum variance portfolio only, we eliminate the impact of the imprecision in the prediction of the returns.
II.B Multivariate ARMA-GARCH Models
The required predictions for both the returns and the conditional covariances of the returns are derived from multivariate ARMA-GARCH models. Since the seminal contribution of Engle (1982), ARCH and GARCH type models have become standard tools to model financial market data. Modelling and predicting financial data has to take into account the widespread phenomenon ofvolatility clustering, i.e. that periods of sustainedly high volatility and periods of sustainedly low volatility are present. This volatility clustering can e.g. be modelled by ARCH or GARCH type models.4 During the last two decades an enormous variety of GARCH models has been developed, see e.g. Bollerslev, Engle and Nelson (1994) or Gourieroux (1997) for overviews of some of the developed models.
Multivariate ARMA-GARCH models consist of two equations. The first one is an ARMA equation for the returns,rtsay. Thus, themean equationis of the formrt=c+A1rt−1+· · ·+ Aprt−p+εt+B1εt−1+· · ·+Bqεt−q withAi, Bj ∈Rn×n.The innovationεtis allowed to have time-varying conditional covariance, denoted by Σt =cov(εt, εt|It−1). The second equation is, appropriately parameterized, an ARMA equation for the conditional covariance matrix Σt and is used to model time dependance structure. More precisely, thevariance equationis an ARMA equation in Σtand εt. If the variance equation is only modelled as an autoregression in Σt, the model is termed an ARCH model.
Preliminary model selection shows that for our application the lag lengths required in both the mean and the variance equation are at most equal to 1. For this reason the following description of the implemented models is in terms of the ARMA(1,1)-GARCH(1,1) case. This simplifies the mean equation to
rt=c+Art−1+εt+Bεt−1
using for simplicityA=A1 and B=B1. We allow for two possible distributions of εtin the empirical part of the paper. Normally distributed innovations andt-distributed innovations,
4An alternative model class is given by stochastic volatility models, see e.g. Harvey, Shephard and Ruiz (1994).
A B εt
AR(1) diag diagonal 0 N(0,Σt) MA(1) diag 0 diagonal N(0,Σt) AR(1) full unrestr. 0 N(0,Σt) AR(1) diag t diagonal 0 t-distr.
MA(1) diag t 0 diagonal t-distr.
ARMA(1,1) full t unrestr. unrestr. t-distr.
naive 0 0 –
Table 1: Specifications of the mean equation.
where in the latter case the degree of freedom of the innovation distribution is estimated itself. The latter possibility is included in order to allow for stronger leptokurtic behavior.
The unrestricted ARMA(1,1) formulation of the mean equation results in most cases in a large number of insignificant parameters. Therefore, in more parsimonious specifications of the mean equation, either A or B or both matrices are restricted to be either diagonal or 0-matrices. See Table 1 for a list of all implemented mean equations. The performance of the portfolios based on the estimated ARMA-GARCH models is compared to thenaiveportfolio, where both the return and covariance predictions are given by the sample mean and the sample covariance, respectively, over the estimation period.
In the estimation of multivariate GARCH models two aspects have to be considered.
Firstly, positive semi-definiteness and symmetry of the estimated conditional covariance ma- trix has to be guaranteed. Secondly, the number of parameters to be estimated grows rapidly with the number of assets. For circumventing the first problem the literature proposes a vari- ety of multivariate GARCH models that guarantee positive semi-definiteness and symmetry of the estimate of Σt, some of them discussed below.
The unrestricted GARCH ordiagonal-vecmodel (Bollerslev, Engle and Wooldridge (1988)) constitutes the natural starting point for the discussion and is therefore described first. The variance equation of the diagonal-vec model is given by:
Σt=P0+P1(εt−1εt−1) +Q1Σt−1
where denotes the Hadamard product and P0 ∈ Rn×n, P1 ∈ Rn×n and Q1 ∈ Rn×n for an application with n assets. Taking the symmetry restriction into account, the diagonal- vec model leads to 63 parameters to be estimated in our application with six index returns series. However, in this formulation it additionally has to be ensured that the resulting
estimated Σtis positive semi-definite, which complicates the likelihood optimization problem.
For this reason we focus on the estimation of alternative formulations of GARCH(1,1) models that incorporate the restrictions that the estimated Σt has to be positive semi-definite and symmetric and do not consider the diagnonal-vec model further. One popular formulation in the empirical literature is known as BEKK model (see Engle and Kroner, 1995). The BEKK(1,1) model’s variance equation is
Σt=P0P0+P1(εt−1εt−1)P1+Q1Σt−1Q1
with P0, P1, Q1 given as above. The BEKK model results in more parameters than the diagonal-vec model, however its formulation incorporates symmetry and positive semi-definite- ness of Σt and its estimate.
The second implemented version of GARCH(1,1) models is thevector-diagonalmodel Σt=P0P0+p1p1(εt−1εt−1) +q1q1Σt−1
with vectors p1, q1 ∈ Rn and P0 as above. It is obvious that this formulation reduces the number of estimated parameters whilst symmetry and positive semi-definiteness of Σtremain ensured.
An alternative strategy for parameter reduction consists in transforming the multivariate problem into a set of (essentially) univariate problems. This means that after appropriate transformations the components of the conditional variance series are modelled with standard univariate GARCH type models. We have implemented three variance equations following this strategy: the CCC, the PC and thepure diagonal models.
In theconstant conditional correlation (CCC) model (Bollerslev (1990)), the conditional covariance matrix is modelled as
Σt=DtRDt
where R ∈ Rn×n is the constant conditional correlation matrix and Dt = diag(σ1t, . . . , σnt) denotes the diagonal matrix of the conditional standard deviations of the individual returns series. The seriesσitare then modelled in our application with univariate GARCH, EGARCH or PGARCH models (see the description below).
Related in spirit to the CCC model is the principal components (PC) model,5 which is based on a singular value decomposition of Σt as its first step
Σt=NtΛtNt
5The implementation of principal components models in S-PLUS GARCH 1.3 Release 2is flawed.
withNt denoting the matrix of singular vectors corresponding to the singular value decom- position of Σt and Λt = diag(σ21t, . . . , σnt2 ), where σ2it are the conditional variances of the individual series (as well as the singular values of Σt). Again, the individual series σ2it are modelled with univariate GARCH models.
Assuming that the returns are conditionally uncorrelated, i.e. that Σtis diagonal for allt, one can directly model the individual volatility series with univariate GARCH models. This approach is often termedpure diagonal GARCH model. However, one should note that the residuals used in this univariate modelling of the volatilities are derived from the multivariate specification of the mean equation. Hence, the results differ from a completely univariate GARCH analysis, where also the mean equations are specified for each of the return series separately.
Let us finally turn to a brief description of the underlying univariate GARCH models used. Hence, from now on we deal only with one volatility series σit and one residual or innovation seriesεit. The basic model is the GARCH model of Bollerslev (1986), which in its GARCH(1,1) form is given by
σit2 =pi+pi1ε2it−1+qi1σit−12
withpi, pi1, qi1∈R. Here, the conditionpi1+qi1 <1 is necessary for covariance stationarity of the underlying return series. In order to be able to model asymmetric behavior of volatility in response to positive or negative shocks, the standard GARCH specification has been extended in various ways. Two of these extensions have been used in this study, theexponentialGARCH (EGARCH) model introduced by Nelson (1991) and thepower GARCH (PGARCH) model, see e.g. Ding, Engle and Granger (1993). The univariate EGARCH(1,1) model has the following variance equation
lnσ2it=pi+pi1|εit−1|+γiεit−1
σit−1 +qi1lnσ2it−1 Finally the variance equation of the PGARCH(1,1) model is given by
σitd =pi+pi1(|εit−1|+γiεit−1)di+qi1σdit−1i
withγi, pi, pi1, qi1∈Rand where the parameter di ∈R can be estimated as well.
II.C Prediction of Conditional Mean and Covariance of ARMA-GARCH Models
For the portfolio optimization problem introduced above, predictions for both the returns as well as the conditional covariances of the returns are computed from all described ARMA- GARCH models. If the investment horizon is larger than one period, multistep predictions are needed. Consider, as is the case in our empirical application, that rebalancing takes place every 3 months, but data are available on a monthly frequency. In this case one needs to cumulate the one-period returns over the longer investment horizon. Denote by
r[t+1:t+3]=rt+1+· · ·+rt+3
the cumulative returns over 3 periods.6 Then it follows that the conditional covariance matrix of the cumulative return vectorr[t+1:t+3] is given by
cov(r[t+1:t+3], r[t+1:t+3]|It) = cov(rt+1+rt+2+rt+3, rt+1+rt+2+rt+3|It)
=
3
i=1
cov(rt+i, rt+i|It) +
3
i,j=1,i=j
cov(rt+i, rt+j|It) (1)
Thus, we see that estimates of the conditional variances and covariances of the returnsrt+i fori= 1,2,3 are required. In the context of ARMA-GARCH models it is important to note that these predictions for the conditional covariances ofrt+i differ from the predictions for the conditional variances of the residualsεt+i. The general formula for computing h−step ahead predictions of the conditional variances of rt+h from multivariate ARMA(p,q)-GARCH(k,l) models is presented in the Appendix.7 The predictions for the conditional variances of εt+i can be easily computed for specified variance equation, thus we focus on the computation of the conditional variances and covariances of rt+h only. To illustrate the issue consider a model with an AR(1) mean equation, i.e.
rt=c+Art−1+εt
where, as above, εt has the conditional covariance matrix Σt =cov(εt, εt|It−1). Now denote by Σrt+1,tthe conditional covariance matrix ofrt+1givenIt. Then, it immediately follows that Σrt+1,t = cov(rt+1, rt+1|It) = cov(Art+εt+1, Art+εt+1|It) = cov(εt+1, εt+1|It) = Σt+1. We
6This follows directly from the definition of the 1-period returns, calculated as the logarithmic difference of asset prices.
7Multistep prediction in univariateGARCH models is presented in Baillie and Bollerslev (1992).
introduce the notation Σt+h,t to denote the conditional variance matrix of εt+h with h ≥ 1 given It. Hence, with this notation Σt+1 = Σt+1,t. Thus, the conditional variance of rt+2 givenIt, denoted by Σrt+2,t can be computed as:
Σrt+2,t = cov(rt+2, rt+2|It)
= cov(Art+1+εt+2, Art+1+εt+2|It)
= cov(Art+1, Art+1|It) +cov(Art+1, εt+2|It) +cov(εt+2, Art+1|It) + cov(εt+2, εt+2|It)
= Acov(rt+1, rt+1|It)A+Acov(rt+1, εt+2|It) +cov(εt+2, rt+1|It)A + cov(εt+2, εt+2|It)
= Acov(εt+1, εt+1|It)A+cov(εt+2, εt+2|It)
= AΣt+1,tA+ Σt+2,t
ascov(rt+1, εt+2|It) = 0. Along the same lines the recursion can be continued to obtain Σrt+3,t: Σrt+3,t = cov(rt+3, rt+3|It)
= cov(Art+2+εt+3, Art+2+εt+3|It)
= cov(Art+2, Art+2|It) +cov(Art+2, εt+3|It) + cov(εt+3, Art+2|It) +cov(εt+3, εt+3|It)
= Acov(rt+2, rt+2|It)A+Acov(rt+2, εt+3|It) + cov(εt+3, rt+2|It)A+cov(εt+3, εt+3|It)
= A(Acov(εt+1, εt+1|It)A+cov(εt+2, εt+2|It))A + cov(εt+3, εt+3|It),
= A2cov(εt+1, εt+1|It)(A)2+Acov(εt+2, εt+2|It)A+cov(εt+3, εt+3|It)
= A2Σt+1,t(A)2+AΣt+2,tA+ Σt+3,t
= AΣrt+2,tA+ Σt+3,t
using the result for Σrt+2,tandcov(rt+2, εt+3|It) = 0.It can be shown that the recursion noted in the last line of the above derivation also holds for larger prediction horizons, hence, for the AR(1) mean equation one obtains Σrt+h,t=AΣrt+h−1,tA+ Σt+h,t forh≥1 and Σrt+1,t = Σt+1. In order to computecov(r[t+1:t+3], r[t+1:t+3]|It), the covariances have to be calculated along similar lines as the variance terms. Then summing up all required variance and covariance
terms delivers the result, see equation (1). In the Appendix the expression for the conditional covariance matrix of the cumulativeh-period returns from ARMA(p,q)-GARCH(k,l) models is derived. This formula for the conditional variance forms the basis for actual predictions by replacing the theoretical quantities by their estimates.
III Data and Results
In the previous section we have illustrated how multistep predictions are obtained for ARMA- GARCH models. These become potentially useful for portfolio management if the data fre- quency is higher than the rebalancing frequency. In this section we assess the practical implications of this result for portfolio selection by comparing the portfolio performance with higher frequency rebalancing (1-month) to lower frequency (3-month) rebalancing using higher frequency (1-month) data. Consequently, the former portfolio selection has to be based on 1- step predictions and the latter on 3-step predictions. The quantitative importance of correct multistep predictions is evaluated by additionally computing several performance measures of portfolios rebalanced at a 3-month frequency but ”incorrectly” based on 1-step predictions.
In the course of this procedure a large number of multivariate ARMA-GARCH models are implemented, see Table 3 in the Appendix for the list of 66 implemented models. This allows us to identify the set of models leading to the best portfolio performance, according to optimality criteria such as gross return, net return or the Sharpe ratio. Furthermore the impact of transaction costs on the portfolio performance of the three described approaches is computed. This is done to evaluate the trade-off between higher transaction costs and faster adjustment to new information, when rebalancing occurs monthly. When considering transaction costs, these are assumed to equal 0.3 % of the portfolio turnover.
In the comparison we track an internationally diversified portfolio denominated in Swiss francs over the 1990ies. The portfolio wealth is invested in six world regions. The Mor- gan Stanley Capital International (MSCI) indices for the U.S., Switzerland, Great Britain, Japan, Europe (excluding Great Britain) and Pacific (excluding Japan) are the investment instruments.8 We use monthly return data from February 1972 to December 2001 for the six indices. The MSCI world index denominated in Swiss Francs is used as benchmark.
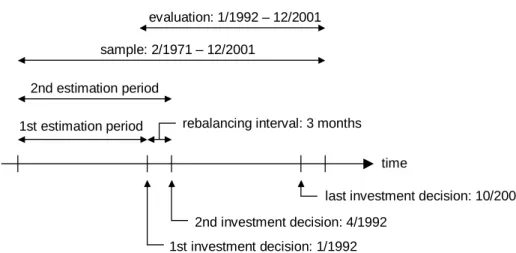
The evaluation with quarterly (respectively monthly) rebalancing proceeds in the following
8Note that we do not include a risk free asset in order to focus on the effect of ARMA-GARCH predicted correlation structures on portfolio performance.
time rebalancing interval: 3 months
last investment decision: 10/2001 2nd investment decision: 4/1992
1st investment decision: 1/1992 1st estimation period
2nd estimation period
sample: 2/1971 – 12/2001
evaluation: 1/1992 – 12/2001
Figure 1: Timing of the evaluation (quarterly rebalancing).
steps (see the timing illustrated in Figure 1):
(1) The monthly return data from February 1972 up to the date of the investment decision are used to predict the returns and the covariances of the six regional indices. 67 different predictions are computed: From 66 ARMA-GARCH models and the naive predictions.
(2) The corresponding global minimum variance portfolios are calculated.
(3) The realized 3- and 1-month returns are calculated.
(4) The investment decision is repeated every 3 (1) months from January 1, 1992 to October 1, (December 1) 2001 and the portfolios are rebalanced accordingly.
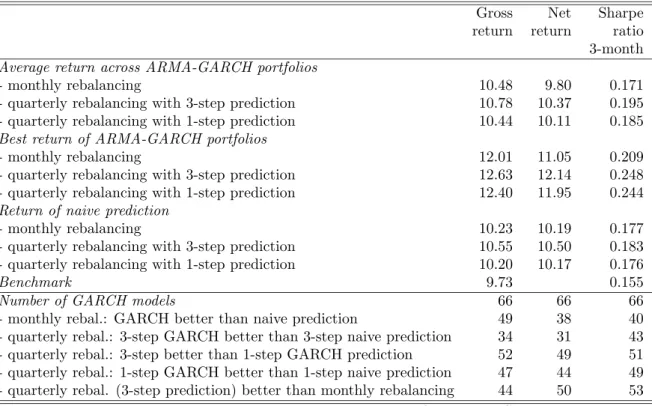
Table 2 exhibits a summary of the results presented in detail in Table 3 in the Appendix.
The latter table shows the detailed results from the evaluation and juxtaposes the results from monthly rebalancing and quarterly rebalancing for both the ”correct” 3-step prediction and the ”incorrect” 1-step prediction method. In Table 3 we report the gross and net return as well as the Sharpe ratio of the portfolios based on 66 ARMA-GARCH models. For comparison, the results obtained from the naive portfolio, based on sample means and covariances, and the MSCI world index as benchmark portfolio are displayed too. Gross return denotes the mean annualized return of the portfolio computed over the evaluation period, net return denotes the mean annualized return of the portfolio after deducting transaction costs and the Sharpe ratio is given by net excess return (i.e. net return minus riskfree rate9) divided by
9The 3-month (respectively 1-month) deposit rate is used as riskfree rate. Before December 1996 the deposit rate is approximated by the LIBOR minus five basis points.
Table 2: Main Results of Performance Comparison
Gross Net Sharpe return return ratio 3-month Average return across ARMA-GARCH portfolios
- monthly rebalancing 10.48 9.80 0.171
- quarterly rebalancing with 3-step prediction 10.78 10.37 0.195 - quarterly rebalancing with 1-step prediction 10.44 10.11 0.185 Best return of ARMA-GARCH portfolios
- monthly rebalancing 12.01 11.05 0.209
- quarterly rebalancing with 3-step prediction 12.63 12.14 0.248 - quarterly rebalancing with 1-step prediction 12.40 11.95 0.244 Return of naive prediction
- monthly rebalancing 10.23 10.19 0.177
- quarterly rebalancing with 3-step prediction 10.55 10.50 0.183 - quarterly rebalancing with 1-step prediction 10.20 10.17 0.176
Benchmark 9.73 0.155
Number of GARCH models 66 66 66
- monthly rebal.: GARCH better than naive prediction 49 38 40
- quarterly rebal.: 3-step GARCH better than 3-step naive prediction 34 31 43 - quarterly rebal.: 3-step better than 1-step GARCH prediction 52 49 51 - quarterly rebal.: 1-step GARCH better than 1-step naive prediction 47 44 49 - quarterly rebal. (3-step prediction) better than monthly rebalancing 44 50 53 This table summarizes the results presented in Table 3 in the Appendix. Gross return denotes the mean annualized return of the portfolio. Net return denotes the mean annualized return of the portfolio after deducting transaction costs. Sharpe ratio (3-step) denotes the mean net excess return (i.e. net return minus riskfree rate) divided by the portfolio’s standard deviation based on quarterly returns. 3-step (1-step) indicates the use of the correct multi-step (incorrect 1-step) predictions in quarterly rebalanced portfolios.
the portfolio’s standard deviation.10 We report the 1-month Sharpe ratio using the standard deviation computed from monthly returns and the 3-month Sharpe ratio based on quarterly returns.11
We need to clarify at this point how we derive multistep predictions for the naive portfolio strategy, which is based on sample means and covariances. Since in the quarterly rebalancing the investor is interested in the prediction of the 3-month returns and their covariances, we base our naive predictions for the 3-month return on the sample mean and covariance matrix of the monthly return series aggregated to 3-month returns.12
10More detailed tables including further risk adjusted performance measures such as Jensen’s alpha, Treynor’s measure as well as shortfall are available from the authors upon request.
11The Sharpe ratio of the annualized monthly returns cannot directly be compared to the Sharpe ratio of annualized quarterly returns, as the latter have lower volatility almost by construction. We therefore compare the 3-month Sharpe ratios of quarterly and monthly rebalanced portfolios. For monthly rebalanced portfolios, Table 3 in the Appendix shows both, the 1- and 3-month Sharpe ratios.
12This seems to be more natural than to simply use the empirical mean and covariance matrix of the returns series at the monthly frequency. The latter are used as ”incorrect” forecasts for the quarterly rebalancing of
Let us start by discussing the performance of ARMA-GARCH predictions used for monthly adjusted portfolios, which requires only 1-step predictions. The best performing portfolio in terms of gross return (12.01%), net return (11.05%) as well as Sharpe ratio (1-month 0.159, 3-month 0.209) is the ARMA(1,1)-BEKK(1,1) portfolio with t-distributed innovations. Note already here that t-distributed innovations only lead to superior portfolio performance for monthly adjusted portfolios. The best quarterly adjusted portfolio is based on a model estimated under the assumption of normality. The ARMA(1,1)-BEKK(1,1) portfolio with t-distributed innovations substantially outperforms the naive portfolio, with gross return of 10.23%, net return of 10.19% and 1-month Sharpe ratio of 0.124. Considering e.g. gross re- turns, 49 of the 66 ARMA-GARCH models result in portfolio strategies which outperform the naive portfolio. The average annualized gross return (10.48%) across all 66 ARMA-GARCH portfolios is 75 basis points higher than the mean return of the benchmark but only 25 basis points above the return of the naive portfolio. However, the average net return over ARMA- GARCH portfolios is below the naive portfolio (-39 basis points) and only marginally (7 basis points) above the benchmark.
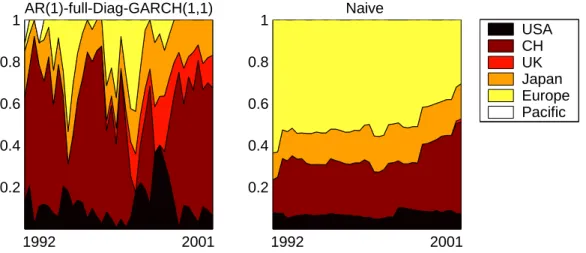
Let us now turn to the quarterly portfolio rebalancing. The AR(1)-full-Diag-GARCH(1,1) yields the best portfolio: gross return of 12.63%, net return of 12.14% and 3-month Sharpe ra- tio of 0.248. This compares to the corresponding naive portfolio’s performance of 10.55% gross return, 10.50% net return and 3-month Sharpe ratio equal to 0.183. For illustration, the asset allocations of these two portfolio strategies are displayed in Figure 2. From this figure a typi- cal feature of portfolios based on GARCH models becomes visible: The larger amount of asset reallocations compared to e.g. the naive portfolio. This difference of course is important when comparing net returns, see below. Again, a majority, now 34 out of the 66 ARMA-GARCH portfolios, show higher gross returns than the corresponding naive portfolio. This lower pro- portion, compared to monthly rebalancing (with 49 out of 66), can mainly be attributed to the poor performance of quarterly rebalanced principal components-GARCH portfolios.13 The average annualized gross return across all ARMA-GARCH portfolios (10.78%) is now 105 ba- sis points above the benchmark and 23 basis points above the naive portfolio. Again, as with monthly rebalanced portfolios, the average net return across all ARMA-GARCH portfolios is lower than the net return of the naive portfolio. Note, however, that despite this lower
the naive portfolio.
13Principal components models perform poor even though we use a corrected algorithm supplied by Insightful Corporation after pointing out the errors in the released version. See Footnote 2.
1992 2001 0.2
0.4 0.6 0.8
1AR(1)-full-Diag-GARCH(1,1)
1992 2001
0.2 0.4 0.6 0.8
1 Naive
USA CH UK Japan Europe Pacific
Figure 2: Asset allocations of the best and the naive quarterly rebalanced portfolios.
average the majority of ARMA-GARCH portfolios outperforms the naive portfolios. This fact, holding for both monthly and quarterly rebalancing, shows that model selection and evaluation are important when applying ARMA-GARCH models for portfolio management.
It may be important to note that the above presented results are sensitive to the evaluation period. Investigation of the performance over the last 1, 3 or 5 years shows instabilities in the ranking of portfolio strategies. This instability underlines the impact of the downturn in the world stock markets starting mid 1999 on portfolio selection.
One might expect that returns of quarterly adjusted portfolios are, at least when ignor- ing transaction costs, lower than those of monthly rebalanced portfolios, due to the quicker adaption to new information in the latter case. Surprisingly, this is not the case. The av- erage gross return on quarterly rebalanced portfolios is 30 basis points higher than that of monthly rebalanced portfolios and the best performing portfolios (3-month: AR(1)-full-Diag- GARCH(1,1) and 1-month: ARMA(1,1)-BEKK(1,1)t-distribution) differ by 62 basis points.
2/3 of the quarterly rebalanced ARMA-GARCH portfolios result in higher gross returns than the corresponding monthly adjusted portfolios. The consideration of transaction cost aggra- vates this difference: 50 ARMA-GARCH portfolios with quarterly rebalancing exceed the net returns of the monthly portfolio based on the same ARMA-GARCH model. An almost identical picture emerges when taking the Sharpe ratio as performance measure. Thus we see that surprisingly quarterly rebalancing based on monthly data performs better than monthly rebalancing, when the portfolio optimization is based on ARMA-GARCH predictions.
Let us now turn specifically to the assessment of the value of correct multistep versus
incorrect 1-step predictions of returns and covariances based on ARMA-GARCH models. The above favorable results of quarterly rebalanced portfolios, based on correct 3-step predictions, are possibly driven by two factors: The use of monthly data and the use of correct multistep predictions. In order to single out the value of the correct predictions, we compare the results next with quarterly rebalanced portfolios based on (incorrect) 1-step predictions. These results are again contained in Table 3 in the Appendix and summarized in Table 2. 52 out of the 66 ARMA-GARCH portfolios exhibit higher gross returns with the correct multistep method than with the incorrect 1-step prediction. The mean difference is 32 basis points.
Note that the generally poor performing principal components models account for most of the cases where the incorrect predictions perform better. Excluding these models, the correct method leads in 46 out of 48 cases to better performance. The average over-performance is then 69 basis points. Again, an almost identical picture emerges for net returns and the Sharpe ratio. The substantial advantage of using the correct multistep prediction is also present for the naive portfolio strategy.
The results are briefly summarized as follows: Considering gross returns the correctly predicted quarterly rebalanced portfolios perform best, followed by the monthly rebalanced portfolios and the incorrectly predicted quarterly rebalanced portfolios. This ranking holds in particular for both the average across all ARMA-GARCH portfolios and the respective best ARMA-GARCH portfolios. This is striking as one expects for gross returns, i.e. where trans- action costs are ignored, monthly rebalanced portfolios to outperform quarterly rebalanced portfolios. Looking at the average net return across all ARMA-GARCH models, the correctly predicted quarterly rebalanced portfolios perform again best, now followed by the incorrectly predicted quarterly rebalanced portfolios and the monthly rebalanced portfolios. The inferior performance of the monthly rebalanced portfolios, even compared to the quarterly rebalanced portfolios based on incorrect multistep predictions, is explained by the higher transaction costs due to the higher rebalancing frequency. The naive portfolio is, both in terms of gross and net returns, outperformed by the majority of ARMA-GARCH portfolios. This holds even when the latter are based on incorrect predictions. Basing the quarterly portfolio decision on correct multistep predictions leads in virtually all cases to performance gains.
IV Summary and Conclusions
In this paper we have derived the closed form solution for multistep predictions of the con- ditional mean and covariance for ARMA-GARCH models and have illustrated their value for portfolio management. Multistep predictions of the conditional means and covariances are e.g. needed for mean-variance portfolio analysis when the rebalancing frequency is lower than the data frequency. In order to deal with this problem we have in addition derived the explicit formula for the conditional covariance matrix of the corresponding cumulative higher frequency returns. The closed form solution for the general ARMA(p,q)-GARCH(k,l) case is provided in the Appendix along with a convenient recursive representation.
The practical relevance of these results has been assessed empirically with an application to six regional MSCI indices using a large variety of ARMA-GARCH models. Based on monthly data the portfolio performance of monthly and quarterly rebalanced portfolios is investigated.
The quarterly rebalancing decision is based on either the (model consistent) correct 3-step predictions or is incorrectly based on 1-step predictions. The evaluation period is January 1992 to December 2001. Some observations emerge: The first observation is that basing the quarterly rebalancing decision on correct multistep predictions is for almost all portfolios advisable. I.e. for almost all ARMA-GARCH models the return of the corresponding portfolio is higher when the rebalancing decision is based on the correct multistep predictions. This holds for gross returns, net returns and also the Sharpe ratio. The second main observation is the fact that for gross returns, i.e. when neglecting transaction costs, quarterly rebalanced portfolios based on multistep predictions lead to better performance than monthly adjusted portfolios. The latter in general outperform quarterly adjusted portfolios based on 1-step predictions. For net returns, even the quarterly adjusted portfolios based on 1-step predictions outperform (on average) the monthly adjusted portfolios. This is a surprising result, as a priori one would expect - at least for gross returns - that monthly rebalanced portfolios outperform quarterly adjusted portfolios. This conjecture, based on the argument that monthly adjusted portfolios incorporate new information faster, is not validated for our empirical example.
The third observation is that by basing the portfolio decision on (predictions from) ARMA- GARCH models one can substantially outperform the naive portfolio and the benchmark.
This fact that portfolios that rely upon volatility models can outperform naive (or static) portfolios is also found for daily data e.g. by Fleming et al. (2001). Fourthly, we have observed
that no particular class of GARCH models leads to superior performance and we have finally seen that models with t-distributed innovations lead to better portfolio performance for the monthly adjusted portfolios only.
An important theoretical question that is left open for future research is the derivation of multistep predictions for multivariate GARCH-in-Mean models. See Karanasos (2001) or Nilsson (2002) for some results concerning prediction for this model class. An important empirical issue that requires further exploration is to assess the value of multistep predictions at higher data frequencies, to explore e.g. the performance of weekly portfolio allocation based on daily data. This might lead to interesting results as the volatility effects are stronger at higher frequencies which should increase the value of correct conditional multistep predictions of conditional covariances.
Appendix: Multistep ARMA-GARCH Predictions
In this appendix we derive multistep predictions for the conditional means and covariances of mul- tivariate ARMA(p,q)-GARCH(k,l) models. We derive both themean squared error (MSE) predictor and the conditional MSE. Related to the portfolio optimization problem in the main text we also derive the predictions for the conditional variance of the forecast of the sum of the variable (in our case returns)h-steps ahead. These are required in the portfolio optimization problem where the data frequency is higher than the rebalancing frequency, see the discussion in Section 2.
In the discussion we abstain from deriving also the multistep prediction formula for the conditional variance of the innovations εt. Obtaining these is a standard prediction problem for the ARMA type variance equation. Thus, this result is dependent of the precise formulation of the variance equation and easily available if the variance equation is specified. Furthermore note also that multistep predictions of the conditional variances of the innovationsεtare directly available in various software packages, whereas the conditional variances of multistep predictions of the returns themselves are to our knowledge not implemented in software packages.
Note that the limits for h → ∞ of the derived results for the minimum MSE predictor of the mean and variance are finite only for stationary processes. Also note that the derivations do not apply to ARCH-in-Mean models, where by construction the prediction of the mean is coupled with the prediction of the conditional variance.
To facilitate the actual implementation of the results we also derive a recursive representation of the result, compare the AR(1) example in Section 2.3.
In relation to the empirical application presented in the main text we finally derive in detail the closed form representation of the conditional variance matrix of the returns over 3 periods ahead for all mean equations implemented empirically, i.e. for ARMA(1,1), AR(1), and MA(1) mean equations.
The cumulative returns over anh−period horizon, henceforth denoted as r[t+1:t+h], are straight- forwardly calculated from the single period returns,rt+i, as follows
r[t+1:t+h]=rt+1+· · ·+rt+h
Thus, the conditional covariance matrix of the cumulated returnsr[t+1:t+h] is
cov(r[t+1:t+h], r[t+1:t+h]|It) = cov(rt+1+· · ·+rt+h, rt+1+· · ·+rt+h|It)
= h i=1
cov(rt+i, rt+i|It) + h i,j=1,i=j
cov(rt+i, rt+j|It) (2)
where It denotes again the information set at time t. One clearly sees from this equation that the conditional variance matrix of r[t+1:t+h] is composed of the (conditional) variances and covari- ances of the one-period returns in rt+i for i = 1, . . . , h. We thus see that for the calculating cov(r[t+1:t+h], r[t+1:t+h]|It) it is necessary to derive the MSE predictor of rt+i and the correspond- ing conditional variances and covariances.
General Case
Letrtbe ann-dimensional ARMA(p, q),p, q∈N, process with GARCH errors rt=c+
p i=1
Airt−i+ q
i=1
Biεt−i+εt
(3)
wherec∈Rn, εt∼W N(0,Σt), with Σt=cov(εt, εt|It−1) and A1, . . . , Ap, B1, . . . , Bq ∈Rn×n matri- ces. In the derivation of the minimum MSE predictors ofrt+i and their conditional covariances it is