Testen Sie, ob es eine signifikante Abhängigkeit zwischen der Wahl des Mathekurses und dem Bestehen der Prüfung gibt. Verwenden Sie dabei das Signifikanzniveau α = 0, 05.

1. Aufgabe: Es soll untersucht werden, ob die Wahl des Mathekurses (Leistungskurs oder Grundkurs) beim Abitur einen Einfluss auf das Bestehen der Prüfung zur Vorlesung „Höhere Mathematik I“ im Studium hat. Dazu liegen folgende Daten vor.

Grundkurs Leistungskurs

Bestanden 45 25

Nicht bestanden 25 5

Testen Sie, ob es eine signifikante Abhängigkeit zwischen der Wahl des Mathekurses und dem Bestehen der Prüfung gibt. Verwenden Sie dabei das Signifikanzniveau α = 0, 05.

Lösung:

H

: Das Bestehen ist von der Wahl des Mathekurses unabhängig.

H

: Das Bestehen ist von der Wahl des Mathekurses abhängig.

h

1 2 h

1 45 25 70

2 25 5 30

h

70 30 n=100

= ⇒

hi··h·j

n

1 2 h

1 49 21 70

2 21 9 30

h

70 30 n=100 t =

³

49

+

+

+

´

= 3, 63 (oder t = 100 ·

³

70·70

+

+

+

´

= 3, 63)

(oder auch, da hier eine Vierfeldertafel vorliegt:

t = 100(45 · 5 − 25 · 25)

70 · 30 · 70 · 30 = 3, 63) K =

n

t | t > χ

o

p = 2 und q = 2 und χ

= 3, 84.

t = 3, 63 6> 3, 84 = ⇒ t 6∈ K = ⇒ H

wird angenommen.

D.h. es gibt keine signifikante Abhängigkeit zwischen den beiden Merkmalen Bestehen und Wahl des Mathekurses.

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

2. Aufgabe: Eine Lieferung von Spritzgussteilen soll mit Hilfe einer Stichprobe kon- trolliert werden. Der Hersteller und der Abnehmer einigen sich wie folgt. Eine Liefer- ung mit einem Ausschussanteil p ≤ 0, 015 ist gut und eine mit p ≥ 0, 05 ist schlecht.

Das Risiko des Herstellers (Produzenten) beträgt α = 0, 025 und das des Abnehmers (Konsumenten) β = 0, 025.

Eine gute Lieferung soll höchstens mit Wahrscheinlichkeit α abgelehnt und eine schlechte höchstens mit Wahrscheinlichkeit β angenommen werden. Gibt es für n = 500 (n,c)-Stichprobenpläne, die diesen beiden Forderungen genügen? Falls ja, welchen Stichprobenplan würde der Produzent wählen?

Lösung:

Produzent: α = 0, 025 und p

= 0, 015 Konsument: β = 0, 025 und p

= 0, 05 n = 500 c =?

Rechnung mit der Normalverteilungs-Approximation: z

= z

= z

= 1, 96 np

+ z

p np

(1 − p

) ≤ c ≤ np

− z

q

np

(1 − p

) 500 · 0, 015 + 1, 96 p

500 · 0, 015 · 0, 985 ≤ c ≤ 500 · 0, 05 − 1, 96 p

500 · 0, 05 · 0, 95 12, 83 ≤ c ≤ 15, 45

Es gibt damit 3 mögliche (n, c)-Pläne:

(n, c) = (500, 13) (n, c) = (500, 14) (n, c) = (500, 15)

Der Produzent würde aus diesen drei Plänen den Plan mit c=15 wählen, da in diesen Fall die Annahmewahrscheinlichkeit der Lieferung am größten ist.

Hinweis: Seit WS 2013/2014 wird bei der Normalverteilungs-Approximation folgen- de Motifikation verwendet:

np

+ z

p

np

(1 − p

)−0, 5 ≤ c ≤ np

− z

q

np

(1 − p

)−0, 5 500 · 0, 015 + 1, 96 p

500 · 0, 015 · 0, 985 − 0, 5 ≤ c ≤ 500 · 0, 05 − 1, 96 p

500 · 0, 05 · 0, 95 − 0, 5 12, 33 ≤ c ≤ 14, 95

Es gibt damit 2 mögliche (n, c)-Pläne:

(n, c) = (500, 13) (n, c) = (500, 14)

Der Produzent würde aus diesen zwei Plänen den Plan mit c=14 wählen, da in diesen Fall die Annahmewahrscheinlichkeit der Lieferung am größten ist.

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

3. Aufgabe: Für 20 Fahrzeuge eines Typs wurden das Alter, die gefahrenen Kilome- ter und der aktuelle Preis erfasst. Mit diesen Daten wurde folgendes Statgraphics- Ergebnis erstellt.

Multiple Regression - Preis

Alter Kilometer

Standard T

Parameter Estimate Error Statistic P-Value

CONSTANT 12526,3 574,898 21,7888 0,0000

Alter -827,245 42,2323 -19,588 0,0000

Kilometer -0,00635206 0,00918315 -0,691708 0,4990

Analysis of Variance

Source Sum of Squares Df Mean Square F-Ratio P-Value

Model 4,94745E7 2 2,47372E7 192,35 0,0000

Residual 2,05767E6 16 128604, Total (Corr.) 5,15322E7 18

a) Wie lautet die geschätzte Regressionsfunktion?

b) Bestimmen Sie das Bestimmtheitsmaß B .

c) Welchen Verkaufspreis würden Sie mit obigem Modell für ein 3 Jahre altes Auto, welches nur 15000 Kilometer gefahren ist, prognostizieren?

Lösung:

y - Preis x

- Alter x

- Kilometer

a)

ˆ

y(x) = 12526, 3 − 827, 245 · x

− 0, 00635206 · x

b)

B = SSE

SST = 4, 94745 · 10

5, 15322 · 10

= 0, 96 c) x =

µ x

x

¶

=

µ 3 15000

¶

ˆ

y(x) = 12526, 3 − 827, 245 · 3 − 0, 00635206 · 15000 = 9949, 28

4. Aufgabe: Der Abteilungsleiter bemüht sich um möglichst optimale Arbeitsbe- dingungen für seine Mitarbeiter. So wurde bei einer Befragung unter anderem die Wohlfühltemperatur am Arbeitsplatz erfragt. Der Abteilungsleiter vermutet, dass es geschlechtsspezifische Unterschiede gibt. Es liegen folgende Daten (in

C) vor.

Männer 19 20 21 21,5 22,5 23,5 24 24,5

Frauen 22 23 23 24 24 25 25,5 26 26,5 27

Die Wohlfühltemperatur ist nicht normalverteilt. Testen Sie zum Signifikanzniveau α = 0, 05, ob die (erwartete) Wohlfühltemperatur der Frauen signifikant größer als die der Männer ist.

Lösung:

X

- zufällige Wohlfühltemperatur bei den Männern EX

= µ

X

- zufällige Wohlfühltemperatur bei den Frauen EX

= µ

Die Wohlfühltemperatur ist nicht normalverteilt. = ⇒ Wilcoxon-Rangsummentest:

1. H

: µ

≥ µ

gegen H

: µ

< µ

2. α = 0, 05

3. T = R

(Rangsumme der ersten Stichprobe)

4. K = {t | t ≤ w

} n

= 8, n

= 10, w

= 56 = ⇒ K = {t | t ≤ 56}

5.

x

19 20 21 21,5 22,5 23,5 24 24,5

x

22 23 23 24 24 25 25,5 26 26,5 27

Rang(x

) 1 2 3 4 6 9 11 13

Rang(x

) 5 7,5 7,5 11 11 14 15 16 17 18

t = 1 + 2 + 3 + 4 + 6 + 9 + 11 + 13 = 49

6. t = 49 < 56 = ⇒ t ∈ K = ⇒ H

wird abgelehnt. D.h. die erwartete Wohlfühltemperatur der Frauen ist signifikant größer als die der Männer.

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

Abgasfilters auf den Geräuschpegel von PKW untersucht werden. Dazu wurden die Modelle nach ihrer Größe in die 3 Klassen „klein“, „mittel“ und „groß“ eingeteilt.

Außerdem gibt es 3 Typen des Abgasfilters.

Analysis of Variance for Geräuschpegel - Type I Sums of Squares Source Sum of Squares Df Mean Square F-Ratio P-Value MAIN EFFECTS

A:Größe 3381,09 2 1690,55 138,52 0,0000

B:Type 401,066 2 200,533 16,43 0,0000

INTERACTIONS

AB 169,345 4 42,3362 3,47 0,0149

RESIDUAL 549,212 45 12,2047

TOTAL (CORRECTED)

4500,71 53

a) Wie lautet die Modellgleichung?

Lösung:

X

- Geräuschpegel, α

- Effekt vom Faktor Größe β

- Effekt vom Faktor Type, γ

- Wechselwirkungseffekt µ - allgemeiner Erwartungswert, ε

- zufälliger Fehler.

Modellgleichung:

X

= µ + α

+ β

+ γ

+ ε

i = 1, .., 3, j = 1, .., 3 und k = 1, .., 6 Faktor Größe: p − 1 = 2 = ⇒ p = 3

Faktor Type: q − 1 = 2 = ⇒ q = 3

N − 1 = 53 = ⇒ N = 54 = p · q · n = ⇒ n = 6

b) Welche Hypothesen werden in der obigen Tabelle getestet und wie lauten die Testentscheidungen bei α = 0, 03?

Lösung:

H

: α

= 0 für alle i gegen H

: α

6= 0 für mindestens ein i p = 0, 0000 < 0, 03 = α = ⇒ H

wird abgelehnt.

H

: β

= 0 für alle j gegen H

: β

6= 0 für mindestens ein j p = 0, 0000 < 0, 03 = α = ⇒ H

wird abgelehnt.

H

: γ

= 0 für alle (i, j) gegen H

: γ

6= 0 für mindestens ein (i, j ) p = 0, 0149 < 0, 03 = α = ⇒ H

wird abgelehnt.

D.h. es gibt signifikante Effekte durch die Größe und durch den Typ

und durch Wechselwirkungen zwischen Größe und Typ.

Wechselwirkungseffekt zwischen der Größenklasse „groß“ und dem Filtertyp 3.

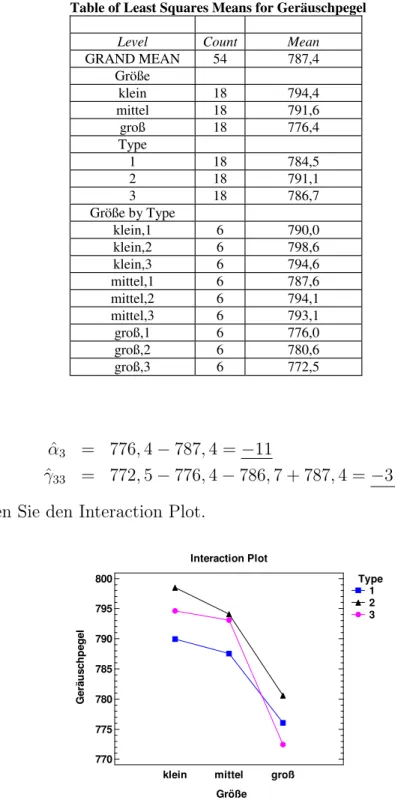
Table of Least Squares Means for Geräuschpegel

Level Count Mean

GRAND MEAN 54 787,4

Größe

klein 18 794,4

mittel 18 791,6

groß 18 776,4

Type

1 18 784,5

2 18 791,1

3 18 786,7

Größe by Type

klein,1 6 790,0

klein,2 6 798,6

klein,3 6 794,6

mittel,1 6 787,6

mittel,2 6 794,1

mittel,3 6 793,1

groß,1 6 776,0

groß,2 6 780,6

groß,3 6 772,5

Lösung:

ˆ

α

= 776, 4 − 787, 4 = −11 ˆ

γ

= 772, 5 − 776, 4 − 786, 7 + 787, 4 = −3, 2 d) Betrachten Sie den Interaction Plot.

Interaction Plot

Größe 770

775 780 785 790 795 800

Geräuschpegel

klein mittel groß

Type 1 2 3

Welchen Filtertyp sollte man in welcher Größenklasse wählen, um den Ge- räuschpegel gering zu halten?

Lösung:

Bei der Größe „klein“ und „mittel“ sollte der Filtertyp 1 und bei der Größe „groß“

der Filtertyp 3 gewählt werden..

a) Welche Hypothese testet der folgende Test und wie lautet die Testentscheidung bei α = 0, 04?

Tests for Normality for IQ

Test Statistic P-Value

Shapiro-Wilk W 0,937324 0,507142

Lösung:

H

: IQ ist normalverteilt gegen H

: IQ ist nicht normalverteilt p = 0, 507 > 0, 04 = α = ⇒ H

wird angenommen.

D.h. IQ unterscheidet sich nicht signifikant von einer Normalverteilung.

b) In einem Warenkorb sind 7 Güter. Bei jedem dieser Güter ist der Preis (von der Basiszeit zur Berichtszeit) um 7% gestiegen und die verkauften Mengen um 7% gesunken. Wie groß ist damit der Umsatzindex?

Lösung:

Preis um 7% gestiegen: p

(j ) = 1, 07 · p

(j) j = 1, ..., 7

verkauften Mengen um 7% gesunken: q

(j) = 0, 93 · p

(j ) j = 1, ..., 7

U

= P

p

(j) · q

(j) P

j=0

p

(j) · q

(j)

= P

1, 07 · p

(j) · 0, 93 · q

(j) P

j=0

p

(j) · q

(j)

= 1, 07 · 0, 93 · P

p

(j ) · q

(j) P

j=0

p

(j ) · q

(j)

= 1, 07 · 0, 93 = 0, 9951

tion von Kendall (Kendalls τ )? Kurze Begründung!

Plot of y vs x

0 1 2 3 4 5

x 12

17 22 27 32 37 42

y

Lösung:

Es liegt ein streng monoton wachsender Zusammenhang vor. (Alle ¡

2

¢ = ¡

2

¢ = 10 Paare sind konkordant.) Die Ränge liegen auf einer Geraden mit positiven Anstieg. = ⇒ τ = r

= 1.

d) Bei der stochastischen Prozesskontrolle durch eine Mittelwertkarte wird der Stichprobenumfang von 15 auf 12 geändert. Wie ändert sich damit die Wahrscheinlichkeit für „blinden Alarm“ (Fehler 1. Art) und wie die für

„unterlassenen Alarm“ (Fehler 2. Art)?

Lösung:

P(„blinder Alarm“)=P(„Fehler 1.Art“)= α ist nicht vom Stichprobenumfang n abhängig und bleibt damit gleich. P(„unterlassener Alarm“)=P(„Fehler 2.Art“)= β wird größer, da der Stichprobenumfang kleiner wird.

e) Die Zufallsgrößen X und Y sind beide normalverteilt mit Erwartungswert 3 und Standardabweichung 3.

i. Wie groß ist E(X · Y ), falls X und Y stochastisch unabhängig sind?

ii. Wie groß kann E(X ·Y ) höchstens sein? Denken Sie dabei an die Beschrän- kung der Korrelation.

Lösung:

i. X, Y unanhängig:

E(X · Y ) = EX · E(Y ) = 3 · 3 = 9 ii.

Corr(X, Y ) = Cov(X, Y )

p Var(X)Var(Y ) ≤ 1

= ⇒ Cov(X, Y ) ≤ p

Var(X) · p

Var(Y ) = 3 · 3 = 9

Cov(X, Y ) = E(X · Y ) − EX · E(Y ) = E(X · Y ) − 3 · 3 ≤ 9

= ⇒ E(X · Y ) ≤ 18.