Bestimmen Sie die Werte der folgenden Doppelintegrale:

(1)

Themen:

Mehrfachintegrale – Doppelintegrale

Aufgabe A1:

Bestimmen Sie die Werte der folgenden Doppelintegrale:

a)

3

1 2

0

...

cos

x x

y x y

dydx I

b)

1 1

1

...

u v

u

dvdu e

v u I

c)

1

0 0

2

...

y y

x y x

dxdy e I

Lösungen:

a)

3

1

3

1 2

3

1 2

0

3

1

2

0

sin sin 0

sin cos

x x

x x x

x

y x

x x y y x

y

dydx x dx x x dx xdx

I

2 4 1 2 9

3 1 2 12

x

b)

1 1

1 u v

u

dvdu e v u I

Innere Integration:

u u

u v v

u

u v e dv uv v e e u u u e

e

₂¹ ² ¹ ₁ ₂¹ ₂¹

2

1

Äußere Integration:

1 pI 1

1 1

2 1 2

2 2

u u u

u u

u

u u

u

u e e du

e g f

e g u du f

e u du

e u

1 1

1

2 1 2 1 2 2

2 u e

^u

e

^u _u

e

^u

u

_u

e e

Normale Cosinus - Integration, Umkehrung

der Kettenregel

Hier möglich, da unabhängig von !

Funktionsterm für die äußere

Integration

ersetzen Uneigentliches

Integral

(2)

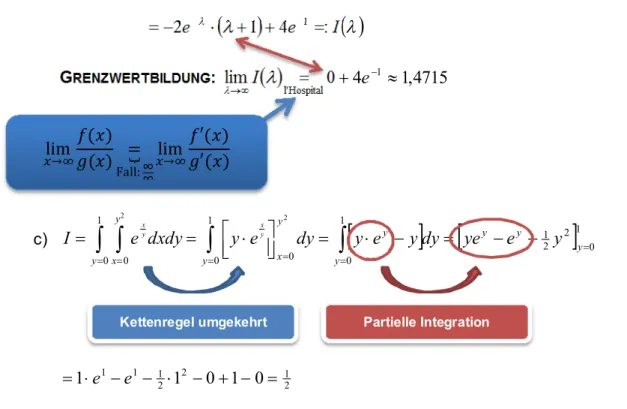
I e

e 1 4 :

2

¹

G RENZWERTBILDUNG : lim 0 4

¹

1 , 4715

Hospital

l'

e

I

c)

1

0

1 0 2 2 1 0

1

0

1

0 0

2 2

y

y y

x y y

y y x

y e ye dy y e y dy e

y dxdy

e

I

^y^x ^y^x

2 2 1

2 1 1

1

1 0 1 0

1 e e

Aufgabe A2:

Die in Figur 1 skizzierte trapezförmige Grenzfläche A zweier dielektrischer Medien enthält die ortsabhängige Oberflächenladung x , y k x

²

y mit k 1 , 5 10

¹⁰

As/cm

⁵

. Berechnen Sie die Gesamtladung Q auf der Grenzfläche nach der Formel

A

dA y x

Q , .

Figur 1: Trapezförmige Grenzfläche.

Lösung:

= 0

= + 1

= 0 und = 4

lim ( ) ( ) =

Fall:

lim ( ) ( )

Kettenregel umgekehrt Partielle Integration

(3)

Aus der Skizze sind die Integrationsgrenzen zu entnehmen. Da y von x abhängt, inte- grieren wir zuerst nach y . Es ist dabei x , y k x

²

y .

dx x x x dx

x x k dx y

x k

dydx y x k

Q

x k x

x

x y x

x

y

4

0

2 3 4 2 4

0 2 2 2 1 4

0

1 0 2 2 2 1 4

0 1

0

2

1 2

8 15

4 2656 0 3 3 4 1 2 5 1 5 1

2

x x x

_x

k 2 , 656 10

k

As

Aufgabe A3:

Berechnen Sie mit Hilfe der Integralrechnung das Volumen der Dreieckspyramide, die durch die Koordinatenachsen im kartesischen Koordinatensystem und die Ebene mit der Koordi- natengleichung x

₁

2 x

₂

3 x

₃

12 im ersten Oktanten begrenzt wird.

Figur 2: Skizze der gesuchten Dreieckspyramide.

Lösung:

Lösung ohne Integralrechnung:

Aus der Koordinatengleichung können wir sofort die drei Spurpunkte ablesen:

1 12

3

2

₂ ₃ ₁₂¹ ₁ ₆¹ ₂ ₄¹ ₃

1

x x x x x

x

Möglich, da von den

Variablen unabhängig! 1. Binomische Formel

Mathematik fertig, nur Zahlenwert für noch eingesetzt

Davon die Kehrwerte nehmen

( / / )

Dreieck: = 12 6 = 36 ^FE

ergibt

(4)

Da wir eine Pyramide mit der Grundfläche A vorliegen haben, können wir wie folgt das Volumen derselben berechnen:

48 4

3

36

1 3

1

A h

V

_P

VE.

Lösung mit Integralrechnung:

Hier formen wir erst einmal nach z ( z x

₃

) um (nach den anderen Variablen ist dies aber auch möglich):

y x z

z y x x

x

₁

2

₂

3

₃

12 2 3 12 4

₃¹ ₃²

Die Integrationsgrenzen entnehmen wir aus folgender Skizze (Betrachtung der Pyramide von oben):

Nun können wir das Integral aufstellen ( z ist die Integrandfunktion, die Grenzen sind dem rechten Teil der Skizze zu entnehmen) und berechnen:

VE 3 48

144 12 12

12 12 12 12

12 2

2 2

2 24 6

6 6

4 4 4

,

2 3 12 31 2

3 361 12

0 2

3 361 12

0 2 121

12

0

2 121 363

2 61 12

0

2 21 31 21 31

12

0

2 6 1

0 2 3 1 3 1 12

0 2 6 1

0

3 2 3 1 )

(

x x

x

x y x

x

y A

P

x x

x dx x

x

dx x x x

x x dx

x x

dx y

xy y dydx

y x dA

y x z V

Etwas umständlicher die „Lösung ohne Integralrechnung“, aber es funktioniert!

6

12 90°

6 ⁼

= 12

= und =

2. Binomische Formel mit Minusklammer

(5)

Aufgabe A4:

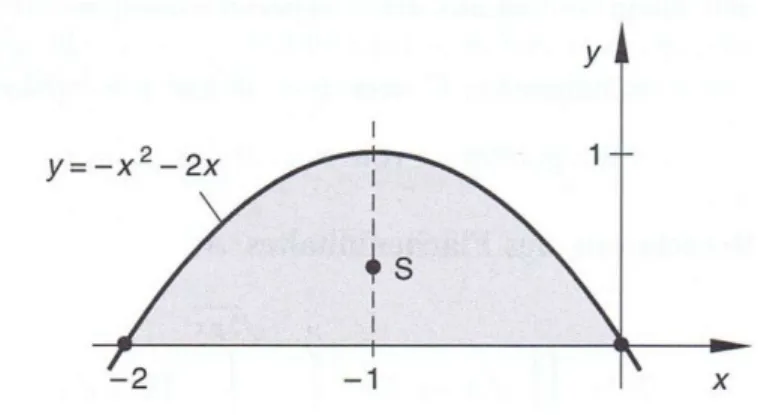
Bestimmen Sie den Schwerpunkt S der zwischen der Parabel y x

²

2 x und der x - Achse gelegenen Fläche.

Figur 3: Parabel und Schwerpunkt.

Lösung:

Wir benötigen für die Berechnung erst einmal den Flächeninhalt. Diesen können wir mit dem stinknormalen Einfachintegral berechnen

¹

:

Flächenberechnung:

FE 4

2 2

2

₃¹ ³ ² ⁰₂ ₃¹ ³ ² ₃⁸ ₃⁴

0

2

x dx x x

x A

Anschließend können wir uns der eigentlichen Schwerpunktberechnung zuwenden, indem wir die Formel aus dem Skript bemühen. Durch die offensichtliche Symmetrie zur Achse

1 x muss der x -Wert des Schwerpunkts natürlich x

_S

1 sein:

Berechnung des Schwerpunktes (nur der y -Wert ist zur berechnen):

5 2 15 16 8 16 3

8 3 8

4 3 8 4

3 2 2 1 4 3 4

3 1

3 32 5

0 32 2 3 3 4 4 5 5 1 0

2

2 3 4 BF

1.

0

2 2 2 0

2

2 0 2 21 0

2 2

0 3

4 )

(

1 ²

2

x x

x x y x

x x

y A

S A

x x x dx

x x x

dx x x dx

y dydx

y ydA

y

Damit ist der Schwerpunkt S 1

₅²

.

Aufgabe A5:

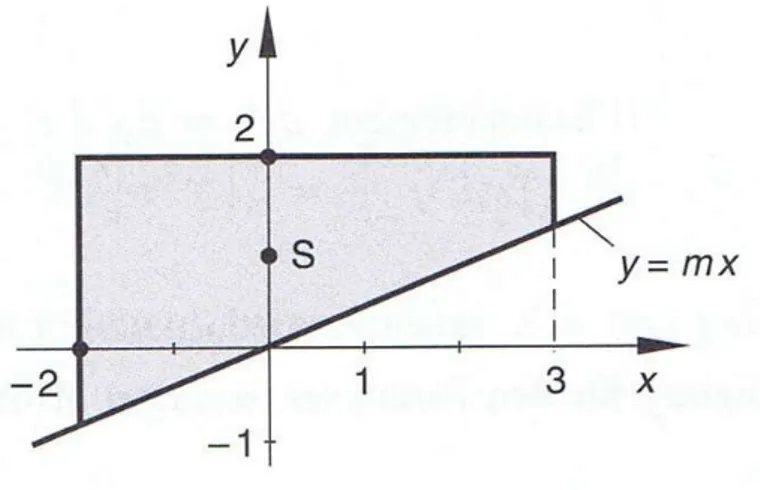
Die in Abbildung 3 skizzierte trapezförmige Fläche wird von unten von der Geraden y mx berandet.

( 2 ) = ( + 2 )

(6)

a) Wie muss man die Steigung m wählen, damit der Flächenschwerpunkt S auf der y - Achse liegt?

b) Bestimmen Sie die genaue Position des Schwerpunktes.

Figur 4: Schwerpunktanpassung.

Lösungen:

a) Damit der Schwerpunkt auf der y -Achse liegt, müssen wir x

_S

0 fordern. Die Grenzen beim Integrieren ergeben sich aus Figur 4. Wir formulieren daher:

0 0

3

2 2 3

2 2 1 )

( 1

x y mx A

A

S A

xdA xdydx xdydx

x Integralberechnung:

7 3 3

35

3 3 8

2 3 3 2 3

2

2 3

2 3 2

2 2

0 5

4 9 9 2

m m

x x dx mx x dx

xy

xdydx

^m _x

x x

mx y x y mx

b) Um die Koordinaten des Schwerpunkts zu bestimmen, müssen wir nur noch die y - Koordinaten berechnen, die x -Koordinate kennen wir bereits aus Teil a). Zuerst kümmern wir uns den Flächeninhalt, den wir nach der bekannten Formel aus dem 2.

Semester berechnen:

b

a

dx x g x f

A ( ) ( )

für den Flächeninhalt zwischen den Schaubildern zweier Funktionen f und g in den

gegebenen Grenzen.

(7)

Flächeninhalt:

A x

x dx x

x

14 FE 2 125

2

₁₄³ ² ³₂

3

2 7 3

Berechnung der fehlenden Koordinate:

98 1 98 98 875 125 4 14

125 6 2 14

125 14

125 2 14 125

14 125

14 1

98 24 98

3 81 2 3 983

3

2

2 989 3

2 2 2 2 1 3

2 2

)

( ⁷

3 7

3

x

x x

x y

x y x

A S

x x

dx x dx

y ydydx

A ydA y

Der Schwerpunkt ist also S 0 1 . Aufgabe A6:

Berechnen Sie

A

dA y

x

I 3

² ²

4 . Die Fläche ist in Figur 5 abgebildet.

Figur 5: Fläche für Aufgabe 6.

Lösung:

Aufgrund der Rotationssymmetrie bietet es sich an, in Polarkoordinaten zu rechnen. Dazu müssen wir die Transformationsregeln beachten:

84 42 2 2

2 4

3 2 4

3 4 sin

cos 3

4 3

3 1 2 3 3

1 2 2

0 3

1 2

2

0 3

1

2 2

) (

2 2

r r

r

r A

r r dr

r r drd

r r

drd r r

r dA

y x I

= cos ^und = sin =

(8)

Radius: r 1 (unten) und r 1 sin

²

(oben) Winkel: 0 (unten) und

₂

(oben, Viertelkreis) Aufgabe A7:

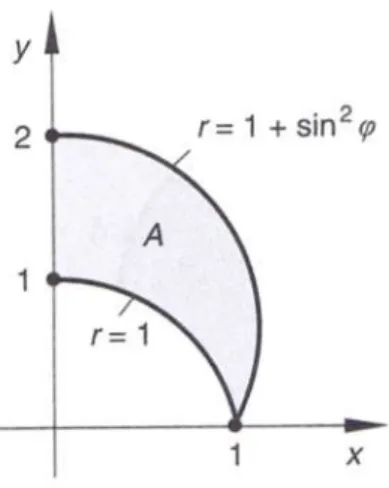
Berechnen Sie den Flächeninhalt A des im ersten Quadranten gelegenen Flächenstücks, das durch die Kurve r 1 sin

²

und den Einheitskreis berandet wird ( r , sind Polarko- ordinaten, Figur 6 zeigt die Fläche).

Figur 6: Fläche zu Aufgabe 7.

Lösung:

Die Integrationsgrenzen sind Figur 6 zu entnehmen. Dabei gilt:

Damit können wir die Flächenberechnung unter Berücksichtigung der Transformationsregeln durchführen:

2

0

2 4

21 2

0 1.BF

sin 1

1 2 21 2

0 sin 1

1 )

(

...

sin 2

2

sin

2

d r

rdrd dA

A

_r

r A

32 ... 11 2

...

¹₂ ₂ ^sin₄² ^sin⁴ ₄^cos ₄³ ₂ ^sin₄² ₀²

Integrale:

2 2 sin 21

21

2

sin cos

sin x dx x x x x

^x

x x

xdx

ⁿ_n ⁿ _n ⁿ

n 1

sin

2 1

cos sin

1