Kryptographische Algorithmen
Wintersemester 2006/2007
Prof. Dr. Steffen Reith reith@informatik.fh-wiesbaden.de
Fachhochschule Wiesbaden
Fachbereich Design Informatik Medien
Erstellt von: Eugen Wittmann Zuletzt ¨uberarbeitet von: Steffen Reith
Email: reith@informatik.fh-wiesbaden.de Erste Version: August 2006
Version: 755
Date: 2007-01-23
Inhaltsverzeichnis
1. Symmetrische Kryptosysteme 1
1.1. Blockchiffren . . . 1
1.2. Einige Grundlagen ¨uber endliche K¨orper . . . 2
1.3. AES – Advanced Encryption Standard . . . 4
1.4. Modes of Operation . . . 7
1.5. Stream Ciphers . . . 8
2. Einige Grundlagen der Rechnerarithmetik 9 2.1. Stellenwertsysteme . . . 10
2.2. Die klassischen Algorithmen . . . 10
2.2.1. Die Addition und Subtraktion . . . 10
2.2.2. Die Multiplikation . . . 11
2.2.3. Die Division . . . 14
2.3. Die Exponentiation . . . 16
3. Public-Key Kryptographie 17 3.1. Einige Grundlagen aus der elementaren Zahlentheorie . . . 17
3.1.1. Der gr¨oßte gemeinsame Teiler . . . 17
3.1.2. Restklassenringe . . . 19
3.2. Das RSA Public-Key Kryptosystem . . . 21
3.2.1. RSA – Schl¨usselerzeugung . . . 21
3.2.2. RSA – Ver- und Entschl¨usselung . . . 23
3.2.3. Angriffe auf RSA . . . 23
3.2.4. Primzahlerzeugung . . . 24
4. Der Diffie-Hellman Schl¨usselaustausch & Diskrete Logarithmen 27 5. Hashfunktionen und Anwendungen 29 5.1. Die Merkle-Damg˚ard Konstruktion (Merkle’s meta method) . . . 30
5.2. Digitale Signaturen . . . 31
5.3. Challenge-Response Verfahren . . . 32
6. Zero-Knowledge Protokolle 32 6.1. Das Fiat-Shamir Protokoll . . . 34
7. ECC – Elliptic Curve Cryptography 35 7.1. Das Gruppengesetz . . . 38
7.2. Der Diffie-Hellman Key-Exchange mit Elliptischen Kurven . . . 41
A. Elementare Begriffe und Schreibweisen 43 A.1. Mengen . . . 43
A.1.1. Die Elementbeziehung und die Enthaltenseinsrelation . . . 43
A.1.2. Definition spezieller Mengen . . . 43
A.1.3. Operationen auf Mengen . . . 44
A.1.4. Gesetze f¨ur Mengenoperationen . . . 44
A.1.5. Tupel (Vektoren) und das Kreuzprodukt . . . 44
A.1.6. Die Anzahl von Elementen in Mengen . . . 45
A.2. Relationen und Funktionen . . . 45
A.2.1. Eigenschaften von Relationen . . . 45
A.2.2. Eigenschaften von Funktionen . . . 46
A.2.3. Permutationen . . . 47
B. Einige formale Grundlagen von Beweistechniken 47
B.1. Direkte Beweise . . . 48
B.1.1. Die Kontraposition . . . 49
B.2. Widerspruchsbeweise . . . 49
B.3. Der Schubfachschluss . . . 50
B.4. Gegenbeispiele . . . 50
B.5. Induktionsbeweise und das Induktionsprinzip . . . 50
B.5.1. Die vollst¨andige Induktion . . . 50
B.5.2. Induktive Definitionen . . . 51
B.5.3. Die strukturelle Induktion . . . 52
Stichwortverzeichnis 53
Literatur 57
1. Symmetrische Kryptosysteme
Definition 1 Ein symmetrisches Kryptosystembesteht aus einer Abbildung E:M×K →C,
sodass f¨ur jeden Schl¨ussel k∈K gilt:
Ek:M →C mit Ek(m) =E(m, k)
ist invertierbar. Dabei sind die Elementem∈M die Plaintexte,Cist die Menge der Ciphertexte und K die Menge der Schl¨ussel. Ek ist die Verschl¨usselungsfunktion f¨ur den Schl¨ussel k und Dk=def Ek−1 die dazugeh¨orige Entschl¨usselungsfunktion.
Bemerkung 2
• Wir nehmen an, dass f¨ur Ek und Dk ”effiziente“ Algorithmen existieren, d.h. wir k¨onnen in der Praxis schnell ver- und entschl¨usseln.
• Die Algorithmen f¨ur Ek und Dk sind bekannt (Kerckhoffsches Prinzip).
• Der Schl¨ussel k∈K muss geheim gehalten werden.
• Die gebr¨auchlichen symmetrischen Kryptosysteme sind sehr effizient, d.h. Implementie- rungen dieser Methoden ver- und entschl¨usseln sehr schnell (etwa 1000-mal schneller als asymmetrische Kryptosysteme (siehe Abschnitt 3)).
1.1. Blockchiffren
Definition 3 Ein Blockchiffre (engl. block cipher) ist ein symmetrisches Kryptosystem mit M =C ={0,1}n.
Dabei heißt n die Blockl¨ange.
Bemerkung 4
• F¨ur einen festen Schl¨ussel k ist Ek (bzw. Dk) eine Permutation (siehe Abschnitt A.2.3) auf {0,1}n.
• Es gibt 2n verschiedene Plaintexte.
Aus der elementaren Kombinatorik folgt dann: Es gibt 2n! Permutationenπ:{0,1}n→ {0,1}n, also potentielle Verschl¨usselungsfunktionenEk bzw. Entschl¨usselungsfunktionenDk. Angenom- men wir legen eine Ordnung auf diesen Permutationen fest1, dann ben¨otigen wir log2(2n!) Bits, um den Index einer solchen Permutation aufzuschreiben. Es gilt (Formelsammlung):
ln(m!)≈(m+1
2) ln(m)−m+1
2ln(2π), also:
log2(2n!) ≈ (2n+12) log2(2n)−2nlog2(e) + 12log2(2π)
≈ 2n(n−log2(e)) + 1 2n+1
2log2(2π)
| {z }
klein, ≈12n+1.3
≈ 2n(n−1.44)
Bei einer Blockl¨ange von 64 Bit br¨auchten wir etwa 270Bit f¨ur den Schl¨ussel, wenn jeder m¨ogli- chen Permutation ein Schl¨ussel/Index zugeordnet sein soll. Dies ist in der Praxis unm¨oglich und deshalb werden dort ¨ublicherweise Schl¨ussell¨angen von 56 bis 256 Bit verwendet.
1D.h. jede Permutation bekommt einen eindeutigen Index / Nummer.
1.2. Einige Grundlagen ¨uber endliche K¨orper
Definition 5 Die Struktur(F,+,·) heißt K¨orper(engl.Field), wenn sie folgende Eigenschaften hat:
(i) (F,+,·) ist ein kommutativer Ring (mit Einselement).
(ii) F¨ur alle a∈F\ {0}
| {z }
=F∗
existiert eina0 mita·a0 = |{z}1
Eins- element
=a0·a.
Dabei heißt a0 ”inverses Element“ bzgl. der K¨orpermultiplikation.
Beispiel 6
• (R,+,·),(C,+,·) und (Q,+,·) sind K¨orper.
• (Z,+,·) ist kein K¨orper.
Bekannt ist, dass Zn ={0, . . . , n−1}mit der Restklassen-Addition und Multiplikation einen kommutativen Ring bildet.
Satz 7 (Zn,+,·) ist ein (endlicher) K¨orper gdw. n∈PRIMES.
Beweis: Sp¨ater, da die entsprechenden Grundlagen f¨ur die Public-Key Kryptosysteme ben¨otigt
werden. #
Definition 8
(i) Ein K¨orper mit einer endlichen Anzahl von Elementen heißt endlicher K¨orper.
(ii) Die Anzahl von Elementen eines K¨orpers F heißt die Ordnung von F. Endliche K¨orper mit q Elementen werden auch mit GF(q) bezeichnet (Galois Field).
(iii) SeiF ein endlicher K¨orper (wichtig) undp6= 0die kleinste Zahl, sodass1 + 1 +| {z· · ·+ 1}
p-mal
= 0 gilt, dann heißt p die Charakteristik von F.
Bemerkung 9
• Die Charakteristik eines endlichen K¨orpers ist immer eine Primzahl.
• Im Fall der symmetrischen Verschl¨usselungsverfahren interessieren uns nur K¨orper der Charakteristik 2.
• (Zp,+,·) mitp Primzahl ist ein endlicher K¨orper der Charakteristik p.
Wir schreiben kurz: GF(p).
Definition 10 Ein Polynom ¨uber einem K¨orper F ist ein Ausdruck der Form b(x) = bn−1xn−1+bn−2xn−2+· · ·+b2x2+b1x+b0.
Dabei istxdieUnbekanntedes Polynoms und diebi∈F heißen die Koeffizientendes Polynoms.
Die kleinste Zahl l mit der Eigenschaft das bj = 0 f¨ur alle j > l gilt, heißt der Grad des Polynoms.
Es ist offensichtlich, dass beliebige Polynome leicht als String ¨uberF gespeichert werden k¨on- nen. Dazu werden die einzelnen Koeffizientenbi in einer bestimmten Reihenfolge aufgeschrieben, wobei sich aus der Position eines Koeffizienten im String leicht wieder der dazugeh¨orige Index ergibt.
Beispiel 11 Sei F = GF(2), dann lassen sich alle Polynome mit Grad kleiner 8 wie folgt in einem Byte speichern:
Sei
b(x) = b7x7+b6x6+· · ·+b1x+b0, dann wird b(x) als Bitstring
b7b6. . . b1b0
gespeichert. Dabei ist b7 das most significant bit(msb) und b0 das least significant bit (lsb).
D.h. Polynome ¨uber GF(2) kann man kurz auch als Hexadezimalzahlen schreiben.
Beispiel 12 Seip(x) =x6+x4+x2+x+ 1 ein Polynom ¨uber GF(2), dann wird es durch den Bitstring 0101 0111 oder durch 0x57 repr¨asentiert.
Definition 13 Wir notieren die Menge aller Polynome mit der Unbekanntenx¨uberF mitF[x].
Die Menge der Polynome ¨uberF mit der Unbekanntenxund einem Grad kleiner alslbezeichnen wir mit F[x]|l.
Betrachten wirF[x]|lmit der normalen Polynomaddition (Symbol⊕), dann ist (F[x]|l,⊕) eine kommutative (abelsche) Gruppe.
Beispiel 14 SeiF =GF(2), dann ist 0x57| {z }
∈GF(2)[x]
⊕ 0x83| {z }
∈GF(2)[x]
= 0xD4| {z }
∈GF(2)[x]
, denn
x6+x4+x2+x+ 1⊕x7+x+ 1 = x7+x6+x4+x+ 2 + (x+x) + (1 + 1)
= x7+x6+x4+x+ 2, und dieses Polynom entspricht 1101 0100, also 0xD4.
Die normale Polynommultiplikation ist assoziativ, kommutativ und distributiv mit der Poly- nomaddition. Seim(x) ein Polynom ¨uberF, dann definieren wir die Polynommultiplikation von a, b∈F[x] modulom(x) (Symbol⊗) als den Rest vona(x)·b(x) bei der Polynomdivision durch m(x) (kurz:a·bmodm). Seim(x)∈F[x] vom Grad l, dann ist (F[x]|l,⊕,⊗) ein kommutativer Ring mit dem Reduktionspolynomm(x). Meist schreiben wir aus Bequemlichkeitsgr¨unden statt (F[x]|l,⊕,⊗) auch (F[x]|l,+,·).
Definition 15 Ein Polynom d∈GF(p)[x] mitp prim, heißt irreduzibel, wenn keine Polynome a, b ∈GF(p)[x]\GF(p) (d.h. der Grad von a und b ist gr¨oßer als 0) existieren, sodass d(x) = a(x)·b(x).
Satz 16 Sei m ∈ GF(p)[x] ein irreduzibles Polynom vom Grad n, dann ist (GF(p)[x]|n,+,·) mit dem Reduktionspolynom m(x) ein K¨orper der Ordnung pn und Charakteristik p.
Beweis: Siehe beliebiges Algebrabuch. #
Bemerkung 17 Der K¨orper (GF(p)[x]|n,+,·) wird gew¨ohnlich mit GF(pn) bezeichnet.
Beispiel 18 Das Polynom m(x) = x8 +x4+x3 +x + 1 ist irreduzibel ¨uber GF(2), d.h. die Menge der Polynome ¨uber GF(2)modulom(x) bilden einen K¨orper (bezeichnet mit GF(28)) der Charakteristik 2. Es gilt z.B.: 0x57⊗0x83 = 0xC1, denn
(x6+x4+x2+x+ 1)·(x7+x+ 1) x13+x11+x9+x8+x7
⊕ x7+x5+x3+x2+x
⊕ x6+x4+x2+x+ 1
x13+x11+x9+x8+x6+x5+x4+x3+ 1
zu
p5 p6 p7
p9
p11 p10
p13 p14 p0
p2 p3 p1
p4 p8 p12
k15 k5
k6 k7
k9
k11 k10
k13 k14 k0
k2 k3 k1
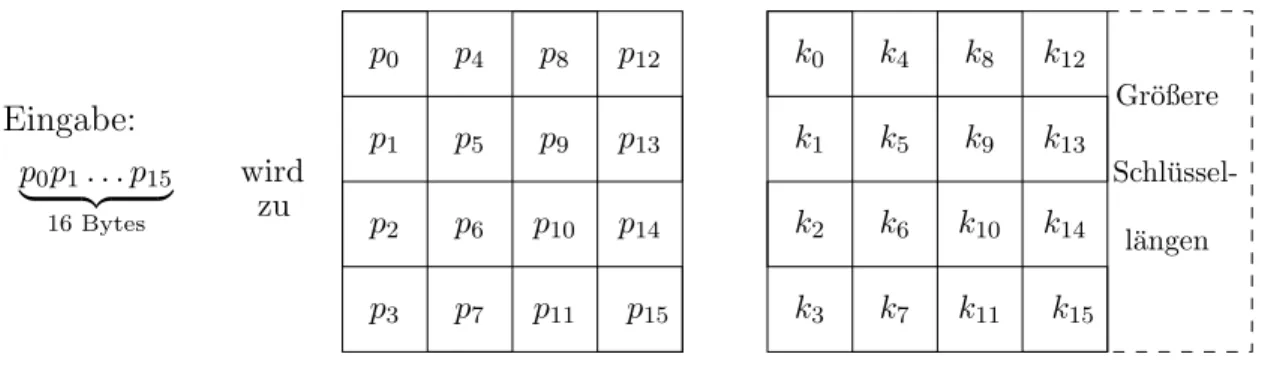
k4 k8 k12 Eingabe:
p0p1. . . p15
| {z }
16Bytes
Gr¨oßere
l¨angen Schl¨ussel- wird
p15
Abbildung 1: Layout von
”State“ und
”Schl¨ussel“
und weiterhin
(x13+x11+x9+x8+x6+x5+x4+x3+ 1) : (x8+x4+x3+x+ 1) =x5+x3
⊕ (x13+x9+x8+x6+x5) x11+x4+x3+ 1
⊕ (x11+x7+x6+x4+x3)
Rest: x7+x6+ 1 , 1100 0001 , 0xC1.
1.3. AES – Advanced Encryption Standard
Im Januar 1997 startete das NIST (US National Institute of Standards and Technology) eine Initiative, um den DES (Data Encryption Standard) und triple-DES zu ersetzen. Nach der ersten Runde wurden 15 Kandidaten akzeptiert (u.a.
”Magenta“ – Deutsche Telekom). Die Kandida- ten wurden nach Sicherheit, Implementierbarkeit und Kosten (Hardware, Speicherbedarf, . . . ) bewertet. Die zweite Runde erreichten f¨unf Kandidaten. Schließlich wurde Rijndael zum Sieger gek¨urt und mit leichten Ver¨anderungen zum AES (Advanced Encryption Standard) gemacht.
Der AES besitzt eine Blockl¨ange von 128 Bit und Schl¨ussell¨angen von 128, 192 und 256 Bit.
Der Einfachheit halber beschr¨anken wir uns hier auf den Fall von 128 Bit Schl¨usseln, d.h. es gilt AES : {0,1}128
| {z }
Plaintext
× {0,1}128
| {z }
Schl¨ussel
→ {0,1}128
| {z }
Ciphertext
.
Damit besteht die Eingabe und Ausgabe von AES aus 16 Bytes, und der AES arbeitet auf einer Datenstruktur die
”State“ genannt wird. Das Layout des States und des Schl¨ussels zeigt Abbildung 1.
In unserem Spezialfall hat der Schl¨ussel das gleiche Layout wie der”State“. Mit Hilfe des States und eines erweiterten Schl¨ussel (sp¨ater mehr) werden elf Runden durchgef¨uhrt (die Rundenan- zahl h¨angt von der Schl¨ussell¨ange ab). F¨ur die Runden i mit 0 ≤ i≤ 9 werden die folgenden Operationen ausgef¨uhrt:
Round(state, expandedKey[i]) { SubBytes(state);
ShiftRows(state);
MixColumns(state);
AddRoundKey(state, expandedKey[i]);
}
Die letzte Runde besteht aus den Schritten:
FinalRound(state, expandedKey[10]) { SubBytes(state);
ShiftRows(state);
AddRoundKey(state, expandedKey[10]);
}
• SubBytes: Hier werden alle Bytes gem¨aß einer Tabelle (S-Box) ersetzt.
Tabelle
Die genaue Struktur der verwendeten S-Box ergibt sich durch die Funktiong: GF(28)→ GF(28), g:a7→b=a−1 und eine nachfolgende affine Transformation (siehe z.B. [DR02, Seite 36]). Da der K¨orper GF(28) nur 256 Element enth¨alt, l¨asst sich eine kleine Tabelle (,S-Box) berechnen, welche die Verkn¨upfung der beiden Abbildungen als”Lookup-Table“
enth¨alt.
Die zuSubBytesinverse Operation heißt InvSubBytes.(Also affine Transformation−1 und dann a7→b=a−1.)
• ShiftRows: Hier werden die Zeilen des
”States“ rotiert a b c d
e f g h
i j k l
n o p m
rotiere 0 rotiere 1 rotiere 2 rotiere 3 a b c d
f g h e
k l i j
n o m p
wirdzu
Die zu ShiftRowsinverse Funktion heißt InvShiftRows.
• MixColumns: DerMixColumns-Schritt arbeitet auf den Spalten des
”States“. Dabei werden die Spalten als Polynom ¨uber dem K¨orper GF(28) (Ordnung 256) aufgefasst und modulox4+1 mit dem festen Polynom c(x) = c3x3 +c2x2+c1x+c0 ∈ GF(28)[x] multipliziert. Dabei giltc0, c1, c2, c3 ∈GF(28) und in der oben beschriebenen Hex-Notation von Elementen aus GF(28) ist c0 = 0x02,c1 = 0x01,c2 = 0x01 und c3= 0x02.
Anschaulich:
·c(x) modx4+ 1
b3,1 b3,0
b2,0 b2,1 b2,2 b2,3 b1,0 b1,1 b1,2 b1,3 b0,0 b0,1 b0,2 b0,3
b3,2 b3,3 a3,1
a3,0
a2,0 a2,1 a2,2 a2,3 a1,0 a1,1 a1,2 a1,3 a0,0 a0,1 a0,2 a0,3
a3,2 a3,3
wird zu
des
Key
S[a3] S[a2] S[a1] RC[·]
S[a0] Konstruktion XOR
Extended Key
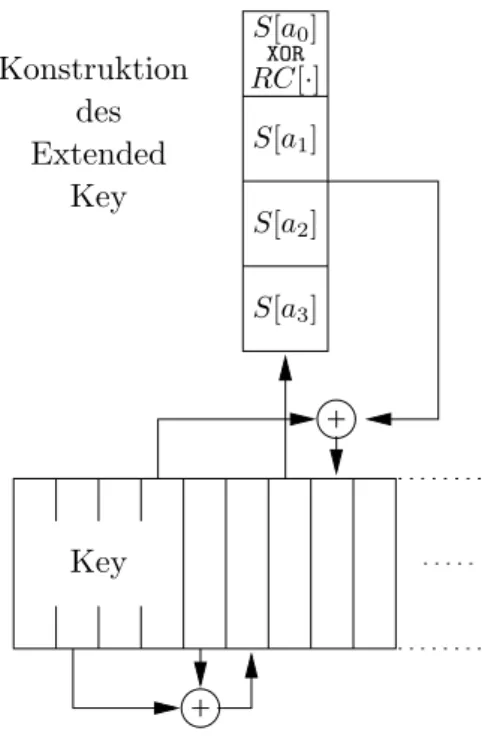
Abbildung 2: Veranschaulichung der Generierung desexpandedKey
Der zu MixColumns inverse Schritt heißt InvMixColumns und verwendet das Polynom d(x) = 0x0Bx3+ 0x0Dx2+ 0x09x+ 0x0E∈GF(28)[x].
Obwohl dieser Schritt sehr aufwendig erscheint, kann er mit Lookup-Tabellen sehr effizient implementiert werden.
• AddRoundKey: Hier wird der”State“ bitweise mit dem ”expandedKey[i]“ XOR-verkn¨upft, wo- bei 0 ≤ i ≤ Nr (Rundenzahl). Da bei unserem Spezialfall Nr = 10 gilt, besteht der
”expandedKey“ aus elf 4x4-Byte Bl¨ocken.
Entschl¨usselt wird durch:
InvFinalRound(state, expandedKey[10]) { AddRoundKey(state, expandedKey[10]);
InvShiftRows(state);
InvSubBytes(state);
}
Und f¨ur 9≥i≥0:
InvRound(state, expandedKey[i]) { AddRoundKey(state, expandedKey[i]);
InvMixColumns(state);
InvShiftRows(state);
InvSubBytes(state);
}
Nun stellt sich noch die Aufgabe, wie man aus dem Key (128 Bit) den ”expandedKey“ (auch
”Key Schedule“ genannt) berechnet. Zuerst wird der 128 Bit-Schl¨ussel in den ”Expanded Key“
kopiert. Eine neue Spalteiwird aus den Spalteni−1 undi−4 (allgemein: iminus Spaltenzahl des Keys) bestimmt. Ist i kein Vielfaches von 4 (der Spaltenzahl des Keys), dann werden die Spalteni−1 undi−4 bitweiseXOR-verkn¨upft. Istiein Vielfaches von 4, dann wird der Prozess
m1m2m3 ml
c1 c2 c3 cl
f f f f
m =
c =
Entschl¨usselung analog mitf−1
=⇒
Abbildung 3: Der ECB-Mode wie folgt modifiziert:
Seia0a1a2a3die Spaltei−1, dann berechne (S[a0]XORRC[i/4])S[a1]S[a2]S[a3] und verkn¨upfe diese Spalte XORmit der Spaltei−4. Dabei istS[·] die S-Box desSubBytes-Schritts und RC[·]
sind so genannte ”Roundconstants“, wobei RC[i]∈ GF(28) und RC[0] = x0 (d.h. 0x01 in der Hex-Notation),RC[1] =x1 (d.h. 0x02), . . .RC[j] =x·RC[j−1]. Eine graphische Veranschau- lichung dieses Prozesses findet sich in Abbildung 2.
1.4. Modes of Operation
In der Praxis werden oft Daten ¨ubertragen, deren Gr¨oße unterschiedlich zur Blockgr¨oße eines Block Ciphers ist. Deshalb brauchen wir eine Erweiterung, die es erm¨oglicht mit Daten beliebiger Gr¨oße arbeiten zu k¨onnen.
Sei nunn, r ∈N,n≥r undf:{0,1}n→ {0,1}n die Verschl¨usselungsfunktion einer Blockchif- fre (mit fixem Keyk). Zerlege den Plaintext m=m1m2. . . ml in Bl¨ocke der Gr¨oßer. Sollte die L¨ange unserer Nachricht nicht durchr teilbar sein, so wird am Ende”aufgef¨ullt“ (”Padding“).
Electronic Codebook Mode (ECB-Mode): Eine offensichtliche L¨osung ist r = n zu w¨ahlen und f auf die Bl¨ocke mi mit 1 ≤ i ≤l anzuwenden (siehe Abbildung 3). Die Verschl¨us- selung arbeitet also wie ein Codebuch und verschl¨usselt gleiche Plaintextbl¨ocke in gleiche Cipherbl¨ocke.
Vorteil: Ubertragungsfehler betreffen nur den jeweiligen Block.¨
Nachteil: Erich erh¨alt Informationen ¨uber den Plaintext. (Er kann z.B. z¨ahlen, wie oft gewisse Plaintextbl¨ocke ¨ubertragen werden. Weiterhin werden ”Replay Attacken“, evtl. mit ver¨anderter Reihenfolge der Bl¨ocke, m¨oglich.). Aus diesen Gr¨unden ist eine Verbesserung notwendig.
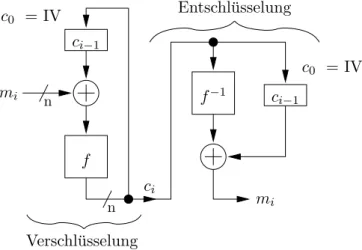
Cipher-Block Chaining Mode (CBC-Mode): W¨ahle r = n und ein c0 ∈ {0,1}n als Initiali- sierungsvektor (kurz IV). Der Plaintextblock mi wird mit dem letzten Ciphertextblock XOR-verkn¨upft und dann mit dem Blockchiffre verschl¨usselt, d.h. ci =f(mi⊕ci−1). Wir erhalten also einen um ein Block l¨angeren Ciphertext c=c0c1. . . cl.
Die Daten k¨onnen mit m1 =f−1(ci)⊕ci−1, 1≤i≤l wieder entschl¨usselt werden (siehe Abbildung 4).
Vorteil: Gleiche Bl¨ocke mit unterschiedlicher ”Vorgeschichte“ werden unterschiedlich ver- schl¨usselt.
Nachteil : Ein ¨Ubertragungsfehler in Block ci betrifft die Entschl¨usselung von Block ci und ci+1. (
”Self-synchronizing“)
Cipher-Feedback Mode (CFB-Mode): Die Funktionen lsbl(·) und msbl(·) bestimmen die l
”least significant“ bzw.”most significant“ Bits eines Bitstrings. Mit ”||“ soll die Konkate- nation von Bitstrings notiert werden.
Verschl¨usselung ci n n
f
f−1 ci−1 ci−1
mi
mi c0 =IV
c0 =IV Entschl¨usselung
Abbildung 4: Der CBC-Mode
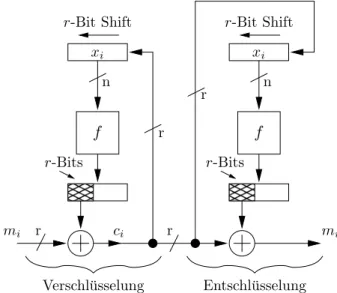
Der Plaintext ist in Bl¨ocke der L¨anger mit 1≤r≤neingeteilt und wir verschl¨usseln wie folgt:
for (i= 1; i≤l; i++) { ci = mi ⊕ msbr(f(xi));
xi+1 = lsbn−r(xi) || ci; }
return c1, . . . , cl;
Dabei ist x1 ein beliebiger (zuf¨allig gew¨ahlter) Initialisierungsvektor und auch der Fall r = 1 ist m¨oglich.
Vorteil: Sender und Empf¨anger k¨onnen den (aufwendigen) Blockchiffre (fast) gleichzeitig anwenden (minimale Verz¨ogerung).
Nachteil: Ein Bitfehler im Block ci betrifft die Entschl¨usselung von diesem und der n¨ach- sten dn/re Bl¨ocke (”Self-synchronizing“).
1.5. Stream Ciphers
Wir haben beim CFB-Mode gesehen, dass einzelne Bits verschl¨usselt werden k¨onnen, d.h. die Blockgr¨oße ist n= 1.
Definition 19 SeiK das Schl¨usselalphabet,M das Plaintextalphabet undCdas Cipheralphabet, dann ist ein Stream CipherE∗ eine Abbildung:
E∗:M∗×K∗→C∗, E∗(m, k) =c,
wobei E∗ den Strom m = m1m2m3. . . ∈ M∗ in den Strom c = c1c2c3. . . ∈ C∗ mit Hilfe des Schl¨usselstroms k=k1k2k3. . .∈K∗ verschl¨usselt. Dazu wird die Abbildung
E:M ×K →C
verwendet, die f¨ur jeden Schl¨usselbuchstaben k ∈ K bijektiv ist. Es gilt ci = E(mi, ki) f¨ur i= 1,2,3, . . ..
n
r-Bits r-Bits
xi
xi
n f
ci
r r
f r
r
mi
Verschl¨usselung Entschl¨usselung
r-Bit Shift
mi
r-Bit Shift
Abbildung 5: Der CFB-Mode
Beispiel 20 (Vernam’s One-Time Pad, ca. 1919) Sei M =def K =def C=def {0,1} und E:{0,1} × {0,1} → {0,1}, (m, k)7→m|{z}⊕
XOR
k.
Die Ver- und Entschl¨usselung von Bitstrings funktioniert mit:
E∗(m, k) = c1c2c3. . . , wobei ci =mi⊕ki und D∗(c, k) = m1m2m3. . . , wobei mi=ci⊕ki.
Jedes Bit im Schl¨usselstrom wird unabh¨angig und zuf¨allig gew¨ahlt. Dies ist ein Nachteil, da sehr viele echte Zufallsbits erzeugt und transportiert werden m¨ussen. Der Schl¨usselstrom darf nicht zweimal verwendet werden, denn angenommenmund m0 werden mitkzu cundc0 verschl¨usselt, dann kann Erich m⊕m0 = c⊕c0 berechnen und erh¨alt so Informationen ¨uber den Plaintext (z.B. wenn m⊕m0 = 0).
Bemerkung 21 In der Praxis werden oft pseudozuf¨allige Schl¨usselstr¨ome verwendet (erzeugt via Feedback-Shift-Register oder Blockchiffren + CFB-Mode). Mehr dazu in [MvOV97].
Bemerkung 22 Ist der Schl¨usselstrom eine zuf¨allige Bitfolge, dann kann man zeigen, dass die- ses Verfahren nicht gebrochen werden kann (vgl. Shannon’s Theorieund
”Perfekte Sicherheit“).
2. Einige Grundlagen der Rechnerarithmetik
Wie wir noch sehen werden, arbeiten viele Verfahren der Public-Key Kryptographie mit großen nat¨urlichen Zahlen mit bis zu 4096 Bit (ca. 1200 Dezimalstellen). Aus diesem Grund bildet eine Bibliothek zum Rechnen mit großen Zahlen die Basis f¨ur viele Algorithmen der Public-Key Kryptographie. Die dazu ben¨otigten Algorithmen sollen in diesem Abschnitt kurz vorgestellt werden. Details und Erweiterungen finden sich in [Knu98] und umfassende Informationen zur Implementation gibt [Wel01].
2.1. Stellenwertsysteme
Ublicherweise repr¨asentieren Digitalcomputer nat¨urliche Zahlen in Bin¨ardarstellung einer fester¨ L¨ange, d.h. eine Zahl wird als geordnete Folge
(xn−1xn−2. . . x1x0)2,wobei xi ∈ {0,1} und 1≤i < n,
dargestellt. Die Zahlnwird oftRegisterbreitegenannt. Die Folge (xn−1xn−2. . . x1x0)2 repr¨asen- tiert dann den Wert
x=
n−1X
i=0
xi2i
Das Gewicht der iten Zifferxi ist also eine 2er Potenz und 2 wird als Basis des Zahlensystems bezeichnet. Offensichtlich kann man auch andere BasenB f¨ur eine Zahlendarstellung verwenden.
Ublicherweise kommen z.B. noch¨ B = 16 (Hexadezimaldarstellung), B = 10 (Dezimaldarstel- lung), B= 8 (Oktaldarstellung) oder B= 60 (Sexagesimaldarstellung) zu Einsatz.
IstB ≥2 die Basis einer Zahlendarstellung, so nennen wir dieseB-n¨are Darstellung. Der Ein- fachkeit halber verwenden wir f¨ur den Wert x=Pn−1
i=0 xi2i auch (xn−1xn−2. . . x1x0)2, d.h. wir unterscheiden nicht zwischen Wert und der jeweiligen Darstellung.
2.2. Die klassischen Algorithmen
In diesem Abschnitt sollen die klassischen Algorithmen zur Addition, Subtraktion und Multipli- kation und Division von Zahlen inB-n¨arer Darstellung vorgestellt werden, die ¨ublicherweise f¨ur die BasisB = 10 verwendet werden.
2.2.1. Die Addition und Subtraktion
Sei B≥2 die Basis unserer Zahlendarstellung und
a = (an−1an−2. . . a1a0)B b = (bn−1bn−2. . . b1b0)B zwei Zahlen in B-n¨arer Darstellung. Es gilt:
a+b = n−1P
i=0
aiBi+n−1P
i=0
biBi
= n−1P
i=0
(ai+bi)Bi
Da die Ziffern ai, bi ∈ {0, . . . B−1} sind, gilt 0≤(ai +bi) ≤ 2(B −1) f¨ur 0 ≤i < n, d.h. die Summe ai +bi kann evtl. nicht mehr als einzelne Ziffer dargestellt werden. Offensichtlich ist 2(B−1) = 2B−2 = 1·B1+ (B−2)·B0 = (1B−2)B, d.h. die Summeai+bi kann alsB-n¨are Ziffer plus einem ¨Ubertrag von maximal 1 auf die n¨achste Ziffer darstellt werden.
Damit ergibt sich Algorithmus 1 zur Addition von zwei Zahlen, wennaundbdie gleiche Anzahl von Ziffern haben.
Bemerkung 23
• Die spezielle Wahl der Basis B hat keinen Einfluß auf Algorithmus 1, d.h. wir w¨ahlen B so, dass
– m¨oglichst wenige Schleifendurchl¨aufe ben¨otigt werden und
– der verarbeitende Prozessor die Summe a[i] +b[i] +carry effizient2 berechnen kann.
2Der ¨Ubertrag auf eine n¨achste Ziffer wird ¨ublicherweise mit dem englischen Wort”carry“ bezeichnet.
Algorithmus 1 : Addition zweier nat¨urlicher Zahlen
Eingabe: Zwei Zahlena= (an−1. . . a1a0)B,b(bn−1. . . b1b0)B und die Anzahl der Ziffernn Ergebnis: Die Summe c= (cn−1. . . c1c0)B von aund bund einen evtl. ¨Ubertrag
/* Initalisiere den Z¨ahler */
i= 0;
/* Initalisiere den ¨Ubertrag */
carry = 0;
for(i= 0; i < n; i++) { t=a[i] +b[i] + carry;
c[i] =tmodB;
/* tdivB */
carry =bBtc;
}
/* Gebe einen evtl. ¨Uberlauf zur¨uck */
returncarry;
• F¨ur 32-Bit Prozessoren bietet sich B = 232 an, da diese Wahl daf¨ur sorgt, dass der Pro- zessor die Summe a[i] +b[i] +carry effizient mit zwei Maschinenbefehlen berechnen kann.
• Bei einer C-Implementierung bietet es sich an, die Zahlen als Array vom Typ unsigned longabzuspeichern, wobei die erste Arraykomponente die Anzahl der Ziffern der jeweiligen Zahl enth¨alt.
Die Subtraktion kann mit einem sehr ¨ahnlichen Algorithmus implementiert werden, wenn a und bdie gleiche Anzahl von Ziffern hat (siehe Algorithmus 2).
Beispiel 24 Sei B = 10. Dann ergeben sich bei der Berechnung von 1372−1285 = 0087 mit Algorithmus 2 die folgenden Zwischenwerte:
i a[i] b[i] t c[i] borrow
0 2 5 7 7 0
1 7 8 8 8 0
2 3 2 10 0 1
3 1 1 10 0 1
Beobachtung 25 Die Algorithmen 1 und 2 haben eine Laufzeit von O(n), wobei ndie Anzahl der Ziffern der Zahlen a und b ist.
2.2.2. Die Multiplikation Sei B≥2 und
a = (an−1an−2. . . a1a0)B b = (bn−1bn−2. . . b1b0)B
Algorithmus 2 : Subtraktion zweier nat¨urlicher Zahlen
Eingabe: Zwei Zahlena= (an−1. . . a1a0)B,b(bn−1. . . b1b0)B und die Anzahl der Ziffernn Ergebnis: Die Differenzc= (cn−1. . . c1c0)B von aund b und einen evtl. Unterlauf
/* Initalisiere den Z¨ahler */
i= 0;
/* borrow==1, wenn von der aktuellen Stelle nicht geborgt wurde */
borrow = 1;
for(i= 0; i < n; i++) { if (borrow==1) {
t=B+a[i]−b[i];
} else{
t= (B−1) +a[i]−b[i];
}
c[i] =tmodB;
/* tdivB */
borrow =bBtc;
}
/* Gebe einen evtl. Unterlauf zur¨uck */
returnborrow;
zwei Zahlen in B-n¨arer Darstellung, dann gilt a·b = (n−1P
i=0
aiBi)·(n−1P
i=0
biBi)
= b0·(n−1P
i=0
aiBi) +b1B1·(n−1P
i=0
aiBi) +· · ·+bn−1Bn−1·(n−1P
i=0
aiBi)
= n−1P
i=0
aib0Bi+n−1P
i=0
aib1Bi+1+· · ·+n−1P
i=0
aibn−1Bi+(n−1)
= n−1P
j=0 n−1P
i=0
aibjBi+j (?)
Damit ergibt sich f¨ur zwei Zahlenaundbderen DarstellungnZiffern lang ist, dass das Produkt a·baus maximal (n−1)(n−1)+1+1 = 2nsignifikanten Stellen besteht. F¨ur eine Implementierung ist die Summendarstellung (?) nicht effizient nutzbar, da erst die Produkte aibj berechnet und gespeichert werden m¨ussten. Sei c[i+j] die (i+j)te Stelle der Zahl a·b, dann berechnen wir einfacher
t=c[i+j] +a[i]·[j] + carry,
wobei carry der ¨Ubertrag aus der Berechnung der letzten Stelle ist. Da 0≤c[i+j], a[i], b[i],carry≤ (B−1) ist, gilt 0≤t≤(B−1) + (B−1)2+ (B−1) = 2B−2 +B2−2B + 1 =B2−1 und weiterhin
B2−1 = (B−1)
| {z }
Ziffer
·B1+ (B−1)
| {z }
Ziffer
·B0.
Deshalb kanntin zweiB-n¨aren Ziffern gespeichert werden. Die zweite Ziffer vontdient als ¨Uber- trag f¨ur die n¨achste Berechnung, d.h. der folgende Algorithmus besteht aus zwei verschachtelten Schleifen, wobei die ¨außere Schleife die Teilprodukte bj·(an−1. . . a1a0)B berechnet.
Beispiel 26 SeiB = 10, a= (123)10 und b= (987)10, dann ist a·b= (121401)10, da sich mit Algorithmus 3 folgende Werte ergeben:
Algorithmus 3 : Multiplikation zweier nat¨urlicher Zahlen
Eingabe: Zwei Zahlena= (an−1. . . a1a0)B,b(bn−1. . . b1b0)B und die Anzahl der Ziffernn Ergebnis: Das Produktc= (c2·n−1. . . c1c0)B vona undb
/* Initalisiere das Ergebnisarray */
for(i= 0; i <2·n; i++) { c[i] = 0;
}
/* F¨uhre die eigentliche Multiplikation durch */
for(j= 0; j < n; j++) { carry = 0;
for (i= 0; i < n; i++) {
t=c[i+j] +a[i]·b[j] + carry;
c[i+j] =tmodB ; carry=bBtc;
}
c[i+n] = carry;
}
i j carry t c[0] c[1] c[2] c[3] c[4] c[5]
0 0 0 21 1 0 0 0 0 0
0 1 2 26 6 0 0 0 0 0
0 2 2 29 1 6 9 2 0 0
1 0 0 20 1 0 9 2 0 0
1 1 2 27 1 0 7 2 0 0
1 2 2 22 1 0 7 2 2 0
2 0 0 14 1 0 4 2 2 0
2 1 1 11 1 0 4 1 2 0
2 2 1 12 1 0 4 1 2 1
Bemerkung 27
• Algorithmus 3 ben¨otigt eine Funktion um zwei Ziffern der BasisB multiplizieren zu k¨onnen.
W¨ahlt man B = 232, so ist die evtl. in C nicht immer direkt m¨oglich (evtl. kein 64 Bit Datentyp auf 32 Bit Rechnern).
• Die Laufzeit dieses Algorithmus istO(n2). Es existiert ein asymptotisch schnellerer Multi- plikationsalgorithmus mitO(nlognlog logn), der die FFT (Fast Fourier Transformation) benutzt. Allerdings ist hier der Overhead (,die Konstante, die durch dieO-Notation ver- borgen wird) extrem groß. F¨ur kryptographische Zwecke ist deshalb der O(n2)-Algorithmus dennoch schneller. Evtl. kann die Karatsuba-Multiplikation mit O(nlog2n) = O(n1.58496) zum Einsatz kommen.
• Die Wahl der Basis hat starke Auswirkungen auf die Laufzeit. Sei die Laufzeit einer kon- kreten Implementierung c·n2, wobeic eine Konstante ist, dann ergibt sich im FallB = 232 f¨ur (an−1. . . a0)232 ·(bn−1. . . b0)232 eine Laufzeit von c ·n2. W¨ahlt man nun B = 216 so sind die beiden Zahlen in dieser Darstellung doppelt so lang, d.h. (a02·n−1. . . a00)216
bzw. (b02·n−1. . . b00)216, womit sich eine Laufzeit von c·(2n)2 = 4·c·n2 ergibt. D.h. das Verdoppeln der Anzahl der Bits der Basis verkleinert die Laufzeit auf ein Viertel.
2.2.3. Die Division
Im Vergleich zu den Algorithmen f¨ur Addition, Subtraktion und Multiplikation, erzeugt der Divisionsalgorithmus mit Abstand den gr¨oßten Implementierungsaufwand, was durch seine ver- gleichsweise komplexe Struktur bedingt ist.
Ab jetzt gehen wir davon aus, dass a > b. Wir suchen also einen Algorithmus der q und 0≤r < bbestimmt, sodass
a=q·b+r
gilt, d.h.q=bacundr =amodb. Es kann gezeigt werden, dasq undreindeutig bestimmt sind.
Definition 28 SeiB ≥2 eine beliebige Basis. Wir sagen eine Zahl c= (cn−1cn−2. . . c1c0)B ist normalisiert, wenncn−1 ≥ bB2c gilt.
Soll q = bac und r = amodb berechnet werden, dann k¨onnen a und b mit einer Zahl d so multipliziert werden, dassb normalisiert ist. Es gilt:
a = qb+r ad = qbd+rd,
d.h. durch die Normalisierung ¨andert sich q nicht und der berechnete Rest rdmuss noch durch d geteilt werden, um r zu enthalten. Ab jetzt gehen wir davon aus, dassb bei der Berechnung vonq =bacundr =amodbschon normalisiert ist, allerdings muss dann ber¨ucksichtigt werden, dass aevtl. eine Stelle l¨anger wird:
2n+ 1 Stellen
z }| {
(a2na2n−1. . . a0)B:
nStellen
z }| { (bn−1. . . b0)B=
nStellen
z }| {
(qn−1. . . q0)B und Rest
nStellen
z }| { (rn−1. . . r0).
Soll der klassische Divisionsalgorithmus durchf¨uhrt werden, so m¨ussen die verschiedenen qi be- rechnet oder geraten werden, um dann in jedem Schritt qi·b von a abziehen zu k¨onnen. Bei großen Basen ist es also sehr ineffizient qi durch Probieren aller M¨oglichkeiten zu ermitteln. Sei nun
ˆ
qi =def min
µ¹aj+nB+aj+n−1 bj−1
º
, B−1
¶
Satz 29 Seia= (anan−1. . . a0)B und b= (bn−1. . . b0)B, wobeib normalisiert, dann gilt bei der Durchf¨uhrung des Divisionsalgorithmus f¨ur qi,0≤i < n:
ˆ
qi−2≤qi≤qˆi
Beweis: Siehe [Knu98, Abschnitt 4.3.1, Theorem A und Theorem B]. # Beobachtung 30
• Die vorl¨aufige Ziffer qˆi unterscheidet sich, unabh¨angig von der Basis, maximal um2 von der wirklichen Ziffer qi und
• qˆi ist nie zu klein.
• Die Wahrscheinlichkeit, dassqˆi um 2zu groß ist, betr¨agt B2. Dies bedeutet aber auch, dass spezielle Tests der Software f¨ur diesen Fall ben¨otigt werden.
Mit Hilfe dieser Techniken ergibt sich Algorithmus 4.
Algorithmus 4 : Division zweier nat¨urlicher Zahlen
Eingabe: Zwei Zahlena0 = (a02n−1. . . a01a00)B,b0(b0n−1. . . b01b00)B und die Anzahl nder Ziffern des Divisors
Ergebnis: Der Quotientq= (qn−1. . . q1q0)B und der Restr = (rn−1. . . r1r0)B, so dass a0 =qb0+r
berechne den Normalisierungsfaktord;
(a2n. . . a1a0)B=a0·d;
(bn−1. . . b1b0)B=b0·d;
for(i≤n; i≤0; i++) { ˆ
q = min(bai+nB+ab i+n−1
n−1 c, B−1);
sei aneu= (ai+n. . . ai)B−qˆ·(bn−1. . . b0)B;
/* qˆ zu groß */
if (aneu<0) {
aneu=aneu+ (bn−1. . . b0)B; ˆ
q–;
}
/* qˆ immer noch zu groß (sehr selten) */
if (aneu<0) {
aneu=aneu+ (bn−1. . . b0)B; ˆ
q–;
}
ersetze (ai+n. . . ai) durch aneu; qi= ˆq;
}
denormalisierer;
returnr undq;
Beispiel 31 SeiB = 10undn= 3. Wir dividieren723604 durch203. Es ergeben mit Hilfe von Algorithmus 4 die folgenden Zwischenwerte:
i a6 a5 a4 a3 a2 a1 a0 b2 b1 b0 qˆ q3 q2 q1 q0 qbˆ
− 0 7 2 3 6 0 4 2 0 3 − − − − − −
− 2 8 9 4 4 1 6 8 1 2 − − − − − −
3 2 4 3 6 4 1 6 8 1 2 28/8 = 3 − − − − 3·812 = 2436
3 0 4 5 8 4 1 6 8 1 2 − 3 − − − −
2 0 4 0 6 0 1 6 8 1 2 45/8 = 5 3 − − − 5·812 = 4060
2 0 0 5 2 4 1 6 8 1 2 − 3 5 − − −
1 0 0 4 8 7 2 6 8 1 2 52/8 = 6 3 5 − − 6·812 = 4872
1 0 0 0 3 6 9 6 8 1 2 − 3 5 6 − −
0 0 0 0 3 2 4 8 8 1 2 36/8 = 4 3 5 6 − 4·812 = 3248
0 0 0 0 0 4 4 8 8 1 2 − 3 5 6 4 −
− 0 0 0 0 1 1 2 8 1 2 − 3 5 6 4 −
Somit erhalten wir den Quotienten q = (3564)10 und den Restr = (0112)10
Damit zeigt sich, dass effiziente Algorithmen f¨ur die Addition, Subtraktion, Multiplikation und Division von nat¨urlichen bzw. ganzen Zahlen existieren. Ein Algorithmus heißt dabei effizient, wenn seine Laufzeit durch ein Polynom p(n) beschr¨ankt ist, wobei n die Anzahl der Bits ist,
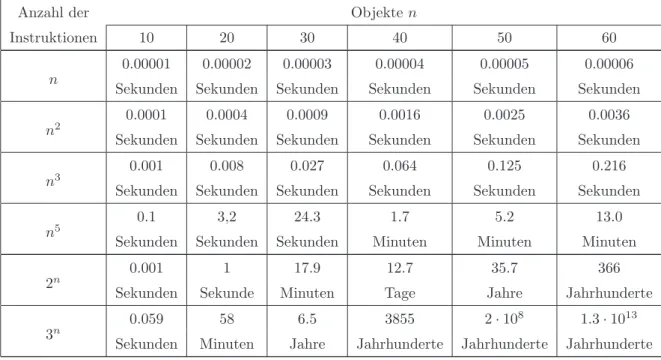
Anzahl der Objekte n
Instruktionen 10 20 30 40 50 60
0.00001 0.00002 0.00003 0.00004 0.00005 0.00006 n Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden
0.0001 0.0004 0.0009 0.0016 0.0025 0.0036
n2
Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden
0.001 0.008 0.027 0.064 0.125 0.216
n3
Sekunden Sekunden Sekunden Sekunden Sekunden Sekunden
0.1 3,2 24.3 1.7 5.2 13.0
n5
Sekunden Sekunden Sekunden Minuten Minuten Minuten
0.001 1 17.9 12.7 35.7 366
2n
Sekunden Sekunde Minuten Tage Jahre Jahrhunderte
0.059 58 6.5 3855 2·108 1.3·1013
3n
Sekunden Minuten Jahre Jahrhunderte Jahrhunderte Jahrhunderte
Abbildung 6: Rechenzeitbedarf von Algorithmen auf einem
”1-MIPS“-Rechner
die gebraucht werden, um die Eingabe zu kodieren (siehe Abbildung 6). Es ergeben sich die folgenden Laufzeiten f¨ur die klassischen Algorithmen:
• Addition / Subtraktion:O(n)
• Multiplikation / Division:O(n2) mit der
”Schulmethode“
2.3. Die Exponentiation
Offensichtlich ist die triviale Methodeab=a|·a·a{z·. . .·a}
b−mal
zu langsam, denn dieser Algorithmus braucht O(2n) Multiplikationen. Dies ist also kein effizienter Algorithmus. Die folgende Idee f¨uhrt zum Ziel: F¨ur a2n berechne
à . . .³¡
a2¢2´···!2 ,
wobei genau n-mal quadriert wird. D.h. f¨ur a16 ben¨otigen wir nur 4 Multiplikationen statt 16 Multiplikationen bei der naiven Methode.
Es stellt sich die Frage, wie wir dieses Vorgehen f¨ur Zahlen anwenden, die keine Zweierpotenz sind. Da jede nat¨urliche Zahl als Summe von Zweierpotenzen (Bin¨ardarstellung) geschrieben werden kann, ergibt sich f¨ur e∈N:
e = 2n−1en−1+ 2n−2en−2+· · ·+ 21e1+ 20e0, miten−1 = 1
= (2n−2en−1+ 2n−3en−2+· · ·+ 20e1)·2 +e0 ... (vergleiche”Horner-Schema“)
= (. . .((2en−1+en−2)·2 +en−3)·2 +. . .+e1)·2 +e0,
Algorithmus 5 : Exponentiation zweier nat¨urlicher Zahlen Eingabe: Zwei Zahlenx= (xn−1. . . x1x0)B,e= (en−1. . . e1e0)B Ergebnis:xe
/* Initalisiere tempor¨are Variable */
y=x;
/* Arbeite alle Bits der Bin¨ardarstellung von e ab */
for(i= BitLength(e)−2; i≥0; i–) { y=y2·xBit(e,i);
}
returny;
Dann ergibt sich
xe = x(...((2en−1+en−2)·2+en−3)·2+···+e1)·2+e0
= ¡
x(...((2en−1+en−2)·2+en−3)·2+···+e1)¢2
·xe0 ... (miten−1 = 1)
= µ
. . .³¡
x2·xen−2¢2
·xen−3
´2
·. . .
¶2
·xe0.
D.h. wir ben¨otigen n−1 Schritte, umxe zu berechnen. Diese Methode zur Potenzierung heißt
”Repeated square-and-multiply“ (siehe Algorithmus 5). Offensichtlich betr¨agt die Laufzeit von Algorithmus 5 dann O(n3).
3. Public-Key Kryptographie
Die Grundlage der Public-Key Kryptographie ist die Idee, einen ¨offentlichen Verschl¨usselungs- schl¨ussel (im”Telefonbuch“) und einen geheimen Entschl¨usselungsschl¨ussel zu verwenden. Dabei soll es unm¨oglich sein, aus dem ¨offentlichen Schl¨ussel den privaten Schl¨ussel zu berechnen, und es darf nur mit Hilfe des geheimen Schl¨ussels m¨oglich sein, die Nachricht zu entschl¨usseln.
Funktionen, bei denen es (praktisch) unm¨oglich ist, aus dem Bild das Urbild zu berechnen, nennt man Einwegfunktionen (engl. one-way functions). Kann man das Urbild mit Hilfe ei- nes Geheimnisses doch (effizient) berechnen, so nennt man eine solche Einwegfunktion auch Trapdoor-Funktion. Solche Funktionen suchen wir, um Public-key Kryptographie betreiben zu k¨onnen.
Da viele bekannte Public-Key Kryptosysteme Ergebnisse aus der Algebra und Zahlentheorie verwenden, m¨ussen/d¨urfen wir Mathematik betreiben.
3.1. Einige Grundlagen aus der elementaren Zahlentheorie
Zist das Symbol f¨ur die geordnete Menge{. . . ,−3,−2,−1,0,1,2,3, . . .}derganzen Zahlen und N das Symbol f¨ur die Menge dernat¨urlichen Zahlen {0,1,2,3, . . .}.
Bekannt ist, dass Z mit der normalen Zahlenaddition und -multiplikation ein kommutativer Ring mit Einselement ist.
3.1.1. Der gr¨oßte gemeinsame Teiler
Definition 32 Wir sagen a teilt n (kurz:a|n), wenn es eine ganze Zahlb gibt mit n=a·b.
Teilt anicht n, so schreibt man kurz a-n.
Satz 33 Seien a, b, c∈Z, dann gilt: