All order α ′ -expansion of superstring trees from the Drinfeld associator
Volltext
Abbildung
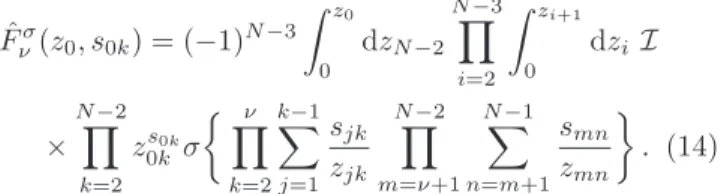
ÄHNLICHE DOKUMENTE
компоненты, что и теория предприятия (см. Остальные компоненты описания теории требуют специального рассмотрения. В качестве примера следствий из данной
компоненты, что и теория предприятия (см. Остальные компоненты описания теории требуют специального рассмотрения. В качестве примера следствий из данной
Previous articles determined the image of the absolute Galois group of K up to commensurability in its action on all prime-to-p 0 torsion points of ϕ, or equivalently, on the
We study a certain compactification of the Drinfeld period domain over a finite field which arises naturally in the context of Drinfeld moduli spaces.. Its boundary is a disjoint
R¨ utsche: Absolute Irreducibility of the Residual Representation and Adelic Openness in generic characteristic for Drinfeld modules, Diss.. Serre: Abelian ℓ-adic representations
Traulsen, Galois representations associated to Drinfeld modules in special characteristic and the isogeny conjecture for
Thus Proposition 6.5 implies that up to scalar multiples there exists exactly one G der -equivariant endomorphism of V ⊗2 of rank 1.. Moreover, again by Proposition 6.5 the same
Парадигмой этой теории должен стать нормоцентрический подход, трактующий такие аномалии не как девиации, а как вариации нормы, что позволяет отказаться от