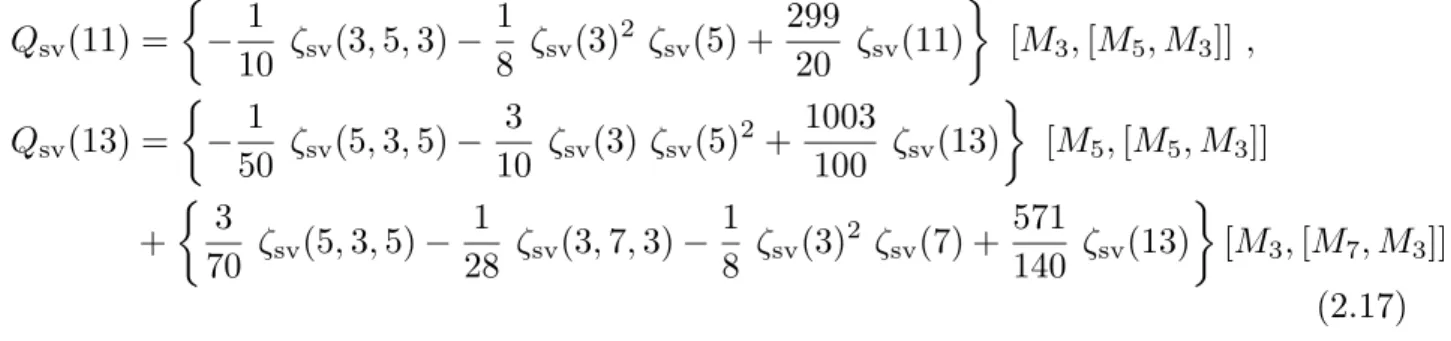Closed Superstring Amplitudes, Single–Valued Multiple Zeta Values and Deligne Associator

MPP–2013–278

Closed Superstring Amplitudes, Single–Valued Multiple Zeta Values and Deligne Associator

S. Stieberger

Max–Planck–Institut f¨ ur Physik

Werner–Heisenberg–Institut, 80805 M¨ unchen, Germany

Abstract

We revisit the tree–level closed superstring amplitude and identify its α

–expansion as

series with single–valued multiple zeta values as coefficients. The latter represent a subclass

of multiple zeta values originating from harmonic polylogarithms at unity. Moreover, in

terms of a non–commutative Hopf algebra the closed superstring amplitude can be cast

into the same algebraic form as the open superstring amplitude: the closed superstring

amplitude essentially is the single–valued version of the open superstring amplitude. This

fact points into a deeper connection between gauge and gravity amplitudes than what is

implied by Kawai–Lewellen–Tye relations. Finally, we give an explicit representation of

the Deligne associator in terms of beta functions modulo squares of commutators of the

underlying Lie algebra. This form of the associator can be interpreted as the four–point

closed superstring amplitude.

1. Introduction

During the last years a great deal of work has been addressed to the problem of re- vealing and understanding the hidden mathematical structures of scattering amplitudes in both field– and string theory, for a recent review cf. [1]. Particular emphasis on the underlying algebraic structure of amplitudes seems to be especially fruitful and might eventually yield an alternative way of constructing perturbative amplitudes by methods residing in arithmetic algebraic geometry. In particular, studying motivic aspects of am- plitudes has dramatically changed our view of how to write amplitudes in terms of simple objects, cf. [2] for an early and [3] for a recent reference. Although motivic amplitudes seem to be mathematically more complicated, they are much more structured, organized and canonical objects.

In perturbative string theory, it is the dependence on the inverse string tension α

, i.e.

the nature of the underlying string world–sheet describing the string interactions, which provides an extensive and rich structure in the analytic expressions of the amplitudes.

Some of the motivic concepts have recently matured in describing tree–level superstring amplitudes [4]. By passing from the multiple zeta values (MZVs) entering as coefficients in the α

–expansion of the amplitude to their motivic versions [2,5] and then mapping the latter to elements of a Hopf algebra reveals the motivic structure of the superstring amplitude. In this way the motivic superstring amplitude becomes a rather simple and well organized object. At the same time it is completely insensitive to a change of the basis of the underlying MZVs.

Perturbative gauge and gravity amplitudes in string theory seem to be rather different due to the unequal world–sheet topology of open and closed strings. Although in prac- tice some properties of scattering amplitudes in both gauge and gravity theories suggest a deeper relation originating from string theory, it is not clear how and whether more symmetries or analogies between open and closed string amplitudes can be found. Finding more similarities between the latter is one aim of this article.

In Ref. [4] the closed superstring tree–level amplitude has been given in terms of a Hopf algebra structure and it has been observed, that in contrast to the open string case only MZVs of a special class show up in its α

–expansion. In Section 2 we revisit the tree–level closed superstring amplitude and identify the coefficients of its power series in α

as single–valued multiple zeta values (SVMZVs). The latter represent a subclass of MZVs originating from single–valued harmonic polylogarithms (SVMPs) at unity [6,7]. In his recent work [8] Brown has introduced the map sv, which maps the algebra of non–

commutative words describing the open superstring amplitude to a smaller subalgebra,

which describes the space of SVMZVs. In Section 3 we find, that the closed superstring

amplitude essentially follows from the open superstring amplitude by applying this map sv.

The Drinfeld associator [9,10], which is an infinite series in two non–commutative variables with coefficients being MZVs, has been argued to be the generating function of the open superstring amplitudes [11,12]. In Section 4 we identify the Deligne associator [13], which has SVMZVs as coefficients in its series, to be the relevant object describing closed su- perstring amplitudes. More precisely, we give an explicit representation of the Deligne associator in terms of beta functions modulo squares of commutators of the underlying Lie algebra and this form can be interpreted as the four–point closed superstring amplitude.

Finally, in Section 5 we give some concluding remarks.

2. Closed superstring amplitudes and single–valued multiple zeta values

In this Section we want to illuminate the observations on the α

–expansion of the graviton amplitude [4] in view of Browns recent work on SVMZVs [8].

The string world–sheet describing the tree–level string S–matrix of N gravitons has the topology of a complex sphere with N insertions of graviton vertex operators. Of the latter N − 3 are integrated on the whole sphere leading to the following type of complex

integrals 

 

N Y

j =2

Z

z

d ² z j



  Y

1≤i<j≤N

|z i − z j | ^s

(z j − z i ) ⁿ

, (2.1)

with z ₁ = 0, z N

= 1, z N = ∞, the set of integers n ij ∈ Z and the real numbers s ij = α

(k i + k j ) ² = 2α

k i k j . The latter describe the ¹ ₂ N (N − 3) independent kinematic invariants of the scattering process involving N external momenta k i , i = 1, . . . , N and α

is the inverse string tension. The integrals (2.1) can be considered as iterated integrals on P ¹ \{0, 1, ∞} integrated independently on all choices of paths.

One of the key properties of graviton amplitudes in string theory is that at tree–level they can be expressed as sum over squares of (color ordered) gauge amplitudes in the left–

and right–moving sectors. This map, known as Kawai–Lewellen–Tye (KLT) relations [14], gives a relation between a closed string tree–level amplitude M involving N closed strings and a sum of squares of (partial ordered) open string tree–level amplitudes. We may write these relations in matrix notation as follows

M(1, . . . , N ) = A ^t S A , (2.2)

with the vector A encoding a basis of (N − 3)! open string subamplitudes and some

(N −3)! ×(N −3)! intersection matrix S. The KLT relations are insensitive to the compact-

ification details or the amount of supersymmetries of the superstring background. Hence,

the following discussions and results on N –graviton tree–level scattering are completely general. In the following let us first review some aspects of open superstring amplitudes A.

Tree–level scattering of N open strings involves (N − 3)! independent color ordered subamplitudes [15,16]. The latter can be collected in an (N − 3)!–dimensional vector A, which can be expressed as [4]

A = F A , (2.3)

with the (N − 3)!–dimensional vector A encoding the Yang–Mills basis and the period matrix F , given by ¹

F = P Q : exp

 

 X

n

ζ ₂ n +1 M ₂ n +1

 

 : , (2.4)

with the (N − 3)! × (N − 3)! matrices P = 1 + X

n

ζ ₂ ⁿ P ₂ n , P ₂ n = F | _ζ

2

, M ₂ n +1 = F | _ζ

,

(2.5)

and:

Q := 1 + X

n

Q n = 1 + 1

5 ζ _3,5 [M ₅ , M ₃ ] + 3

14 ζ ₅ ² + 1 14 ζ _3,7

[M ₇ , M ₃ ] +

9 ζ ₂ ζ ₉ + 6

25 ζ ₂ ² ζ ₇ − 4

35 ζ ₂ ³ ζ ₅ + 1 5 ζ ₃ , 3 , 5

[M ₃ , [M ₅ , M ₃ ]] + . . . . (2.6) Above we have have adapted to the following definition of MZVs

ζ n

,...,n

:= ζ(n 1 , . . . , n r ) = X

0<k

<...<k

Y r l=1

k _l

ⁿ

, n l ∈ N ⁺ , n r ≥ 2 , (2.7)

with r specifying the depth and w = P r

l =1 n l denoting the weight of the MZV ζ n

,...,n

. Furthermore, we have used the MZV basis constructed in [17]. Note, that for any N the tree–level open superstring amplitude assumes the form (2.3) with (2.4). The only ingre- dients are the (N − 3)! × (N − 3)! matrices P _2n and M _2n+1 , whose entries are polynomials in degree 2n and 2n + 1 in the kinematic invariants s ij , respectively. The matrices P _2n and

1 The ordering colons : . . . : are defined such that matrices with larger subscript multiply ma- trices with smaller subscript from the left, i.e. : M

M

:=

M

M

, i ≥ j ,

M

M

, i < j . The generalization

to iterated matrix products : M

M

. . . M

: is straightforward.

M 2n+1 have been thoroughly investigated in [18]. Moreover, the form of the expressions (2.4), (2.5) and (2.6) is bolstered by the algebraic structure of motivic MZVs and their decomposition [5]. In fact, the operator F is isomorphic to the decomposition operator of motivic MZVs [4].

Applying the open string results (2.4) to the graviton amplitude (2.2) gives rise to [4]:

M = A ^t G A , (2.8)

with the matrix ² G = F ^t S F = S ₀



exp

 

 X

r

+1

ζ r M _r ^t

 







t

Q Q e exp

 

 X

s

+1

ζ s M s

 

 , (2.9) and the intersection form S 0 defined by:

S ₀ = P ^t S P . (2.10)

An other interpretation of S ₀ is, that it makes sure, that the field–theory limit of the graviton amplitude (2.8) is correctly reproduced: M(1, . . . , N )| _α

= A ^t S 0 A, i.e.

G| _α

= S ₀ .

It has already been observed in [4] (extending the results [19]), that one implication of the specific form of (2.9) is, that only a certain subclass of MZVs appears in the α

– expansion of the graviton amplitude (2.8). In fact, in Eq. (2.9) the product QQ e is given by [4]

Q Q e = 1 + 2 Q ₁₁ + 2 Q ₁₃ + 2 Q ₁₅ + . . . , (2.11) with Q e = Q |

(r)→(−1)^r+1Q(r)

and Q _(r) any nested commutator of depth r appearing in (2.6). As a consequence the product (2.11) is free of odd powers in even depth commutators Q _(2n) . Furthermore, the specific form of (2.9) involves, that MZVs of even weight or depth

≥ 2 only enter through the product (2.11) starting at weight w = 11 [4].

The subclass of MZVs appearing in (2.9) can be identified as single–valued multiple zeta values

ζ _sv (n ₁ , . . . , n r ) ∈ R (2.12) originating from single–valued multiple polylogarithms at unity and studied recently in [8]

from a mathematical point of view. Let us now illuminate (2.9) in view of this subclass of

2 Note, that the transpositions involved in the expression : exp P

r

ζ

M

:

lead to a reversal of the matrix multiplication order compared to the ordered product : exp P

s

ζ

M

: without transposition, i.e. : : exp P

r∈2N⁺+1

ζ

M

:

= 1 + ζ

M

+ ζ

M

+

ζ

M

+ ζ

M

+

ζ

ζ

M

M

+

ζ

M

+ ζ

M

+

ζ

M

+ ζ

ζ

M

M

+

ζ

ζ

M

M

+ ζ

M

+ . . . .

MZVs. The numbers (2.12) satisfy the same double shuffle and associator relations than the usual MZVs and many more relations [8]:

ζ _sv (2) = 0 ,

ζ sv (2n + 1) = 2 ζ 2n+1 , n ≥ 1 . (2.13) Furthermore, for instance we have:

ζ _sv (3, 5) = −10 ζ ₃ ζ ₅ ,

ζ sv (3, 7) = −28 ζ 3 ζ 7 − 12 ζ ₅ ² ,

ζ _sv (3, 3, 5) = 2 ζ ₃ , 3 , 5 − 5 ζ ₃ ² ζ ₅ + 90 ζ ₂ ζ ₉ + 12

5 ζ ₂ ² ζ ₇ − 8

7 ζ ₂ ³ ζ ₅ ² , (2.14) ζ _sv (3, 5, 5) = 2 ζ ₃ , 5 , 5 + 10 ζ ₅ ζ ₃ , 5 + 50 ζ ₃ ζ ₅ ² + 275 ζ ₂ ζ ₁₁ + 20 ζ ₂ ² ζ ₉ ,

ζ _sv (3, 3, 7) = 2 ζ ₃ , 3 , 7 + 12 ζ ₅ ζ ₃ , 5 + 14 ζ ₃ ² ζ ₇ + 60 ζ ₃ ζ ₅ ² + 407 ζ ₂ ζ ₁₁ + 112

5 ζ ₂ ² ζ ₉ − 64 35 ζ ₂ ³ ζ ₇ . The matrix (2.9) can be written purely in terms of SVMZVs (2.12) as follows:

G = S ₀ 1 + ζ _sv (3) M ₃ + ζ _sv (5) M ₅ + 1

2 ζ _sv (3) ² M ₃ ² + ζ _sv (7) M ₇ + 1

2 ζ _sv (3) ζ _sv (5) {M ₃ , M ₅ } + ζ _sv (9) M ₉ + 1

3! ζ _sv (3) ³ M ₃ ³ + 1

2 ζ _sv (5) ² M ₅ ² + 1

2 ζ _sv (3) ζ _sv (7) {M ₃ , M ₇ } + Q sv (11) + ζ sv (11) M 11 + 1

8 ζ sv (3) ² ζ sv (5) {M 3 , {M 3 , M 5 }}

+ 1

4! ζ _sv (3) ⁴ M ₃ ⁴ + 1

2 ζ _sv (3) ζ _sv (9) {M ₃ , M ₉ } + 1

2 ζ _sv (5) ζ _sv (7) {M ₅ , M ₇ } + Q _sv (13) + ζ _sv (13) M ₁₃ (2.15) + 1

8 ζ _sv (3) ² ζ _sv (7) {M ₃ , {M ₃ , M ₇ }} + 1

4 ζ _sv (3) ζ _sv (5) ² {M ₃ , M ₅ ² } + 1

2 ζ _sv (3) {M ₃ , Q _sv (11)} + 1

2 ζ _sv (7) ² M ₇ ² + 1

2 ζ _sv (3) ζ _sv (11) {M ₃ , M ₁₁ } + 1

2 ζ _sv (5) ζ _sv (9) {M ₅ , M ₉ } + 1

48 ζ _sv (3) ³ ζ _sv (5) {M ₃ , {M ₃ , {M ₃ , M ₅ }}} + . . . , with:

Q sv (11) = 1

5 ζ sv (3, 3, 5) + 1

8 ζ sv (3) ² ζ sv (5)

[M 3 , [M 5 , M 3 ]] , Q _sv (13) =

1

25 ζ _sv (3, 5, 5) − 1

4 ζ _sv (3) ζ _sv (5) ²

[M ₅ , [M ₅ , M ₃ ]] (2.16) +

1

14 ζ _sv (3, 3, 7) − 3

35 ζ _sv (3, 5, 5) − 1

16 ζ _sv (3) ² ζ _sv (7)

[M ₃ , [M ₇ , M ₃ ]] .

Note, that in (2.15) the terms (2.11) containing MZVs of even weight or depth ≥ 2 comprise into the expressions Q sv (n), which can be written purely in terms of SVMZVs.

A different representation in terms of the SVMZV basis chosen in [8] gives:

Q sv (11) =

− 1

10 ζ sv (3, 5, 3) − 1

8 ζ sv (3) ² ζ sv (5) + 299

20 ζ sv (11)

[M 3 , [M 5 , M 3 ]] , Q _sv (13) =

− 1

50 ζ _sv (5, 3, 5) − 3

10 ζ _sv (3) ζ _sv (5) ² + 1003

100 ζ _sv (13)

[M ₅ , [M ₅ , M ₃ ]]

+ 3

70 ζ _sv (5, 3, 5) − 1

28 ζ _sv (3, 7, 3) − 1

8 ζ _sv (3) ² ζ _sv (7) + 571

140 ζ _sv (13)

[M ₃ , [M ₇ , M ₃ ]].

(2.17)

3. Motivic open and closed superstring amplitudes

In this Section we find a striking similarity between the open superstring amplitude A and the closed superstring amplitude M thus giving a new relation between gauge and gravity amplitudes at the level of the underlying Hopf algebra.

Motivic MZVs ζ ^m are defined as elements of a certain algebra H = L

w≥0 H w over Q, which is graded for the weight and equipped with the period homomorphism per : H → R, which maps ζ _n ^m

_,...,n

to ζ n

,...,n

, i.e. per(ζ _n ^m

_,...,n

) = ζ n

,...,n

. The motivic versions of the SVMZVs (2.12) have been defined in [8] and are denoted by ζ _sv ^m (n ₁ , . . . , n r ). The latter satisfy all motivic relations of MZVs and ζ _sv ^m (2) = 0 [8]. The motivic SVMZVs span a subalgebra H ^sv ⊂ H. There exist a homomorphism H → H ^sv , which maps each ζ _n ^m

_,...,n

to ζ _sv ^m (n 1 , . . . , n r ).

A list of generators of H ^sv _w up to weight w = 14 is collected in Tables 1–2 below.

w 2 3 4 5 6 7 8 9 10

H

− ζ

(3) − ζ

(5) ζ

(3)

ζ

(7) ζ

(3) ζ

(5) ζ

(9) ζ

(5)

ζ

(3)

ζ

(3) ζ

(7)

dim(H

) 0 1 0 1 1 1 1 2 2

Table 1: Generators of H

for 2 ≤ w ≤ 10 .

w 11 12 13 14

H

ζ

(11) ζ

(3) ζ

(9) ζ

(13) ζ

(3) ζ

(3, 3, 5) ζ

(3, 3, 5) ζ

(5) ζ

(7) ζ

(3, 5, 5) ζ

(3)

ζ

(5) ζ

(3)

ζ

(5) ζ

(3)

ζ

(3, 3, 7) ζ

(7)

ζ

(3)

ζ

(7) ζ

(3) ζ

(11) ζ

(3) ζ

(5)

ζ

(5) ζ

(9)

dim(H

) 3 3 5 5

Table 2: Generators of H

for 11 ≤ w ≤ 14 .

Note, that the generators of Tables 1–2 are those, which appear in (2.15), subject to the period map per.

To explicitly describe the structure of the algebra H Brown has introduced an auxiliary algebra U , the (trivial) algebra–comodule [5]:

U = Qhf ₃ , f ₅ , . . .i ⊗

Q[f ₂ ] . (3.1) The first factor U

= U

f ₂ U is a cofree Hopf–algebra on the cogenerators f _2r+1 in degree 2r + 1 ≥ 3, whose basis consists of all non–commutative words in the f _2i+1 . The multipli- cation on U

is given by the shuffle product III . The Hopf–algebra U

is the algebra of all words constructed from the alphabet {f ₃ , f ₅ , f ₇ , . . .} and is isomorphic to the space of non–

commutative polynomials in f _2i+1 . The element f ₂ commutes with all f _2r+1 . Again, there is a grading U k on U and we have the non–canonical isomorphism: H ≃ U . Furthermore, there exists a morphism φ of graded algebra–comodules

φ : H −→ U , (3.2)

normalized by:

φ ζ _n ^m

= f n , n ≥ 2 . (3.3)

The map (3.2), which respects the shuffle multiplication rule

φ(x 1 x 2 ) = φ(x 1 ) III φ(x 2 ) , x 1 , x 2 ∈ H , (3.4) sends every motivic MZV to a non–commutative polynomial in the f i .

The motivic period matrix F ^m , where all MZVs ζ n

,...,n

are replaced by their motivic objects ζ _n ^m

_,...,n

, has been introduced and studied in [4]. Furthermore, in this reference the map of F ^m under φ has been computed, with the result:

φ(F ^m ) = X

k=0

f ₂ ^k P 2k

! 

  X

p =0

X

i1,...,ip

∈2N++1

f i

f i

. . . f i

M i

. . . M i

M i



  . (3.5)

Furthermore, in [4] the motivic version of G ^m has been introduced and an expression for φ(G ^m ) has been given. We want to rewrite the latter in view of the recent work of Brown [8] and eventually find a striking similarity between φ(F ^m ) and φ(G ^m ).

Similar to the construction of U in Ref. [8] Brown has introduced a model U ^sv for H ^sv via the the homomorphism

sv : U

−→ U

, (3.6)

with

w 7−→ X

uv=w

u III e v , (3.7)

and e v being the reversal of the word v. For the image U ^sv under (3.6) we have the isomorphism: H ^sv ≃ U ^sv . For instance we have [8]

sv(f a ) = 2f a , sv(f a f b ) = 2 (f a f b + f b f a ) , sv(f a f b f c ) = 2 (f a f b f c + f a f c f b + f c f a f b + f c f b f a ) , sv(f a f b f c f d ) = 2 (f a f b f c f d + f a f b f d f c + f a f d f b f c + f a f d f c f b

+ f d f a f b f c + f d f a f c f b + f d f c f a f b + f d f c f b f a ) ,

(3.8)

for the odd integers a, b, c, d. Evidently, we can extend the map (3.6) to U with:

sv(f ₂ ) = 0 . (3.9)

Let us now return to the matrix G, given in (2.9) and (2.15) and compute the image φ(G ^m ). The latter has been given in [4] as:

φ(G ^m ) = S 0



  X

p =0

X

i1,...,ip

∈2N+ +1

M i

M i

. . . M i

X p k=0

f i

f i

. . . f i

III f i

f i

. . . f i



  .

(3.10) By making profit out of the map (3.6) and using relations like (3.8) we can cast (3.10) into the compact form:

φ(G ^m ) = S 0



  X

p=0

X

i1,...,ip

∈2N+ +1

M i

M i

. . . M i

sv(f i

f i

. . . f i

)



  . (3.11)

After comparing (3.11) with (3.5) and using (3.9) we find:

φ(G ^m ) = S ₀ sv(φ(F ^m )) . (3.12)

Finally, due to (3.12) the motivic open superstring amplitude A ^m

φ(A ^m ) = X

k=0

f ₂ ^k P _2k

! 

  X

p=0

X

i1,...,ip

∈2N+ +1

f i

. . . f i

M i

. . . M i



  A , (3.13)

and the motivic closed superstring amplitude M ^m

φ(M ^m ) = A ^t S ₀



  X

p=0

X

i1,...,ip

∈2N+ +1

M i

. . . M i

sv(f i

. . . f i

)



  A , (3.14)

respectively, can be related as follows:

φ(M ^m ) = A ^t S ₀ sv(φ(A ^m )) , (3.15) with the intersection matrix S ₀ defined in (2.10) and the vector A of Yang–Mills sub- amplitudes introduced in (2.3). Note, that the map φ can be inverted. Hence, not any information on the motivic amplitudes A ^m or M ^m is lost by considering the objects φ(A ^m ) and φ(M ^m ) and the full superstring amplitudes (2.3) and (2.8) can be recovered from the images φ(A ^m ) and φ(M ^m ), respectively.

To conclude, the image (3.5) of the motivic period matrix F ^m under φ is the uniform form for both the open and closed superstring amplitude.

4. Deligne associator and closed superstring amplitudes

In his recent work [8] Brown has identified SVMZVs as elements of the Deligne associ- ator [13], i.e. the coefficients of the latter are the values of SVMPs at one. In this Section we give an explicit representation of the Deligne associator in terms of beta functions mod- ulo squares of commutators of the underlying Lie algebra. This form of the associator can be interpreted as the four–point closed superstring amplitude and also allows to extract the form of the N –point closed superstring amplitude.

The unique solution to the KZ equation ³ [20]

d

dz L e

,e

(z) = L e

,e

(z) e 0

z + e 1

1 − z

, (4.1)

3 Partial differential equations based on Lie algebras appear in the context of conformal field

theory.

with the generators e 0 and e 1 of the free Lie algebra g can be be given as generating series of multiple polylogarithms as [6]

L e

,e

(z) = X

w∈{e

,e

L w (z) w , (4.2)

with the symbol w ∈ {e ₀ , e ₁ }

denoting a non–commutative word w ₁ w ₂ . . . in the letters w i ∈ {e ₀ , e ₁ }.

The generating series of SVMPs is defined by [6]

L e

,e

(z) = L

_,−e

(z)

L e

,e

(z) , (4.3) where e

₁ is determined recursively by the following fixed–point equation

Z(−e ₀ , −e

₁ ) e

₁ Z (−e ₀ , −e

₁ )

= Z (e ₀ , e ₁ ) e ₁ Z (e ₀ , e ₁ )

, (4.4) with the Drinfeld associator L e

,e

(1) ≡ Z(e ₀ , e ₁ ). The latter is given by the non–

commutative generating series of (shuffle-regularized) MZVs [21]

Z (e ₀ , e ₁ ) = X

w

e

,e

ζ(w) w = 1 + ζ ₂ [e ₀ , e ₁ ] + ζ ₃ ([e ₀ , [e ₀ , e ₁ ]] − [e ₁ , [e ₀ , e ₁ ])

+ ζ 4

[e 0 , [e 0 , [e 0 , e 1 ]]] − 1

4 [e 0 , [e 1 , [e 0 , e 1 ]]] + [e 1 , [e 1 , [e 0 , e 1 ]]] − 5

4 [e 0 , e 1 ] ²

+ . . . , (4.5) with ζ (e ₁ e ⁿ ₀

. . . e ₁ e ⁿ ₀

) = ζ n

,...,n

, the shuffle product ζ(w ₁ )ζ (w ₂ ) = ζ(w _{1 III} w ₂ ) and ζ(e ₀ ) = 0 = ζ(e ₁ ).

The Deligne canonical associator W is related to the Drinfeld associator Z through the following equation [8]

W ◦ ^σ Z = Z , (4.6)

with the Ihara action ◦ and the anti–linear map σ : Che 0 , e 1 i → Che 0 , e 1 i with σ(e i ) 7→ −e i . The equation (4.6) can be solved recursively in length of words as [8]:

W (e 0 , e 1 ) = ^σ Z (e 0 , W e 1 W

)

Z(e 0 , e 1 ) . (4.7) The unique solution to (4.4) is e

₁ = W e 1 W

. As a consequence, Eqs. (4.3) and (4.7) allow to express the Deligne associator W as [8]:

L(1) = W (e 0 , e 1 ) = Z (−e 0 , −e

₁ )

Z(e 0 , e 1 ) . (4.8) In analogy to the motivic version of the Drinfeld associator (4.5)

Z ^m (e 0 , e 1 ) = X

w∈{e

,e

ζ ^m (w) w (4.9)

in Ref. [8] Brown has given the motivic single–valued associator as a generating series W ^m (e 0 , e 1 ) = X

w∈{e

,e

ζ _sv ^m (w) w , (4.10)

whose period map per gives the Deligne associator W (e ₀ , e ₁ ). Note, that the motivic SVMZVs ζ _sv ^m (w) satisfy the same double shuffle and associator relations than the motivic MZVs ζ ^m (w). Hence, in a first step we can work out the sum (4.10) in the same way as (4.9) by applying various shuffle and associator relations, in the second step we replace the symbols ζ ^m (w) by ζ _sv ^m (w). Finally, in the last step the latter are replaced thanks to relations such as (the motivic versions of) (2.13) and (2.14). As a result we obtain:

W ^m (e ₀ , e ₁ ) = 1 + 2 ζ ₃ ^m ([e ₀ , [e ₀ , e ₁ ]] − [e ₁ , [e ₀ , e ₁ ]) + 2 ζ ₅ ^m

[e ₀ , [e ₀ , [e ₀ , [e ₀ , e ₁ ]]]]

− 1

2 [e 0 , [e 0 , [e 1 , [e 0 , e 1 ]]]] − 3

2 [e 1 , [e 0 , [e 0 , [e 0 , e 1 ]]]] + (e 0 ↔ e 1 )

+ . . . . (4.11) The associator Z is group–like. Therefore, its logarithm ln Z can be expressed as a Lie series in the elements e ₀ and e ₁ . Due to Drinfeld we have [10]

ln Z (e ₀ , e ₁ ) = X

k,l

z kl u kl mod g

, (4.12)

with (ad x y = [x, y])

u kl = (−1) ^k ad ^k−1 _e

ad ^l−1 _e

[e ₀ , e ₁ ] , (4.13) and g

= [[g, g], [g, g]] the second commutant of the Lie algebra g. The coefficients z kl are extracted from the generating function

Γ(1 − u) Γ(1 − v)

Γ(1 − u − v) = 1 + X

k,l≥1

z kl u ^k v ^l

= 1 − ζ ₂ u v − ζ ₃ u v(u + v) − 2

5 ζ ₂ ² u v(u ² + 1

4 uv + v ² ) + . . . , (4.14) which in turn gives rise to

ln Z(e ₀ , e ₁ ) = −(uv)

Γ(1 − u) Γ(1 − v) Γ(1 − u − v) − 1

[e ₀ , e ₁ ] mod g

, (4.15) with:

u = −ad e

, v = ad e

. (4.16)

Furthermore, we have

Z (e ₀ , e ₁ ) = 1 − (uv)

Γ(1 − u) Γ(1 − v) Γ(1 − u − v) − 1

[e ₀ , e ₁ ] mod (g

) ² , (4.17)

which reproduces (4.5) up to squares of commutators (g

) ² = [g, g] ² .

In Ref. [11] by making use of the Ihara bracket [22] the Drinfeld associator (4.5) has been written in a form, which very much resembles the structure of the period matrix F , given in (2.4). In particular, the terms Q n containing the MZVs of depth greater than one are accompanied by Ihara brackets. In a limit, where the latter vanishes, a correspondence can be established between the four–point open superstring amplitude A

A(1, 2, 3, 4) = Γ(1 + s) Γ(1 + u)

Γ(1 + s + u) A , (4.18)

with the two kinematic invariants s = α

(k 1 + k 2 ) ² and u = α

(k 1 + k 4 ) ² and the associator.

If we work modulo g

then a commutative realization of the Ihara bracket is established and (4.18) can be related to (4.15) [11].

A natural question is, whether the four–point closed superstring amplitude (2.8) can be related to the Deligne associator W (e ₀ , e ₁ ). The four–graviton amplitude (2.8)

M(1, 2, 3, 4) = G |A| ² , (4.19)

can be obtained from (2.9)

G = S 0 exp

 

 −2 X

n≥1

ζ 2n+1 M 2n+1

 

 , (4.20)

with

M 2n+1 = − 1 2n + 1

s ²ⁿ⁺¹ + u ²ⁿ⁺¹ − (s + u) ²ⁿ⁺¹

, (4.21)

and the normalization:

S ₀ = −π su

s + u . (4.22)

Hence, we have:

M(1, 2, 3, 4) = |S ₀ | Γ(s) Γ(u) Γ(−s − u)

Γ(−s) Γ(−u) Γ(s + u) |A| ² . (4.23) In the case under consideration the expansion (2.15) of (4.20) becomes rather simple, all Q sv (n) disappear and the Poisson brackets become trivial.

By borrowing the arguments given below Eq. (4.10) the (motivic) Deligne associator

(4.10) can also be cast in a form, where MZVs of depth greater than one are accompanied

by Ihara brackets. Note, that this step essentially amounts to replacing ζ ^m by ζ _sv ^m in the

(motivic) Drinfeld associator. Hence, to find a correspondence between (4.23) and the

Deligne associator, we also need to work in a commutative realization of the Ihara bracket, i.e. modulo g

.

In this limit, based on the closed superstring amplitude (4.23) we conjecture the following expression for the Deligne associator W (e 0 , e 1 )

ln W (e ₀ , e ₁ ) = X

k,l

w kl u kl mod g

, (4.24)

with the coefficients w kl extracted from the generating function:

− Γ(−u) Γ(−v) Γ(u + v)

Γ(u) Γ(v) Γ(−u − v) = 1 + X

k,l

w kl u ^k v ^l

= 1 − 2ζ ₃ u v(u + v) − 2ζ ₅ u v(u + v)(u ² + uv + v ² ) + . . . . (4.25) With (4.25) the sum (4.24) gives:

ln W (e 0 , e 1 ) = −2 ζ 3 ([e 0 , [e 0 , e 1 ]] − [e 1 , [e 0 , e 1 ]) + . . . . (4.26) Eqs. (4.24) and (4.25) can be combined into:

ln W (e ₀ , e ₁ ) = (uv)

Γ(−u) Γ(−v) Γ(u + v) Γ(u) Γ(v) Γ(−u − v) + 1

[e ₀ , e ₁ ] mod g

, (4.27) which gives rise to:

W (e 0 , e 1 ) = 1 + (uv)

Γ(−u) Γ(−v) Γ(u + v) Γ(u) Γ(v) Γ(−u − v) + 1

[e 0 , e 1 ] mod (g

) ² . (4.28) Expanding (4.28) w.r.t. u and v reproduces the Deligne associator W (e ₀ , e ₁ ) modulo ⁴ squares of commutators (g

) ² :

W (e ₀ , e ₁ ) = 1 + 2ζ ₃ ([e ₀ , [e ₀ , e ₁ ]] − [e ₁ , [e ₀ , e ₁ ]) + 2 ζ ₅

[e ₀ , [e ₀ , [e ₀ , [e ₀ , e ₁ ]]]]

− 1

2 [e ₀ , [e ₀ , [e ₁ , [e ₀ , e ₁ ]]]] − 3

2 [e ₁ , [e ₀ , [e ₀ , [e ₀ , e ₁ ]]]] + (e ₀ ↔ e ₁ )

+ . . . .

(4.29)

Note, that the form (4.29) agrees with the motivic version (4.11). It can be verified, that the expressions (4.27) and (4.15) indeed fulfill (4.8), i.e.

ln W (e 0 , e 1 ) = − ln Z(−e 0 , −e

₁ ) + ln Z (e 0 , e 1 ) mod g

, (4.30)

4 Note, that expanding (4.28) yields the ζ

–term [e

, [e

, [e

, [e

, e

]]]] − 2[e

, [e

, [e

, [e

, e

]]]] +

2[e

, [e

, [e

, [e

, e

]]]] − [e

, [e

, [e

, [e

, e

]]]], which modulo squares of commutators (g

)

agrees

with [e

, [e

, [e

, [e

, e

]]]] −

[e

, [e

, [e

, [e

, e

]]]] −

[e

, [e

, [e

, [e

, e

]]]] + (e

↔ e

).

modulo double commutators and e

₁ = W e 1 W

. This relation (4.30) can be checked order by order in a basis of MZVs.

To conclude, the Deligne associator (4.28) assumes a similar form as the four–graviton amplitude (4.23) just as the Drinfeld associator resembles the four–gluon amplitude [11].

The relation (4.6) should be interpreted as KLT relation for the associators. It should be straightforward to use the Deligne associator (4.8) as a tool for setting up recursion relations for general N –graviton amplitudes in lines of [12].

5. Concluding remarks

In this work we have revisited the α

–expansion of the closed superstring amplitude (graviton amplitude) at tree–level with particular emphasis on its underlying algebraic structure and transcendentality properties.

After mapping the motivic open and closed superstring amplitudes onto a non–

commutative Hopf–algebra we have observed a striking similarity (3.12) between the two amplitudes communicated by the map (3.6). In the writings (3.13) and (3.14) the α

– expansions of the tree–level open and closed superstring amplitude take an uniform form suggesting an even deeper connection between gauge and gravity amplitudes than what is implied by KLT relations [14]. Anyhow, correspondences between perturbative gauge–

and gravity–theories are established in field–theory through the double copy construction [23] and in string theory through the Mellin correspondence [24]. Furthermore, recently interesting uniform descriptions of gauge– and gravity amplitudes in field–theory have been presented in [25].

The relation (3.15) relates two very different superstring amplitudes by the map (3.6).

It would be interesting to understand the role of the map sv at the level of the perturbation theory of open and closed strings or from the nature of the underlying string world–sheets.

Note, that a large class of Feynman integrals in four space–time dimensions lives in the subspace of SVMZVs or SVMPs, cf. Refs. [26,27]. As pointed out in [8] by Brown, this fact opens the interesting possibility to replace general amplitudes with their single–

valued versions (defined by the map sv), which should lead to considerable simplifications.

In string theory this simplification occurs by replacing gluon amplitudes (3.13) with their single–valued versions describing graviton amplitudes (3.14), which seem to be considerably simpler.

Through the Γ σ –decomposition B σ (s, u) = ^Γ(s)Γ(u) _Γ(s+u) , σ ∈ GT the Drinfeld associator

(4.15) is related to the structure of the Lie algebra of the Grothendieck–Teichm¨ uller group

GT [28]. The latter plays a role in revealing the underlying Lie algebra structure of the

open superstring amplitude. Hence, the Deligne associator (4.27) should be related to the

underlying algebra of the α

–expansion of closed superstring amplitude, cf. also Refs. [29]

for related research.

Finally, the structure underlying the motivic open and closed superstring amplitudes in terms of a Hopf algebra is not only a tool to conveniently express these amplitudes but rather seems to be an intrinsic feature, which might allow to compute the latter by first principles. Eventually, some or all aspects of string perturbation theory might be reduced to algebraic methods based on arithmetic algebraic geometry.

Acknowledgments

I wish to thank Hidekazu Furusho for useful comments.

References

[1] H. Elvang and Y.-t. Huang, “Scattering Amplitudes,” [arXiv:1308.1697 [hep-th]].

[2] A.B. Goncharov, “Galois symmetries of fundamental groupoids and noncommutative geometry,” Duke Math. J. 128 (2005) 209-284. [arXiv:math/0208144v4 [math.AG]].

[3] J. Golden, A.B. Goncharov, M. Spradlin, C. Vergu and A. Volovich, “Motivic Ampli- tudes and Cluster Coordinates,” [arXiv:1305.1617 [hep-th]].

[4] O. Schlotterer and S. Stieberger, “Motivic Multiple Zeta Values and Superstring Am- plitudes,” [arXiv:1205.1516 [hep-th]], to appear in J. Phys. A: Math. Theor.

[5] F. Brown, “On the decomposition of motivic multiple zeta values,” in ‘Galois- Teichm¨ uller Theory and Arithmetic Geometry’, Advanced Studies in Pure Mathe- matics 63 (2012) 31-58 [arXiv:1102.1310 [math.NT]].

[6] F. Brown, “Single-valued multiple polylogarithms in one variable,” C.R. Acad. Sci.

Paris, Ser. I 338, 527-532 (2004).

[7] O. Schnetz, “Graphical functions and single-valued multiple polylogarithms,”

[arXiv:1302.6445 [math.NT]].

[8] F. Brown, “Single-valued periods and multiple zeta values,” [arXiv:1309.5309 [math.NT]].

[9] V.G. Drinfeld, “Quasi Hopf algebras,” Alg. Anal. 1, 114 (1989); English translation:

Leningrad Math. J. 1 (1989), 1419-1457.

[10] V.G. Drinfeld, “On quasitriangular quasi-Hopf algebras and on a group that is closely connected with Gal(Q/Q),” Alg. Anal. 2, 149 (1990); English translation: Leningrad Math. J. 2 (1991), 829-860.

[11] J.M. Drummond and E. Ragoucy, “Superstring amplitudes and the associator,” JHEP 1308 , 135 (2013). [arXiv:1301.0794 [hep-th]].

[12] J. Broedel, O. Schlotterer, S. Stieberger and T. Terasoma, “All order alpha’-expansion of superstring trees from the Drinfeld associator,” [arXiv:1304.7304 [hep-th]].

[13] P. Deligne, “Le groupe fondamental de la droite projective moins trois points,” in:

Galois groups over Q, Springer, MSRI publications 16 (1989), 72-297; “Periods for the fundamental group,” Arizona Winter School 2002.

[14] H. Kawai, D.C. Lewellen and S.H.H. Tye, “A Relation Between Tree Amplitudes Of Closed And Open Strings,” Nucl. Phys. B 269, 1 (1986).

[15] N.E.J. Bjerrum-Bohr, P.H. Damgaard and P. Vanhove, “Minimal Basis for Gauge Theory Amplitudes,” Phys. Rev. Lett. 103, 161602 (2009) [arXiv:0907.1425 [hep-th]].

[16] S. Stieberger, “Open & Closed vs. Pure Open String Disk Amplitudes,” arXiv:0907.2211 [hep-th].

[17] J. Bl¨ umlein, D.J. Broadhurst and J.A.M. Vermaseren, “The Multiple Zeta Value Data Mine,” Comput. Phys. Commun. 181, 582 (2010). [arXiv:0907.2557 [math-ph]].

[18] J. Broedel, O. Schlotterer and S. Stieberger, “Polylogarithms, Multiple Zeta Values

and Superstring Amplitudes,” Fortsch. Phys. 61 , 812 (2013). [arXiv:1304.7267 [hep-

th]].

[19] S. Stieberger, “Constraints on Tree-Level Higher Order Gravitational Couplings in Superstring Theory,” Phys. Rev. Lett. 106, 111601 (2011) [arXiv:0910.0180 [hep-th]].

[20] V.G. Knizhnik and A.B. Zamolodchikov, “Current Algebra and Wess-Zumino Model in Two-Dimensions,” Nucl. Phys. B 247, 83 (1984).

[21] T.Q.T. Le and J. Murakami, “Kontsevich’s integral for the Kauffman polynomial,”

Nagoya Math. J. 142 (1996), 39-65.

[22] Y. Ihara, “Some arithmetic aspects of Galois actions on the pro-p fundamental group of P\{0, 1, ∞},” Proc. of Symposia in Pure Mathematics Vol. 70 (2002).

[23] Z. Bern, J.J.M. Carrasco and H. Johansson, “New Relations for Gauge-Theory Am- plitudes,” Phys. Rev. D 78, 085011 (2008) [arXiv:0805.3993 [hep-ph]]; “Perturbative Quantum Gravity as a Double Copy of Gauge Theory,” Phys. Rev. Lett. 105, 061602 (2010) [arXiv:1004.0476 [hep-th]];

Z. Bern, T. Dennen, Y.-t. Huang and M. Kiermaier, “Gravity as the Square of Gauge Theory,” Phys. Rev. D 82, 065003 (2010) [arXiv:1004.0693 [hep-th]].

[24] S. Stieberger and T.R. Taylor, “Superstring Amplitudes as a Mellin Transform of Supergravity,” Nucl. Phys. B 873 , 65 (2013) [arXiv:1303.1532 [hep-th]]; “Super- string/Supergravity Mellin Correspondence in Grassmannian Formulation,” Phys.

Lett. B 725 , 180 (2013) [arXiv:1306.1844 [hep-th]].

[25] F. Cachazo, S. He and E.Y. Yuan, “Scattering Equations and KLT Orthogonal- ity,” [arXiv:1306.6575 [hep-th]]; “Scattering of Massless Particles in Arbitrary Dimen- sion,” [arXiv:1307.2199 [hep-th]]; “Scattering of Massless Particles: Scalars, Gluons and Gravitons,” [arXiv:1309.0885 [hep-th]];

S. Litsey and J. Stankowicz, “Kinematic Numerators and a Double-Copy Formula for N = 4 Super-Yang-Mills Residues,” [arXiv:1309.7681 [hep-th]].

[26] L.J. Dixon, C. Duhr and J. Pennington, “Single-valued harmonic polylogarithms and the multi-Regge limit,” JHEP 1210, 074 (2012). [arXiv:1207.0186 [hep-th]];

F. Chavez and C. Duhr, “Three-mass triangle integrals and single-valued polyloga- rithms,” JHEP 1211, 114 (2012). [arXiv:1209.2722 [hep-ph]];

V. Del Duca, L.J. Dixon, C. Duhr and J. Pennington, “The BFKL equation, Mueller- Navelet jets and single-valued harmonic polylogarithms,” [arXiv:1309.6647 [hep-ph]].

[27] S. Leurent and D. Volin, “Multiple zeta functions and double wrapping in planar N = 4 SYM,” Nucl. Phys. B 875, 757 (2013). [arXiv:1302.1135 [hep-th]].

[28] Y. Ihara, “On beta and gamma functions associated with the Grothendieck–

Teichm¨ uller group,” in: Aspects of Galois Theory, London Math. Soc. Lecture Notes 256 (1999), 144-179; “On beta and gamma functions associated with the Grothendieck-Teichm¨ uller group. II,” J. reine u. angew. Math. 527 (2000), 1-11;

H. Furusho, “Multiple zeta values and Grothendieck-Teichm¨ uller groups,” AMS Con- temporary Math., Vol. 416, (2006), 49-82

[29] H. Furusho, “Four groups related to associators,” [arXiv:1108.3389 [math.QA]]; “p-

adic multiple zeta values II. Tannakian interpretations,” American Journal of Math-

ematics, Vol. 129 (2007), 1105-1144.