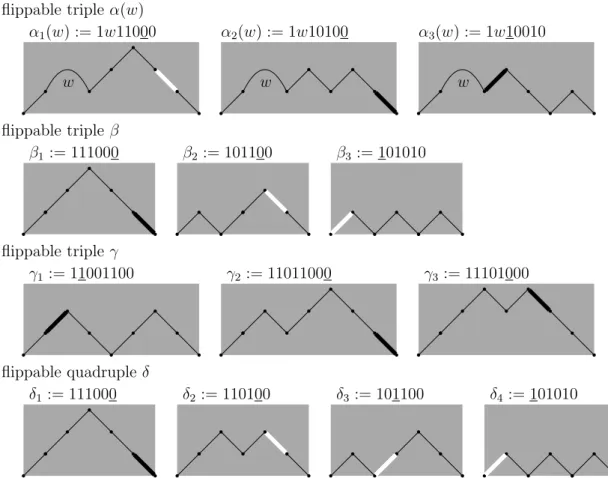
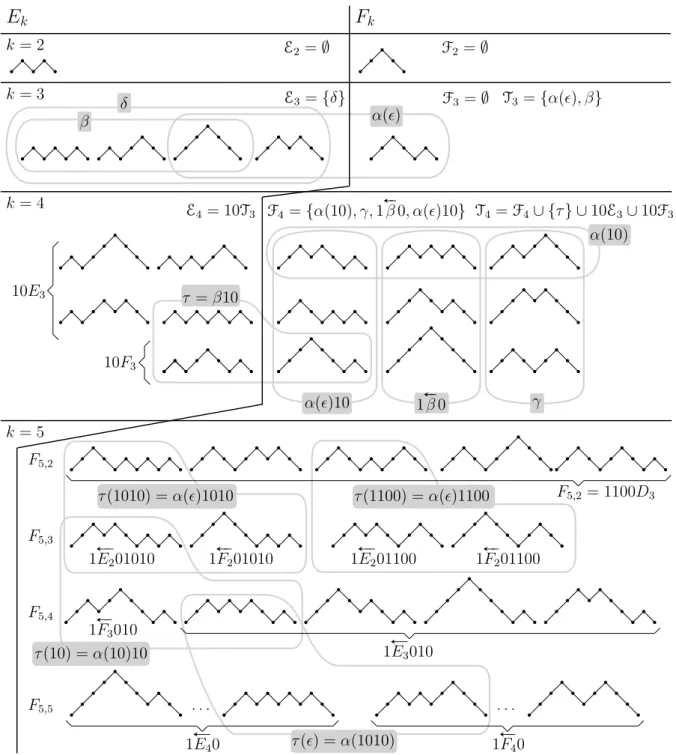
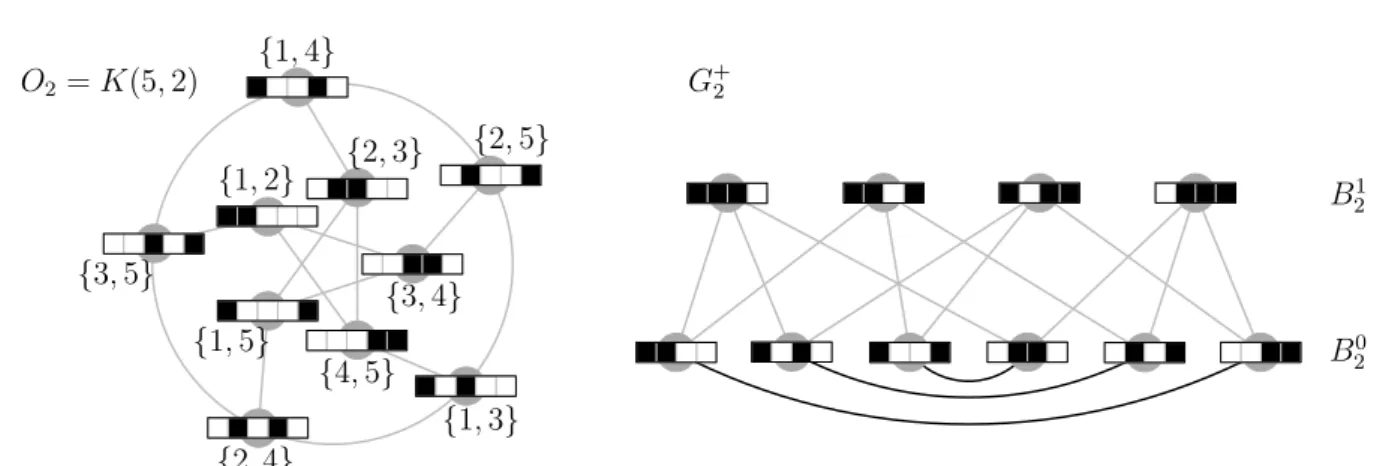
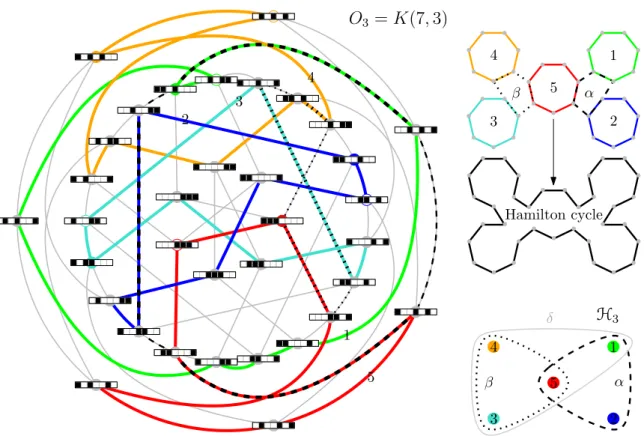
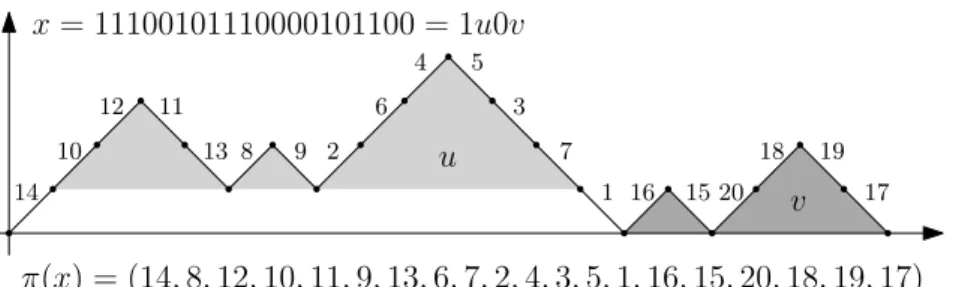
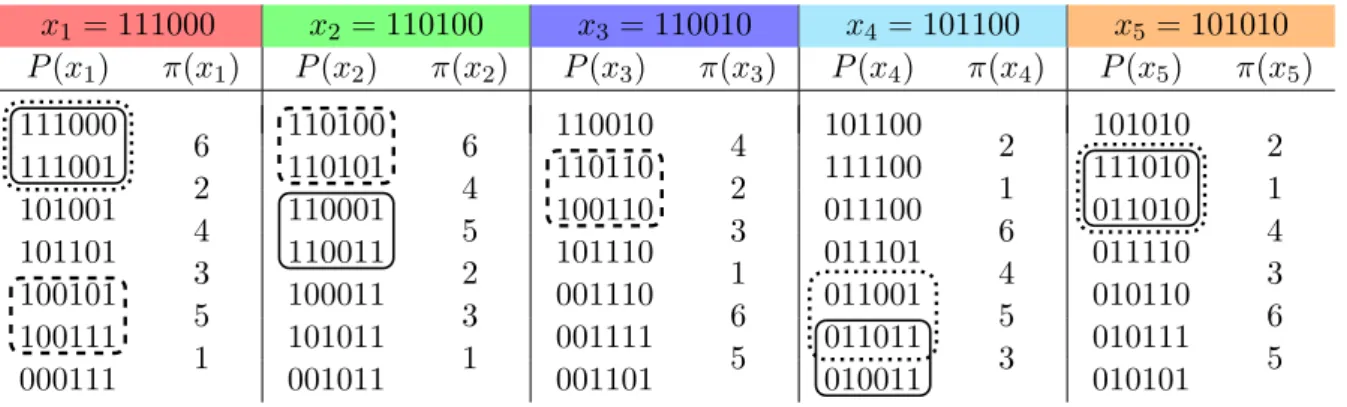
, k) with k > 3 and a > 0 have a Hamilton cycle. We also prove that K(2k + 1, k) has at least 2
22
0
0
Volltext
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
Abbildung
+3
ÄHNLICHE DOKUMENTE
[r]
Der obige Beweis zeigt allgemeiner, dass alle endlichen Untergruppen der multiplikativen Gruppe eines Körpers zyklisch sind. 2 Gleichungen über einem
[r]
[r]
Goldener Schnitt, Fibonacci-Zahlen, Pascalsches Dreieck Präsenzübungen (für Mi,
[r]
Lösung zu Aufgabe 2: (Bayes im Oberrabensteiner Nationalpark) bayes.tex Sei O das Ereignis, dass der Ausgang im Osten liegt und W das Ereignis, dass er sich im Westen befindet.. Für
(b) Um welche andere Strecke können Länge und Breite vergrößert und die Höhe verkleinert werden, wenn sich dieselbe Volumszunahme wie in Frage (a) ergeben