mω j 2 , j = 1, 2, 3

Der harmonishe Oszillator

DasEinzigewasSierehnenkönnen,isteinKastenpotential,derTunneleekt,

das Wasserstoatom und vor allem der harmonishe Oszillator. Wenn Sie so

einen haben, freuen Sie sih. Wenn niht, nähern Sie so lange, bis Sie einen

haben.

aus: Die besten Sprühe vonProfessoren

In diesem Kapitel werden wir das nahdem freien Teilhen einfahste physikalishe Sys-

tem, den harmonishen Oszillator, untersuhen. Ein gutes Verständnis des quantisierten

Oszillatorsistunabdingbarbeider Untersuhung vonkomplizierterenQuantensystemen.

Viele Näherungen in der Festkörperphysik, Quantenfeldtheorie usw. beruhen in tiefster

Ordnung auf der Lösung für den harmonishen Oszillator. Die Maxwellgleihungen im

Vakuum führen nah einer Fouriertransformation auf ein System von unendlih vielen

ungekoppelten harmonishen Oszillatoren.

WirwerdendieShrödingergleihungfürden

3

m

und Federkonstanten

mω _j ² , j = 1, 2, 3

H =

3

X

j=1

H j (p j , x ^j ),

H j (p, x) = 1

2m p ² + m

2 ω _j ² x ²

untersuhen.

H

ψ(t,

) = e ^{−iEt/ ~} ψ(

).

Die zeitunabhängige Funktion

ψ(

)

Eψ(

) = Hψ(

) = X

j

H _j (p _j , x ^j )ψ(

)

mitEnergie

E

ψ(

)

tintegrierbar ist.Nur quadratintegrierbare

ψ

DerHamiltonoperatoristdieSummevondreikommutierendeneindimensionalenOpe-

ratoren.Diesekönnengleihzeitigdiagonalisiertwerden.Esfolgt,dassdieEigenfunktionen

faktorisieren

ψ(

) = ψ 1 (x ¹ )ψ 2 (x ² )ψ 3 (x ³ )

Eψ(x) = − ~ ²

2m ψ ^′′ (x) + mω ²

2 x ² ψ(x),

zu lösen. Dies wird uns im nähsten Abshnitt mitalgebraishen Methoden gelingen.

Aus Masse und Kreisfrequenz des Oszillatorssowie der Naturkonstanten

~

α = r ~

mω .

Misstman dieMasse inKilogrammund dieKreisfrequenz in Sekunden, dann ergibtsih

α[

] ≈ 10 ⁻¹⁷ (mω) ^−1/2 .

Selbst für makroskopishe Oszillatorenist

α

7.1 Auf- und Absteigeoperatoren

Umfortzufahren, isteshilfreih,dendimensionslosen Absteigeoperator

a

giertes,den Aufsteigeoperator

a ^†

a = 1

√ 2 x

α + iαp

~

, a ^† = 1

√ 2 x

α − iαp

~

.

Oft nennt man

a

a ^†

DaOrts-undImpulsoperatornihtkommutieren,

[x, p] = i ~

und Aufsteigeoperator niht:

[a, a ^† ] = [αx + i p

2 ~ α , αx − i p

2 ~ α ] = 1

2 ~ ( − i[x, p] + i[p, x]) = 1.

Natürlihvertaushen

a

a ^†

[a, a] = [a ^† , a ^† ] = 0 , [a, a ^† ] = 1.

Da weiterhin

a ^† a =

αx − ip

2 ~ α αx + ip 2 ~ α

= α ² x ² + p ²

(2 ~ α) ² + i 2 ~ [x, p]

= mω

2 ~ x ² + 1

2mω ~ p ² − 1 2

gilt,kann der Hamilton-Operatordurh

a ^† a

H = ~ ω a ^† a + ¹ ₂

≡ ~ ω N + ¹ ₂

.

Der Operator

N = a ^† a

0 ≤ h aψ | aψ i = h ψ | N | ψ i .

ImfolgendenwerdenwirdieEigenwerteundEigenfunktionenvon

N

H

7.1.1 Energien und Eigenfunktionen

Wir wollen das Spektrum (die möglihen Eigenwerte

E n

H

braishen Beziehungen (7.7) und (7.8) nden, ohne dabei die spezielle Darstellung (7.6)

zu benutzen.Löstman sihnämlihvondieserDarstellung,dannkannmandiefolgenden

ResultatezumBeispielaufdieErzeugungundVernihtungvonPhononen oderPhotonen

übertragen.

Der Zustand mit kleinster Energie, der Grundzustand des harmonishen Oszillators,

muÿ oensihtlih minimales

N

| n i

N

N | n i = a n | n i ,

a n ≥ 0

Die Eigenwerte des Besetzungszahloperators

N

| n i

a n

[ N, a ^† ] = a ^† aa ^† − a ^† a ^† a = a ^† [a, a ^† ] = a ^†

[N, a] = a ^† aa − aa ^† a = [a ^† , a]a = − a

haben

a ^† | n i

a | n i

a n + 1

a n − 1

Na ^† | n i = a ^† (N + 1) | n i = (a n + 1)a ^† | n i

Na | n i = a (N − 1) | n i = (a n − 1)a | n i .

a ^†

a

a ^†p

p

a ^p

p

WirwollenzuerstdieFragenahdem kleinstenEigenwert von

N

h an | an i = h n | N | n i = a _n h n | n i

istfür

a n 6 = 0

| n i

a | n i

a n 6 = 0

a n − 1

Eigenwert von

N

N

a n ∈

⁰

und deshalbistder kleinsteEigenwert von

N

0

| 0 i

a

N | 0 i = 0 ⇐⇒ a | 0 i = 0.

Damitwäregezeigt,dass

| n i ∼ a ^†n | 0 i

N

a n = n

ist.Die Eigenwerte von

N

0

Es habe nun

| n − 1 i

1

β

| n i = βa ^† | n − 1 i

so bestimmen, dass auh

| n i

1 = ^! h n | n i = | β | ²

n − 1 | aa ^† | n − 1

= | β | ² h n − 1 | (N +

) | n − 1 i = n | β | ² .

Ist der Grundzustand

| 0 i

| n i = 1

√ n a ^† | n − 1 i = 1

p n(n − 1) a ^†2 | n − 2 i = . . . = 1

√ n! a ^†n | 0 i

ebenfallsauf Eins normiert. Insbesondere sind die Eigenwerte

n = 0, 1, 2, . . .

N

obenunbeshränkt.DieseEigenwertekönnenniht entartet sein.Wäre

n

so gäbe es mindestenszwei unabhängigeZustände

| n i = 1

√ n! a ^†n | 0 i

| n ˜ i = 1

√ n! a ^†n | ˜0 i ,

dieaus zwei vershiedenen Zuständen mitBesetzungszahl

0

n

Erzeugungsoperators gewonnen würden. Wirhaben aber bereits gezeigt,dass

a | 0 i = 0

a | ˜0 i = 0

gelten muÿ. Wir werden unten beweisen, dass es nur einen Zustand

| 0 i

a

annihiliertwird. Alsosind die Eigenwerte von

N

•

N

{ 0, 1, 2, . . . }

von

a ^†

| 0 i

0

Mit dem Spektrum des Besetzungszahloperators kennen wir mit(7.8) auh die Energie-

eigenwerte

H | n i = E n | n i , E n = ~ ω n + ¹ ₂

.

DieOperatoren

a ^†

a

~ ω

SpektrumdesharmonishenOszillatorsistäquidistantund

a ^†

a

Zur expliziten Konstruktion der Eigenfunktion im Ortsraum,

ψ n (x) = h x | n i

wir zur Ortsdarstellung (7.6) für den Absteige- und Aufsteigeoperator zurük. In dieser

Darstellung ist

p = ^~ _i ∂ x

aψ 0 = 0

aψ 0 =

αx + 1 2α ∂ x

ψ 0 = 0.

Die Lösung dieser Dierentialgleihung erster Ordnung isteine Gauÿshe Funktion

ψ 0 (x) = 2α ²

π 1/4

e ^−α

^x

, α ² = mω

2 ~ ,

unddieEindeutigkeitderLösungimpliziert,dassderGrundzustand

| 0 i

ψ n (x) = 1

√ n! (a ^† ) ⁿ ψ 0 (x) = 1

√ n!

mω π ~

1/4

αx − 1 2α ∂ x

n

e ^−α

^x

berehnet werden. Zum Beispielndet man für den ersten angeregtenZustand

ψ 1 (x) =

r 2mω

~ · x · ψ 0 (x).

Die höheren angeregten Zustände

ψ n

H n (ξ)

n

ψ _n (x) = mω π ~

1/4 1

√ 2 ⁿ n! H _n √ 2αx

· e ^−α

^x

.

Die Hermite-Polynome

H n

niedrigsten Ordnungen lauten

H 0 (ξ) = 1 H 1 (ξ) = 2ξ H 2 (ξ) = 4ξ ² − 2 H 3 (ξ) = 8ξ ³ − 12ξ

H 4 (ξ) = 16ξ ⁴ − 48ξ ² + 12 H 5 (ξ) = 32ξ ⁵ − 160ξ ³ + 120ξ

| ψ n | ²

x n = 0

n = 1 n = 2

In der Abbildungsind dieWahrsheinlihkeitsdihten

w n (x) = | ψ n (x) | ² = 1

√ π 1

2 ⁿ n! H _n ² (x)e ^−x

für die Zustände mit den

3

~ /mω

ψ n

(ψ n , ψ m ) = δ nm .

Es ist kein Zufall, dass

ψ _n

n

diesen Sahverhalt später für dieallgemeine Shrödingergleihung diskutieren.

Die Lösungen des dreidimensionalen Oszillators (7.3) sind nun einfah Produkte der

Lösungen (7.14) des eindimensionalen Oszillatoren,

ψ n

,n

,n

(

) = ψ n

(x ¹ )ψ n

(x ² )ψ n

(x ³ ),

mit den Eigenfunktionenen

ψ n

(x )

n → n i , x → x ⁱ , ω → ω i

1

E n

,n

,n

= ~

3

X

i=1

ω i (n i + ¹ ₂ ).

7.1.2 Interpretationen

In diesemAbshnitt werden wir diegewonnen Resultateinterpretieren undweiter ergän-

zen.Zuerstinvertierenwir dieBeziehungen(7.6)umden Orts-undImpulsoperatordurh

den Auf- und den Absteigeoperator auszudrüken,

x = 1

2α a ^† + a)

p = i ~ α a ^† − a

.

Damit lassen sih die Erwartungswerte von Ort und Impuls in den Energie-Eigenzu-

ständen

| n i

wieAuf- undAbsteigeoperatoraufdienormierten

| n i

a ^† | n i = √

n + 1 | n + 1 i

abgeleitet. Um die Wirkung von

a

| n i

n

n − 1

aa ^† | n − 1 i =

√ n a | n i .

aa ^† = a ^† a + 1 = N + 1

a | n i = √

n | n − 1 i .

Also noh einmalzusammengefasst:

a ^† | n i = √

n + 1 | n + 1 i

a | n i = √

n | n − 1 i .

Da Ort und Impuls linearvon

a

a ^†

x | n i

p | n i

| n − 1 i

| n + 1 i

| n i

x | n i

p | n i

| n i

EigenzuständensitztruhtderOszillatorimMittelamUrsprungundhateinenvershwin-

denden mittleren Impuls,

h n | x | n i = h n | p | n i = 0

Shwankungen vonOrt und Impuls bestimmen. Wegen

x ² = ~

2mω a ^† a ^† + aa + a ^† a + aa ^†

p ² = − mω

2 a ^† a ^† + aa − a ^† a − aa ^†

nden wir folgendenErwartungswert für

x ²

n

h n | x ² | n i = ~

2mω h n | (a ^† a + aa ^† ) | n i

= ~

2mω h n | (2N + 1) | n i = ~

mω n + ¹ ₂

und ganz analog

h n | p ² | n i = ~ mω

2 h n | (aa ^† + aa ^† ) | n i = ~ mω n + ¹ ₂ .

Da dieMittelwertevon

x

p

| n i

h n | (∆x) ² | n ih n | (∆p) ² | n i = ~ ² n + ¹ ₂ 2

≥ ~ ²

4 , n = 0, 1, 2, . . .

ImGrundzustandhatder OszillatorsdasnahderUnshärferelationkleinstmöglihePro-

dukt der Unshärfen,

∆x · ∆p = ~ /2

Produkt der Unshärfen jedoh zu, für groÿe Energienproportionalzu

n

Uminterpretation: Im harmonishen Potential haben zwei benahbarte Energiewer-

te den Abstand

~ ω

ω

| n i

n

~ ω

N

zahloperator,daerdieQuanten zählt.Wegen

a ^† | n i ∼ | n + 1 i

a ^†

wegen

a | n i ∼ | n − 1 i

a

a ^†

a

Diese Interpretation wird benutzt zur Beshreibung der Shwingungsbewegung der

atomaren Bausteine in Molekülen, der Gitteratome in Kristallen und bei der Quantisie-

rung des freien elektromagnetishen Feldes. In allen drei Fällenbasiert die Beshreibung

auf Systemen ungekoppelter, eindimensionaler harmonisher Oszillatoren, die im Allge-

meinenvershiedeneFrequenzenhaben.BeiderDiskussionderHohlraumstrahlunghaben

wir dies explizit gesehen. Die durh

a ^† , a

Nützlihe Formeln: Folgende Formeln sind bei der Behandlung von harmonishen

Oszillatoren hilfreih:

[N, a ^p ] = − pa ^p , [N, a ^{† p} ] = pa ^{† p} , [a, a ^{† n} ] = na ^{† (n−1)} .

Siekönnenmühelosaus

[a, a ^† ] = 1

N = a ^† a

7.2 Kohärente Zustände

Durh Überlagerung von Eigenfunktionen können Zustände konstruiert werden, für die

der mittlere Ort und Impuls die klassishe Bewegung des Oszillators vollführen. Solhe

kohärentenZustände bildendieBrükezwishen derklassishenMehanik undder Quan-

tenmehanik. Sie wurden bereits von E. Shrödinger zu Beginn der Wellenmehanik

eingeführt [45℄. In der zitierten Arbeit untersuhte er niht-zerieÿende Wellenpakete.

Kohärente Zustände haben diese interessante Eigenshaft.

Wirhabengesehen,dassimGrundzustanddasProduktausOrts-undImpulsunshärfe

minimal ist. Dies gilt auh, wenn wir die Wellenfunktion im Ortsraum vershieben, d.h.

für

ψ _ξ (x) = ψ ₀ (x − x ₀ ) , ξ = αx ₀ =

r mω

2 ~ x ₀ .

Die Zustände

ψ ξ

exp(iηp/ ~ )

Argument einer Wellenfunktion um

η

ψ ξ (x) = e ^−ix

^{p/ ~} ψ 0 (x) ^(7.15) = e ^ξa

^−ξa ψ 0 (x).

WirbenutzendieBaker-Campbell-Hausdor-Formel 1

zurUmformungdesaufdenGrund-

zustand wirkendenunitären Operators.Wegen

[a, a ^† ] =

e ^ξa

^−ξa = e ^−ξ

^/2 e ^ξa

e ^−ξa ,

und da

a

exp( − ξa)ψ 0 = ψ 0

zu

ψ ξ (x) = e ^−ξ

^/2 e ^ξa

ψ 0 (x).

1

siehez.B.meinMehanikSkript

Wirlösenuns nunvonderOrtsdarstellungundwehselnzur DirashenShreibweise.Die

kohärenten Zustände werden mit

| ξ i

h x | ξ i = ψ _ξ (x)

ξ

diese

| ξ i = e ^−|ξ|

^/2 e ^ξa

| 0 i .

Diese Zustände sind Eigenzustände des niht-hermiteshen Absteigeoperators.Dies zeigt

man amshnellsten mitHilfe der Formel

e ^−ηa

ae ^ηa

= a − η[a ^† , a] + η ²

2 [a ^† , [a ^† , a]] + . . . = a + η

wie folgt,

a | ξ i = e ^−|ξ|

^/2 e ^ξa

(a + ξ) | 0 i = ξ | ξ i .

DerEigenwertvon

| ξ i

ξ

alfunktion in(7.20) und mahen Gebrauhvonder Darstellung(7.11)für dieangeregten

Zustände des Oszillators,so erhalten wir

| ξ i = e ^−|ξ|

^/2

∞

X

n=0

ξ ⁿ

√ n! | n i .

DiekohärentenZuständesindeine Überlagerungunendlih vielerEnergie-Eigenzustände.

Nun ist es relativeinfah, diejenige Lösung der zeitabhängigen Shrödingergleihung

anzugeben, die zur Zeit

t = 0

| ξ i

diebekannte Zeitabhängigkeit der Energie-Eigenzustände in(7.23) einzusetzen,

| ξ i (t) = e ^−|ξ|

^/2

∞

X

n=0

ξ ⁿ

√ n! e ^−iE

^{t/ ~} | n i = e ^−iωt/2

e ^−|ξ|

^/2 X (ξe ^−iωt ) ⁿ

√ n! | n i

.

Der Ausdruk zwishen den Klammern ist oensihtlih wieder ein kohärenter Zustand,

allerdingsmitzeitabhängigem Parameter

ξ(t) = e ^−iωt ξ(t)

stand bleibt alsozu allen Zeiten kohärent,

| ξ i (t) = e ^−iωt/2 ξ(t)

, ξ(t) = e ^−iωt ξ.

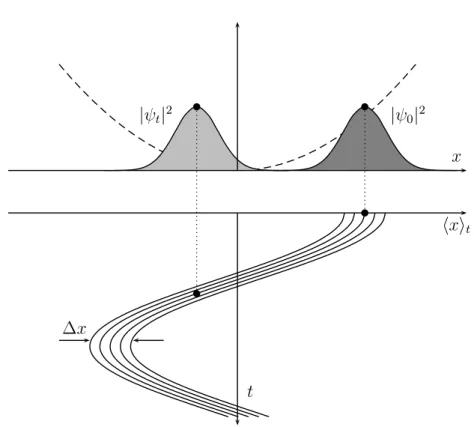
Die Wellenfunktion und zugehörige Wahrsheinlihkeitsdihte imOrtsraum haben damit

diefolgende Zeitentwiklung,

ψ _ξ (t, x) = h x | ξ(t) i = e ^−iωt/2 ψ ₀ x − e ^−iωt x ₀

ψ ξ (t, x)

2 =

ψ 0 x − x(t)

2 , x(t) = x 0 cos ωt.

Diese lässt eine einfahe Deutung zu: das anfänglihvershobene Gauÿshe Wellenpaket

shwingt harmonishum den Koordinatenursprung.

7.2.1 Erwartungswerte und Unshärfen

Beider Berehnung vonErwartungswerten imkohärenten Zustand

| ξ i

a | ξ i = ξ | ξ i

h x i ^ξ ≡ h ξ | x | ξ i ^(7.15) = 1

2α h ξ | (a ^† + a) | ξ i = 1 α ℜ ξ,

und für den mittlerenImpuls

h p i ^ξ = h ξ | p | ξ i ^(7.15) = i ~ α h ξ | (a ^† − a) | ξ i = mω α ℑ ξ.

Im letzten Shritt setzten wir für

α

Zustand mit Parameter

ξ

Parameter

ξ(t)

h x i ^ξ (t) = x(t) = x 0 cos ωt

h p i ^ξ (t) = − mωx 0 sin ωt = m x(t). ˙

Nihtunerwartet ist der mittlereOrt gleihdem Maximum der Wahrsheinlihkeitdihte

imOrtsraum.ErbeshreibtdieklassisheShwingungsbewegungdes harmonishenOszil-

latorsmitAmplitude

x 0

ω

aa ^† + a ^† a = 2a ^† a + 1

x ²

p ²

h x ² i ^ξ = 1 4α ²

a ^†2 + 2a ^† a + a ² + 1

ξ = 1

(2α) ² + x 2

ξ

h p ² i ξ = − ( ~ α) ²

a ^†2 − 2a ^† a + a ² − 1

ξ = ( ~ α) ² + p 2

ξ .

Die Zeitentwiklung dieser Erwartungswerte erhält man wieder, wenn man

ξ

ξ(t)

aus (7.24) ersetzt. Insbesondere sind für die Erwartungswerte rehts das Quadrat der

Mittelwerte (7.25)einzusetzen.

ImGegensatzzummittlerenOrtundmittlerenImpulssindOrts-undImpulsunshärfe

zeitunabhängig,

(∆x) ²

ξ = 1

4α ² = ⇒ ∆x = r ~

2mw (∆p) ²

ξ = ~ ² α ² = ⇒ ∆p =

r m ~ ω

2

DiekohärentenZuständezerieÿenalsowederimOrts-nohimImpulsraum.DasProdukt

derOrts-undImpulsunshärfeistsoklein,wieesnahderUnshärferelationnurseinkann,

h (∆x) ² i ^ξ · h (∆p) ² i ^ξ = ~ ²

4 .

Zusammenfassend haben unsere Rehnungen gezeigt, dass die Wellenfunktion

ψ ξ

ne Shwingung mitKreisfrequenz

ω

x 0

dass sih dabei dieOrts- und Impulsunshärfen niht ändern. Der Zustand ist das quan-

tenmehanishe Analogon des shwingenden Massenpunktes der klassishen Mehanik.

Der zusammengesetzte Zustand

| ξ i

Betrahten wir zum Beispiel einen makroskopishen Oszillator mit

m = 1

Shwingungsdauer von

T = 0.63

Länge

10

α ∼ 2 · 10 ¹⁵

⁻¹

∆x ∼ 2 · 10 ⁻¹⁸

∆p ∼ 2 · 10 ⁻¹⁷

.

SeineOrtsunshärfeistalsoetwadrei Gröÿenordnungenkleineralseindurhshnittliher

Kerndurhmesser. Auf eine derartigeGenauigkeitkann man keine makroskopishe Länge

messen. Für die Beshreibung eines makroskopishen Oszillators sind die Gesetze der

klassishen Mehanik also mehr alsausreihend.

Jeder kohärente Zustand ist eine Superposition von unendlihvielen Eigenzuständen

| n i

N

sharf. Die Wahrsheinlihkeit, mit der man den Zustand

| n i

antrit, ist durh das Betragsquadrat der Koezienten

α n

gegeben,

| α _n | ² = |h n | ξ i| ² = | ξ | ²ⁿ

n! e ^−|ξ|

= ⇒ X

| α _n | ² = 1.

Diese Gleihung zeigt, dass der Anteil des Zustandes

| n i

n

h x i ^t

t

x

| ψ t | ² | ψ 0 | ²

∆x

Abbildung7.1:DieBewegungdesWellenpakets kannmitderZeitabhängigkeitdesErwar-

tungswertes der Koordinatesamtihrer Unshärfe veranshauliht werden. Für kohärente

Zustände ist dieUnshärfezeitunabhängig.

Zustand

| ξ i

F (z) ≡ h e ^zN i ^ξ = X

| α n | ² e ^zn = e ^{− ξξ ¯} X ( ¯ ξξ) ⁿ

n! e ^zn = exp ¯ ξξe ^z exp ¯ ξξ

ndet man diemittlereBesetzungszahl als erste Ableitungnah dem Parameter

z

h N i ξ = X

n | α _n | ² = F ^′ (0) = ¯ ξξ.

Das mittlereQuadrat der Besetzungszahl istgleihder zweiten Ableitung amUrsprung,

h N ² i ξ = F ^′′ (0) = ¯ ξξ + ( ¯ ξξ) ² = h N i ξ + h N i ² ξ .

Die Unshärfeder Besetzungszahl

N

| ξ i

∆N = q

h N ² i ξ − h N i ² ξ = q

h N i ξ = | ξ | ,

und ist äquivalent zu folgender Energieunshärfe

∆E = ~ ω∆N = ~ ω q h N i ^ξ .

Aus (7.27,7.29)entnehmen wir, dass

∆N · ∆x = 1

2 x 0

∆x x 0

= 1

2 h N i ^−1/2 ξ ,

gelten, eine für kohärente Zustände harakteristishe Form der Unshärferelationen. Um

das Teilhen imOrtsraum zu lokalisieren, brauht man groÿe Besetzungszahlen.

Zwei kohärenteZustände sind niemalsorthogonal,

h ξ | ξ ^′ i =

Z ψ ¯ 0 (x − x 0 )ψ 0 (x − x ^′ ₀ ) = e ^−(ξ−ξ

⁾

^/2 , ξ = αx 0 , ξ ^′ = αx ^′ ₀ .

Für eine groÿe Dierenz der Parameter

ξ

ξ ^′

Dann sind dieentsprehenden kohärenten Zustände in guter Näherungorthogonal.

Die kohärenten Zustände

| ξ i

t = 0

| ξ, β i

Ortsraum ebenfallseine Gauÿshe Form,

ψ ξ,β (0, x) = h x | ξ, β i = ∼ e ^−βα

^(x−x

⁾

.

Ähnlihwiefür kohärenteZustände kann mandieLösungen

ψ ξ,β (t, x)

∆x∆p =

~ /2

∆x

∆p

die Impulsunshärfe sehr klein (und entsprehend die Ortsunshärfe groÿ). Gequetshte

Zustände nden sih zuerst in den Arbeiten [44℄. Für eine ausführlihe Diskussion die-

ser interessanten Zustände des harmonishen Oszillators verweise ih auf [46℄ oder die

Lehrbüher über Quantenoptik.