Anwendung der Multireferenzstörungstheorie auf elektronische Anregungsenergien von polycyclischen aromatischen Kohlenwasserstoffen
BACHELORARBEIT
zur Erlangung des akademischen Grades
Bachelor of Science (B. Sc.) im Studiengang Chemie
von Joris Theunissen
Heinrich-Heine-Universität Düsseldorf
Institut für Theoretische Chemie und Computerchemie
September 2016
1. Gutachterin: Frau Prof. Dr. Christel M. Marian 2. Gutachter: Herr Prof. Dr. Rainer Weinkauf
i
Hiermit versichere ich diese Bachelorarbeit selbstständig und ohne die Hilfe Dritter angefertigt zu haben. Dabei habe ich keine anderen als die angegebenen Quellen für wörtliche oder inhaltliche entnommene Stellen verwendet. Diese Arbeit hat in gleicher oder ähnlicher Form noch keiner Prüfungsbehörde vorgelegen.
Düsseldorf, den 13. September 2016
___________________
(Joris Theunissen)
ii Danksagung
Zunächst möchte ich mich bei Frau Prof. Dr. Christel M. Marian bedanken, dafür mir ermöglicht zu haben diese Bachelorarbeit in ihrem Arbeitskreis zu schreiben. Des weiteren für die Auswahl und Bereitstellung des bearbeiteten Themas.
Des weiteren Dank an Adrian Heil für die Betreuung während der Bearbeitungszeit, dass ich bei Fragen mich an ihn wenden konnte.
Ebenso möchte ich mich bei Herrn Prof. Dr. Rainer Weinkauf als Zweitkorrektor dieser Arbeit bedanken.
Zuletzt möchte ich mich auch bei meiner Familie und allen guten Freunden bedanken, die mich während meiner Bachelorarbeit, aber auch bereits während der gesamten Studienzeit, unterstützt und motiviert haben.
iii Kurzzusammenfassung
In dieser Arbeit wurden verschieden Anregungsenergien von kleinen polycyclischen aromatischen Kationen auf MR-MP2-Niveau mit den Programmen RIMR und MRCI berechnet. Die verwendeten Kationen waren, das Acenaphthylen-Kation, das Anthracen- Kation, das Azulen-Kation, das Naphthalin-Kation, das Pyren-Kation und das Tetracen- Kation. Dabei wurde ein Vergleich der beiden Programme durchgeführt, bei dem sich herausgestellt hat, dass durch die iterative Verbesserung des verwendeten Referenzraums die Anzahl der Referenzen, für jede weitere durgeführte Rechnung, in RIMR deutlich größer wurde im Vergleich zu MRCI. Der für die erste Rechnung vorgegebene Referenzraum war allerdings der selbe.
Im weiteren wurden die vertikalen Anregungsenergien der Kationen an der Struktur der neutralen Moleküle mit RIMR berechnet. Die erhaltenen Ergebnisse wurden verglichen mit experimentellen Ergebnissen aus der Photoelektronenspektroskopie (PES) und zusätzlich mit den von Hirata, Head-Gordon, Szczepanski und Vala[1] unter Verwendung von TDDFT und der Tamm-Dancoff-Näherung (TDA). Dabei hat sich herausgestellt, dass einzelne Ergebnisse der MR-MP2 Berechnungen durchaus schlechter sein können als die TDA-Ergebnisse, allerdings liefern die MR-MP2-Berechnungen im allgemeinen bessere Ergebnisse im Vergleich zu den experimentell Bestimmten Werten.
Zuletzt wurden ebenfalls noch die Anregungsenergien an der Struktur der Kationen berechnet und verglichen mit Ergebnissen der Absorptionsspektroskopie. Hier hat sich gezeigt, dass auf MR-MP2-Basis größere Abweichungen von experimentellen Daten erhalten werden, als beim Vergleich der vertikalen Anregungsenergien mit den Ergebnissen der PES.
iv
v
Inhaltsverzeichnis
Abkürzungsverzeichnis vii
1. Einleitung 1
2. Theoretischer Hintergrund 3
2.1 Photoelektronenspektroskopie 3
2.2 Franck-Condon-Prinzip 6
2.3 Dichtefunktionaltheorie 7
2.4 Multireferenz Møller-Plesset Störungstheorie 9
2.5 Gruppentheorie und Symmetrieelemente 12
3. Verwendete Methoden und technische Details 15
4. Auswertung und Diskussion 17
4.1 Vergleich MRCI und RIMR 19
4.2 Vertikale Anregungsenergien an der neutralen Struktur 25 4.3 Anregungsenergien an der kationischen Struktur 31
4.4 Ionisierungsenergien 35
5. Zusammenfassung und Ausblick 37
6. Quellenverzeichnis 38
Anhang
Charaktertafeln III
MO-Diagramme und Orbitale V
Tabellen XVIII
vi
Abkürzungsverzeichnis
MR-MP2 - Multireferenz Møller-Plesset Störungstheorie zweiter Ordnung E(MR-MP2) - Energiekorrekturterm zweiter Ordnung
RIMR - resolution of identity multi-reference MRCI - multireference configuration interaction µEh - µ-Hartree (Energieeinheit)
PES - Photoelektronenspektroskopie GS - ground state (engl. Grundzustand)
E - Energie
c.ref² - Summe der Koeffizientenquadrate des Referenzraums Anr.E - Anregungsenergie
ΔAnr.E - Differenz der Anregungsenergien verw. E - verworfene Energiesumme korr. E - Korrelationsenergie
DFT - Dichtefunktionaltheorie
ROKS - restricted open-shell Kohn-Sham Orbitale TDDFT - time-dependent density functional theory
(engl. zeitabhängige Dichtefunktionaltheorie) TDA - Tamm-Dancoff approximation
UKS - unrestricted Kohn-Sham (unbegrenzte Kohn-Sham Methode) UHF - unrestricted Hartree-Fock (unbegrenzte HF-Methode)
HOMO / H - highest occupied molecular orbital (engl. höchstes besetztes Molekülorbital)
SOMO / S - singly occupied molecular orbital (engl. einfach besetztes Molekülorbital)
LUMO / L - lowest unoccupied molecular orbital (engl. niedrigstes unbesetztes Molekülorbital)
RMSD - Root-mean-square deviation
1 1. Einleitung
In der Quantenchemie wird, wie in den meisten anderen Bereichen, danach gestrebt bestehende Verfahren zu verbessern und neue Verfahren zu finden, die bessere Ergebnisse liefern als ihre Vorgänger. Diese sollen dabei allerdings kosteneffizient bleiben.
Die Eignung der Multireferenz-Störungstheorie zweiter Ordnung (MR-MP2) für die Berechnung von Anregungsenergien der Radikalkationen kleiner aromatischer Systeme (Abbildung 1) soll in dieser Arbeit getestet werden und die Resultate mit experimentellen Daten verglichen werden.[1]
Zudem bietet die Arbeit von Hirata, Head-Gordon, Szczepanski und Vala[1], aus der die experimentellen Werte entnommen wurden, eigene Berechnungen zu den verwendeten Molekülen. Abweichend wurden dort die Anregungsenergien mittels zeitabhängiger Dichtefunktionaltheorie (TDDFT) und der Tamm-Dancoff Näherung berechnet. Die Ergebnisse beider Methoden sollen verglichen werden und, wenn möglich, festgestellt werden, ob sich eine der beiden besser zur Beschreibung kleiner aromatischer Systeme eignet.
Abbildung 1: Azulen Abbildung 2: Naphthalin Abbildung 3: Anthracen
Abbildung 4: Tetracen Abbildung 5: Acenaphthylen Abbildung 6: Pyren
Experimentell lassen sich die errechneten Anregungsenergien mittels Photoelektronen- Spektroskopie (PES) ermitteln. Verglichen werden diese mit den Anregungsenergien der Radikal-Kationen von Azulen, Naphthalin, Acenaphthylen, Anthracen, Tetracen und Pyren.
Berechnet wurden alle wichtigen Werte mit dem RIMR-Programm.
2
Zusätzlich wurden noch Anregungen mit dem MRCI-Program berechnet, dies geschah lediglich für die drei kleineren Moleküle Azulen, Naphthalin und Acenaphthylen. Im Vergleich der beiden Programme liegt die Vermutung nahe, dass die Ergebnisse ähnlich sein sollten, da beide Programme gleich aufgebaut sind. Das RIMR-Programm nutzt lediglich eine weitere Näherung.
3 2. Theoretischer Hintergrund
2.1. Photoelektronen-Spektroskopie
Zur praktischen Überprüfung der Anregungsenergien ist die PES geeignet. Mit ihr lassen sich einige elektronische Eigenschaften von Molekülen gut bestimmen bzw. unter Zuhilfenahme physikalisch-chemischen Wissens berechnen.
Die PES basiert auf dem photoelektrischen Effekt, der besagt, dass Elektronen mittels Lichteinstrahlung aus Atomen und Molekülen geschossen werden können.[2] Dies ist nur durch einen Impuls möglich, den Licht durch die Beschreibung als Teilchens, genauer als Photon, aufweist. Die dabei erhaltene kinetische Energie und damit korrelierte Geschwindigkeit (1) des herausgelösten Elektrons hängt von der Energie des eingestrahlten Photons (2) ab. Allerdings lässt sich ein Energieunterschied zwischen der Energie des eingestrahlten Photons und der kinetischen Energie des austretenden Elektrons feststellen (3), dies lässt sich durch die Bindungsenergie des Elektrons i (Ei) erklären. Die Bindungsenergie ist die Energie, die benötigt wird um das jeweilige Elektron aus dem Molekül heraus zu lösen.
� ( −) =1
2 �² (1)
�ℎ = ℎ ∗ (2)
� = �ℎ − � (3)
Die in den Formeln (1) bis (3) erhaltenen Variablen und Konstanten beschreiben die Masse des Elektrons ( = 9.1094∗10−31 kg), die Geschwindigkeit des austretenden Elektrons (�), das Plancksche Wirkungsquantum (ℎ = 6.626∗10−34 Js) und die Frequenz des eingestrahlten Lichts ( ).
Zu bemerken ist, dass der photoelektrische Effekt nur bei Einstrahlung mit Licht einer bestimmten, materialspezifischen Wellenlänge und bei kleineren auftritt. Je kleiner die Wellenlänge ( ) eines Lichtquants ist, desto größer ist seine Energie (4) (vergleiche auch (2)).
Dies lässt sich ebenfalls über die oben genannte Bindungsenergie des Elektrons erklären, da diese zunächst aufgebracht werden muss, damit das Elektron aus dem Molekül heraus gelöst wird und sich detektieren lässt.
4
= ℎ ∗ (4)
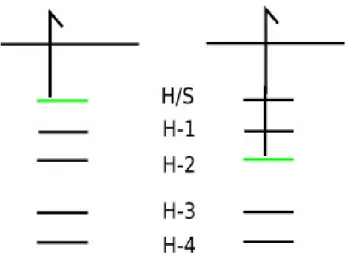
Das erhaltene PE-Spektrum enthält verschiedene Peaks denen eine Energie zugeordnet werden kann, bei dieser handelt es sich um die Energie, die benötigt wird, dass Elektron aus dem Molekül zu lösen. Da die Moleküle mit Photonen der gleichen Energie beschossen wurden, lässt sich die Energie nach (3) einfach berechnen. Je mehr Energie dem Elektron zugeordnet wird, aus einem desto energetisch tiefer liegenden Orbital wurde das Elektron herausgelöst.[3] Der erste Peak beschreibt zudem die Ionisationsenergie des Moleküls. Die Anregungsenergien werden erhalten in dem alle Peaks relativ zum ersten, dieser beschreibt den Grundzustand des Kations in der PES von neutralen Molekülen, berechnet werden, dass heißt, der erste Peak wird auf null gesetzt.
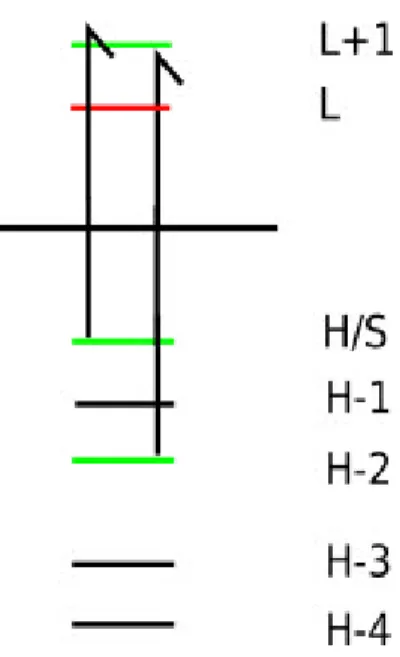
Abbildung 7: Zustände erhalten mit PES, grüne Orbitale: einfach besetztes Orbital nach Photoneneinstrahlung, schwarz:
doppelt besetztes Orbital
Die in Abbildung 7 dargestellten kationischen Zustände wurden durch Photoneneinstrahlung auf zwei neutrale Moleküle erzeugt. Im linken wurde ein Elektron aus dem HOMO geschossen, im rechten aus dem HOMO-2. Die ermittelte Energie zum entfernen des Elektrons aus dem HOMO ergibt die Ionisierungsenergie und stellt gleichzeitig den Grundzustand des Kations dar. Ebenfalls ist eine Energie für das herausschießen des Elektrons aus dem HOMO-2 ermittelt. Die Differenz der beiden Energien der Zustände ist gleich zu setzen mit der Anregungsenergie vom HOMO-2 ins HOMO/SUMO des Kations.
Gleiches gilt für die Differenz aller anderen entstandenen Zustände zum Grundzustand des Kations.
5
Allerdings sind im PES nicht alle Zustände sichtbar, die in den theoretischen Anregungsspektren berechnet werden. Dies liegt daran, das in PES jeweils ein Photon nur ein einziges Elektron anregen oder aus dem Molekül herausschießen kann.[23] Die Energie des detektierten Elektrons ist somit abhängig von einem eingestrahlten Photon. Allerdings können theoretisch auch Anregungen wie in Abbildung 8 berechnet werden, die in der PES nicht oder nur schwer zu erkennen sind.
Abbildung 8: Im PES 'unsichtbare' Anregung, Legende wie Abbildung 7, rot: leeres/virtuelles Orbital
Bei der hier dargestellten Anregung handelt es sich um das herausschießen eines Elektrons aus dem HOMO um das Kation zu erzeugen, gleichzeitig allerdings findet eine Anregung vom HOMO-2 ins LUMO+1 statt. Dieser Zustand beschreibt eine Anregung vom HOMO-2 ins LUMO+1 des Kations und ist mittels PES kaum nachweisbar, da dieser Zustand nicht mit durch wechselwirken eines Photons mit einem Elektron zustande kommt. Laut Cederbaum und Deleuze[23] lassen sich diese Zustände allerdings mit etwas Aufwand mittels PES trotzdem nachweisen, sind dabei allerdings nicht eindeutig bzw. können auch durch Verunreinigungen und andere Ursachen für ein Rauschen im Spektrum fehlinterpretiert werden.
6 2.2 Franck-Condon-Prinzip
Das Franck-Condon-Prinzip beruht auf der Annahme, dass sich die elektronische Anregung, durch die geringe Masse der Elektronen, in deutlich geringeren Zeitabständen abspielt, als die Änderung der Kernkoordinaten.[3] Deswegen kann davon ausgegangen werden, dass die Kernkoordinaten unveränderlich bleiben, dies ist analog zur Born-Oppenheimer-Näherung.
Es ist davon aus zu gehen, dass die Anregung aus der Gleichgewichtsgeometrie erfolgt, da hier die Wahrscheinlichkeitsdichte des Grundzustands, aus dem angeregt wird, am größten ist.
Das Franck-Condon-Prinzip sagt aus, dass eine vertikale Anregung in den Zustand stattfindet, bei dem die Überlappung der Wahrscheinlichkeitsdichte am größten ist.[3] Die Wahrscheinlichkeitsdichte entspricht dabei dem Quadrat der Wellenfunktion Ψ². Auch andere Anregungen sind möglich, allerdings mit deutlich geringeren Intensitäten.
Abbildung 9: Franck-Condon-Effekt[3]
7 2.3 Dichtefunktionaltheorie
Wenn nicht anders aufgeführt, ist der nachfolgende Abschnitt mit den Quellen [4] und [5] als Referenz entstanden.
Das Lösen der Schrödingergleichung (5) mittels Wellenfunktionstheorien wie der Hartree- Fock Theorie ist komplex. Wellenfunktionen hängen vom Spin und drei Raumkoordinaten jedes einzelnen Elektrons ab, wodurch sie in Mehrelektronensystemen nicht mehr direkt lösbar ist. Ebenso werden Systeme mit sehr vielen Elektronen immer komplexer, da die Wellenfunktion die Koordinaten aller Elektronen enthält, diese aber wiederum korreliert sind.
Das heißt, dass die Koordinaten jedes Elektrons abhängig sind von der Bewegung jedes anderen Elektrons.
�Ψ= Ψ (5)
Des weiteren birgt die Wellenfunktion selbst keine Informationen, stattdessen werden alle Informationen nur durch das Wirken eines Operators auf die Wellenfunktion erhalten. Die Aufenthaltswahrscheinlichkeit des Elektrons wird zum Beispiel durch das Quadrieren der Wellenfunktion erhalten.
Einfacher ist es, die Schrödingergleichung über eine physikalische Observable zu lösen, die alle nötigen Informationen beschreibt. Geeignet ist hierfür die Elektronendichte. Sie bietet sich an, da der Hamilton-Operator lediglich abhängig ist von der Position der Kerne, den Kernladungszahlen und der Gesamtanzahl der Elektronen. Die Elektronendichte ergibt integriert über den gesamten Raum die Anzahl der Elektronen (6).
= �( ) (6)
Dass die Elektronendichte eindeutig Grundzustandsenergie, Grundzustands-Hamilton- Operator und -Wellenfunktion beschreibt, wird im ersten Hohenberg-Kohn-Theorem bewiesen.[6]
Das exakte Dichtefunktional [�] ist nicht bekannt, weswegen ein etwas anderer Ansatz verwendet werden muss. Dabei wird ein Hartree-Fock ähnlicher Ansatz verwendet, bei dem die Elektronendichte über die sogenannten Kohn-Sham-Orbitale beschrieben werden. Die Kohn-Sham-Gleichung (7) ist der Hartree-Fock-Gleichung (8) ähnlich, dabei wird lediglich
8
der Austauschterm in HF durch ein Austausch-Korrelationspotential in der DFT ersetzt. Die berechnete Grundzustandsenergie des Systems ist dabei, bei Verwendung des „hypothetisch exakten Potentials“, genau. Im Gegensatz zu HF beinhaltet die Grundzustandsenergie nach DFT auch die Korrelationsenergie.[6]
ℎ�� =−12∇i2− |rZk
i−rk|+ r′
ri−r′ dr′
M
k=1 + Vxc (7)
ℎ� =−12∇i2− |rZk
i−rk| M
k=1 + i≠j rijjdr (8)
Die ROKS-Orbitale kommen bei offenschaligen Molekülen zum Einsatz. Funktionale und Wellenfunktionen werden dabei angepasst, damit sie einfach besetzte Orbitale besser beschreiben. Genutzt werden unterschiedliche Methoden. Okazaki, Sato, Yoshihiro, Ueno und Kashiwagi[7] beschreiben die Trennung der Elektronendichte in die Dichte für alpha- und beta-Spin Elektronen (9). Für Elektronen in halb besetzten Orbitalen wird alpha-Spin angenommen. Demnach werden die Terme, aus denen die Funktionale bestehen, über den unterschiedlichen Spin genauer beschrieben.
�= � +� (9)
Eine andere Methode wurde von Roemelt, Maganas, DeBeer und Neese[8] beschrieben. In ihrer Arbeit werden die Kohn-Sham Matrizen über die voll besetzten Orbitale und die halb besetzten Orbitale getrennt beschrieben.
Alternative Herangehensweisen wären die Verwendung von unrestricted Kohn-Sham (UKS) Methoden oder unrestricted Hartree-Fock Methoden (UHF). Durch diese Methoden erhaltene Wellenfunktionen haben allerdings den Nachteil, dass sie keine exakten Eigenfunktionen des Quadrats des Drehimpulsoperators sind.[7] In Berechnungen mit UKS-Methoden sind immer Einflüsse durch den Elektronenspin enthalten, wodurch die Berechnungen unzuverlässig werden bei der Untersuchung von offenschaligen Molekülen. Eine Verbesserung der Wellenfunktionen wird durch das Ausprojizieren der Anteile mit anderen Spinmultiplizitäten erreicht, allerdings sind solche Berechnungen sehr Zeit- und Kosten aufwändig, weswegen sie sich meist nicht lohnen.[7]
9
2.4 Multireferenz Møller-Plesset Störungstheorie
Anregungen lassen sich bereits gut mit DFT -Methoden berechnen, sodass zu experimentellen Daten vergleichbare Ergebnisse erhalten werden, allerdings lassen sich durch Verwendung der DFT-Methoden keine systematischen Verbesserungen erzielen. Dies liegt daran, dass es kein Funktional gibt, das gleichzeitig die Potentiale in Kernnähe, aber auch im molekularen Randbereich ausreichend gut beschreibt.[6] Einige DFT-Methoden bieten allerdings noch weitere Nachteile. Mittels TDDFT lassen sich nur Einfachanregungen gut berechnen.[1][9]
Zudem werden in der TDDFT nur gemittelte Austausch-Korrelations-Funktionale verwendet, wodurch die gesamte Methode nur näherungsweise gute Ergebnisse liefert.[9]
Bessere Lösungen bieten hier störungstheoretische Ansätze. Die Störungstheorie der Quantenchemie versucht im Allgemeinen eine Wellenfunktion mittels Störung zu verbessern.
Die betrachtete Störung liegt in der Differenz zwischen der wahren Elektron-Elektron- Wechselwirkung und der genäherten Elektron-Elektron-Wechselwirkung der HF-Theorie.[6]
Die Schrödingergleichung (5) ändert sich in der Störungstheorie. Dabei wird der tatsächliche Hamiltonoperator beschrieben über die Summe eines ungestörten Hamiltonoperators und den gestörten Hamiltonoperator, der Faktor λ ist der Störparameter.[5]
�Ψ= (�0+λ�′)Ψ= Ψ (10)
Demnach sind sowohl die Eigenfunktion Ψ sowie der Eigenwert E des Hamiltonoperators von λ abhängig. Für den Fall, dass keine Störung vorliegt, = 0, entspricht der tatsächliche Hamiltonoperator dem ungestörten Hamiltonopertator (11).
�Ψ=�0Ψ (11)
Gleiches gilt auch für die Wellenfunktion und die Energie des Systems, da diese Eigenfunktion und Eigenwert des Hamiltonoperators sind. Für den Fall, das eine Störung vorliegt, > 0, lassen sich die Wellenfunktion (12) und die Energie (13) als Taylorreihe beschreiben.
Ψ= Ψ =0+∂Ψ
∂λ =0 +∂2Ψ
∂λ2 =0 2
2! + … (12)
10
= =0 +
=0 + 22
=0 2
2! + … (13)
Durch die Einführung der beiden Korrekturterme k-ter Ordnung (14), werden die beiden Taylorreihen gekürzt zu (12.2) und (13.2).[5]
Ψ( ) = 1
!
∂kΨ
∂λk =0
( )= 1
! =0 (14)
Ψ=Ψ(0)+ Ψ(1)+ 2Ψ(2)+⋯+ Ψ( )+⋯ (12.2)
E = (0)+ (1)+ 2 (2)+⋯+ ( )+⋯ (13.2)
Für diese Taylorreihen werden meist nur die ersten Terme verwendet, die hinreichend genaue Ergebnisse liefern sollten.[5] Wie viele der Terme tatsächlich genutzt werden, ist allerdings im wesentlichen von der Methode und der gewünschten Genauigkeit abhängig.
Die Wellenfunktion ist normiert, Ψ(0) Ψ(0) = 1, und alle gestörten Wellenfunktionen müssen orthogonal zur ungestörten Wellenfunktion sein, Ψ(0) Ψ( ) = 0. Unter diesen Bedingungen lassen sich die Korrekturen erster und zweiter Ordnung in wenigen Schritten herleiten. Die Herleitungen sowie die genauen Energie- und Wellenfunktionskorrekturen lassen sich in der Literatur nachlesen: [4], [5], [10]
Zu bemerken ist hier lediglich, dass sich die Korrekturen jeweils mit Hilfe der gestörten Wellenfunktion und dem gestörten Hamiltonoperator –2 Ordnung berechnen lassen.
Die im folgenden beschriebene Møller-Plesset Störungstheorie ist in weiten Teilen aus den Literaturquellen [6] und [15] entnommen, wenn nicht anders vermerkt.
In der Störungstheorie wird von einer ungestörten Wellenfunktion Ψ(0) ausgegangen. In der MR-MP2 Theorie, ist diese basiert auf einer CI-Referenzfunktion nullter Ordnung (15).
Ψ(0)= Ψ0 (15)
Zur Beschreibung einer Störung reicht eine ungestörte Wellenfunktion nicht aus. Deswegen werden ebenfalls Wellenfunktionen höherer Ordnung definiert. Die Wellenfunktion erster
11
Ordnung wird über die Konfigurationen Ψ1 erzeugt, die durch Einfach- und Doppelanregungen von Ψ0 erhalten werden (16).
Ψ(1)= Ψ1 (16)
Die in (17) enthaltenen Anregungsoperatoren beschreiben die Anregungen von den besetzten Orbitalen r und s in die unbesetzten Orbitale p und q.
Ψ1 ≡Erp Ψ0 ∪erspq Ψ0 (17)
Der ungestörte Hamiltonoperator ist ebenfalls von Bedeutung für die Störungstheorie. Er ist wichtig für die Störung � =� − �0, wobei � dem tatsächlichen Hamiltonoperators des gestörten Systems entspricht. Durch die Orthogonalität der Funktionsräume nullter (Ψ(0)) und erster Ordnung (Ψ(1)), entspricht �0 (18). Dabei beschreiben � und � Projektoren auf die Funktionsräume nullter und erster Ordnung und die Summe an spin-gemittelter Einteilchen- Fockoperatoren (�) (19). Die Matrixelemente der Fockoperatoren haben bezüglich der Raumorbitale r und s die in (20) beschriebene Form.
�0 = �0 �0+� � +⋯ (18)
= � (�) (19)
= ℎ + [ − 2 ] (20)
In (20) entspricht ℎ dem Einelektronen-Hamiltonian und ist ein Element der Dichtematrix erster Ordnung für die ungestörte Wellenfunktion. Somit erhaltene Energiekorrekturen sind unveränderlich bezüglich der Rotation aller besetzten und unbesetzten Orbitale des Systems.
Der Koeffizient aus Gleichung (16) lässt sich durch das Lösen der inhomogenen Gleichungen (21) im Folgenden berechnen:
Ψ1 �0 − 0 Ψ1 =− Ψ1 � Ψ(0) (21)
12
Die Møller-Plesset Störungstheorie wird meist bist zur zweiten Ordnung berechnet (MR-MP2), allerdings sind auch Berechnungen mit Störungen höherer Ordnung möglich (MP3 oder MP4), diese werden hier allerdings nicht weiter aufgeführt.
Die Energiekorrektur zweiter Ordnung E(MR-MP2) lässt sich nach folgender Formel berechnen (22)
MR−MP2 = − Ψ1 � Ψ(0) (22)
Zur Verbesserung der Ergebnisse ist es ebenfalls möglich, den Fockoperator anzupassen, da der in (20) beschriebene Operator eine nicht immer geeignete Beschreibung offenschaliger gegenüber geschlossenschaliger Zustände liefert.[6]
Im verwendeten Program RIMR wird noch die RI-Näherung (Resolution of the Identity) verwendet, dabei werden die Mehrzentrenintegrale vereinfacht. Im speziellen die Vierzentren- Integrale durch einfacher zu berechnende Zwei- und Dreizentren-Integrale beschrieben (23).
� = ( �) (23)
"Da aber die Multiplikation rechenintensiv ist, ist die Verwendung von RI nur dort sinnvoll, wo, wie beim Coulombteil von HF und DFT, auf diese Multiplikation verzichtet werden kann, weil die Dreizentrengrößen direkt zur Coulomb-Matrix bzw. -energie kontrahiert werden können, oder aber transformierte Integrale gebildet werden müssen, deren Berechnung auf dem konventionellen Weg sehr aufwändig ist, wie zum Beispiel bei MP2."[24]
2.5 Gruppentheorie und Symmetrieelemente
Der nachfolgende Abschnitt soll nur einen groben Überblick verschaffen, wodurch sich die irreduzible Darstellung der einzelnen Anregungszustände verändern kann. Dies kann bei unterschiedlichen Rechnungen oder Methoden passieren, wodurch im Vergleich zwischen der eigenen Rechnung und einem Vergleichswert der selbe Anregungszustand mit einer leicht veränderten Symmetrie angegeben wird.
13
Eine ausführlichere Erklärung zu diesem Thema findet sich in Quantentheorie der Moleküle von Joachim Reinhold[10], aber auch andere Literaturquellen bieten ausführlichere Informationen.
Im Anhang auf Seite IV befinden sich die beiden Charaktertafeln der in dieser Arbeit wichtigen Punktgruppen, mit diesen werden die nachfolgenden Erklärungen verdeutlicht.
Zunächst sind in der ersten Spalte die einzelnen irreduziblen Darstellungen aufgeführt, die die jeweilige Punktgruppe besitzt. In der ersten Zeile sind die Symmetrieoperationen aufgeführt, die die jeweilige Punktgruppe auszeichnet. Die einzelnen Zellen der Charaktertafeln beinhalten die Information, ob die jeweilige irreduzible Darstellung symmetrisch (1) oder antisymmetrisch (-1) bezüglich des jeweiligen Symmetrieoperators sind. Für diese beiden Punktgruppen wichtige Symmetrieelemente sind die Einheit E, C2-Drehachsen C2, Spiegelebenen σ und das Inversionszentrum i. Zusätzlich ist bei den Drehachsen angegeben zu welcher Achse des Koordinatensystems (x, y oder z im dreidimensionalen Raum) diese parallel ist und bei den Spiegelebenen in welcher Ebene des Raums (xy, xz oder yz) sie sich aufspannt.
Wenn die zu berechnenden Moleküle für verschiedene Rechnungen mit unterschiedlichen Programmen modelliert werden, muss die Anordnung des Moleküls nicht die selbe sein, da jedes Programm die Moleküle in andere Raumrichtungen ausrichten kann. Durch die unterschiedliche Anordnung im Raum verändern sich die Symmetrieoperationen, die für den jeweiligen Anregungszustand durchgeführt werden können. Dies hat dann zur Folge, dass sich die irreduzible Darstellung dieser Zustände ändert. Allerdings können nicht irgendwelche irreduzible Darstellungen vertauscht werden, sondern nur solche, die bei Umorientierung im Raum ineinander überführt werden.
Die A1 bzw. Ag Zustände sind total symmetrisch bezüglich Inversion und Spiegelungen, wohingegen A2 bzw. Au Zustände total antisymmetrisch diesbezüglich sind. Zustände mit diesen Symmetrien weisen diese Symmetrie immer auf, unabhängig davon wie das Molekül im Raum angeordnet ist. Im Gegensatz dazu kann es je nach Anordnung passieren, dass bei C2v Molekülen die Zustände B1 und B2 vertauschen. Beide sind antisymmetrisch bezüglich der Drehung um die C2-Achse, allerdings ändert sich die Symmetrie der beiden irreduziblen Darstellungen bezüglich der beiden Spiegelebenen. Wird ein planares Molekül zwischen den beiden Programmen so gedreht, dass es einmal z.B. in der xz-Ebene liegt und einmal in der yz-Ebene, dann vertauschen die Symmetrien der Zustände B1 und B2.
14
Ähnliches geschieht, wenn ein Molekül der Punktgruppe D2h im Raum gedreht wird. Hier gilt allerdings, dass nur die Zustände B1g, B2g und B3g bzw. B1u, B2u und B3u miteinander vertauschbar sind. Dies liegt daran, dass die Bng-Zustände symmetrisch bezüglich Inversion und einer Spiegelung, sowie antisymmetrisch bezüglich der anderen beiden Spiegelungen sind, die Bnu-Zustände sind allerdings antisymmetrisch bezüglich Inversion und einer Spiegelung, sowie symmetrisch bezüglich der beiden anderen Spiegelungen. Alleine die unterschiedliche Symmetrie der Inversion betreffend verhindert, dass Bng- mit Bnu-Zuständen tauschen. Zusätzlich muss hier berücksichtigt werden, dass nur jeweils zwei der irreduziblen Darstellungen tauschen können. Sind die Zustände B2u und B3u im Vergleich zu Literaturquellen vertauscht, dann gilt somit gleichzeitig, dass B1u-Zustände in der Literatur und der eigenen Rechnung als diese aufgezählt werden müssen, ansonsten handelt es sich um eine andere Anregung.
15
3. Verwendete Methoden und technische Details
Die durchgeführten Geometrieoptimierungen wurden alle mit dem Turbomole 7.0 Programmpaket[11][12][13] durchgeführt. Alle Moleküle, sowohl in kationischer als auch in neutraler Struktur, wurden unter Verwendung des B3-LYP Hybrid-Dichtefunktionals und des SV(P) Basissatzes mit jobex[12][13] optimiert. Dabei wurde die Symmetrie der Moleküle ebenfalls berücksichtigt. Azulen und Acenaphthylen wurden in C2v-Symmetrie optimiert, Naphthalin, Anthracen, Tetracen und Pyren hingegen unter Vorgabe der D2h-Symmetrie. Im Anschluss wurde mit aoforce[19][20][21] eine Frequenzanalyse durchgeführt um zu verifizieren, dass es sich tatsächlich um eine Minimumstruktur und keinen Übergangszustand handelt. Die Einelektronenintegrale wurden mit oneint und die Zweielektronenintegrale mit ritraf berechnet. Mit Hilfe des Programms Dalton[14] wurden die ROKS-Orbitale berechnet, die für offenschalige Systeme gut geeignet sind. Zusätzlich wurde das Funktional von B3-LYP in BH-LYP geändert. Im Anschluss wurden alle kernnahen Molekülorbitale mit einer Energie unterhalb -10 Hartree eingefroren, da aus diesen Orbitalen keine Anregungen stattfinden, ebenfalls wurden alle virtuellen Orbitale oberhalb einer Energie von zwei Hartree eingefroren.
Grund dafür ist, dass diese Orbitale energetisch zu hoch liegen, damit eine Anregung in diese stattfinden kann.
Die Anregungen wurden für alle Moleküle in kationischer und neutraler Geometrie unter Verwendung des RIMR-Programms[15][6] mittels MR-MP2 berechnet. Zusätzlich wurden mit Hilfe des MRCI-Programs[15][16][17] die Anregungen für die kleinen Moleküle, Naphthalin, Azulen und Acenaphthylen, unter Verwendung der neutralen Geometrie berechnet um beide Programme miteinander vergleichen zu können. In beiden Programmen wurde allerdings nicht wie in [15] HF-Orbitale, sondern BH-LYP-Orbitale verwendet. Dabei wurde die Multireferenz-Störungstheorie zweiter Ordnung mit g0-Operator verwendet. Die Verwendung der g0-Option bedeutet, dass der ungestörte Fockoperator für die durchgeführten Berechnungen verwendet wurde. In RIMR wurden die Anregungen mit einem $esel-Wert 0.1 und 0.01 berechnet, in MRCI nur mit einem $esel-Wert 0.1. Der $esel-Wert ist in beiden Programmen ein Selektionsschwellwert. Er definiert ab welchem Wert Konfigurationen ausgewählt werden und ist in der Einheit µEh angegeben.
In den jeweiligen Inputs wurden für jedes Molekül noch weitere Angaben gemacht. So wurde die Anzahl der beteiligten Elektronen und Orbitale festgelegt, die an den Anregungen
16
teilnehmen sollten und zusätzlich die Anzahl der berechneten Zustände (im weiteren Wurzeln genannt) für jede irreduzible Darstellung / Art der Anregung.
Die genauen Inputs wurden für jede Rechnung / jeden Vergleich neu gewählt und finden sich deswegen in der Auswertung und Diskussion im jeweiligen Abschnitt. Dabei ist zu beachten, dass nach durchgeführten Berechnung, auf Basis der erhaltenen Ergebnisse, von beiden Programmen (RIMR und MRCI) ein neuer Referenzraum vorgeschlagen und in einer weiteren, als neuer Input möglichen, Datei ausgegeben wird. Bei dieser iterativen Bestimmung des Referenzraums werden noch weitere Anregungen für den Referenzraum berücksichtigt, die durch das Programm als relevant berechnet werden und nicht durch Schwellwerte, wie z.B. den $esel-Wert, aussortiert werden, dabei allerdings nicht im Referenzraum der vorangegangenen Rechnung liegen.
17 4. Auswertung und Diskussion
Bevor die Ergebnisse aufgelistet und diskutiert werden, sind zunächst die irreduziblen Darstellungen der Grundzustände der Moleküle aufgelistet. Zusätzlich ist angegeben, welche Punktgruppe die Moleküle haben. Diese sind für alle Rechnungen und den jeweiligen Input von Bedeutung:
Tabelle 1: Molekülsymmetrien bei vorausgesetzter neutraler Geometrie
Molekül Punktgruppe irr. Darstellung GS
Acenaphthylen+ C2v b2
Anthracen+ D2h b2g
Azulen+ C2v a2
Naphthalin+ D2h au
Pyren+ D2h b2g
Tetracen+ D2h au
Für die Benennung der Orbitale gibt es einen Sonderfall. Alle doppelt besetzten Orbitale sind energetisch absteigend mit HOMO-1 (H-1), HOMO-2 (H-2), HOMO-3 (H-3), usw.
bezeichnet, die unbesetzten Orbitale energetisch aufsteigend mit LUMO (L), LUMO+1 (L+1), LUMO+2 (L+2) usw. Das einfach besetzte Orbital ist als HOMO/SOMO bezeichnet und wird in den Tabellen mit S abgekürzt. Ein als HOMO (H) bezeichnetes Molekülorbital ist bei den Kationen in dieser Arbeit nicht bezeichnet, sondern gilt als das höchste mit zwei Elektronen besetzte Orbital der neutralen Moleküle.
Auf der nachfolgenden Seite sind die MO-Diagramme aller sechs Kationen aufgeführt, verwendet wurden dabei die ROKS-Orbitalstrukturen und -energien an der neutralen Geometrie. Die blau markierten Orbitale sind dabei alle besetzten, einfach und doppelt, unbesetzte sind rot. Bilder zum Aussehen der hier aufgeführten Orbitale finden sich im Anhang (I: Orbitalbilder zu den MO-Diagrammen). Das jeweils energetisch höchste blau markierte Orbital in jedem Diagramm ist das HOMO/SOMO.
18
Abbildung 10: MO-Diagramm (ROKS) des Acenaphthylenkations
Abbildung 11: MO-Diagramm (ROKS) des Azulenkations
Abbildung 12: MO-Diagramm (ROKS) des Anthracenkations
Abbildung 13: MO-Diagramm (ROKS) des Naphthalinkations
Abbildung 14: MO-Diagramm (ROKS) des Pyrenkations
Abbildung 15: MO-Diagramm (ROKS) des Tetracenkations
19 4.1 Vergleich MRCI und RIMR
Für einen Vergleich der beiden Programme ist es von Bedeutung, dass der Input für die erste Rechnungen mit beiden Programmen, jeweils für das selbe Molekül, gleich ist. Eine Änderung des Referenzraums hätte zur Folge, dass Anregungen in die Berechnungen mit einbezogen werden, die vorher nicht von Bedeutung waren und somit können sich auch Energien und andere Werte verändern und verlieren eventuell ihre Vergleichbarkeit. Durch die iterative Bestimmung des Referenzraums geht allerdings ein Teil der Vergleichbarkeit verloren.
Für die Moleküle Acenaphthylen und Azulen wurden für den Referenzraum elf Elektronen aus den höchsten sechs besetzten Orbitalen und zusätzlich die sechs untersten unbesetzten Orbitale verwendet und mit diesem für jede irreduzible Darstellung fünf Wurzeln berechnet, lediglich für die Darstellung, in der auch der Grundzustand liegt, wurden sechs berechnet, Grundzustand und fünf Anregungen. Der Referenzraum des Naphthalins wurde auf neun Elektronen in den fünf obersten besetzten und die fünf niedrigsten unbesetzten Orbitale festgelegt und für jede irreduzible Darstellung vier Anregungen berechnet. Wiederum wurde die Wurzel für die Darstellung in dem der Grundzustand liegt um eins erhöht.
Betrachtet werden nur der Grundzustand, jene Zustände, die im späteren Verlauf mit Literaturwerten verglichen werden, und alle weiteren, die nicht in der Literaturquelle aufgeführt werden, allerdings in den Programmen RIMR und MRCI unter den verwendeten Methoden energetisch zwischen den in der Literaturquelle aufgeführten liegen. Ein Vergleich mit experimentellen Werten entfällt, da hier der anfängliche Input nicht verbessert wurde und somit hohe Abweichungen entstehen können.
In der nachfolgenden Tabelle 2 sind die berechnete Anregungsenergie (Anr.E) und die Summe des Koeffizientenquadrats der im Referenzraum liegenden Anregungen (c.ref²) aufgeführt, in Tabelle 3 die berechneten Ergebnisse der verworfenen Energiesummen (verw.
E) sowie der Korrealationsenergie (korr. E). Die Energien der einzelnen angeregten Zustände werden nicht aufgeführt, da diese über die jeweilige Anregungsenergie verglichen werden.
Die Anregungsenergie berechnet sich aus der Differenz zwischen Energie des Zustands und Energie des Grundzustands.
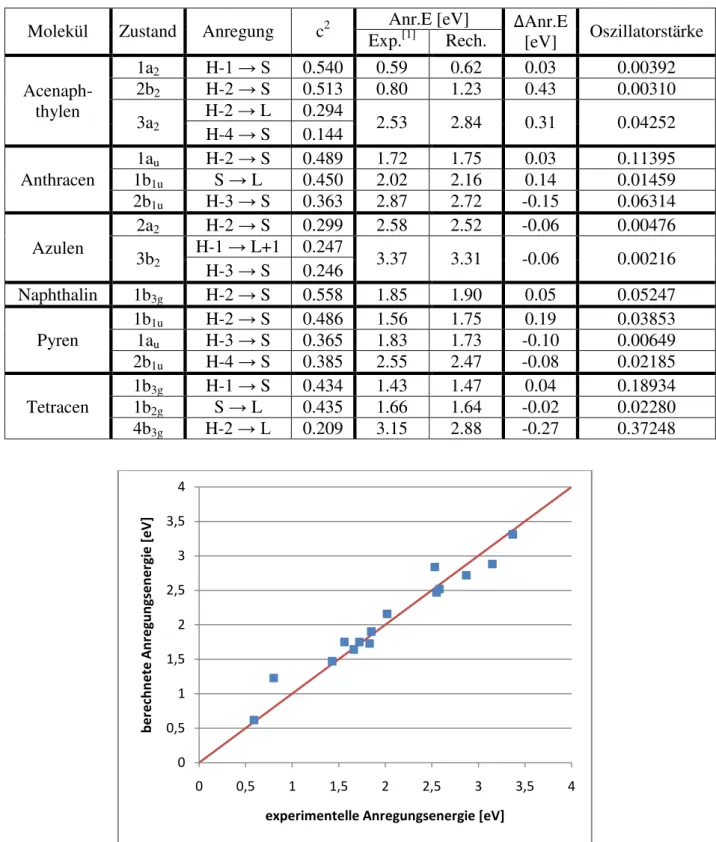
Die einzelnen Anregungen der Zustände mit einem Anteil über einem Prozent, sowie ihr Anteil können im Anhang Tabellen (Tabelle T12 bis T17) gefunden werden.
20
Vorab sollte erwähnt werden, dass der 2a2 Zustand im Acenaphthylen in der Berechnung mit RIMR Programm energetisch höher liegt, als die im späteren Verlauf dieser Bachelorarbeit mit der Literatur[1] verglichenen Anregungen, deswegen ist sie als letztes aufgeführt.
Allerdings liegt dieser Zustand in der Berechnung mit MRCI zwischen 2b2 und 3b2, weswegen er hier mit aufgeführt ist. Diese Abweichung eines Zustands tritt nur beim 2a2 des Acenaphthylens auf und bei keinem der anderen untersuchten.
Tabelle 2: wichtige Daten aus den MR-MP2 Rechnungen im Vergleich des MRCI- und RIMR-Programms
Molekül Zustand
MRCI RIMR
ΔAnr.E [eV]
Anr.E [eV]
c.ref² Hauptanr. Anr.E [eV]
c.ref² Hauptanr.
Acenaph- thylen+
1b2 - 0.668 - - 0.685 - -
1a2 0.31 0.653 H-1 → S 0.35 0.681 H-1 → S 0.04 2b2 0.89 0.659 H-2 → S 0.96 0.686 H-2 → S 0.06 3b2 2.42 0.652 H-3 → S 2.31 0.674 H-3 → S 0.11 3a2 2.46 0.647 H-4 → S 2.53 0.677 H-4 → S 0.07 2a2* 2.38 0.650 S → L 2.69 0.681 S → L 0.31
Azulen+
1a2 - 0.705 - - 0.722 - -
1b2 1.08 0.695 H-1 → S 1.13 0.721 H-1 → S 0.05 2a2 2.40 0.691 H-2 → S 2.46 0.718 H-2 → S 0.06 2b2 2.52 0.684 S → L 2.61 0.716 S → L 0.09 3a2 2.82 0.691 H-1 → L 2.77 0.714 H-1 → L 0.04 3b2 3.08 0.687 H-3 → S 3.11 0.713 H-3 → S 0.04 4a2 3.26 0.679 H-1 → L 3.31 0.708 H-1 → L 0.05 1a1 3.53 0.662 H-4 → S 3.61 0.698 H-4 → S 0.08
Naphthalin+
1au - 0.711 - - 0.723 - -
1b1u 0.71 0.706 H-1 → S 0.74 0.724 H-1 → S 0.03 1b3g 1.75 0.697 H-2 → S 1.82 0.720 H-2 → S 0.07 1b2g 2.57 0.691 H-3 → S 2.62 0.716 H-3 → S 0.05 1ag 2.96 0.676 H-4 → S 2.87 0.706 H-4 → S 0.09 1b1g 3.13 0.657 H-5 → S 3.32 0.667 H-5 → S 0.19 2b2g 3.39 0.688 S → L 3.36 0.715 S → L 0.03
21
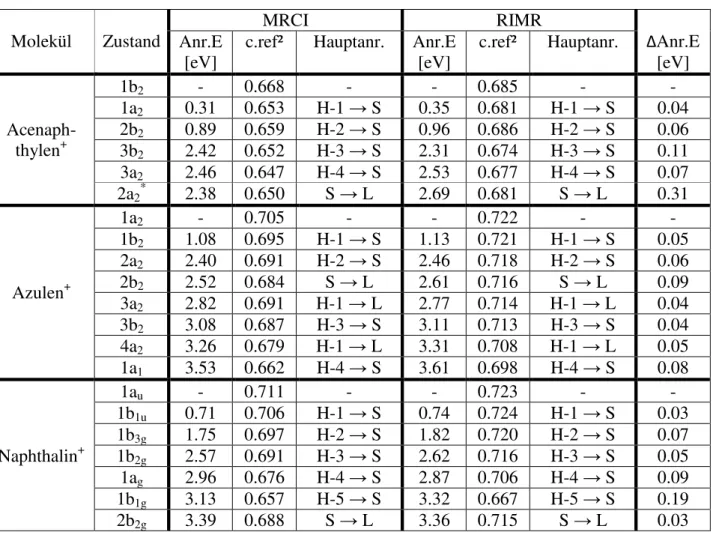
Abbildung 16: Korrelationsdiagramm der Anregungsenergien berechnet mit MRCI und RIMR
Für die Grundzustandsenergien fällt auf, dass diese mit RIMR für alle drei Moleküle höher berechnet wurde als mit MRCI. Dabei ist die Abweichung beim Naphthalin mit 0.18 eV noch am geringsten, aber auch Azulen (0.21 eV) und Acenaphthylen (0.30 eV) weisen ähnliche Abweichungen auf. Zudem ist c.ref² der einzelnen Zustände in RIMR für jeden Zustand höher als in MRCI, was bedeutet, dass die Anteile der Anregungen, die im Referenzraum liegen, in RIMR größer sind oder durch die iterative Bestimmung des Referenzraums mehr Anregungen in diesem liegen. Das Koeffizientenquadrat beschreibt den Anteil der jeweiligen Anregung am betrachteten Zustand, somit beschreibt die Summe der Koeffizientenquadrate der im Referenzraum liegenden Anregungen den Anteil der Anregungen für den Zustand die im Referenzraum liegen. Für die hier betrachteten Moleküle sinkt im allgemeinen c.ref² bei steigender Anregungsenergie, was damit zusammenhängt, dass in den höheren Anregungen die Wahrscheinlichkeit für Anregungen aus den tiefen Orbitalen wahrscheinlicher wird.
Die Anregungsenergien aus Tabelle 2 sind zusätzlich in den Abbildungen 14 bis 16 graphisch dargestellt.
0 0,5 1 1,5 2 2,5 3 3,5 4
0 0,5 1 1,5 2 2,5 3 3,5 4
Anregungsenergie RIMR [eV]
Anregungsenergie MRCI [eV]
22
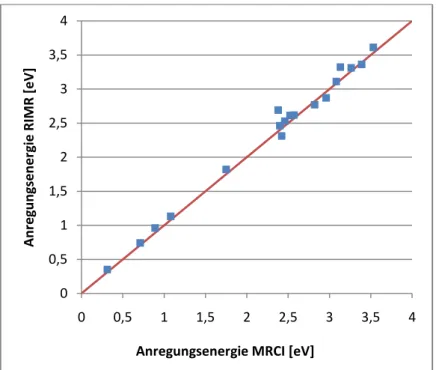
Abbildung 17: MR-MP2 Anregungsenergien der ersten Zustände des Acenaphthylens
Abbildung 18: MR-MP2 Anregungsenergien der ersten Zustände des Azulens
Abbildung 19: MR-MP2 Anregungsenergien der ersten Zustände des Naphthalins 0,0
0,5 1,0 1,5 2,0 2,5 3,0
1a2 2b2 3b2 3a2 2a2
Energie [eV]
Zustand
Acenaphthylen
MRCI RIMR
0,0 1,0 2,0 3,0 4,0
1b2 2a2 2b2 3a2 3b2 4a2 1a1
Energie [eV]
Zustand
Azulen
MRCI RIMR
0,00 1,00 2,00 3,00 4,00
1b1u 1b3g 1b2g 1ag 1b1g 2b2g
Energie [eV]
Zustand
Naphthalin
MRCI RIMR
23
Im Vergleich der Anregungsenergien in den beiden Programmen ist zu erkennen, dass meistens die Anregungsenergie mit RIMR größer berechnet wird. Davon abweichend wurden die Energien in den folgenden Zuständen mittels MRCI als größerer Wert berechnet:
Acenaphthylen 3b2; Azulen 3a2; Naphthalin 1ag und 2b2g. Da die Zustände unterschiedlicher Art sind lässt sich hier keine Regelmäßigkeit feststellen.
Lässt man den 2a2 Zustand des Acenaphthylens außen vor, liegt der Betrag des Unterschieds in der Anregungsenergie (ΔAnr.E), berechnet nach (24), in den beiden Programmen zwischen 0.03 eV und 0.19 eV. Die Unterschiede in den meisten Zuständen liegen zwischen 0.03 eV und 0.07 eV, lediglich fünf der 17 angeregten Zustände, exklusive 2a2 des Acenaphthylens, haben größere Abweichungen.
�� . = |� . RIMR − � . MRCI | (24)
Tabelle 3: verworfene Energiesumme und Korrelationsenergie berechnet mit MRCI und RIMR
Molekül Zustand
MRCI RIMR Δ(RIMR-MRCI)
verw. E
[eV] korr. E
[eV] verw. E
[eV] korr. E
[eV] verw. E
[eV] korr. E [eV]
Acenaph- thylen+
1b2 -2.47 -34.74 -3.18 -33.69 -0.71 1.05 1a2 -2.42 -35.78 -3.48 -34.15 -1.06 1.63 2b2 -3.32 -35.56 -4.15 -33.95 -0.83 1.61 3b2 -4.21 -36.07 -5.17 -35.00 -0.96 1.07 3a2 -5.37 -36.60 -6.63 -35.28 -1.26 1.32 2a2* -5.75 -36.53 -5.64 -34.76 0.11 1.77
Azulen+
1a2 -1.33 -29.16 -2.07 -28.08 -0.74 1.08 1b2 -1.59 -29.86 -2.51 -28.38 -0.92 1.48 2a2 -2.49 -30.05 -3.62 -28.83 -1.13 1.22 2b2 -2.32 -30.34 -3.15 -28.83 -0.83 1.51 3a2 -2.63 -29.98 -3.40 -28.94 -0.77 1.04 3b2 -3.13 -30.44 -4.09 -29.27 -0.96 1.17 4a2 -2.59 -30.75 -3.76 -29.46 -1.17 1.29 1a1 -1.84 -32.03 -3.04 -30.13 -1.20 1.90
Naphthalin+
1au -1.02 -28.61 -1.44 -27.77 -0.42 0.84 1b1u -1.15 -28.93 -1.92 -27.83 -0.77 1.10 1b3g -1.37 -29.51 -2.26 -28.13 -0.89 1.38 1b2g -1.25 -29.67 -2.21 -28.35 -0.96 1.32 1ag -1.20 -31.04 -2.44 -29.35 -1.24 1.69 1b1g -0.94 -32.12 -1.49 -31.54 -0.55 0.58 2b2g -1.42 -29.74 -2.53 -28.45 -1.11 1.29
24
Für die verworfene Energiesumme und die Korrelationsenergie ist zunächst auffällig, dass die verworfene Energiesumme in RIMR vom Betrag her in fast allen Zuständen größer ist als in MRCI und die Korrelationsenergie vom Betrag her immer kleiner. Einzige Ausnahme bildet der 2a2 Zustand des Acenaphthylens, hier ist die verworfene Energiesumme in RIMR vom Betrag her kleiner als in MRCI.
Die Unterschiede in der Korrelationsenergie liegen meist zwischen 1.00 eV und 2.00 eV, lediglich die Zustände 1au (0.84 eV) und 1b1g (0.58 eV) des Naphthalins weisen geringere Abweichungen zwischen den beiden Programmen auf. Für die verworfene Energiesumme lässt sich eine ähnliche Tendenz finden, hier liegen die meisten Abweichungen zwischen -0.70 eV und -1.26 eV. Ebenfalls zeigen hier der 1au- (-0.42 eV) und 1b1g-Zustand (-0.55 eV) des Naphthalins andere Abweichungen, allerdings ist die verworfenen Energiesumme zusätzlich im 2a2-Zustand des Acenaphthalens als einziger Zustand mit RIMR größer berechnet worden als in MRCI.
Die Unterschiede zwischen den beiden Programmen sind vor allem in der Anregungsenergie größer als erwartet. Im Durchschnitt, ohne 2a2 des Acenaphthylens, liegen diese bei etwa 0.07 eV. Bei der Suche nach der Ursache wurde eine unterschiedliche Konfiguration der beiden Programme gefunden. Der $sthr-Wert gibt an, welche Anregungen für weitere Rechnungen, mit iterativer Bestimmung des Referenzraums, berücksichtigt werden. Dabei werden in MRCI Anregungen mit ² < $ ℎ nicht weiter berücksichtigt. Dieser Wert ist standardmäßig auf 0.003 festgelegt. In RIMR bestimmt dieser Wert ebenfalls einen Selektionswert für Anregungen, hier allerdings werden Anregungen verworfen deren Wert der Amplitude in intermediärer Normierung geringer ist als $sthr. Vorgegeben war ein Wert von 0.02, anders als beschrieben.[6] Quadriert man diesen Wert beziehen sich diese immer noch nicht auf die Koeffizienten, somit sind beide Werte nicht vergleichbar. Damit ist keine exakte Vergleichbarkeit der beiden Programme gegeben, es kann nur versucht werden, diese möglichst genau anzugleichen.
Durch den anderen Ausschlusswert wurden mit RIMR für die zweite und dritte iterative Berechnung deutlich mehr Referenzen verwendet, als in MRCI. Zum Beispiel wurden für die zweite Berechnung des Naphthalins 1351 Referenzen mit RIMR-Programm und nur 467 Referenzen mit MRCI-Programm verwendet. Für die dritte iterative Rechnung wurden dann mit MRCI-Programm 481 Referenzen verwendet, während im RIMR-Programm immer noch 1351 angegeben waren. Durch diesen Unterschied geht die tatsächliche Vergleichbarkeit der
25
beiden Programme verloren, allerdings ist deswegen davon aus zu gehen, dass die Ergebnisse mittels RIMR-Programm genauer sind und dies nicht nur durch die Verwendung einer weiteren Näherung, sondern auch durch die höhere Anzahl an Referenzen für weitere Berechnungen.
Im nächsten Abschnitt sollen für den besseren Vergleich die Anregungen des Acenaphthylens nach der ersten Berechnung verglichen werden, dabei wird allerdings der 2a2-Zustand vernachlässigt. In diesen Ergebnissen wird eine Abweichung durch die iterative Verbesserung des Referenzraums, und dabei unterschiedlicher verwendeter Schwellwerte ($sthr-Wert) in den beiden Programmen, ausgeschlossen, da auf die Verbesserung durch die Programme vorgeschlagene Referenzen verzichtet wird.
Tabelle 4: Anregungsenergien des Acenaphthylenkations
Molekül Zustand
MRCI RIMR ΔAnr.E
MP2 [eV]
Anr.E MP2 [eV]
c.ref² Anr.E MP2 [eV]
c.ref²
Acenaph- thylen+
1b2 - 0.667 - 0.667 -
1a2 0.3342 0.653 0.3345 0.653 0.0003
2b2 0.8232 0.652 0.8229 0.652 0.0003
3b2 2.2406 0.627 2.2399 0.627 0.0007
3a2 2.4578 0.641 2.4579 0.641 0.0001
Der Unterschied im Wert der MP2 Rechnung, die in dieser Arbeit betrachtet wird, entsteht durch die bereits angesprochene, weitere Näherung in RIMR. Hier ist ebenfalls zu erkennen, dass der Unterschied zwischen beiden Programmen wie erwartet gering ist. Die größeren Unterschiede, die in den Tabellen 2 und 3 auftreten entstehen Großteils durch den veränderten
$sthr-Wert und die damit verbundene Erhöhung der Anzahl Referenzanregungen. Zu beachten ist, dass hier auch mit beiden Programmen auch der selbe Wert für c.ref² erhalten wird. Somit liegen in beiden Programmen Anregungen mit gleichem Anteil im Referenzbereich.
4.2 Vertikale Anregungsenergien an der neutralen Struktur
Für die vertikalen Anregungsenergien, berechnet mit der neutralen Struktur, werden die beiden Rechnungen mit den $esel-Werten 0.1 und 0.01 verglichen mit den experimentellen Werten[1][18] und den in der jeweiligen Literaturquelle mit TDDFT ermittelten Ergebnissen.
26
Tetracen ließ sich mit dem voreingestellten $sthr-Wert nur mit einer reduzierten Anzahl an Wurzeln berechnen, da mit dem voreingestellten Wert für die zweite iterative Berechnung, bei der Anzahl an Wurzeln der anderen Moleküle (insgesamt 33), ca. 2500
Referenzen berechnet wurden. Deswegen wurden die Berechnungen für Tetracen mit
$ ℎ = 0.031≙ ² ≈0.001 durchgeführt. Mit diesem Wert ließen sich die Rechnungen ohne eine Reduzierung der Wurzeln durchführen. Als diese Verbesserung gefunden wurde, war bereits zu erkennen, dass die Ergebnisse mit einem $esel-Wert von 0.01 besser waren, als die mit 0.1, wie im folgenden noch herausgestellt wird. Somit wurden die verbesserten Rechnungen für Tetracen nur noch mit $ = 0.01 durchgeführt.
Aufgrund dessen, dass in der Arbeit von Hirata[1] keine Ergebnisse für Naphthalin aufgeführt sind, musste eine andere Literaturquelle[18] herangezogen werden, hier entfällt der Vergleich mit den in der Arbeit berechneten Ergebnissen.
Als ersten Input wurden für die Moleküle Acenaphthylen und Azulen der Referenzraum auf elf Elektronen aus den sechs höchsten besetzten und die sechs niedrigsten unbesetzten Orbitale begrenzt, dabei wurden für jede irreduzible Darstellung fünf Wurzeln berechnet, lediglich für den Grundzustand wurde eine weitere Wurzel berechnet. Der Referenzraum der anderen Moleküle wurde wie folgt festgelegt: Naphthalin neun Elektronen aus den fünf höchsten besetzten und die fünf niedrigsten unbesetzten Orbitale; Anthracen 13 Elektronen aus den sieben höchsten besetzten und die drei niedrigsten unbesetzten Orbitale; Pyren elf Elektronen aus den sechs höchst besetzten und den sechs niedrigsten unbesetzten Orbitale und Tetracen 13 Elektronen aus den sieben höchsten besetzten Orbitalen und die sieben niedrigsten unbesetzten Orbitale. Für diese Moleküle wurden jeweils vier Wurzeln pro irreduzibler Darstellung berechnet und zusätzlich der Grundzustand. Einzige Ausnahme bildet das Tetracen, hier wurden ebenfalls vier Wurzeln pro irreduzibler Darstellung berechnet, allerdings keine zusätzliche für den Grundzustand, sondern für die irreduziblen Darstellungen b2g und b3g. Grund hierfür ist, dass vor der verbesserten Konfiguration des Programms, erkannt wurde, dass in diesen Darstellungen die meisten wichtigen Anregungen liegen.
Es ist anzumerken, dass in der Tabelle 5, auf der nachfolgenden Seite, die Abweichungen vom Literaturwert in roter Schrift markiert sind, wenn diese im Betrag größer sind, als die Abweichung der zu vergleichenden Quelle. Handelt es sich um eine Anregung aus einem - Orbital ist dies vermerkt, ansonsten handelt es sich bei allen anderen Orbitalen um - bzw.
*-Orbitale.
27
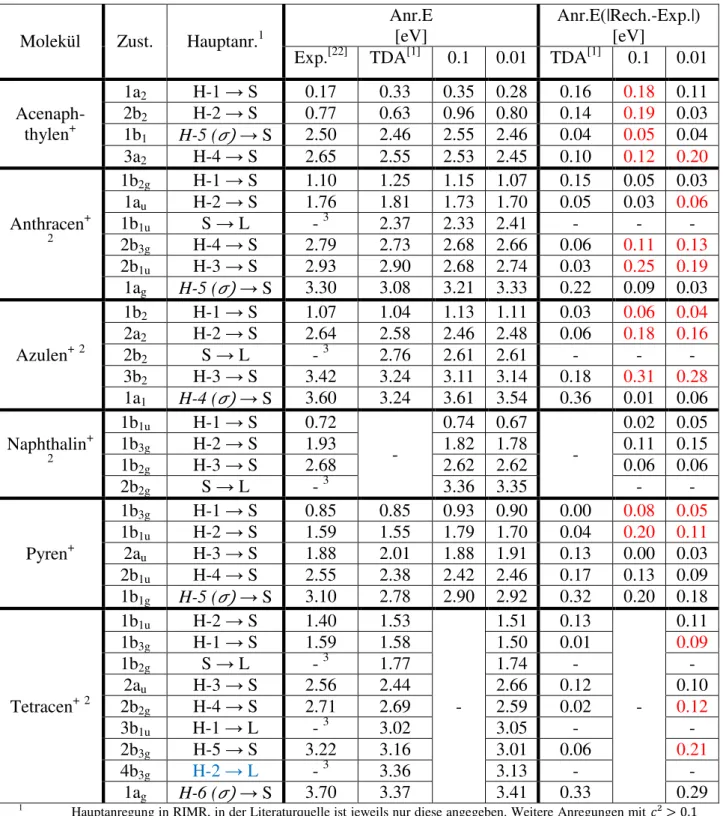
Tabelle 5: vertikale Anregungsenergien der Kationen an neutraler Struktur im Vergleich
Molekül Zust. Hauptanr.1
Anr.E [eV]
Anr.E(|Rech.-Exp.|) [eV]
Exp.[22] TDA[1] 0.1 0.01 TDA[1] 0.1 0.01 Acenaph-
thylen+
1a2 H-1 → S 0.17 0.33 0.35 0.28 0.16 0.18 0.11 2b2 H-2 → S 0.77 0.63 0.96 0.80 0.14 0.19 0.03 1b1 H-5 (�) → S 2.50 2.46 2.55 2.46 0.04 0.05 0.04 3a2 H-4 → S 2.65 2.55 2.53 2.45 0.10 0.12 0.20
Anthracen+
2
1b2g H-1 → S 1.10 1.25 1.15 1.07 0.15 0.05 0.03 1au H-2 → S 1.76 1.81 1.73 1.70 0.05 0.03 0.06
1b1u S → L - 3 2.37 2.33 2.41 - - -
2b3g H-4 → S 2.79 2.73 2.68 2.66 0.06 0.11 0.13 2b1u H-3 → S 2.93 2.90 2.68 2.74 0.03 0.25 0.19 1ag H-5 (�) → S 3.30 3.08 3.21 3.33 0.22 0.09 0.03
Azulen+2
1b2 H-1 → S 1.07 1.04 1.13 1.11 0.03 0.06 0.04 2a2 H-2 → S 2.64 2.58 2.46 2.48 0.06 0.18 0.16
2b2 S → L - 3 2.76 2.61 2.61 - - -
3b2 H-3 → S 3.42 3.24 3.11 3.14 0.18 0.31 0.28 1a1 H-4 (�) → S 3.60 3.24 3.61 3.54 0.36 0.01 0.06 Naphthalin+
2
1b1u H-1 → S 0.72
-
0.74 0.67
-
0.02 0.05
1b3g H-2 → S 1.93 1.82 1.78 0.11 0.15
1b2g H-3 → S 2.68 2.62 2.62 0.06 0.06
2b2g S → L - 3 3.36 3.35 - -
Pyren+
1b3g H-1 → S 0.85 0.85 0.93 0.90 0.00 0.08 0.05 1b1u H-2 → S 1.59 1.55 1.79 1.70 0.04 0.20 0.11 2au H-3 → S 1.88 2.01 1.88 1.91 0.13 0.00 0.03 2b1u H-4 → S 2.55 2.38 2.42 2.46 0.17 0.13 0.09 1b1g H-5 (�) → S 3.10 2.78 2.90 2.92 0.32 0.20 0.18
Tetracen+2
1b1u H-2 → S 1.40 1.53
-
1.51 0.13
-
0.11
1b3g H-1 → S 1.59 1.58 1.50 0.01 0.09
1b2g S → L - 3 1.77 1.74 - -
2au H-3 → S 2.56 2.44 2.66 0.12 0.10
2b2g H-4 → S 2.71 2.69 2.59 0.02 0.12
3b1u H-1 → L - 3 3.02 3.05 - -
2b3g H-5 → S 3.22 3.16 3.01 0.06 0.21
4b3g H-2 → L - 3 3.36 3.13 - -
1ag H-6 (�) → S 3.70 3.37 3.41 0.33 0.29
1 Hauptanregung in RIMR, in der Literaturquelle ist jeweils nur diese angegeben. Weitere Anregungen mit ² > 0.1 sind in der Tabellen im Anhang aufgelistet.
2 Vertauschung jeweils zweier Zustände (Rechnung zu Literaturquelle): Anthracen - b3g und b2g, Azulen - b1 und b2, Naphthalin - b2g und b3g, Tetracen - b2g und b3g
3 zusätzliche Anregungen in virtuelle/nicht besetzte Orbitale sind mit PES nicht nachweisbar.
28
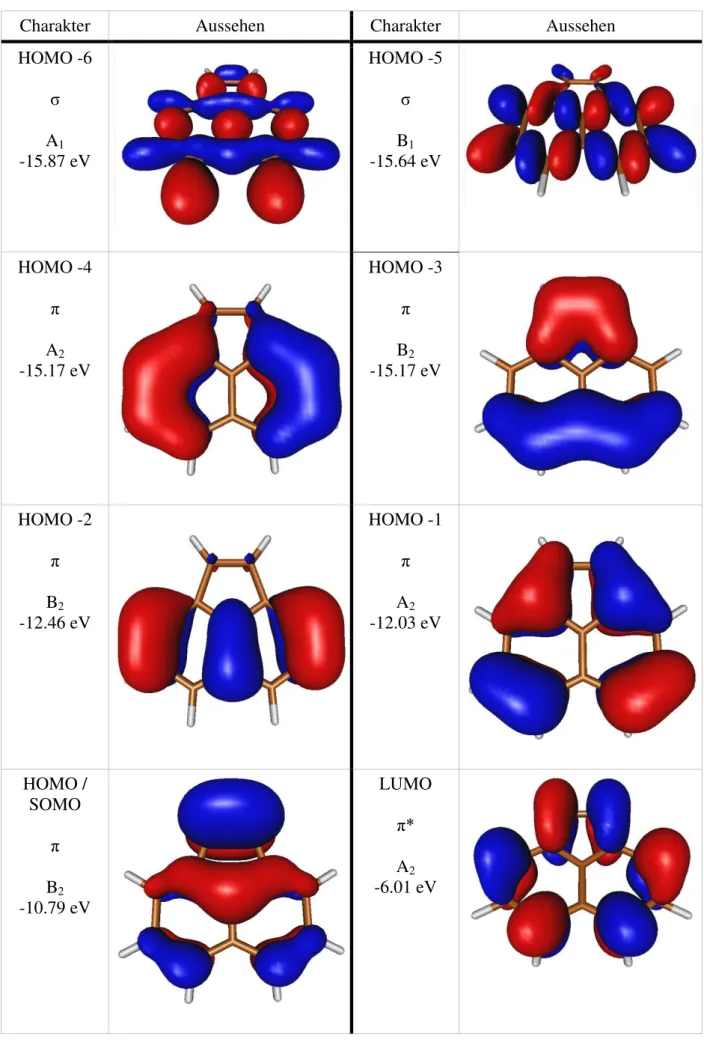
Abbildung 20: Korrelationsdiagramm Anr.E TDA[1] zu PES[22]
Abbildung 21: Korrelationsdiagramm Anr.E MR-MP2 zu TDA[1]
Abbildung 22: Korrelationsdiagramm Anr.E MR-MP2 zu PES[22]
Abbildung 23: Korrelationsdiagramm Anr.E MR-MP2 mit unterschiedlichem $esel-Wert
Es gab bei einigen Anregungen Abweichungen zwischen Literatur und eigener Berechnung.
So findet die 2b3g Anregung beim Anthracen in der Literaturquelle nicht aus dem HOMO-4 statt, sondern aus dem HOMO-3, genau umgekehrt verhält es sich mit der 2b1u Anregung, hier finden laut Literaturquelle die Anregung aus dem HOMO-4 statt. Grund dafür ist eine Veränderung der Orbitalenergien zwischen den beiden Methoden. In der Arbeit von Hirata[1]
wurde das B-LYP-Funktional und der 6-31G** Basissatz für die Kationen verwendet, während für diese Arbeit das BH-LYP-Funktional und der SV(P)-Basissatz verwendet wurde.
Wie in Abschnitt 2.5 erklärt, kann es nicht vorkommen, dass diese beiden Zustände durch eine andere Raumorientierung des Moleküls vertauscht sind. Wie in den MO-Diagrammen am Anfang des Kapitels 4 zu erkennen, sind diese beiden Orbitale fast entartet, da die Orbitale unterschiedlicher Form sind (siehe Anhang I: Orbitalbilder zu den MO-Diagrammen),
0 0,5 1 1,5 2 2,5 3 3,5 4
0 0,5 1 1,5 2 2,5 3 3,5 4
Anregungsenergie TDA [eV]
experimentelle Anregungsenergie [eV]
0 0,5 1 1,5 2 2,5 3 3,5 4
0 0,5 1 1,5 2 2,5 3 3,5 4
Anr.E MR-MP2 $esel=0.01 [eV]
Anregungsenergie TDA [eV]
0 0,5 1 1,5 2 2,5 3 3,5 4
0 0,5 1 1,5 2 2,5 3 3,5 4
Anr.E MR-MP2 $esel=0.01 [eV]
experimentelle Anregungsenergie [eV]
0 0,5 1 1,5 2 2,5 3 3,5 4
0 0,5 1 1,5 2 2,5 3 3,5 4
Anr.E MR-MP2 $esel=0.01 [eV]
Anr.E MR-MP2 $esel=0.1 [eV]
![Abbildung 9: Franck-Condon-Effekt [3]](https://thumb-eu.123doks.com/thumbv2/1library_info/4530415.1596180/14.892.118.594.519.837/abbildung-franck-condon-effekt.webp)