ASYMPTOTICPROPERTIESOFTHE
NONPARAMETRICPARTINPARTIAL
LINEARHETEROSCEDASTIC
REGRESSIONMODELS
HuaLiang,WolfgangHardleandAxelWerwatz
AbstractThispaperconsidersestimationoftheunknownfunctiong()inthepartiallinearregressionmodelYi=XTi
+g(Ti)+"iwithheteroscedasticerrors.Werstconstructaclassofestimatesgnofgandprovethat,underappropriateconditions,gnisweak,meansquareerrorconsistent.Ratesofconvergenceandasymptoticnormalityfortheestimatorgnarealsoestablished.
Key W ords and Phrases:Key words and phrases:
Asymptoticnormality,consistency,heteroscedasticity,kernelestimation,ratesofconvergence,partiallinearmodel,semipara-metricmodels.1INTRODUCTIONSemiparametricmodelscombinetheexibilityofnonparametricmodelingwithstructuralparametriccomponents.OnesuchmodelthathasreceivedalotofattentionintheliteratureisthesemiparametricpartiallinearregressionmodelYi=X Ti+g(Ti)+"ii=1:::n(1)HuaLiangisAssociateProfessorofStatistics,InstituteofSystemsScience,ChineseAcademyofSciences,Beijing100080,China.WolfgangHardleisProfessorofEconometrics,AxelWerwatzisDr.ofEconomics.BothoflatterareattheInstitutfurStatistikundOkonometrie,Humboldt-UniversitatzuBerlin,D-10178Berlin,Germany.ThisresearchwassupportedbySonderforschungsbereich373\QuantikationundSimu-lationOkonomischerProzesse".TherstauthorwassupportedbyAlexandervonHumboldtFoundation.TheauthorswouldliketothankMr.KnutBartelsforhisvaluablecommentswhichgreatlyimprovedthepresentationofthispaper.1
whereXandTare(possibly)multidimensionalregressors,avectorofunknownparame-ters,g()anunknownsmoothfunctionand"anerrortermwithmeanzeroconditionalonXandT:Well-knownapplicationsintheeconometricsliteraturethatcanbeputintheformof(1)arethehumancapitalearningsfunction(Willis(1986))andthewagecurve(BlanchowerandOswald(1994)).Inbothcases,log-earningsofanindividualarerelatedtopersonalcharacteristics(sex,maritalstatus)andmeasuresofaperson'shumancapitallikeschoolingandlabormarketexperience.Economictheorysuggestsanon-linearrelationshipbetweenlog-earningsandlabormarketexperience,whichthereforeplaystheroleofthevariableTin(1).Thewagecurveisobtainedbyincludingthelocalunemploymentrateasanadditionalregressor,withapossiblynon-linearinuence.RendtelandSchwarze(1995),forinstance,estimateg()asafunctionofthelocalunemploymentrateusingsmoothing-splinesandndaU-shapedrelationship.Undervariousassumptions,severalauthorshaveconsideredestimationofin(1)ataparametricrate.Chen(1988),Heckman(1986),Robinson(1988),Schick(1996)andSpeck-man(1988)constructed pn;consistentestimatorsof.Cuzick(1992a)studiedecientestimationofwhentheerrordensityisknown.Ecientestimationwhentheerrordistri-butionisofanunknownformistreatedinCuzick(1992b)andSchick(1993).Inthispaper,wewillinsteadfocusonderivingtheasymptoticpropertiesofanesti-matoroftheunknownfunctiong().Weconsideritsconsistency,weakconvergencerateandasymptoticnormality.Wewillderivetheseresultsforaspecicversionof(1)withnonstochasticregressors,heteroscedasticerrorsandTunivariate.Theremainderofthispaperisorganizedasfollows.Inthefollowingsectionwewilldescribemethodsforestimatingandg().Weproveconsistencyandasymptoticnormalityoftheestimatorofg()insections3and4.Weillustratetheusefulnessoftheestimatorandtherelevanceoftheasymptoticdistributionresultsforappliedworkbyasmall-scaleMonteCarlostudyandanempiricalillustrationinthenalsectionofthepaper.
2THEESTIMATORSpecically,weconsiderestimationofg()(and)inthefollowingpartiallinear,semipara-metricregressionmodel:Yi=X Ti+g(Ti)+"ii=1:::n(2)2
whereisanunknownpdimensionalparametervector,g()anunknown,smoothfunctionfrom01]toIR 1,(X1T1),(X2T2):::areknown,nonrandomdesignpointsand"1:::"nareindependentmeanzerorandomerrorswithnonconstantvariance.Weallowthevarianceof"todependonXandTinanarbitraryway.Previousworkinaheteroscedasticsettinghasfocusedonthenonparametricregressionmodel(i.e.=0).Mulleretal.(1987)proposedanestimateofthevariancefunctionbyusingkernelsmoother,andthenprovedthattheestimateisuniformlyconsistent.HallandCarroll(1989)consideredconsistencyofestimatesofg():Eubanketal.(1990)proposedtrigonometricseriestypeestimatorsgofg.Theyinvestigatedasymptoticapproximationsoftheintegratedmeansquarederrorandthepartialintegratedmeansquarederrorofg.Theheteroscedasticversionof(1)with6=0hasbeenconsideredinSchick(1996)butheconsidersweightedleastsquaresestimationof.Wefocusonnonparametricestimationofg()asafunctionofT.Supposeweknew:Thenwemayestimateg()bynonparametricregressionofYi;X Ti(thevariationinYinotaccountedforbythelinearcomponentX Ti)onTi:Intheliteratureonecanndvariousmethodsforestimatingg()nonparametrically,e.g.,kernel,nearestneighbor,orthogonalseries,piecewisepolynomialandsmoothingsplines.SeeHardle(1990)foranextensivediscussionoftheirstatisticalproperties.Alltheseestimatorsmaybewrittenasweightedlocalaveragesoftheobservedvaluesofthedependentvariablewiththeweightsdependingonthevaluesoftheexplanatoryvariables.Inourcase,wecanwrite(stillassumingthatisknown):^g(t)= nXi=1 !ni(t)(Yi;X Ti)(3)where!ni(t)=!ni(tT1T2:::Tn)areweightfunctionsthatdependontheobservationsT1:::Tn.Forinstance,aGasser-Muller-typekernelestimatortakes!ni(t)= 1h Zsis
i;1 K t;shn ds1infors0=0sn=1si= 12 (T(i)+T(i+1)):HereT(1):::T(n)aresampleorderstatistics,K()isthekernelfunctionandhdenotesthebandwidth.SeeRemark5belowfordetails.Giventheestimator^g(t)asdenedin(3)wemayestimatebytheleastsquaresregres-sionofYi=X Ti+^g(Ti)+i3
Yi; nXj=1 !nj(Ti)Yj= nXi; nXj=1 !nj(Ti)Xj oT+i
eYi= fX Ti+i(4)Thatis,weestimatebythegeneralizedleastsquaresestimatorLS=( fX T
fX) ;1
fX T
eY(5)where fX=( fX1::: fXn) Tand eY=( eY1::: eYn) Tarethepresmootheddesignandresponsevariables.Inthenalstepweobtainthefeasibleestimatorofg()bysubstitutingLSfortheunknownin(3):gn(t)= nXi=1 !ni(t)(Yi;X TiLS)(6)Furthermotivationfortheestimatorsdenedin(5)and(6)isgiveninSpeckman(1988)andGao,etal.(1995).NotethoughthatLSisnotanecientestimatorinthesenseofasymptoticnormality.Inthefollowingsectionwestateandprovetheweak,meansquareerrorconsistencyandgivetheratesofconvergenceofgn(t)undervariousassumptions.
3CONSISTENCYRESULTSAlltechnicalpreliminariesneededintheproofsofthefollowingresultsarecollectedinAppendix6aslemmas.Forconvenienceandsimplicity,wealwaysletCdenotesomepositiveconstantnotdependingonn:Wewillusethefollowingassumptions.
Assumption 1.
Thereexistcontinuousfunctionshj()denedon01]suchthateachelementofXisatisesxij=hj(Ti)+uij1in1jp(7)whereuijisasequenceofrealnumberswhichsatisfylimn!1 1n Pni=1ui=0andlimn!1 1n nXi=1 uiu Ti=B(8)isapositivedenitematrix,andlimsupn!1 1an max1kn kXi=1 ujim <1form=1:::p(9)4
holdsforallpermutations(j1:::jn)of(12:::n)whereui=(ui1:::uip) Tan=n 1=2logn:
Assumption 2.
(a) Pni=1!ni(t)!1asn!1(b) Pni=1j!ni(t)jCforalltandsomeconstantC(c) Pni=1
j!ni(t)jI(jt;Tij>a)!0asn!1foralla>0(d)supinj!ni(t)j=Of(logn) ;1
g:Denotent= n Pni=1! 2ni(t) o
;1:
Assumption 3.
(a)supn(nt)sup1inj!ni(t)j<1andnt=o(n)(b) pntsup1inj!ni(t)j=O(n ;=2)forsome1>>0(c) Pni=1! 2ni(t)E" 2i= 20=nt+o(1=nt)forsome 20>0:Remark 1.
Assumption1isacommonrequirementforprovingconsistencyofinthepartiallinearmodel(1).Infact,(7)ofAssumption1isparalleltothecasehj(Ti)=E(xijjTi)anduij=xij;E(xijjTi) when(XiTi)arerandomvariables.(8)issimilartotheresultofthestronglawoflargenumbersforrandomerrors.(9)issimilartolawoftheiteratedlogarithm.MoredetaileddiscussionsmaybefoundinSpeckman(1988)andGaoetal.(1995).Theorem 1.
UnderAssumptions1and2Efgn(t)g!g(t)asn!1ateverycontinuitypointofthefunctiong:Pro of.
Decomposethedierencegn(t);g(t)asfollowsbydirectcalculation.gn(t);g(t)= nXj=1 !nj(t)fg(Ti)+"i;X Ti( fX TfX) ;1
fX T
eg(T);X Tj( fX T
fX) ;1
fX T
e"g;g(t)
whereeg(T)=feg(T1):::eg(Tn)g Tandeg(Ti)=g(Ti); Pnj=1!nj(Ti)g(Tj)ande"justlike fX:ItfollowsthatEfgn(t)g;g(t)= nnXi=1 !ni(t)g(Ti);g(t) o
; nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
eg(T)(10)
5
ThersttermtendstozerobyLemmaA.1(i).BylemmasA.2andA.1(i)andCauchy-Schwarzinequality,weknowthateveryelementof( fX TfX) ;1fX T
eg(T)iso(n ;1=2),i.e.,
n( fX T
fX) ;1
fX T
eg(T) oj =o(n ;1=2)forj=1:::p(11)Itsucestoshowthateveryelementof Pni=1!ni(t)XiisO(n 1=2).Observethatn
Xi=1 !ni(t)xij= nXi=1 !ni(t)fhj(Ti)+uijgSincehj()iscontinuous, Pni=1!ni(t)hj(Ti)convergestoh(t)onthecontinuitypointofh(t)bythesameproofasoneforLemmaA.1(i).Moreover,byAbel'sinequalityandAssumption2(d),
nXi=1 !ni(t)uij sup1in j!ni(t)jmax1kn kXi=1 ujim =O(n 1=2)Thusn
Xi=1 !ni(t)xij=O(n 1=2)(12)andwecompletetheproofofTheorem1.
#
Theorem1showsthatgn(t)isanasymptoticallyunbiasedestimatorofg(t)ateverycontinuitypointofg(t).Thenextresult,Theorem2,willdemonstratethatgn(t)isalsomeansquare-errorconsistent.Theorem 2
AssumetheconditionsofTheorem1holdexceptAssumption2(d)whichisreplacedbysupinj!ni(t)j=of(logn) ;1g:ThenEfgn(t);g(t)g 2
!0asn!1:
Pro of.
ItfollowsfromtheCr;inequalitywithr=2thatEfgn(t);g(t)g 2CE
nXi=1 !ni(t)g(Ti);g(t) 2+CE nXi=1 !ni(t)"i 2
+CE
nXi=1 !ni(t)( fX T
fX) ;1
fX T
eg(T)
2+CE
nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
e"
2(13)IntheproofofTheorem1weobtainedthattherstandthirdtermsof(13)convergetozeroasntendstoinnity.Thesecondcanbeshowntobeordero(1)bydirectcalculation.Weshallnowprovethefourthtermalsoconvergestozero.Denote( fX TfX) ;1fX T=(ji)pn:E nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T"
2=E nnXi=1 !ni(t) pXk=1 nXl=1 xikkl"l o2
= nXl=1 nXi=1 pXk=1 !ni(t)xikkl 2 2l
6
Itfollowsfromtheargumentsfor(12)thatthisequalstoO(n) Pnl=1 2kl.Since Pnl=1 2klandtheelementsofthek;throwof( fX TfX) ;1havethesameorderO(n ;1).ItfollowsthatE
nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T"
2=o(1):(14)Furthermore,wecaneasilyshowthatE nXi=1 !ni(t)X Ti( fX T
fX) ;1 nXk=1 fXk nnXl=1 !nl(Tk)"k o 2=o(1):(15) Combining(14)and(15)ensuresthatthefourthtermof(13)iso(1),andthuscompletestheproofofTheorem2.
#
Thefollowingresultgivestheweakconvergencerateofgnunderstrongerassumptionsonf!ni(t)gthanthosegiveninAssumption2.Herewelisttheseassumptions.Assumption 2'.
Theweightfunctions!ni(t)satisfy:(a)suptj Pni=1!ni(t);1j=OP(n ;1=3logn)(b)supt Pni=1j!ni(t)jI(jt;Tij>cn)=O(dn)wherednandcnaren ;1=3logn(c)suptmax1inj!ni(t)j=OP(n ;2=3):
Theorem 3.
Assumeg()andhj()areLipschitzcontinuousoforder1andAssumptions1and2'hold.Thengn(t);g(t)=OP(n ;1=3logn):Pro of.
ByLemmaA.1(ii),nXi=1 !ni(t)g(Ti);g(t)=OP(n ;1=3logn):
UsingAssumption2'(c)andChebyshev'sinequalitywehaven
Xi=1 !ni(t)"i=OP(n ;1=3logn):
Thesimilarargumentsasthatfor(11)and(12)yieldn
Xi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
eg(T)=OP(n ;1=3logn):
7
Finally,observethat Pni=1!ni(t)uij=O(1)andthen Pni=1!ni(t)xij=O(1)forj=1:::p:Thus,bytheargumentsfor(14)and(15),E
nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
e"
2=O(n ;1):(16)
whichentailsn
Xi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
e"=OP(n ;1=3logn):
ThiscompletestheproofofTheorem3.
# Remark 2.
Wecanconcludefromtheaboveargumentsthatlimsupn!1 (n 2=3log ;2n)Efgn(t);g(t)g 2<1:Theorem4givestheasymptoticvarianceofgn(t):Theorem 4.
UnderAssumptions1,2'and3,ntVarfgn(t)g! 20asn!1:Pro of.
ntVarfgn(t)g=ntE nnXi=1 !ni(t)"i o2+ntE nnXi=1 !ni(t)X Ti( fX TfX) ;1
fX T
e" o2
;2ntE nnXi=1 !ni(t)"i o
nnXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
e" o
Thersttermconvergesto 20:Thesecondtermtendstozeroby(16),andthenthethirdtermalsotendstozerobytheCauchy-Schwarzinequality.
#
4ASYMPTOTICNORMALITYInthenonparametricregressionmodel,Liang(1995)provedasymptoticnormalityforin-dependent"i'sunderthemildconditions.Inthissection,weshallconsidertheasymptoticnormalityofgnundertheAssumptions1,2'and3.
Theorem 5.
Assumethat"1"2:::"nareindependentrandomvariableswithE"i=0andinfi 2i>c>0forsomec:ThereexistsafunctionG(u)satisfyingZ
10 uG(u)du<1(17) suchthatP(j"ij>u)G(u)fori=1:::nandlargeenoughu:(18)8
Ifmax1in! 2ni(t)
Pni=1! 2ni(t) !0asn!1:(19) Thengn(t);Egn(t)
qVarfgn(t)g ;! LN(01)asn!1:
Remark 3.
Thecondition R10uG(u)du<1istoguaranteesupi 2i<1:
The pro of of Theorem 5.
AtrstfromtheproofofTheorem4,weobtainthatVarfgn(t)g= nXi=1 ! 2ni(t) 2i+o nnXi=1 ! 2ni(t) 2i oFurthermoregn(t);Egn(t); nXi=1 !ni(t)"i= nXi=1 !ni(t)X Ti( fX T
fX) ;1
fX T
e"=OP(n ;1=2)
whichyields
Pni=1!ni(t)X Ti(fX T
fX) ;1
fX T
e"
qVarfgn(t)g =OP(n ;1=2n 1=2t)=oP(1) Itfollowsthatgn(t);Egn(t)
qVarfgn(t)g = Pni=1!ni(t)"i
q
Pni=1! 2ni(t) 2i +oP(1) def= nXi=1 a ni"i+oP(1) wherea ni= !
ni(t)
p
P
n
i=1!2ni(t) i :Letani=a nii,obviouslysupii<1dueto R
10vH(v)dv<1:Theproofofthetheoremimmediatelyfollowsfromtheconditions(17){(19)andLemmaA.4.
# Remark 4.
If"1:::"nareindependentidenticallydistributed,thenEj"1j 2<1andthecondition(19)ofTheorem5canyieldtheresultofTheorem5.Assumption 2".
Theweightfunctions!ni(t)satisfy:(a) Pni=1!ni(t);1=o(n ;1=2t)(b) Pni=1j!ni(t)jI(jt;Tij>c 0n)=o(d 0n)wherec 0nandd 0nareo(n ;1=2t):
9
Theorem 6.
Supposethatg(t)isLipschitzcontinuousoforder1.AssumetheconditionsofTheorem5holdwiththepreviousAssumption2"replacingAssumption2'.Thengn(t);g(t)qVarfgn(t)g ;! LN(01)asn!1:
Pro of.
Infact,recalltheconclusionofTheorem5,itsucestoshowthatEgn(t);g(t)qVarfgn(t)g = pntfEgn(t);g(t)g+o(1)=o(1):Forc 0n=o(n ;1=2t).Notethat
jEgn(t);g(t)j nXi=1 j!ni(t)fg(Ti);g(t)gjfI(jTi;tj>c 0n)+I(jTi;tjc 0n)g
+jg(t)j
nXi=1 !ni(t);1
(gc 0n)B+2C nXi=1 j!ni(t)jI(jTi;tj>c 0n)+C nXi=1 !ni(t);1 whereC=supt2 01]jg(t)jand(gc 0n)=sup
jt;t0 jc0 n jg(t);g(t 0)j:Assumption2"andthepreviousargumentsyieldtheconclusionofTheorem6.
# Remark 5.
Inthisremark,weshallgiveconcreteweightfunctionsf!ni(t)i=1:::ngwhichsatisfytheassumptionsgivenintheformercontext,inordertoexplainthereasonabilityoftheresultsestablishedinprevioussectionscarefully.Assume!ni(t)= 1hn Zsisi;1 K t;shn ds1in(20)wheres0=0sn=1andsi= 12 (T(i)+T(i+1))1in;1:hnisasequenceofbandwidthparameterswhichtendstozeroasn!1andK()isakernelfunction,whichissupportedtohavecompactsupportandtosatisfysupp(K)=;11]supjK(x)jC<1 ZK(u)du=1andK(u)=K(;u)
ObviouslyAssumptions2(a),(b)and(d)aresatisedfortheweightfunctionsgivenin(20).If
Z
juj ah ;1 n K(u)du=o(1)
10
ThenAssumption2(c)holdalso.Infactn
Xi=1 !ni(t)I(jTi;tj>a)= 1hn nXi=1 Zsisi;1 K t;shn dsI(jTi;tj>a)
1hn Z
jT
i;sj a;maxjT
i;T
i;1j K t;shn ds
1hn Z
juj h ;1 n(a;maxjTi;T
i;1j) K(u)du=o(1) Nowletustakehn=Cn ;1=3forsomeC>0andsuppose
Z
juj ah;1 n K(u)du=O(n ;1=3logn) ThereexistconstantsC1C2>0suchthatC1n min1in jTi;Ti;1jmax1in jTi;Ti;1j C2nThenwecantakent=nhn,andAssumptions3and2"hold.Theorems5and6implythat
qnhnfgn(t);g(t)g;! LN(0 20)asn!1:
Thisisjusttheclassicalconclusioninnonparametricregressionestimation.
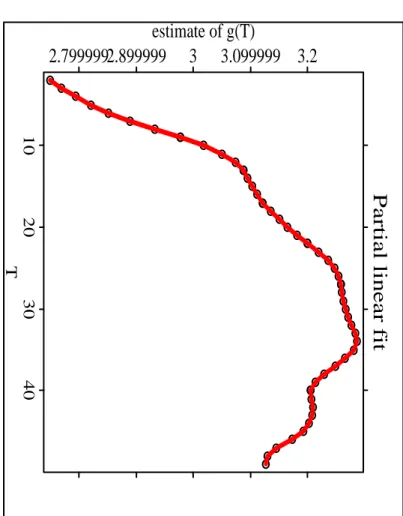
5NUMERICALEXAMPLESInthissectionwewillillustratethenite-samplebehaviouroftheestimatorbyapplyingittorealdataandbyperformingasmallsimulationstudy.Intheintroductionwealreadymentionedthehuman-capitalearningsfunctionasawell-knowneconometricapplicationthatcanbeputintotheformofapartiallinearmodel.Ittypicallyrelatesthelogarithmofearningstoasetofexplanatoryvariablesdescribinganindividual'sskills,personalcharacteristicsandlabourmarketconditions.Specically,weestimateandg()inthemodellnYi=X Ti+g(Ti)+"i(21)whereXcontainstwodummyvariablesindicatingthelevelofsecondaryschoolingapersonhascompletedandTisameasureoflabourmarketexperience(denedasthenumberofyearsspentinthelabourmarketandapproximatedbysubtracting(yearsofschooling+6)fromaperson'sage).11
Partial linear fit
10203040T
2.7999992.899999 3 3.099999 3.2 estimate of g(T)
Figure1:Relationshipoflog-earningsandlabour-marketexperience
Undercertainassumptions,theestimateofcanbeinterpretedastherateofreturnfromobtainingtherespectivelevelofsecondaryschooling.Regardingg(T),humancapitaltheorysuggestsaconcaveform:rapidhumancapitalaccumulationintheearlystageofone'slabormarketcarrerareassociatedwithrisingearningsthatpeaksomewhereduringmidlifeanddeclinethereafterashoursworkedandtheincentivetoinvestinhumancapitaldecrease.Toallowforconcavity,parametricspecicationsoftheearnings-functiontypicallyincludeTandT 2inthemodelandobtainapositiveestimateforthecoecentofTandanegativeestimateforthecoecientofT 2.Fornonparametrictting,weuseaNadaraya-Watsonweightfunctionwithquartickernel(15=16)(1;u 2) 2I(juj1)andchosethebandwidthusingcross-validation.Theestimateofg(T)isdepictedinFigure1.Inasamplesizethatislowerthaninmostempiricalinvestigationsofthehumancapitalearningsfunctionweobtainanestimatethatnicelyagreeswiththeconcaverelationshipenvisionedbyeconomictheoryandoftenconrmedbyparametricmodeltting.Wealsoconductedasmallsimulationstudytogeturtherinsightsintothesmall-sample12
Simulation comparation
00.51T
0 0.5 1
g(T) and its estimate values
Figure2:Estimatesofthefunctiong(T)performanceoftheestimatorofg().WeconsiderthemodelYi=X Ti+sin(Ti)+sin(X Ti+Ti)"ii=1:::n=300where"iisstandardnormallydistributedandXiandTiaresampledfromauniformdistri-butionon01]:Weset=(10:75) Tandperformed100replicationsofgeneratingsamplesofsizen=300andestimatingg():Figure2depictsthe"true"curveg(T)=sin(T)(solid-line)andanaverageofthe100estimatesofg()(dashed-line).Theaverageestimatenicelycapturestheshapeofg():
6APPENDIXInthisappendixwestatesomeusefullemmas.
Lemma A.1.
SupposethatAssumption2(a)-(c)holdandg()andhj()arecontinuous.Then(i)max1in Gj(Ti); nXk=1 !nk(Ti)Gj(Tk) =o(1)13
Furthermore,ifg()andhj()areLipschitzcontinuousoforder1andAssumption2'(a)-(c)and2(b)hold.Then(ii)max1in Gj(Ti); nXk=1 !nk(Ti)Gj(Tk) =O(cn+dn) forj=0:::p:WhereG0()=g()andGl()=hl()forl=1:::p:
Pro of.
Weonlypresenttheproofof(ii)forg().Theproofsofothercasesand(i)aresimilar.ObservethatnXi=1 !ni(t)fg(Ti);g(t)g= nXi=1 !ni(t)fg(Ti);g(t)g+ nnXi=1 !ni(t);1 og(t)
= nXi=1 !ni(t)fg(Ti);g(t)gI(jTi;tj>cn) + nXi=1 !ni(t)fg(Ti);g(t)gI(jTi;tjcn)+ nnXi=1 !ni(t);1 og(t)ByAssumption2'(b)andLipschitzcontinuityofg()n
Xi=1 !ni(t)fg(Ti);g(t)gI(jTi;tj>cn)=O(dn)(22)andn
Xi=1 !ni(t)fg(Ti);g(t)gI(jTi;tjcn)=O(cn):(23)(22)-(23)andAssumption2(a)completetheproofofLemmaA.1.
Lemma A.2.
UnderAssumptions1and2'.limn!1 1n fX TfX=B
Pro of.
Denotehns(Ti)=hs(Ti); Pnk=1!nk(Ti)xks.Itfollowsfromxis=hs(Ti)+uisthatthe(sm)elementof fX TfX(sm=1:::p)isnXi=1 exisexim= nXi=1 uisuim+ nXi=1 hns(Ti)uim+ nXi=1 hnm(Ti)uis+ nXi=1 hns(Ti) hnm
(Ti)
def= nXi=1 uisuim+ 3Xq=1 R (q)nsm
Thestronglawoflargenumberimpliesthatlimn!11=n Pni=1uiu Ti=BandLemmaA.1meansR (3)nsm=o(n),whichandCauchy-SchwarzinequalityshowthatR (1)nsm=o(n)andR (2)nsm=o(n):Thiscompletestheproofofthelemma.14
ThefollowingLemmaisaslightversionofTheorem9.1.1ofChowandTeicher(1988).Wethereforedonotgiveaproof.
Lemma A.3.
Letnkk=1:::knbeindependentrandomvariableswithEnk=0andE 2nk= 2nk<1:Assumethatlimn!1 Pknk=1 2nk=1andmax1kkn 2nk!0:Then
Pk
nk=1nk! LN(01)indistributionifandonlyifk
n
Xk=1 E 2nkI(jnkj>)!0forany>0asn!1:
Lemma A.4.
LetV1:::VnbeindependentrandomvariableswithEVi=0andinfiEV 2i>C>0forsomeconstantnumberC:ThefunctionH(v)satisfying R10vH(v)dv<1suchthatPfjVkj>vgH(v)forlargeenoughv>0andk=1:::n:(24)Alsoassumethatfanii=1:::nn1gisasequencerealnumberssatisfying Pni=1a 2ni=1:Ifmax1injanij!0thenfora 0ni=ani=i(V)n
Xi=1 a 0niVi;! LN(01)asn!1:
Pro of.
Denotenk=a 0nkVkk=1:::n:Wehave Pnk=1E 2nk=1:Moreover,itfollowsthatnXk=1 E 2nkI(jnkj>)= nXk=1 a 0nk 2EV 2kI(jankVkj>)
nXk=1 a 2nk 2k EV 2kI(max1kn jankVkj>)
(infk 2k) ;1supk EfV 2kI(max1kn jankVkj>)g:Itfollowsfromthecondition(24)thatsupk EfV 2kI(max1kn jankVkj>)g!0asn!1:LemmaA.4isthereforederivedfromLemmaA.3.
15
REFERENCESBlanchowerandOswald(1994).Blanchower,D.G.andOswald,A.J.(1994).TheWageCurve,MITPressCambridge,MA.Carroll,R.J.(1982).Adaptingforheteroscedasticityinlinearmodels,AnnalsofStatistics,
10
,1224-1233.Chen,H.(1988).Convergenceratesforparametriccomponentsinapartlylinearmodel.AnnalsofStatistics,16
,136-146.Chow,Y.S.andTeicher,H.(1988).ProbabilityTheory.2ndEdition,Springer-Verlag.Cuzick,J(1992a).Semiparametricadditiveregression.JournaloftheRoyalStatisticalSociety,SeriesB,54
,831-843.Cuzick,J(1992b).Ecientestimatesinsemiparametricadditiveregressionmodelswithunknownerrordistribution.AnnalsofStatistics,20
,1129-1136.Engle,R.F.,Granger,C.W.J.,Rice,J.andWeiss,A.(1986).Semiparametricestimatesoftherelationbetweenweatherandelectricitysales.JournaloftheAmericanStatisticalAssociation,81
,310-320.Eubank,R.L.,Hart,J.D.andSpeckman,P.(1990).Trigonometricseriesregressionestima-torswithanapplicationtopartiallylinearmodel.JournalofMultivariateAnalysis,32
,70-83.Gao,J.T.,Hong,S.Y.andLiang,H.(1995).Convergenceratesofaclassofestimatesinpartlylinearmodels.ActaMathematicaeSinicaSeriesNew,38
,658-669.Hall,P.andCarroll,R.J.(1989)Variancefunctionestimationinregression:theeectofestimatingthemean.JournaloftheRoyalStatisticalSociety,SeriesB,51
,3-14.Hardle,W.(1990).AppliedNonparametricRegression.CambridgeUniversityPress,NewYork.Heckman,N.E.(1986).Splinesmoothinginpartlylinearmodels.JournaloftheRoyalStatisticalSociety,SeriesB,48
,244-248.Liang,H.(1995).Anoteonasymptoticnormalityfornonparametricmultipleregression:thexeddesigncase.Soo-ChowJournalofMathematics,395-399.Muller,H.G.andStadtmuller,U.(1987).Estimationofheteroscedasticityinregressionanalysis.AnnalsofStatistics,15,
610-625.Rendtel,U.andSchwarze,J.(1995).ZumZusammenhangzwischenLohnhoeheundArbeit-slosigkeit:NeueBefundeaufBasissemiparametrischerSchaetzungenundeinesverall-gemeinertenVarianz-KomponentenModells.GermanInstituteforEconomicResearch(DIW)DiscussionPaper118,Berlin,1995.Robinson,P.W.(1987).Asymptoticallyecientestimationinthepresenceofheteroscedas-ticityofunknownform.Econometrica,55
,875-891.16
Schick,A.(1993).Onecientestimationinregressionmodels.AnnalsofStatistics,
21
,1486-1521.Schick,A.(1996).Weightedleastsquaresestimatesinpartlylinearregressionmodels.Statistics&ProbabilityLetters,27
,281-287.Speckman,P.(1988).Kernelsmoothinginpartiallinearmodels.JournaloftheRoyalSta-tisticalSociety,SeriesB,50
,413-436.Willis,R.J.(1986).WageDeterminants:ASurveyandReinterpretationofHumanCapitalEarningsFunctionsin:Ashenfelter,O.andLayard,R.TheHandbookofLaborEco-nomics,Vol.1NorthHolland-ElsevierSciencePublishersAmsterdam,1986,pp525-602.17
![Figure 2: Estimates of the function g(T )performanceoftheestimatorofg().WeconsiderthemodelYi=XTi+sin(Ti)+sin(XTi+Ti)"ii=1:::n =3 00where"iisstandardnormallydistributedandXiandTiaresampledfrom au niform distri-butionon01]:Weset=(10:75)Tandperformed1](https://thumb-eu.123doks.com/thumbv2/1library_info/5612483.1691656/13.1188.687.1093.185.711/figure-estimates-function-performanceoftheestimatorofg-weconsiderthemodelyi-iisstandardnormallydistributedandxiandtiaresampledfrom-butionon-tandperformed.webp)