Bayesian Inference for High-Dimensional Data with Applications to Portfolio Theory
Volltext
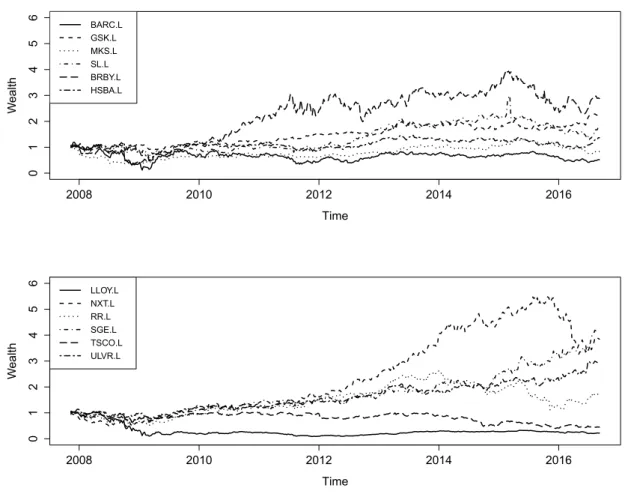
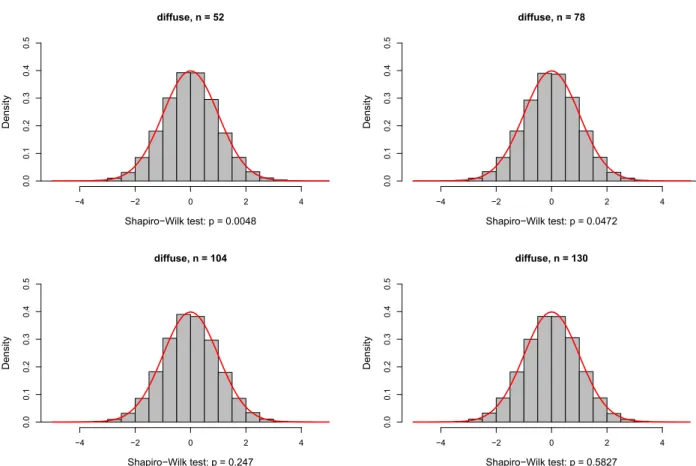
Abbildung


ÄHNLICHE DOKUMENTE
Inwiefern sind E-Portfolios ein geeignetes Instrument, um selbstgesteuerte Lernprozesse zu unterstützen?...
It will be shown that the mean-variance hedging problem in nance of this context is a special case of the linear quadratic optimal stochastic control problem discussed in Section 5,
We measure the (annualized) average ΔMPPM over a random hedge fund portfolio as the MPPM of the alternative asset strategy (90% invested into the original pension fund and 10%
I drilled holes for the screw connected to the holder. Unfortunately the screws did not fit after my first try, and I had to re-drill the holes. The next time, I will check the size
In the aftermath of any agreement, the United States (and the international community) must also maintain the will and capability to take effec- tive action, including the use
Keywords: Catastrophes, Insurance, Risk, Stochastic optimization, Adaptive Monte Carlo, Nonsmooth optimization, Ruin probability.... 3 2.3 Pareto
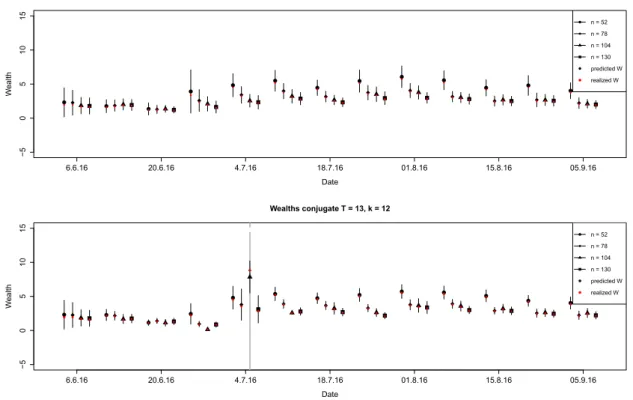
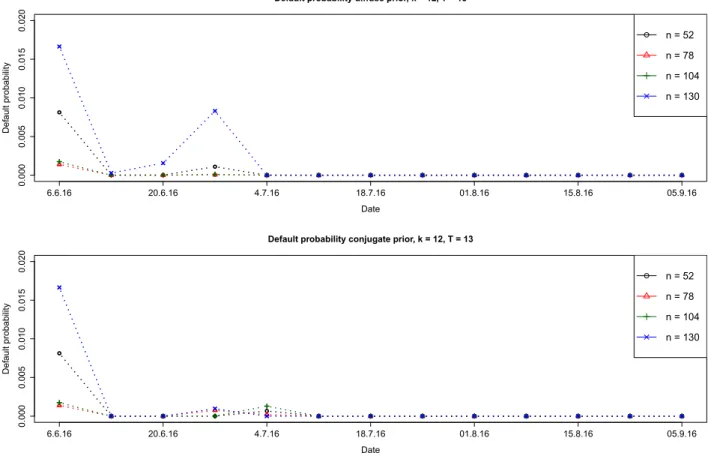
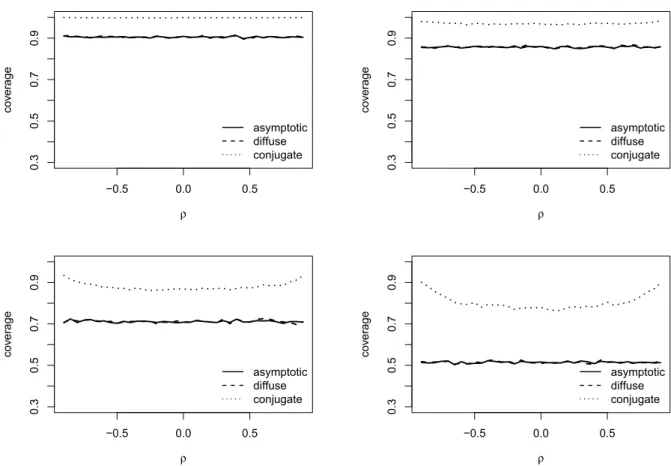
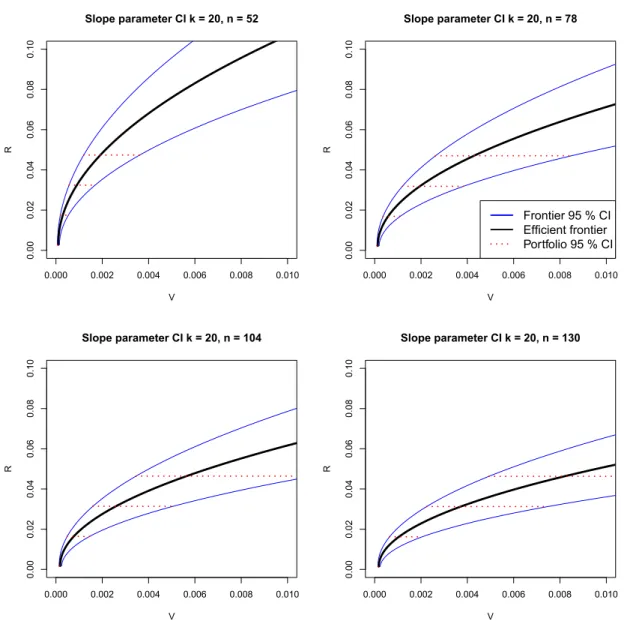
In this section, we discuss the procedure of a typical Bayesian portfolio selection. On the basis of her forecast of future stock returns, she optimally allocates the
Based on the normality assumption and on ¯ r and S as plug-in estimates, the distri-.. This will cause large short positions in the constructed portfolio. In the following, we