Anwendung der stereographischen Projektion auf Konstruktionen im nichteuklidischen Raume

Research Collection

Doctoral Thesis

Anwendung der stereographischen Projektion auf Konstruktionen im nichteuklidischen Raume

Author(s):

Mettler, Ernst Publication Date:

1916

Permanent Link:

https://doi.org/10.3929/ethz-a-000092028

Rights / License:

In Copyright - Non-Commercial Use Permitted

This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.

ETH Library

Anwendung stereographischen Projektion ^auf Konstruktionen ^im

nichteuklidischen Räume.

(5X5) ex©

Von der

Eidgenössischen Technischen Hochschule in Zürich

zur Erlangung ^der

Würde eines Doktors der Mathematik

genehmigte

Promotionsarbeit

vorgelegt ^von

Ernst Mettler,

aus Stäfa.

Referent: Herr Prof. Dr. M. GROSSMANN.

Korreferent: Herr Prof. Dr. L. KOLLROS.

165

ZÜRICH a 1916.

Diss.-Druckerei Gebr. Leemann & Co.

Stockerstr. 64.

Leer

^-

Vide

^-

Empty

LIEBEN ELTERN

AUS DANKBARKEIT GEWIDMET.

Leer

^-

Vide

^-

Empty

Der Zweck der

vorliegenden

Arbeit soll

sein,

die fundamen¬

talen, projektiven

Konstruktionen

anzugeben,

^{welche sich auf} die beiden nichteuklidischen Räume

beziehen.1)

Die

Festlegung

^der

Maßgeometrie

im Räume und damit die

Grundlage

^{für das} Konstruieren

geschieht

^durch die Annahme der absoluten Fläche. Zu diesem Zwecke bilden wir den nichteukli¬

dischen Raum auf den euklidischen ab. In diesem wählen wir nun

als das Bild des absoluten Gebildes des

hyperbolischen

^Raumes der Einfachheit halber eine reelle

Kugel

^und

repräsentieren

^die

imaginäre

^{absolute Fläche des}

elliptischen

^{Raumes durch eine} solche. Diese

Festsetzung auferlegt jedoch

^der

Allgemeinheit

keine

Einschränkungen,

^{da die}

Kugel

^{für eine}

allgemeine

^el¬

liptische

^{Fläche zweiten} Grades des nichteuklidischen Raumes

angesehen

^{werden kann. Für unsere} Konstruktionen ist die absolute Fläche als

gegeben

zu

betrachten;

wir operieren ^mit ihren

Punkten,

^{als wären es}

eigentliche

^{Punkte des} nichteukli¬

dischen Raumes. Sobaldaber auf

(diese

Art und Weise die Methoden der Konstruktionen entwickelt

sind,

^{so lassen} sie sich auch mit

Leichtigkeit

^{auf den Fall}

übertragen,

^wo die absolute Fläche nur

indirekt

gegeben ist.2)

Für die

Durchführung

^der Konstruktionen benützen wir die

stcreographische Abbildung

^{der im} euklidischen Räume

*) ^{Für die} entsprechenden Aufgaben ^{in der} hyperbolischen ^und elliptischen

Ebene vgl.: ^Großmann, M., ^Die fundamentalen Konstruktionen der nicht¬

euklidischen Geometrie (Programm ^der Thurgauischen Kantonsschule, ^Frauen¬

feld 1904).

2) ^{Groß mann,} M., ^Die Zentralprojektion ^{in der absoluten Geometrie} (Verhandlungen ^{des V.} Internationalen Mathematikerkongresses ⁱⁿ Cambridge, 1912).

— 6 ^—

als absolute Fläche des nichteuklidischen Raumes angenommenen

Kugel

^{auf die Bildebene.}

Eine Ebene trifft die

Kugel

^{in einem}

Kreise,

^{der sich be¬}

kanntlich durch diese

Abbildung

^{wieder als Kreis}

projiziert.

^Durch die Annahme eines Kreises in der Bildebene ist dann auch rück¬

wärts eine Ebene bestimmt;durch zwei

Kreise,

^{als ihre}

Potenzlinie,

eine

Gerade,

und durch drei

Kreise,

^{als ihr}

gemeinsamer

^Potenz¬

punkt,

^{ein Punkt} des betreffenden nichteuklidischen Raumes.

Es wird

jedoch

^{von Vorteil}

sein,

^{noch weitere}

Bestimmungsarten

der Raumelemente zu benützen. Z. B. bestimmen wir

häufig

^die

Lage

eines Punktes durch seine

Zentralprojektion

^{und das}

„Bild"

einer durch ihn

gehenden Ebene;

^die

Festlegung

^{einer Geraden}

geschieht

durch die Bilder der beiden

Punkte,

in denen sie die angenommene

Kugel

^trifft.

Sind zwei Geraden durch die Bilder ihrer

Durchstoßpunkte

durch die

Kugel bestimmt,

^{so schneiden sie}

sich,

^{wenn diese vier} Punkte auf einem Kreise

liegen;

^{dieser Kreis ist dann das Bild} der durch

die

beiden Geraden

gehenden

^Ebene.

Liegen

^{die vier} Punkte nicht auf einem

Kreis,

^{so sind} die Geraden windschief.

Die Ebenen eines Büschels bilden sich ab als ein Kreisbüschel und zwar sind die

Grundpunkte

^des Kreisbüschels reell oder

imaginär, je

nachdem der

Träger

^des Ebenenbüschels die

Kugel

in zwei reellen oder

imaginären

Punkten trifft.

Das Bild des absoluten Poles einer

Ebene,

d. h. des Poles der Ebene in

Bezug

auf die als absolute Fläche angenommene

Kugel,

fällt in den

Mittelpunkt

^des

Kreises,

der das Bild der Ebene ist. Demnach schneiden sich die Bilder zweier

Geraden,

die

bezüglich

^der

Kugel konjugiert polar sind, rechtwinklig,

Ebenso treffen sich die Bilder zweier

Ebenen,

^{von denen die} eine durch den absoluten Pol der andern

geht,

^{unter rechten} Winkeln.

Durch die Annahme zweier Kreise

kj

^und

k2

^{und derenMittel¬}

punkte Ki

und

K2

ⁱⁿ der Bildebene sind im Räume zwei Ebenen

E]

und

E2

^und ihre absoluten Pole bestimmt. Die

gegenseitige Lage

^von

Ej

^und

E2

ist durch die Kreise

ki

und

k2 völlig gegeben.

Schneiden sich

kj und,k2

^inden

Punkten Ui

^und

TJ2,

so ist

Vi U2

^=s das Bild der

Schnittgeraden

von

Ei

^und

E2; KiK2

^{=s* ist das}

Bild der zu s

konjugierten

^{Polaren. Ein Kreis}

k,

^der

kx

^und

k2 rechtwinklig trifft,

stellt das Bild einer durch s*

gehenden

^Ebene E

dar;

^{ihr Pol K}

liegt notwendigerweise

^{auf s. Die}

Schnittgeraden

von E mit

Ej

^und

E2

treffen s* in den

Durchstoßpunkten Px

^und

P2

von s* durch

Ex

^und

E2.

^{Durch die Punkte}

Ki, Pls K2, P2

^{ist die} absolute Involution auf s* bestimmt. Somit kann also auf einfache Weise die absolute Involution auf einerGeraden

angegeben werden,

ohne die

Fixierung

des absoluten Gebildes. Das heißt:

Die meisten

projektiven

Konstruktionen kön¬

nen

durchgeführt werden,

^{ohne daß das absolute} Gebilde in

Bezug

auf unsere Bildebene

festge¬

legt

ist.

Es betrifft dies diese

Konstruktionen,

in denen der Bildebene

nur die

Bedeutung

^als

solche,

^{aber keine weitere zukommt.}

Spielt

sie aber in einer

Aufgabe

^{eine besondere}

Rolle,

^{d. h. sind} in ihr

gewisse

Konstruktionselemente

gegeben

^oder

gesucht,

so

muß die

gegenseitige Lage

^von Bildebene und absoluter Fläche

gegeben

^{sein. Diese}

Festlegung

^{werden wir}

später

^{in den be¬}

treffenden

Aufgaben

^vornehmen.

Durch diese

eindeutige Abbildung gelangen

^{wir zu einfachen} Konstruktionen. Wir

geben

ⁱⁿ

Folgendem

^die

Lösungen

^{der funda¬}

mentalen

Aufgaben

^der

hyperbolischen

^und

elliptischen

^Geometrie.

I. TEIL

Die hyperbolische ^Geometric

§

^1. Definitionen und

Hauptsätze

^der

hyperbolischen

^Geometrie.

Um uns in den

folgenden Betrachtungen

kürzer fassen zu

können, geben

^{wir eine}

Zusammenstellung

^der

wichtigsten

^von

uns

gebrauchten

Definitionen und Sätze.

1. Das absolute Gebilde des

hyperbolischen

^{Raumes ist eine}

reelle,

^nicht

degenerierte

^{Fläche zweiten Gra¬}

des,

^die sogenannte absolute Fläche.

2. Die Punkte im Innern der absoluten Fläche nennen wir reale

Punkte,

^im

Gegensatz

^{zu den}

äußern,

^{den idealen}

Punkten,

^{die für} ein

hyperbolisches

^Wesen

unzugänglich

^sind.

Eine

Ebene,

die reale Punkte

enthält,

heißt eine reale

Ebene,

eine

solche,

^{die nur} ideale Punkte

besitzt,

^{eine ideale} Ebene.

Analog

unterscheiden wir zwischen realen und idealen Geraden.

3. Jede

eigentliche

^{oder reale Gerade hat zwei}

reelle,

^unend¬

lich ferne

Punkte;

^{es sind dies ihre}

Schnittpunkte

mit der abso¬

luten Fläche. Wir nennen sie die beiden Enden der Ge¬

raden. Zwei

Geraden,

die in einer Ebene

liegen,

^{treffen sich in} einem realen oder idealen

Punkt,

oder in einem Punkte der absoluten Fläche.

Demzufolge

unterscheiden wir zwischen sich

schneidenden,

nichtschneidenden und

parallelen

Geraden.

4. Die unendlich fernen Punkte einer Ebene

liegen

^{auf der} Schnittkurve der Ebene und der absoluten Fläche. Ihre Gesamtheit bildet den

absolutenKegelschnitt

derbetreffenden Ebene.

5. Die durch einen Punkt

gelegten

Ebenen zerfallen

bezüglich

einer nicht durchihn

gehenden

^{Ebene in}

schneidende,

^nicht¬

schneidende und einfach unendlich viele

parallele.

^Schnei¬

dende Ebenen treffen sich in einer

realen,

nichtschneidende in einer idealen Geraden. Die

parallelen

^{Ebenen umhüllen den}

Kegel

zweiten

Grades,

der den Punkt mit dem absoluten

Kegel¬

schnitt, der Ebene verbindet. Zwei Ebenen sind also

parallel,

^wenn ihre

Schnittgerade

^eine

Tangente

^der absoluten Fläche ist.

6. Durch die Annahme der absoluten Fläche und zweier Kon¬

stanten ist die

hyperbolische

Geometrie bestimmt.

7. Wir definieren als den Abstand r der Punkte A und B

r ⁼

klgCABUiUs),

wo

Ui

^und

U2

^die beiden Enden ihrer

Verbindungsgeraden sind,

und k eine

beliebige,

reelle Konstante bedeutet. Sind

Ex

^und

E2

zwei

Ebenen, TI1

und

IT2

die

Tangentialebenen

von ihrer Schnitt¬

geraden

an die absolute

Fläche,

^{so ist der Winkel} q> der beiden Ebenen

Ej

^und

E2 gegeben

^durch

cf⁼k' i

lg (Ei E2 ir± n2). (k' reell,

ⁱ⁼

f

^—

1).

8. Demnach haben zwei reale Punkte einen reellen

eindeutigen

Abstand. Zwei

Ebenen,

die sich in einer realen Geraden

treffen,

bilden einen reellen

Winkel,

^dessen

Messung

^{die Periode 2k'?r} besitzt. Einer vollen

Umdrehung entspricht

der Winkel 4k'ji.

9. Der Winkel zweier sich schneidender Geraden a und b wird

dargestellt

durch den

Ebenenwinkel,

den die beiden Ebenen

bilden,

^{welche die Geraden mit dem absoluten Pol der Ver¬}

bindungsebene

^{von a und b verbinden.}

10. Ist

F^

⁼

SSa'kXlXk=0 ^(i.

^{k =}

^1,

^2,

^{3, 4j}

die

Gleichung

^{der absoluten Fläche in} Punktkoordinaten und

dieselbe in

Ebenenkoordinaten,

^{wo --a.kX.Xk und}

ZZa^^

zwei

indefinite, quadratische

^Formen

bedeuten,

^{und setzt man}

\- 10 ^—

so läßt sich die Größe des Abstandes r der beiden Punkte A

(x1(

x2,x3,

x4)

^{und B}

(y1(

y2, y3,

YÙ

^{ausdrücken in der Form}

r ⁼

klg ^y+faly ^-Fxx -Fyy F)ty

^—

>Fxy ^—Fxx'Fyy

oder

F

cos- ^{- xv}

2ki

|/Fxx-Fyy

^2ki

J/ ^Fxx-Fyy

Für den Winkel zweier Ebenen

Ei (£1, §2, £s, £4)

^und

E2 {%,

t]3, rls,

W

erhalten wir die

Bestimmungsgleichungen

COS ^rr-r⁼--^== ^< Sltl prV", ⁼

/

^{— ~ ~ >}

2k

y(!>,, 0),v

^{2k f}

<p|r Qrr]

11. Zwei Ebenen stehen

rechtwinklig aufeinander,

^{wenn die} eine durch den absoluten Pol der andern

geht,

^{denn es ist dann}

<%? =-0,

^also <p^—Yn.

12. Von den 15 fach unendlich vielen Kollineationen des Raumes transformieren 6 fach unendlich viele die absolute Fläche in sich selbst. Eine

jede

solche Kollineation ist eine

Bewegung

des

hyperbolischen Raumes,

^{da durch sie} die Maßverhältnisse

uhgeändert bleiben.2)

Diese Definitionen und Sätze führen nun

infolge

^ihrer pro¬

jektiven Eigenschaften

zu einfachen Konstruktionen der metrischen

Aufgaben

^des

hyperbolischen

Raumes.

§

^2.

Winkelhalbierungs-

^und Mittelnormalebenen.

1.

Aufgabe.

Es sind die

Winkelhalbierungsebenen

^eines Ebenenwinkels zu bestimmen.

Auflösung, a)

^Die Scheitelkante ist eine reale Gerade. Sind die beiden Ebenen

Ex

^und

E2 gegeben

durch ihre beiden absoluten Kreise

~kt

^und

k2 (vgl. Fig. 1),

^{so ist ihre} ge¬

meinsame Potenzlinie die

Schnittgerade

^s der beiden Ebenen.

Die

Verbindungsgerade

^{s* der Punkte}

Kx

^und

K2

^{ist die kon-} x) Clebsch-Lindemann, Vorlesungen ^über Geometrie, ^IL Band.

2) Klein, F., Vorlesungen über nichteuklidische Geometrie.

jugierte

^{Polare zu s}

bezüglich

der absoluten

Fläche,

da die

Mittelpunkte Kt

^und

K2

die Bilder der Pole der Ebenen

Ex

^und

Eg

bedeuten. Die

Schnittpunkte Pi

^und

P2

^{von s* mit}

Ei

^und

E2

^sind die Pole ^von s in

Bezug

auf die Kreise

ki

^und

k2.

Sie können

am einfachsten

gefunden werden,

^{indem wir durch s* eine Ebene} E* legen. ^Ihr

Bild,

^{der Kreis}

k*,

^schneidet

kx

^und

k2 orthogonal.

Die

Schnittpunkte

^von s* und k* sind die beiden Enden von

s*,

d. h. die

Schnittpunkte Ui

und

U2

^{mit der}

Kugel.

^{Da aber s*}

eine ideale Gerade

ist,

so sind

Ui

^und

U2 konjugiert imaginär.

Sie sind die

Doppelpunkte

^der

elliptischen Polinvolution

^{auf s*}

bezüglich k*;

^{diese ist}

gegeben

^{durch die}

Punktepaare Ki, Pi

und

K2,

P2. ^E* steht normal auf s, somit bilden ihre Schnittger¬

raden _ai und _a2 mit

Ei

^und

E2

denselben Winkel wie

Ei

und

E2.

Die

Aufgabe

ist demnach auf die Geometrie der Ebene zurück¬

geführt.

Sind

Vi

und

Wi

^die

Schnittpunkte

^von ai mit k*und

V2

^and

W2 diejenigen

^von a2, ^so ist der

Schnittpunkt

M der Geraden

Vi W2

und V2

Wi

ein Punkt der Wüikelhalbierenden. ^M

liegt

^auf

s*,

^da A der Pol ist von s* in

Bezug

auf k*. Die Ebene E durch Munds

ist eine der

gesuchten Halbierungsebenen.

Die Geraden

WiW2

und

Vi V»

^{treffen sich auf s* in M'=K.} AM' halbiert den Winkel

von ai und _a2 ebenfalls. Somit halbiert auch ^E' durch M' und s

den Winkel von

Ei

^und

E2.

^{Wie aus der}

Figur

ersichtlich

ist,

fällt der Pol K' von E' mit M _zusammen; d. h.: Die beiden

— 12 ^—

Winkelhalbierenden eines Ebenenwinkels stehen normal aufeinander. Die Kreise k und k7 sind die Bilder dieser Ebenen.

b)

^Die Scheitelkante s des Ebenenwinkels ist eine ideale Gerade. Wir

geben

^die

Auflösung,

^{weil wir}

uns

später

^darauf

berufen,

obsehon das Verfahren dasselbe

ist,

wie im ersten Falle. Für ein

hyperbolisches

Wesen fällt die

Bedeutung

^dieser Winkelhalbierenden als solche

dahin,

^{da der} Winkel der beiden Ebenen

imaginär

^{ist. Die}

Halbierungsebene

stellt aber den Ort von allen Punkten

dar,

die von

Et

^und

E2 gleiche

Abstände haben.

Die Involution auf der Geraden

s*, gegeben

durch die Punkte¬

paare

Px, Kx

^und

P2, K2,

ist in diesem Falle

hyperbolisch (Fig. 2)

; also sind die

Doppelpunkte Ux

^und

U2

^{reell. Wir bestimmen} den

Mittelpunkt

^{M der Strecke}

Px P2

^als

Schnittpunkt

^von

Vt W2

und V2

Wx-

Die Ebene E durch M und s ist die

Halbierungsebene

-des Ebenenwinkels. Denn ist

<Ti ⁼

k'

i

lg (E,

^E

JI, 77,),

(f2⁼

k'

i

lg (E E2 nt /T2),

wo

H1

^und

JT2

^die

Tangentialebenen

^{von s} an die absolute Fläche

bedeuten,

^so

folgt

^aus

(Pi

^M

Ux U2)

⁼

(Ex

^E

Ih JT2), (M P2

Ux

U2)

⁼

(E E2 n, n2)

^und

(Pi

^M

Ux U2)

⁼

(M P2 Ux U2).

Die zweite Winkelhalbierende Ebene F/ ist in diesem Falle

ideal;

ihr Pol K' fällt mit M zusammen.

2.

Aufgabe.

Gesucht ist die Mittelnormalebene einer Strecke AB.

Auflösung.

Die Mittelnormalebene ist die

Ebene,

^welche den

Mittelpunkt

^{M der Strecke A B mit der}

konjugierten

Polaren der Geraden AB verbindet.

Wir bestimmen

(Fig. 3)

^die

^Gerade,

^{auf der die Punkte}

A und B

liegen,

^{durch ihre Enden}

Ui

^und

U2.

^Zur

Aufsuchung

des

Mittelpunktes

^{M von AB}

legen

^{wir durch} AB eine Ebene

E,

die durch ihren absoluten

Kegelschnitt

^k

gegeben

^{ist. Ist}

Q

der Pol der Geraden AB in

Bezug

^auf

k,

^{so ist M der}

Schnittpunkt

von

Vi

W2 ^und

V2 W*.

Die Ebene durch M und

Q

^{K ist die} ge¬

suchte Mittelnormalebene E*.

Als

Anwendung

^der beiden ersten

Aufgaben geben

^{wir noch} die

Lösung

der beiden

folgenden.

3. A uf_gabe. Es ist der

Mittelpunkt

^der einbeschriebenen

Kugel

eines Tetraeders zu konstruieren.

Auflösung. Pl5 P2, P3, P4

^{seien die Ecken} des Tetraeders

(Fig. 4).

^{Die Bilder}

k12, k13

^und

k23

^der Winkelhalbierenden Ebenen

von

PXP2P3

^und

PiP8P4, PiP3P2

^und

P^P^

^und

P2P3Pt

^und

P2P3P4

besitzen als ihren

gemeinsamen Potenzpunkt

den Mittel¬

punkt

M des Tetraeders. Denn wir haben

gezeigt,

daß die Punkte der Winkelhalbierenden

gleiche

Abstände haben von den Ebenen des betreffenden

Ebenenwinkels,

also hat M denselben Abstand

von allen Tetraederflächen. D. h. die durch die sechs Kanten

— 14 ^—

gelegten

Winkelhalbierenden schneiden sich in einem Punkte.

Je

drei,

^{die durch eine Ecke}

gehen,

treffen sich in einer Geraden.

Die

Fußpunkte

der Lote von M auf die Flächen sind die Berüh¬

rungspunkte.

^{Nehmen wir an Stelle der}

angegebenen

^Winkel¬

halbierenden

diejenigen

^der

Außenwinkel,

^so erhalten wir vier

neue

Punkte,

^{die die}

gleiche Eigenschaft besitzen,

^{wie M. Es} sind dies die

Mittelpunkte

^der anbeschriebenen

Kugeln.

In der

Figur

^{wurden die}

Eckpunkte Pi

und P2

festgelegt

auf ihrer

Verbindungsgeraden U12 V«,

^und

P3, P4

^durch

U34 V34.

Die Winkelhalbierenden von zwei Tetraederflächen können nach

Aufgabe

^{1 leicht}

gefunden werden,

sobald die Enden der Kanten und die Bilder der die Flachen enthaltenden Ebenen bestimmt sind. Um die Enden von

PiP3

^zu

bestimmen,

legen ^wir durch

U12,1]34, V34

^den

Kreis,

der das Bild der Ebene

U12P3P4

ist. Das zweite Ende W der Geraden

U12P3

^{ist der}

Schnittpunkt

^von

U13 P3

^{mit dem}

angegebenen

^Kreis. Der Kreis durch

W, Ui2, Vj.2

ist das Bild der Ebene

Pi P3 P3

^{und trifft}

Px P3

^{in den}

gesuchten

Punkten.

4.

Aufgabe.

^Man konstruiere den

Mittelpunkt

^{der um¬}

schriebenen

Kugel

^eines Tetraeders.

Auflösung.

^Der

Mittelpunkt

^der umschriebenen

Kugel

ist der

Schnittpunkt

der Mittelnormalebenen der sechs Tetraeder¬

kanten.

Sind in

Figur

⁵

Pi, P2, P3, P4

^{die Ecken des}

Tetraeders,

^so

ist seine

Lage

bestimmt durch die Geraden

U12 V12

und

U34 V34

und durch die Bilder von

Pt, P2, P3, P4.

^{Mit Hilfe der Pole}

A13

und

A2o

^von

Pj P3

^und

P2 P3 bezüglich

^des absoluten Kreises

k123

^der Ebene

Pi P2 P3

konstruieren wir uns den

Mittelpunkt Mi2j

^des umschriebenen Kreises des Dreiecks

PiP2P3.

^Die

Mittelnormalebenen von

Px P2, P2 P3

^und

P3 Pi gehen

^durch

M123

und den absoluten Pol

P123

der Ebene

Pi P2 P3.

mi23 ⁼ Mi23

Pi23

^{ist ihre}

Schnittgerade.

Wir finden den

Mittelpunkt

M unserer

gesuchten Kugel,

^{indem wir diese} Konstruktion nochmals durch¬

führen;

^{z. B. für die Ebene}

PiP3P4.

^{Die Geraden} mi23 und _mi34

ergeben

^{als ihren}

Schnittpunkt

^den

Mittelpunkt M;

^{sie schneiden}

sich,

da sie in der Mittelnormalebene von

P^ liegen.

^{M hat}

gleiche

^{Abstände von}

P4, P2, P3, P4,

denn die Punkte von m123 sind

gleich

weit von

Pl5 P2, P3

^und

diejenigen

^von m13i

gleich

weit von

Pj, P3. P4

entfernt.

— 16 ^—

§

^3. Abstandsfläche eines Punktes und einer Ebene.

5.

Aufgabe.

^Ist eine

Kugel gegeben

^{durch das Zentrum} M und den Radius

MP,

^so sind weitere Punkte derselben und ihre Schnittkurve mit einer Ebene

anzugeben.

Auflösung.

^Bedeutet

Pt

^ein weiterer Punkt der

Kugel

um M durch P und sind

Ui

^und

Vx

^die Enden der Geraden

MPx,

so

gilt (vgl. ^Fig. 6)

(MP!UiVi

⁼

(MPUV).

Demnach stehen alle

Kugeln

ⁱⁿ räumlich kol¬

linearer

Beziehung

^{zur absoluten}

Fläche,

^{sind also} Flächen zweiten Grades. Der

Mittelpunkt

^M ist Kollineations- zentrum; ^die absolute Polarebene von M ist Kollineationsebene.

Sind R und S die beiden noch fehlenden

Diagonalpunkte

^des

vollständigen

^Vierecks

UVUiVi,

^so liefern die Geraden RP und SP auf

UiVi

bekanntlich zwei weitere

Kugelpunkte Px

^und

P2.

Der

Schnittpunkt

von R

P4

und U V oder von S

Px

^{und UV}

gibt

den zu P diametralen Punkt P'. Auf diese Art können

beliebig

viele Punkte der

Kugel gefunden

werden. Die

Tangentialebene

in einem Punkte der Fläche ist die Normalebene zu seinem

Radius, geht

^{also durch die}

konjugierte

^Polare seines Radius. Diese

Eigenschaft folgt

aus der kollinearen

Beziehung

^der

Kugel

^und der absoluten Fläche.

Um den

Kugelkreis,

der in der Ebene B

liegt,

^zu

bestimmen,

legen

^{wir durch das Lot Mil} von M auf E eine Ebene E*

(k*

^sei ihr absoluter

Kegelschnitt; vgl. Fig. 7).

^{Wir bestimmen die}

auf der

Schnittgeraden

^{s von E und E*}

gelegenen Kugelpunkte Pi

^und

P2

^{mit Hilfe der}

vorigen Aufgabe.

Dadurch"ist der Kreis in E vollkommen bestimmt. Für dieKonstruktion weiterer Elemente des Kreises benützt man die

Kollineation,

^{die zwischen dem}

Kugelkreis

^und dem absoluten

Kegelschnitt

^{von E besteht.}

Demnach lassen sich die fundamentalen

Aufgaben

^{über die}

Kugel

^{auf einfache} Art. durch räumliche oder ebene Zentral- kollineation lösen. Als

Beispiel geben

^{wir noch die}

Auflösung folgender Aufgabe:

Gesucht ist die

Durchdringungskurve

^zweier

Kugeln.

Ist der Abstand der beiden Zentren M und M'* kleiner als die Summe der beiden

Radien,

^so besteht die vollständige ^Durch¬

dringungskurve

ⁱⁿ einem reellen und einem

imaginären

^Kreis.

Ist ein Punkt des reellen Kreises

gegeben,

^so kann derselbe nach

obiger Aufgabe

^leicht

angegeben

^werden. Sind aber die beiden

Kugeln anderweitig gegeben,

^{so bestimmt man die beiden}

Ebenen,

welche die

Durchdringungskurve enthalten,

^wie

folgt:

In

Figur

^{8 seien} die beiden

Kugeln

^{bestimmt durch die} Zentren M und M' und

je

^{einem Punkt A und}

A',

^{welche der} Einfachheit halber so angenommen

wurden,

^daß sie mit M und M' in einer Ebene

liegen.

^{Von dem}

gemeinsamen

Polartetraeder der beiden Flächen sind zwei

gegenüberliegende

^Kanten

bestimmt;

es sind dies die Geraden MM' und ihre absolute Polare s. Die

Aufgabe

vierten Grades reduziert sich somit auf solche vom

zweiten Grade. Ist S der

Durchstoßpunkt

^{von s} durch die Ebene

— 18 ^—

MM'A

A',

^{so ist S}

Träger

^{von einerlei} Polarinvolution

bezüglich

der beiden in* dieser Ebene

liegenden Kugelkreise.

Wir bestimmen zu A und A' die beiden Polaren

bezüglich

dieser Kreise mit Hilfe der

Kollineation,

welche zwischen den Kreisen und k besteht. Schneiden sich die Polaren von A in A* und

diejenigen

^{von A'-in}

A'*,

^so bestimmen die Strahlen von

S

nach-A, A*,

A'und A'* die

angegebene

Involution. Die

Doppel¬

strahlen x=x' und _y⁼

y' geben,

^{mit s}

verbunden,

^die

Ebenen,

welche die

vollständige Durchdringungskurve

^beider

Kugeln

^ent¬

halten. Damit ist die

Aufgabe

^{auf die}

vorhergehende

^zurück¬

geführt.

A*

9

PA"

r V: ?.'• A

Af\^'

y:

*. **"* ^

"

%

1°:/

J*~''''"

*s"

Jïff.â.

Abstandsfläche einer Ebene. Besitzt eine

Kugel

^ein ideales

Zentrum,

^so

geht

sie in die Abstandsfläche einer Ebene über. Sie berührt die absolute Fläche

längs

^{des absoluten}

Kegel¬

schnittes der Polarebene des

Kugelzentrums.

^Die

Aufgaben

^über die Abstandsflächen einer Ebene werden

gleich durchgeführt,

^wie

diejenigen

^{über die}

Kugeln.

Ebenso erhalten wir auf

gleiche

Weis© die

Lösung

^der

folgenden Aufgabe:

Man bestimme die

Durchdringungskurve

^einer

Kugel

^und einer Abstandsfläche. D. h. es ist damit die

Aufgabe gelöst:

Es ist der Ort aller Punkte zu

bestimmen,

^{die von einem} festen Punkt und einer festen Ebene

vorgeschriebene

^Abstände

haben.

! [

Sind die Zentren zweier

Kugeln

^ideale

Punkte,

^{und haben} die Kugeln

gleiche Radien,

^{so haben die} Punkte der Durch-

dringungskurve

^{von den beiden} Polarebenen der

Kugelmittel¬

punkte gleiche

Abstände. DieTeile der zerfallenden Kurve vierter

Ordnung liegen

^{in den} Winkelhalbierenden Ebenen des ange¬

gebenen

Ebenenwinkels.

Es bleibt noch zu

bemerken,

^{daß diese}

letzten,

^{für uns} identischen

Aufgaben,

^{für ein}

hyperbolisches

^{Wesen von ver¬}

schiedener Natur sind.

Aus den

angegebenen Eigenschaften folgt

^{der Satz:}

Berühren zwei Flächen

zweiten

Grades eine dritte

je längs

^{einem reellen oder}

imaginären Kegelschnitt,

^so

gehen

^{durch die}

Schnittgerade

die beiden

Ebenen,

^{die die}

Kegelschnitte

^ent¬

halten,

^{noch zwei}

Ebenen,

in denen die vollstän¬

dige Durchdringungskurve

^{der beiden erstem} Flächen

liegt.

Dieser Satz ist eine

Verallgemeinerung

^des Steiner'schen Satzes über

doppeltberührende Kegelschnitte.3)

§

^4.

Drehungen

^und

Schraubungen

^des

hyperbolischen

^Raumes.

Jede

Bewegung

^des

hyperbolischen

^Raumes ist bekanntlich eine

Kollineatiön,

^{die die abso¬}

lute Fläche in sich überführt. Wir beschränken uns

in

Folgendem

auf die

Drehungen

^{des Raumes um eine Gerade.}

6.

Aufgabe.

^{Man drehe den}

hyperbolischen

^{Raum um} eine Gerade um einen

gegebenen

Winkel co. Gesucht ist die End¬

lage

eines

beliebigen

^{Punktes P.}

Auflösung.

^{Bleibt bei} unserer

Bewegung

^{eine Gerade} g

fest,

so verhalten sich ihre

Schnittpunkte

^{mit der absoluten} Fläche und die

Tangentialebenen

^{in ihnen}

gleich.

^Mit g bleibt also auch ihre

absolute, konjugierte

Polare

g*

^fest.

Ist _g eine reale Gerade

(Fig. 9),

d. h. sind ihre

Schnittpunkte

mit der absoluten Fläche

reell,

so haben wir es mit einer wirk¬

lichen

Drehung

^{um eine Gerade zu} tun, wobei ^alle Punkte Kreise

(Kegelschnitte) beschreiben,

^{die in} Normalebenen zu g

liegen.

3) ^{S teine}r, Werke, ^Bd. II, pag. 469.

— 20 ^—

Sind die

Schnittpunkte

von g mit der absoluten Fläche da¬

gegen

imaginär (Fig. 10),

^{g also eine ideale}

Gerade,

so besteht die

Drehung

^um g in einer

Verschiebung

^{des Raumes}

längs g*.

Alle Punkte beschreiben zu

g* aequidistante

^Kurven

(Kegel¬

schnitte).

Für unser Denken besteht zwischen diesen beiden Fällen kein

Unterschied,

^{da wir mit idealen}

Punkten,

^{Geraden und} Ebenen

gleich operieren,

wie mit realen. Diese

Übereinstimmung

ist aber für ein

hyperbolisches

Wesen nicht vorhanden.

E sei die

Ebene,

ⁱⁿ der der Punkt P und die Gerade _g

liegt.

Der

Drehungswinkel

^{co und der Sinn der}

Drehung

^seien

gegeben

durch die Punkte A und B auf

g*.

Wir

legen

durch P die Normalebene E* zu g und haben nun die

Aufgabe

der Ebene

vor uns: Es ist die

hyperbolische

^{Ebene E* um einen}

gegebenen

Winkel zu drehen.

Der

Schnittpunkt

^{M von E* und}gist dasZentrum der

Drehung.

Sind

U, Ui

^und

V, Vi

^{die Enden der Geraden} MA und MB und

U', U'i diejenigen

^von

MP,

^{so liefert}

ViU'i

^auf

g*

einen Punkt

T,

^{der mit}

Ui

^verbunden auf k*

V'i ergibt. V'iM

^{ist die} ge¬

drehte Gerade M P. Schneidet

U'i Y\ g*

ⁱⁿ

S,

^{so trifft SP}

Vi

M in P'. P' ist der um die Gerade g um den Winkel a> ge¬

drehte Punkt P.

Wie aus der

Figur

ersichtlich ist, sind die Strecken AB und À' B' einander

gleich.

^Denn die Geraden von M nach den Punkten

Ui, Vi, W, Wi entsprechen

^{den Geraden von} M nach

Vi, U'i, Wi,

^W in der Polarinvolution um T

bezüglich

des Kreises

g*.

^{Die Ge¬}

rade

g"

trifft die beiden

projektiven

Büschel in den Punkten

A,B,

W,

W1

^und

B', A', Wi,

^{W. Es ist also}

(ABWWJ

⁼

(B'A'WiW);

^{d. h. AB = A'B'. Wir}

finden,

^daß

gleiche

Strecken auf

g*

^von Punkten auf _{g unter}

gleichen

Winkeln

gesehen

^werden. Diesen Satz hätten wir schon in

Aufgabe

1 aufstellen können. Denn wir

mußten,

^{um dieWinkel¬}

halbierende eines Ebenenwinkels zu

bestimmen, die,

^{von den} beiden Ebenen auf der

konjugierten

^{Polaren ihrer}

Schnittgeraden, herausgeschnittene

Strecke halbieren. Der

Mittelpunkt

^{der be¬}

treffenden Strecke

gab

^uns einen Punkt der Winkelhalbierenden.

Analytisch hängt

der Winkel co mit der Strecke AB⁼r durch

folgende

^Formel zusammen:

10 cos 7TP

r 2k

cos -TT-.—⁼

Sln

2¥

Ist die

Endlage

^einer

beliebigen

Geraden

gesucht,

^{so drehen} wir zwei ihrer Punkte P und

Q

^{auf die oben}

angegebene

^Weise.

P'

Q'

^{ist die}

gedrehte

^{Gerade P}

Q.

Wir haben

gesehen,

daß bei einer

Drehung

^um g die zu ihr

konjugierte

Polare

g*

^{fest bleibt,}

g*

wird in sich verschoben und zwar steht die Größe der

Drehung

^um g in einem bestimmten Verhältnis zu der

Verschiebung

^auf

g*.

^Es

gilt

somit der Satz:

Jede

Drehung

^des

hyperbolischen

^{Eaumes um} eine Gerade ist eine

Verschiebung längs

^ihrer

konjugierten Polaren,

^und

umgekehrt.

Führen wir zwei

Drehungen

aus, die eine um g, die andere

um

g*,

^{so ersetzen wir die}

Drehung

^um

g*

^{durch die}

entsprechende Verschiebung längs

g. Dadurch schrauben wir den Raum in

Bezug

auf g als

Schraubungsaxe.

^{Aus dem}

Vorigen folgt aber,

daß mit _g auch

g*

^{eine Axe oder}

Schraubung

^{ist. Jede Schrau¬}

bung

des

hyperbolischen

^{Raumes besitzt zwei}

- 22 ^-

Axen,

^die

bezüglich

des absoluten Gebildes kon¬

jugiert

^{sind. Für ein}

hyperbolisches

Wesen kommt

jedoch

nur die reale der beiden Axen in Betracht.

Abstandsfläche einer Geraden. Bei der Schrau¬

bung bewegt

^sich

jeder

Punkt auf einer Abstandsfläche der Axe g. Eine solche ist durch _g und einen Punkt ^P bestimmt.

Liegt

P auf g

selbst,

^so

degeneriert

^{die Fläche in die Gerade g und}

zwar in das Stück der

Geraden,

das die realen Punkte enthält.

Ebenso ist die absolute Fläche eine Abstandsfläche von g, denn bei der

Schraubung bewegt

^{sich diese in} sich selbst.

Legen

^wir durch P und g die

Ebene,

^{so schneidet diese} die Abstandsfläche in einer Abstandslinie

km

^von g. Die

Tangente

^{in P an}

km

^steht normal zum

Lote,

^{das von P auf} g

gefällt

werden kann. Eine Ebene durch P normal zu g, d. h. die Ebene durch P und

g*,

trifft die Abstandsfläche in einem Kreis

kn,

^{mit dem Durchsto߬}

punkt

^von g als

Mittelpunkt.

^Die

Tangente

^{in P an diesen Kreis} ist normal zu dem

entsprechenden

^{Radius. Hieraus}

folgt,

^daß die

Tangentialebene

ⁱⁿ einem

beliebigen

Punkte der Fläche nor¬

mal steht auf der durch den

Berührungspunkt gehenden

^Trans¬

versalen von g und

g*.

^{Durch die}

Drehung

^der Meridiankurve

km

^um g oder der

Drehung

^des Normalschnittes

kn

^um

g*

^er¬

zeugen diese Kurven die Fläche. Diese berührt demnach die absolute Fläche in zwei

Punkten,

^{den beiden Enden von} g.

Umnoch die Methode einer

speziellen Drehung

^zu

entwickeln, geben

wir die

Auflösung

^der

folgenden

7.

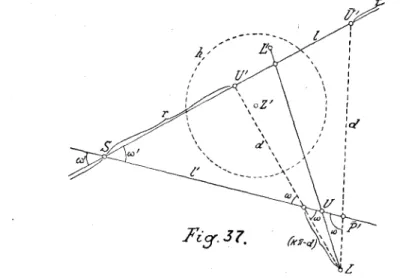
Aufgabe.

^Es ist die Ebene E in die BildebeneJTum¬

zuklappen.

Auflösung.

^{In den bereits}

gelösten Aufgaben gelangten

wir immer zu den

Lösungen,

^ohne daß wir das absolute Gebilde

gegenüber

^{unserer Tafel}

festlegten.

^Die

angegebenen Lösungen

sind,

^wie aus den Konstruktionen

folgt,

^{auch für}

jede beliebige

Lage

^{der zu Grunde}

gelegten Kugel gültig.

^{In dieser}

Aufgabe

spielt

^{aber die} Bildebene eine besondere

Rolle,

^{somit muß die} absolute Fläche der

Lage

^und Gestalt nach

gegeben sein;

^damit istdann auch das

Projektionszentrum

unserer

Abbildung

^bestimmt.

Wir erhalten die einfachsten

Konstruktionen,

^{indem wir die} Bildebene ^ffdurch das Zentrum der absoluten

Kugel legen.

^Durch die

Angabe

des absoluten

Kegelschnittes

h von ITsind die not¬

wendigen Festlegungen getroffen.

^Der

Mittelpunkt

^{von h stellt} sowohl das Bild des Poles H von Ff wie auch die

Normalprojektion

Z' des

Projektionszentrums

^{Z dar. h} ist der Distanzkreis von

Z,

der sogenannte

Hauptkreis.

E sei in

Figur

11 wie immer durch k und das Bild K ihres Poles

gegeben,

^{s sei ihre}

Schnittgerade

mit

Ff;

^{s* die zu s kon¬}

jugierte

^{Polare. Zur}

Lösung

^unserer

Aufgabe legen

^{wir durch}

s* die zu s normale Ebene

E',

^deren

Spur

^{mit dem Bilde von s*}

zusammenfällt. Durch die

Umlegung

^{von E' in n}fällt ihr absoluter

Kegelschnitt

ⁱⁿ

h,

^{Z in}

[Z]

^{und s* in}

[s*].

^Die

Schnittgerade

^AB

von E' und Ekommt in

[A] [B]

^zu

liegen.

^{Ist P ein Punkt von A}

B,

so erhalten wir

[P]

^als

Schnittpunkt

^{der Geraden P}

[Z]

^und

[A] [B].

Bei der

Umklappung

^{von E in n dreht sich E' in sich um S.}

Die

Umklappungen

^{von A und B fallen in}

(A)

^und

(B),

^insofern wir eine bestimmte der beiden

möglichen Umklappungen

^heraus¬

greifen;

im andern Falle vertauschen sich die Punkte

(A)

^und

— 24 ^—

(B).

^{Wir finden}

(P)

^durch

Vermittlung

^des

Schnittpunktes [M]

von

[s*]

^und

LA] (A),

^{denn es ist}

S[P]

⁼

S(P).

^{Die Zentral¬}

projektion

^{M von}

[M]

^{ist das Bild des} Poles einer Winkelhal¬

bierenden Ebene von E und ^ITund stellt das Zentrum der Kol- lineation

dar,

^{die zwischen den Elementen von E und den ent¬}

sprechenden

^der

Umklappung

^{besteht. Somit erhalten wir auf} einfache Weise die

Umklappung

eines weiteren Punktes

Q

^von E wie

folgt:

^Ist g ⁼

PQ,

^{so ist}

(g)

^die

Verbindung

^von

(P)

^mit dem

Schnittpunkt

^von g und s.

(Q)

⁼

(g)

^XM

Q.

^{An Stelle von}

g könnte auch A

Q

^{oder B}

Q

genommen werden.

Natürlich kann diese

Lösung

^{auch erreicht} werden durch die

Methode,

^{die in}

Aufgabe

6 entwickelt

wurde;

^{die oben an¬}

gegebene

^{ist aber für diesen}

speziellen

^Fall

vorzuziehen,

^da die Konstruktion nur das Ziehen von Geraden erfordert.

8.

Aufgabe.

^Eine

gegebene

^{Strecke A}B soll auf einer andern Geraden _g von P aus

abgetragen

^werden.

Auflösung.

Man

projiziert

^{die Strecke auf} eine Trans¬

versale der Geraden AB und g und von da auf _g selbst. Dann verschiebt man ihre

Projektion,

bis der eine oder andere End¬

punkt

in P fällt.

Die Gerade AB sei durch ihre Enden U und

V,

^{die Gerade}

g durch

Ui

^und

Vi

^{im Räume}

festgelegt.

^Da g und AB wind¬

schief

"sind,

^dürfen

U, V, Ui, Vi

^{nicht auf} einem Kreise

liegen (Fig. 12),

Durch P und AB

legen

wir die Ebene E

(k

^{sei ihr abso¬}

luter

Kegelschnitt).

^Wir

projizieren

die Strecke AB von T aus auf die durch P

gehende

^{und in E}

liegende

^Gerade

g'.

A' B' ⁼ AB.

Vom Punkte T _aus, der in der Ebene Efder beiden Geraden _g und

g' liegt, projizieren

^{wir A'B' auf} g und erhalten A"B".

A"B"=AB.

Wir haben noch A"B" auf _g zu verschieben bis A" oder B" mit P zusammenfällt. D. h. wir drehen den Raum um die

konjugierte

Polare zu g. Die weitere

Auflösung gibt Aufgabe

^6.

Die

Lösung

^kann

verschiedenartig gestaltet

^werden. Bei¬

spielsweise

könnte A' B' auf

g'

^{so verschoben}

werden,

^{bis A' in}

P fällt. Dann schneidet der

Kreis,

^der durch den verschobenen Punkt B'

geht,

P als Zentrum besitzt und in E'

liegt,

g in den gesuchten Punkten.

Wir

geben

für den zweiten Teil der oben

gelösten Aufgabe,

also für die

Verschiebung

einer Strecke auf der durch sie be¬

stimmten Geraden eine zweite

Lösung.

Dadurch werden wir eine Konstruktionsmethode kennen

lernen,

^{die zu den denkbar ein¬}

fachsten

Lösungen führt,

^{und die aus der von uns benützten} sofort

hergeleitet

werden kann.

Legen

^wir durch einen Punkt des

hyperbolischen

Raumes das

Ebenenbündel,

^{so wird dasselbe in unserer}

Abbildung

^durch ein Kreisbündel

dargestellt.

Das Bild des betreffenden Punktes hat in

Bezug

auf alle Kreise des Büschels dieselbe Potenz k2.

Die realen Punkte des

hyperbolischen

^Raumes besitzen eine nega¬

tive,

die idealen eine

positive,

^{die Punkte der} absoluten Fläche eine verschwindende Potenz. Ordnet man nun

jedem

^{Punkte P} des

hyperbolischen

Raumes einen beistimmten Punkt P' des eukli¬

dischen Raumes zu und zwar so, daß die

Normalprojektion

^von

P' auf die Bildebene zusammenfällt mit der

stereographischen Projektion

^{von P} und daß die Kote z' von P'

gleich

^ist

Y— k2,

wo k? die oben definierte Potenz

bedeutet,

^{so hat man damit} den

hyperbolischen

Raum auf den euklidischen

abgebildet.

Um eine

eindeutige Abbildung

^zu

besitzen,

^bestimmen

wir,

^{daß immer}

nur der

positive

Wert von

Y

^—k2 genommen werden soll. Damit wird der

hyperbolische

^Raum

eindeutig

^{auf einen durch die} Bildebene bestimmten euklidischen Halbraum

abgebildet.

Den realen Punkten des

hyperbolischen

^Raumes

entsprechen

^die

reellen,

^{den idealen die}

imaginären

^Punkte des euklidischenHalb¬

raumes und den Punkten der absoluten Fläche

diejenigen

^der Bildebene.

— 26 ^—

Diese

Abbildung

^{ist identisch mit}

derjenigen,

^{die von Poin-}

c a ré

angegeben wurde.4) Legen wir,

^{wie in}

Aufgabe 7,

^die Bildebene durch das Zentrum der absoluten

Kugel

^{und wählen} wir ZZ' als z-Axe und ^Z' als

Nullpunkt

^eines

rechtwinkligen Koordinatensystems,

^so

entspricht

^{dem Punkte P}

(x,

y,

z)

des

hy¬

perbolischen

^Raumes der Punkt P'

(x', y', z')

^des

euklidischen,

wenn

x'=7. ^y'

⁼

ri

^{und Z' =}

7Z7P2~(s2 ^{+ y2+z2),}

wo r den Radius der als absolute Fläche angenommenen

Kugel

bedeutet. Hieraus

folgt,

^{wie auch aus den}

angeführten

geo¬

metrischen

Betrachtungen,

^daß

jeder

^{Ebene des}

hyperbolischen

Raumes eine

Halbkugel

des euklidischen Raumes

entspricht.

Diese

Halbkugel

trifft die Bildebene normal und zwar in dem Bilde des absoluten Kreiseis der

entsprechenden

^{Ebene des}

hyperbo¬

lischen Raumes. Jeder Geraden

entspricht

^ein

Halbkreis,

dessen Ebene normal zur Bildebene steht und dessen

Endpunkte

^die Bilder der Enden der Geraden sind.

Wir wollen diese

Abbildung

für die

Lösung

^{der oben er¬}

wähnten Aufgabe ^benützen.

Soll AB auf _g von A' aus

abgetragen werden,

^{so halbieren} wir BA'. Wir bestimmen zu A den

symmetrischen

Punkt B' in

Bezug

auf den

Halbierungspunkt.

^A'B' ist die verschobene Strecke AB.

Ist in

Figur

^{13 die Gerade} g, welche die Strecke AB

enthält,

bestimmt durch die beiden Enden U und

V,

^{so wird}

ihr, gemäß

ihrer

Abbildung,

der Halbkreis über U

V,

dessen

Normalprojektion

mit g

zusammenfällt, zugeordnet.

Die

Umlegung

^{dieses Halb¬}

kreises sei

[g].

^{Den Punkten A und B}

entsprechen

^{in der Um¬}

legung

^{die Punkte}

[A]

^und

[B].

^{Ziehen wir in}

[B]

^und

[A]

^die

Tangenten

an

[g],

^so treffen sich diese in einem Punkte

[Mi],

dessen

Normalprojektion

^{M der}

Mittelpunkt

von BA' ist. Denn

es ist leicht zu

zeigen,

daß

(BMU V)

⁼

(M

^A'U

V).

^{Um die} Strecke AM von M aus nach V hin

abzutragen,

^{bestimmt man}

*) Poincaré, ^H., Wissenschaft und Hypothese (Autor, ^{deutsche Aus¬}

gabe ^von Lindemann) 1904, pag. 42 ff. und Anmerkung 19, pag. 257ff.

den

Schnittpunkt [M'J

^der

Tangente

ⁱⁿ

|A]

^{und M}

[MJ.

^Ist

[M'J [B'J

euklidisch

gleich [M'J[A],

^so bestimmt die

Normalprojektion

^von

[B'J

^auf g den Punkt B'. Es ist AM⁼

MB,

^{also AB=A'B'.}

Dieses

Beispiel zeigt,

^{wie mit Hilfe dieser}

Abbildung

^die

Aufgaben

^der

hyperbolischen

^{Geometrie auf} einfache Weise durch euklidische Konstruktionen

gelöst

werden können.

9.

Aufgabe.

^Eine

Bewegung

^des

hyperbolischen

^Raumes ist

gegeben

durch

Anfangs-

^und

Endlage

^eines Punktes und durch

Anfangs-

^und

Endlage

zweier durch ihn

gehender

normaler Ge¬

raden. Gesucht sind zwei

Geraden,

^{um welche der Kaum} ge¬

dreht werden

muß,

^damit

Anfangs-

^und

Endlage zusammenfallen;

insbesondere ist die

Schraubungsaxe

^{zu bestimmen.}

Auflösung.

Ist die

Anfangslage gegeben

^{durch P und} die durch ihn

gehenden

normalen Geraden

UUi

^und

YVX,

^die

Endlage

^{durch P'} und die

entsprechenden

^Geraden

U'U'i

^und V

V\ (Fig. 14),

^{so sind durch die}

Zuordnung

dieser Elemente sechs Konstante bestimmt. Aus den 6 fach unendlich vielen Kol-

lineationen,

^{die die absolute} Fläche in sich

überführen,

^wird demnach eine

spezielle herausgegriffen.

^{Damit ist aber die Be¬}

wegung noch nicht

eindeutig

^{bestimmt. Es muß noch}

angegeben werden,

ⁱⁿ welchem Sinne sich die Enden der Geraden ent¬

sprechen

^{sollen. Wir}

legen fest,

^{daß die}

Halbgerade

^{PU in P'U'} und PV in P'V

übergehen

^{soll. Damit haben wir}

erreicht,

^daß einer bestimmten Halbebene der Ebene PUV eine bestimmte der Ebene P' U'V

entspricht. Bringen

^{wir P mit}

P',

^{U mitU'} und V mit V zur

Deckung,

^{so fällt} auch die Normale W

Wi

^durch P zur Ebene PUV mit seiner

entsprechenden W'W'i

zusammen.

— 28 ^—

Durch das

Entsprechen

der

Halbgeraden

^{PW und P'W wird} einem bestimmten Halbraum der

Anfangslage

^{ein bestimmter} der

Endlage zugeordnet.

Zur

Lösung

^unserer

Aufgabe

^{drehen wir den Raum um die}

Sclmittgerade

^{der Ebenen PU V und P'U'}

V,

^{bis P in die Ebene}

P'U' V fällt. Dann dreht man noch um die

Gerade,

^{welche durch} den absoluten Pol der Ebene P'U'V

geht,

^{bis die}

gedrehten

Punkte P,

U,

V in ihre

entsprechenden P', U',

V zu

liegen

kommen.

Mit Hilfe der

Aufgabe

^{6 drehen}wir den Raum um die Schnitt¬

gerade

^{a der Ebenen P}U V und F U' V

(Fig. 14). P", U",

V" seien die

gedrehten

^Punkte

P, U,

^V.

P, U,

^{V und}

P", U",

V"

entsprechen

sich in der Involution mit dem Pol einer der Winkelhalbierenden Ebenen der beiden als Zentrum. Es sind also zwei Fälle

möglich.

Es ist der Pol zu

wählen,

^der drei solche Punkte

P", U",

^V"

liefert,

welche dann mit

P', U',

^{V auch} wirklich durch eine endliche

Drehung

^oder

Verschiebung

^zur

Deckung gebracht

^{werden können.}

Ist M der Punkt der Ebene P' U'

V,

^um welchen sie

gedreht

werden

muß,

^daß P" in

P',

^{U" in} U' und V" in V

übergeht,

^so