FUNCTIONAL ANALYSIS Theo B¨uhler Dietmar A. Salamon

(1)

FUNCTIONAL ANALYSIS

Theo B¨ uhler Dietmar A. Salamon

ETH Z¨urich

E-mail address: math@theobuehler.org E-mail address: salamond@math.ethz.ch

(2)

space, dual operator, Arzel`a–Ascoli, uniform boundedness, open mapping, closed graph, Hahn–Banach, James space, weak and weak* topology, Banach–Alaoglu, Banach–Dieudonn´e, Eberlein-ˇSmulyan, Kre˘ın–Milman,

ergodic theorem, closed image theorem, compact operator, Fredholm theory, spectral theory, functional calculus, Gelfand representation, spectral measure, unbounded operator, strongly continuous semigroup,

infinitesimal generator, Hille–Yosida–Phillips, analytic semigroup.

Abstract. This book provides an introduction to the subject of Func- tional Analysis for third year students of mathematics and physics with a basic knowledge of first year analysis and linear algebra as well as some complex analysis, point set topology, and measure and integration.

(3)

Preface

These are notes for the lecture course “Functional Analysis I” held by the second author at ETH Z¨urich in the fall semester 2015. Prerequisites are the first year courses on Analysis and Linear Algebra, and the second year courses onComplex Analysis,Topology, and Measure and Integration.

The material of Section 1.4 on elementary Hilbert space theory, Sub- section 5.4.2 on the Stone–Weierstraß Theorem, and the appendix on the Lemma of Zorn and Tychonoff’s Theorem was not covered in the lectures.

These topics were assumed to have been covered in previous lecture courses.

They are included here for completeness of the exposition.

The material of Subsection 2.4.4 on the James space, Section 5.5 on the functional calculus for bounded normal operators, and Chapter 6 on unbounded operators was not part of the lecture course (with the exception of some of the basic definitions in Chapter 6 that are relevant for infinitesimal generators of strongly continuous semigroups). From Chapter 7 only the basic material on strongly continuous semigroups in Section 7.1, on their infinitesimal generators in Section 7.2, and on the dual semigroup in Sec- tion 7.3 were included in the lecture course.

28 February 2018 Theo B¨uhler

Dietmar A. Salamon

ix

(8)

(9)

Introduction

Classically, functional analysis is the study of function spaces and linear operators between them. The relevant function spaces are often equipped with the structure of a Banach space and many of the central results re- main valid in the more general setting of bounded linear operators between Banach spaces or normed vector spaces, where the specific properties of the concrete function space in question only play a minor role. Thus, in the modern guise, functional analysis is the study of Banach spaces and bounded linear operators between them, and this is the viewpoint taken in the present book. This area of mathematics has both an intrinsic beauty, which we hope to convey to the reader, and a vast number of applications in many fields of mathematics. These include the analysis of PDEs, differential topology and geometry, symplectic topology, quantum mechanics, probability theory, geometric group theory, dynamical systems, ergodic theory, and approximation theory, among many others. While we say little about specific applications, they do motivate the choice of topics covered in this book, and our goal is to give a self-contained exposition of the necessary background in abstract functional analysis for many of the relevant applications.

The book is addressed primarily to third year students of mathematics or physics, and the reader is assumed to be familiar with first year analysis and linear algebra, as well as complex analysis and the basics of point set topology and measure and integration. For example, this book does not include a proof of completeness and duality forL^p spaces.

There are naturally many topics that go beyond the scope of the present book, such as Sobolev spaces and PDEs, which would require a book on its own and, in fact, very many books have been written about this subject; here we just refer the interested reader to [19, 28, 30]. We also

xi

(10)

restrict the discussion to linear operators and say nothing about nonlinear functional analysis. Other topics not covered include the Fourier transform (see [2, 48, 79]), maximal regularity for semigroups (see [76]), the space of Fredholm operators on an infinite-dimensional Hilbert space as a clas- sifying space for K-theory (see [5, 6, 7, 42]), Quillen’s determinant line bundle over the space of Fredholm operators (see [71, 77]), and the work of Gowers [31] and Argyros–Haydon [4] on Banach spaces on which every bounded linear operator is the sum of a scalar multiple of the identity and a compact operator. Here is a description of the contents of the book, chapter by chapter.

Chapter 1 discusses some basic concepts that play a central role in the subject. It begins with a section on metric spaces and compact sets which includes a proof of the Arzel`a–Ascoli theorem. It then moves on to establish some basic properties of finite-dimensional normed vector spaces and shows, in particular, that a normed vector space is finite-dimensional if and only if the unit ball is compact. The first chapter also introduces the dual space of a normed vector space, explains several important examples, and contains an introduction to elementary Hilbert space theory. It then introduces Banach algebras and shows that the group of invertible elements is an open set. It closes with a proof of the Baire category theorem.

Chapter 2 is devoted to the three fundamental principles of functional analysis. They are theUniform Boundedness Principle(a pointwise bounded family of bounded linear operators on a Banach space is bounded), theOpen Mapping Theorem (a surjective bounded linear operator between Banach spaces is open), and the Hahn–Banach Theorem (a bounded linear functional on a linear subspace of a normed vector space extends to a bounded linear functional on the entire normed vector space). An equivalent formu- lation of the Open Mapping Theorem is theClosed Graph Theorem(a linear operator between Banach spaces is bounded if and only if it has a closed graph) and a corollary is theInverse Operator Theorem(a bijective bounded linear operator between Banach spaces has a bounded inverse). A slightly stronger version of the Hahn–Banach theorem, with the norm replaced by a quasi-seminorm, can be reformulated as the geometric assertion that two convex subsets of a normed vector space can be separated by a hyperplane whenever one of them has nonempty interior. The chapter also discusses reflexive Banach spaces and includes an exposition of the James space.

The subjects of Chapter 3 are the weak topology on a Banach spaceX and the weak* topology on its dual space X^∗. With these topologies X andX^∗are locally convex Hausdorff topological vector spaces and the chapter begins with a discussion of the elementary properties of such spaces. The central result of the third chapter is the Banach–Alaoglu Theorem which

(11)

Introduction xiii

asserts that the unit ball in the dual space is compact with respect to the weak* topology. This theorem has important consequences in many fields of mathematics. The chapter also contains a proof of the Banach–Dieudonn´e Theorem which asserts that a linear subspace of the dual space of a Banach space is weak* closed if and only if its intersection with the closed unit ball is weak* closed. A consequence of the Banach–Alaoglu Theorem is that the unit ball in a reflexive Banach space is weakly compact, and the Eberlein–

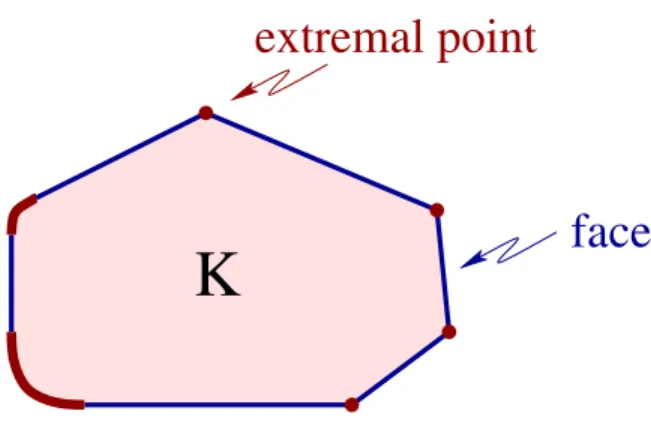
ˇSmulyan Theorem asserts that this property characterizes reflexive Banach spaces. The Kre˘ın–Milman Theorem asserts that every nonempty compact convex subset of a locally convex Hausdorff topological vector space is the closed convex hull of its extremal points. Combining this with the Banach–

Alaoglu Theorem, one can prove that every homeomorphism of a compact metric space admits an invariant ergodic Borel probability measure. Some properties of such ergodic measures can be derived from an abstract functional analytic ergodic theorem which is also established in this chapter.

The purpose of Chapter 4 is to give a basic introduction to Fredholm operators and their indices including the stability theorem. A Fredholm operator is a bounded linear operator between Banach spaces that has a finite-dimensional kernel, a closed image, and a finite-dimensional cokernel.

Its Fredholm index is the difference of the dimensions of kernel and cokernel.

The stability theorem asserts that the Fredholm operators of any given index form an open subset of the space of all bounded linear operators between two Banach spaces, with respect to the topology induced by the operator norm.

It also asserts that the sum of a Fredholm operator and a compact operator is again Fredholm and has the same index as the original operator. The chapter includes an introduction to the dual of a bounded linear operator, a proof of the closed image theorem which asserts that an operator has a closed image if and only if its dual does, an introduction to compact operators which map the unit ball to pre-compact subsets of the target space, a characterization of Fredholm operators in terms of invertibility modulo compact operators, and a proof of the stability theorem for Fredholm operators.

The purpose of Chapter 5 is to study the spectrum of a bounded linear operator on a real or complex Banach space. A first preparatory section discusses complex Banach spaces and the complexifications of real Banach spaces, the integrals of continuous Banach space valued functions on compact intervals, and holomorphic operator valued functions. The chapter then introduces the spectrum of a bounded linear operator, examines its elementary properties, discusses the spectra of compact operators, and establishes the holomorphic functional calculus. The remainder of this chapter deals exclusively with operators on Hilbert spaces, starting with a discussion of complex Hilbert spaces and the spectra of normal and self-adjoint operators.

It then moves on to C* algebras and the continuous functional calculus for

(12)

self-adjoint operators, which takes the form of an isomorphism from the C* algebra of complex valued continuous functions on the spectrum to the smallest C* algebra containing the given operator. The next topic is the Gelfand representation and the extension of the continuous functional calculus to normal operators. The chapter also contains a proof that every normal operator can be represented by a projection valued measure on the spectrum, and that every self-adjoint operator is isomorphic to a direct sum of multiplication operators on L² spaces.

Chapter 6 is devoted to unbounded operators and their spectral theory. The domain of an unbounded operator on a Banach space is a linear subspace. In most of the relevant examples the domain is dense and the operator has a closed graph. The chapter includes a discussion of the dual of an unbounded operator and an extension of the closed image theorem to this setting. It then examines the basic properties of the spectra of unbounded operators. The remainder of the chapter deals with unbounded operators on Hilbert spaces and their adjoints. In particular, it extends the functional calculus and the spectral measure to unbounded self-adjoint operators.

Strongly continuous semigroups of operators are the subject of Chap- ter 7. They play an important role in the study of many linear partial differential equations such as the heat equation, the wave equation, and the Schr¨odinger equation, and they can be viewed as infinite-dimensional ana- logues of the exponential matrix S(t) :=e^tA. In all the relevant examples the operator Ais unbounded. It is called the infinitesimal generatorof the strongly continuous semigroup in question. A central result in the subject is the Hille–Yosida–Phillips Theorem which characterizes the infinitesimal generators of strongly continuous semigroups. The dual semigroup is not always strongly continuous. It is, however, strongly continuous whenever the Banach space in question is reflexive. The chapter also includes a basic treatment of analytic semigroups and their infinitesimal generators. It closes with a study of Banach space valued measurable functions and of solutions to the inhomogeneous equation associated to a semigroup.

Each of the seven chapters ends with a problem section, which we hope will give the interested reader the opportunity to deepen their understanding of the subject.

(13)

Chapter 1

Foundations

This introductory chapter discusses some of the basic concepts that play a central role in the subject of Functional Analysis. In a nutshell, functional analysis is the study of normed vector spaces and bounded linear operators.

Thus it merges the subjects of linear algebra (vector spaces and linear maps) with that of point set topology (topological spaces and continuous maps).

The topologies that appear in functional analysis will in many cases arise from metric spaces. We begin in Section 1.1 by recalling the basic definitions and list several examples of Banach spaces that will be used to illustrate the theory throughout the book. The central topic is the study of compact sets and the main results are the characterization of sequentially compact subsets of a metric space in terms of open covers and the Arzel`a–Ascoli theorem which gives a compactness criterion for subsets of the space of continuous functions on a compact metric space. Section 1.2 moves on to the study of finite-dimensional normed vector spaces. It shows that any two norms on a finite-dimensional vector space are equivalent, and that a normed vector space is finite-dimensional if and only if the unit ball is compact. The section also contains a brief introduction to bounded linear operators and to product and quotient spaces. Section 1.3 introduces the dual space of a normed vector space and explains several important examples. Section 1.4 contains a brief introduction to elementary Hilbert space theory, including a proof of the Cauchy–Schwarz inequality and the Riesz representation theorem. Section 1.5 examines some basic properties of power series in Banach algebras. It shows, via the geometric series, that the space of invertible operators on a Banach space is open and that the map that assigns to an invertible operator its inverse is continuous. The Baire category theorem is the subject of Section 1.6.

1

(14)

1.1. Metric Spaces and Compact Sets

This section begins by recalling the basic definitions of a metric space and a Banach space and gives several important examples of Banach spaces. It then moves on to the study of compact subsets of a metric space and shows that sequential compactness is equivalent to the condition that every open cover has a finite subcover (Theorem 1.1.4). The second main result of this section is the Arzel`a–Ascoli theorem, which characterizes the precompact subsets of the space of continuous functions from a compact metric space to another metric space, equipped with the supremum metric, in terms of equicontinuity and pointwise precompactness (Theorem 1.1.11).

1.1.1. Banach Spaces.

Definition 1.1.1 (Metric Space). A metric space is a pair (X, d) consisting of a set X and a function d:X×X→R that satisfies the following axioms.

(M1)d(x, y)≥0 for allx, y∈X, with equality if and only ifx=y.

(M2)d(x, y) =d(y, x) for allx, y∈X.

(M3)d(x, z)≤d(x, y) +d(y, z) for all x, y, z∈X.

A functiond:X×X →R that satisfies these axioms is called adistance function and the inequality in (M3) is called thetriangle inequality. A subset U ⊂ X of a metric space (X, d) is called open (or d-open) if, for everyx∈U, there exists a constantε >0 such that theopen ball

B_ε(x) :=B_ε(x, d) :={y∈X|d(x, y)< ε}

(centered at x with radius ε) is contained in U. The set of d-open subsets of X will be denoted by

U(X, d) :={U ⊂X|U is d-open}.

It follows directly from the definitions that the collectionU(X, d)⊂2^X of d-open sets in a metric space (X, d) satisfies the axioms of a topology (i.e. the empty set and the setXare open, arbitrary unions of open sets are open, and finite intersections of open sets are open). A subsetF of a metric space (X, d) is closed (i.e. its complement is open) if and only if the limit point of every convergent sequence inF is itself contained inF.

Recall that a sequence (x_n)n∈N in a metric space (X, d) is called a Cauchy sequence if, for every ε >0, there exists an n0 ∈N such that any two integersn, m≥n0 satisfy the inequalityd(xn, xm)< ε. Recall also that a metric space (X, d) is calledcompleteif every Cauchy sequence inX converges.

(15)

1.1. Metric Spaces and Compact Sets 3

The most important metric spaces in the field of functional analysis are the normed vector spaces.

Definition 1.1.2 (Banach Space). A normed vector space is a pair (X,k·k) consisting of a real vector space X and a function

X→R:x7→ kxk satisfying the following axioms.

(N1)kxk ≥0 for allx∈X, with equality if and only if x= 0.

(N2)kλxk=|λ| kxk for all x∈X and λ∈R. (N3)kx+yk ≤ kxk+kyk for allx, y∈X.

Let (X,k·k) be a normed vector space. Then the formula

(1.1.1) d(x, y) :=kx−yk

for x, y ∈ X defines a distance function on X. The resulting topology is denoted byU(X,k·k) :=U(X, d). Xis called aBanach spaceif the metric space (X, d) iscomplete, i.e. if every Cauchy sequence inX converges.

Here are six examples of Banach spaces.

Example 1.1.3. (i) Fix a real number 1≤p <∞. Then the vector space X =Rⁿ of all n-tuples x= (x₁, . . . , x_n) of real numbers is a Banach space with the norm-function

kxk_p :=

n

X

i=1

|x_i|^p

!1/p

for x= (x₁, . . . , x_n)∈Rⁿ. For p = 2 this is the Euclidean norm. Another norm on Rⁿ is given by kxk_∞:= max_i=1,...,n|x_i|forx= (x₁, . . . , x_n)∈Rⁿ. (ii) For 1 ≤ p < ∞ the set of p-summable sequences of real numbers is denoted by

`^p :=

(

x= (xi)i∈N∈R^N

∞

X

i=1

|x_i|^p <∞ )

.

This is a Banach space with the norm kxk_p := (P∞

i=1|x_i|^p)^1/p for x ∈ `^p. Likewise, the space `^∞⊂R^N of bounded sequences is a Banach space with the supremum norm kxk_∞:= sup_i∈_N|x_i|forx= (x_i)i∈N∈`^∞.

(iii)Let (M,A, µ) be a measure space, i.e.M is a set,A ⊂2^M is aσ-algebra, and µ:A →[0,∞] is a measure. Fix a constant 1≤p <∞. A measurable functionf :M →Ris called p-integrableifR

M|f|^pdµ <∞ and the space of p-integrable functions on M will be denoted by

L^p(µ) :=

f :M →R

f is measurable and Z

M

|f|^pdµ <∞

.

(16)

The function L^p(µ)→R:f 7→ kfk_p defined by

(1.1.2) kfk_p:=

Z

M

|f|^pdµ 1/p

is nonnegative and satisfies the triangle inequality (Minkowski’s inequality).

However, in general it is not a norm, because kfk_p = 0 if and only if f vanishes almost everywhere (i.e. on the complement of a set of measure zero). To obtain a normed vector space, one considers the quotient

L^p(µ) :=L^p(µ)/∼, where

f ∼g ⇐⇒^def f =g almost everywhere.

The function f 7→ kfk_p descends to this quotient space and, with this norm, L^p(µ) is a Banach space (see [75, Theorem 4.9]). In this example it is often convenient to abuse notation and use the same letterf to denote a function in L^p(µ) and its equivalence class in the quotient space L^p(µ).

(iv) Let (M,A, µ) be a measure space, denote by L^∞(µ) the space of bounded measurable functions, and denote by

L^∞(µ) :=L^∞(µ)/∼

the quotient space, where the equivalence relation is again defined by equality almost everywhere. Then the formula

(1.1.3) kfk_∞:= ess sup|f|= inf c≥0

f ≤c almost everywhere defines a norm on L^∞(µ), andL^∞(µ) is a Banach space with this norm.

(v) Let M be a topological space. Then the space C_b(M) of bounded continuous functions f : M → R is a Banach space with the supremum norm

kfk_∞:= sup

p∈M

|f(p)|

forf ∈C_b(M).

(vi) Let (M,A) be a measurable space, i.e. M is a set and A ⊂ 2^M is a σ-algebra. A signed measure on (M,A) is a function µ : A → R that satisfies µ(∅) = 0 and isσ-additive, i.e. µ(S∞

i=1A_i) = P∞

i=1µ(A_i) for every sequence of pairwise disjoint measurable setsAi ∈ A. The space M(M,A) of signed measures on (M,A) is a Banach space with the norm given by (1.1.4) kµk:=|µ|(M) := sup

A∈A

µ(A)−µ(M \A) forµ∈ M(M,A) (see [75, Exercise 5.34]).

(17)

1.1.2. Compact Sets. Let (X, d) be a metric space and letK ⊂X. Then the restriction of the distance function d to K×K is a distance function, denoted by dK :=d|K×K:K×K→R, so (K, dK) is a metric space in its own right. The metric space (X, d) is called (sequentially) compact if every sequence in X has a convergent subsequence. The subset K is called (sequentially) compact if (K, d_K) is compact, i.e. if every sequence inK has a subsequence that converges to an element of K. It is calledprecom- pact if its closure is sequentially compact. Thus K is compact if and only if it is precompact and closed. The subset K is called completeif (K, dK) is a complete metric space, i.e. if every Cauchy sequence inK converges to an element of K. It is calledtotally bounded if it is either empty or, for everyε >0, there exist finitely many elementsξ₁, . . . , ξ_m∈K such that

K⊂

m

[

i=1

Bε(ξi).

The next theorem characterizes the compact subsets of a metric space (X, d) in terms of the open subsets ofX. It thus shows that compactness depends only on the topologyU(X, d) induced by the distance functiond.

Theorem1.1.4 (Characterization of Compact Sets). Let (X, d) be a metric space and let K ⊂X. Then the following are equivalent.

(i) K is sequentially compact.

(ii) K is complete and totally bounded.

(iii) Every open cover of K has a finite subcover.

Proof. See page 7.

Let (X,U) be a topological space. Then condition (iii) in Theorem 1.1.4 is used to define compact subsets ofX. Thus a subsetK⊂Xis calledcom- pact if every open cover of K has a finite subcover. Here an open cover ofK is a collection (U_i)i∈I of open subsetsU_i ⊂X, indexed by the elements of a nonempty setI, such thatK ⊂S

i∈IUi, and a finite subcover is a finite collection of indicesi1, . . . , im ∈I such thatK ⊂Ui1 ∪ · · · ∪Uim. Thus The- orem 1.1.4 asserts that a subset of a metric space (X, d) is sequentially compact if and only if it is compact as a subset of the topological space (X,U) with U =U(X, d). A subset of a topological space is called precompact if its closure is compact. Elementary properties of compact sets include the fact that every compact subset of a Hausdorff space is closed, that every closed subset of a compact set is compact, and that the image of a compact set under a continuous map is compact (see [45, 61]).

(18)

We give two proofs of Theorem 1.1.4. The first proof is more straight- forward and uses the axiom of dependent choice. The second proof is taken from Herrlich [34, Prop 3.26] and only uses the axiom of countable choice.

The axiom of dependent choice asserts that, if X is a nonempty set and A : X → 2^X is a map that assigns to each element x∈X a nonempty subsetA(x)⊂X, then there exists a sequence (xk)k∈NinXsuch thatxk+1 ∈A(xk) for allk∈N. In the axiom of dependent choice the first element of the sequence (x_k)k∈N can be prescribed. To see this, letx1 ∈X, define Xe as the set of all tuples of the form ex= (n,x₁, . . . ,x_n) withn∈N and x_k∈A(xk−1) for k= 2, . . . , n, and for ex= (n,x₁, . . . ,x_n)∈Xe define the set A(e ex) :={(n+ 1,x1, . . . ,xn,x)|x∈A(xn)}. Then Xe is nonempty andA(e ex) is nonempty for everyex∈X. Now apply the axiom of dependente choice to A.e

Theaxiom of countable choiceasserts that, if (A_k)_k∈_N is a sequence of nonempty subsets of a set A, then there exists a sequence (ak)k∈N in A such that a_k∈A_k for all k∈N. This follows from the axiom of dependent choice by takingX:=N×AandA(k,a) :={k+1}×A_k+1for (k,a)∈N×A.

Lemma 1.1.5. Let (X, d) be a metric space and let K ⊂ X. Then the following are equivalent.

(i) Every sequence inK has a Cauchy subsequence.

(ii) K is totally bounded.

Proof of (ii)=⇒(i) in Lemma 1.1.5. The argument only uses the axiom of countable choice. Assume thatK is totally bounded and let (xn)n∈N

be a sequence in K. We prove that there exists a sequence of infinite sub- setsN⊃T₁ ⊃T₂⊃ · · · such that, for all k, m, n∈N,

(1.1.5) m, n∈Tk =⇒ d(xm, xn)<2^−k.

Since K is totally bounded, it follows from the axiom of countable choice that there exists a sequence of ordered finite subsets

S_k={ξ_k,1, . . . , ξ_k,m_k} ⊂K such that

K⊂

mk

[

i=1

B₂^−k−1(ξ_k,i) for all k∈N.

Since xn∈K for alln∈N, there must exist an index i∈ {1, . . . , m₁} such that the open ball B_1/4(ξ_1,i) contains infinitely many of the elements x_n. Leti₁ be the smallest such index and define the set

T1 :={n∈N|xn∈B_1/4(ξ1,i1)}.

(19)

This set is infinite and satisfies d(x_n, x_m)≤d(x_n, ξ_1,i₁) +d(ξ_1,i₁, x_m)<1/2 for all m, n∈T₁. Now fix an integer k ≥ 2 and suppose, by induction, that Tk−1 has been defined. Since Tk−1 is an infinite set, there must exist an index i∈ {1, . . . , m_k} such that the ballB₂^−k−1(ξk,i) contains infinitely many of the elements xn with n∈Tk−1. Leti_k be the smallest such index and define

T_k:={n∈Tk−1|xn∈B₂^−k−1(ξ_k,i_k)}.

This set is infinite and satisfies d(xn, xm)≤d(xn, ξk,i_k) +d(ξk,i_k, xm)<2^−k for allm, n∈T_k. This completes the induction argument and the construction of a decreasing sequence of infinite setsT_k⊂Nthat satisfy (1.1.5).

We prove that (xn)n∈N has a Cauchy subsequence. By (1.1.5) there exists a sequence of positive integers n1< n2 < n3 <· · · such thatn_k∈T_k for all k∈N. Such a sequence can be defined by the recursion formula

n1:= minT1, nk+1 := min

n∈Tk+1

n > nk

fork∈N. It follows that nk, n` ∈Tk and hence

d(x_n_k, x_n_`)<2^−k for`≥k≥1.

Thus the subsequence (x_n_k)k∈N is a Cauchy sequence. This shows that (ii) implies (i) in Lemma 1.1.5. The converse will be proved on page 9.

First proof of Theorem 1.1.4. We prove that (i) implies (iii) using the axiom of dependent choice. Assume that the set K is nonempty and sequentially compact, and let {U_i}_i∈I be an open cover of K. Here I is a nonempty index set and the mapI →2^X :i7→U_i assigns to each indexian open set U_i ⊂X such that K⊂S

i∈IU_i. We prove in two steps that there exist indicesi₁, . . . , i_m ∈I such thatK ⊂Sm

j=1U_i_j.

Step 1. There exists a constant ε > 0 such that, for every x ∈ K, there exists an index i∈I such thatBε(x)⊂Ui.

Assume, by contradiction, that there is no such constantε >0. Then

∀ε >0 ∃x∈K ∀i∈I Bε(x)6⊂Ui.

Take ε= 1/n forn∈N. Then the set {x ∈K|B_1/n(x) 6⊂Ui for alli∈I} is nonempty for every n ∈N. Hence the axiom of countable choice asserts that there exists a sequence x_n∈K such that

(1.1.6) B_1/n(xn)6⊂Ui for all n∈Nand all i∈I.

Since K is sequentially compact, there exists a subsequence (xnk)k∈N that converges to an element x∈K. Since K ⊂S

i∈IUi, there exists an i∈I such that x∈U_i. SinceU_i is open, there is an ε >0 such thatB_ε(x)⊂U_i. Sincex= limk→∞x_n_k, there is ak∈Nsuch thatd(x, x_n_k)< ₂^ε and _n¹

k < ₂^ε. ThusB_1/n_k(xnk)⊂B_ε/2(xnk)⊂Bε(x)⊂Ui in contradiction to (1.1.6).

(20)

Step 2. There exist indices i₁, . . . , i_m ∈I such thatK ⊂Sm j=1U_i_j.

Assume, by contradiction, that this is wrong. Let ε >0 be the constant in Step 1. We prove that there are sequences xn∈K and in∈I such that (1.1.7) Bε(xn)⊂Uin, xn∈/ Ui1 ∪ · · · ∪Uin−1

for all n∈N(with n≥2 for the second condition). Choose x₁ ∈K. Then, by Step 1, there exists an indexi1 ∈I such thatBε(x1)⊂Ui1. Now suppose, by induction, thatx1, . . . , x_kandi1, . . . , i_khave been found such that (1.1.7) holds for n≤k. Then

K6⊂Ui1 ∪ · · · ∪Ui_k.

Choose an element x_k+1∈K\(U_i₁ ∪ · · · ∪U_i_k). By Step 1, there exists an index i_k+1 ∈I such that B_ε(x_k+1)⊂U_i_k+1. Thus the existence of sequences xn and in that satisfy (1.1.7) follows from the axiom of dependent choice. More precisely, letXbe the set of all pairsx= (x, J) such thatJ is a finite subset ofI andx∈K\S

j∈JUj. Forx= (x, J)∈XletA(x) be the set of all pairsx⁰ = (x⁰, J⁰)∈X, whereJ⁰ =J∪{i⁰},i⁰ ∈I, andB_ε(x⁰)⊂U_i⁰. Then A(x)6=∅ for all x∈X by assumption and the choice ofε in Step 1.

Thus there is a sequencex_n= (x_n, J_n)∈Xsuch thatx_n+1 ∈A(x_n) for alln.

So Jn\Jn−1 ={i_n} is a singleton such that Bε(xn) ⊂Uin for each n∈N.

Moreoveri₁, . . . , in−1∈J_nand sox_n∈K\Sn−1

k=1U_i_k for each integer n≥2.

Thus the sequences (xn)n∈Nand (in)n∈N satisfy (1.1.7) as claimed.

By (1.1.7) we haved(x_n, x_k) ≥εfor k6=n, so (x_n)n∈N does not have a convergent subsequence, contradicting (i). This shows that (i) implies (iii).

We prove that (iii) implies (ii) without using any version of the axiom of choice. Thus assume that every open cover of K has a finite subcover.

Assume thatK is nonempty and fix a constantε >0. Then the setsB_ε(ξ) forξ∈Kform a nonempty open cover ofK. Hence there exist finitely many elements ξ1, . . . , ξm ∈K such that K ⊂Sm

i=1Bε(ξi). This shows that K is totally bounded.

We prove thatK is complete. Let (xn)n∈N be a Cauchy sequence in K and suppose, by contradiction, that (xn)n∈N does not converge to any element of K. Then no subsequence of (x_n)n∈N can converge to any element of K. Thus, for every ξ ∈ K, there is an ε > 0 such that B_ε(ξ) contains only finitely many of thex_n. For ξ ∈K let ε(ξ)>0 be half the supremum of the set of all ε∈ (0,1] such that #{n∈N|xn∈Bε(ξ)}<∞. Then the set {n∈N

xn ∈B_ε(ξ)(ξ)} is finite for every ξ ∈K. Thus{B_ε(ξ)(ξ)}_ξ∈K is an open cover of K that does not have a finite subcover, in contradiction to (iii). This shows that (iii) implies (ii).

That (ii) implies (i) was shown in Lemma 1.1.5, using the axiom of countable choice, and this completes the first proof of Theorem 1.1.4.

(21)

The above proof of Theorem 1.1.4 requires the axiom of dependent choice and only uses the implication (ii) =⇒(i) in Lemma 1.1.5. The second proof follows [34, Prop 3.26] and only requires the axiom of countable choice.

Proof of (i)=⇒(ii) in Lemma 1.1.5. The proof follows [34, Prop 3.26]

and only uses the axiom of countable choice. We argue indirectly and assume that K is not totally bounded and hence also nonempty. Then there exists a constant ε >0 such that K does not admit a finite cover by balls of radius ε, centered at elements of K. We prove in three steps that there exists a sequence in K that does not have a Cauchy subsequence.

Step 1. For n∈N define the set Kn:=

(x1, . . . , xn)∈Kⁿ

if i, j∈ {1, . . . , n} andi6=j thend(xi, xj)≥ε

.

There is a sequence(x_k)k∈NinKsuch that(x_n(n−1)/2+1, . . . , x_n(n+1)/2)∈K_n for every integer n≥1.

We prove that K_n is nonempty for every n ∈ N. For n = 1 this holds because K is nonempty. If it is empty for some n ∈ N then there exists an integer n ≥1 such that Kn6=∅ and Kn+1 =∅. In this case, choose an element (x1, . . . , xn)∈Kn. Since Kn+1=∅, this implies K⊂Sn

i=1Bε(xi), contradicting the choice of ε. Since Kn6=∅for all n∈N, the existence of a sequence (x_k)k∈N as in Step 1 follows from the axiom of countable choice.

Step 2. For every collection ofn−1elements y1, . . . , yn−1 ∈K, there is an integerisuch that ⁽ⁿ⁻¹⁾ⁿ₂ < i≤ ⁿ⁽ⁿ⁺¹⁾₂ andd(yj, xi)≥ ^ε₂ forj= 1, . . . , n−1.

Otherwise, there exists a mapν :{⁽ⁿ⁻¹⁾ⁿ₂ + 1, . . . ,ⁿ⁽ⁿ⁺¹⁾₂ } → {1, . . . , n−1}

such thatd(x_i, y_ν(i))< ^ε₂ for alli. Since the target space ofνhas smaller car- dinality than the domain, there is a pairi6=jin the domain withν(i) =ν(j) and so d(xi, xj)≤d(xi, y_ν(i)) +d(y_ν(j), xj)< ε, in contradiction to Step 1.

Step 3. There exists a subsequence (x_k_n)n∈N such that k₁ = 1 and (1.1.8) (n−1)n

2 < k_n≤ n(n+ 1)

2 , d(x_k_m, x_k_n)≥ ε

2 for m < n.

Definek1 := 1, fix an integern≥2, and assume, by induction, that the inte- gersk1, k2, . . . , kn−1have been found such that (1.1.8) holds withnreplaced by any number n⁰ ∈ {2, . . . , n−1}. Then, by Step 2, there exists a unique smallest integer kn such that ⁽ⁿ⁻¹⁾ⁿ₂ < kn ≤ ⁿ⁽ⁿ⁺¹⁾₂ and d(xkm, xkn) ≥ ^ε₂ for m= 1, . . . , n−1. This proves the existence of a subsequence (xkn)n∈N

that satisfies (1.1.8). The sequence (x_k_n)n∈N in Step 3 does not have a Cauchy subsequence. This shows that (i) implies (ii) in Lemma 1.1.5.

(22)

Second proof of Theorem 1.1.4. A sequentially compact metric space is complete, because a Cauchy sequence converges if and only if it has a convergent subsequence. Hence the equivalence of (i) and (ii) in Theorem 1.1.4 follows directly from Lemma 1.1.5.

We prove that (ii) implies (iii), following the argument in [34, Prop 3.26].

Assume thatKis complete and totally bounded. Suppose, by contradiction, that there is an open cover{U_i}_i∈I ofKthat does not have a finite subcover.

Then K6=∅. Forn, m∈N define An,m :=







(x1, . . . , xm)∈K^m

K⊂

m

[

j=1

B_1/n(xj)





 .

Then, for everyn∈N, there exists anm∈Nsuch thatAn,m 6=∅, becauseK is totally bounded and nonempty. For n∈N let m_n∈N be the smallest positive integer such that A_n,m_n 6=∅. Then, by the axiom of countable choice, there is a sequencea_n= (x_n,1, . . . , x_n,m_n)∈A_n,m_n for n∈N.

Next we construct a sequence (y_n)n∈NinKsuch thatT_n

ν=1B_1/ν(y_ν)∩K cannot be covered by finitely many of the sets U_i for anyn∈N. For n= 1 definey₁ :=x_1,k, where

k:= min

j ∈ {1, . . . , m₁}

the set B1(x1,j)∩K cannot be covered by finitely manyUi

.

Assume, by induction, that y1, . . . , yn−1 have been chosen such that the set Tn−1

ν=1B_1/ν(y_ν)∩K cannot be covered by finitely many of the U_i and definey_n:=x_n,k, where

k:= min

j∈ {1, . . . , m_n}

the setB_1/n(xn,j)∩Tn−1

ν=1B_1/ν(yν)∩K cannot be covered by finitely many U_i

.

This completes the construction of the sequence (yn)n∈N. It satisfies d(yn, ym)< 1

m + 1 n ≤ 2

m forn > m≥1,

because B_1/n(yn)∩B_1/m(ym) 6= ∅. Hence (y_n)n∈N is a Cauchy sequence in K. Since K is complete, the limit y^∗ := limn→∞yn exists and is an element of K. Choose an index i^∗ ∈ I such that y^∗ ∈ Ui^∗ and choose a constantε^∗>0 such thatB_ε^∗(y^∗)⊂U_i^∗.Then

B_1/n(y_n)⊂B_ε^∗(y^∗)⊂U_i^∗

for n sufficiently large in contradiction to the choice of y_n. This proves that (ii) implies (iii).

That (iii) implies (ii) was shown in the first proof without using the axiom of choice. This completes the second proof of Theorem 1.1.4.

(23)

It follows immediately from Theorem 1.1.4 that every compact metric space is separable. Here are the relevant definitions.

Definition 1.1.6. Let X be a topological space. A subset S ⊂ X is called dense in X if its closure is equal to X or, equivalently, every nonempty open subset ofX contains an element ofS. The spaceXis called separableif it admits a countable dense subset. (A set is calledcountable if it is either finite or countably infinite.)

Corollary 1.1.7. Every compact metric space is separable.

Proof. Let n∈ N. Since X is totally bounded by Theorem 1.1.4, there exists a finite setSn⊂Xsuch thatX =S

ξ∈SnB_1/n(ξ).HenceS :=S

n∈NSn

is a countable dense subset of X by the axiom of countable choice.

Corollary 1.1.8. Let (X, d) be a metric space and let A ⊂ X. Then the following are equivalent.

(i) A is precompact.

(ii) Every sequence inA has a subsequence that converges in X.

(iii) A is totally bounded and every Cauchy sequence in A converges in X.

Proof. That (i) implies (ii) follows directly from the definitions.

We prove that (ii) implies (iii). By (ii) every sequence inAhas a Cauchy subsequence and so A is totally bounded by Lemma 1.1.5. If (x_n)n∈N is a Cauchy sequence inA, then by (ii) there exists a subsequence (xni)i∈N that converges in X, and so the original sequence converges in X because a Cauchy sequence converges if and only if it has a convergent subsequence.

We prove that (iii) implies (i). Let (xn)n∈Nbe a sequence in the closureA ofA. Then, by the axiom of countable choice, there exists a sequence (an)n∈N

inA such thatd(xn, an)<1/n for alln∈N. Since Ais totally bounded, it follows from Lemma 1.1.5 that the sequence (a_n)n∈N has a Cauchy subsequence (a_n_i)i∈N. This subsequence converges in X by (iii). Denote its limit bya. Thena∈Aanda= limi→∞a_n_i = limi→∞x_n_i. ThusAis sequentially

compact. This proves Corollary 1.1.8.

Corollary1.1.9. Let (X, d)be a complete metric space and letA⊂X.

Then the following are equivalent.

(i) A is precompact.

(ii) Every sequence inA has a Cauchy subsequence.

(iii) A is totally bounded.

Proof. This follows directly from the definitions and Corollary 1.1.8.

(24)

1.1.3. The Arzel`a–Ascoli Theorem. It is a recurring theme in functional analysis to understand which subsets of a Banach space or topological vector space are compact. For the standard Euclidean space (Rⁿ,k·k₂) the Heine-Borel Theorem asserts that a subset ofRⁿ is compact if and only if it is closed and bounded. This continues to hold for every finite-dimensional normed vector space and, conversely, every normed vector space in which the closed unit ball is compact is necessarily finite-dimensional (see The- orem 1.2.11 below). For infinite-dimensional Banach spaces this leads to the problem of characterizing the compact subsets. Necessary conditions are that the subset is closed and bounded, however, these conditions can no longer be sufficient. For the Banach space of continuous functions on a compact metric space a characterization of the compact subsets is given by a theorem of Arzel`a and Ascoli which we explain next.

Let (X, d_X) and (Y, d_Y) be metric spaces and assume thatXis compact.

Then the space

C(X, Y) :=

f :X→Y

f is continuous

of continuous maps fromXtoY is a metric space with the distance function (1.1.9) d(f, g) := sup

x∈X

dY(f(x), g(x)) forf, g∈C(X, Y).

This is well defined because the function X → R : x 7→ dY(f(x), g(x)) is continuous and hence is bounded because X is compact. That (1.1.9) satisfies the axioms of a distance function follows directly from the definitions.

When X is nonempty, the metric space C(X, Y) with the distance function (1.1.9) is complete if and only if Y is complete, because the limit of a uniformly convergent sequence of continuous functions is again continuous.

Definition 1.1.10. A subset

F ⊂C(X, Y)

is called equi-continuous if, for everyε >0, there exists a constantδ >0 such that, for all x, x⁰∈X and all f ∈F,

d_X(x, x⁰)< δ =⇒ d_Y(f(x), f(x⁰))< ε.

It is called pointwise compactif, for every elementx∈X, the set F(x) :=

f(x) f ∈F

is a compact subset of Y. It is called pointwise precompactif, for every elementx∈X, the setF(x) has a compact closure in Y.

Since every continuous map defined on a compact metric space is uniformly continuous, every finite subset ofC(X, Y) is equi-continuous.

(25)

Theorem 1.1.11 (Arzel`a–Ascoli). Let (X, d_X) and (Y, d_Y) be metric spaces such that X is compact and let F ⊂C(X, Y). Then the following are equivalent.

(i) F is precompact.

(ii) F is pointwise precompact and equi-continuous.

Proof. We prove that (i) implies (ii). Thus assume F is precompact.

That F is pointwise precompact follows from the fact that the evaluation mapC(X, Y)→Y :f 7→evx(f) :=f(x) is continuous for everyx∈X.

Since the image of a precompact set under a continuous map is again precompact (Exercise 1.7.1), it follows that the setF(x) = evx(F) is a precompact subset of Y for every x∈X.

It remains to prove thatF is equi-continuous. AssumeF is nonempty and fix a constantε >0. Since the setF is totally bounded by Lemma 1.1.5, there exist finitely many maps f₁, . . . , f_m ∈F such that

(1.1.10) F ⊂

m

[

i=1

B_ε/3(f_i).

Since X is compact, each function f_i is uniformly continuous. Hence there exists a constant δ >0 such that, for alli∈ {1, . . . , m}and all x, x⁰∈X, (1.1.11) d_X(x, x⁰)< δ =⇒ d_Y(f_i(x), f_i(x⁰))< ε

3. Now let f ∈F and letx, x⁰ ∈X such that

(1.1.12) dX(x, x⁰)< δ.

By (1.1.10) there exists an indexi∈ {1, . . . , m}such thatd(f, fi)< ₃^ε. Thus d_Y(f(x), f_i(x))< ε

3, d_Y(f(x⁰), f_i(x⁰))< ε 3. Moreover, it follows from (1.1.11) and (1.1.12) that

dY(fi(x), fi(x⁰))< ε 3.

Putting these last three inequalities together and using the triangle inequality, we find

d_Y(f(x), f(x⁰))≤d_Y(f(x), f_i(x)) +d_Y(f_i(x), f_i(x⁰)) +d_Y(f_i(x⁰), f(x⁰))

≤ ε 3+ ε

3+ ε 3

=ε.

This shows that F is equi-continuous, and thus we have proved that (i) implies (ii).

(26)

We prove that (ii) implies (i). Let (f_n)n∈N be a sequence in F and let (x_k)k∈N be a dense sequence in X (Corollary 1.1.7). We prove in three steps that (fn)n∈N has a convergent subsequence.

Step 1. There exists a subsequence (gi)i∈N of (fn)n∈N such that the sequence (gi(x_k))i∈N converges in Y for everyk∈N.

Since F(x_k) is precompact for each k, it follows from the axiom of dependent choice (page 6) that there is a sequence of subsequences (f_n_k,i)i∈N such that, for eachk∈N, the sequence (f_n_k+1,i)i∈Nis a subsequence of (f_n_k,i)i∈N

and the sequence (f_n_k,i(x_k))i∈N converges in Y. Thus the diagonal subse- quencegi :=fni,i satisfies the requirements of Step 1.

Step 2. The subsequence(gi)i∈Nin Step 1 is a Cauchy sequence inC(X, Y).

Fix a constantε >0. Then, by equi-continuity, there exists a constantδ >0 such that, for all f ∈F and allx, x⁰ ∈X,

(1.1.13) d_X(x, x⁰)< δ =⇒ d_Y(f(x), f(x⁰))< ε 3.

Since the ballsBδ(xk) form an open cover ofX, there exists anm∈Nsuch that X=Sm

k=1B_δ(x_k). Since (gi(x_k))i∈N is a Cauchy sequence for each k, there exists an N ∈Nsuch that, for all i, j, k∈N, we have

(1.1.14) 1≤k≤m, i, j≥N =⇒ dY(gi(xk), gj(xk))< ε/3.

We prove thatd(g_i, g_j)< εfor alli, j≥N. To see this, fix an elementx∈X.

Then there exists an index k∈ {1, . . . , m} such that dX(x, xk)< δ. This implies dY(gi(x), gi(xk))< ε/3 for all i∈N, by (1.1.13), and so

d_Y(g_i(x), g_j(x))≤d_Y(g_i(x), g_i(x_k)) +d_Y(g_i(x_k), g_j(x_k)) +d_Y(g_j(x_k), g_j(x))

< ε 3 + ε

3 +ε 3

=ε

for all i, j ≥N by (1.1.14). Hence d(g_i, g_j) = maxx∈Xd_Y(g_i(x), g_j(x))< ε for all i, j≥N and this proves Step 2.

Step 3. The subsequence (g_i)i∈N in Step 1 converges inC(X, Y).

Letx∈X. By Step 2, (gi(x))i∈Nis a Cauchy sequence inF(x). SinceF(x) is a precompact subset ofY, the sequence (gi(x))i∈Nhas a convergent subsequence and hence converges inY. Denote the limit byg(x) := limi→∞gi(x).

Then the sequenceg_iconverges uniformly togby Step 2 and sog∈C(X, Y).

Step 3 shows that every sequence inF has a subsequence that converges to an element ofC(X, Y). HenceF is precompact by Corollary 1.1.8. This

proves Theorem 1.1.11.

(27)

Corollary 1.1.12 (Arzel`a–Ascoli). Let (X, d_X) be a compact metric space, let (Y, d_Y) be a metric space, and let F ⊂C(X, Y). Then the following are equivalent.

(i) F is compact.

(ii) F is closed, pointwise compact, and equi-continuous.

(iii) F is closed, pointwise precompact, and equi-continuous.

Proof. That (i) implies (ii) follows from Theorem 1.1.11, because every compact subset of a metric space is closed, and the image of a compact set under a continuous map is compact. Here the continuous map in question is the evaluation mapC(X, Y)→Y :f 7→f(x) associated tox∈X. That (ii) implies (iii) is obvious. That (iii) implies (i) follows from Theorem 1.1.11, because a subset of a metric space is compact if and only if it is precompact

and closed. This proves Corollary 1.1.12.

When the target spaceY is the Euclidean space (Rⁿ,k·k₂) in part (i) of Example 1.1.3, the Arzel`a–Ascoli Theorem takes the following form.

Corollary 1.1.13 (Arzel`a–Ascoli). Let (X, d) be a compact metric space and letF ⊂C(X,Rⁿ). Then the following holds.

(i) F is precompact if and only if it is bounded and equi-continuous.

(ii) F is compact if and only if it is closed, bounded, and equi-continuous.

Proof. Assume F is precompact. ThenF is equi-continuous by Theo- rem 1.1.11, and is bounded, because a sequence whose norm tends to infinity cannot have a convergent subsequence. Conversely, assume F is bounded and equi-continuous. Then, for each x∈X, the set F(x)⊂Rⁿ is bounded and therefore is precompact by the Heine–Borel Theorem. HenceF is precompact by Theorem 1.1.11. This proves (i). Part (ii) follows from (i) and the fact that a subset of a metric space is compact if and only if it is precompact and closed. This proves Corollary 1.1.13.

Exercise 1.1.14. This exercise shows that the hypothesis that X is compact cannot be removed in Corollary 1.1.13. Consider the Banach space C_b(R) of bounded continuous real-valued functions on R with the supremum norm. Find a closed bounded equi-continuous subset of Cb(R) that is not compact.

There are many versions of the Arzel`a–Ascoli Theorem. For example, Theorem 1.1.11, Corollary 1.1.12, and Corollary 1.1.13 continue to hold, with the appropriate notion of equi-continuity, whenXis any compact topological space. This is the content of the following exercise.

(28)

Exercise 1.1.15. LetX be a compact topological space and let Y be a metric space. Then the spaceC(X, Y) of continuous functionsf :X→Y is a metric space with the distance function (1.1.9). A subsetF ⊂C(X, Y) is calledequi-continuousif, for everyx∈X and everyε >0, there exists an open neighborhoodU ⊂X ofx such thatdY(f(x), f(x⁰))< εfor allx⁰ ∈U and all f ∈F.

(a) Prove that the above definition of equi-continuity agrees with the one in Definition 1.1.10 wheneverX is a compact metric space.

(b) Prove the following variant of the Arzel`a–Ascoli Theorem for compact topological spacesX.

Arzel`a–Ascoli Theorem. Let X be a compact topological space and let Y be a metric space. A set F ⊂ C(X, Y) is precompact if and only if it is pointwise precompact and equi-continuous.

Hint 1: If F is precompact, use the argument in the proof of Theo- rem 1.1.11 to show thatF is pointwise precompact and equi-continuous.

Hint 2: Assume F is equi-continuous and pointwise precompact.

Step 1. The set F :={f(x)|x∈X, f ∈F} ⊂Y is totally bounded.

Show that F is precompact (Exercise 1.7.1) and use Corollary 1.1.8.

Step 2. The set F is totally bounded.

Letε >0. CoverF by finitely many open ballsV₁, . . . , V_n of radiusε/3 and coverX by finitely many open setsU1, . . . , Um such that

sup

x,x⁰∈U_i

sup

f∈Fd_Y(f(x), f(x⁰))< ε/3 fori= 1, . . . , m.

For any functionα:{1, . . . , m} → {1, . . . , n}define Fα:=

f ∈F

f(Ui)∩V_α(i)6=∅ fori= 1, . . . , m .

Prove that d(f, g) = sup_x∈XdY(f(x), g(x))< ε for all f, g∈Fα. Let A be the set of all α such that Fα6=∅. Prove that F =S

α∈AFα and choose a collection of functions fα∈Fα, one for each α∈A.

Step 3. The set F is precompact.

Use Lemma 1.1.5 and Step 3 in the proof of Theorem 1.1.11 to show that every sequence inF has a subsequence that converges in C(X, Y).

In contrast to what one might expect from Exercise 1.1.14, there is also a version of the Arzel`a–Ascoli theorem for the space of continuous functions from an arbitrary topological spaceXto a metric spaceY. This version uses the compact-open topology onC(X, Y) and is explained in Exercise 3.7.5.

(29)

1.2. Finite-Dimensional Banach Spaces 17

1.2. Finite-Dimensional Banach Spaces

The purpose of the present section is to examine finite-dimensional normed vector spaces with an emphasis on those properties that distinguish them from infinite-dimensional normed vector spaces, which are the main subject of functional analysis. Finite-dimensional normed vector spaces are complete, their linear subspaces are closed, linear functionals on them are continuous, and their closed unit balls are compact. Theorem 1.2.11 below shows that this last property characterizes finite-dimensionality. Before en- tering into the main topic of this section, it is convenient to first introduce the concept of a bounded linear operator.

1.2.1. Bounded Linear Operators. The second fundamental concept in functional analysis, after that of a Banach space, is the notion of a bounded linear operator. In functional analysis it is common practice to use the term linear operator instead of linear map, although both terms have the exact same meaning, namely that of a map between vector spaces that preserves addition and scalar multiplication. The reason lies in the fact that the relevant normed vector spaces in applications are often function spaces and then the elements of the space on which the operator acts are themselves functions. If domain and target of a linear operator arenormed vector spaces, it is natural to impose continuity with respect to the norm topologies. This underlies the following definition.

Definition 1.2.1 (Bounded Linear Operator).

Let (X,k·k_X) and (Y,k·k_Y) be real normed vector spaces. A linear operator A:X →Y

is called boundedif there exists a constant c≥0 such that (1.2.1) kAxk_Y ≤ckxk_X for all x∈X.

The smallest constant c ≥ 0 that satisfies (1.2.1) is called the operator norm of A and is denoted by

(1.2.2) kAk:=kAk_L(X,Y₎:= sup

x∈X\{0}

kAxk_Y kxk_X .

A bounded linear operator with values inY =Ris called abounded linear functional on X. The space of bounded linear operators from X to Y is denoted by¹

L(X, Y) :=

A:X→Y

A is linear and bounded .

Then (L(X, Y),k·k_L(X,Y₎) is a normed vector space. The resulting topology on L(X, Y) is called the uniform operator topology.

1Many authors use the notationB(X, Y) for the space of bounded linear operators.

(30)

Theorem1.2.2. Let(X,k·k_X)and(Y,k·k_Y)be real normed vector spaces and let A:X→Y be a linear operator. The following are equivalent.

(i) A is bounded.

(ii) A is continuous.

(iii) A is continuous at x= 0.

Proof. We prove that (i) implies (ii). If Ais bounded then Ax−Ax⁰

Y =

A(x−x⁰) Y

≤ kAk

x−x⁰ X

for all x, x⁰ ∈ X and so A is Lipschitz-continuous. Since every Lipschitz- continuous function is continuous, this shows that (i) implies (ii). That (ii) implies (iii) follows directly from the definition of continuity.

We prove that (iii) implies (i). Thus assume A is continuous at x = 0.

Then it follows from the ε-δ definition of continuity with ε = 1 that there exists a constant δ >0 such that, for allx∈X,

kxk_X < δ =⇒ kAxk_Y <1.

This implieskAxk_Y ≤1 for everyx∈Xwithkxk_X =δ. Now letx∈X\{0}.

Then kδkxk⁻¹_X xk_X =δ and sokA(δkxk⁻¹_X x)k_Y ≤1. Multiply both sides of this last inequality by δ⁻¹kxk_X to obtain the inequality

kAxk_Y ≤δ⁻¹kxk_X

for all x∈X. This proves Theorem 1.2.2.

Recall that the kernel and image of a linear operator A : X → Y between real vector spaces are the linear subspaces defined by

ker(A) :={x∈X|Ax= 0} ⊂X, im(A) :={Ax|x∈X} ⊂Y.

If X and Y are normed vector spaces and A :X → Y is a bounded linear operator, then the kernel ofA is a closed subspace of X by Theorem 1.2.2.

However, its image need not be a closed subspace ofY.

Definition 1.2.3 (Equivalent Norms). LetXbe a real vector space.

Two normsk·kand k·k⁰ on X are calledequivalent if there is a constant c≥1

such that

1

ckxk ≤ kxk⁰ ≤ckxk for all x∈X.

FUNCTIONAL ANALYSIS Theo B¨uhler Dietmar A. Salamon