DerRiesz-Dunford’scheFunktionalkalk¨ul Seminararbeit

(1)

Seminararbeit

Der Riesz-Dunford’sche Funktionalkalk¨ ul

im Rahmen des Seminars zu Funktionalanalysis im Wintersemester 2009/2010

Christoph Neuner 9. Februar 2010

(2)

Inhaltsverzeichnis

1 Ziel und Motivation 1

2 Vorbereitung f¨ur den Funktionalkalk¨ul 2

2.1 Integration in einer Banachalgebra . . . 3 2.2 Zum Thema Integrationswege . . . 3 2.3 Der Cauchy’sche Integralsatz und die Cauchy’schen Integralformeln . . . 5 3 Der Funktionalkalk¨ul f¨ur holomorphe Funktionen 6 3.1 Der Hauptsatz . . . 7 3.2 Eine Anwendung . . . 10

Literatur 11

(3)

1 Ziel und Motivation

Sei f : ∆ → C, mit ∆ ⊆ C, eine holomorphe Funktion und ein Element a einer komplexen Banachalgebra mit Eins gegeben. Es stellt sich die Frage, wie der Ausdruck f(a), also die “Er- weiterung” vonf von einem komplex- auf ein banachraumwertiges Argument, vernünftigerweise erklärt werden kann. Eine Antwort liefert der in dieser Arbeit vorgestellte Funktionalkalkül.

Dieser firmiert in der Literatur wahlweise unter Funktionalkalkül von F. Riesz (dem Schöpfer) und/oder Dunford (welcher ihn auf der Grundlage von Riesz’ Ideen weiterentwickelte) oder schlicht als Funktionalkalkül für holomorphe Funktionen.

Als bekannt darf an dieser Stelle der Funktionalkalk¨ul f¨ur Polynome vorausgesetzt werden, welcher den Ring der Polynome homomorph in den Ring der n×nMatrizen abbildet und im wesentlichen folgendes leistet: Sei

f : z7→

m

X

i=0

α_izⁱ, (1)

dann ist f(T) f¨ur eine quadratische MatrixT ∈C^n×nerkl¨art durch (setze T⁰ :=I) f : T 7→

m

X

i=0

αiTⁱ.

Insbesondere bedeutet das, dass man, wenn man weiß, wie man mit Polynomen rechnet, auch weiß, wie man mit (quadratischen) Matrizen zu rechnen hat.

Eine erste Idee ergibt sich zwanglos aus dem Faktum, dass (vorerst auf ganzC) holomorphe Funktionen ebendort auch analytisch sind und damit eine Darstellung als Potenzreihe, etwa mit Anschlusspunkt 0, haben. Das bedeutet, dass in (1) die Summe bis∞ geführt wird, wobei diese Reihe überall konvergiert. Es erscheint also möglich, wie oben das komplexe Argument z durch die Matrix T zu ersetzen, wobei Konvergenz nun im Sinne von Konvergenz in der Operatornorm zu verstehen ist. Die Menge an zulässigen holomorphen Funktionen kann sogar insofern erweitert werden, als dass nur der Konvergenzradius der zugehörigen Potenzreihe echt größer als die Operatornorm der einzusetzenden MatrixT sein muss.

Leider st¨oßt diese Vorgangsweise recht schnell an ihre Grenzen, was an einem Beispiel illus- triert werden soll.

Beispiel 1. Betrachte die Exponentialfunktion, welche holomorph in der ganzen komplexen Ebene ist und zu folgender Potenzreihe f¨uhrt:

exp(z) =

∞

X

n=0

1 n!zⁿ.

Für reguläre Matrizen wäre es nun wünschenswert, auch eine Inverse zu exp(.) zu haben. Der logische Kandidat, der natürliche Logarithmus

ln(z+ 1) =

∞

X

n=1

(−1)ⁿ⁺¹zⁿ n

konvergiert jedoch nur auf der offenen Einheitskreisscheibe um die Null. Daher findet man sich der Situation ausgesetzt, zwar für beliebigeT eine Funktionexp(T), aber im FallkTk ≥1 keine Umkehrfunktionln(T+I) erklären zu können.

Das Beispiel lehrt, dass es einer Verallgemeinerung des Funktionalkalk¨uls auf holomorphe Funktionen bedarf, die ohne Potenzreihen auskommt.

(4)

2 Vorbereitung f¨ ur den Funktionalkalk¨ ul

In diesem Abschnitt sollen die nötigen Konzepte bereitgestellt werden, die anschließend für den Kalkül benötigt werden. Zunächst eine Reihe von Definitionen, die der Kalkül benötigen wird.

Definition 2 (komplexe Banachalgebra mit Eins). Eine komplexe BanachalgebraA ist

• ein Banachraum (A,k.k) ¨uberC,

• auf dem zusätzlich eine bilineare, assoziative Verknüpfung·:A×A→A erklärt ist.

• Außerdem gilt f¨ur beliebige Elementea, b∈A die Absch¨atzungka·bk ≤ kak · kbk.

• Schlussendlich heißt A eine komplexe Banachalgebra mit Eins, fallsA ¨uber ein multipli- kativ neutrales Elementemitkek= 1 verf¨ugt.

Definition 3 (Resolventenmenge, Spektrum, Resolvente). SeiA eine Banachalgebra mit Eins und a∈A. Dann heißt

• ρ(a) ={λ∈C: (λe−a) ist invertierbar} die Resolventenmenge,

• σ(a) =C\ρ(a) das Spektrum und

• die Abbildung

R_λ(a) :

ρ(a) → A

λ 7→ (λe−a)⁻¹ die Resolvente.

Bekannte Resultate in der Theorie der Banachalgebren besagen, dass die Resolventenmenge offen, das Spektrum kompakt und die Resolvente auf ρ(a) holomorph ist. Neben Eigenschaften von Banachalgebren, welche den Zielraum f¨ur unseren Funktionalkalk¨ul stellen werden, sind noch Charakterisierungen von Funktionen wichtig, die am Ende den Ausgangsraum ausmachen werden.

Definition 4 (Holomorphie, Analytizit¨at). Sei ∆ eine offene Teilmenge vonC,z₀ ∈∆ und eine Funktion f : ∆→C. Dann heißtf

• komplex differenzierbar inz0, wenn der Limes

h→0lim

z0+h ∈ ∆

f(z0+h)−f(z0) h

existiert. In diesem Fall wird der Limes mitf⁰(z0) bezeichnet.

• holomorph in z₀, wennf in einer Umgebung vonz₀ komplex differenzierbar ist.

• analytisch inz0, wenn eine PotenzreiheP∞

n=0αn(z−z₀)ⁿexistiert, die in einer Umgebung von z₀ gegen die Funktion f(z) konvergiert.

• analytisch bzw. holomorph in ∆, wennf in jedem Punkt von ∆ die jeweilige Eigenschaft hat.

Für den Fall, dass f in einen komplexen, normierten Raum (E,k.k) abbildet, werden die an- geführten Punkte über die Norm erklärt, beispielsweise die komplexe Differenzierbarkeit

f(z)−f(z₀)

z−z₀ −f⁰(z₀)

z→z₀

−−−−→0.

(5)

Schlussendlich wird noch folgendes integrationstechnisch wichtige Konzept ben¨otigt.

Definition 5 (Integrationsweg). Ein Integrationsweg Γ ist das Bild einer stetigen Abbildung γ : [0,1]→C, wobei Γ endliche L¨ange hat (d.h. Γ ist rektifizierbar).

Da im weiteren Verlauf gegebenenfalls aus dem Kontext heraus stets klar ist, ob wir gerade von der Bildmenge Γ oder der zugrundeliegenden Abbildung γ sprechen, unterlassen wir ab sofort diese Unterscheidung und verwenden f¨ur beides den selben Buchstaben.

2.1 Integration in einer Banachalgebra

Es wird sich zeigen, dass der Funktionalkalkül über Integrale aufgebaut werden kann. Aus diesem Grund sei hier kurz erwähnt, wie in einer Banachalgebra ein Integral erklärt ist.

Gegeben seien ein Integrationsweg Γ, ein komplexer BanachraumE und eine Funktionf : Γ→ E, welche stetig sein soll. Dann k¨onnen wir das Integral vonf uber Γ definieren als Grenzwert¨ von Riemann’schen Summen:

Z

Γ

f(λ)dλ:= limX

k

f(Γ(ξk))(Γ(λk)−Γ(λk−1))

Dabei sind dieλkdie Unterteilungspunkte der verwendeten Zerlegung undξkein Wert aus dem Intervall [λk−1, λ_k]. Der Grenzübergang wird dann wie beim Riemann-Integral üblich über die Verfeinerung der Zerlegung vorgenommen.

Dieses auf Banachräume verallgemeinerte Riemann-Integral hat einige elementare Eigen- schaften, von denen die folgenden drei später noch benötigt werden: Es ist linear, d.h. für geeignete f, g∈C(Γ, E) und α∈E

Z

Γ

αf(λ)dλ=α Z

Γ

f(λ)dλ (2)

Z

Γ

f(λ) +g(λ)dλ= Z

Γ

f(λ)dλ+ Z

Γ

g(λ)dλ. (3)

Außerdem gilt die praktische Absch¨atzung

Z

Γ

f(λ)dλ

≤max

λ∈Γ kf(λ)k ·µ(Γ), (4)

wobei µ(Γ) die L¨ange des Integrationswegs Γ bezeichnen soll, und das Integral kann mit den stetigen linearen Funktionalen des Banachraums vertauscht werden, d.h.

e⁰ Z

Γ

f(λ)dλ

= Z

Γ

e⁰[f(λ)]dλ ∀e⁰ ∈E⁰. (5)

2.2 Zum Thema Integrationswege

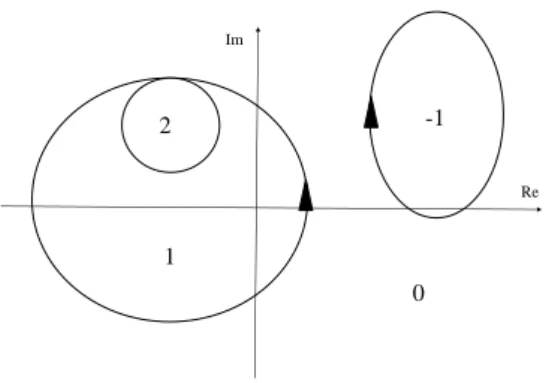
Eine genauere Betrachtung verdienen die Voraussetzungen, die wir im Funktionalkalk¨ul an die verwendeten Integrationswege stellen. Sei daherγ eine geschlossene und rektifizierbare Kurve in Cundλ6=γ(t)∀t∈[0,1]. Zu dieser Kurve kann die stets ganzzahlige sogenannte Windungszahl

n(γ;λ) := 1 2πi

Z

γ

1 ζ−λdζ

definiert werden. Sie ist auf jedem vonγumrissenen Teilgebiet in der komplexen Ebene konstant und z¨ahlt ihrem Namen getreu, wie oft sich eine Kurve um einen fraglichen Punktλwindet.

Allgemein wird γ positiv orientiert genannt, falls alle Punkte der komplexen Ebene als Windungszahl ein n∈N0 haben. Im Rahmen dieser Arbeit ben¨otigen wir die folgende spezielle

(6)

Definition 6. Ein Integrationswegγ wird einfach positiv orientiert genannt, falls

∀λ∈C\γ : n(γ;λ) = 1

0

Diese einfach positiv orientierten Integrationswege legen auch eine Kategorisierung der Punkte der komplexen Ebene nahe, indem das Innere bzw. ¨Außere von γ als jenes Gebiet bezeichnet wird, auf dem die Windungszahl konstant 1 bzw. 0 ist.

Die Verallgemeinerung auf den Fall, dass Γ eine Sammlung geschlossener, rektifizierbarer Kurven{γ₁, . . . , γ_m}ist, stellt nun keine Schwierigkeit mehr da:

Definition 7. Γ ={γ₁, . . . , γ_m}heißt einfach positiv orientiert, falls gilt (a) γi∩γj =∅ ∀ i6=j

(b) ∀λ∈C\Γ =C\Sm

i=1γ_i : n(Γ;λ) :=Pm

i=1n(γ_i;λ) = 1

0

Dazu passend heißt die Menge ins(Γ)≡ {λ: n(Γ;λ) = 1} das Innere und entsprechenderweise out(Γ)≡ {λ: n(Γ;λ) = 0}das ¨Außere von Γ.

Im

Re

0 2

1

-1

Abbildung 1: Bereiche der komplexen Ebene mit unterschiedlicher Windungszahl - bemerke, dass Definition 6 zufolge in den folgenden Abschnitten keine der gezeigten Kurven zul¨assig ist

Es ist somit nicht weiter verwunderlich, dass im Fall einer in einer Umgebung von Γ stetigen Funktion f die Festsetzung

Z

Γ

f(λ)dλ:=

m

X

i=1

Z

γi

f(λ)dλ getroffen wird.

Lemma 8. Zu zwei Mengen ∆⊆Coffen undK ⊂∆ kompakt findet man stets eine Sammlung Γ endlich vieler einfach positiv orientierter geschlossener Kurven, die einerseits ganz in ∆\K verlaufen und andererseitsK ⊂ins(Γ) und C\∆⊂out(Γ) leisten.

Beweis. Da K kompakt ist, hat jede Überdeckung von K durch offene Mengen eine endliche Teilüberdeckung. Insbesondere kann man K durch offene Kreisscheiben U_r_i(k_i) mit k_i ∈ K, r_i > 0 und U_r_i(k_i) ⊂ ∆ überdecken, eine endliche Teilüberdeckung {U_r₁(k₁), . . . , U_r_n(k_n)}

ausw¨ahlen und die Vereinigung V := Sn

i=1Uri(ki) betrachten. Man erh¨alt die Inklusionskette

(7)

K ⊂ V ⊂V ⊂ ∆. Insbesondere ist ∂V ⊂ ∆\K. Der Rand ist aus Kreisbögen aufgebaut und hat nur endlich viele, genauer: m ≤n Komponenten. Zudem sind alle Teile von ∂V ohne Be- schränkung der Allgemeinheit (ansonsten müssen einfach die Radien ri angepasst werden) dop- pelpunktfrei und disjunkt, weswegen∂V einfach positiv orientiert werden kann. Damit erfüllen die so konstruierten Kurven alle Anforderungen des Lemmas.

2.3 Der Cauchy’sche Integralsatz und die Cauchy’schen Integralformeln Die beiden nächsten hier vorgestellten Sätze, die das Skelett für den Funktionalkalkül bilden, sind ein Import aus der komplexen Analysis, besser gesagt eine Verallgemeinerung auf den für uns wichtigen Fall von komplexen Banachräumen.

In Anlehnung an [KA], Kapitel 11.3 zuerst eine

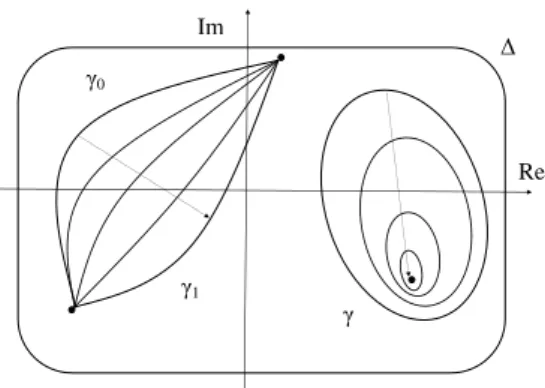
Definition 9(stetige Deformierbarkeit). Sei ∆⊆Cein Gebiet undγ₀, γ₁zwei Integrationswe- ge. Sei Γ : [0,1]×[0,1]→∆ stetig, mit Γ(t,0) =γ0(t) und Γ(t,1) =γ1(t), jeweils f¨urt∈[0,1].

Dann heißenγ₀ und γ₁ stetig ineinander deformierbar.

Im

Re Δ γ₀

γ1

γ

Abbildung 2: zur stetigen Deformierbarkeit in ∆ von γ0 zu γ1 - Skizze zu den zwei F¨allen im Cauchy’schen Integralsatz

Satz 10(Cauchy’scher Integralsatz). Seif : ∆→E, wobei ∆⊆Cein Gebiet,E ein komplexer Banachraum undf in ∆ holomorph ist.

1) F¨ur zwei Integrationswege Γ₁ und Γ₂ mit gleichen Anfangs- und Endpunkten, die zudem in

∆ stetig ineinander deformiert werden k¨onnen, folgt Z

Γ1

f(λ)dλ= Z

Γ2

f(λ)dλ.

2) Im Fall eines geschlossenen Integrationsweges Γ, dessen Inneres nur Punkte aus ∆ enth¨alt (oder ¨aquivalent dazu: Γ ist stetig deformierbar zu einem einpunktigen Integrationsweg), gilt

Z

Γ

f(λ)dλ= 0.

Zur Illustration sei hier kurz gezeigt, wie sich Beweise oftmals verallgemeinern lassen, wenn man den bekannten Fall von C-wertigen Funktionen bereits zur Verf¨ugung hat.

(8)

Beweis. ad 1): Laut (5) gilt∀e⁰ ∈E⁰: e⁰

Z

Γ1

f(λ)dλ

= Z

Γ1

e⁰[f(λ)]dλ=^∗ Z

Γ2

e⁰[f(λ)]dλ=e⁰ Z

Γ2

f(λ)dλ

.

Dabei wird bei * ausgenützt, dass e⁰◦f eine holomorphe, C-wertige Funktion ist, für die laut komplexer Analysis bereits eine Version des Cauchy’schen Integralsatzes existiert. Nachdem obige Gleichheit für beliebige Funktionalee⁰ gilt, müssen die Argumente identisch sein und der erste Teil des Satzes ist bewiesen.

ad 2): Der zweite Fall folgt direkt aus dem ersten, wenn man beachtet, dass man erstens einen geschlossenen Integrationsweg an zwei beliebigen, nicht identischen Punkten in zwei Integrati- onswege unterteilen kann, wo der Endpunkt des einen der Anfangspunkt des anderen ist, und sich zweitens das Vorzeichen des Integrals umdreht, wenn man die Orientierung des Integrati- onsweges verkehrt.

Satz 11 (Cauchy’sche Integralformeln). Sei wieder f : ∆ → E, wobei ∆ ⊆ C ein einfach zusammenh¨angendes Gebiet, E ein komplexer Banachraum undf in ∆ holomorph ist. Zudem sei Γ ein geschlossener, rektifizierbarer, einfach positiv orientierter Integrationsweg, der ein λ∈∆ umschließt.

Dann istf beliebig oft differenzierbar und es gelten die Formeln f⁽ⁿ⁾(λ) = n!

2πi Z

Γ

f(ζ)

(ζ−λ)ⁿ⁺¹dζ ∀n∈N0. (6)

Zudem folgt, dassf um jeden Punktλ₀ ∈∆ in eine Potenzreihe in der Gestalt f(λ) =

∞

X

k=0

α_k(λ−λ₀) α_k ∈E

entwickelt werden kann, deren Konvergenz zumindest im gr¨oßten offenen Kreis umλ₀, der ganz in ∆ liegt, gesichert ist.

Ein Beweis dieses Satzes kann in [HE] (Satz 97.2) gefunden werden, welcher wiederum die Eigenschaft (5) der stetigen linearen Funktionale ausn¨utzt.

Die wichtigste Aussage des obigen Satzes ist (6) im Fall n= 0:

f(λ) = 1 2πi

Z

Γ

f(ζ)

ζ−λdζ. (7)

Kurz gesagt erm¨oglicht uns diese Formel, den Funktionswert einer holomorphen Funktionf an einer festen Stelleλuber die Werte auszudr¨¨ ucken, die diese Funktion auf einem (wie auch immer deformierten) Kreis rund umλannimmt, wenn man noch mit geeigneten Faktoren multipliziert.

Ersetzt man in (7)λ∈Cdurch ein Elementaeiner komplexen BanachalgebraA, so erhält man im Integranden an Stelle von (ζ−λ)⁻¹ einfach die Resolvente (ζe−a)⁻¹ =R_ζ(a), während die Funktion f im Zähler unverändert bleibt und aus der gesamten rechten Seite ein banachraumwertiges Riemann-Integral wird, welches, wie bereits weiter oben erwähnt, auch kein unlösbares Problem darstellt.

3 Der Funktionalkalk¨ ul f¨ ur holomorphe Funktionen

Nach allen Vorbereitungen sind wir nun soweit, den Ausdruckf(a) sinnvoll zu erkl¨aren.

(9)

Definition 12. Sei A eine Banachalgebra mit Eins, sowie a ∈ A. Zudem sei eine Funktion f : ∆ → C gegeben, die in ∆ holomorph ist, und das kompakte Spektrum σ(a) echt in ∆ enthalten. F¨ur eine ganz in ρ(a)∩∆ verlaufende Sammlung Γ von einfach positiv orientierten Integrationswegen setze

f(a) := 1 2πi

Z

Γ

f(ζ)(ζe−a)⁻¹dζ= 1 2πi

Z

Γ

f(ζ)Rζ(a)dζ. (8)

An dieser Stelle wird also der Nutzen von Lemma 8 klar, wobei jedoch keine Eindeutigkeit des gefundenen Γ gew¨ahrleistet werden kann. Deshalb erg¨anzen wir die Definition durch folgendes Lemma 13. Durch (8) ist f(a) wohldefiniert.

Beweis. Zu zeigen ist die Unabh¨angigkeit der Definition vom gew¨ahlten Integrationsweg. Seien dazu also Γ ={γ₁, . . . , γm} und Λ ={λ₁, . . . , λk} zwei Sammlungen von einfach positiv orientierten Kurven im Holomorphiebereich ∆ von f, mit σ(a) ⊂ ins(Γ) bzw. σ(a) ⊂ ins(Λ). Wir fassen Γ und Λ durch die Festsetzung γ_m+i := λ⁻¹_i , das bedeutet also durch Umkehrung der Orientierung von Λ vermittelsλ⁻¹_i (t) :=λi(1−t), in der Menge Σ :={γ₁, . . . , γm+k}zusammen.

Speziell ¨andert sich f¨ur das so verkehrte Λ in jedem Punkt das Vorzeichen der Windungszahl.

Sei ζ /∈ ∆\σ(a) beliebig. Dann ist ζ entweder Teil der Menge C\∆ (welche leer ist f¨ur eine

¨

uberall holomorphe Funktion) oder im Spektrum vonaund es gilt:

ζ ∈C\∆ : n(Σ;ζ) =

m+k

X

i=1

n(γ_i;ζ) =n(Γ;ζ)−n(Λ;ζ) = 0−0 = 0 ζ ∈σ(a) : n(Σ;ζ) = 1−1 = 0

Also ist Σ eine Sammlung geschlossener Kurven in ∆\σ(a) mit der Eigenschaft n(Σ;ζ) = 0

∀ζ /∈ ∆\σ(a), d.h. C\∆∪σ(a) ⊆ out(Σ). Ergo enth¨alt das “Innere” von Σ nur Punkte aus

∆\σ(a) (zwar ist nicht gew¨ahrleistet, dass die Windungszahl hier stets 1 ist, aber dieses Detail spielt im weiteren keine Rolle). Außerdem istf(ζ) auf ∆ undRζ(a) auf der Resolventenmenge holomorph und damit hat deren Produkt diese Eigenschaft auf ∆\σ(a). Mit dem Cauchy’schen Integralsatz erhalten wir

0 = Z

Σ

f(ζ)R_ζ(a)dζ = Z

Γ

f(ζ)R_ζ(a)dζ− Z

Λ

f(ζ)R_ζ(a)dζ

und als Konsequenz liefert jede Wahl von Integrationswegen dasselbe Ergebnis. Damit ist die Wohldefiniertheit gezeigt.

3.1 Der Hauptsatz

Mit diesem Wissen k¨onnen wir nun den Funktionalkalk¨ul formulieren. Im Gegensatz zum vor- hergehenden Teil liegt unser Hauptaugenmerk nun nicht mehr darauf, wie man gewisse Elemente von A in eine spezielle Funktion einsetzen kann, sondern wie man bei festem a ∈ A mit ver- schiedenen holomorphen Funktionen rechnet.

Der Zielraum des Funktionalkalküls ist eine gegebene komplexe Banachalgebra A. Darum erscheint es zweckmäßig, als Ausgangsraum eine Struktur zur Verfügung zu stellen, die möglichst viele Eigenschaften mitAteilt, um den Kalkül zu einem Algebrenhomomorphismus zu machen.

Konkret f¨uhrt dies zur Funktionenalgebra

Hol(a) :={f |f : ∆f →C, ∆f ⊆Coffen,σ(a)⊂∆f, f holomorph in ∆f}.

(10)

Dabei hängt der Holomorphiebereich jeweils von der betrachteten Funktion ab. Deshalb sind die algebraischen Operationen f +g und f ·g nur auf dem Schnitt ∆_f ∩∆_g erklärt, während die Skalarmultiplikation αf mit α ∈ C keine Probleme bereitet. Es ist allerdings notwendig, zwei Funktionen f, g ∈ Hol(a) als äquivalent anzusehen, wenn sie auf dem Schnitt ihrer Ho- lomorphiebereiche übereinstimmen: ganz offensichtlich sollf +g−g=f gelten, jedoch ist die linke Seite auf ∆f ∩∆g definiert, was unter Umständen nicht mit dem Definitionsbereich der rechten Seite, ∆_f, zusammenpasst und zu Widersprüchen führen würde, wenn man besagte Aquivalenzrelation außer Acht l¨¨ asst. Auf diese Weise ist Hol(a) dann tatsächlich unter allen Operationen abgeschlossen.

Satz 14 (Funktionalkalk¨ul f¨ur holomorphe Funktionen). Sei A eine Banachalgebra mit Eins, a∈A.

(a) Die Funktion

Φ_a:

Hol(a) → A f 7→ f(a)

ist ein Algebrenhomomorphismus. Insbesondere ist f(a)g(a) =g(a)f(a).

(b) Seif : z7→P∞

k=0α_kz^k mitα_k ∈C und KonvergenzradiusR > r(a) (Spektralradius, i.e.

der betragsm¨aßig gr¨oßte Spektralpunkt). Dann gilt f ∈ Hol(a) undf(a) =P∞

k=0α_ka^k. (c) Seif : z7→1. Dann gilt f(a) =e.

(d) Seif : z7→z. Dann gilt f(a) =a.

(e) Istf(λ)6= 0 ∀λ∈σ(a). Dann besitztf(a) die Inverse f(a)⁻¹ =

1 f

(a).

(f) Seien f1, f2, . . . , f ∈ Hol(a) mit demselben Holomorphiebereich ∆. Konvergiert die Folge f_n gleichm¨aßig gegenf auf jeder beliebigen kompakten Menge K⊂∆, so gilt

kf_n(a)−f(a)k−−−−→^n→∞ 0

Interessanterweise legen die Homomorphieeigenschaft, sowie (c), (d) und (f) den Funktio- nalkalk¨ul bereits eindeutig fest. Ein Beweis f¨ur diese Aussage kann in [CO] VII. Proposition 4.8 nachgeschlagen werden.

Beweis. ad (a): Zuerst folgt (αf+βg)(a) =αf(a)+βg(a) direkt aus der Linearit¨at des Integrals laut (2) und (3). Es bleibt also nur noch (f g)(a) =f(a)g(a) zu zeigen.

Seien dazu also f, g ∈ Hol(a), ∆ ihr gemeinsamer Holomorphiebereich, sowie Γ und Λ zwei Sammlungen einfach positiv orientierter geschlossener Integrationswege mit der zus¨atzlichen Eigenschaft σ(a)⊂ ins(Γ)⊂ins(Γ)⊂ins(Λ)⊂∆. Dann gilt:

f(a)g(a) =− 1 4π²

Z

Γ

f(z)Rz(a)dz Z

Λ

g(ζ)R_ζ(a)dζ

=

=− 1 4π²

Z

Γ

Z

Λ

f(z)g(ζ) Rz(a)Rζ(a) dζdz=

=∗ − 1 4π²

Z

Γ

Z

Λ

f(z)g(ζ)(ζ−z)⁻¹ [Rz(a)−Rζ(a)]dζdz=

=− 1 4π²

Z

Γ

f(z) Z

Λ

g(ζ) (ζ−z) dζ

| {z }

=:A

Rz(a) dz+ 1 4π²

Z

Λ

g(ζ) Z

Γ

f(z) (ζ−z) dz

| {z }

=: B

R_ζ(a)dζ

(11)

Bei * wird die aus der Funktionalanalysis bekannte Resolventengleichung (ζ−z)R_z(a)R_ζ(a) = R_z(a)−R_ζ(a) für die Umformung verwendet und im letzten Integral lässt sich die Vertauschung der Integrationsreihenfolge mit dem Satz von Fubini für Riemann-Integrale rechtfertigen: Γ und Λ sind im wesentlichen die stetigen Bilder kompakter Intervalle und der Integrand ist holomorph (f, g auf ∆,R_ζ(a) auf ρ(a) und _ζ−z¹ auf C\{z =ζ}, ihr Produkt damit auf dem Schnitt dieser drei offenen Mengen, in welchem auch Γ und Λ liegen), daher insbesondere stetig, also mithin integrierbar, womit sich Fubini anwenden lässt. Schlussendlich gilt: z ∈ Γ ⊂ ins(Λ), weshalb nach (7) A = 2πi g(z) folgt. Wegen ζ ∈ Λ ⊂ out(Γ) ist der Integrand von B in ganz ins(Γ) holomorph und laut Satz 10 ergibt sichB= 0. Obige Rechnung fortgesetzt ist somit

f(a)g(a) = 1 2πi

Z

Γ

f(z)g(z)R_z(a) dz= (f g)(a) (9)

und (a) ist gezeigt. Das Kommutieren vonf(a) undg(a) ist eine simple Konsequenz der punktweise erkl¨arten abelschen Multiplikation in C, wie aus (9) ohne Weiteres ersichtlich ist.

ad (c), (d): Sei f ein allgemeines Monom, also f : z7→ z^k f¨urk ≥0. Eine solche Funktion ist, wie jedes Polynom, auf ganz C holomorph. Daher kann mittels γ(t) = Rexp(2πit), mit R > kak und t ∈ [0,1] ein spezieller Integrationsweg gew¨ahlt werden, da das Spektrum eines Elements a∈A immer im abgeschlossenen Kreis mit Radiuskakliegt und sicher σ(a)⊂ins(γ) folgt. Damit haben wir

f(a) = 1 2πi

Z

γ

z^kR_z(a)dz =

= 1 2πi

Z

γ

z^k(ze−a)⁻¹dz=

= 1 2πi

Z

γ

z^k−1(e−a

z)⁻¹dz =

=∗ 1 2πi

Z

γ

z^k−1

∞

X

n=0

a z

n

dz=

=

∞

X

n=0

1 2πi

Z

γ

1 z^n−k+1dz

| {z }

=







0 n6=k 1 n=k

aⁿ=

=a^k

Bei * wurde verwendet, dass |z| = R und daher ^a_z

< 1 gilt, weswegen sich (e− â_z)⁻¹ als gleichmäßig konvergente Neumann-Reihe schreiben lässt und die Vertauschung von Summe und Integral gerechtfertigt ist. Sowohl (c) als auch (d) folgen nun klarerweise als Spezialfälle des eben gezeigten.

ad (f): Sei Γ ={γ₁, . . . , γm}eine einfach positiv orientierte Sammlung geschlossener Kurven,

(12)

wie ¨ublich mit σ(a)⊂ins(Γ).

2πkf_n(a)−f(a)k= Z

Γ

f_n(z)R_z(a)dz− Z

Γ

f(z)R_z(a)dz

=

m

X

i=1

Z

γi

f_n(z)R_z(a)dz− Z

γi

f(z)R_z(a)dz

≤

m

X

i=1

Z

γi

fn(z)Rz(a)dz− Z

γi

f(z)Rz(a)dz

=

m

X

i=1

Z

γi

(f_n−f)(z)[ze−a]⁻¹dz

≤

m

X

i=1

Z

γi

|(f_n−f)(z)|

[ze−a]⁻¹

| {z }

∗

≤Mi

dz ≤

∗∗≤

m

X

i=1

M_i

|{z}<∞

· kγ_ik

|{z}<∞

·max

z∈γ_i{|(f_n−f)(z)|}

| {z }

−n→∞−−→ 0

n→∞

−−−−→0

Da die Zuordnung z 7→

[ze−a]⁻¹

stetig auf γ_i für jedes i∈ {1, . . . , m} ist - schließlich sind die Resolvente und die Norm beides stetige Funktionen - ist insbesondere die Verknüpfung der zwei Funktionen auf jedem Integrationsweg γi durch ein Mi beschränkt, was * erklärt. Die Abschätzung bei ** ergibt sich wegen (4).

ad (b): F¨ur festesn undpn(z) :=Pn

k=0αkz^k folgt mit (a), (c) und (d)pn(a) =Pn

k=0αka^k. Sei nun also f(z) =P∞

k=0α_kz^k mit einem gewissen Konvergenzradius R > r(a). Dann konvergiert die Folge derp_nsicher punktweise gegenf und sogar gleichm¨aßig auf kompakten Teilmen- gen von {z∈C:|z|< R}. Mit dem gerade bewiesenen (f) folgt daherp_n(a)→f(a).

ad (e): Wenn f am Spektrum von a nicht verschwindet, dann gibt es wegen der Stetigkeit von f insbesondere eine offene Umgebung U des Spektrums, auf derf nicht Null wird. Es folgt daher aus der Holomorphie von f jene von ¹_f auf U und ¹_f geh¨ort sicherlich zu Hol(a). Es gilt nun trivialerweise die Gleichung f(λ)

1 f

(λ) =

1 f

(λ)f(λ) = 1 f¨urλ ∈ U und mit (a) und (c) ist daher klar, dass _f¹ invers zuf ist. Damit ist der Satz vollst¨andig bewiesen.

3.2 Eine Anwendung

Zum Abschluss und Ausblick sei hier noch eine erste Verwendungsmöglichkeit für den Funktio- nalkalkül vorgestellt, namentlich ein Spektralabbildungssatz.

Satz 15 (Spektralabbildungssatz). Seif ∈Hol(a). Dann gilt σ(f(a)) =f(σ(a)).

Beweis. ⊆: Sei µ ∈ σ(f(a)). Angenommen es gelte µ /∈ f(σ(a)), d.h. µ−f(λ) 6= 0 für jeden Spektralpunkt. Laut der Aussage (e) des Funktionalkalküls hätte also µe−f(a) eine Inverse, ein Widerspruch zur Voraussetzung. Also muss σ(f(a))⊆f(σ(a)) gelten.

⊇: Sei jetztµ∈f(σ(a)), d.h.µ=f(ζ) f¨ur ein gewissesζ ∈σ(a). Auf ∆_f definieren wir nun g(λ) :=

( _f(λ)−f

(ζ)

λ−ζ λ6=ζ f⁰(ζ) λ=ζ .

(13)

Diese Festsetzung ist sinnvoll, weil nach Definition 4 g(λ) gegen g(ζ) konvergieren muss. Die Holomorphie vererbt sich von f auf g und wir erhalten g ∈ Hol(a). Damit kann Φ_a auf g angewandt werden:

g(λ)(ζ−λ) =f(ζ)−f(λ)

⇓Φ_a

g(a)(ζe−a) =f(ζ)e−f(a) =µe−f(a)

Wir treffen an dieser Stelle die Annahme, dassµ /∈σ(f(a)), d.h. µe−f(a) ist invertierbar und wir erhalten

(µe−f(a))⁻¹g(a)

(ζe−a) = (ζe−a)

(µe−f(a))⁻¹g(a)

=e.

Es ist alsoζe−ainvertierbar, womit wir wiederum einen Widerspruch zur Annahme erhalten.

Also muss auchf(σ(a))⊆σ(f(a)) sein und der Satz ist bewiesen.

Literatur

[HE] Harro Heuser:Funktionalanalysis - Theorie und Anwendung, Wiesbaden: B. G. Teubner Verlag, 4. Auflage 2006.

[CO] John B. Conway:A Course in Functional Analysis, New York: Springer, 1985.

[KA] Michael Kaltenb¨ack: Analysis II f¨ur Technische Mathematik, Vorlesungsskriptum, Wien, 2008.

Anmerkung: Als Einf¨uhrung und ¨Ubersicht zum Thema ist zudem auch die Seite http://en.wikipedia.org/wiki/Holomorphic_functional_calculus

zu empfehlen, von wo auch Beispiel 1 in gek¨urzter Form ¨ubernommen wurde.