∂Tν(x) ∂xµ x=x0 aµ= ˜aν (2) ∂2Tν(x) ∂xµ1∂xµ2 x=x0 aµ1aµ2 = 0 (3) Diesgiltwohlgemerktfürallea, x0∈R4.Wirshlieÿenalso,daTalsmindestensC2vorausgesetzt,undsomitdieHessishe symmetrish,dasswirausdemVershwindenderquadratishenFormdasVershwindenderMatrixfolgernkön

Prof.Dr.R.Verh,M.Teuhler,A.Knospe

. .

Inst. f. Theoretische Physik

UNIVERSITAT LEIPZIG

Wintersemester 2008/09

Musterlösungen zuÜbungen zurAllgemeinen Relativitätstheorie

Aufgabenblatt 1

Aufgabe 1

GeradenwerdenaufGraden abgebildet,d.h.∀a, x0∈R⁴∃˜a,x˜0∈R^4,sodass:

T^ν(aτ+x0) = ˜a^ντ+ ˜x^ν₀, ∀τ ∈R

Wobeizubeahtenist,dassfüra6= 0^auh˜a6= 0^{,denndieWeltliniendürfennihtzuPunkten}degenerieren,dieAbbildung mussalsobijektiv sein.Wirerhaltenalso:

T^ν(x0) = ˜x^ν₀ ⁽¹⁾

∂

∂τT^ν(aτ +x0) = ∂T^ν(x)

∂x^µ x=x0

a^µ= ˜a^{ν (2)}

∂²T^ν(x)

∂x^µ1∂x^µ2 x=x0

a^µ1a^µ2 = 0 ⁽³⁾

Diesgiltwohlgemerktfürallea, x0∈R^{4.Wirshlieÿenalso,da}T^{alsmindestens}C²vorausgesetzt,undsomitdieHessishe symmetrish,dasswirausdemVershwindenderquadratishenFormdasVershwindenderMatrixfolgernkönnen.

∂²T^ν(x)

∂x^µ1∂x^µ2 _x=x

0

= 0 ∀µ1, µ2, ν, x0 ⁽⁴⁾

Somitfolgerndaswir alle höherenAbleitungen bilden können unddiese vershwinden. T ^{lässtsih so in eine}Taylorreihe umnullentwikeln.

T(x) =B·x+X, x∈R^{4 (5)}

,wobei

X=T(0) B^µν = ∂T^µ

∂x^ν(0)

Aufgabe 2

β= tanh (θ), γ= cosh(θ), γβ= sinh(θ) ⁽⁶⁾

x^′0= cosh(θ)x⁰−sinh(θ)ⁿ·^{x (7)}

x

′

||= cosh(θ)^x_||−sinh(θ)x^{0n (8)}

x

′

⊥=^x_⊥ ⁽⁹⁾

Wirführenim R^{3 denProjektor}P(ⁿ)^{auf den}eindimensionalenUnterraum{αⁿ|α∈R}^{ein,welherin(bzglderStandart-}

basis)dieFormP(ⁿ)ⁱ_j =nⁱnj^,bzw.in Matrixshreibweise

P(ⁿ) =





n¹n1 n¹n2 n¹n3

n²n1 n²n2 n²n3

n³n1 n³n2 n³n3



=|ⁿi hⁿ| ⁽¹⁰⁾

Λ(ⁿ, θ) =

coshθ −^nTsinhθ

−ⁿsinhθ coshθP(ⁿ)

+

0 ^0T

0 Id^(3×3)−P(ⁿ)

=

coshθ −^nTsinhθ

−ⁿsinhθ Id^(3×3)+ (coshθ−1)P(ⁿ)

=

coshθ −sinhθhⁿ|

− |ⁿisinhθ Id^(3×3)+ (coshθ−1)|ⁿi hⁿ|

(11)

Nunkönnenwir indieFormeleinsetzen,wobeiauf dieReihenfolgevon hⁿ| ^und|ⁿi^{zu ahtenist, z.B.erhältmandie3x3}

raumartigeUntermatrixin folgenderWeise:

Λ(ⁿ, θ1)Λ(ⁿ, θ2)|raumartiger Teil=|ⁿisinhθ1sinhθ2hⁿ|+ (Id^(3×3)+ (coshθ1−1)|ⁿi hⁿ|)(Id^(3×3)+ (coshθ2−1)|ⁿi hⁿ|)

= sinhθ1sinhθ2|ⁿi hⁿ|+Id^(3×3)+ (coshθ2+ coshθ2−2)|ⁿi hⁿ|+ (coshθ1−1)(coshθ2−1)|ⁿi hⁿ|ⁿi hⁿ|

= (sinhθ1sinhθ2+ coshθ1coshθ2−1)|ⁿi hⁿ|+Id^(3×3)

DieanderenMatrixelementefolgeninähnliherWeise.Wirerhalten:

Λ(ⁿ, θ1)Λ(ⁿ, θ2) =

coshθ1coshθ2+ sinhθ1 sinhθ2 −(coshθ1sinhθ2+ sinhθ1coshθ2)hⁿ|

− |ⁿi(coshθ2sinhθ1+ sinhθ2coshθ1) (sinhθ1sinhθ2+ coshθ1coshθ2−1)|ⁿi hⁿ|+Id^(3×3)

Nunistnurnoh zuverwenden,dasscoshθ= cos(iθ)^und sinhθ=−isin(iθ)^:

cosh(θ1+θ2) = cos(i(θ1+θ2)) = cos(iθ1) cos(iθ2)−sin(iθ1) sin(iθ2) = coshθ1coshθ2+ sinhθ1sinhθ2

sinh(θ1+θ2) =−isin(i(θ1+θ2) =−isin(iθ1) cos(iθ2)−isin(iθ2) cos(iθ1) = sinhθ1coshθ2+ sinhθ2coshθ1

undwirerhaltendasgesuhte:

Λ(ⁿ, θ1)Λ(ⁿ, θ2) =

cosh(θ1+θ2) −sinh(θ1+θ2)hⁿ|

− |ⁿisinh(θ1+θ2) Id^(3×3)+ (cosh(θ1+θ2)−1)|ⁿi hⁿ|

= Λ(ⁿ, θ1+θ2)

Aufgabe 3

Minkowski-Diagrammebildenmitunter(wennmansieeinmalverstandenhat)sehranshaulihSituationeninderspeziellen

Relativitätstheorieab. Deshalbwollen wirhiernoheinmalmit einerGegenüberstellungzubekannten Verhältnissen imR³

kurzerklären,wiesiezu konstruierensind,und wiemanetwasausihnen abliest.Dazu betrahtemandieTabelleauf der

nähstenSeite.

Standart(Euklid-)R^{3 Minkowski-}R⁴

DieLänge vonVektorenwirdmitHilfeeinerMetrikgemessen:

gµν =





1 0 0 0 1 0 0 0 1



 ηµν=









1 0 0 0

0 −1 0 0

0 0 −1 0

0 0 0 −1









GewisseTransformationen lassendie Metrikinvariant und bilden so die Einheitssphäreauf dieEinheitssphäre

ab. Bei Minkowskisind jedoh Vektoren der Länge -1 möglih,wodurh die Einheitssphäre in vier disjunkte

Gebieteaufspaltet:

FührtmannuneineTransformation(spezielleineRotationodereinenBoost)aus,solassensihdieKoordinaten

der(Standart-)BasisvektorendesneuenSystemsindasaltemittelsderInversenmatrixberehnenundeintragen:

cosϕ sinϕ

−sinϕ cosϕ 1 0

=

cosϕ

−sinϕ

coshθ sinhθ sinhθ coshθ

1 0

=

coshθ sinhθ

cosϕ sinϕ

−sinϕ cosϕ 0 1

=

sinϕ cosϕ

coshθ sinhθ sinhθ coshθ

0 1

=

sinhθ coshθ

Nunlassen sihKoordinaten Linien beiderSysteme in ein Diagramm eintragenlassen,man kannalso so gle-

ihzeitiginzweiSystemenablesen:

1

2

3

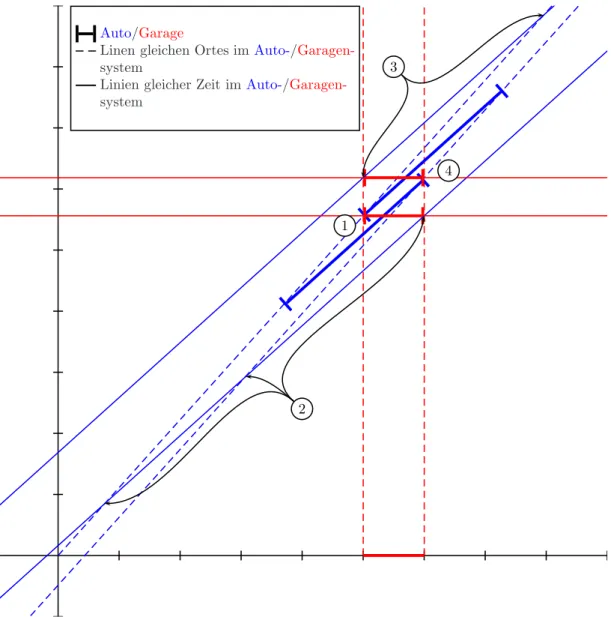
4 Auto/Garage

Linen gleichen Ortes imAuto-/Garagen- system

Linien gleicher Zeit im Auto-/Garagen- system

Abbildung1:Raumzeitdiagramm derSituationbei v=0.9,mit einerRuhelängeder Garage,sowiedesAutosvon1.

NummernstehenfürEreignisseundPfeilemarkierenwosihdasAutozugleihenZeitpunktaufhieltimAutosystem:

(1)ShlieÿenderVordertürderGarage,(2)ShlieÿenderHintertürderGarage,(3)ÖnenderVordertürderGarage,

(4)ÖnenderHintertürderGarage

Hier nun also noh das Problem in Worten behandelt. l(...) heiÿt immer die Länge im Ruhesystem. Indizes V und H

bezeihnenVorder-bzw.Hintertor;↑^und↓ ^{ÖnenundShlieÿen.}

wirzunähsteinmaldieZeitdierenz vonShlieÿendesVordertoresundÖnendesHintertores imAutosystemaus:

∆x^′0_V↓H↑=γ(∆x⁰_V↓H↑−β∆x¹) = γl(Garage)−l(Auto)

β −γβl(Garage) = l(Garage)−γl(Auto) γβ

Insbesondere ist diese Dierenz bei gleiher Ruhelängevon Auto und Garage negativ, dass heiÿt dasfür den Autofahrer

geshiehtdasÖnendesHintertoresvordemShlieÿendesVordertores.ZuletztberehnenwirnohdieStrekediezwishen

beidenEreignissenimAutosystemgemessenwird:

∆x^′1_V↓H↑=γ(∆x¹_V↓H↑−β∆x⁰_V↓H↑) =γl(Garage)−γl(Garage) +l(Auto) =l(Auto)

DasheiÿtimAutosystemsinddieEreignissegenaudieLängedesAutosvoneinanderentfernt,dasAutopasstalsoebenfalls

indieGarage.DasProblemistkonsistentin beidenSystemen.