Programmiermethoden des Wissenschaftlichen Rechnens

Programmiermethoden des Wissenschaftlichen Rechnens

Winter semester 2018/2019 Prof. Dr. Marc Alexander Schweitzer Clelia Albrecht and Albert Ziegenhagel

Exercise sheet 5.

1 Einf¨ uhrung

In dem noch jungen Forschungsgebiet des wissenschaftlichen Rechnens werden der tech- nische Sachverstand der Ingenieure, die numerischen Verfahren der Mathematiker und die modernen Methoden und Rechner der Informatiker gleichgewichtig interdisziplin¨ ar eingesetzt. Die mathematische Vorausberechnung technischer Prozesse, kurz numerische Simulation genannt, ist dabei ein wichtiges Ziel.

Durch die numerische Simulation kann beispielweise der Aufbau kostspieliger Ver- suchsaufbauten vermieden werden. Dar¨ uberhinaus lassen sich in vielen F¨ allen Aussagen treffen, bei denen dies auf Grund technischer Unzul¨ anglichkeiten sonst nicht m¨ oglich w¨ are, oder ein praktisches Experiment sich von vornherein verbietet.

Ein wichtiges Beispiel f¨ ur den Einsatz der numerischen Simulation ist die Berechnung von Str¨ omungsvorg¨ angen wie die Umstr¨ omung eines Flugzeugfl¨ ugels, der Luftwiderstand eines Automobils, Verbrennungsvorg¨ ange in Kraftwerken, sowie Schmelzprozesse und Kristallwachstum bei der Halbleiterfertigung. Aber auch bei der Wettervorhersage, in der Geologie, der Bioinformatik, der Mechanik (Elastizit¨ atstheorie) und in vielen anderen Gebieten der Physik und der Chemie kommen Simulationsmethoden zum Einsatz.

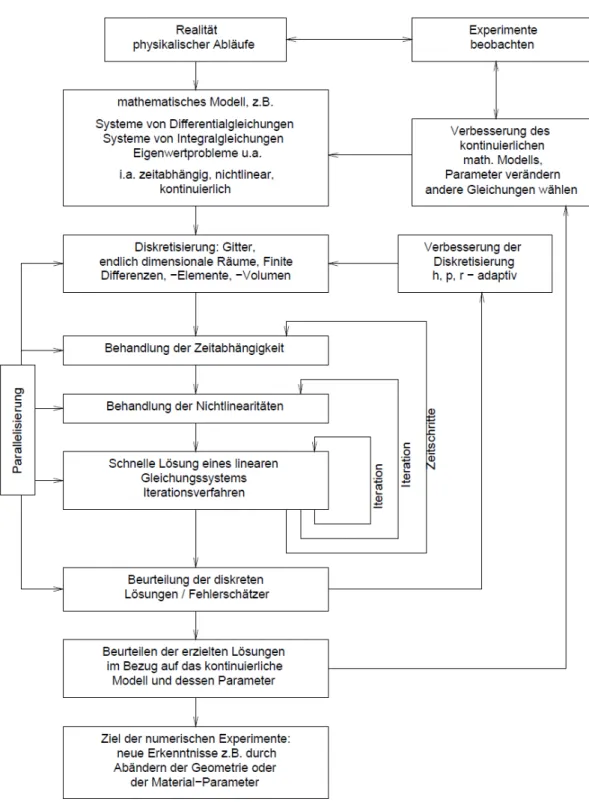
Das folgende Vorgehen ist dabei charakteristisch: Aus der Beobachtung der Realit¨ at wird

ein mathematisches Modell entwickelt, das nach geeigneter Diskretisierung n¨ aherungs-

weise gel¨ ost wird. Mittels geeigneter Visualisierungsmethoden k¨ onnen die Ergebnisse

interpretiert werden. Gegebenenfalls m¨ ussen dann die numerischen L¨ osungsverfahren

oder das Modell nachgebessert werden (vergleiche hierzu auch Abbildung 1).

2 Die Problemstellung: Inkompressible viskose Str¨ omun- gen

Im Praktikum wollen wir diese Schritte an einem konkreten Beispiel aus der Str¨ omungs- mechanik erlernen. Wir betrachten dazu die Behandlung viskoser, instation¨ arer, lamina- rer Str¨ omungen.

Dabei beschr¨ anken wir uns auf inkompressible Medien, wie beispielsweise Wasser, die, wie der Name sagt, nicht komprimierbar sind. Luft w¨ are hingegen ein Beispiel f¨ ur ein kom- pressibles Medium, bei dem ein und dieselbe Masse unterschiedliche Volumina ausf¨ ullen kann. Die Viskosit¨ at beschreibt die Z¨ ahigkeit des Mediums. So besitzt Luft eine sehr ge- ringe, Wasser eine etwas gr¨ oßere und Honig eine hohe Viskosit¨ at. Bei nicht zu hohen Ge- schwindigkeiten und nicht zu geringen Viskosit¨ aten sind Str¨ omungen relativ regelm¨ aßig und wenig mischungsintensiv, d.h. laminar und nicht turbulent. Instation¨ ar bedeutet schließlich, dass sich die Str¨ omung im Gegensatz zu station¨ aren Str¨ omungen mit der Zeit ver¨ andern kann.

Beispiele aus der Praxis sind in den Abbildungen 2 und 3 zu sehen.

3 Das mathematische Modell: Die Navier–Stokes–

Gleichungen

Instation¨ are, inkompressible, viskose, laminare Str¨ omungen lassen sich durch die Navier–

Stokes–Gleichungen beschreiben. Der Einfachheit halber beschr¨ anken wir uns dabei auf den zweidimensionalen Fall und legen ein kartesisches Koordinatensystem zu Grunde.

Dann erhalten wir ein System partieller Differentialgleichungen, bestehend aus den zwei Impulsgleichungen

∂u

∂t + ∂p

∂x = 1 Re

∂ ² u

∂x ² + ∂ ² u

∂y ²

− ∂(u ² )

∂x − ∂(uv)

∂y + g _x , (1)

∂v

∂t + ∂p

∂y = 1 Re

∂ ² v

∂x ² + ∂ ² v

∂y ²

− ∂(uv)

∂x − ∂(v ² )

∂y + g _y (2)

und der Kontinuit¨ atsgleichung

∂u

∂x + ∂v

∂y = 0, (3)

das zun¨ achst auf dem rechteckigen Gebiet Ω := [0, a] × [0, b] ⊂ R ² in dem Zeitintervall [0, t _end ] gel¨ ost werden soll. ¹

Dabei sind die drei gesuchten Gr¨ oßen

• u : Ω × [0, t end ] → R die Geschwindigkeit des Fluids in x–Richtung,

• v : Ω × [0, t _end ] → R die Geschwindigkeit des Fluids in y–Richtung,

• p : Ω × [0, t _end ] → R der Druck.

Die reelle Zahl Re ist die Reynoldszahl, die die Z¨ ahigkeit des Fluids angibt. Je kleiner Re ist, umso z¨ aher ist das Fluid.

1

Neben der hier verwendeten Formulierung mit den Unbekannten (u, v, p) existiert auch eine Formu-

lierung mit der Stromfunktion ψ und der Wirbelfunktion ω als Unbekannte (siehe auch Blatt 2).

Abbildung 1: Typische Vorgehensweise in einem Teilgebiet des Wissenschaftlichen Rech-

nens

Abbildung 2: Str¨ omung ¨ uber einen Hohl- raum

Abbildung 3: Str¨ omung ¨ uber eine Stufe

g x : Ω × [0, t end ] → R und g y : Ω × [0, t end ] → R sind ¨ außere Kr¨ afte, etwa die Erdanzie- hung oder andere Beschleunigungen, denen das System unterworfen ist. In der Literatur findet man h¨ aufig nicht die obige, komponentenweise Notation sondern die kompaktere Schreibweise

∂u

∂t + ∇ · (u ⊗ u) = g − ∇p + ν∆u ,

∇ · u = 0 .

Dabei ist u = (u, v) ^T bzw. (u, v, w) ^T in 3D, g = (g _x , g _y {, g _z }) ^T und u ⊗ u die 2 × 2 (3 × 3) Matrix u · u ^T . Die Divergenz ∇· einer Matrix ist dabei wie ¨ ublich der Vektor der Divergenzen der Spalten.

Zu Beginn (t = 0) seien Anfangsbedingungen u = u ₀ (x, y) und v = v ₀ (x, y) vorge- geben, die (3) erf¨ ullen. Zus¨ atzlich sind zu allen Zeitpunkten Bedingungen an den 4 Gebietsr¨ andern erforderlich, so dass wir insgesamt ein Anfangs–Randwertproblem erhal- ten.

F¨ ur die Formulierung der Randbedingungen bezeichne w 1 die Geschwindigkeitskompo- nente senkrecht zum Rand (in Normalenrichtung), w ₂ die Geschwindigkeitskomponente parallel zum Rand (in Tangentialrichtung) und ∂w 1 /∂n bzw. ∂w 2 /∂n die Ableitung in Normalenrichtung.

Am senkrechten Rand gilt also

w 1 = u, w 2 = v, ∂w 1

∂n = ∂u

∂x , ∂w 2

∂n = ∂v

∂x , und am waagrechten Rand gilt

w 1 = v, w 2 = u, ∂w 1

∂n = ∂v

∂y , ∂w 2

∂n = ∂u

∂y .

F¨ ur Punkte (x, y) des festen Randes Γ := ∂Ω sind folgende Randbedingungen m¨ oglich:

1. Haftbedingung (no–slip): w ₁ (x, y) = 0, w ₂ (x, y) = 0.

(Fluid haftet am Rand) 2. Rutschbedingung (free–slip): w ₁ (x, y) = 0, ∂w ₂ (x, y)/∂n = 0.

(keine Reibung am Rand) 3. Einstr¨ ombedingung (inflow): w 1 (x, y) = w ⁰ ₁ , w 2 (x, y) = w ⁰ ₂ .

w ₁ ⁰ , w ⁰ ₂ gegeben

4. Ausstr¨ ombedingung (outflow): ∂w ₁ (x, y)/∂n = 0, ∂w ₂ (x, y)/∂n = 0.

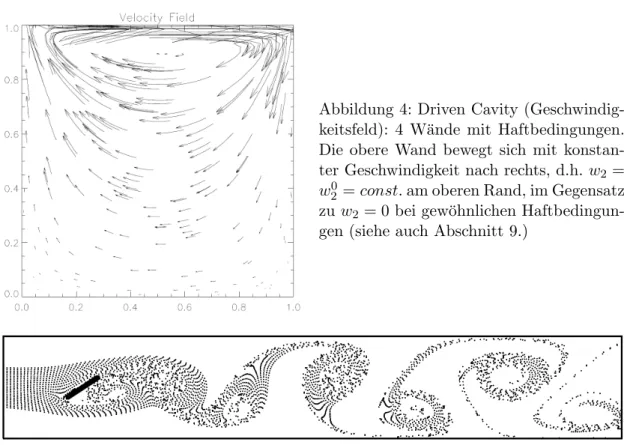
Abbildung 4: Driven Cavity (Geschwindig- keitsfeld): 4 W¨ ande mit Haftbedingungen.

Die obere Wand bewegt sich mit konstan- ter Geschwindigkeit nach rechts, d.h. w ₂ = w ₂ ⁰ = const. am oberen Rand, im Gegensatz zu w 2 = 0 bei gew¨ ohnlichen Haftbedingun- gen (siehe auch Abschnitt 9.)

Abbildung 5: Str¨ omung ¨ uber einen schr¨ agen Balken (Streichlinien): links: Einstr¨ omung (inflow), rechts: Ausstr¨ omung (outflow) oben und unten starre W¨ ande (no-slip)

Sind an allen R¨ andern die Geschwindigkeiten selbst und nicht deren Normalenablei- tungen vorgegeben, so muss zus¨ atzlich das Randintegral ¨ uber die Geschwindigkeiten senkrecht zum Rand Null sein, d.h.

Z

Γ

u v

· n ds = 0

Beispiele f¨ ur Str¨ omungen mit unterschiedlichen Randbedingungen sind etwa:

Mit physikalisch richtigen Randbedingungen erhalten wir insgesamt ein

” gut–gestell- tes“Problem, das eine eindeutige L¨ osung besitzt.

Diese L¨ osung ist jedoch im allgemeinen Fall nicht analytisch berechenbar, d.h. sie kann nicht in einer geschlossenen Formel angegeben werden. Sie ist meist nur numerisch ap- proximierbar.

4 Die Diskretisierung

Mit dem Begriff Diskretisierung beschreibt man in der Numerik den ¨ ubergang von ei- nem kontinuierlichen Problem zu einem Problem, das nur in endlich vielen Punkten betrachtet wird. Im einfachsten Fall wird das Gebiet Ω durch ein Gitter ¨ uberdeckt, und das zu l¨ osende Problem wird statt auf dem ganzen Gebiet jetzt nur noch in den Kreuzungspunkten der Gitterlinen betrachtet. Das Gitter habe in x–Richtung imax und in y–Richtung jmax Zellen der gleichen Gr¨ oße, so dass die Gitterlinien die Abst¨ ande δx := a/imax und δy := b/jmax haben. Die Zelle mit dem Index (i, j) entspricht dem Gebiet [(i − 1) δx, i δx] × [(j − 1) δy, j δy]. Die Differentialoperatoren lassen sich dann durch Differenzensterne ersetzen. Gem¨ aß der Definition der Ableitung

df

dx := lim

δx→0

f (x + δx) − f (x)

δx

j j+1

j-1

i-1 i i+1

i,j

i+2 Zelle (i,j) Zelle (i+1,j)

i,j i+1,j

p i,j p i+1,j

u i+1,j

v i,j-1 v

i+1,j-1

v v

u i-1,j u

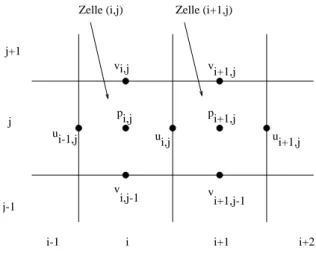
Abbildung 6: Staggered Grid

wird so im Eindimensionalen der kontinuierliche Differentialoperator df /dx durch den Differenzenoperator δf /δx := (f (x + δx) − f (x))/δx zur Schrittweite δx approximiert, indem die Limesbildung weggelassen wird. x und x + δx sind dabei Gitterpunkte. Wir erhalten so die Methode der finiten Differenzen ² . Anschaulich ist klar, dass eine Verfei- nerung des Gitters, d.h eine Verkleinerung der Schrittweite δx, zu einer besseren Appro- ximation des Differentialquotienten f¨ uhrt.

Im Fall der Navier–Stokes–Gleichungen wird zur Diskretisierung des Gebietes Ω oftmals ein versetztes Gitter (“staggered grid”) verwendet, bei dem die verschiedenen gesuch- ten Variablen nicht in den selben Gitterpunkten liegen. Wir verwenden ein Gitter, in dem der Druck p nur in den Mittelpunkten der Zellen, die Geschwindigkeit u nur in den Mittelpunkten der senkrechten Zellkanten und die Geschwindigkeit v nur in den Mittelpunkten der waagrechten Zellkanten betrachtet wird. Den Index (i, j) tragen der Druck im Mittelpunkt der Zelle (i, j), die u–Geschwindigkeit an der rechten Kante und die v–Geschwindigkeit an der oberen Kante der Zelle (i, j). Der Druck p i,j liegt also bei den Koordinaten ((i − 0.5) δx, (j − 0.5) δy), u _i,j bei den Koordinaten (i δx, (j − 0.5) δy) und v i,j bei den Koordinaten ((i − 0.5) δx, j δy) (vgl. Abbildung 6).

Die Punkte f¨ ur u, v und p geh¨ oren also zu drei, hier nicht dargestellten Gittern, die jeweils um eine halbe Maschenweite versetzt sind.

In Folge dessen kommen nicht alle Werte auf dem Rand des Gebietes zu liegen. So gibt es etwa auf den senkrechten R¨ andern keine v–Werte und auf den waagrechten R¨ andern keine u–Werte. Daher wird noch eine Randschicht aus Gitterzellen mitgef¨ uhrt (vgl. Abbildung 7), und die Randbedingungen werden durch eine Mittelung der n¨ achstliegenden Werte erf¨ ullt.

Weiterhin wird auch das Zeitintervall [0, t _end ] in gleiche Teilintervalle [n δt, (n + 1) δt], n = 0, . . . , t _end /δt − 1 zerlegt. Werte f¨ ur u, v und p werden also nur zu den Zeitpunkten n δt betrachtet.

Die Navier–Stokes–Gleichungen werden jetzt wie folgt diskretisiert:

Zun¨ achst wollen wir die Ortsableitungen behandeln. Die Impulsgleichung (1) wird in den Mittelpunkten der senkrechten Kanten, die Impulsgleichung (2) wird in den Mittelpunk- ten der waagrechten Kanten, und die Kontinuit¨ atsgleichung (3) wird in den Zellmittel- punkten ausgewertet.

Die Ausdr¨ ucke in Gleichung (1) ersetzen wir am Mittelpunkt der rechten Kante der Zelle (i, j), i = 1, . . . , imax − 1, j = 1 . . . , jmax, durch

2

Daneben existieren eine Reihe anderer Diskretisierungsverfahren, wie finite Elemente oder finite

Volumen.

Rand des Gebietes

i=0 i=1 i=2 i=ibar i=ibar+1 j=0

j=1 j=2 j=jbar j=jbar+1

Abbildung 7: Gebiet mit Randzellen

∂(u ² )

∂x

i,j

:= 1 δx

u _i,j + u _i+1,j 2

2

−

u i−1,j + u _i,j 2

2 ! + α 1

δx

|u _i,j + u _i+1,j | 2

(u _i,j − u _i+1,j )

2 − |u _i−1,j + u _i,j | 2

(u i−1,j − u _i,j ) 2

, ∂(uv)

∂y

i,j

:= 1 δy

(v _i,j + v _i+1,j ) 2

(u _i,j + u _i,j+1 )

2 − (v i,j−1 + v i+1,j−1 ) 2

(u i,j−1 + u _i,j ) 2

+ α 1

δy

|v _i,j + v i+1,j | 2

(u i,j − u i,j+1 )

2 − |v _i,j−1 + v i+1,j−1 | 2

(u i,j−1 − u i,j ) 2

, (4) ∂ ² u

∂x ²

i,j

:= u _i+1,j − 2u _i,j + u i−1,j

(δx) ² ,

∂ ² u

∂y ²

i,j

:= u _i,j+1 − 2u _i,j + u i,j−1

(δy) ² ,

∂p

∂x

i,j

:= p _i+1,j − p _i,j

δx .

Die Ausdr¨ ucke in Gleichung (2) ersetzen wir am Mittelpunkt der oberen Kante der Zelle (i, j), i = 1, . . . , imax, j = 1 . . . , jmax − 1, durch

∂(uv)

∂x

i,j

:= 1 δx

(u _i,j + u _i,j+1 ) 2

(v _i,j + v _i+1,j )

2 − (u i−1,j + u i−1,j+1 ) 2

(v i−1,j + v _i,j ) 2

+ α 1

δx

|u _i,j + u i,j+1 | 2

(v i,j − v i+1,j )

2 − |u i−1,j + u i−1,j+1 | 2

(v i−1,j − v i,j ) 2

, ∂(v ² )

∂y

i,j

:= 1 δy

v i,j + v i,j+1

2

2

−

v i,j−1 + v i,j

2

2 ! + α 1

δy

|v _i,j + v i,j+1 | 2

(v i,j − v i,j+1 )

2 − |v _i,j−1 + v i,j | 2

(v i,j−1 − v i,j ) 2

, (5) ∂ ² v

∂x ²

i,j

:= v _i+1,j − 2v _i,j + v i−1,j

(δx) ² ,

∂ ² v

∂y ²

i,j

:= v _i,j+1 − 2v _i,j + v i,j−1

(δy) ² ,

∂p

∂y

i,j

:= p _i,j+1 − p _i,j δy

und die Terme in der Kontinuit¨ atsgleichung (3) ersetzen wir im Mittelpunkt der Zelle

(i, j), i = 1, . . . , imax, j = 1 . . . , jmax, durch ∂u

∂x

i,j

:= u i,j − u i−1,j

δx ,

∂v

∂y

i,j

:= v i,j − v i,j−1

δy . (6)

Dabei ist α ein Parameter zwischen 0 und 1. Mit α = 0 erh¨ alt man f¨ ur die Differen- tialoperatoren eine Approximation 2. Ordnung, d.h. der Approximationsfehler hat die Genauigkeit O(δx ² ) bzw. O(δy ² ). Diese Approximation kann jedoch f¨ ur geringe Visko- sit¨ atswerte, oder wenn die Ableitungsterme ∂/∂x bzw. ∂/∂y mit wesentlich gr¨ oßeren Faktoren in das Problem eingehen als die Ableitungsterme ∂ ² /∂x ² und ∂ ² /∂y ² , zu Os- zillationen in der L¨ osung f¨ uhren. In solchen F¨ allen muss das sogenannte Donor–Cell–

Schema (α = 1) verwendet werden, das nur eine Approximation 1. Ordnung liefert. In der Praxis benutzt man eine Mischung aus beiden Verfahren mit α ∈ [0, 1]. Der Para- meter α sollte dabei etwas gr¨ oßer als der maximale Wert von |u δt/δx| und |v δt/δy| im Gitter gew¨ ahlt werden.

Bei der Diskretisierung der Impulsgleichungen (1) und (2) bez¨ uglich der Zeit werden die Terme auf der linken Seite zum Zeitpunkt t n+1 und die Terme auf der rechten Seite zum Zeitpunkt t n ausgewertet. Die Zeitableitung ∂u/∂t zur Zeit t n+1 wird durch den Diffe- renzenquotienten 1. Ordnung (u ⁽ⁿ⁺¹⁾ − u ⁽ⁿ⁾ )/δt ersetzt. Dies entspricht einem expliziten Zeitschritt–Verfahren mit Hilfe der Euler–Formel ³ .

Die Kontinuit¨ atsgleichung (3) wird zum Zeitpunkt t _n+1 ausgewertet.

5 Der Algorithmus

Das gesamte L¨ osungsverfahren l¨ aßt sich nun mit den folgenden Einzelschritten beschrei- ben.

5.1 Die Zeitschleife

In einer ¨ außeren Iterationsschleife wird beginnend beim Zeitpunkt t = 0 die Zeit solange um δt erh¨ oht, bis die Endzeit t _end erreicht ist. Im Zeitschritt n (n = 0, 1, . . .) werden die Differentialgleichungen wie oben beschrieben diskretisiert. Dabei seien die Werte zum Zeitpunkt t n bereits bekannt, und die Werte zum Zeitpunkt t n+1 sollen berechnet werden. In der kompakten Notation hat der gesamte Algorithmus die folgende Form (Transport Schritt)

F ⁽ⁿ⁾ − u ⁽ⁿ⁾

∂t = g − ∇ · (u ⁽ⁿ⁾ ⊗ u ⁽ⁿ⁾ ) + ν∆u ⁽ⁿ⁾ (7) (Projektions-Schritt) L¨ ose das Sattelpunkt Problem

u ⁽ⁿ⁺¹⁾ − F ⁽ⁿ⁾

∂t = −∇p ⁽ⁿ⁺¹⁾ (8)

∇ · u ⁽ⁿ⁺¹⁾ = 0 . (9)

Dies geschieht, indem man auf Gleichung (8) den Divergenzoperator anwendet und Glei- chung (9) ausnutzt. Dann erh¨ alt man die sogenannte Druck-Poisson Gleichung

∆p ⁽ⁿ⁺¹⁾ = 1

∂t ∇ · F ⁽ⁿ⁾ .

3

Es gibt auch implizite Verfahren, bei denen auf der rechten Seite auch Werte zum Zeitpunkt t

vorkommen. Diese erlauben wesentlich gr¨ oßere Zeitschritte. Die L¨ osung der entstehenden Gleichungssy-

steme ist aber meist wesentlich aufwendiger.

Verfahren der obigen Bauart werden in der Literatur als Splitting-Methoden bezeichnet.

Der Grund liegt in der getrennten (gesplittet) Behandlung der Impulsgleichung bzw.

der Kontinuit¨ atsgleichung. Die entkoppelte Behandlung beider Gleichungen hat enorme algorithmische Vorteile. Splitting Methoden sind deshalb die wohl effizientesten Metho- den f¨ ur die instation¨ aren, inkompressiblen Navier-Stokes Gleichungen. Ihr Prototyp ist (1968) von A.J. Chorin (unabh¨ anging davon auch durch R. Temam) angegeben worden, so daß man oft auch die Bezeichnung Chorinsche Projektionsmethode liest.

5.2 Die diskreten Impulsgleichungen

Die diskreten Impulsgleichungen werden so umgestellt, dass auf der linken Seite nur noch die Geschwindigkeit u ⁽ⁿ⁺¹⁾ _i,j bzw. v _i,j ⁽ⁿ⁺¹⁾ stehen. Dann erhalten die Gleichungen die Form

u ⁽ⁿ⁺¹⁾ _i,j = F _i,j ⁽ⁿ⁾ − δt

δx (p ⁽ⁿ⁺¹⁾ _i+1,j − p ⁽ⁿ⁺¹⁾ _i,j ) (10)

i = 1, . . . , imax − 1, j = 1, . . . , jmax;

v _i,j ⁽ⁿ⁺¹⁾ = G ⁽ⁿ⁾ _i,j − δt

δy (p ⁽ⁿ⁺¹⁾ _i,j+1 − p ⁽ⁿ⁺¹⁾ _i,j ) (11)

i = 1, . . . , imax, j = 1, . . . , jmax − 1.

Die Terme F _i,j ⁽ⁿ⁾ und G ⁽ⁿ⁾ _i,j beinhalten die in den diskreten Impulsgleichungen vorkom- menden Geschwindigkeiten zum Zeitpunkt n. Mit den diskretisierten Ausdr¨ ucken aus (4) und (5) sind dies:

F _i,j := u _i,j + δt 1 Re

∂ ² u

∂x ²

i,j

+ ∂ ² u

∂y ²

i,j

!

−

∂(u ² )

∂x

i,j

−

∂(uv)

∂y

i,j

+ g _x

! (12) i = 1, . . . , imax − 1, j = 1, . . . , jmax;

G _i,j := v _i,j + δt 1 Re

∂ ² v

∂x ²

i,j

+ ∂ ² v

∂y ²

i,j

!

−

∂(uv)

∂x

i,j

−

∂(v ² )

∂y

i,j

+ g _y

! (13) i = 1, . . . , imax, j = 1, . . . , jmax − 1.

5.3 Die Druckgleichung

Jetzt k¨ onnen wir die durch die rechten Seiten von (10) und (11) gegebenen Ausdr¨ ucke f¨ ur die Geschwindigkeiten u ⁽ⁿ⁺¹⁾ _i−1,j , u ⁽ⁿ⁺¹⁾ _i,j , v _i,j−1 ⁽ⁿ⁺¹⁾ und v ⁽ⁿ⁺¹⁾ _i,j in die diskrete Kontinuit¨ ats- gleichung der Zelle (i, j) einsetzen und erhalten eine Gleichung, die nur noch Druckwerte zum Zeitpunkt t n+1 und (bereits bekannte) Geschwindigkeiten zum Zeitpunkt t n enth¨ alt:

p ⁽ⁿ⁺¹⁾ _i+1,j − 2p ⁽ⁿ⁺¹⁾ _i,j + p ⁽ⁿ⁺¹⁾ _i−1,j

(δx) ² + p ⁽ⁿ⁺¹⁾ _i,j+1 − 2p ⁽ⁿ⁺¹⁾ _i,j + p ⁽ⁿ⁺¹⁾ _i,j−1

(δy) ² =

1 δt

F _i,j ⁽ⁿ⁾ − F _i−1,j ⁽ⁿ⁾

δx + G ⁽ⁿ⁾ _i,j − G ⁽ⁿ⁾ _i,j−1 δy

!

, (14) i = 1, . . . , imax, j = 1, . . . , jmax.

Dies ist die bekannte Form einer diskretisierten Poisson–Gleichung f¨ ur die Gr¨ oße p ⁽ⁿ⁺¹⁾

∂ ² p ⁽ⁿ⁺¹⁾

∂x ² + ∂ ² p ⁽ⁿ⁺¹⁾

∂y ² = rhs

auf dem Gebiet Ω mit einer beliebigen rechten Seite rhs. Zur eindeutigen L¨ osbarkeit

ben¨ otigen wir aber noch die Randwerte p _i,j (i = 0, imax + 1, j = 0, jmax + 1), F _i,j

(i = 0, imax) und G _i,j (j = 0, jmax), die wir aus den Impulsgleichungen am Rand gewinnen k¨ onnen (siehe unten).

Jetzt ist es m¨ oglich, die Druckgleichung (14) mit einem beliebigen Verfahren zur L¨ osung linearer Gleichungssysteme zu l¨ osen. Da direkte Verfahren wie die Gaußelimination bei sehr großen Problemen (hier imax · jmax Unbekannte) einen zu großen Rechenaufwand besitzen, kommen bei der numerischen L¨ osung partieller Differentialgleichungen gew¨ ohn- lich iterative Gleichungsl¨ oser zum Einsatz. Bei unserem Problem haben wir jeweils f¨ ur die L¨ osung der Gleichungssysteme eine recht gute N¨ aherung: den Druck p ⁽ⁿ⁾ aus dem alten Zeitschritt. Nur iterative Verfahren k¨ onnen das effizient ausnutzen.

Ein klassisches iteratives Verfahren ist das Gauß–Seidel–Verfahren, bei dem, ausgehend von einem Startwert, in jedem Zyklus sukzessive alle Zellen abgelaufen werden und in der Zelle (i, j) der Druck in dieser Zelle so ge¨ andert wird, dass die zugeh¨ orige Gleichung exakt erf¨ ullt wird.

Eine verbesserte Variante ist das SOR–Verfahren:

it = 1, . . . , itmax i = 1, . . . , imax

j = 1, . . . , jmax

p ^it+1 _i,j := (1 − ω) p ^it _i,j + (15)

ω 2( _(δx) ¹

+ _(δy) ¹

)

p ^it _i+1,j + p ^it+1 _i−1,j

(δx) ² + p ^it _i,j+1 + p ^it+1 _i,j−1

(δy) ² − rhs _i,j

!

rhs i,j ist die rechte Seite der Druckgleichung (14) f¨ ur die Zelle (i, j) und ω ist ein Pa- rameter (Relaxationsfaktor), der aus dem Intervall ]0, 2] gew¨ ahlt werden muss (h¨ aufig ω = 1.7). F¨ ur ω = 1 ergibt sich das Gauß–Seidel–Verfahren. Die Iteration wird abgebro- chen, wenn die maximale Anzahl von Iterationsschritten itmax erreicht ist oder wenn das Residuum

res :=





imax

X

i=1 jmax

X

j=1

p _i+1,j − 2p _i,j + p i−1,j

(δx) ² + p _i,j+1 − 2p _i,j + p i,j−1

(δy) ² − rhs _i,j 2

/(imax · jmax)





1/2

(16) eine vom Benutzer zu w¨ ahlende Toleranzgrenze ε unterschritten hat.

Als Startwert der Iteration zur Berechnung der Druckwerte p ⁽ⁿ⁺¹⁾ dienen jeweils die Druckwerte zum Zeitpunkt n.

Mit den so berechneten Druckwerten zum Zeitpunkt t _n+1 k¨ onnen dann auch die Ge- schwindigkeitswerte u und v zum Zeitpunkt t _n+1 gem¨ aß (10) und (11) berechnet werden.

5.4 Die Randwerte f¨ ur die diskreten Gleichungen bei Haftbedingungen Bei der Berechnung von F und G nach (12) und (13) wird f¨ ur i = 1, imax und j = 1, jmax auf u– und v–Werte zugegriffen, die auf dem Gebietsrand oder sogar außerhalb liegen k¨ onnen. Wir wollen uns hier zun¨ achst auf Haftbedingungen beschr¨ anken, bei denen die kontinuierlichen Geschwindigkeiten am Rand jeweils 0 sein sollen. Also setzen wir f¨ ur die Werte, die direkt auf dem Rand liegen

u _0,j = 0, u _imax,j = 0, j = 1, . . . , jmax v _i,0 = 0, v _i,jmax = 0, i = 1, . . . , imax. (17) An den 4 R¨ andern erhalten wir somit die weiteren Bedingungen:

v 0,j = −v _1,j , v imax+1,j = −v _imax,j , j = 1, . . . , jmax,

u _i,0 = −u _i,1 , u _i,jmax+1 = −u _i,jmax , i = 1, . . . , imax. (18)

i Rand Fluid

va vr v

Da weiterhin auf den senkrechten R¨ andern keine v–Werte und auf den waagrechten R¨ andern keine u–Werte liegen, wird hier der Randwert 0 durch eine Mittelung der Werte zu beiden Seiten des Randes erzielt:

v r := v a + v i

2 = 0 ⇒ v a = −v _i . Wie schon erw¨ ahnt, wird der Druck am Rand aus den diskreten Impulsgleichungen her- geleitet, und zwar durch Multiplikation mit dem jeweiligen Normalenvektor. Es ergibt sich insgesamt:

p _0,j = p _1,j , p _imax+1,j = p _imax,j , j = 1, . . . , jmax;

p i,0 = p i,1 , p i,jmax+1 = p i,jmax , i = 1, . . . , imax (19) und

F 0,j = u 0,j , F imax,j = u imax,j , j = 1, . . . , jmax,

G _i,0 = v _i,0 , G _i,jmax = v _i,jmax , i = 1, . . . , imax. (20) 5.5 Die Stabilit¨ atsbedingung

Um die Stabilit¨ at des numerischen Algorithmus zu gew¨ ahrleisten und keine Oszillatio- nen zu erzeugen, m¨ ussen schließlich die folgenden drei Stabilit¨ atsbedingungen an die Schrittweiten δx, δy und δt gestellt werden:

2

Re δt < (δx) ² (δy) ²

(δx) ² + (δy) ² , |u _max | δt < δx, |v _max | δt < δy. ⁴ (21)

|u _max | und |v _max | sind die maximalen Absolutwerte der vorkommenden Geschwindigkei- ten.

Basierend auf diesen Stabilit¨ atsbedingungen kann eine adaptive Zeitschrittweitensteue- rung verwendet werden. Dabei wird δt f¨ ur den n¨ achsten Zeitschritt so gew¨ ahlt, dass jede der drei Bedingungen erf¨ ullt ist:

δt := τ min Re 2

1 δx ² + 1

δy ² −1

, δx

|u _max | , δy

|v _max |

!

. (22)

Der Faktor τ ∈]0, 1] ist ein Sicherheitsfaktor.

5.6 Zusammenfassung

Abschließend sei der Algorithmus nochmals ¨ ubersichtlich dargestellt:

4

Die letzten beiden Bedingungen sind die sogenannten Courant–Friedrichs–Levi–(CFL)–Bedingungen.

Einlesen der Problemparameter Setze t := 0, n := 0

Belege u, v, p mit Anfangswerten Solange t < t end

W¨ ahle δt nach (22)

Setze die Randwerte f¨ ur u und v gem¨ aß (17),(18) Berechne F ⁽ⁿ⁾ und G ⁽ⁿ⁾ gem¨ aß (12),(13),(20)

Berechne die rechte Seite rhs der Druckgleichung (14) Setze it := 0

Solange it < itmax und res > ε

Setze die Randwerte f¨ ur den Druck gem¨ aß (19) F¨ uhre einen SOR-Zyklus gem¨ aß (15) durch

Berechne das Residuum res der Druckgleichung gem¨ aß (16) it := it + 1

Berechne u ⁽ⁿ⁺¹⁾ und v ⁽ⁿ⁺¹⁾ gem¨ aß (10),(11)

Gegebenenfalls Ausgabe der Werte u, v, p zur Visualisierung t := t + δt

n := n + 1

Ausgabe der Werte u, v, p zur Visualisierung

6 Die Problemgr¨ oßen und Datenstrukturen

Der oben beschriebene Algorithmus soll im Praktikum in der Programmiersprache Py- thon und C++ realisiert werden. Er ben¨ otigt die folgenden Gr¨ oßen, die, bis auf die Variablen t, it, delx und dely, am besten in einer Eingabedatei zur Verf¨ ugung gestellt werden. REAL steht dabei jeweils f¨ ur float in Python bzw. einen template parameter in C++, der wahlweise float oder double sein kann.

• Geometriegr¨ oßen:

REAL xlength Gebietsl¨ ange in x–Richtung REAL ylength Gebietsl¨ ange in y–Richtung

Das Berechnungsgebiet ist somit Ω = [0, xlength] × [0, ylength].

int imax Anzahl der inneren Zellen in x–Richtung int jmax Anzahl der inneren Zellen in y–Richtung REAL delx L¨ ange einer Zelle in x–Richtung δx REAL dely L¨ ange einer Zelle in y–Richtung δy

• Gr¨ oßen f¨ ur die Zeititeration:

REAL t aktuelle Zeit REAL t end Endzeit t _end REAL delt Zeitschrittweite δt

REAL tau Sicherheitsfaktor f¨ ur die Zeitschrittweitensteuerung τ

REAL del vec Zeitabstand, in dem Daten zur Visualisierung in eine Datei ge- schrieben werden sollen

• Parameter f¨ ur die Druckiteration:

int itermax Maximale Anzahl von Druck-Iterationen pro Zeitschritt int it Z¨ ahler f¨ ur die SOR–Iterationen

REAL res Norm des Residuums der Druckgleichung

REAL eps Genauigkeitskriterium ε f¨ ur die Druckiteration (res < eps) REAL omg Relaxationsfaktor ω f¨ ur die SOR-Iteration

REAL alpha Upwind-Differencing-Faktor α

• Problemabh¨ angige Gr¨ oßen:

REAL Re Reynoldszahl Re

REAL GX,GY ¨ außere Kr¨ afte g _x , g _y , z.B. Gravitation

REAL UI,VI,PI Anfangsbelegung der Geschwindigkeiten und des Drucks Weiterhin sollen die folgenden Felder der Dimension [0,imax+1]x[0,jmax+1] als Da- tenstrukturen verwendet werden:

• Datenfelder

Matrix<REAL> U Geschwindigkeit in x–Richtung Matrix<REAL> V Geschwindigkeit in y–Richtung Matrix<REAL> P Druck

Matrix<REAL> RHS Rechte Seite f¨ ur die Druckiteration

Matrix<REAL> F,G F, G

Exercise 32. (Driven Cavity)

a) Schreiben Sie unter Verwendung obiger Gr¨ oßen und Datenstrukturen die Prozeduren, welche die folgigen Funktionalit¨ aten bereitsstellen:

• Einlesen einer Parameterdatei zu welcher der Dateipfad ¨ ubergeben wird.

Zus¨ atzlich werden die Werte delx, dely aus imax und xlength bzw. jmax und ylength bestimmt. Eine Beispiel Eingabdedatei mit dem Namen driven cavity input.txt ist auf der Praktikumswebsite zu finden.

• Initialisieren der Felder U,V,P mit den konstanten Werten UI,VI und PI als Anfangswerte.

• Berechnen der Schrittweite delt f¨ ur den n¨ achsten Zeitschritt nach (22). War der aus der Parameterdatei eingelesene Wert f¨ ur tau negativ, so soll anstatt der berechneten Zeitschrittweite direkt der aus der Parameterdatei eingelesene Wert f¨ ur delt verwendet werden.

• Setzen der Randwerte f¨ ur die Felder U und V gem¨ aß der Formeln (17) und (18).

• Berechnen von F und G gem¨ aß (12) und (13). Dabei m¨ ussen am Rand die Formeln (20) angewendet werden.

• Berechnung der rechten Seite der Druckgleichung (14).

• SOR–Iteration f¨ ur die Druck–(Poisson–)Gleichung gem¨ aß (15). In jeder Iteration m¨ ussen zun¨ achst die Randwerte f¨ ur P gem¨ aß (19) gesetzt werden. Die Iteration wird abgebrochen, wenn die Norm des Residuums res die Toleranzgrenze eps unterschreitet oder die maximale Iterationsanzahl itermax erreicht ist. Nach dem Abbruch soll die Anzahl der ben¨ otigten Iterationen zur¨ uckgegeben werden und in res die aktuelle Gr¨ oße der Norm des Residuums stehen.

• Berechnen der neuen Geschwindigkeiten gem¨ aß (10) und (11).

• Ausgabe der berechneten Daten U,V,P in eine Datei. Die Ausgabe soll nicht nach jedem Zeitschritt erfolgen, sondern nur in den Zeitabst¨ anden del vec, wobei del vec aus der Eingabedatei eingelesen wird. ⁵

Bei jeder Ausgabe werden nacheinander die aktuellen Werte der Felder U,V und P jeweils zeilenweise geschrieben. Die Werte sollen jeweils im Mittelpunkt der Zellen liegen. Dazu m¨ ussen die Werte von U und V nach der Formel (a 1 + a 2 )/2 noch aus geeigneten Kantenwerten gemittelt werden.

Die Form der Ausgabedatei ist trivial. Man schreibt einfach die Werte folgender Variablen untereinander in eine Datei:

xlength ylength imax jmax

Feld U(x,y) Feld V(x,y) Feld P(x,y)

b) Als erstes Beispiel soll ein typisches Modellproblem der numerischen Str¨ omungsme- chanik, das sogenannte “Driven–Cavity–Problem” (zu deutsch “Nischenstr¨ omung“) simuliert werden. Es handelt sich dabei um einen mit Fl¨ ussigkeit gef¨ ullten Topf, ¨ uber den ein Band mit konstanter Geschwindigkeit gezogen wird. Dabei werden an allen 4 R¨ andern Haftbedingungen verwendet. Lediglich am oberen Rand wird die Geschwin- digkeit in x–Richtung u nicht auf 0 sondern auf 1 gesetzt, um das gezogene Band zu

5

Da der jeweilige Zeitschritt delt aus einer Zeitschrittweitensteuerung ermittelt wird, k¨ onnen die Werte f¨ ur del vec nicht a priori so bestimmt werden, dass die jeweils zugeh¨ orige

” Aktionszeit“ in der

Zeitschleife genau erreicht wird. In der Regel ist jedoch delt klein gegen del vec, so dass die jeweilige

Aktion beim ersten ¨ uberschreiten der zugeh¨ origen Aktionszeit ausgef¨ uhrt werden kann.

simulieren. Im Programm wird dies realisiert, indem die Randwerte am oberen Rand auf

u i,jmax+1 = 2.0 − u i,jmax , i = 1, . . . , imax gesetzt werden.

Als weitere Parameter sollen verwendet werden:

imax = 50 jmax = 50 xlength = 10 ylength = 10 delt = 0.02 t end = 2.0 tau = 0.5 del vec = 2.0 eps = 0.001 omg = 1.7 alpha = 0.5 itermax = 100 GX = 0.0 GY = 0.0 Re = 10

UI = 0.0 VI = 0.0 PI = 0.0

c) Implementiere obige Funktionalit¨ at in Python. Der Aufruf des Programms soll wie folgt aussehen:

python3 driven_cavity.py --input <parametersfile> --output <outputfile>

wobei <parametersfile> der Dateipfad zu einer Eingabedatei und <outputfile>

der Basis-Dateiname der Ausgabedateien sein soll. Die Ausgabedateien sollen einen Suffix erhalten, welcher sie durchnummeriert. Beispielsweise w¨ urde ein Aufruf

python3 driven_cavity.py --input param.in --output dc_output

dateien mit den den Namen dc output 001, dc output 002, dc output 002, ... er- zeugen.

Zum Parsen der Kommandozeilen Parameter kann das Packet argparse verwendet werden.

d) Implementiere ein Python programm welches die generierten Ausgabedateien einließt und mittels matplotlib das Vektorfeld der Geschwindigkeiten aus U und V als auch das Skalarfeld P visualisiert. Der Aufruf soll wie folgt aussehen

python3 visualize.py --input <inputfile>

wobei <inputfile> der Pfad zu einer der w¨ ahrend der Simulation generierten Aus- gabedateien ist.

e) Implementiere die gesamte obige Funktionalit¨ at in C++. Der Aufruf des Programms soll wie folgt aussehen:

driven_cavity.exe <parametersfile> <outputfile>

Achte auf eine Vern¨ unftige Struktur deines Programms in Klassen und Dateien. Ver-

wende alle bisher gelernten Paradigmen, wo dies sinnvoll ist. Das Kompilieren des

Programms soll mittels einer CMake Datei gesteuert werden.