HOCHSCHULE HANNOVER

HOCHSCHULE HANNOVER Name ...

Fakultät II Abt. M SS 2017 Matrikelnummer ...

Übungsklausur Experimentalphysik 2

1 2 3 4 SUM

/25 /30 /30 /25 /110

1. Auftrieb Ein Holzquader mit einer Höhe von 10 cm schwebt zwischen einer Wasser- und Öl-Schicht (siehe Bild rechts). Die Dichte von Öl ist

790 3

Öl kg m

  ^ , die Dichte von Wasser kann mit _W 1000kg m^3 angenommen werden.

a. Wie groß ist der Druckdifferenz p_S des Schweredrucks zwischen der oberen und unteren Fläche des Quaders?

b. Wie groß ist die Dichte _Hz des Holzquaders?

2. Harmonische Schwingungen

Das Diagramm zeigt das Oszillogramm eines harmonisch schwingenden Federpendels mit der schwingenden Masse von

B 14,3

m  g. Bei t0 beträgt die Auslenkung des Pendels 0, 43

x  m.

a. Bestimmen Sie die Eigenfrequenz f₀, die Federkonstante D, die Phasenverschiebung ₀ (Nullphasenwinkel) einer cosinus- förmigen Schwingungsfunktion, die maximale

Geschwindigkeit v_max und die maximale Beschleunigung a_max.

b. Berechnen Sie die momentane Geschwindigkeit zum Zeitpunkt t₁2, 72s.

Ein physikalisches Pendel besteht aus 2 gleich schweren Kugeln (Radius r), die auf einen halb so schweren Stab der Länge 0,9 m symmetrisch gesteckt sind, der durch die Schwerpunkte der Kugeln geht.

Das Pendel ist in D drehbar gelagert.

Angaben zur Geometrie: L1=0,3 m, L2=0,2 m, r=0,1 m.

a. Berechnen Sie die Schwingungsdauer T0 für freie ungedämpfte Schwingungen bei kleinen Winkelauslenkungen.

3. Gedämpfte Schwingungen (Beschleunigungssensor)

Bei einem Federschwinger sind die Masse m = 30 g, die Federkonstante 1,5 /

D N m und die Dämpfungskonstante b = 0,12 N*s/m bekannt.

a. Der Schwinger befindet sich im Gleichgewicht. Im Moment t=0 bekommt der Schwinger wegen der Wirkung einer konstante Kraft F die Beschleunigung a=0,5 m/s². Welche Elongation erreicht der Schwinger nachdem die Schwingungen infolge der Dämpfung abgeklungen sind?

b. Der Federschwinger befindet sich in Gleichgewicht und bekommt in Moment t=0 wegen eines Stoßes die Geschwindigkeit v0 = 10 mm/s. Berechnen Sie die Bewegung des Schwingers x(t). Untersuchen Sie zunächst, ob der Schwing-, Kriech– oder aperiodische Grenzfall vorliegt.

c. Wann wird in b) die maximale Auslenkung erreicht und wie groß ist diese?

FACHHOCHSCHULE HANNOVER Name ...

Fakultät II Abt. M SS 2015 Übungsklausur

Experimentalphysik 2

d. Der Schwinger bewegt sich wegen der Wirkung einer konstanten Kraft F, wie im a). Die Schwingungen sind abgeklungen. In einen Moment ist die äußeren Kraft F weg. Wie verändert sich die Bewegung des Schwingers? Beschreiben es qualitativ, ohne Lösen der mathematischen Gleichungen.

4. Erzwungene Schwingungen

Ein Auto, vereinfacht dargestellt als Masse-Feder-System (m = 800 kg, D 2 10⁵N m/ , zunächst ohne Dämpfung, fährt mit horizontaler und konstanter Geschwindigkeit 36 km/h über eine Straße mit vielen Bodenwellen im jeweiligen Abstand von 5 m und Gesamthöhe 20 cm, die sinusförmig modelliert werden können.

a. Mit welcher Frequenz wird der Stoßdämpfer angeregt?

b. Welche Amplitude stellt sich beim Befahren ein?

c. Welche kritische Reisegeschwindigkeit vkrit sollte vermieden werden und warum?

d. Nun mit Dämpfung: Wie müsste die Abklingkonstante   gewählt werden, damit bei der kritischen Reisegeschwindigkeit aus (c) die Federamplitude maximal 10% größer als die Amplitude der äußeren Anregung wird?

Hilfsmittel: je eine der freigegebenen Physik1 und Physik 2-Formelsammlungen, Taschenrechner Bearbeitungszeit: 90 Minuten

Bearbeitungshinweise: Der Lösungsweg muss erkennbar und nachvollziehbar sein.

Die Aufgaben sind soweit wie möglich buchstabenmäßig durchzurechnen. Geben Sie die Ergebnisse der Zahlenrechnung mit sinnvoller Ziffernzahl an. Für die Erdbeschleunigung kann g = 10 m/s² verwendet werden.

Lösungen:

Lösungen zur Aufgabe 1:

a. Tiefendruck Oberseite: p h( 1, 5cm)_Öl g h (1)

3 2

( 1,5 ) 790 10 0, 015 118,5

p h cm  kg m^  ms^  m Pa (2) Tiefendruck Unterseite: p h⁽ ^{11, 5}cm⁾



Öl^0,10mW^{0, 015}m



g (3)

 

( 11, 5 ) 790 0,10 1000 0, 015 10

p h cm      Pa (4)

( 11,5 ) 940

p h cm  Pa (5)

Druckdifferenz:  pS



^{940 118, 5}



Pa^{821, 5}Pa mit g 10m s^2 (6)



922,14 116, 25



805,9

p Pa Pa

    mit g9,81m s^2 (7)

b. Schwebebedingung: F_AF_g (8)



ÖlVÖl WVW



 g HqVHqg (9)



ÖlVÖlWVW



HqVHq (10)



Öl^{0, 085}mW^{0, 015}



Hq^0,10 (11)

Ergebnis: ^{790 0, 085} 1000 0, 015 ^{3 3}

821,5

Hq 0,10

m kg m kg m

  ^{   }  ^ (12)

Lösungen zur Aufgabe 2 Teil 1:

a. Eigenfrequenz: ₀ ¹

0

1 1

1, 45 0, 69

f s

T s

    (1)

Eigenkreisfrequenz: ₀ 2 f₀ 9,11s^1 (2)

Federkonstante:

2

2 2

0 2

0

4 1,186

B B

D m m kg s

T

  ^

     (3)

Funktion der harmonischen Schwingung:

Entweder: ^{x t}

 

^{ x0 sin}



^{0 t 0,sin}



⁽⁴⁾

oder: x t

 

 x0 cos



0 t 0,cos



(5)

Aus Diagramm folgt: x₀ 0,82cm (6)

Anfangsbedingung Gl. (4): x t



0



0, 43cm x0 sin



0 0 0,sin



 x0 sin



0,sin



(7) Nullphasenwinkel: _0,sin arcsin ^{0, 43} 31, 627 0, 5519

  ^0,82^   (8) Nullphasenwinkel: _0,cos arccos ^{0, 43} 58, 373 1, 019

  ^0,82^   (9) Geschwindigkeitsfunktion: v t

 

x t( ) x0 0cos



0 t 0,sin



(10) Maximale Geschwindigkeit: _{max 0 0} 0, 0082 ² 0, 07467 ¹

0, 69

v x m ms

s

  ^

     (11)

Beschleunigungsfunktion: a t

 

x t( )  x0 0²sin



0 t 0,sin



(12) Maximale Beschleunigung:

2

2 2

max 0 0 2 2

0, 0082 4 0, 6799

0, 69

a x m ms

s

  ^

     (13)

b. Amplitudenfunktion: x t

 

 x0 sin



0 t 0,sin



(10) Geschwindigkeitsfunktion: ^{v t}

 

^{x t( ) x0 0cos}



^{0 t 0,sin}



⁽¹¹⁾

Zeitpunkt t₁2, 72s: v t

 

1 x t( )1  x0 0cos



0 t1 0,sin



(12)

 

1

2 2

0, 0082 cos 2, 72 0, 5519

0, 69 0, 69

v t m s

s s

   

      

  (13)

 

1 0, 07336 ¹

v t  m s^ (14)

Alternativ: x t

 

 x0 cos



0 t 0,cos



(15) Geschwindigkeitsfunktion: v t

 

x t( )  x0 0sin



0 t 0,cos



(16)

 

1

2 2

0, 0082 sin 2, 72 1, 019

0, 69 0, 69

v t m s

s s

   

       

  (17)

 

1 0, 07336 ¹

v t  m s^ (18)

Lösungen zur Aufgabe 2 Teil 2:

Geometrie der Anordnung: Für die Länge des Stabendes L₃ , die oben und unten aus der Kugel herausragt, gilt: L_Stab     2 L₃ 2 r L₁ L₂ (1)

 

3 0, 5 _Stab 2 1 2

L   L    r L L (2)

 

3 0, 5 0, 9 2 0,1 0, 2 0, 3 0,1

L       m m (3)

Abstand Drehpunkt – Schwerpunkt h:

 

3 2 0, 45 0,1 0,1 0, 2 0, 05 2

Lstab

h   L r L     m m (4)

alternativ: _{3 3} 0, 45 0,1 0,1 0,3 0, 05

2 Lstab

h   L r L       m (5) Massenträgheitsmoment der Massen oberhalb des Drehpunktes:

, ,

o Stab o Kugel o

J J J (6)

Stab oben:

2 ,

1 2

3 2

Stab

Stab

Stab o Stab

Stab

L h

J m L h

L

  

   

      

 

(7)

2 ,

1 2

3 2 2

Stab

Kugel Stab

Stab o

Stab

L h

m L

J h

L

  

   

      

 

(8)

 

^{2 2}

,

1 0, 45 0, 05

0, 45 0, 05

3 2 0, 9

Kugel Stab o

J m   m

    

  (9)

 

^{2 2}

,

4 0, 4

6 9

Kugel Stab o

J m  m

  

  (10)

2 2

,

8 0, 01185

Stab o 675 Kugel Kugel

J  m m  m m (11)

Kugel oben: _, ^{2 2 2}₂ ²0,1² 0, 2^{2 2}

5 5

Kugel o Kugel Kugel Kugel

J  m r m L m   m (12)

2 2 ,

11 0, 044

Kugel o 250 Kugel Kugel

J  m m  m m (13)

Trägheitsmoment oben: J_o J_{Stab o,} J_{Kugel o,} (14)

2 2

8 10 11 27 377

6750 6750

o Kugel Kugel

J     m m  m m (15) 0, 05585 2

o Kugel

J  m m (16)

Massenträgheitsmoment der Massen unterhalb des Drehpunktes:

, ,

u Stab u Kugel u

J J J (17)

Stab unten:

2 ,

1 2

3 2 2

Stab

Kugel Stab

Stab u

Stab

L h

m L

J h

L

  

   

      

 

(18)

 

^{2 2}

,

1 0, 45 0, 05

0, 45 0, 05

3 2 0, 9

Kugel Stab u

J  m     m

  (19)

 

^{2 2}

,

5 0, 5

6 9

Kugel Stab u

J m  m

  

  (20)

2 2

,

5 0, 02315

Stab u 216 Kugel Kugel

J  m m  m m (21)

Kugel unten: _, ^{2 2 2}₁ ² 0,1² 0, 3^{2 2}

5 5

Kugel u Kugel Kugel Kugel

J  m r m L m    m

  (22)

2 2

,

47 0, 094

Kugel u 500 Kugel Kugel

J  m m  m m (23)

2

, ,

5 47

216 500

u Stab u Kugel u Kugel

J J J   m m (24)

Trägheitsmoment unten: _{, ,} 3163 ^{2 2}

0,117148 27000

u Stab u Kugel u Kugel

J J J  m m  kg m (25)

Massenträgheitsmoment: ^{377 3163 2}

6750 27000

ges o u Kugel

J J J   m m (26)

2 2

1508 3163 4671

27000 27000

ges Kugel Kugel

J   m m  m m (27)

173 2

ges 1000 Kugel

J  m m (28)

0,173 2

ges Kugel

J  m m (29)

Gesamtmasse des Pendels: 1

2 2,5

ges Kugel 2 Kugel Kugel

m  m  m  m (30)

Eigenkreisfrequenz des physikalischen Pendels:

0 2

2, 5 0,173

ges Kugel

ges Kugel

m g h m g h

J m m

  ^{ }  ^{ }

 (31)

2

1

0 2

2,5 10 0, 05

2, 688 0,173

ms m

m s

  ^{  }  ^

 (32)

Schwingungsdauer: _{0 1}

0

2 2

2,175 2,888

T s

s

 

 ^

   (33)

Lösungen zur Aufgabe 3:

a. Masse des Schwingers: m0, 03kg (1)

Federkonstante: D1, 5N m^1 (2)

Dämpfungskonstante: b0,12N s m^1 (3)

Eigenkreisfrequenz:

2

1 0

1, 5 7, 0711

0, 03

D kg s

m kg s

   ^  ^ (4)

Abklingkonstante:

2 1

0,12 1

2 2 0, 03 2 b kg m s s m

m kg s

    ^{ }  ^

 (5)

Es gilt: a t



0



0, 5m s^2 a00

Kraft bei t 0 ^{F t}



^0



^{ m a t}



^0



^{0, 03kg0, 5ms2 0, 015N (6)}

Elongation des Schwingers:

 

00 1

0 0, 015

0, 01 1 1, 5

F t N

x m cm

D N m^

     (7)

--- Zua. Untersuchung zum Schwingverhalten.

(war nicht gefordert und dient nur der Erläuterung):

Es ist 2, 0s^1     ₀ 7, 0711s^1 (8)

also handelt es sich um einen Schwingfall.

Zum Zeitpunkt t 0 ist die Amplitude ^{x t}



^0



^{0 und für t  ist} x t



  



x00. Es gilt ferner, das ^{x t}



^0



^{0 und} x t



0



a00 0, 5m s^2.

Die Amplitudenfunktion kann wie folgt ausgedrückt werden:

Amplitudenfunktion: ( ) 00 1 ^t sin



_e



cos



_e



e

x t x e ^   t  t



    

       

 

  (9)

mit: x₀₀ 0, 01m (10)

Eigenkreisfrequenz: _e  ₀²²  7, 0711²2, 0² s^1 6, 78236s^1 (11) Geschwindigkeitsfunktion:

   

00 ^{t 02} sin



_e



e

v t x t x e ^   t



        (12)

Beschleunigungsfunktion:

   

00 ^{t 02} sin



_e



e

a t v t d x e t

dt

  



   

      

  (13)

 

^{00 02}

  

^{t sin}

 

^{e e t cos}

 

^e



e

a t x   e ^  t  e ^  t

 ^{   }

       (14)

 

00 ^{02 t}



_e cos



_e



sin



_e

 

e

a t x  e ^   t   t

 ^{ }

        (15)

Probe:



0



00 ⁰² 1



_e cos



_e 0



sin



_e 0

 

e

a t x     

         (16)



0



00 0² 0, 01 7, 0711^{2 2} 0, 5 ²

a t x   m s^  m s^ (17)

Beschleunigungswert entspricht der Aufgabenstellung.

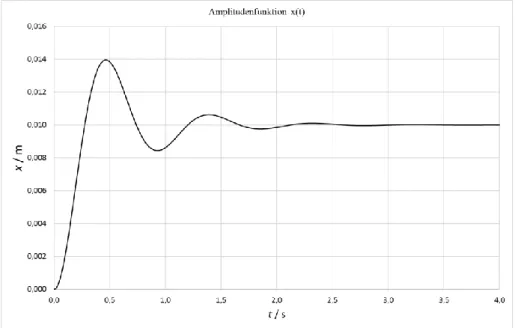
Abb. 1: Amplitudenfunktion zu Aufgabe 3a)

Abb. 2: Geschwindigkeitsfunktion zu Aufgabe 3a)

Abb. 3: Beschleunigungsfunktion zu Aufgabe 3a)

3b. Zum Zeitpunkt t 0 erhält der Schwinger durch einen Stoß die Anfangsgeschwindigkeit:



0



0 10 ¹ 0, 01 ¹

v t  v  mm s^  ms^ (18)

Es gilt: 2, 0s^1     ₀ 7, 0711s^1 (19)

also handelt es sich um einen Schwingfall.

Amplitudenfunktion:

  

⁰



^{t sin}



e



e

x t x t e ^  t

 ^{ }

     (20)

(laut Formelsammlung Schrewe)

Hinweis: Herleitung der Lösung aus der allgemeinen Lösung der DGL:

Allgemeine Lösung: x t

 

e^{ ß t}



a^sin



e  t



b ^cos



et

 

mit a b,  (21) und v t

 

e^{ t}



aeb

   

^cos et  bea

  

^sin et  (22) Anfangsbedingungen: ^{x t}



^0



^{0 und} v t



0



v0 0, 01ms^1 (23)

Es folgt: ^{x t}



^0



^{ 0 1}



^{a  0 b 1}



⁽²⁴⁾

und somit: b0 (25)

ferner gilt: v t



0



v0  1 



a_eb



 1



b_ea



0 (26

Es folgt: v₀ a_eb (27)

Da b0 folgt: ⁰

e

a v

 (28)

Amplitudenfunktion:

 

^{0 ß t sin}



e



e

x t v e  t

 ^{ }

    (29)

Geschwindigkeitsfunktion:

 

0 ^t cos

 

_e sin

 

_e

e

v t v e ^  t   t



   

     

  (30)

c) Beim Maximum der Auslenkung hat die Geschwindigkeitsfunktion eine Nullstelle:

Bestimmung der Nullstelle:

 

_m 0 0 ^tm cos



_{e m}



sin



_{e m}



e

v t v e ^  t   t



   

      

  (31)

Es folgt: ^cos



e m



^sin



e m



e

t  t

 

  (32)

 

tan _{e m}t ^e

 (33)

Lösung: _m ¹ arctan ^e

e

t 

 

 

  

  (34)

Ergebnis: ¹ ₁arctan^{6, 78236} 0,18932

6, 78236 2, 0

tm s

s^

  (35)

--- Hinweis: Die Lage des Maximums ist nicht identisch mit dem Wert für ein (1/4) der

Periodendauer T_e.

Es gilt: ² ₁ 0, 23160

4 4 2 6, 78236

e e

T s

s

 

 ^

  

 (36)

Relative Abweichung: ⁴ 0,18932 0, 23160

22, 3%

0,18932

m e

m

t T t

 

   (37)

---

3c) Amplitude bei tt_m

 

m ^{0 ß tm sin}



e m



e

x t v e  t



      (38)

 

¹ 2,0 0,18923



1



1

0, 01

sin 6, 78236 0,18932 6, 78236

m

x t m s e s s

s

   

     (39)

Amplitudenmaximum: x t

 

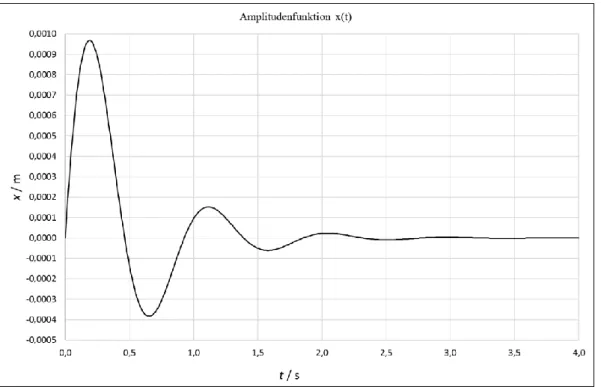
m ^{9, 686 10} ^4m^0,9686mm (40)

Amplitudenfunktion für Aufgabe 3b) und 3c)

Abb. 4: Amplitudenfunktion zu Aufgabe 3b) und 3c)

3d) Zur Darstellung der Amplitudenfunktion nach Aufgabenstellung d) kann man die Amplitudenfunktion von Aufgabe 3a) erweitern.

Die Amplitudenfunktion von Aufgabe 3a soll zum Beispiel für 0 t 4s gelten.

   

( ) 00 1 ^t sin _e cos _e

e

x t x e ^   t  t



    

       

 

  (41)

für 0 t 4s

Ab t₁4s wirkt keine äußere Kraft mehr. Da der Einschwingvorgang aus Aufgabe 3a) abgeklungen ist, beträgt die Amplitude bei x t



4s



x00 0, 01m.

Für 4s  t lautet die Amplitudenfunktion:

 ¹

       

00 1 1

( ) ^{t t} sin _e cos _e

e

x t x e ^   t t  t t



    

       

  für 4s  t (42)

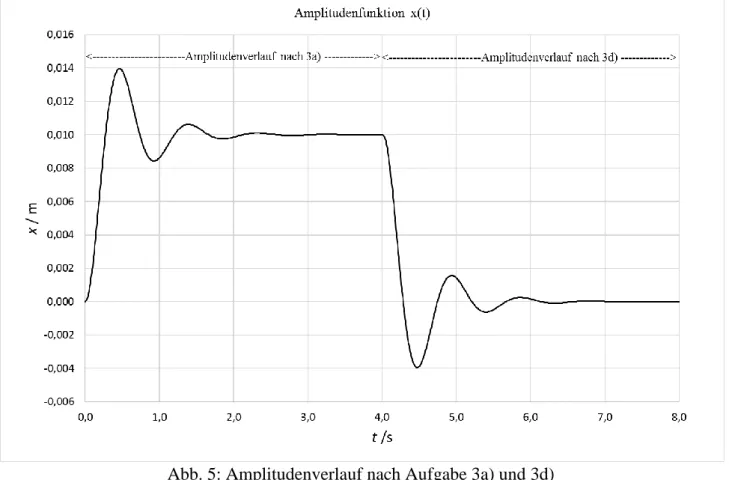
Mit t₁4, 0s.

Abb. 5: Amplitudenverlauf nach Aufgabe 3a) und 3d)

--- Lösung der Aufgabe 4

Masse: m_PKW 800kg (1)

Federkonstante: D_PKW  2 10⁵N m/ (2)

Geschwindigkeit: v₀ 36km h^110m s^1 (3)

Periode der Bodenwellen: S_BW 5m (4)

4a) Periode der Schwingung, die beim Befahren der Bodenwellen mit v₀ entsteht.

1 0

5 0, 5

10

BW a

S m

T s

v m s^

   (5)

Anregungskreisfrequenz durch die Bodenwellen:

2 2 1

12, 56

a 0, 5

a

T s s

 

    ^ (6)

Anregungskreisfrequenz durch die Bodenwellen:

1 1 1

0, 5 2, 0

a a

T s s

    ^ (7)

Hinweis: Hier wird für die Frequenz _a verwendet, weil f_a für die Beschleunigungsamplitude der erzwungenen Schwingung benötigt wird.

4b) Die Höhe der Bodenwellen beträgt 0,2 m (Differenz von maximaler und minimaler Amplitude). Die Amplitude der Anregungsschwingung beträgt: x₀₀ 0,1m.

Für die Amplitudenüberhöhung gilt (siehe Vorlesung):

 

   

  ^{ }

2

0 0 0 0 0

2 2

2 2

0 0

2 0 0

, , , ,

0, ,

2

a a

a a

a a

x x

x f

      

     



 

  

(8) Da das Auto zunächst ohne Dämpfung betrachtet werden soll, ist  0.

Gl. (8) vereinfacht sich zu:

 

     

2 2

0 0 0 0

2 2

2 2 2

0 0 0

0

, , 0

0, ,

a

a a

a

x x

    

      

  

  

(9) Aus Gl. (1) und (2) ergibt sich die Eigenkreisfrequenz der ungedämpften Schwingung:

5 2 1

1 0

2 10 15,811

800

PKW PKW

D kg m s m

m kg s

   ^{  }  ^ (10)

Amplitudenüberhöhung:

 

     

2 2

0 0 0

2 2 2 2

0 0 0

, , 0 15,811

2, 710

0, , 15,811 12,56

a

a a

x x

   

    

   

   (11)

Amplitude: ^x0



^{a 12, 56s1,0 15,811s1, 0}



^{2, 710 0,1 m0, 271m (12)}

4c) Eine kritische Reisegeschwindigkeit ist gegeben, wenn:

1 0 15,811

a s

   ^ (13)

Reisegeschwindigkeit:

1

1 1

0

5 15,811

12, 58 45, 3

2 2

BW BW a

a

S S m s

v ms kmh

T



 

  

 

     (14)

4d) Die Federamplitude ist dann 10% größer als die Amplitude der äußeren Anregung, wenn der Wert der Amplitudenüberhöhung gleich 1,1 ist.

Die Reisegeschwindigkeit soll gleich der kritischen Geschwindigkeit sein, also

1 0 15,811

a s

   ^ (15)

Amplitudenüberhöhung:

 

    ^{ }

2 2

0 0 0 0 0

2 2

2 2

0 0

0 0

, ,

0, , 2 2

a

a a

a

x x

     

       

  

  

(16)

Einsetzen von Gl. (15)

 

 

2 2

0 0 0 0 0 0

0 0 0

, ,

0, , 2 2 2 1,1

a

a a

x x

      

       

    

 (17)

Abklingkonstante:

1 0 15,811 1

7,1868 2 1,1 2, 2

s s

    ^  ^

 (18)

Schrewe, 14.06.2017