Kapitel 5

Hochschule Karlsruhe w University of Applied Sciences w Fakultät für Informatik

Prof. Dr. Dirk W. Hoffmann

Kapitel 5

!

Standardschaltnetze

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Inhalt und Lernziele

§ Inhalt

§ Vorstellung der wichtigsten Standardelemente

§ Nur kombinatorische Logik, kein Gedächtnis

§ Multiplexer

§ Demultiplexer

§ PALs, PLAs

§ Halbaddierer, Volladdierer

§ Carry-Ripple-Addierer

§ Carry-Look-Ahead-Addierer

§ ALU

§ Lernziele

§ Kenntnis über Aufbau und Funktion der Schaltelemente

2

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Multiplexer

3

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6:Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂ ^s₁^s₀^x₁)_(s₂ ^s₁ ^s₀ ^x₂) _ (s₂ ^s₁^s₀^x₃)_(s₂ ^s₁ ^s₀ ^x₄) _ (s₂ ^s₁^s₀^x₅)_(s₂ ^s₁ ^s₀ ^x₆) _ (s₂ ^s₁^s₀^x₇)_(s₂ ^s₁ ^s₀ ^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6: Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂^s₁^s₀^x₁)_(s₂^s₁ ^s₀^x₂) _ (s₂^s₁^s₀^x₃)_(s₂^s₁ ^s₀^x₄) _ (s₂^s₁^s₀^x₅)_(s₂^s₁ ^s₀^x₆) _ (s₂^s₁^s₀^x₇)_(s₂^s₁ ^s₀^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6: Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂^s₁^s₀ ^x₁)_(s₂^s₁^s₀ ^x₂) _ (s₂^s₁^s₀ ^x₃)_(s₂^s₁^s₀ ^x₄) _ (s₂^s₁^s₀ ^x₅)_(s₂^s₁^s₀ ^x₆) _ (s₂^s₁^s₀ ^x₇)_(s₂^s₁^s₀ ^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6:Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂^s₁^s₀ ^x₁)_(s₂ ^s₁^s₀ ^x₂) _ (s₂^s₁^s₀ ^x₃)_(s₂ ^s₁^s₀ ^x₄) _ (s₂^s₁^s₀ ^x₅)_(s₂ ^s₁^s₀ ^x₆) _ (s₂^s₁^s₀ ^x₇)_(s₂ ^s₁^s₀ ^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Multiplexer-Implementierung

4

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6: Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂^s₁^s₀ ^x₁)_(s₂^s₁^s₀ ^x₂) _ (s₂^s₁^s₀ ^x₃)_(s₂^s₁^s₀ ^x₄) _ (s₂^s₁^s₀ ^x₅)_(s₂^s₁^s₀ ^x₆) _ (s₂^s₁^s₀ ^x₇)_(s₂^s₁^s₀ ^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

Abbildung 7.6:Realisierung eines 1-aus-8- Multiplexers mit Hilfe der elementaren Lo- gikgatter

208 7 Standardschaltnetze

s₀ x₁

x₂

2:1

MUX y

s₀ s₁ x₁

x₃ x₂

x₄ 4:1

MUX y

s₂ s₀ x₁

x₃ x₅ x₇ x₂ x₄ x₆ x₈

8:1

MUX y

s₁

s₀ y

0 x₁

1 x₂

s₁ s₀ y

0 0 x₁

0 1 x₂

1 0 x₃

1 1 x₄

s₂ s₁ s₀ y s₂ s₁ s₀ y

0 0 0 x₁ 1 0 0 x₅

0 0 1 x₂ 1 0 1 x₆

0 1 0 x₃ 1 1 0 x₇

0 1 1 x₄ 1 1 1 x₈

Abbildung 7.5: Multiplexer-Bausteine verschiedener Größen

gang y durch. Alle anderen Eingänge werden durch den Multiplexer faktisch vom Rest der Schaltung abgetrennt, so dass die dort anliegen- den Signalwerte für den Ausgangswert keine Rolle spielen. Da mit m Steuerleitungen 2^m verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Eingänge eines Multiplexers in aller Regel einer Zweierpotenz. Abbildung 7.5 fasst die Wahrheitstabellen und Schaltsymbole von Multiplexern verschiedener Größe zusammen.

An dieser Stelle wollen wir uns der Frage zuwenden, wie sich ein Multiplexer-Baustein mit Hilfe der elementaren Logikgatter implemen- tieren lässt. Hierzu überführen wir die Wahrheitstabelle des 1-aus-8- Multiplexers in einen booleschen Ausdruck und erhalten das folgende Ergebnis:

y = (s₂^s₁^s₀ ^x₁)_(s₂ ^s₁^s₀ ^x₂) _ (s₂^s₁^s₀ ^x₃)_(s₂ ^s₁^s₀ ^x₄) _ (s₂^s₁^s₀ ^x₅)_(s₂ ^s₁^s₀ ^x₆) _ (s₂^s₁^s₀ ^x₇)_(s₂ ^s₁^s₀ ^x₈)

Das hieraus resultierende Schaltnetz ist in Abbildung 7.6 dargestellt.

Wie das Strukturbild bereits vermuten lässt, ist der Flächenbedarf großer Multiplexer-Bausteine nicht unerheblich. Implementieren wir die Schaltung, wie hier gezeigt, als zweistufiges Schaltnetz, so benö- tigen wir zur Umsetzung eines 1-aus-n-Multiplexers n UND-Gatter mit jeweils log₂n+1 Eingängen. Gehen wir davon aus, dass die Größe ei- nes UND-Gatters proportional mit der Anzahl seiner Eingänge steigt,

x₁

s₂ s₁ s₀ x₂

x₃ x₄ x₅ x₆ x₇ x₈

≥1

y

&

&

&

&

&

&

&

&

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Multiplexer-Anwendungen

§ Steuerung des Datenflusses

5

Analogie: Schienenverkehr
 Multiplexer entspricht 


der Weichensteuerung Hier steuert der Multiplexer,


ob das Ergebnis des Addierers oder des Multiplizierers

weiterverwendet werden soll.

∑

∏ ?

Addierer

Multiplizierer

s₀ x₁

x₂

Abbildung 7.2:Ein einfaches Rechenwerk.

In Abhängigkeit der Steuerleitung s₀ wer- den die Operanden x₁ und x₂ entweder ad- diert (s₀ = 0) oder multipliziert (s₀ = 1).

x₁ x₂

s₀

y

Abbildung 7.3: Schienenanalogon. Das Verhalten eines Multiplexers ist dem einer Schienenweiche vergleichbar. In Abhängig- keit des Stellsignals wird genau einer der Eingänge mit dem Ausgang verbunden.

∑

∏

y Addierer

Multiplizierer

s₀ x₁

x₂

2:1 MUX

Abbildung 7.4:Mit Hilfe von Multiplexern werden Datenströme kanalisiert. In Abhän- gigkeit der Steuerleitung wird entweder das obere Eingangssignal (s₀ = 0) oder das un- tere Eingangssignal (s₀ = 1) auf den Aus- gang durchgeschaltet.

7.2 Multiplexer und Demultiplexer 207

Multiplexer

Multiplexer kommen immer dann zum Einsatz, wenn eine Signalleitung mit einem Wert beschaltet werden soll, der potenziell aus mehreren ver- schiedenen Quellen stammen kann. In anderen Worten: Ein Multiplexer führt Datenpfade gezielt zusammen.

Als Beispiel betrachten wir die in Abbildung 7.2 skizzierte Schaltung.

Das dargestellte Rechenwerk nimmt zwei Zweierkomplementzahlen x

und x

entgegen und berechnet in Abhängigkeit der Steuerleitung s

entweder die Summe oder das Produkt der beiden Operanden. Zu die- sem Zweck hält die Schaltung intern sowohl eine Addier- als auch eine Multipliziereinheit vor, die durch das Auftrennen der Eingangsleitun- gen vollständig parallel arbeiten. In anderen Worten: Zu jedem Zeit- punkt stehen intern sowohl die Summe als auch das Produkt der Ope- randen zur Verfügung.

Damit an den ausgehenden Signalleitungen der korrekte Wert ausge- geben wird, muss das Rechenwerk in Abhängigkeit der Steuerleitung s

eines der beiden internen Ergebnisse auswählen und nach außen lei- ten. Anders als bei der eingangsseitigen Verzweigung können wir die Datenpfade jedoch nicht einfach physikalisch miteinander verbinden.

Stattdessen benötigen wir eine Schaltkomponente, die in der Lage ist, mehrere Datenquellen als Eingabe entgegenzunehmen und eine davon in Abhängigkeit der Steuersignale auf den Ausgang durchzuschalten.

Genau dies ist die Aufgabe eines Multiplexers. Bildlich gesprochen entspricht das Verhalten eines Multiplexers, wie in Abbildung 7.3 ge- zeigt, exakt dem Funktionsprinzip einer Zugweiche. In Abhängigkeit des Stellsignals wird genau eines der beiden ankommenden Schienen- segmente mit dem nachfolgenden Schienenstrang verbunden.

Abbildung 7.4 zeigt, wie sich die Implementierung des oben skizzier- ten Rechenwerks mit Hilfe eines 1-aus-2-Multiplexers vervollständigen lässt. Ist s

gleich 0, so wird der Ausgang y mit dem oberen Eingang des Multiplexers und damit mit der Summe aus x

und x

beschrieben.

Ist s

gleich 1, so wird der untere Eingang und damit das Produkt aus x

und x

durchgeschaltet.

Neben dem hier eingesetzten 1-aus-2-Multiplexer stehen in der Praxis auch deutlich größere Varianten zur Verfügung. Im allgemeinen Fall verfügt ein 1-aus-n-Multiplexer (n:1 MUX) über die Eingangsleitungen x

bis x

, die Steuerleitungen s

bis s

und eine einzige Ausgangslei- tung y. In Abhängigkeit der Wertebelegung von s

bis s

schaltet der Multiplexer genau eine der Eingangsleitungen x

bis x

auf den Aus-

∑

∏ ?

Addierer

Multiplizierer

s₀ x₁

x₂

Abbildung 7.2: Ein einfaches Rechenwerk.

In Abhängigkeit der Steuerleitung s₀ wer- den die Operanden x₁ und x₂ entweder ad- diert (s₀ = 0) oder multipliziert (s₀ = 1).

x₁ x₂

s₀

y

Abbildung 7.3: Schienenanalogon. Das Verhalten eines Multiplexers ist dem einer Schienenweiche vergleichbar. In Abhängig- keit des Stellsignals wird genau einer der Eingänge mit dem Ausgang verbunden.

∑

∏

y Addierer

Multiplizierer

s₀ x₁

x₂

2:1 MUX

Abbildung 7.4: Mit Hilfe von Multiplexern werden Datenströme kanalisiert. In Abhän- gigkeit der Steuerleitung wird entweder das obere Eingangssignal (s₀ = 0) oder das un- tere Eingangssignal (s₀ = 1) auf den Aus- gang durchgeschaltet.

7.2 Multiplexer und Demultiplexer 207

Multiplexer

Multiplexer kommen immer dann zum Einsatz, wenn eine Signalleitung mit einem Wert beschaltet werden soll, der potenziell aus mehreren ver- schiedenen Quellen stammen kann. In anderen Worten: Ein Multiplexer führt Datenpfade gezielt zusammen.

Als Beispiel betrachten wir die in Abbildung 7.2 skizzierte Schaltung.

Das dargestellte Rechenwerk nimmt zwei Zweierkomplementzahlen x

und x

entgegen und berechnet in Abhängigkeit der Steuerleitung s

entweder die Summe oder das Produkt der beiden Operanden. Zu die- sem Zweck hält die Schaltung intern sowohl eine Addier- als auch eine Multipliziereinheit vor, die durch das Auftrennen der Eingangsleitun- gen vollständig parallel arbeiten. In anderen Worten: Zu jedem Zeit- punkt stehen intern sowohl die Summe als auch das Produkt der Ope- randen zur Verfügung.

Damit an den ausgehenden Signalleitungen der korrekte Wert ausge- geben wird, muss das Rechenwerk in Abhängigkeit der Steuerleitung s

eines der beiden internen Ergebnisse auswählen und nach außen lei- ten. Anders als bei der eingangsseitigen Verzweigung können wir die Datenpfade jedoch nicht einfach physikalisch miteinander verbinden.

Stattdessen benötigen wir eine Schaltkomponente, die in der Lage ist, mehrere Datenquellen als Eingabe entgegenzunehmen und eine davon in Abhängigkeit der Steuersignale auf den Ausgang durchzuschalten.

Genau dies ist die Aufgabe eines Multiplexers. Bildlich gesprochen entspricht das Verhalten eines Multiplexers, wie in Abbildung 7.3 ge- zeigt, exakt dem Funktionsprinzip einer Zugweiche. In Abhängigkeit des Stellsignals wird genau eines der beiden ankommenden Schienen- segmente mit dem nachfolgenden Schienenstrang verbunden.

Abbildung 7.4 zeigt, wie sich die Implementierung des oben skizzier- ten Rechenwerks mit Hilfe eines 1-aus-2-Multiplexers vervollständigen lässt. Ist s

gleich 0, so wird der Ausgang y mit dem oberen Eingang des Multiplexers und damit mit der Summe aus x

und x

beschrieben.

Ist s

gleich 1, so wird der untere Eingang und damit das Produkt aus x

und x

durchgeschaltet.

Neben dem hier eingesetzten 1-aus-2-Multiplexer stehen in der Praxis

auch deutlich größere Varianten zur Verfügung. Im allgemeinen Fall

verfügt ein 1-aus-n-Multiplexer (n:1 MUX) über die Eingangsleitungen

x

bis x

, die Steuerleitungen s

bis s

und eine einzige Ausgangslei-

tung y. In Abhängigkeit der Wertebelegung von s

bis s

schaltet der

Multiplexer genau eine der Eingangsleitungen x

bis x

auf den Aus-

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Schaltnetzsynthese mit Multiplexern

6

210 7 Standardschaltnetze

ErsterSchritt

x₃ x₂ x₁ y

0 0 0 0

0 0 1 0

0 1 0 1

0 1 1 0

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 1

y

ZweiterSchritt

x₂ x₁ y₀

0 0 0

0 1 0

1 0 1

1 1 0

x₂ x₁ y₁

0 0 0

0 1 1

1 0 1

1 1 1

y₀

y₁ MUX x₃

y

DritterSchritt

x₁ y₀₀

0 0

1 0

x₁ y₀₁

0 1

1 0

x₁ y₁₀

0 0

1 1

x₁ y₁₁

0 1

1 1

MUX x₂ y₀₀

y₀₁

MUX x₂ y₁₀

y₁₁

MUX x₃

y

VierterSchritt

MUX x₂ 0

¬x₁

MUX x₂ x₁

1

MUX x₃

y

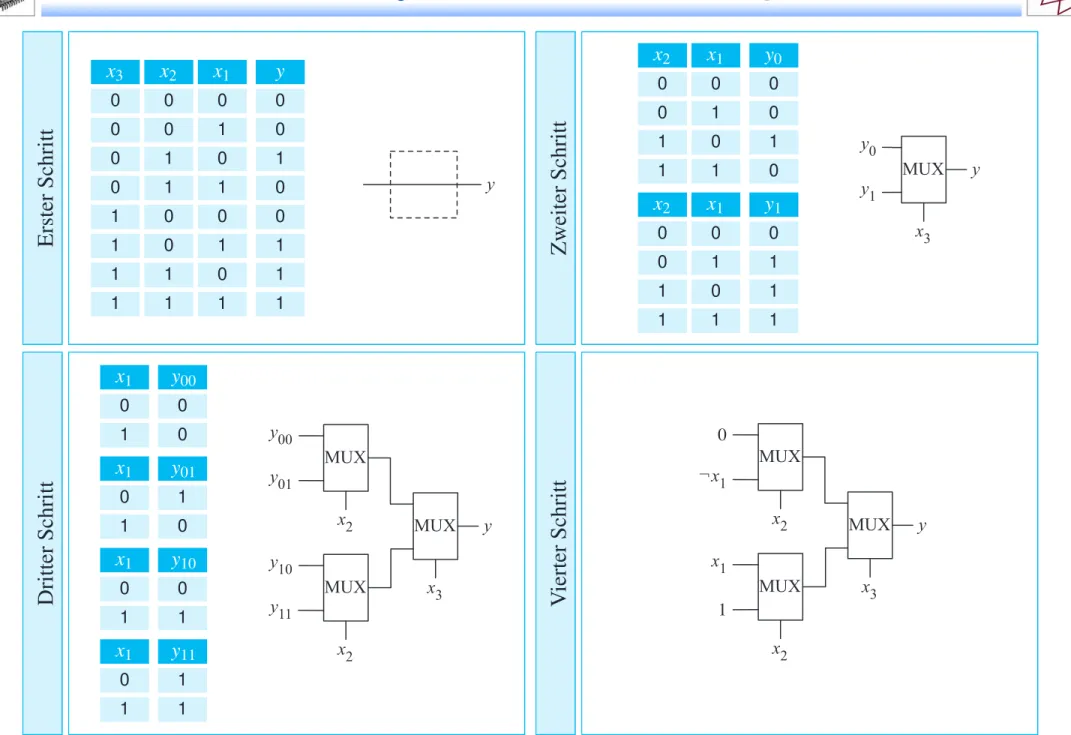
Abbildung 7.8:Schrittweise Transformation einer beliebigen booleschen Funktion in ein Multiplexer-Schaltnetz

nur erdenkliche boolesche Funktion zu implementieren. Als Ausgangs- punkt verwenden wir die Wahrheitstafeldarstellung einer booleschen Funktion f(x₁, . . . ,x_n)und setzen diese schrittweise in eine Multiplexer- basierte Schaltung um. Hierzu unterteilen wir die Tabelle jeweils in eine obere und eine untere Hälfte, so dass die Variablenbelegungen der obe- ren Hälfte durch die Bedingung x_n = 0 und die Belegungen der unte- ren Hälfte durch die Bedingungx_n=1charakterisiert sind. Folgerichtig können wir die boolesche Funktion erzeugen, indem wir die Steuerlei- tung eines 1-aus-2-Multiplexers mit der Variablenx_n beschalten und an dem oberen bzw. unteren Eingang des Multiplexers die boolesche Funk- tion der oberen bzw. unteren Hälfte der Wahrheitstafel erzeugen. Durch die wiederholte Zerlegung entsteht ein Schaltnetz für f, das ausschließ- lich aus 1-aus-2-Multiplexern besteht.

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Demultiplexer

7

y₁ y₂

s₀ x

Abbildung 7.10: Genau wie im Falle des Multiplexers ist das Verhalten eines Demul- tiplexers mit dem einer Weiche vergleich- bar. Beide Bausteine unterscheiden sich le- diglich in der Flussrichtung der ein- und ausgehenden Signale.

s₂ s₁ s₀

y₁ y₂ y₃ y₄ y₅ y₆ y₇ y₈

&

&

&

&

&

&

&

&

x

Abbildung 7.11: Realisierung eines 1-zu- 8-Demultiplexers mit Hilfe der elementaren Logikgatter

7.2 Multiplexer und Demultiplexer 211

x

y₁ y₂

s₀ 1:2 DEMUX

s₀ s₁

y₁ y₃ y₂ y₄ 1:4

DEMUX x

s

y

y

0

x

1 0

x

s

s

y

y

y

y

0 0

x

0 1 0

x

1 0 0 0

x

1 1 0 0 0

x

Abbildung 7.9: Demultiplexer-Bausteine verschiedener Größen

Demultiplexer

Bewirken Multiplexer die kontrollierte Zusammenführung von Daten- pfaden, so bewerkstelligen Demultiplexer deren Aufspaltung. Entspre- chend verfügt ein 1-zu-n-Demultiplexer (1:n DEMUX) über eine einzi- ge Eingangsleitung x, die Steuerleitungen s

bis s

und n Ausgangslei- tungen y

, . . . , y

. In Abhängigkeit der Wertebelegung schaltet der De- multiplexer das Eingangssignal x auf genau eine der Ausgangsleitungen y

bis y

durch und belegt alle anderen Ausgänge mit 0. Abbildung 7.9 zeigt die Wahrheitstabellen und Schaltsymbole eines 1-zu-2- und ei- nes 1-zu-4-Demultiplexers. Da mit n Steuerleitungen 2

verschiedene Möglichkeiten unterschieden werden können, entspricht die Anzahl der Ausgänge eines typischen Demultiplexers in aller Regel einer Zweier- potenz.

Das Schienenanalogon, das wir zur Veranschaulichung des Multiplexer- Verhaltens herangezogen haben, können wir in direkter Weise auf die Demultiplexer-Schaltung übertragen, indem wir schlicht die Richtung drehen. Wie in Abbildung 7.10 gezeigt, wird der ankommende Schie- nenstrang in Abhängigkeit des Stellsignals mit genau einem der beiden ausgehenden Schienenstränge verbunden.

Aus der Wahrheitstabelle des Demultiplexers lässt sich unmittelbar eine

einstufige Implementierung ableiten. Jedes der Ausgangssignale y

kann

durch ein einzelnes UND-Gatter erzeugt werden, das neben dem Ein-

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Demultiplexer-Anwendungen (2)

§ Realisierung von logischen Funktionen

§ Der Decoder erzeugt alle 2

Minterme seiner n Steuerleitungen

§ Ein ODER-Gatter erzeugt die Einsmenge der Funktion

8

c b a y

0 0 0 0

0 0 1 0

0 1 0 1

0 1 1 0

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 1

1 DX

c a

≥1

y(a,b,c)

b

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Programmierbare Logikbausteine

9

& ≥1

&

&

&

&

1 1

1 1

x

x

x

x

≥1

≥1

≥1

≥1

y

y

y

y

UND-Matrix ODER-Matrix

... ...

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Beispiel

10

& ≥1

&

&

&

&

1 1

1 1

x

x

x

x

≥1

≥1

≥1

≥1

f

f

f

f

UND-Matrix ODER-Matrix

5.

Technische Informatik I • Hochschule Karlsruhe • Prof. Dr. D. W. Hoffmann

Addierer

§ Halbaddierer

§ Addiert zwei Binärziffern

§ Ergebnis ist der Summenwert und ein Übertrag

§ Es werden 2 Eingänge und zwei Ausgänge benötigt

11

Fall 1 Fall 2

0

+ 0

= 0 0

0

+ 1

= 0 1

Fall 3 Fall 4

1

+ 0

= 0 1

1

+ 1

= 1 0

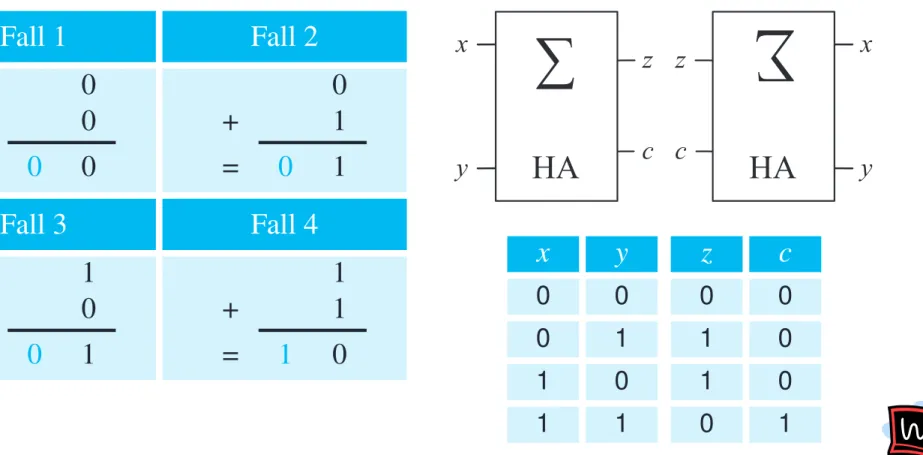
Tabelle 7.1: Bei der Addition zweier Binär- ziffern müssen wir vier Fälle unterscheiden.

x

y

=

&

z c

∑

HA

x

y

=

&

z c

∑

HA

x y z c

0 0 0 0

0 1 1 0

1 0 1 0

1 1 0 1

Abbildung 7.22: Schaltsymbol und Wahr- heitstafel eines Halbaddierers

x

y

=1

&

z c

Abbildung 7.23: Implementierung der Halbaddiererschaltung

218 7 Standardschaltnetze

7.5 Addierer

Die Durchführung arithmetischer Operationen gehört zu den Kernauf- gaben eines jedes Computersystems. In diesem Abschnitt werden wir die verschiedenen Möglichkeiten kennen lernen, wie sich die Additi- on in Form eines Schaltnetzes implementieren lässt. Hierzu werden wir mit dem Halb- und dem Volladdierer zunächst die arithmetischen Ba- siskomponenten einführen und anschließend zeigen, wie sich diese zu komplexen Addierwerken kombinieren lassen. Auch hier werden wir unser besonderes Augenmerk wieder auf die Laufzeit und den Flächen- verbrauch der betreffenden Schaltungen richten.

7.5.1 Halb- und Volladdierer

Der Halbaddierer ist die einfachste arithmetische Basiskomponente und bildet die Addition zweier Binärziffern x und y nach. Da beide Summan- den nur die Werte 0 und 1 annehmen können, müssen wir lediglich die vier in Tabelle 7.1 dargestellten Fälle unterscheiden. Wie die Rechen- beispiele zeigen, setzt sich das Ergebnis der Addition aus dem Summen- bit z und dem Übertragsbit c (Carry-Bit) zusammen, so dass der Halb- addierer neben den beiden Eingangsleitungen x und y über insgesamt zwei Ausgangsleitungen verfügt. Das Schaltsymbol des Halbaddierers ist zusammen mit seiner Wahrheitstafel in Abbildung 7.22 dargestellt.

Die Wahrheitstabelle ergibt sich ohne Umwege aus den binären Additi- onsregeln.

Wie aus der Tabelle hervorgeht, ist das Summenbit genau dann gleich 1, wenn einer der beiden Summanden gleich 1, der andere dagegen gleich 0 ist. Dagegen wird das Übertragsbit nur dann gesetzt, wenn beide Sum- manden gleich 1 sind. Damit erhalten wir für die booleschen Funktionen von z und c das folgende Ergebnis:

z = x

= x

c = x

^ x

Aus den beiden Gleichungen ergibt sich ohne Umwege die in Abbil- dung 7.23 skizzierte Implementierung, die aus lediglich zwei Logikgat- tern besteht.

Mit Hilfe von Halbaddierern sind wir in der Lage, beliebige Dualziffern zu addieren, für die vollständige Addition mehrziffriger Dualzahlen ist die Funktionalität jedoch noch nicht ausreichend. Als Beispiel betrach- ten wir die Berechnung der Summe 92 + 106, die zusammen mit dem

Fall 1 Fall 2

0

+ 0

= 0 0

0

+ 1

= 0 1

Fall 3 Fall 4

1

+ 0

= 0 1

1

+ 1

= 1 0

Tabelle 7.1: Bei der Addition zweier Binär- ziffern müssen wir vier Fälle unterscheiden.

x

y

=

&

z c

∑

HA

x

y

=

&

z c

∑

HA

x y z c

0 0 0 0

0 1 1 0

1 0 1 0

1 1 0 1

Abbildung 7.22: Schaltsymbol und Wahr- heitstafel eines Halbaddierers

x

y

=1

&

z c

Abbildung 7.23: Implementierung der Halbaddiererschaltung

218 7 Standardschaltnetze

7.5 Addierer

Die Durchführung arithmetischer Operationen gehört zu den Kernauf- gaben eines jedes Computersystems. In diesem Abschnitt werden wir die verschiedenen Möglichkeiten kennen lernen, wie sich die Additi- on in Form eines Schaltnetzes implementieren lässt. Hierzu werden wir mit dem Halb- und dem Volladdierer zunächst die arithmetischen Ba- siskomponenten einführen und anschließend zeigen, wie sich diese zu komplexen Addierwerken kombinieren lassen. Auch hier werden wir unser besonderes Augenmerk wieder auf die Laufzeit und den Flächen- verbrauch der betreffenden Schaltungen richten.

7.5.1 Halb- und Volladdierer

Der Halbaddierer ist die einfachste arithmetische Basiskomponente und bildet die Addition zweier Binärziffern x und y nach. Da beide Summan- den nur die Werte 0 und 1 annehmen können, müssen wir lediglich die vier in Tabelle 7.1 dargestellten Fälle unterscheiden. Wie die Rechen- beispiele zeigen, setzt sich das Ergebnis der Addition aus dem Summen- bit z und dem Übertragsbit c (Carry-Bit) zusammen, so dass der Halb- addierer neben den beiden Eingangsleitungen x und y über insgesamt zwei Ausgangsleitungen verfügt. Das Schaltsymbol des Halbaddierers ist zusammen mit seiner Wahrheitstafel in Abbildung 7.22 dargestellt.

Die Wahrheitstabelle ergibt sich ohne Umwege aus den binären Additi- onsregeln.

Wie aus der Tabelle hervorgeht, ist das Summenbit genau dann gleich 1, wenn einer der beiden Summanden gleich 1, der andere dagegen gleich 0 ist. Dagegen wird das Übertragsbit nur dann gesetzt, wenn beide Sum- manden gleich 1 sind. Damit erhalten wir für die booleschen Funktionen von z und c das folgende Ergebnis:

z = x

= x

c = x

^ x

Aus den beiden Gleichungen ergibt sich ohne Umwege die in Abbil- dung 7.23 skizzierte Implementierung, die aus lediglich zwei Logikgat- tern besteht.

Mit Hilfe von Halbaddierern sind wir in der Lage, beliebige Dualziffern

zu addieren, für die vollständige Addition mehrziffriger Dualzahlen ist

die Funktionalität jedoch noch nicht ausreichend. Als Beispiel betrach-

ten wir die Berechnung der Summe 92 + 106, die zusammen mit dem