Die Quantenmechanik verstehen
Volltext
Abbildung


ÄHNLICHE DOKUMENTE
lingg Maschine, oder bei konstantem Druck, wie in Ericssons Maschine, Stattfinden, SO daß die spezifische Wärme (. konstant ist, sind
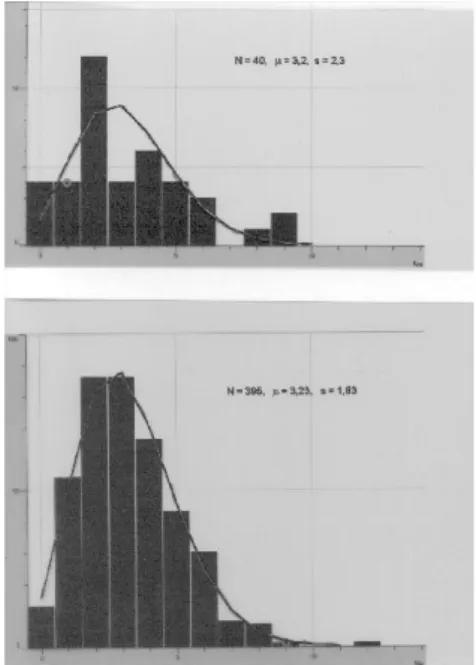
Die Verteilung der Teilchen auf die beiden H¨ alften ver¨ andert sich jeweils nach Ablauf einer festen Zeiteineit (Takt): 10% der sich in A befindlichen Teilchen diffun- dieren nach
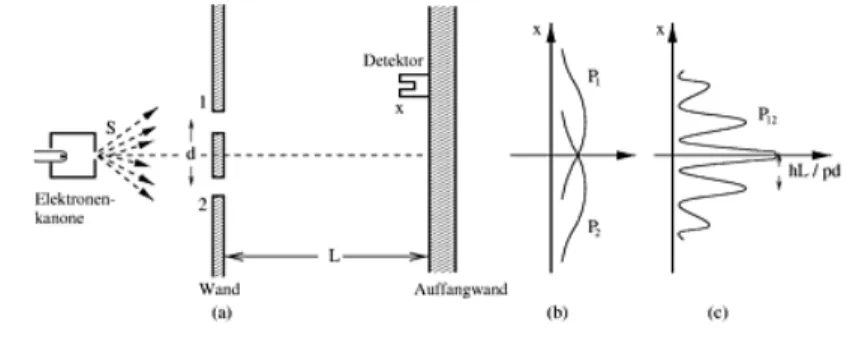
das Verhalten eines Elektrons kann durch eine De-Broglie-Welle mit einer von Zeit und Raum abhängigen Amplitude beschrieben werden. Einen stationären Zustand eines
Ein Teil des Lichts geht durch den Spalt hindurch und trifft auf einen Beobachtungsschirm im Abstand L zwischen Spalt und Schirm von 2 m. Das Licht wird gebeugt, denn es wird auch
• Die Atome können – trotz der in der Regel großen Verstimmung des Wellenleiter- lasers gegen den atomaren Übergang – auch durch Streuung eines Photons aus der stehenden Welle in
Jahrhundert gab es starke experimentelle Hinweise, dass elektromagnetis- che Felder nicht nur Wellen-Eigenschaften besitzen, sondern auch Eigenschaften, die man mit Teilchen
• Verformungssimulation einer Lochwelle unter Drehmomentbelastung (Abaqus CAE 6.12-3 und Z88Aurora)5. • Validierung der Ergebnisse mittels eines
Auf diese Weise kann nicht gesagt werden, welche von den Moden des Plasmas, die mit den Teilchen resonant wechselwirken k¨onnen, auch angeregt sind.. Die Beobachtung einer Ab-