Bachelorarbeit Heinrich-Heine-UniversitätDüsseldorf

(1)

Heinrich-Heine-Universität Düsseldorf

Bachelorarbeit

im Studiengang Chemie

zur Erlangung des akademischen Grades Bachelor of Science

Thema:

Validierung verschiedener DFT/MRCI-Hamiltonoperatoren anhand der UV/Vis-Spektren von Tris(2,2’-bipyridin)-M(II) Komplexen

(M = Fe, Ru, Os)

Autor: Tobias Kretschmer <tobias.kretschmer@hhu.de>

MatNr. 2397038 Version vom: 26. August 2018

Erstgutachterin: Prof. Dr. Christel Marian Zweitgutachter: PD Dr. Oliver Weingart

(2)

2

Zusammenfassung

In der folgenden Arbeit werden die vier zum jetzigen Zeitpunkt existierenden Hamil- tonoperatoren für DFT/MRCI im Hinblick auf Rechnerressourcen und Genauigkeit untersucht. Dafür werden für drei Tris(2,2’-bipyridin)-M(II) Komplexe (M=Fe, Ru, Os) DFT/MRCI-Rechnungen mit allen Operatoren durchgeführt. Dabei werden je drei Kombinationen aus Parametersatz und Selektionsschwellenwert (standard 1.0, short 0.8 und standard 0.8) genutzt. Die Genauigkeit wird durch den Vergleich mit experimentellen Absorptionsspektren [1] [2] bestimmt. Es hat sich gezeigt, dass Original und R2018, sowie R2016 und R2017, meist ähnliche Spektren ergeben. Von der Kombina- tion standard 0.8 ist für Original und R2018 abzuraten. Bei R2016 und R2017 kommt es hier zu Fehlerkompensation. Insgesamt ist standard 1.0 eine solide Wahl. Oft lassen sich jedoch mit short ähnlich gute Ergebnisse bei geringerem Rechenaufwand erzielen.

Für die betrachteten Komplexe können experimentell ermittelte Übergänge am Besten zugeordnet werden. Allerdings gibt R2018 meist den Verlauf der Spektren am Bes- ten wieder. Aufgrund der für R2016 und R2017 oft aufgetretenen Fehlerkompensation ist deren Genauigkeit für andere Übergangsmetallkomplexen, wo diese Fehlerkompen- sationen möglicherweise nicht auftreten, anzuzweifeln. In diesem Fall ist R2018 mit standard 1.0 zu bevorzugen.

(3)

3

Danksagung

Zuerst gilt mein Dank Frau Prof. Dr. Christel M. Marian, die mir die Anfertigung dieser Arbeit in ihrem Arbeitskreis ermöglicht hat. Des weiteren möchte ich mich bei ihr herzlich für die hilfreichen Anregungen und die konstruktive Kritik bei der Erstellung dieser Arbeit bedanken.

Bedanken möchte ich mich außerdem bei Adrian Heil für die Betreuung während der Bearbeitungszeit, sowie für die vielen hilfreichen Anmerkungen und Erklärungen.

Zuletzt möchte ich mich auch bei meinen Eltern und Geschwistern, sowie allen guten Freunden bedanken, die mich immer unterstützt und motiviert haben.

(4)

Inhaltsverzeichnis 4

Inhaltsverzeichnis

Abkürzungsverzeichnis 5

1 Einleitung 6

1.1 Moleküle . . . 6

2 Theorie 7 2.1 Elektronische Anregung . . . 7

2.1.1 Anregungsarten . . . 7

2.1.2 Franck-Condon-Prinzip . . . 8

2.2 Experimentelle Absorptionsspektren . . . 9

2.3 Dichtefunktionaltheorie . . . 9

2.4 DFT/MRCI . . . 11

2.4.1 Original . . . 11

2.4.2 R2016 . . . 11

2.4.3 R2017 . . . 12

2.4.4 R2018 . . . 12

2.4.5 Dämpfungsfunktion . . . 12

2.5 Symmetrie . . . 13

2.5.1 Symmetrieelemente und Symmetrieoperatoren . . . 13

2.5.2 Charaktertafel und Transformation . . . 14

2.5.3 Abelsche Molekülpunktgruppe . . . 15

3 Methoden 16 3.1 Verwendete Programme . . . 16

3.2 Basissätze . . . 16

3.3 Funktionale . . . 17

3.3.1 BH-LYP . . . 17

3.3.2 PBE0 . . . 18

4 Auswertung und Diskussion 18 4.1 MO-Schemata . . . 20

4.2 Tris(2,2’-bipyridin)-Ru(II) . . . 20

4.2.1 Kristallstruktur . . . 20

4.2.2 MO-Schema . . . 21

4.2.3 Zuordnung . . . 23

4.2.4 Spektren . . . 24

4.2.5 Fazit . . . 28

4.3 Tris(2,2’-bipyridin)-Os(II) . . . 28

4.3.2 MO-Schema . . . 29

4.3.3 Zuordnung . . . 30

4.3.4 Spektren . . . 31

4.3.5 Fazit . . . 34

4.4 Tris(2,2’-bipyridin)-Fe(II) . . . 34

4.4.2 MO-Schema . . . 36

4.4.3 Zuordnung . . . 36

4.4.4 Spektren . . . 37

(5)

Abkürzungsverzeichnis 5 4.4.5 Fazit . . . 40

5 Fazit 41

Literaturverzeichnis 43

Anhang 46

6 Anhang 46

6.1 Kristallstrukturen . . . 46 6.2 Spektren . . . 49 6.3 Orbitale . . . 58

Eidesstattliche Erklärung 58

(6)

1 Einleitung 6

1 Einleitung

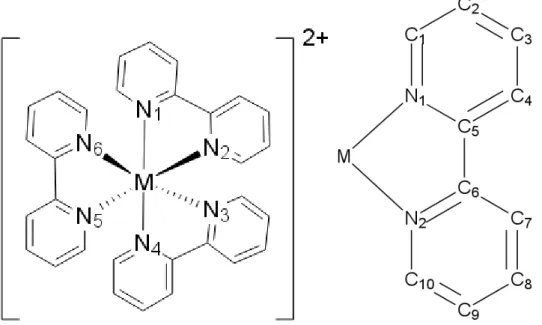
Eine der grundlegenden Aufgaben der Quantenchemie ist die Vorhersage und Beschrei- bung chemischer Eigenschaften, wie z.B. Dipolmomente, Bindungslängen und Ener- gien. Dabei kommt Übergangsmetallkomplexen, aufgrund ihrer photophysikalischen Eigenschaften, ein besonderes Interesse zu. Es konnte gezeigt werden, dass DFT/MR- CI (Abschnitt 2.4) eine dafür geeignete Methode ist [3]. In den letzten Jahren wurde die DFT/MRCI-Methode weiterentwickelt, wodurch jetzt neben dem ersten Opera- tor, welcher in dieser Arbeit als Original bezeichnet wird (Abschnitt 2.4.1), auch die neuen Operatoren R2016 (Abschnitt 2.4.2), R2017 (Abschnitt 2.4.3) und R2018 (Ab- schnitt 2.4.4) zur Verfügung stehen. Außerdem gibt es für jeden Operator zwei Selek- tionsschwellenwerte (0.8 und 1.0), sowie die Parametersätze short und standard. Im Rahmen dieser Bachelorarbeit werden diese vier Operatoren unter Nutzung der Kom- binationen short 0.8, standard 0.8 und standard 1.0 für drei Tris(2,2’-bipyridin)-M(II) Komplexe (M=Ru, Os, Fe) Abbildung 1 untersucht und die Ergebnisse der Rechnung mit experimentellen Quellen [1] [2] verglichen.

1.1 Moleküle

Abbildung 1: Tris(2,2’-bipyridin)-M(II) Komplex, M=Ru, Os, Fe; die gestrichelten Li- nien sind C2-Achsen

Die Moleküle besitzen eine hohe Absorptionsrate im sichtbaren Bereich, was auf Über- gänge mit hohem MLCT-Charakter (Abschnitt 2.1.1) zurückzuführen ist [1]. Aufgrund dieser Übergänge werden die Moleküle als Photosensibilisator und Photokatalysator eingesetzt[2]. Außerdem fungieren sie als Prototypen für andere Metall-Polypyridyl- Komplexe [2]. Der Tris(2,2’-bipyridin)-Ru(II) Komplex ist besonders gut untersucht.

Der Ru-Komplex findet zusätzlich Anwendung als Redoxkatalysator und lichtsammeln- der Farbstoff [1]. Für Osmium kommen spinabhängige relativistische Effekte zum Tra- gen.

(7)

2 Theorie 7

2 Theorie

2.1 Elektronische Anregung

2.1.1 Anregungsarten

In Übergangsmetallkomplexen gibt es fünf Anregungsarten:

MC (Abbildung 2, metal-centered): Die Ladungsverteilung ändert sich nur am Metall- atom (hier Zentralatom). Die Liganden sind davon nicht oder nur wenig beeinflusst.

Abbildung 2: Beispiel MC

MLCT (Abbildung 3, metal-to-ligand charge transfer): Es findet eine Ladungsübertra- gung (charge transfer) vom Metall auf den Liganden statt.

Abbildung 3: Beispiel MLCT

LMCT (Abbildung 4, ligand-to-metal charge transfer): Es findet eine Ladungsübertra- gung (charge transfer) vom Ligand auf das Metall statt.

Abbildung 4: Beispiel LMCT

LC (Abbildung 5, ligand-centered): Die Ladungsverteilung ändert sich innerhalb der einzelnen Liganden. Das Zentralatom wird davon nicht beeinflusst.

Abbildung 5: Beispiel LC

(8)

2 Theorie 8 LLCT (ligand-to-ligand charge transfer): Es findet eine Ladungsübertragung (charge transfer) vom einem Liganden auf einen anderen Liganden statt. Eine Anregung dieser Art findet bei den untersuchten Molekülen nicht statt. Beispiele für diese Anregungsart sind in Paper [4] beschrieben.

2.1.2 Franck-Condon-Prinzip

Mit Hilfe des Franck-Condon-Prinzips lassen sich Aussagen über die Intensität elek- tronischer Anregung treffen. Grundlage ist dabei die der Born-Oppenheimer-Näherung analoge Überlegung, dass sich die Elektronen, aufgrund ihrer weitaus geringeren Masse, wesentlich schneller bewegen [5]. Deswegen wird angenommen, dass bei einer elektronischen Anregung, die eine Änderung des Elektronenzustands bedingt, die Kerngeometrie nahezu gleichbleibt und sich erst im Nachhinein ändert (siehe Abbildung 6) [5]. Dies wird auch als vertikale Anregung bezeichnet, da sich bei einer Auftragung der Energie gegen die Kerngeometrie bei einer Anregung nur die Energie ändert. Da die Wahr- scheinlichkeitsdichte im Grundzustand bei der Gleichgewichtsgeometrie maximal ist, wird eine Anregung meist aus dieser Geometrie heraus erfolgen [5]. Die Wahrschein- lichkeitsdichte ergibt sich aus dem Quadrat der Wellenfunktion. Aufgrund des Franck- Condon-Prinzips ist es hinreichend für die Modellierung von Absorptionsspektren nur die Geometrie im Grundzustand zu berechnen.

Abbildung 6: Franck-Condon-Prinzip [6]

(9)

2 Theorie 9

2.2 Experimentelle Absorptionsspektren

Für Tris(2,2’-bipyridin)-M(II) Komplexe (M=Ru, Os, Fe) gibt es eine Vielzahl an experimentellen Absorptionsspektren. Neben vielen Messungen in diversen Lösungsmitteln befinden sich darunter auch Messungen in kristalliner Umgebung [7] [8] [9]. Letztere sind aufgrund von Umgebungseinflüssen jedoch nicht hoch aufgelöst. Für einen mög- lichst guten Vergleich sind experimentelle Spektren in Abwesenheit einer chemischen Umgebung vorzuziehen. Dies ist mit Hilfe der Photodissoziationsspektroskopie möglich [1] [2]. Deswegen wurden die Ergebnisse der Messenger Tagging Photodissoziationss- pektren von Xu et al [1] [2] für den Vergleich mit dem Experiment genutzt. In den verwendeten Quellen [1] [2] wurde für die Aufnahme des Absorptionsspektrums in einer kryogenen Ionenfalle N₂ an das Molekül angebracht (messenger tagging). Anschließend wurde das Molekül unter Abspaltung des vorher angebrachten Stickstoffs spektrosko- pisch untersucht (photodissociation spectroscopy) [1] [2]. Voraussetzung für den Erhalt hochaufgelöster Spektren des Moleküls ist unter anderem, dass die Anbringung von N₂ die Eigenschaften des Moleküls nicht oder nur geringfügig ändert [1] [2].

2.3 Dichtefunktionaltheorie

Der Abschnitt ist mit der Quelle [10] als Referenz entstanden. Die Dichtefunktio- naltheorie (DFT) ist eine Theorie, in der sich die Energie und andere Eigenschaften eines Moleküls mit Hilfe eines Funktionals der Elektronendichteρ(ab hier: Dichte) berechnen lassen. Ein Funktional ist eine Funktion, welche als Argument eine Funktion besitzt, die wiederum von Parametern abhängig ist. Mit DFT lässt sich im Gegensatz zu Hartree-Fock auch die Korrelationsenergie mit berücksichtigen. Antriebskraft für die Entwicklung der DFT ist der Umstand, dass die Wellenfunktion von vier Koordi- naten (Spin und drei Raumkoordinaten) pro Elektron abhängig und nicht intuitiv ist.

Anstelle der Wellenfunktion wollte man eine physikalische Observable benutzen. Da der Hamilton-Operator ˆH (Gleichung 1)

Hˆ = ˆT_k(R_α) + ˆT_e(r_i) + ˆV_ke(r_i, R_α) + ˆV_ee(r_i, r_j) + ˆV_kk(R_α, R_β) (1) nur von der Position R und Ladung der Kerne Z, sowie der Anzahl an Elektronen N abhängig ist, erscheint die Dichte als geeignete Wahl. Das Integral der Dichte über den gesamten Raum ergibt die Anzahl der Elektronen (Gleichung 2). Zusätzlich konnte gezeigt werden, dass zwischen der Dichte und Ort und Ladung der Kerne ein Zusam- menhang besteht (Gleichung 3).

N =

Z

ρ(r)dr (2)

∂ρ(r_A)

∂rA

=−2Z_Aρ(r_A) (3)

(10)

2 Theorie 10 Mit dem 1. Hohenberg-Kohn Theorem (Hohenberg-Kohn Existence Theorem) konnte gezeigt werden, dass die Grundzustandsdichte den Hamiltonoperator und damit auch die Wellenfunktion bestimmt. Mit dem 2. Hohenberg-Kohn Theorem (Hohenberg-Kohn Variational Theorem) wurde gezeigt, dass die Dichte einem Variationsprinzip folgt. Da- mit ist die aus einer Dichte folgende Energie größer oder gleich der echten Grundzu- standsenergieE₀ (Gleichung 4).

E[ρ]≥E₀ (4)

Allerdings ist weder die Dichte noch das exakte Dichtefunktional bekannt. In der Kohn- Sham-DFT ergibt sich die Elektronendichte aus den optimierten Kohn-Sham-Orbitalen (Gleichung 5).

ρ=

N

X

i=1

|ψ|² (5)

Die Formulierung des GesamtenergieE_ges[ρ(r)] (Gleichung 6) geschieht über eine klas- sische Formulierung der WechselwirkungenV_ne[ρ(r)] undV_ee[ρ(r)], sowie die kinetische Energie von nicht-wechselwirkenden Elektronen T_e[ρ(r)].

E_ges[ρ(r)] = T_e[ρ(r)] +V_ne[ρ(r)] +V_ee[ρ(r)] +E_XC[ρ(r)] (6) T_e[ρ(r)] ergibt sich analog zu Hartree-Fock aus der Summe der kinetischen Energieter- men T_i der Teilchen (Gleichung 7).

Te[ρ(r)] =

N

X

i=1

Ti (7)

Zusätzlich gibt es noch den KorrekturtermE_XC[ρ(r)]. Dieser enthält neben Austausch- wechselwirkung und Korrelationsenergie auch Korrekturen für die Selbstwechselwir- kung. Das zugehörige Funktional heißt Austauschkorrelationsfunktional. Demzufolge lässt sich die Schrödingergleichung (Gleichung 8)

HΨ =ˆ EΨ (8)

für Kohn-Sham-DFT als Summe der Einelektronenoperatoren, welche die Pseudoei- genwertgleichung (Gleichung 9)

h^KS_i ψ_i =_iψ_i (9)

erfüllen, schreiben. h^KS_i (Gleichung 10) ist hierbei als h^KS_i =−1

2∇²_i −

n

X

α=1

Z_α

|r_i−R_α| +

Z ρ(r)

|r_i−r|dr+V_XC (10) VXC = ∂E_XC

∂ρ (11)

(11)

2 Theorie 11 definiert. Weitere Informationen zu den Dichtefunktionalen gibt es in Abschnitt 3.3.

2.4 DFT/MRCI

DFT/MRCI ist eine von S.Grimme und M.Waletzke [11]entwickelte Methode, die Dich- tefunktionaltheorie und Multi-Reference Configuration-Interaction kombiniert. Sie ist für das BH-LYP Funktional (Abschnitt 3.3.1) parametrisiert und ermöglicht auch die Berechnung von großen Molekülen. Da für die genaue Beschreibung von Grund- und angeregten elektronischen Zuständen sowohl dynamische als auch nicht-dynamische Korrelationseffekte berücksichtigt werden müssen, ist die grundlegende Idee hinter DFT/MRCI, die dynamischen Korrelationen mit Kohn-Sham DFT und die nicht dynamischen mit MRCI zu beschreiben [11]. Aus den Kohn-Sham Orbitalen werden an Spin -und Raumsymmetrie angepasste configuration state functions (CSFs) konstruiert. Da nur die wichtigsten CSFs benutzt werden, ergibt sich ein relativ geringer Re- chenaufwand. Die Matrixelemente eines Hamiltonoperators zwischen zwei CSFs lassen sich in Diagonalelemente mit gleichwertiger räumlicher Besetzung und Außerdiago- nalelemente mit Ein- oder Zwei-Elektronen Unterschieden unterteilen [11] [12]. Die Diagonalelemente der DFT/MRCI-Hamiltonoperatoren basieren auf einer Korrektur der exakten Elemente mit KS Orbitalenergien und skalierten Zweielektronenintegralen [11]. Die Außerdiagonalelemente mit gleichartiger räumlicher Besetzung werden exakt berechnet und skaliert, um zu den Korrekturen der Diagonalelemente zu passen [11].

Um Doppeltzählungen zu vermeiden, werden die Außerdiagonalelemente mit Ein- oder Zwei-Elektronen-Unterschieden abhängig von ihrer Energiedifferenz auf Null skaliert (Dämpfungsfunktion) [11].

2.4.1 Original

Im Hamiltonoperator von S.Grimme und M.Waletzke wurde eine exponentielle Dämp- fungsfunktion gewählt (Gleichung 12).

H_nn⁰ =p₁∗exp(−p₂∗∆E⁴)∗H_nn^CI0[12] (12) Mit Original lassen sich nur Singulett- und Triplettzustaende berechnen [13]. Original besitzt unterschiedliche Parametersaetze für Singuletts und Tripletts [14].

2.4.2 R2016

R2016 benutzt keine exponentielle Dämpfungsfunktion. Stattdessen wird der Arku- stangens verwendet (Gleichung 13).

H_nn⁰ = p1

1 +p₂∗∆E⁵∗arctan(p₂∗∆E⁵)H_nn^CI⁰[12] (13)

(12)

2 Theorie 12 R2016 wurde erstellt um die Schwächen von Original bei der Beschreibung von Bi- Chromophoren [13] zu beheben. R2016 besitzt einen eigenen Parametersatz, der sowohl für Singuletts als auch Tripletts anwendbar ist [14]. Dieser enthält weniger Empirie als Original [14].

2.4.3 R2017

R2017 und R2016 haben die gleiche Dämpfungsfunktion [12]. Für R2017 wurde ein Pa- rametersatz auf einen Selektionsschwellenwert von 0.8 E_h und ein Parametersatz auf einen Selektionsschwellenwert von 1.0 E_h optimiert [13]. Mit beiden Parametersätzen lassen sich nun neben Singulett- und Triplettzuständen auch Dublett- und Quartett- zustände berechnen [13].

2.4.4 R2018

Für die Dämpfungsfunktion von R2018 wurde wieder eine Exponentialfunktion verwendet. Diese unterscheidet sich nur im Exponenten der Energiedifferenz zum Original.

(Gleichung 14)

Hnn⁰ =p₁∗exp(−p₂∗∆E⁶)∗H_nn^CI⁰[12] (14) R2018 wurde erstellt um die Schwächen der anderen Operatoren bei der Beschrei- bung von Übergangsmetallkomplexen zu beheben [12]. Es wurde festgestellt, dass die Dämpfungsfunktion einen grossen Einfluss auf die Anregungsenergie von Übergangs- metallkomplexen hat [12]. Für R2018 wurde ein Parametersatz auf einen Selektions- schwellenwert von 0.8E_h und ein Parametersatz auf einen Selektionsschwellenwert von 1.0E_h optimiert [12]. Diese Parametersätze sind für Singuletts, Dubletts, Tripletts und Quartetts anwendbar.

2.4.5 Dämpfungsfunktion

In Abbildung 7 und Abbildung 8 sind die Dämpfungsfunktionen für die einzelnen Ope- ratoren zu sehen. Original und R2016 benutzen für einen Selektionsschwellenwert von 0.8 und von 1.0 den selben Parametersatz. R2017 und R2018 haben für beide Selekti- onsschwellenwerte einen eigenen darauf optimierten Parametersatz [12]. Der Parame- tersatz standard ist für einen Selektionsschwellenwert von 1.0 optimiert, während short für 0.8 optimieret ist. Bei der Kombination standard 0.8 ist der Parametersatz nicht für diesen Selektionsschwellenwert optimiert. Die neueren Operatoren beginnen alle unge- fähr beim gleichen Wert. Original beginnt bei einem höheren Wert. Die Verläufe von R2016 und R2017 ähneln sich stark. Bei einem Selektionsschwellenwert von 1.0 fällt der Graph von R2018 später und stärker ab [12]. Im Bereich des Selektionsschwellen- werts 1.0 weist er einen geringeren Wert auf als die anderen Operatoren [12]. Bei der

(13)

2 Theorie 13 Kombination standard 0.8 befinden sich alle Graphen beim Selektionsschwellenwert bei höheren Werten. Aus ihren Verläufen ergeben sich Hypothesen 8 und 9 (Abschnitt 4).

Abbildung 7: Dämpfungsfunktion von allen Hamiltonoperatoren optimiert auf einen Selektionsschwellenwert von 1.0E_h [12]

Abbildung 8: Dämpfungsfunktion von allen Hamiltonoperatoren optimiert auf einen Selektionsschwellenwert von 0.8E_h [12]

2.5 Symmetrie

2.5.1 Symmetrieelemente und Symmetrieoperatoren

Die Tris(2,2’-bipyridin)-M(II) Komplexe (M=Ru, Os, Fe) haben die PunktgruppeD₃, welche sich dadurch auszeichnet, dass sie neben einer dreizähligen Drehachse (C₃) auch drei dazu senkrechte zweizählige Drehachsen (C₂) besitzt ˆC₃ beschreibt eine Drehung von 120 ^◦ um die C₃-Achse, während ˆC₂ eine Drehung von 180 ^◦ um eine der drei

(14)

2 Theorie 14 C₂-Achsen beschreibt. In Abbildung 1 gehen die drei C₂-Achsen durch je eine der Bin- dungen zwischen den beiden Pyridyl-Ringen des Bipyridins und das Metallatom. Sie befinden sich in der Zeichenebene und sind in Abbildung 1 als gestrichelte Linien einge- zeichnet. DieC₃-Achse ist orthogonal zur Zeicheneben und geht durch das Metallatom.

Die Identität ˆE beschreibt eine Drehung um 360 ^◦. 2.5.2 Charaktertafel und Transformation

Tabelle 1: Charaktertafeln der PunktgruppenD₃ und C₂ D₃ Eˆ 2 ˆC₃ 3 ˆC₂

A₁ 1 1 1 A₂ 1 1 -1

E 2 -1 0

C₂ Eˆ Cˆ₂

A 1 1

B 1 -1

Anhand der Charaktertafel (Tabelle 1) lässt sich die Symmetrie der Orbitale bestimmen. In der ersten Spalte befinden sich die Namen der irreduziblen Darstellungen der Punktgruppe und in der ersten Zeile die Symmetrieoperationen der jeweiligen Punkt- gruppe.D3 enthält einmal die Identität E, eineC3-Achse und dreiC2-Achsen, während C₂ einmal die Identität E und eine C₂-Achse enthält. Bei 1 verhalten sich die Orbitale symmetrisch zu der Symmetrieoperation, weswegen sie ihr Vorzeichen beibehalten. Bei -1 verhalten sie sich antisymmetrisch zu der Symmetrieoperation, was eine Umkehr der Vorzeichen der Orbitale zu Folge hat. Da DFT/MRCI nurD_2h und Untergruppen als Symmetrie benutzen kann, wurde für das Molekül bei der DFT/MRCI-Rechnung C₂-Symmetrie benutzt. Damit transformiert A₁ zu A, A₂ zu B und E zu A und B.

A₁ =







1 1 1 1 1 1







A₂ =







1 1 1

−1







E =







2

−1

−1 0 0 0







(15)

Um die Symmetrie des Übergangs zu bestimmen, muss das direkte Produkt der irreduziblen Darstellungen der beteiligten Orbitale gebildet und ausreduziert werden.

Dies ist für alle in den Rechnungen vorkommenden Symmetriekombinationen in Glei- chung 16 bis Gleichung 20 zu sehen.

A₁⊗A₁ =A₁ (16)

A₁⊗A₂ =A₂ ⊗A₁ =A₂ (17)

(15)

2 Theorie 15

A₁⊗E =E⊗A₁ =E (18)

E⊗A₂ =E (19)

E⊗E =A1⊕A2⊕E (20)

Übergänge mit einer E-Symmetrie treten dabei immer paarweise auf. Da E zu A und B transformiert, können nur zwei Zustände mit ähnlicher Energie und Orbitalbeteili- gung gemeinsam einen E-Zustand bilden. Für A1 und A2 gilt dies nicht, da sie nicht entartet sind.

2.5.3 Abelsche Molekülpunktgruppe

Bei einer abelschen Punktgruppe wird bei einer Hintereinanderausführung der Sym- metrieoperationen in beliebigen Reihenfolgen immer das gleiche Ergebnis erhalten.D₃ ist keine abelsche Punktgruppe, da ˆC₃ · Cˆ₂ 6= ˆC₂ · Cˆ₃ ist, was durch Abbildung 9 veranschaulicht wird:

Abbildung 9: Beispiel zur Verdeutlichung einer abelschen Punktgruppe (unten) und einer nichtabelschen (oben)

(16)

3 Methoden 16

3 Methoden

3.1 Verwendete Programme

Die Moleküle wurden mit dem Spartan-Programm [15] [16] konstruiert. Die Geome- trien wurden mittels Turbomole [17] [18] mit der Methode DFT (Abschnitt 2.3) [19]

[20] im elektronischem Grundzustand und in D3-Symmetrie unter Verwendung des PBE0-Dichtefunktionals (Abschnitt 3.3.2) optimiert. Dabei wurde eine SV(P)-Basis (Abschnitt 3.2) für die Liganden und ein skalarrelativistisches effektives Rumpfpoten- tial (ECP) mit dem zugehörigen Basissatz (Abschnitt 3.2) für das Metallatom verwendet (ECP-10-MDF für Eisen, def-ECP für Osmium und Ruthenium). Auch die Schwin- gungsfrequenzen wurden mittels Turbomole bestimmt. Die Orbitale wurden mit dem Programm rimp2prep [21], welches zum Turbomole-Paket gehört, eingefroren. Die angeregten Singlett- und Triplettzustände wurden mit dem DFT/MRCI (Abschnitt 2.4) Programm berechnet. Dabei wurde das BH-LYP-Dichtefunktional (Abschnitt 3.3.1) benutzt. Die Gaußverbreiterung der berechneten Spektren wurde mit dem Programm Plotter [22] durchgeführt. Das Programm Gnuplot [23] wurde zum Erstellen der Spek- tren verwendet. Die Orbitale wurden mit dem Programm Jmol [24] angezeigt. Die experimentellen Absorptionsspektren wurden mit dem Programm Engauge Digitizer [25] digitalisiert.

3.2 Basissätze

Der für alle Nichtmetallatome verwendete def-SV(P) Basissatz ist eine Split-Valence Basis, d.h. für die Atomorbitale der inneren Schalen wird eine Funktion und für die Valenzorbitale je zwei Funktionen verwendet [26]. Im Falle von def-SV(P) sind diese Funktionen kontrahierte Gaußfunktionen [26]. Zusätzlich enthält der Basissatz noch Polarisationsfunktionen für alle Atome außer Wasserstoff [26]. Für Eisen wurde der ECP-10-MDF Basissatz verwendet [20].

Für Ruthenium und Osmium wurde als skalarrelativistisches effektives Rumpfpotential def-ECP [27] und für Eisen ECP-10-MDF [28] benutzt. Da bei schwereren Elementen viele nicht-Valenzelektronen berechnet werden müssen, werden die Wechselwirkungen der inneren Elektronen durch ein effektives Potential angenähert, welches auf die Va- lenzelektronen wirkt [28] [27]. Dieses effektive Potential wird auch Pseudopotential genannt. Bei ECP-10-MDF werden 10 Elektronen durch das Pseudopotential ersetzt, welches unter Annahme eines neutralen Moleküls erstellt wird [29].

Bei ab initio SCF (self consistent field) mit anschließender CI (configuration interaction) Rechnung an Übergangsmetallverbindungen stellen Pseudopotentiale eine einfache und effiziente Methode dar, sowohl den Rechenaufwand zu senken, als auch relativistische Effekte zu berücksichtigen [27]. Für die verwendeten ECPs wurde ein quasirelati-

(17)

3 Methoden 17 vistisches semilokales Pseudopotential V^qr(r_i)Gleichung 21 bei allen Atomen [28] [27]

verwendet.

V^qr(r_i) =−Q r +^X

l

X

j

X

k

Cljkexp^−α^ljk^r²ⁱ Plj (21) Q ist hier die Kernladung undP_ljist der Projektionsoperator auf den Hilbert-Unterraum mit Winkelsymmetrie j. C_ljkund α_ljk sind Parameter.

Für die erste Reihe der Übergangsmetalle werden die innersten 10 (Neon-Konfiguration) [28], für die zweite Reihe 28 und für die dritte Reihe 60 Elektronen durch das Pseudo- potential ersetzt [27].

3.3 Funktionale

Bei der Geometrieoptimierung wurde das PBE0-Dichtefunktional und für DFT/MRCI das BH-LYP-Dichtefunktional benutzt. Mit den Dichtefunktionalen lässt sich in der Dichtefunktionaltheorie aus der Dichte die Austauschwechselwirkung und die Korre- lationsenergie errechnen. Mit dem exakten Dichtefunktional liefert die Dichtefunktio- naltheorie exakte Ergebnisse. Da das exakte Dichtefunktional nicht bekannt ist, werden Näherungen benutzt. Häufig bestehen die Funktionale aus einem Term für Austausch- wechselwirkung und einem für Korrelationsenergie (Gleichung 22).

E_XC[ρ(r)] =E_X[ρ(r)] +E_C[ρ(r)] (22) Hybridfunktionale sind Funktionale, welche einen Teil der Austauschwechselwirkung aus der Hartree-Fock Theorie (HF) und den Rest aus anderen Quellen, wie z.B. LDA, LSDA, GGA und empirisch gefittete wie in B88 (Becke 1988), beziehen. LDA steht für local density approximation und ist eine Näherung, bei der die Austausch-Korrelations- Energie nur von der Dichte am Punkt r abhängig ist. LSDA (local spin density approximation) berücksichtigt zusätzlich noch den Spin. Bei der GGA (generalized gradient approximation) wird der Gradient der Dichte (Gleichung 23) mit einbezogen.

∂ρ(r)

∂r (23)

3.3.1 BH-LYP

BH-LYP ist ein Hybridfunktional aus Becke H&H für Austauschwechselwirkung und LYP für Korrelation. Becke H&H ist aus der Überlegung entstanden, die Austausch- wechselwirkung exakt, über die Austauschenergie der Kohn-Sham OrbitaleEX, zu be- handeln und die Korrelationsenergie über LSDA (E_C^LSDA) zu errechnen (Gleichung 24) [30].

E_XC =E_X +E_C^LSDA (24)

(18)

4 Auswertung und Diskussion 18

Zusammen mit dem LYP-Funktional ergibt sich für BH-LYP Gleichung 25 [11][30].

E_XC^{BHLY P} = 0,5E_X^HF + 0,5E_X^LDA/88+E_C^{LY P} (25) 3.3.2 PBE0

PBE0 ist ein Hybridfunktional, welches auf dem PBE-Funktional aufbaut [31]. Die Austausch-Korrelations-Energie von PBE0 (E_XC^{P BE0}) (Gleichung 26) ergibt sich als Sum- me der Austausch-Korrelations-Energie von PBE (E_XC^GGA) und einem Viertel der Diffe- renz des Hartree-Fock-Austauschs (E_X^HF) mit dem Austausch aus PBE (E_X^GGA) [31].

E_XC^{P BE0} =E_XC^GGA+1

4(E_X^HF −E_X^GGA) (26) Das PBE-Funktional beruht auf GGA und zeichnet sich dadurch aus, dass alle Para- meter fundamentale Naturkonstanten sind [32].

4 Auswertung und Diskussion

Für die Kristallstrukturen wurden die in Abbildung 10 gezeigten Nummerierungen benutzt. Die für die Messung der Absorptionsspektren verwendeten Methoden sind in Abschnitt 2.2 erläutert. Die Symmetrie und die Art des Übergangs wurde anhand von TDDFT-Rechnungen und Vergleiche mit anderen Quellen bestimmt. Bei Zuständen mit E-Symmetrie wurden, aufgrund der in Abschnitt 2.5.2 erläuterten Umstände, die Energien gemittelt und die Oszillatorstärken addiert, um den Zustand zu erhalten.

Aussagen über die Güte werden anhand des RMSD (Gleichung 27) getroffen. Neben den in diesem Kapitel gezeigten Spektren befinden sich weitere Spektren im Abschnitt 6.

Diese enthalten neben den Spektren auch Linienspektren, sowie das experimentelle Spektrum aus den Quellen und das mit engauge digitizer eingelesene Spektrum.

RM SD=

v u u t

1 n

n

X

i

(x_i−x)² (27)

Ziel dieser Arbeit ist es die verschiedenen DFT/MRCI-Ansätze und Parametersät- ze zu validieren und die im Hinblick auf Genauigkeit und Rechnerresourcen optimale Kombination von Operator, Parametersatz und Selektionsschwellenwert Tabelle 2 zu ermitteln. Dazu werden die errechneten Ergebnisse mit experimentellen Absorptionss- pektren verglichen. Für die Rechenzeit t(Parametersatz Selektionsschwellenwert) kann allgemein Gleichung 28 angenommen werden.

t(short0.8E_h)> t(standard0.8E_h)> t(standard1.0E_h) (28)

(19)

Abbildung 10: Nummerierungen für die Kristallstruktur; M=Ru, Os, Fe Dabei zu prüfende Hypothesen sind:

1) Die Kombination aus standard und 1.0 ergibt für den jeweiligen Operator immer die besten Ergebnisse.

2) R2018 ergibt für die jeweilige Kombination die besten Ergebnisse, da er für Über- gangsmetallkomplexe bessere Ergebnisse erzielt als die anderen Operatoren [12].

3) Die besten Ergebnisse für den Ruthenium-Komplex erzielt, da für Eisen zusätzliche Korrelation der Valenz- und der inneren Elektronen berücksichtigt werden muss, wäh- rend für Osmium zusätzlich spinabhängige relativistische Effekte zum Tragen kommen.

4) Der Osmium-Komplex wird besser beschrieben als der Eisen-Komplex, da die rela- tivistischen Effekte teilweise durch das verwendete ECP (Abschnitt 3.2) berücksichtigt wurden.

5) Original und R2018 ähneln sich in ihren Ergebnissen, da sie unter anderem eine ähnliche Dämpfungsfunktion bzw. einen ähnlichen Verlauf der Dämpfungsfunktion besitzen.

6) R2016 und R2017 ähneln sich in ihren Ergebnissen, da sie unter anderem die selbe Dämpfungsfunktion besitzen.

7) R2016 und R2017 unterschätzen die Energien [12].

8) Bei R2016 und R2017 kommt es bei der Kombination standard 0.8 zu Fehlerkom- pensation, da die Dämpfungsfunktion (Abschnitt 2.4.5) bis 0.8 etwas zu hoch liegt und dadurch Energien überschätzt werden.

9) Original und R2018 ergeben für die Kombination standard 0.8 schlechte Ergebnisse, da die Dämpfungsfunktion (Abschnitt 2.4.5) bis 0.8 hoch liegt und dadurch Energien überschätzt werden.

(20)

Tabelle 2: Übersicht über die zu vergleichenden Kombinationen Operator Parametersatz Selektionsschwellenwert

Original standard 1.0

Original short 0.8

Original standard 0.8

R2016 standard 1.0

R2016 short 0.8

R2016 standard 0.8

R2017 standard 1.0

R2017 short 0.8

R2017 standard 0.8

R2018 standard 1.0

R2018 short 0.8

R2018 standard 0.8

4.1 MO-Schemata

In allen MO-Schemata (Abschnitt 4.2.2, Abschnitt 4.3.2 und Abschnitt 4.4.2) sind 17 Orbitale mit den zugehörigen Energien in eV abgebildet. Die 6 energetisch niedrigsten abgebildeten Orbitale sind im Grundzustand besetzte Orbitale. Aus diesen erfolgen fast alle relevanten Anregungen. Die restlichen 11 abgebildeten Orbitale sind im Grundzu- stand unbesetzt. Die 2 energetisch höchsten abgebildeten Orbitale sind d-Orbitale. Alle Komplexe weisen eine pseudooktedrische Struktur auf, wodurch 3 d-Orbitale energetisch abgesenkt und 2 d-Orbitale energetisch angehoben werden. Zusätzlich hat es zur Folge, dass die Orbitale, im Gegensatz zur oktaedrischen Struktur, nicht perfekt entartet sind. Die 3 energetisch niedrigeren abgebildeten d-Orbitale entsprechen dem t_2g Orbital eines oktaedrischen Komplexes, während die energetisch höchsten abgebildeten d-Orbitale deme_2g Orbital entsprechen. Die MC-Übergange (Abschnitt 2.1.1) sind demnach symmetrieverbotene Übergänge, die eine geringe oder keine Oszillatorstärke besitzen. Im Experiment kann die Intensität der MC-Übergänge höher liegen, da die Symmetrie aufgrund der Temperatur kurzzeitig aufgehoben werden kann.

4.2 Tris(2,2’-bipyridin)-Ru(II)

4.2.1 Kristallstruktur

Die Daten wurden nach der Geometrieoptimierung mittels des Programms jmol bestimmt und mit experimentellen Kristallstrukturen [33] verglichen. In Tabelle 12 (An- hang) sind in rot Winkel mit einer Abweichung von über 2,5^◦ und Bindungslängen mit einer Abweichung von über 1pm markiert.

Anhand der Schwingungsfrequenzen wurde überprüft, ob es sich um ein Minimum han- delt. Die optimierte Geometrie enthält keine imaginären Frequenzen und ist damit ein Minimum. Alle Liganden sind im Bezug auf ihre Bindungslängen und Winkel gleich.

(21)

Tabelle 3: Orbitalschema für Tris(2,2’-bipyridin)-Ru(II) E [eV] Besetzung Orbital Symmetrie

A₁ -13.49 2 H-5 a

E -13.42 4 H-4 a

H-3 b

E -12.71 4 H-2 b

H-1 a

A1 -12.63 2 H a

A₂ -6.61 0 L b

E -6.52 0 L+1 a

L+2 b

A₂ -5.76 0 L+3 b

E -5.37 0 L+4 b

L+5 a

A₁ -5.3 0 L+6 a

E -5.18 0 L+7 b

L+8 a

E -3.12 0 L+12 b

L+13 a

Die Bindungslängen weichen bis zu 1,9 pm im Ring und an der Metall-Ligand Bindung (Ru-N) um 2,67 pm ab. Nur die Bindung N1-C5 und C3-C4 haben eine Abweichung kleiner 1 pm zum Experiment. Die Abweichung der Metall-Ligand Bindung lässt sich dadurch erklären, dass diese innerhalb der Rechnung schwer zu beschreiben ist. Die teils hohen Abweichungen der Bindungen im Ring lassen sich durch die Temperatur erklä- ren, welche im Experiment bei 105 K liegt, während die Rechnung von 0 K ausgeht, da die Abweichungen bei einem Vergleich mit bei einer höheren Temperatur experimentell bestimmten Kristallstruktur anstiegen. Die Abweichung der Winkel befindet sich meist unter 1,5^◦. Der einzige Winkel über dieser Abweichung ist N1-C5-C6-N2 mit einer Abweichung von 5,1^◦, welcher die Verdrehung der Ebenen der Pyridyl-Ringe im Bipyridin gegeneinander beschreibt. Der Unterschied beim Winkel N1-C5-C6-N2 und bei der Bindungslänge C4-C5 könnten auf Kristallpackungseffekte zurückzuführen sein, da in der gemessenen Kristallstruktur sich in diesem Bereich das Gegenion P F₆⁻ befindet [33].

4.2.2 MO-Schema

Die in Abschnitt 4.1 getroffenen Aussagen gelten auch für den Ruthenium-Komplex. Die Differenz zwischen demt_2g Orbital und dem e_2g beträgt ca. 9,6 eV. Die Energiediffernz zwischen HOMO (-12,63 eV) und LUMO (6,61 eV) beträgt 6,02 eV. Die energetisch niedrigstgelegenen Anregungen haben MLCT-Charakter. LC-Übergänge treten erst bei höheren Energien auf.

(22)

Abbildung 11: MO-Schema für Tris(2,2’-bipyridin)-Ru(II)

(23)

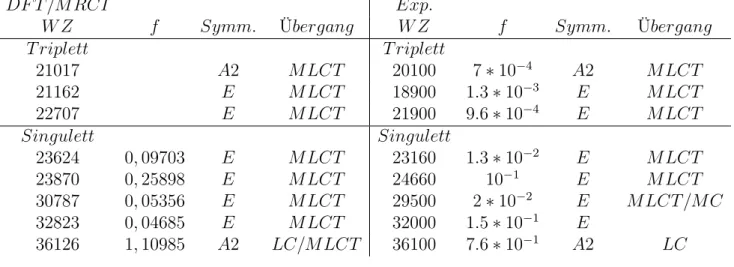
Tabelle 4: Beispiel der Zuordnung für Tris(2,2’-bipyridin)-Ru(II) unter Verwendung der Werte von R2018 standard 1.0, f ist die Oszillatorstaerke und WZ ist incm⁻¹

DF T /M RCI Exp.

W Z f Symm. Übergang W Z f Symm. Übergang

T riplett T riplett

21017 A2 M LCT 20100 7∗10⁻⁴ A2 M LCT

21162 E M LCT 18900 1.3∗10⁻³ E M LCT

22707 E M LCT 21900 9.6∗10⁻⁴ E M LCT

Singulett Singulett

23624 0,09703 E M LCT 23160 1.3∗10⁻² E M LCT

23870 0,25898 E M LCT 24660 10⁻¹ E M LCT

30787 0,05356 E M LCT 29500 2∗10⁻² E M LCT /M C

32823 0,04685 E M LCT 32000 1.5∗10⁻¹ E

36126 1,10985 A2 LC/M LCT 36100 7.6∗10⁻¹ A2 LC

4.2.3 Zuordnung

Die Zuordnung wurde unter Berüksichtigung der Symmetrie, der Oszillatorstärke und den Orbitalen der Übergänge vorgenommen. Experimentelle Werte wurden nur errechneten Übergängen zugeordnet, wenn diese die selbe Symmetrie aufweisen und sich die Oszillatorstärken um maximal den Faktor 10 unterscheiden. Dabei wurden auch die Or- bitale berücksichtigt. D.h. z.B. der Übergang bei 23160cm⁻¹ wurde bei jeder Kombina- tion jedes Operators einem HOMO-1/HOMO-2 -> LUMO Übergang zugeordnet, wäh- rend der Übergang bei 24600cm⁻¹immer HOMO-1/HOMO-2 -> LUMO+1/LUMO+2 Übergängen zugeordnet wurde. Dabei wurde für alle Übergänge außer für den Über- gang bei 36100cm⁻¹ die richtige Anregungsart wiedergegeben. Dieser Übergang ergibt aufgrund seiner hohen Oszillatorstärke einen hohen Peak in den Spektren (u.a. Abbil- dung 15,Abbildung 16, Abbildung 14). Der Übergang enthält neben hohen LC-Anteilen auch hohe MLCT-Anteile. Während LC-Übergänge oftmals eine hohe Intensität aufweisen, ist dies für MLCT-Übergänge eher unwahrscheinlich.

Für die Triplettzustände ist keine Oszillatorstärke angegeben, da nur die Anregungen von T1 nach TX (X>1) berechnet wurden. Für die Anregungsenergie von S0 nach TX wurde Gleichung 29 verwendet.

E(S0→T X) =E(T1)−E(S0) +E(T1→T X) (29) In Tabelle 5 ist in rot der jeweils schlechteste und in grün der jeweils beste Operator einer Kombination aus Selektionsschwellenwert und Parametersatz markiert. Bei der Zuordnung wurde der Wert bei 26230cm⁻¹ (ca. 381 nm) nicht berücksichtigt, da er in anderen Quellen [34]nicht vorkommt und die Oszillatorstärken der meisten berechneten Spektren dieser Arbeit in diesem Bereich (so fern vorhanden) nur sehr gering ausfallen.

Die experimentellen Werte mit 18900 cm⁻¹ (ca. 529 nm), 20100 cm⁻¹ (ca. 498 nm) und 21900cm⁻¹ (ca. 457 nm) sind Triplettzuständen zuzuordnen [35] und wurden mit

(24)

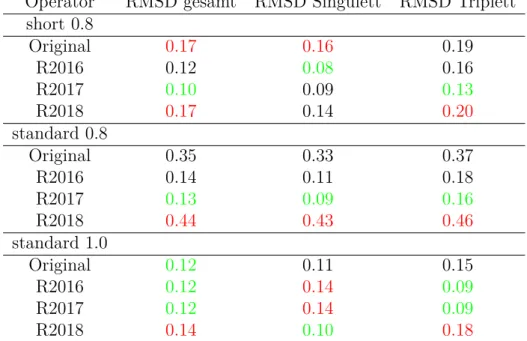
Tabelle 5: RMSD in eV aller Hamiltonoperatoren für Tris(2,2’-bipyridin)-Ru(II); für Singulett wurden 5 Werte und für Triplett 3 Werte, sowie gesamt 8 Werte verglichen

Operator RMSD gesamt RMSD Singulett RMSD Triplett short 0.8

Original 0.17 0.16 0.19

R2016 0.12 0.08 0.16

R2017 0.10 0.09 0.13

R2018 0.17 0.14 0.20

standard 0.8

Original 0.35 0.33 0.37

R2016 0.14 0.11 0.18

R2017 0.13 0.09 0.16

R2018 0.44 0.43 0.46

standard 1.0

Original 0.12 0.11 0.15

R2016 0.12 0.14 0.09

R2017 0.12 0.14 0.09

R2018 0.14 0.10 0.18

errechneten Anregungsenergien von Triplettzuständen verglichen.

4.2.4 Spektren

Das errechnete Spektrum in Abbildung 12 ähnelt dem experimentellen Spektrum [1]

sehr. Auffällig ist, dass im Bereich 350-380 nm das Spektrum der Rechnung eine Inten- sität nahe null aufweist, während die gemessenen Werte deutlich höher liegen (um 0,1).

Anzumerken ist, dass die experimentellen Messwerte [1] in diesem Bereich stark streuen (Abbildung 13) und andere Quellen [34] eine geringere Intensität in diesem Bereich aufweisen. Im Bereich 350-380 nm befindet sich in der Rechnung nur ein Zustand. Dieser hat A₁-Symmetrie und eine Oszillatorstärke von null. Im Bereich 300-350 nm befinden sich in der Rechnung größtenteils MC-Übergänge. Aufgrund von temperaturbedingten Einflüssen ergeben diese im experimentellen Spektrum eine deutlich höhere Intensität.

Weiterhin ist zu beachten, dass der experimentelle Graph im Bereich 450-500 nm später abfällt als der der Rechnung. Dies liegt voraussichtlich an Triplettzuständen, welche in den berechneten Spektren nicht berücksichtigt wurden. Für Abbildung 12 liegen die beiden hohen Oszillatorstärken im Bereich 400-450 nm nahe zusammen, weswegen nur ein Peak, anstelle von zweien, wie im Experiment, zu sehen ist. Nicht in allen Spektren ist die Wiedergabe der zwei Peaks in den Oszillatorstärken sichtbar. Der höchste Peak befindet sich bei ca. 275 nm. Im Bereich 250-275 nm befinden sich LC-Übergänge oder Übergänge mit hohem LC-Anteil. Die restlichen Bereiche haben MLCT-Übergänge.

Die Beschreibung trifft auch auf alle anderen Spektren des Ruthenium-Komplexes zu.

(25)

Abbildung 12: Vergleich der Ergebnisse für die Singulettanregungen der Rechnung mit R2018 standard 1.0 E_h mit experimentellen Daten für Tris(2,2’- bipyridin)-Ru(II)

Abbildung 13: Experimentelle Daten für Tris(2,2’-bipyridin)-Ru(II); die vertikalen schwarzen Balken repräsentieren mit TDDFT errechnete Oszillatorstär- ken (blauverschoben um 800 cm⁻¹) [1]

(26)

Abbildung 14: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (standard 1.0 E_h) mit experimentellen Daten für Tris(2,2’-bipyridin)- Ru(II)

Allerdings sind einige Spektren geringfügig verschoben. Genauere Informationen und weitere Spektren befinden sich im Anhang (Abschnitt 6).

In Abbildung 14 sind die Spektren aller Operatoren mit der Kombination standard 1.0 und das experimentelle Spektrum [1] zu sehen. Hier geben Original und R2018 den groben Verlauf des experimentellen Spektrums [1] sehr gut wieder. Die Spektren mit R2016 und R2017 sind im Vergleich zu den Spektren mit Original und R2018 rotverschoben (zu höheren Wellenlängen). Deswegen wird von ihnen (R2016/R2017) sowohl der Peak bei ca 275 nm, als auch den Peaks bei ca 400 nm, schlechter und die Peaks bei 300-350 besser wiedergegeben, als bei den anderen beiden (Original/R2018).

Für standard 1.0 ergeben alle Operatoren sehr gute Ergebnisse (Tabelle 5) (RMSD unter 0,21 eV). Original, R2016 und R2017 haben mit 0,12 eV das beste Ergebnis, wäh- rend R2018 mit 0,14 eV knapp dahinter liegt. Auffällig ist, dass R2016 und R2017 alle Singulettzustände unterschätzen. Bei Original und R2018 ist für die Singulettzustände kein Trend erkennbar. Original und R2018 ergeben zu hohe Werte für die Triplettzu- stände. Es liegt nahe, dass für R2016 und R2017 eine Fehlerkompensation zwischen der allgemeinen Überschätzung der Triplettenergien jedes Operators und dem Unterschät- zen der Energie für diese beiden Operatoren auftritt. Wenn nur die Singulettzustände berücksichtigt werden, erzielen R2018 (0,10 eV) und Original (0,11 eV) bessere Ergeb- nisse als R2016 (0,14 eV) und R2017 (0,14 eV). Hypothesen 2, 5, 6 und 7 treffen für diese Kombination zu.

In Abbildung 15 sind die Spektren aller Operatoren mit der Kombination short 0.8 und das experimentelle Spektrum [1] zu sehen. Insgesamt ähnelt Abbildung 15 Abbil-

(27)

Abbildung 15: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (short 0.8E_h) mit experimentellen Daten des Tris(2,2’-bipyridin)-Ru(II) dung 14. Im Gegensatz zu Abbildung 14 geben hier jedoch alle Operatoren den groben Verlauf des experimentellen Spektrums [1] sehr gut wieder. Außerdem ist die Rotver- schiebung hier geringer.

Für short 0.8 ergeben alle Operatoren sehr gute Ergebnisse (Tabelle 5) (RMSD unter 0,21 eV). R2016 (0,12 eV)und R2017 haben (0,10 eV) die besten Ergebnisse. Original und R2018 liegen mit 0,17 eV etwas dahinter. Jeder Operator beschreibt die Singu- lettzustände besser als die Triplettzustände. Insgesamt wird von allen Operatoren die Energie überschätzt. Hypothesen 5 und 6 treffen für diese Kombination zu. Hingegen treffen Hypothesen 2 und 7 für diese Kombination nicht zu.

In Abbildung 16 sind die Spektren aller Operatoren mit der Kombination standard 0.8 und das experimentelle Spektrum [1] zu sehen. Abbildung 16 unterscheidet sich deutlich von Abbildung 15 und Abbildung 14. Hier geben R2016 und R2017 den groben Verlauf des experimentellen Spektrums [1] besser wieder, als Original und R2018, wobei R2018 weiter abweicht als Original. Die Rotverschiebung ist hier am stärksten.

Für standard 0.8 ergeben R2016 (0,14 eV) und R2017 (0,13 eV) sehr gute Ergebnisse (RMSD unter 0,21 eV)(Tabelle 5). Original (0,33 eV) und R2018 (0,44 eV) liefern deutlich schlechtere Ergebnisse. Jeder Operator beschreibt die Singulettzustände besser als die Triplettzustände und überschätzt die Energie der Triplettzustände. Insgesamt wird von Original und R2018 Operatoren die Energie deutlich überschätzt. Bei R2016 und R2017 ist für die Singulettzustände kein Trend erkennbar. Es liegt nahe, dass für R2016 und R2017 eine Fehlerkompensation zwischen der Überschätzung der Energien der Zustände durch die Dämpfungsfunktion und dem allgemeinem Unterschätzen der

(28)

Abbildung 16: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (standard 0.8 E_h) mit experimentellen Daten für Tris(2,2’-bipyridin)- Ru(II)

Energie für diese beiden Operatoren auftritt. Hier treffen Hypothesen 5, 6, 7, 8 und 9 für diese Kombination zu. Hypothese 2 trifft für diese Kombination nicht zu.

4.2.5 Fazit

Unter Berücksichtigung der Singulett- und Triplettenergien ist im Hinblick auf Ge- nauigkeit und Rechnerresourcen R2017 mit short 0.8 die optimale Kombination von Operator, Parametersatz und Selektionsschwellenwert, da er eine im Vergleich zu anderen Kombinationen geringere Rechenzeit benötigt und die besten Ergebnisse erzielt.

Hypothese 1 trifft nicht zu. Die Kombination von Original und R2018 mit standard 0.8 ist nicht zu empfehlen.

4.3 Tris(2,2’-bipyridin)-Os(II)

Die Daten wurden nach der Geometrieoptimierung mittels des Programms jmol bestimmt und mit experimentellen Kristallstrukturen [36] verglichen. In Tabelle 13 sind in rot Winkel mit einer Abweichung von über 2,5^◦ und Bindungslängen mit einer Ab- weichung von über 1pm markiert.

Die Bindungslängen weichen bis zu 3,5 pm im Ring und an der Metall-Ligand Bindung (Os-N) um 3,4 pm ab. Nur die Bindung N1-C5 hat eine Abweichung kleiner 1 pm zum Experiment. Die Abweichung der Metall-Ligand Bindung lässt sich dadurch erklären,

(29)

Abbildung 17: MO-Schema für Tris(2,2’-bipyridin)-Os(II)

dass diese innerhalb der Rechnung schwer zu beschreiben ist. Die Abweichung der Win- kel befinden sich unter 2,5^◦. Die Abweichungen der Bindungslängen sind höher als die des Ruthenium-Komplexes.

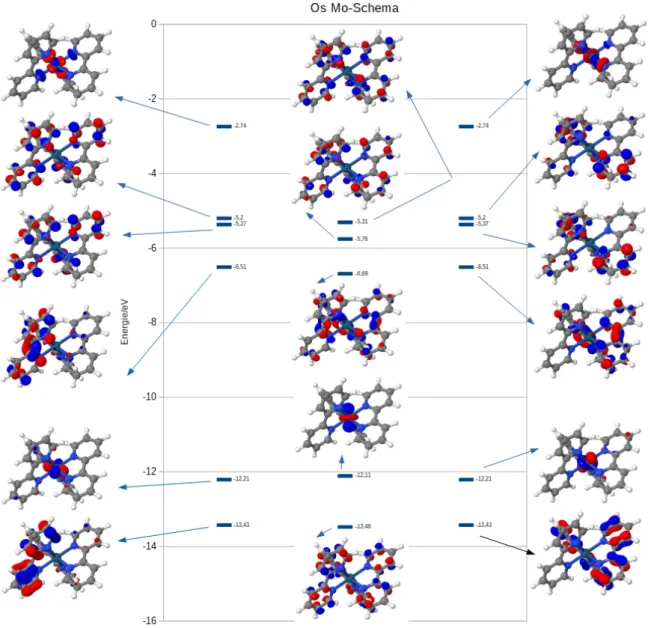
4.3.2 MO-Schema

Das MO-Schema für den Osmium-Komplex in Abbildung 17 ist analog zu dem des Ru-Komplex in Abbildung 11. Das Aussehen der Orbitale ähnelt dem im Ruthenium- Komplex, wobei bei den nahezu entarteten Orbitalen die energetische Reihenfolge teilweise getauscht wurde. Die untersten 3 und die obersten 8 π-Orbitale sind denen im Ru-Komplex energetisch sehr ähnlich (Unterschiede unter 0,03 eV). Das LUMO ist im Osmium-Komplex um 0,08 eV niedriger, währen die d-Orbitale energetisch deutlich höher liegen. Die Differenz zwischen dem t_2g Orbital und dem e_2g beträgt ca. 9,4 eV und ist damit geringer als beim Ru-Komplex. Im Vergleich zum Ruthenium-Komplex

(30)

Tabelle 6: Orbitalschema für Tris(2,2’-bipyridin)-Os(II) E [eV] Besetzung Orbital Symmetrie

A₁ -13.48 2 H-5 a

E -13.43 4 H-4 a

H-3 b

E -12.21 4 H-2 b

H-1 a

A1 -12.11 2 H a

A₂ -6.69 0 L b

E -6.51 0 L+1 b

L+2 a

A₂ -5.76 0 L+3 b

E -5.37 0 L+4 b

L+5 a

A₁ -5.31 0 L+6 a

E -5.2 0 L+7 a

L+8 b

E -2.74 0 L+12 b

L+13 a

ist die Energiediffernz zwischen HOMO (-12,11 eV) und LUMO (6,69 eV) mit 5,42 eV deutlich geringer. Übergänge befinden sich damit in einem ähnlichem energetischen Bereich.

4.3.3 Zuordnung

Die Zuordnung wurde nach den selben Kriterien, wie im entsprechenden Ruthenium- Komplex (Abschnitt 4.2.3) vorgenommen.

In Tabelle 8 ist in rot der jeweils schlechteste und in grün ist der jeweils beste Operator einer Kombination aus Selektionsschwellenwert und Parametersatz markiert. Der Wert Tabelle 7: Beispiel der Zuordnung für Tris(2,2’-bipyridin)-Os(II) unter Verwendung der Werte von R2018 standard 1.0, f ist die Oszillatorstaerke und WZ ist incm⁻¹

T riplett T riplett

18909 E M LCT 16140 1.5∗10⁻2 E

18690 0,00792 A2 M LCT 17740 7∗10⁻³ A2 M LCT

20999 0,18746 E M LCT 20700 5∗10⁻² E M LCT

21932 0,26796 E M LCT 22310 2.1∗10⁻¹ E M LCT

26208 0,01539 A2 M LCT 24160 9.3∗10⁻³ A2 M LCT

30099 0,11446 E M LCT 27890 2.3∗10⁻¹ E M LCT

34621 0,80722 E LC 36530 3.8∗10⁻¹ E LC

(31)

Tabelle 8: RMSD in eV aller Hamiltonoperatoren für Tris(2,2’-bipyridin)-Os(II); insgesamt wurden 7 Werte (1 Triplett und 6 Singuletts) verglichen

Operator RMSD short 0.8 RMSD standard 0.8 RMSD standard 1.0

Original 0,22 0,37 0,24

R2016 0,20 0,23 0,19

R2017 0,21 0,22 0,19

R2018 0,23 0,42 0,22

Abbildung 18: Vergleich der Ergebnisse für die Singulettanregungen der Rechnung mit R2018 standard 1.0 E_h mit experimentellen Daten für Tris(2,2’- bipyridin)-Os(II)

mit 16140cm⁻¹ (ca. 620 nm) wurde mit errechneten Triplettzuständen verglichen [37].

4.3.4 Spektren

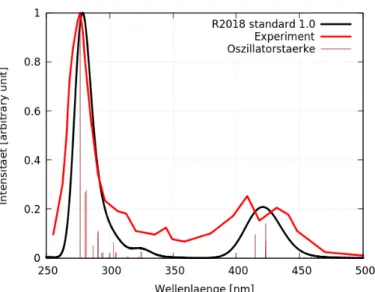
Das errechnete Spektrum in Abbildung 18 ähnelt dem experimentellen Spektrum [2]

sehr. Auffällig ist, dass im Bereich 360-430 nm das Spektrum der Rechnung eine In- tensität nahe null aufweist, während die gemessenen Werte deutlich höher liegen. Im Bereich 360-430 nm befinden sich in der Rechnung nur zwei Zustände. Diese haben eine geringe Oszillatorstärke. Im Bereich von ca. 300-430 nm hat das experimentelle Spek- trum eine deutlich höhere Intensität, als das errechnete Spektrum. Da sich im Bereich 300-430 nm nur Übergänge ohne oder mit nur sehr geringem MC-Anteil befinden, kann diese Abweichung nicht von temperaturbedingten Einflüssen herrühren. Weiterhin ist zu beachten, dass der experimentelle Graph im Bereich 500-550 nm eine höhere Inten- sität aufweist als der der Rechnung. Dies liegt vorraussichtlich an Triplettzuständen, die in den quantenchemisch berechneten Spektren nicht berücksichtigt wurden. Da Os- mium ein Schwermetall ist, kann ein besonders hoher Einfluss der Triplettzustände auf das Spektrum erwartet werden. Der Peak bei ca. 360 nm lässt sich blauverschoben im

(32)

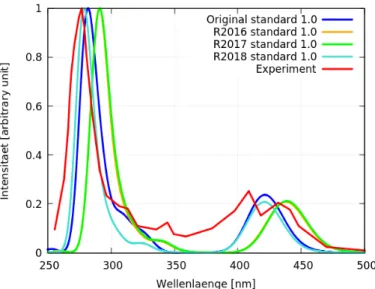
Abbildung 19: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (standard 1.0 E_h) mit experimentellen Daten für Tris(2,2’-bipyridin)- Os(II)

errechneten Spektrum im Bereich von ca. 300-360 nm wiederfinden. Der höchste Peak in Abbildung 18 befindet sich bei ca. 275 nm. Im Bereich 250-290 nm befinden sich LC-Übergänge oder Übergänge mit hohem LC-Anteil und MC-Übergänge mit geringen Oszillatorstärken. Die restlichen Bereiche haben MLCT-Übergänge. Die Beschreibung trifft auch auf alle anderen Spektren für den Osmium-Komplex zu. Allerdings sind einige Spektren verschoben. Genauere Informationen und weitere Spektren befinden sich im Anhang (Abschnitt 6).

In Abbildung 19 sind die Spektren aller Operatoren mit der Kombination standard 1.0 und das experimentelle Spektrum [2] zu sehen. Hier geben alle Operatoren den groben Verlauf des experimentellen Spektrums [2] wieder. Die Spektren mit R2016 und R2017 sind im Vergleich zu den Spektren mit Original und R2018 rotverschoben (zu höheren Wellenlängen). Deswegen wird von ihnen (R2016/R2017) der Peak bei ca. 275-300 nm und der Peak bei ca. 460 nm schlechter, sowie die Peaks bei ca. 300 nm und ca. 360 nm besser, wiedergegeben als bei den anderen beiden (Original/R2018).

Für standard 1.0 ergeben alle Operatoren gute Ergebnisse (Tabelle 8) (RMSD unter 0,31 eV). R2016 und R2017 haben mit 0,19 eV das beste Ergebnis. Hingegen liegen Original mit 0,24 eV und R2018 mit 0,22 eV etwas dahinter. Auffällig ist, dass R2016 und R2017 die Singulettzustände tendenziell unterschätzen, während Original und R2018 die Singulettzustände tendenziell überschätzen. Alle Operatoren ergeben zu hohe Werte für die Triplettzustände. Es liegt nahe, dass für R2016 und R2017 eine Fehlerkompensation zwischen der allgemeinen Überschätzung der Triplettenergien jedes Operators und dem Unterschätzen der Energie für diese beiden Operatoren auftritt.

Dies hat allerdings beim Os-Komplex weniger Auswirkungen auf den RMSD als beim

(33)

Abbildung 20: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (short 0.8E_h) mit experimentellen Daten des Tris(2,2’-bipyridin)-Os(II) Ru-Komplex, da beim Os-Komplex deutlich weniger Triplettzustände berücksichtigt wurden. Hypothesen 5, 6 und 7 treffen für diese Kombination zu. Für diese Kombina- tion trifft Hypothese 2 nicht zu.

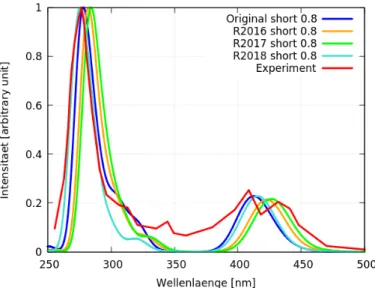
In Abbildung 20 sind die Spektren aller Operatoren mit der Kombination short 0.8 und das experimentelle Spektrum [2] zu sehen. Abbildung 20 und Abbildung 19 ähneln sich stark. Der linke Peak im Spektrum von R2018 ist im Vergleich zu Abbildung 19 rotverschoben.

Für short 0.8 ergeben alle Operatoren gute Ergebnisse (Tabelle 8) (RMSD unter 0,31 eV). R2016 hat mit 0,20 eV das beste Ergebnis, während R2017 mit 0,21 eV, Original mit 0,22 eV und R2018 mit 0,23 eV knapp dahinter liegen. Original unterschätzt die Singulettzustände, während alle Operatoren zu hohe Werte für die Triplettzustände ergeben. Hier treffen Hypothesen 5 und 6 für diese Kombination zu. Hypothesen 2 und 7 treffen für diese Kombination nicht zu.

In Abbildung 21 sind die Spektren aller Operatoren mit der Kombination short 0.8 und das experimentelle Spektrum [2] zu sehen. Es unterscheidet sich, analog zum Ruthenium-Komplex, deutlich von Abbildung 20 und Abbildung 19. Die Spektren mit Original und R2018 sind im Vergleich zu den Spektren mit R2016 und R2017 blauverschoben (zu niedrigeren Wellenlängen). Deswegen werden von ihnen (Original/R2018) der Peak bei ca. 275 nm und der Peak bei ca. 460 nm schlechter wiedergegeben als bei den anderen beiden (R2016/R2017).

(34)

Abbildung 21: Vergleich der Ergebnisse für die Singulettanregungen der Rechnungen (standard 0.8 E_h) mit experimentellen Daten für Tris(2,2’-bipyridin)- Os(II)

Für standard 0.8 ergeben R2016 (0,23 eV) und R2017 (0,22 eV) gute Ergebnisse (Tabelle 8) (RMSD unter 0,31 eV). Original (0,37 eV) und R2018 (0,42 eV) liefern wesentlich schlechtere Ergebnisse. Jeder Operator überschätzt die Energie der Triplettzu- stände. Original und R2018 überschätzen die Energie deutlich. Es liegt nahe, dass für R2016 und R2017 eine Fehlerkompensation zwischen der Überschätzung der Energien der Zustände durch die Dämpfungsfunktion und dem allgemeinem Unterschätzen der Energie für diese beiden Operatoren auftritt. Für diese Kombination treffen Hypothe- sen 5, 6, 7, 8 und 9 zu. Hypothese 2 trifft für diese Kombination nicht zu.

4.3.5 Fazit

Im Hinblick auf Genauigkeit und Rechnerressourcen ist die optimale Kombination von Operator, Parametersatz und Selektionsschwellenwert R2016 mit short 0.8 (0,20 eV), da er eine im Vergleich zu anderen Kombinationen geringere Rechenzeit benötigt und nach R2016 standard 1.0 (0,19 eV) und R2017 standard 1.0 (0,19 eV) die besten Ergeb- nisse erzielt. Hypothese 3 trifft zu und Hypothese 1 trifft nicht zu. Auch für Tris(2,2’- bipyridin)-Os(II) ist die Kombination von Original und R2018 mit standard 0.8 nicht zu empfehlen.

4.4 Tris(2,2’-bipyridin)-Fe(II)

Die Daten wurden nach der Geometrieoptimierung mittels des Programms jmol bestimmt und mit experimentellen Kristallstrukturen [38] verglichen. In Tabelle 14 sind in rot Winkel mit einer Abweichung von über 2,5^◦ und Bindungslängen mit einer Ab-

(35)

Abbildung 22: MO-Schema für Tris(2,2’-bipyridin)-Fe(II) weichung von über 1pm markiert.

Die Bindungslängen weichen bis zu 3,0 pm im Ring und an der Metall-Ligand Bindung (Os-N) um 2,7 pm ab. Nur die Bindungen N1-C1, C1-C2 und C4-C5 haben eine Ab- weichung kleiner 1 pm zum Experiment. Die Abweichung der Metall-Ligand Bindung lässt sich dadurch erklären, dass diese innerhalb der Rechnung schwer zu beschreiben ist. Die Abweichung der Winkel befinden sich unter 2,0^◦. Die Abweichungen der Bin- dungslängen sind höher als die des Ruthenium-Komplexes und geringer als die des Osmium-Komplexes.

(36)

Tabelle 9: Orbitalschema für Tris(2,2’-bipyridin)-Fe(II) E [eV] Besetzung Orbital Symmetrie

A₁ -14 2 H-5 a

E -13,96 4 H-4 a

H-3 b

A1 -13,45 2 H-2 a

E -13,42 4 H-1 b

H a

E -6,61 0 L a

L+1 b

A₂ -6,56 0 L+2 b

A₂ -5,78 0 L+3 b

E -5,46 0 L+4 a

L+5 b

A₁ -5,39 0 L+6 a

E -5,17 0 L+7 b

L+8 a

E -2,49 0 L+16 a

L+17 b

4.4.2 MO-Schema

Das MO-Schema unterscheidet sich deutlich von dem der anderen Komplexe in Ab- bildung 11 und in Abbildung 17. Die in Abschnitt 4.1 getroffenen Aussagen gelten trotzdem auch für den Eisen-Komplex. Grob ähneln die Orbitale denen der anderen Komplexe. Sie weisen aber auch signifikante Unterschiede, wie z.B. Anteile auf den Liganden bei den d-Orbitalen, auf. Zusätzlich sind bei den besetzten Orbitalen, im Ge- gensatz zu den anderen Komplexen, die π-Orbitale energetisch über den d-Orbitalen.

Das HOMO ist entartet. Die Orbitale bei 13,42 eV, 5,78 eV und 5,17 eV lassen sich in den anderen MO-Schemata bei ähnlicher Energie (Unterschiede unter 0,04 eV) wiederfinden. Die besetzten d-Orbitale sind im Vergleich zu den anderen Komplexen abgesenkt, während die unbesetzten d-Orbitale energetisch angehoben sind. Dadurch erhöht sich die Differenz zwischen dem t_2g Orbital und dem e_2g Orbital auf ca. 11,5 eV. Die energetische Differenz zwischen HOMO (13,42 eV) und LUMO (6,61 eV) steigt auf 6,81 eV.

4.4.3 Zuordnung

Die Zuordnung wurde nach den selben Kriterien, wie im entsprechenden Ruthenium- Komplex (Abschnitt 4.2.3) vorgenommen. Allerdings wurden Zustände beim Eisen- Komplex auch dann zugeordnet, wenn ihre Oszillatorstärke über den Faktor 10 abweicht, wenn dies nicht anders möglich war.

In Tabelle 11 ist in rot der jeweils schlechteste und in grün ist der jeweils beste Operator einer Kombination aus Selektionsschwellenwert und Parametersatz markiert.

(37)

Tabelle 10: Beispiel der Zuordnung für Tris(2,2’-bipyridin)-Fe(II) unter Verwendung der Werte von R2018 standard 1.0, f ist die Oszillatorstärke und WZ ist in cm⁻¹

16133 0,00026 E M C 19300 2∗10⁻³ E M LCT /M C

22439 0,00017 E M LCT /M C 19970 3∗10⁻² E M LCT

23852 0,03376 E M LCT /M C 21570 6∗10⁻² E M LCT

24247 0,00056 A2 M LCT 26480 1∗10⁻³ A2 M LCT

24378 0,03723 E M LCT /M C 23230 1∗10⁻² E M C/M LCT

31846 0,04433 E M LCT 29310 1∗10⁻² E M LCT

34912 0,39567 E M LCT /LC 34360 3∗10⁻¹ E LC/M LCT

Tabelle 11: RMSD in eV aller Hamiltonoperatoren für Tris(2,2’-bipyridin)-Fe(II); insgesamt wurden 7 Werte verglichen

Operator RMSD short 0.8 RMSD standard 0.8 RMSD standard 1.0

Original 0,49 0,37 0,31

R2016 0,57 0,35 0,22

R2017 0,43 0,40 0,25

R2018 0,34 0,62 0,27

Es wurden keine Triplettzustände verglichen, da in der der Quelle [2] alle Zustände Singulettzuständen zugeordnet wurden.

4.4.4 Spektren

Zwischen dem experimentellen Spektrum [2] und dem errechneten Spektrum in Abbil- dung 23 besteht nur eine sehr grobe Ähnlichkeit. Der Peak im Bereich von ca. 250-300 nm wird sehr gut wieder gegeben. Die Peaks bei ca. 440-510 nm erscheinen im errechneten Spektrum mit weitaus geringerer Oszillatorstärke und einer starken Blauverschie- bung Der Peak im Bereich 325-350 nm ist im errechneten Spektrum gar nicht zu sehen oder fällt aufgrund einer Rotverschiebung an den Rand des Peaks bei ca. 250-300 nm, wodurch er kaum noch zu erkennen wäre. Letzteres wird als wahrscheinlicher Erachtet, da dem Peak gut errechnete Werte aus diesem Bereich zugeordnet werden konnten.

Ein weiteres Indiz dafür ist der "Knickïm Spektrum bei ca. 300 nm, der von diesem Peak stammen könnte. Weiterhin ist zu beachten, dass sich im Bereich von 330-600 nm größtenteils MC-Übergänge oder Übergänge mit hohem MC-Anteil befinden. Aufgrund von temperaturbedingten Einflüssen ergeben diese im experimentellen Spektrum eine deutlich höhere Intensität. Dadurch ließe sich erklären, dass das errechnete Spektrum in diesem Bereich meist eine nahe 0 aufweist, während das experimentelle Spektrum meist deutlich darüber liegt. Im Bereich von 330 -275 nm befinden sich größtenteils MLCT-Übergänge mit teils hohen LC-Anteilen. Im Bereich von ca. 275-250 nm sind