Renormalisation of Radiative Neutrino Masses
Moritz Ernst Lothar Platscher
München 2015
Renormierung Radiativer Neutrinomassen
Masterarbeit
an der Fakultät für Physik der
Ludwig-Maximilians-Universität München
vorgelegt von
Moritz Ernst Lothar Platscher geboren in Schwäbisch Hall
München, den 30. September 2015
Masterarbeit
am
Max-Planck-Institut für Physik (Werner-Heisenberg-Institut) Föhringer Ring 6
80805 München
eingereicht bei der Fakultät für Physik der Ludwig-Maximilians-Universität München von Moritz Ernst Lothar Platscher
am 30. September 2015
Betreut von: Dr. habil. Georg Raffelt und
Dr. Alexander Merle
Abstract
In this thesis we study the renormalisation group effects which occur in models that gener- ate neutrino masses via radiative effects, i.e. through loop-diagrams. In the present analysis the key features are illustrated by studying one particular such model, the scotogenic model proposed by Ma in 2006. This model is very simple and yet it exhibits all aspects relevant to radiative neutrino mass generation. At the same time, the methods developed are easily generalised to more involved settings. To make the results as self-contained as possible, the necessary field theoretical concepts, as well as the basics of neutrino mass generation are discussed thoroughly.
One of the key results of this work is a numerical study of the renormalisation group equations in the model under consideration. Focussing on the neutrino mixing parameters, it is found that the running can be significant in certain regions of the parameter space.
The regions of interest are identified with the aid of approximate analytical equations, which are derived explicitly. These equations describe the energy scale dependence of the leptonic mixing angles, of the phases, and of all light neutrino masses. We compute the full set of renormalisation group equations, and consider the matching of the various effective theories which result from integrating out the heavy fields. This is done perturbatively up to one-loop order. Both diagrammatic and analytic matching conditions are given and an example of how to calculate the renormalisation group equations is presented. This allows anyone to reproduce the results, making them as transparent as possible.
Finally, it can be seen from the renormalisation group equations that, in certain param-
eter regimes, there is a hierarchy-type problem in the scotogenic model which threatens
to spoil its underlying discrete symmetry. However, this symmetry is crucial to preserve
the phenomenology of the model. Since avoiding this parity problem may spoil electroweak
symmetry breaking, some tension on the parameter space is generated.
The results presented in this thesis have been obtained by the author between Octo-
ber 2014 and September 2015 at the ‘Max-Planck-Institut für Physik (Werner-Heisenberg-
Institut)’ in Munich, Germany, under the supervision of Dr. habil. Georg Raffelt and
Dr. Alexander Merle. Parts of this thesis have been published in references [1, 2].
Contents
1 Introduction 1
2 Theoretical Preliminaries 3
2.1 Regularisation and Renormalisation . . . . 3
2.1.1 Dimensional Regularisation . . . . 4
2.1.2 Renormalisation . . . . 5
2.1.3 The Renormalisation Group and the Callan-Symanzik Equation . . 8
2.2 Effective Field Theories . . . . 11
2.2.1 The Decoupling Theorem . . . . 11
2.2.2 Effective Operators and Matching . . . . 13
2.3 Majorana Fermions . . . . 15
2.3.1 Constructing Majorana Particles . . . . 16
2.3.2 Lepton Number Violating Interactions . . . . 17
3 Massive Neutrinos and Physics Beyond the Standard Model 21 3.1 Neutrino Oscillations . . . . 21
3.2 Tree-Level Mass Generation . . . . 26
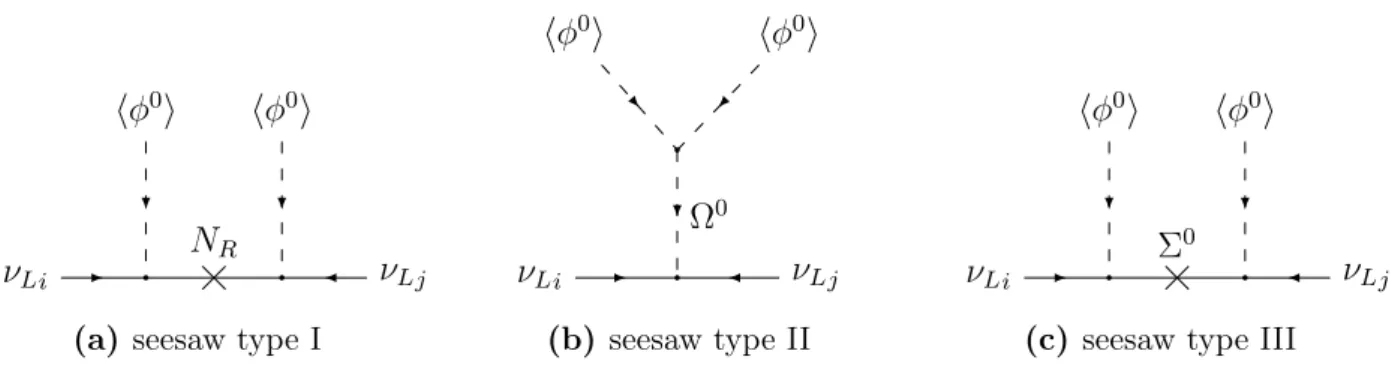
3.2.1 Seesaw Mechanism . . . . 27
3.2.2 Other Tree-Level Mechanisms . . . . 29
3.3 Loop-Level Mass Generation . . . . 30
3.3.1 The Scotogenic Model . . . . 30
3.3.2 More One-Loop Mechanisms . . . . 35
3.3.3 Other Radiative Mechanisms . . . . 35
4 Running Neutrino Masses and Leptonic Mixing Angles 37 4.1 Matching Conditions and the Effective Theories . . . . 37
4.1.1 Calculation of the Relevant Diagrams . . . . 38
4.1.2 Mass Matrix in the Effective Theories . . . . 40
4.1.3 Integrating out the Right-Handed Neutrinos . . . . 42
4.1.4 Integrating out the Inert Scalars . . . . 45
4.2 RGEs of the Scotogenic Model . . . . 46
4.2.1 Computing RGEs – the Neutrino Yukawa Matrix . . . . 46
4.2.2 Full Set of RGEs in the Scotogenic Model . . . . 52
4.3 Analytical RGEs for the Mixing Angles and Masses . . . . 54
4.3.1 Derivation of the Analytical RGEs . . . . 54
4.3.2 Analytical RGEs . . . . 56
5 Numerical Results 61 5.1 General Strategy . . . . 61
5.2 Numerical Analysis . . . . 62
5.2.1 Heavy Scalars . . . . 63
5.2.2 Similar Scalar and Right-Handed Neutrino Masses . . . . 66
5.2.3 Heavy Right-Handed Neutrinos . . . . 68
5.2.4 Inverted Mass Ordering . . . . 70
5.2.5 The Bottom-Up Approach . . . . 71
6 The Parity Problem of the Scotogenic Model 73 6.1 Vacuum Structure and Constraints . . . . 73
6.2 Analytical Estimates . . . . 75
6.3 Numerical Analysis . . . . 77
6.3.1 Breaking Scale . . . . 78
6.3.2 Avoiding the Breaking of Z
2. . . . 79
7 Summary and Outlook 81 A The PMNS Matrix 85 A.1 Diagonalisation of a Complex Symmetric Matrix . . . . 85
A.2 Extraction of Mixing Angles and Phases . . . . 86
B The Clifford Algebra in arbitrary dimensions 87 C Feynman Rules 89 C.1 The Scotogenic Model – Unbroken Electroweak Symmetry . . . . 89
C.2 The Scotogenic Model – Broken Electroweak Symmetry . . . . 95
D Loop Integrals 97 D.1 Computing Loop Integrals . . . . 97
D.2 The One-Point Function . . . . 98
D.3 The Two-Point Functions . . . . 98
D.4 The Three-Point Functions . . . . 99
D.5 The Four-Point Functions . . . . 100
Bibliography 101
Chapter 1 Introduction
The long standing problem of how to extend the Standard Model (SM) of elementary particle physics remains among the greatest challenges of modern science. On the one hand, collider experiments have found that the SM is a very accurate description of nature, highlighted by the discovery of the Higgs boson in 2012 [3, 4]. On the other hand, we see that the SM cannot explain certain phenomena, such as the identity of the observed Dark Matter (DM) in our Universe [5] and the origin of the small, but non-zero neutrino masses . 1 eV [6, 7].
In the absence of any signatures of new particles at colliders and no direct evidence for DM, massive neutrinos are certainly the most compelling signal of physics beyond the Standard Model (BSM). While neutrinos are predicted to be exactly massless in the SM, extending it by right-handed (RH) neutrinos requires severe fine-tuning to explain the light neutrino masses which lie many orders of magnitude below the electroweak scale. A pop- ular remedy to this fine-tuning problem is the seesaw mechanism [8–15] which introduces extremely heavy RH neutrinos. Alternatively, neutrino masses could also be generated at loop-level. This has several interesting consequences beyond the observation that the mass scale of new physics (e.g. the masses of the RH neutrinos) can be reduced to experimentally accessible values. First of all, such models usually require new fields to propagate in the loops which could be produced at colliders. Secondly, these new fields, if electrically neutral and stable against decay into lighter particles, may constitute part of the observed DM.
Furthermore, since a loop-diagram contains more couplings than a comparable tree-level diagram, we may expect that effects beyond leading order could be stronger in radiative neutrino mass models than they are e.g. in the conventional seesaw mechanism. The reason is that, unless cancellations occur, corrections to the couplings will in general add up. This could serve as an explanation for the observed neutrino mixing pattern: a mixing pattern that obeys a certain symmetry at high energies could be modified by running effects to yield the observed mixing pattern at lower energies.
On the other hand, running effects in these models can have consequences that are very
different from the aforementioned ones. Specifically, we can have settings that exhibit a
hierarchy-type problem, which is more than a mere aesthetical flaw. In such cases, one
may find that the discrete symmetry of such a model is endangered to be broken by the running masses. This can be problematic if the DM decays away quickly, and neutrino masses are generated at tree-level yielding unacceptably large values. Avoiding this parity problem can give new constraints on the parameter space of the model. However, one could argue that, if the breaking occurs at some very high energy scale, it is irrelevant as long as the low-energy phenomenology remains unaffected. We return to this discussion when we introduce the parity problem in Chapter 6. It will become clear that, even if this point of view is taken, significant constraints can arise.
To illustrate these rather generic remarks, we use the so-called scotogenic model as our benchmark model, which was proposed in Ref. [16]. Throughout this thesis we work in natural units, where ~ = c = 1, and use a metric signature (+, −, −, −). Unless indicated otherwise, we assume summation over repeated indices. Vectors in three-dimensional Eu- clidean space are indicated by bold-face symbols, while four-vectors in Minkowski space are written in italics.
The structure of this thesis is the following: in Chapter 2 we review the basic field theoretical methods employed throughout this work. In the subsequent Chapter 3 some of the mechanisms which could be responsible for the generation of neutrino masses are discussed. The main results of our work are outlined in Chapter 4, where we discuss the necessary steps to arrive at the running neutrino masses, leptonic mixing angles, and phases. Subsequently, we apply these findings to illustrate the running of the neutrino mixing parameters in Chapter 5, and in Chapter 6 we finally highlight the parity problem.
A summary of the results is given in Chapter 7. Technical details can be found in the
appendices.
Chapter 2 Theoretical Preliminaries
In this chapter we discuss some of the theoretical concepts which will be needed throughout this work and go beyond introductory courses on quantum field theory (QFT). We begin with an introduction to regularisation, renormalisation, and an overview of some relevant renormalisation group methods in Sec. 2.1. Subsequently, we study effective field theories (EFTs) in Sec. 2.2. Finally, Sec. 2.3 is dedicated to the concept of Majorana fermions and lepton number violating interactions. These self-conjugate fermions are often a source of confusion since they are usually not covered in standard courses on QFT. Any unacquainted reader will hopefully benefit from this discussion.
2.1 Regularisation and Renormalisation
To the best of our knowledge, Nature is described on a fundamental level by interacting QFTs. However, as soon as interactions are inserted into the Lagrangian, no closed solu- tions can be found in general. Hence, we are restricted to the use of perturbation theory.
The leading order contributions, often at tree-level, usually yield good first impressions of a given scattering process. Going beyond tree-level calculations, however, one may immedi- ately encounter divergent expressions. Such loop-level expressions involve integrations over momenta, which are not fixed by momentum conservation, and which may not converge in all cases. This makes the assumption of a perturbative expansion seem entirely wrong, a fact which even some of the founding fathers of QFT disapproved of (see e.g. Ref. [17]).
The renormalisation group method enables us to tackle this issue self-consistently and extract predictions concerning the running of coupling ‘constants’ and masses (i.e. their dependence on the energy scale under consideration). This curious behaviour has in fact been verified experimentally, e.g. by measuring the running of the QCD fine structure constant [18].
To illustrate the running, we consider the following toy theory of a real and massive spin-0 boson with quartic self-interactions:
L = 1
2 (∂
µφ) (∂
µφ) − m
22 φ
2− λ
4! φ
4. (2.1)
Even though this toy model is a highly simplified example, it will clarify the most important concepts which generalise straight-forwardly to more complicated and realistic models like those discussed in later chapters.
2.1.1 Dimensional Regularisation
In order to make sense of a perturbation series with divergent coefficients, we first need to find a way of assigning a finite value to the diverging integrals. To this end, we have several options. For example, the one-loop correction to the two-point function in the above theory would be quadratically divergent (
12is a symmetry factor):
− iΣ
(1)=
.
= 1 2 (−iλ)
Z d
4k (2π)
4i
k
2− m
2+ iη ∼ Z
Λ0
dk k
3k
2∼ Λ
2, (2.2)
where Λ is a momentum cut-off. In principle, such a cut-off is a valid regulator. However, it introduces further subtleties, because it can destroy gauge invariance [19].
The most convenient option for our purposes is dimensional regularisation. Here, we use an arbitrary dimension d of space-time such that the integral converges to a well- defined value which is analytically continued even to non-integer dimensions d ≡ 4 − ε [20].
Considering the above integral in d 6= 4 dimensions, we have:
− iΣ
(1)→ −iΣ
(1)d= λ 2
Z d
dk (2π)
d1
k
2− m
2+ iη , (2.3)
which converges for sufficiently small d, as power counting reveals. This integral can be calculated using the following steps:
1. Rotate the k
0-integration contour to go from −i∞ to +i∞. This so-called Wick rotation is shown schematically in Fig. 2.1 and makes explicit use of the pole structure in the k
0-plane [21, 22].
2. Define new integration variables ik
E0≡ k
0and k
E≡ k, i.e. go to Euclidean space.
3. Perform the integral in d = 4 − ε dimensions and expand in powers of ε. This allows one to isolate the divergences as poles at ε = 0.
4. Check whether coupling constants acquire a mass dimension in d 6= 4 dimensions.
For example, the Lagrangian in Eq. (2.1) has a mass dimension d. From its kinetic or
mass terms it follows that the field has a mass dimension [φ] = (d − 2)/2. Applying
this to the interaction, we see that [λ] = ε. We can then introduce λ
0= µ
ελ as the
actual coupling in the Lagrangian, where µ is some arbitrary mass scale and λ is
dimensionless.
2.1 Regularisation and Renormalisation 5
Re k
0Im k
0√ k
2+ m
2− iη
− √
k
2+ m
2+ iη
Figure 2.1:
Wick rotation of the
k0-integration. See also [22], where a similar drawing is shown.
Performing the above steps, one finds:
−iΣ
(1)d= µ
ελ 2
Z d
dk (2π)
d1
k
2− m
2+ iη = i µ
ελ 2
Z d
dk
E(2π)
d1
−k
2E− m
2= −i µ
ελ 2
1 (2π)
dZ
d
d−1Ω Z
∞0
dk k
d−1k
2+ m
2= i λ 32π
2m
22
ε + 1 − γ
E− log (4π) + log µ
2m
2+ O (ε)
,
(2.4)
where R
d
d−1Ω is the the surface area of a d-dimensional unit sphere and γ
E≈ 0.57722 is the Euler-Mascheroni constant. This expression is an analytic function of ε with a simple pole at ε = 0 (d = 4). For all practical purposes, it is sufficient to follow this approach to dimensional regularisation. In some cases, however, one has to be cautious. In Ref. [20], the authors show by a more formal definition of dimensional regularisation that the integral of any polynomial of momenta vanishes:
Z d
dk
(2π)
dk
2α= 0, for α ∈ R. (2.5)
If no care is taken, following the above calculation for m = 0, we can arrive at a result that has a pole at d = 2 and is finite in the limit ε → 0. Alternatively, we can see that if we set m = 0 in Eq. (2.4), we get Σ
(1)d= 0. This ambiguity occurs when external scales are absent. It can be lifted by either following the authors of Ref. [20], or by taking Eq. (2.5) as a definition.
2.1.2 Renormalisation
The next step in the renormalisation programme is to remove the singularity at d = 4 from
Eq. (2.4), so that we may take the limit d → 4. The prescription according to which this
is done is called the renormalisation scheme. To understand the physical implications of choosing a particular renormalisation scheme, let us consider an example. Following the standard procedure and decomposing the full propagator into 1-particle irreducible (1PI)
1contributions, we obtain at the one-loop level [22–24]:
= + . + . . + · · · S(p
2) = i
p
2− m
2+ i
p
2− m
2−iΣ
(1)i p
2− m
2+
+ i
p
2− m
2−iΣ
(1)i
p
2− m
2−iΣ
(1)i
p
2− m
2+ · · ·
= i
p
2− m
2− Σ
(1)`−loop
− −−− → i
p
2− m
2− (Σ
(1)+ Σ
(2)+ · · · ) , (2.6) with Σ
(`)the 1PI `-loop two-point function with amputated external legs. From this equation it is apparent that we can absorb the divergences in Σ
(`)by redefining our fields and parameters in the Lagrangian (2.1). Namely, we replace the bare fields and parameters by renormalised ones:
φ ↔ φ
B≡ Z
12φ
R, (2.7a)
m
2↔ m
2B≡ Z
−1m
2R+ δm
2, (2.7b)
λ ↔ λ
B≡ Z
−2µ
εZ
λλ
R. (2.7c)
Note that the bare quantities are precisely those of the Lagrangian in Eq. (2.1). The subscripts B and R are merely added in this section to avoid any confusion between bare and renormalised quantities. One can think of the quantities Z , δm
2and Z
λas originating from the self-interactions of a freely propagating particle. Thus, they contain all the divergences, while any renormalised quantity is finite. In any experiment, we will measure the renormalised coupling, mass, etc. of a field, which already contain all quantum corrections and are finite.
By splitting Z = 1 + δZ and Z
λ= 1 + δλ, we arrive at a renormalised Lagrangian which is the sum of the original Lagrangian and a counter term Lagrangian. Note that both parts are written in terms of the measurable and finite quantities m
Rand λ
R:
L = L
R+ L
ct= 1
2 (∂
µφ
R) (∂
µφ
R) − m
2R2 φ
2R− µ
ελ
R4! φ
4R+ + 1
2 δZ (∂
µφ
R) (∂
µφ
R) − δm
22 φ
2R− µ
εδλ λ
R4! φ
4R.
(2.8)
Repeating the above calculation in Eq. (2.3) for the renormalised theory, we obtain the renormalised two-point function:
Σ
(1)R= −iΣ
(1)d+ i p
2δZ − δm
2. (2.9)
1Such a diagram isnot disconnected if any internal line is cut.
2.1 Regularisation and Renormalisation 7 We can now specify a renormalisation scheme, i.e. the way in which we subtract the pole at ε = 0 from Eq. (2.4). This subtraction is not unique and in fact this arbitrariness is what leads to the renormalisation group.
2One option is to specify that the renormalised parameters in the Lagrangian correspond to the physically measured ones, in our case the physical mass of a particle. A possible set of renormalisation conditions on the 1PI two point function G
(2)R≡ Σ
(1)R+ Σ
(2)R+ · · · would be:
G
(2)Rp2=m2R
= 0, and (2.10a)
d
d (p
2) G
(2)Rp2=m2R
= 0, (2.10b)
which needs to be fulfilled to all orders in perturbation theory. This leaves the physical mass of the particles, i.e. the location of the pole, at m
R. The second condition fixes the residue of the pole in the propagator to 1, as can be verified by considering Eq. (2.6).
Imposing Eqs. (2.10a) and (2.10b) at one-loop order yields:
3δZ
OS= 0 and δm
2OS= −Σ
(1)dp
2= µ
2= m
2R= λ
R32π
2m
2R2
ε + 1 − γ
E− log (4π)
. (2.11) This is known as the on-shell (OS) scheme.
Alternatively, we can use the counter terms more economically and subtract the divergent parts only. This renormalisation scheme is the so-called minimal subtraction (MS) scheme.
In the MS scheme, we find that again δZ
MS= 0 and:
δm
2MS= λ
32π
2m
2R2
ε . (2.12)
However, one should realise that now m
Ris not necessarily the physical mass of a particle, since the full propagator’s pole structure is modified:
S
MS−1(p
2, µ
2) = p
2− m
2R1 − λ
R32π
21 − γ
E− log (4π) + log µ
2m
2R+ O λ
2R(4π)
4. (2.13) A modified version of this is the MS scheme, where the constant factor [1 − γ
E− log (4π)] is also subtracted.
4In principle, we can subtract an arbitrary dimensionless constant yielding an MS-like scheme where the various renormalisation constants take the form:
δZ
k= X
i≥1
δZ
k(i)˜
ε
i. (2.14)
The common feature of the MS-like schemes is that ε ˜ is a dimensionless constant which diverges in the limit d → 4, and the δZ
k(i)are independent of ε. ˜
2In many cases these ambiguities form a group algebra, but sometimes no inverse transformation exists (cf. the block spin analogy [25]) such that they only form a semi-group.
3It is a coincidence of pureφ4 theory thatΣ(1)d is independent ofp2 and henceδZ= 0.
4In this very simple example, where the self-energy is independent of external momenta, the MS scheme coincides with the OS scheme.
A theory in which all divergences occurring at any loop order can be absorbed into a finite number of counter terms, which are obtained by redefining the existing parameters, is called a renormalisable theory. By counting powers of loop momenta, one can show that a necessary condition for a theory to be renormalisable is that it contains only couplings that have positive or no mass dimension [24, 26]. In contrast, those theories where the couplings have inverse mass dimensionality are non-renormalisable. Non-renormalisable theories are theories in which one would need infinitely many counter terms to cancel all divergences that may occur.
A full proof of renormalisability is much more involved since one has to show that all correlation functions can be made finite at any loop order by a finite number of counter terms. See Refs. [27–29] for examples of such proofs.
2.1.3 The Renormalisation Group and the Callan-Symanzik Equa- tion
As we have seen in the previous section, there is some freedom in how we subtract the divergences and absorb them into the counter terms. In addition, even after choosing a renormalisation scheme, say MS, the mass parameter µ, which has been introduced for dimensional reasons, is still present in our final result in Eq. (2.13). However, the bare Lagrangian is independent of µ and thereby correlation functions of bare fields do not depend on µ. Moreover, we can use Eqs. (2.7) and (2.8) to express a bare correlation function in terms of renormalised quantities:
G
(n)B{x
i}
1≤i≤n; λ
B, m
B≡ h0| T φ
B(x
1)φ
B(x
2) · · · φ
B(x
n) |0i
= Z
n2(µ) h0| T φ
R(x
1)φ
R(x
2) · · · φ
R(x
n) |0i
= Z
n2(µ) G
(n)R{x
i}
1≤i≤n; λ
R, m
R, µ
, (2.15)
where G
(n)Ris the renormalised n-point correlation function and T is the time ordering operator. The fact that bare correlation functions do not depend on µ is parametrised by the so-called Callan-Symanzik equation [30–32]:
µ d
dµ G
(n)B({x
i} ; λ
B, m
B) = 0, from which it follows that
µ ∂
∂µ + β
λ∂
∂λ
R− γ
mm
R∂
∂m
R+ nγ
G
(n)R({x
i} ; λ
R, m
R, µ) = 0. (2.16) Here, β
λ≡ µ
dλdµRis the so-called β-function or renormalisation group equation (RGE) of the running coupling λ
R(µ). The functions γ
m≡ −
mµR
dmR
dµ
and γ ≡
2Zµ dZdµare the anomalous dimensions of the mass m
Rand the field φ
R, respectively.
The above equation states that any change in the renormalisation scheme, which amounts
to a finite and potentially µ-dependent shift of the counter terms, is compensated by an
appropriate change in the scale µ [27]. For example, from Eqs. (2.11) and (2.12) we see
that δm
2OS= δm
2MS+
32πλR2m
2R[1 − γ
E− log (4π)]. This removes some of the arbitrariness
in choosing a renormalisation scheme by relating the scheme to the scale µ.
2.1 Regularisation and Renormalisation 9 The meaning of µ. In more involved calculations than the simple example of a real scalar field, one usually encounters logarithms of the type log
p2 µ2
, where p is an external momentum. To minimise potentially large logarithms due to a poor choice of the renormal- isation scale µ, one chooses µ ∼ E, where E is a typical energy scale for the process, e.g. it could be the centre of mass energy √
s in a scattering process. Thus, µ is to be identified with the energy scale under consideration. In the following Sec. 2.2, an example for such a large logarithm, that can be tamed by a suitable choice of µ, can be found. Before turning to this discussion, however, we will demonstrate how to calculate β-functions in practice.
Calculating β-functions. The MS scheme is a so-called mass-independent scheme be- cause the subtraction of the ε
−1-pole is not specified at a certain energy scale. As a consequence, the counter terms depend only implicitly on the scale µ. This requires some care when calculating β-functions. The following derivation closely follows Refs. [33, 34].
Take some bare coupling or mass Q
B, for which it is true that:
µ d
dµ Q
B= 0. (2.17)
In general, there is a relation:
Q
B= Z
Qµ
DQε(Q + δQ), (2.18)
where Z
Qcontains all contributions stemming from wave function renormalisation con- stants Z [cf. Eq. (2.7a)]. Furthermore, D
Qis the additional mass dimensionality the quantity acquires in d = 4 − ε dimensions. Note that, unless there is some symmetry at work, we should not expect Q to be renormalised multiplicatively, which would imply δQ ∝ Q. Thus, in order to cover the most general case possible, we have introduced δQ as an additive correction. In case Q is indeed renormalised multiplicatively, we will simply find δQ ∝ Q. Inserting Eq. (2.18) into Eq. (2.17), we find:
0 = µ d dµ Q
B=
µ dZ
Qdµ (Q + δQ) + D
Qε Z
Q(Q + δQ) + Z
Qβ
Q+ µ dδQ dµ
µ
DQε, (2.19) where β
Q≡ µ
dQdµis the β-function we aim at. The chain rule can be used to eliminate the factors
dδZdµQand
dδQdµin favour of beta functions of Q and other quantities. These are represented by V
iand Eq. (2.19) can be expressed as (a sum over i is implied):
0 = dδZ
QdQ β
Q(Q + δQ) + dδZ
QdV
iβ
Vi(Q + δQ) + D
Qε Z
Q(Q + δQ)+
+ Z
Qβ
Q+ Z
QdδQ
dQ β
Q+ dδQ dV
iβ
Vi.
(2.20)
At N -loop order, our renormalisation constants will have received contributions from all
loop orders ≤ N . In a mass-independent subtraction scheme they will most generally take
the form given in Eq. (2.14):
Z
Q= 1 +
N
X
i=1
δZ
Q(i)ε
i, δQ =
N
X
i=1
δQ
(i)ε
i, and δV
i=
N
X
j=1
δV
i(j)ε
j. (2.21) Additionally, β
Qmust be finite because it is a function of finite renormalised quantities.
Therefore, we can try the ansatz:
β
Q/Vi= β
Q/V(0)i
+ εβ
Q/V(1)i
+ ε
2β
Q/V(2)i
+ · · · + ε
mβ
Q/V(m)i
−−→
ε→0β
Q/V(0)i
, (2.22)
for some integer m which is not necessarily affiliated with the loop order N . Plugging Eqs. (2.21) and (2.22) into (2.20) and equating coefficients, it is apparent that Z
Qβ
Qgives rise to the only O (ε
m) term. It follows that β
Q/V(n)i
= 0 for n ≥ 2.
At order ε
1, we find:
β
Q(1)= −D
QQ and similarly β
V(1)i
= −D
ViV
i(no sum). (2.23) At order ε
0, Eq. (2.20) reads:
0 = dδZ
Q(1)dQ β
Q(1)Q + dδZ
Q(1)dV
iβ
V(1)i
Q + D
QδZ
Q(1)Q + D
QδQ
(1)+ + β
Q(0)+ β
Q(1)δZ
Q(1)+ dδQ
(1)dQ β
Q(1)+ dδQ
(1)dV
iβ
V(1)i
,
(2.24)
which we can solve for β
Q(0)by using Eq. (2.23). Thereby, the beta function in d = 4 is given by:
β
Q(0)= D
QdδQ
(1)dQ Q + D
VidδQ
(1)dV
iV
i− D
QδQ
(1)+ Q
"
D
QdδZ
Q(1)dQ Q + D
VidδZ
Q(1)dV
iV
i#
. (2.25) This is the final result for the calculation of β-functions in MS-like renormalisation schemes.
It is easily generalised to couplings with tensorial structure, e.g. a Yukawa matrix. The derivations that can be found in Refs. [33, 34] give explicit formulae for such cases. For the concrete case of a matrix-valued quantity Y one obtains, in analogy to Eq. (2.18):
Y
B= µ
DYεZ
L(Y + δY ) Z
R. (2.26) Repeating the above computation yields:
β
Y ε→0= D
YdδY
(1)dY
ijY
ij+ D
VidδY
(1)dV
iV
i− D
YδY
(1)+ +
"
D
YdδZ
L(1)dY
ijY
ij+ D
VidδZ
L(1)dV
iV
i# Y + Y
"
D
YdδZ
R(1)dY
ijY
ij+ D
VidδZ
R(1)dV
iV
i# .
(2.27)
Note that we have assumed a treatment up to N -loop order, but only δQ
(1)and δZ
Q(1)enter
Eq. (2.27). Hence, only the ε
−1contributions to the counter terms are relevant. This fact
can facilitate higher loop calculations significantly.
2.2 Effective Field Theories 11
iΠ
νρR= i(p
2g
νρ− p
νp
ρ) Π
R= ρ . . ν
e
e
+ ρ ν
δZ
AFigure 2.2:
One-loop QED vacuum polarisation and counter term.
2.2 Effective Field Theories
The decoupling of high-energy degrees of freedom is a well-established paradigm throughout the various fields of physics. Examples are easily found: we do not consider the parton structure of the proton when solving the hydrogen atom’s Schrödinger equation. Similarly, we are not interested in the quantum mechanical (QM) energy levels of an individual atom if we study the mechanical properties of a macroscopic solid state system. The crucial observation is that for sufficiently small energy scales the low-energy effective theory is a good approximation of the full theory, which we may not even know. But even if the full theory is known, the approximation can facilitate computations, e.g. at non-relativistic velocities classical mechanics is a good approximation of special or even general relativity and much easier to handle.
2.2.1 The Decoupling Theorem
In QFT, the first proof of the decoupling of heavy fields at energies much smaller than their masses was given in Ref. [35]. The authors have made use of two facts: firstly, for energies much below the mass m of the heavy field, no heavy external states can be produced. Secondly, due to the structure of the propagators [(p
2− m
2)
−1for bosons and
/ p − m
−1for fermions], internal lines of heavy fields are accompanied by a suppression of the form ‘energy scale over heavy mass’, e.g. (p
2− m
2)
−1=
m−12P
n
p2 m2 n, which is valid for p
2< m
2. Therefore, the low-energy effects from the heavy field can be approximated arbitrarily well by truncating the geometric series at a desired order.
To prove the decoupling theorem, a renormalisation scheme needs to be found such that the decoupling is manifest even after renormalisation [27]. Without going into the details of the proof, we illustrate that this is not straight-forward, especially in mass-independent renormalisation schemes such as MS and MS.
In QED, the one-loop vacuum polarisation, i.e. the photon self-energy, is given by the left diagram shown in Fig. 2.2. Using dimensional regularisation, we obtain [22]:
Π(p
2, m
2, µ
2) = − 2α π
Z
1 0dx x(x − 1) 2
ε − γ
E+ log (4π) + log
µ
2m
2− x(1 − x)p
2,
(2.28)
where α =
4πe2is the fine structure constant and m the electron mass.
In the OS renormalisation scheme, we impose that the divergence in the self-energy is cancelled by its counter term δZ
Aat the physical photon mass, i.e. at p
2= 0. This makes the OS scheme mass-dependent. Thereby, we obtain the OS renormalised vacuum polarisation:
Π
(OS)R(p
2, m
2, µ
2) = − 2α π
Z
1 0dx x(x − 1) log
m
2m
2− x(1 − x)p
2| {z }
=x(1−x)p2
m2+O
p4 m4
. (2.29)
In this expression the µ-dependence has dropped out and the expansion of the logarithm is valid for p
2< m
2. Therefore, at energies much below the electron mass, the decoupling of the electrons is taken care off automatically in the OS scheme. However, in the opposite limit, p
2m
2, it contains a large logarithm ∼ log
m2 p2
, as anticipated in the previous section.
5In the MS scheme, in contrast, we subtract only the divergent part (plus constants) from the vacuum polarisation. This way we get:
Π
(MS)R(p
2, m
2, µ
2) = − 2α π
Z
1 0dx x(x − 1) log
µ
2m
2− x(1 − x)p
2| {z }
=−log
m2
µ2−x(1−x)p2
µ2
. (2.30)
Choosing µ
2∼ p
2, we encounter for small energy scales a large logarithm ∼ log
p2 m2
in the expression (2.30). This means that perturbation theory cannot be trusted in the limit p
2m
2because the electrons are not properly decoupled in this renormalisation scheme.
At high energies (p
2m
2), in contrast, this logarithm is small and perturbation theory is applicable.
This illustrates that the use of perturbation theory in QFT requires some caution when considering low-energy effective theories. Also, this example emphasises the intimate rela- tion between EFTs and renormalisation.
To avoid such large logarithms at low energies in mass-independent renormalisation schemes, we make use of the decoupling theorem. According to its proof a renormal- isation scheme must exist in which decoupling is manifest. At the same time, we can switch between the renormalisation schemes at will, because any change in the renormal- isation prescription can be compensated by appropriately changing the renormalisation scale. Thus, we may decouple heavy particles at energy scales far below their masses by hand. This procedure is called integrating out the heavy degrees of freedom and we will describe the procedure in the following subsection.
65In principle, the issue of a large logarithm in this limit can be cured by imposing the cancellation to occur atp2= Λ2. Then the scale Λtakes a role similar to that ofµin the MSscheme.
6This terminology originates from the path integral formalism and in our approach, we should speak of matching instead.
2.2 Effective Field Theories 13 e(p
2)
u(p
1)
ν(p
4)
d(p
3)
. .
W
q =p2−p4q2MW2
−−−−−→
e(p
2)
u(p
1)
ν(p
4)
d(p
3)
Figure 2.3:
Electron capture
pe→nν.2.2.2 Effective Operators and Matching
A well-known example for a low-energy EFT is the Fermi theory of weak interactions.
The process shown in Fig. 2.3 (left diagram) is mediated by a massive W -boson. For energies well below the W mass M
W, we can follow the above reasoning and expand the W -propagator in powers of
q2 MW2
. This procedure yields an effective four-fermion interaction (spin indices are suppressed):
u(p
4) i
√ 2 gγ
µP
Lu(p
2) −ig
µνq
2− M
W2u(p
3) i
√ 2 gγ
νP
Lu(p
1)
q2MW2
−−−−−→ −i g
22M
W2u(p
4)γ
µP
Lu(p
2)u(p
3)γ
µP
Lu(p
1) + O q
2M
W2.
(2.31)
Thus, expanding the W -propagator for small energies has decoupled the W -boson by con- tracting the internal line into an effective vertex (cf. Fig. 2.3, right diagram). The effective coupling constant is given by the Fermi constant G
F=
√2g2
8MW2
, which is suppressed by the mass scale M
W. This amplitude can be obtained from the following interaction Lagrangian:
L
Fermi= G
F√ 2
νγ
µ1 − γ
5e dγ
µ1 − γ
5u
+ h.c. (2.32)
Note that, even though this interaction is non-renormalisable, it is only valid for energies up to approximately M
W. Thus, for energies larger than M
Wwe must turn to the ultraviolet (UV) completion – the Standard Model which is renormalisable!
We can continue the expansion in
q2MW2
and eventually obtain an infinite tower of non-renormalisable effective interactions [36]:
L
eff= X
n≥5
C
nM
Wn−4O
(n), (2.33)
where the operators O
(n)have a mass dimension n. Note that not all of them have to be be realised, e.g. the operator in L
Fermicontributes to O
(6), while O
(5)= 0 in the above example.
This approach, where the UV completion of a theory is known and higher dimensional operators can be related to its couplings, is called top-down. In practice, rather than expanding propagators, one includes terms of the form Eq. (2.33) up to a desired order and matches the couplings C
nto those of the UV completion, e.g. diagrammatically [37].
Of course one can reverse this approach, yielding the so-called bottom-up approach, which does not require the knowledge of any UV theory. We simply include all possible non-renormalisable interaction terms, which should respect the theory’s symmetries, up to a desired order in Λ
−1where Λ represents the scale of new physics. Again, not all of these operators need to be realised in the UV theory, as we have seen above. The down-side of this approach is that, in order to perform loop calculations, more and more effective operators are needed to have enough counter terms that can cancel the occurring divergences due to their non-renormalisable nature. Nevertheless, the bottom-up approach allows one to gain some insight into physics beyond the low-energy EFT. We illustrate this by treating the SM as an EFT in the bottom-up approach. Including effective operators up to a mass dimension D = 5, we find that only one such operator is allowed by the SM gauge symmetry, the so- called Weinberg operator [38]:
L
D=5= 1
4 κ
ij`
cLaiε
abφ
b`
Lej
ε
efφ
f+ h.c. (2.34) In this expression `
Lis the left-chiral lepton doublet and φ is the Higgs doublet. Dimen- sional analysis shows that κ is of mass dimension (−1) and can be expressed in terms of dimensionless couplings y
ijand the scale Λ: κ
ij=
yΛij. From the point of view of neu- trino physics, the most interesting feature of the Weinberg operator is that it gives rise to Majorana neutrino masses as the Higgs acquires a vacuum expectation value (VEV):
1
4 κ
ij`
cLaiε
abφ
b`
Lejε
efφ
f+ h.c.
hφi=(0,v)T
−−−−−−→ v
24Λ y
ij| {z }
≡12(Mν)ij
ν
Licν
Lj+ h.c. (2.35)
It is evident that a natural explanation for the smallness of neutrino masses is a large scale Λ, which is the basic idea of the seesaw mechanism: the larger the scale of new physics Λ is, the smaller the neutrino mass scale. In Chapter 3 we will study potential UV completions of the SM that realise the Weinberg operator.
To summarise, by a bottom-up treatment of the SM as an EFT, we have gained in-
sight into some features of possible UV completions: we expect (light) neutrino masses as
verified experimentally (see next chapter) and lepton number violation through the (Ma-
jorana) neutrinos’ interactions (cf. next section). Finally, we should see some new particles
appearing around a mass scale Λ. However, in case the Weinberg operator is not realised
in the UV completion of the SM, these observations can be altered significantly.
2.3 Majorana Fermions 15
2.3 Majorana Fermions
In any course on QFT the first concept that is introduced is the real scalar field, followed by the complex scalar field and eventually the Dirac field – a complex field describing particles of spin
1/
2. The natural question to ask is whether there is a real solution to the Dirac equation, just as there is a real solution to the Klein-Gordon equation. Thus, we need to verify whether we can impose the additional reality condition ψ = ψ
∗on a fermion field ψ which satisfies the Dirac equation,
(iγ
µ∂
µ− m) ψ(x) ≡ (i / ∂ − m)ψ(x) = 0. (2.36) Here, the γ
µare the so-called Dirac matrices satisfying the anti-commutation relations
{γ
µ, γ
ν} ≡ γ
µγ
ν+ γ
νγ
µ= 2g
µν1 (Clifford algebra), (2.37) where 1 is the identity matrix. To find the equation of motion ψ
∗obeys, we take the complex conjugate of Eq. (2.36). Hence, we see that unless the Dirac matrices are purely imaginary, i.e. γ
µ∗= −γ
µ, we cannot impose ψ = ψ
∗[39]. Clearly, this is not the case in the standard, or Dirac representation of the gamma matrices:
γ
0=
I
20 0 −I
2, γ
i=
0 σ
i−σ
i0
, γ
5≡ iγ
0γ
1γ
2γ
3=
0 I
2I
20
, (2.38) where the latter anti-commutes with all other gamma matrices, I
2is the 2 × 2 identity matrix, and the σ
iare the Pauli matrices.
However, the representation is not unique because, if Eq. (2.37) is satisfied by γ
µ, it will also hold for e γ
µ= U
†γ
µU with a unitary matrix U . By virtue of Eq. (2.36), such a change of basis is achieved by ψ e = U
†ψ. Thus, a representation where the e γ
µare all imaginary can be found – the so-called Majorana representation, named after Ettore Majorana, who first proposed such self-conjugate fermions [40]:
e γ
0=
0 σ
2σ
20
, e γ
1=
iσ
30 0 iσ
3,
e γ
2=
0 −σ
2σ
20
, e γ
3=
−iσ
10 0 −iσ
1.
(2.39)
In this representation the field ψ e solves the Dirac equation (2.36) and we can additionally impose ψ e
∗= ψ. Thereby, we can generalise the reality or e Majorana condition:
ψ e = ψ e
∗⇔ U
†ψ = (U
†ψ)
∗or ψ = U U
Tψ
∗≡ Cψ
T, (2.40)
where we have introduced the charge conjugation matrix C ≡ U U
Tγ
0T, which fulfils the
useful relations C
−1= C
†= C
T= −C [23], and ψ ≡ ψ
†γ
0is the adjoint spinor. In the
standard representation the charge conjugation matrix is given by C = iγ
2γ
0. For a more
compact notation, it is customary to define the charge conjugate spinor CψC
†≡ ψ
c= Cψ
T. The operator C can be thought of as flipping the signs of all U (1) charge quantum numbers.
Therefore, if we impose the Majorana condition:
ψ
c= ψ, (2.41)
the field cannot carry any U (1) charges. This is usually expressed in the statement that Majorana particles are identical to their anti-particles.
Thus, by considering the Majorana basis, we have found that there is a proper, i.e.
Lorentz invariant, way of defining a conjugate fermion field in a general basis.
2.3.1 Constructing Majorana Particles
Now that we have an elementary understanding of what a self-conjugate fermion field is, we address the explicit construction of a theory of such a field. The Fourier expansion for a Majorana field solving (2.36) is given by:
ψ(x) =
Z d
3p (2π)
31 2E
pX
s
![Figure 2.1: Wick rotation of the k 0 -integration. See also [22], where a similar drawing is shown.](https://thumb-eu.123doks.com/thumbv2/1library_info/4013028.1541236/13.892.303.610.171.408/figure-wick-rotation-k-integration-similar-drawing-shown.webp)
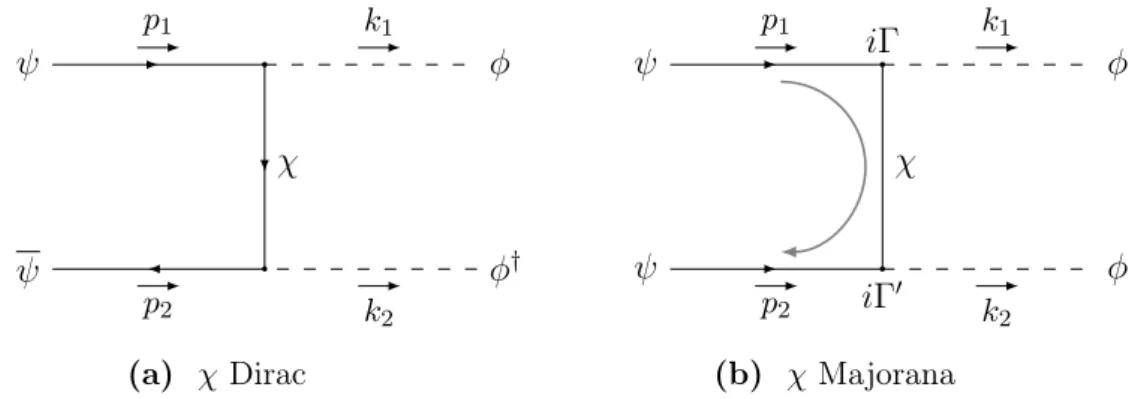
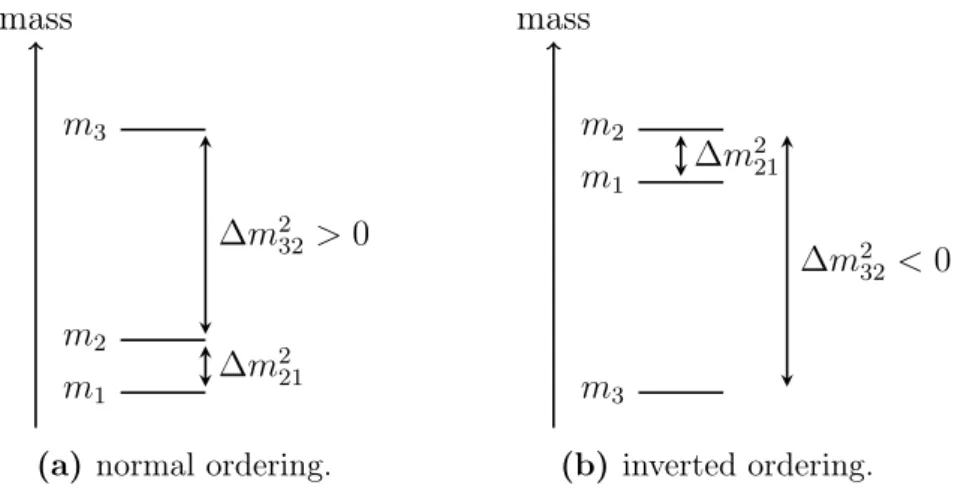
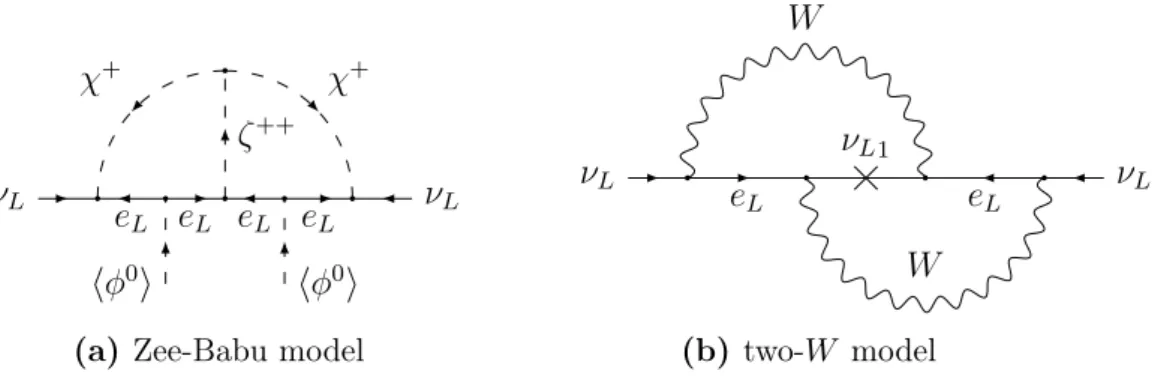
![Table 3.1: Summary: global fit of neutrino oscillation parameters [77].](https://thumb-eu.123doks.com/thumbv2/1library_info/4013028.1541236/34.892.106.803.170.446/table-summary-global-fit-neutrino-oscillation-parameters.webp)
![Figure 3.4: One-loop topologies that realise the Weinberg operator as given in Ref. [90].](https://thumb-eu.123doks.com/thumbv2/1library_info/4013028.1541236/43.892.122.798.174.362/figure-loop-topologies-realise-weinberg-operator-given-ref.webp)