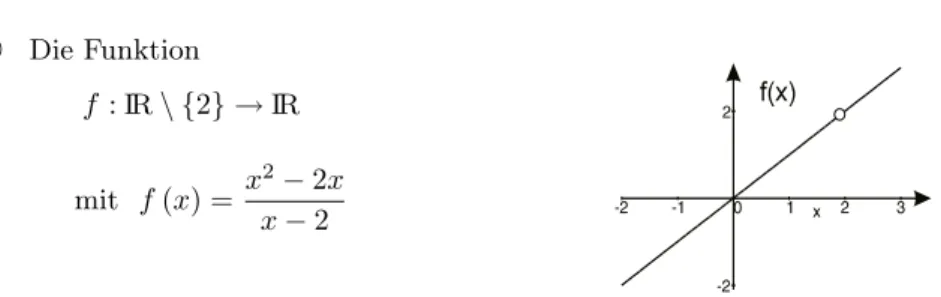6.1 Reelle Zahlenfolgen

6 Grenzwert und Stetigkeit

Grundlegend f¨ur das gesamte Kapitel sind Grenzwerte von Zahlenfolgen. Auf dieser Grundlage baut die Konstruktion des Funktionsgrenzwertes auf, der wiederum f¨ur den Begriff der Stetigkeit ben¨otigt wird. Etwas lax formuliert sind die stetigen Funktionen die Funktionen, die bei einem zusammenh¨angenden Definitionsbereich keine Sprungstelle aufweisen, d.h. ohne Unterbrechung gezeichnet werden k¨onnen. F¨ur diese stetigen Funk- tionen werden wir das Bisektionsverfahren einf¨uhren, um numerisch die Nullstellen dieser Funktionen zu bestimmen.

6.1 Reelle Zahlenfolgen

In den meisten Tests zur Erfassung der Denkf¨ahigkeit von Sch¨ulern und Stu- denten kommt eine Aufgabenstellung der Form vor: Gegeben ist

−1 2, 1

4,−1 6, 1

8, ...

Man m¨oge vier weitere Glieder dieser Folge angeben. Gemeint ist nat¨urlich

−₁₀¹, ₁₂¹,−₁₄¹, ₁₆¹.Etwas schwieriger ist die Aufgabe, eine Gesetzm¨aßigkeit zu finden, um das 100. Glied der Folge zu bestimmen. Hierbei ist dann nach der Formel(−1)ⁿ₂¹_n gefragt, in die man anschließendn= 100einsetzt. Eventuell wird auch gefragt, welchem Wert die Folgenglieder f¨ur großen beliebig nahe kommen. Dann ist der Grenzwert der Folge gesucht. Wir definieren verallge- meinernd:

Definition: (Zahlenfolge). Unter einer reellen Zahlenfolge versteht man eine geordnete Menge reeller Zahlen, indiziert mit 1, 2, 3,. . ..

Notation:(an)_n=a1, a2, a3, . . . , an, . . . .

Die Zahlena1,a2, . . .heißenGliederder Folge,andasn-te Gliedbzw. das allgemeine Gliedder Folge(Bildungsgesetz).

Beispiele 6.1:

1 (an)_n = 1,2,3,4, . . . , n, . . .; an =n.

2 (an)_n = 1, ¹₂, ¹₃, ¹₄, . . . , ¹_n, . . .; an =_n¹. 3 (a_n)_n =−1,+1,−1,+1,−1,+1, . . .; a_n = (−1)ⁿ. 4 (a_n)_n =−¹₂, ¹₄,−¹₆, ¹₈,−₁₀¹, . . .; a_n = (−1)ⁿ ₂¹_n. 5 (an)_n = 0.1,0.11,0.111, 0.1111, . . .; a1= 0.1und

an =a_n−1+ 10⁻ⁿ f¨urn≥2.

Eine Zahlenfolge kann alsdiskrete Funktion F :IN→IR mitn7−→a(n) = a_n aufgefasst werden. Die Funktion F ordnet jeder nat¨urlichen Zahl n genau eine reelle ZahlF(n) =an zu. Hierbei tritt die Variablen als Index auf; die Funktionswerte sind nummeriert.

Darstellung von Zahlenfolgen:Die Glieder einer Folge sind darstellbar auf der reellenZahlengeraden. Z.B. f¨uran= ₂n−1¹ erhalten wir die Folge

(a_n)_n= 1, 1 2, 1

4, 1 8, 1

16, 1 32, . . .

die unten auf dem Zahlenstrahl dargestellt ist. Gem¨aß der Interpretation als diskrete Funktion k¨onnen Folgen auch ¨uber den Funktionsgraphen (siehe rechte Abb.) dargestellt werden. Da die Funktion nur f¨urn∈IN definiert ist, d¨urfen die Punkte nicht verbunden werden!

Folge auf reellem Zahlenstrahl Folge als diskrete Funktion

Grenzwert einer Folge

Um das Verhalten der Folgean = 1−_n¹(n∈IN) f¨ur große nzu diskutieren, erstellen wir eine Wertetabelle

n 1 2 3 4 · · · 10 · · · 100 · · · 1000 · · · 10000 a_n 0 ¹₂ ²₃ ³₄ · · · 0.9 · · · 0.99 · · · 0.999 · · · 0.9999 .

Die Eigenschaften dieser Folge sind, dass

Abb. 6.1.Grenzwert der Folge 1− ¹

n

alle Gliederankleiner als1sind und dass mit wachsendem n die Glieder an sich an die Zahl1 ann¨ahern. Damit wird der Abstand zwischen den Folgengliedernan

und dem Wert1mit wachsendemnklei- ner:

|an−1| →0 f¨ur n→ ∞.

Die Zahl1wird alsGrenzwertder Folgean= 1−_n¹ bezeichnet.

6.1 Reelle Zahlenfolgen 225 Visualisierung mit Maple: Auf der Homepage befindet sich ein Worksheet, bei dem man selbst Folgen spezifiziert und diese Folgen dann - sofern sie einen Grenzwert besitzt - in Form einer Animation dargestellt werden.

Definition: (Grenzwert)

(1) Eine reelle Zahl a heißt Grenzwert oder Limes der Zahlenfolge (a_n)_n∈IN, wenn es zu jedem ε > 0 eine nat¨urliche Zahl n₀ gibt, so dass f¨ur alle n > n0stets gilt

|an−a|< ε.

(2) Eine Folge heißt konvergent,wenn sie einen Grenzwert besitzt. Wir verwenden dann die Notation

an

n→∞−→ a oder lim

n→∞an=a.

(3) Eine Folge heißt divergent,wenn sie keinen Grenzwert besitzt.

Definition (1) besagt, dassader Grenzwert einer Folge ist, wenn der Abstand von Folgengliedern zum Grenzwert, |an−a|, beliebig klein (ε) gew¨ahlt wer- den kann und alle Folgenglieder a_n abn₀ einen noch kleineren Abstand zum Grenzwertabesitzen. Anschaulich formuliert bedeutet dies:

Folgerung:Eine Folge an konvergiert, wenn es einen Grenzwert agibt, so dass der Abstand

d=|an−a| →0 f¨ur n→ ∞.

Bemerkungen:

(1) Konvergiert eine Zahlenfolge gegen einen Grenzwert a, dann h¨angt der Indexn0 von der Wahl des Abstandesεab.

(2) Der Grenzwert einer Zahlenfolge ist eindeutig.

(3) Divergiert eine Folge, so muss nicht notwendigerweisean→ ±∞gelten.

(4) Wir werden S¨atze kennen lernen, mit denen man den Grenzwert einer Fol- ge direkt berechnen kann, ohne auf die obige Definition zur¨uckgreifen zu m¨ussen.

(5) Der Grenzwert einer Folge wird in der Regel nie von den Folgengliedern erreicht.

Beispiele 6.2:

1 Die Folge

(an)_n= 1

n

n

= 1, 1 2, 1

3, 1 4, . . . konvergiert gegen den Grenzwert 0 : lim

n→∞a_n= lim

n→∞

1 n = 0.

Man bezeichnet Folgen, die gegen den Grenzwert0konvergieren, alsNull- folgen.

2 Die Folge (an)_n =

1 + 1

2ⁿ

n

= 1.5, 1.25,1.125,1.0625,1.03125, . . .

konvergiert gegen1,da f¨ur den Abstand der Folgengliederna_n zu1 gilt d=|an−a|=

1 + 1 2ⁿ −1

= 1 2ⁿ

n→∞−→ 0.

3 Die Folge

(a_n)_n= (n)_n= 1, 2,3,4, . . . ist unbeschr¨ankt wachsend und daher divergent.

4

4

(an)_n= ((−1)ⁿ)_n=−1,1,−1,1,−1, . . .

hat zwei sog. H¨aufungspunkte, n¨amlich 1 und −1. Sie konvergiert aber nicht gegeneinenGrenzwert. Daher ist sie divergent.

5 x∈IR fest.

(a_n)_n = (xⁿ)_n=x, x², x³, x⁴, x⁵, . . . , xⁿ, . . . .

F¨urx-Werte mit−1< x <1konvergiert die Folge gegen Null, f¨urx= 1 gegen 1,f¨ur anderex-Werte divergiert die Folge.

Um nachzupr¨ufen, dass Zahlenfolgen konvergent sind, muss nach der Defi- nition von Konvergenz der Grenzwert bereits bekannt sein, da der Abstand d=|a_n−a| bestimmt werden muss. Das folgendeMonotoniekriteriummacht eine Aussage ¨uber die Konvergenz einer Folge, ohne dass der Grenzwert be- kannt ist. Es besagt, dass eine monoton wachsende Folge, die nach oben hin beschr¨ankt ist, stets einen Grenzwert besitzt. Eine Folge, die monoton f¨allt und nach unten beschr¨ankt ist, besitzt ebenfalls einen Grenzwert.

6.1 Reelle Zahlenfolgen 227

Monotonie-Kriterium:

(1) Sei(an)_n eine Folge mit den Eigenschaften

(i) an≤an+1 (Monotonie), (ii) an≤A (Beschr¨anktheit), dann konvergiert die Folge gegen einen Grenzwert a≤A.

(2) Sei(a_n)_n eine Folge mit den Eigenschaften

(i) an≥an+1 (Monotonie), (ii) an≥A (Beschr¨anktheit), dann konvergiert die Folge gegen einen Grenzwert a≥A.

Beispiel 6.3 (Exponentialfolge, mitMaple-Worksheet): Die Folge

an=

1 + 1 n

ⁿ

ist konvergent, da sie eine monoton wachsende Folge darstellt, die nach oben durch 3 beschr¨ankt ist (ohne Beweis):

n 1 10¹ 10² 10³ 10⁴ 10⁵

a_n 2 2.59374 2.70481 2.71692 2.71814 2.71826 Der GrenzwerteheißtEulersche Zahl

e= 2.71828 18284 59045 23536 0287. . . .

Wir stellen den Grenzwert zusammen mit einer ε-Umgebung als Funktions- schaubild f¨ur die Folge(1 + _n¹)ⁿ graphisch dar.

Abb. 6.2.Zum Grenzwert der Folge (1+¹_n)ⁿ

Die Eulersche Zahletritt in vielen naturwissenschaftlichen Zusammenh¨angen auf. Aus mathematischer Sicht ist sie eine der bedeutsamsten reellen Zahlen.

Die Exponentialfunktion basiert aufeals Basis. Wir werden im Kapitel Taylor- Reihen in Beispiel 9.33 eine alternative Methode kennen lernen, um die Zahle

durch eine schneller konvergente Folge zu bestimmen:

e=

∞

X

n= 0

1

n! = 1 + 1 + 1 2!+ 1

3!+ 1

4!+. . .+ 1

n! +. . . .

Beispiel 6.4 (Babylonisches Wurzelziehen, mit Maple-Worksheet):

Dierekursiv definierte Folge

a0=a , an+1 =¹₂

an+ a a_n

(∗)

ist f¨ur jedes a >0 eine monoton fallende Folge, die nach unten durch√ abe- schr¨ankt ist (ohne Beweis).

Der Grenzwert der Folge bestimmt sich aus der Definitionsgleichung von an (∗), indem auf beiden Seiten der Gleichung der Limesn→ ∞gebildet wird. Sei der Grenzwert der Folgeb:= lim

n→∞a_n = lim

n→∞a_n+1, so folgt f¨urb mit den Limesrechenregeln

n→∞lim an+1 = lim

n→∞

1 2

an+ a

a_n

⇒ b = ¹₂ b+a

b

. L¨ost man diese Gleichung nachbauf, folgt

b²=a ⇒ b=√ a.

Somit stellt obige Folge ein N¨aherungsverfahren zur Berechnung von Qua- dratwurzeln dar, das schon den Babyloniern bekannt war. Tats¨achlich ist dies ein Spezialfall des Newton-Verfahrens, das wir in 7.9 einf¨uhren wer- den.

Die folgende Wertetabelle verdeutlicht die schnelle Konvergenz der Folge f¨ura= 2:

n 1 2 3 4 5

an 1.5 1.416666666 1.414215686 1.414213562 1.414213562 Nach 4 Iterationen ist√

2 = 1.414213562bis auf 9 Stellen genau!

Das Monotonie-Kriterium sichert zwar die Konvergenz einer Folge, aber es lie- fert nicht den Grenzwert. Die Limesrechenregeln bei Folgen bieten eine M¨og- lichkeit, den Grenzwert einer Folge f¨ur viele aber nicht alle F¨alle zu berechnen:

6.2 Funktionsgrenzwert 229

Limesrechenregeln bei Folgen:

Seien (a_n)_n und (b_n)_n konvergente Folgen mit lim

n→∞ a_n = a und

n→∞lim bn=b.Seic∈IR.Dann gilt (L1) lim

n→∞c an = c lim

n→∞an =c·a

(L2) lim

n→∞(an±bn) = lim

n→∞an± lim

n→∞bn =a±b (L3) lim

n→∞(an·bn) = lim

n→∞an· lim

n→∞bn =a·b (L4) lim

n→∞

a_n bn

= lim

n→∞an/ lim

n→∞bn =a

b, fallsbn, b6= 0.

Beispiele 6.5 (Ermittlung von Grenzwerten):

1 an= 4n³−6

6n³+ 2n² = 4n³−6 6n³+ 2n² ·

1 n³

1 n³

=4−_n⁶3

6 + ²_n

n→∞−→ 4 6 = 2

3. ² an= n−1

2n²+ 1 = n−1 2n²+ 1·

1 n²

1 n²

=

1 n−_n¹2

2 +_n¹2

n→∞−→ 0 2 = 0.

³ an= 3ⁿ⁺¹+ 2ⁿ

3ⁿ+ 1 = 3ⁿ⁺¹+ 2ⁿ 3ⁿ+ 1 ·

1 3ⁿ

1 3ⁿ

=3 + ²₃n

1 + ¹₃n

n→∞−→ 3 1 = 3, da ²₃ⁿ

→0und ¹₃ⁿ

→0f¨urn→ ∞nach Beispiel 6.2⁵.

Tipp: Bei den Beispielen wird der Quotient mit dem Kehrwert des f¨uh- renden Terms erweitert und dann eine der Regeln angewendet. Diese Um- formungen sind notwendig, damit die Limesrechenregeln f¨urkonvergente Folgen angewendet werden k¨onnen.

6.2 Funktionsgrenzwert

In Abschnitt 6.1 werden Grenzwerte von Zahlenfolgen (xn)_n∈IN untersucht.

Dieser Begriff wird nun direkt auf Funktionsgrenzwerte ausgedehnt, indem Folgen der Form(f(xn))_n∈INbetrachtet werden. Zur Einf¨uhrung untersuchen wir das Verhalten der Funktionf(x) =x² an der Stellex₀= 2.Dazu w¨ahlen wir die Folge

(x_n)_n = 1.9, 1.99,1.999,1.9999, . . .^n→∞−→ 2 und berechnen zu jedem Folgenglied den Funktionswert

(f(xn))_n = 3.61,3.9601,3.996,3.9996, . . .^n→∞−→ 4. DieFolge der Funktionswertekonvergiert gegen den Wert 4.

Um den Funktionsgrenzwert zu gegebener Funktion f an einer Stelle x0 zu erhalten, w¨ahlt man sich eine Zahlenfolgex_n ^n→∞−→ x₀ aus dem Definitionsbe- reich vonf und wendet die Funktion f auf xn an. Dann untersucht man die Konvergenz der Folge (f(x_n))_n (= Grenzwertuntersuchung der Funktion an der Stelle x0). In unserem Beispiel gilt auch f¨ur jede andere Folge(xn)_n, die gegen den Wert 2 konvergiert, dassf(xn)^n→∞−→ 4.Man schreibt daher:

n→∞lim f(x_n) = lim

x→2 (x<2)

f(x) = lim

x→2 (x<2)

x²= 4.

Da die Folgenglieder x < 2, nennt man diesen Grenzwert den linksseitigen Grenzwertvonf(x) =x²an der Stellex₀= 2.

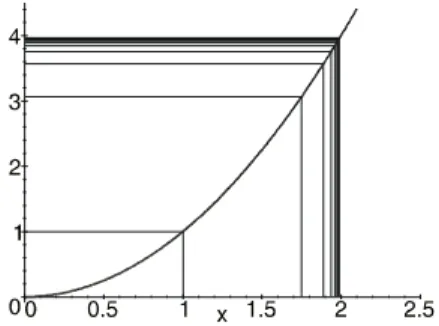
Beispiel 6.6 (Mit Maple-Worksheet). Man kann diesen Sachverhalt an- schaulich darstellen, indem sowohl die Folge(xn)_nals auch die Funktionsfolge (f(xn))_n in ein Schaubild gezeichnet werden. Zur ¨ubersichtlicheren Darstel- lung w¨ahlen wir nun die Folgex_n= 2−_n¹2

n→∞−→ 2:

Abb. 6.3.Linksseitiger Funktionsgrenzwert beix0= 2

Man erkennt, dass diex_n-Werte sich der Zahl2von links ann¨ahern; die Funkti- onswertef(xn)demy-Wert4. Analog erh¨alt man denrechtsseitigenGrenzwert der Funktion beix₀= 2,indem man als Zahlenfolge z.B.

(xn)_n= 2.1,2.01,2.001,2.0001, . . .→2 w¨ahlt. Dazu ist die zugeh¨orige Funktionsfolge

(f(xn))_n= 4.41,4.041,4.004,4.0004, . . .→4.

Auch hier gilt allgemeiner, dass der Funktionsgrenzwert unabh¨angig von der gew¨ahlten Zahlenfolge xn ist.Man schreibt f¨ur den rechtsseitigen Grenzwert

n→∞lim f(xn) = lim

x→2 (x>2)

f(x) = lim

x→2 (x>2)

x²= 4.

F¨ur die Funktion f(x) =x² existieren beix₀= 2also sowohl der linksseitige als auch der rechtsseitige Grenzwert der Funktion und beide sind gleich 4.

6.2 Funktionsgrenzwert 231

Definition: (Funktionsgrenzwert). Eine Funktion f sei in einer Um- gebung vonx0definiert. Gilt f¨urjedeim Definitionsbereich der Funktion liegende Folge (x_n)_n,die gegenx₀konvergiert, stets

n→∞lim f(xn) =g∈IR, so heißtg derGrenzwertvonf(x)f¨ur xn

n→∞−→ x0.

Schreibweise: lim

n→∞f(xn) = lim

x→x0

f(x) =g,wennxn

n→∞−→ x0.

Bemerkungen:

(1) Es wirdnichtgefordert, dassx0 aus dem Definitionsbereich der Funktion ist.

(2) Der Grenz¨ubergang x→ x₀ bedeutet, dass xder Stelle x₀ beliebig nahe kommt,ohneden Wert x0 anzunehmen!

(3) Es kann der Fall eintreten, dass, obwohlx0 ∈/ID,der Funktionsgrenzwert existiert, d.h. der linksseitige mit dem rechtsseitigen Grenzwert ¨uberein- stimmt.

(4) Derlinksseitige Grenzwert wird auch oftmals bezeichnet mit gl:= lim

x→x0

(x<x0)

f(x) = lim

h→0f(x0−h) und derrechtsseitige Grenzwert mit

gr:= lim

x→x0

(x>x₀)

f(x) = lim

h→0f(x0+h) .

Beispiele 6.7:

1 DieHeaviside-Funktion:

f :IR→IR mitf(x) =

0 f¨ur x <0 1 f¨ur x≥0

Die Heaviside-Funktion ist die Funktion, die f¨ur negativex-Werte Null und f¨ur positivex-Werte den Funktionswert 1 besitzt. Sie wird in den Anwen- dungen auch oftmals mit SprungfunktionS(x)bzw. als Einschaltfunktion bezeichnet. Die Heaviside-Funktion besitzt beix₀= 0keinenGrenzwert,

da der rechtsseitige Grenzwert nicht mit dem linksseitigen ¨ubereinstimmt:

g_l= lim

h→0f(x₀−h) = lim

h→0f(−h) = lim

h→00 = 0, g_r= lim

h→0f(x₀+h) = lim

h→0f(h) = lim

h→01 = 1.

2 F¨ur die Funktion

f :IR\ {2} →IR mitf(x) = x²−2x x−2

existiert der Funktionsgrenzwert an der Stellex0= 2,obwohlx0∈/ID:

gl= lim

x→x0

(x<x₀)

f(x) = lim

x→2 (x<2)

x²−2x x−2 = lim

x→2 (x<2)

x= 2,

gr= lim

x→x0

(x>x₀)

f(x) = lim

x→2 (x>2)

x²−2x x−2 = lim

x→2 (x>2)

x= 2.

Der Faktor (x−2) ist im Z¨ahler und Nenner enthalten und kann damit gek¨urzt werden.

3 Die Funktion

f :IR\ {0} →IR mitf(x) = 1 x besitzt inx0= 0 keinenGrenzwert, denn

g_l= lim

h→0f(x₀−h) = lim

h→0=−1

h → −∞, gr= lim

h→0f(x0+h) = lim

h→0= 1

h→+∞.

Nicht f¨ur alle Funktionsgrenzwerte ist die Frage der Konvergenz so einfach zu beantworten wie in den obigen Beispielen. Man braucht dann in der Regel zu- s¨atzliche geometrische ¨Uberlegungen.

6.2 Funktionsgrenzwert 233

Beispiel 6.8. lim

x→0

sin (x)

x =?

Geometrisch entspricht der Grenzwert der Funktion f(x) = sinx

x an der Stelle x0 = 0der Tatsache, dass im Einheitskreis f¨ur0< x < ^π₂ gilt: tanx > x >sinx

⇒ 1

cosx > x

sinx >1⇒cosx < sinx x <1

⇒1 = lim

x→0cosx≤lim

x→0

sinx x ≤1.

Man erh¨alt also insgesamt

x→0lim sinx

x = 1

Beispiel 6.9.Ahnliche geometrische ¨¨ Uberlegungen f¨uhren auf die Formel

x→0lim e^x−1

x = 1.

Denn f¨ur kleine, positivex-Werte ist

1 +x < e^x<1 +x+x².

Damit istx < e^x−1< x(x+1)bzw.1< ^ex_x⁻¹ < x+1. Der Grenz¨ubergang x→0liefert dann die behauptete Formel.

Verhalten der Funktion f¨ur Folgen x → ±∞: Gilt f¨ur jede Fol- ge (xn)_n∈IN aus dem Definitionsbereich von f mit xn

n→∞−→ ∞, dass f(xn) ^n→∞−→ g konvergiert, so heißt g der Grenzwert der Funktion f¨ur x→ ∞:

x→∞lim f(x) =g.

Um die Funktionsgrenzwerte zu berechnen, sowohl f¨ur x_n → x₀ als auch f¨ur xn→ ±∞, gelten dieselben Rechenregeln wie f¨ur reelle Zahlenfolgen:

Rechenregeln f¨ur Funktionsgrenzwerte: Unter der Voraussetzung, dass die Grenzwerte lim

x→x0

f(x)und lim

x→x0

g(x)existieren, gelten folgende Regeln:

(F1) lim

x→x0

c f(x) = c lim

x→x0

f(x).

(F2) lim

x→x0

(f(x)±g(x)) = lim

x→x0

f(x)± lim

x→x0

g(x).

(F3) lim

x→x0

(f(x)·g(x)) = lim

x→x0

f(x)· lim

x→x0

g(x).

(F4) lim

x→x0

f(x)

g(x) =

x→xlim0

f(x)

x→xlim₀g(x), falls lim

x→x0

g(x)6= 0.

Bemerkungen:

(1) Die Regeln gelten auch f¨ur Grenzwerte von Funktionen f¨urx→ ±∞,falls die Grenzwerte lim

x→±∞f(x)und lim

x→±∞g(x)existieren.

(2) F¨ur Grenzwerte vom Typ ⁰₀ und ^∞_∞ gelten die Regeln von l’Hospital,auf die in Abschnitt 7.7.3 n¨aher eingegangen wird!

Beispiele 6.10:

1 lim

x→0

x²−2x+ 5 cosx =

x→0lim x²−2x+ 5

x→0lim cosx =5 1 = 5.

2 lim

x→∞

2x²+ 4 x²−1 = lim

x→∞

2x²+ 4 x²−1 ·

1 x² 1 x²

= lim

x→∞

2 + _x⁴2

1−_x¹2

=2 1 = 2.

3 lim

x→1

x−1 x²−1 = lim

x→1

x−1

(x−1) (x+ 1) = lim

x→1

1 x+ 1 =1

2.

4 lim

x→∞

4 + 2x x²+ 1 = lim

x→∞

4 + 2x x²+ 1 ·

1 x² 1 x²

= lim

x→∞

4 x² +_x² 1 +_x¹2

=0 1 = 0.

5 lim

x→0

√x+ 1−1

x = lim

x→0

√x+ 1−1 √

x+ 1 + 1 x √

x+ 1 + 1

= lim

x→0

(x+ 1)−1 x √

x+ 1 + 1= lim

x→0

√ 1

x+ 1 + 1 = 1 2.

6.3 Stetigkeit einer Funktion 235

6.3 Stetigkeit einer Funktion

Eine Funktion f :IR → IR heißtstetig, wenn der Graph keine Spr¨unge auf- weist. Mit dieser Erkl¨arung hat man sich lange Zeit begn¨ugt, und f¨ur die meis- ten Anwendungen reicht diese anschauliche Interpretation aus. Die Funktion f :IR →IR mitf(x) =x² ist demnach stetig. Um auch Grenzf¨alle wie z.B.

die Funktionf :IR\ {^π₂+k π , k∈ZZ} →IR mitf(x) = tanxklassifizieren zu k¨onnen, ben¨otigt man die folgende pr¨azise Definition:

Quadratfunktion Tangens

Definition: (Stetigkeit). Ist x0 ∈ ID und ist die Funktion f in einer Umgebung vonx0definiert. Die Funktionf heißtstetig inx0, wenn der Funktionsgrenzwert in x₀ existiert und mit dem Funktionswert f(x₀) ubereinstimmt.¨

kurz:f ist inx0∈IDstetig,wenn lim

h→0f(x₀+h) = lim

h→0f(x₀−h) =f(x₀).

Bemerkungen:

(1) Die Stetigkeit im Punktex₀ setzt voraus, dassx₀∈ID. Stellen, an denen f nicht definiert ist, sindDefinitionsl¨ucken.Dort wird die Stetigkeit nicht untersucht.

(2) Istf in jedem Punktx∈ID stetig, so nennt man f einestetige Funktion.

(3) Man kann die Stetigkeit einer Funktion beix₀ auch umformulieren:

x→xlim0

f(x) =f

x→xlim0

x

=f(x₀).

Bei Stetigkeit d¨urfen Grenzwertbildung und Funktionsauswertung vertauscht werden.

Beispiele 6.11:

1 Polynomef :IR→IR mitf(x) =a0+a1x+. . .+anxⁿ sind in jedem Punkt x∈IRstetig.

2 Die Betragsfunktion f :IR→IR mitf(x) =|x|

ist auch bei x₀= 0stetig, da

h→0lim f(x0+h) = lim

h→0f(h) = lim

h→0h= 0

h→0limf(x0−h) = lim

h→0f(−h) = lim

h→0|−h|= 0

f(0) = 0.

3 Die Sprungfunktion (Heavisidefunktion), die zur Beschreibung von Einschaltvorg¨angen dient,S :IR→IR mit

S(x) =

1 f¨ur x≥0 0 f¨ur x <0

ist beix0= 0nicht stetig, da sie einen Sprung aufweist:

h→0lim f(x0+h) = lim

h→0S(h) = 1,

h→0lim f(x0−h) = lim

h→0S(−h) = 0.

4 DieVorzeichenfunktion (Signumfunktion) sign:IR→IR mit

sign(x) =







1fur x >¨ 0 0fur x¨ = 0

−1fur x <¨ 0

ist an der Stellex₀= 0nicht stetig.

6.4 Intervallhalbierungs-Methode 237

5 Die Funktion f :IR\ {2} →IR

mit f(x) =x²−2x x−2

hat an der Stellex0 = 2eine Definitionsl¨ucke. Nach Beispiel 6.7² exis- tieren inx₀= 2der rechtsseitige und linksseitige Grenzwert und stimmen

¨uberein. Man definiert diestetige Erweiterungvonf: f˜:IR→IR mit f˜(x) =

f(x) f¨ur x6= 2 2 f¨ur x= 2 .

Dann ist die Funktion f˜in x0 stetig und damit f¨ur alle x ∈ IR stetig.

Oftmals verzichtet man auf die Notationf˜und verwendet als Bezeichnung f¨ur die stetige Erweiterung wieder den Funktionsnamenf.

6.4 Intervallhalbierungs-Methode

Grundlage f¨ur eine einfache numerische Methode zur Bestimmung von Nullstel- len einer Funktion bildet der folgende, anschauliche Satz: Jede stetige Funktion, die auf einem Intervall[a, b]einen Vorzeichenwechsel hat, besitzt in diesem In- tervall eine Nullstelle (siehe Abb. 6.4):

Abb. 6.4.Intervallhalbierungs-Methode

Zwischenwertsatz:Seif : [a, b]→IR eine stetige Funktion mit (f(a)<

0 und f(b) > 0) oder (f(a) > 0 und f(b) < 0). Dann existiert eine Zwischenstelle ξ∈(a, b)mit der Eigenschaft

f(ξ) = 0.