Master Thesis
Effects of radio-frequency field inhomogeneity on MAS solid- state NMR experiments
Author(s):
Aebischer, Kathrin Publication Date:
2020-09
Permanent Link:
https://doi.org/10.3929/ethz-b-000455492
Rights / License:
In Copyright - Non-Commercial Use Permitted
This page was generated automatically upon download from the ETH Zurich Research Collection. For more information please consult the Terms of use.
on MAS Solid-State NMR Experiments
Kathrin S. Aebischer
Master Thesis
Eidgen¨ ossische Technische Hochschule Z¨ urich
supervised by:
Prof. Dr. Matthias Ernst
September 2020
fields. Different coil designs have been developed to generate these fields. In solid-state NMR probes, solenoid coils wound around the rotor inside the magic-angle-spinning (MAS) stator are most commonly used. The field generated by such a coil is inhomogeneous and depends on the position within the sample space. This rf inhomogeneity is a prevalent problem in NMR which leads to non-ideal rotations of spins in parts of the sample. Radial contributions to the rf field cause time-dependent modulations of the rf amplitude and phase, as spin packets travel through areas with different rf fields during MAS. The influence of these rf modulations on the performance of hetero- and homonuclear recoupling (Rotational Echo Double Resonance and symmetry-based C712) and homonuclear frequency-switched Lee-Goldburg decoupling pulse sequences are studied using numerical simulations and Floquet theory. Significant effects are only observed for frequency-switched Lee-Goldburg decoupling, where time-dependent ampli- tude modulations lead to line broadening.
Experimentally, these effects can be studied by a physical restriction of the sample volume to areas close to the coil windings where modulations are strongest. As an alternative to physical sample restriction, the implementation of band-selective pulses in the spin-lock frame for the application of B1-field selective inversions to spins experiencing selected parts of the rf-field distribution is presented. Any frequency band-selective pulse can be used for this purpose and the family of I-BURP pulses (H. Geen, R. Freeman, Band-Selective Radiofrequency Pulses, J.
Magn. Reson. 93 (1991) 93141) chosen for the measurements demonstrated here. Significant improvements in homonuclear frequency-switched Lee-Goldburg decoupled proton spectra are shown, when parts of the rf-field distribution close to the nominal rf amplitude are selected.
However, residual observed linewidths are not decoupling limited and therefore broadening due to amplitude modulations cannot be studied.
E i g e nstä n d igkeitse rkl äru n g
Die untezeichnete Eigenständigkeitserklärung ist Bestandteil jeder während des Studiums verfassten Semester-, Bachelor- und Master-Arbeit oder anderen Abschlussarbeit (auch der jeweils elektronischen Version).
Die Dozentinnen und Dozenten können auch für andere bei ihnen verfasste schriftliche Arbeiten eine
Ei genständigkeitserklärung verlangen.
lch bestätige, die vorliegende Arbeit selbständig und in eigenen Worten verfasst zu haben. Davon
ausgenommen sind sprachliche und inhaltliche Korrekturvorschläge durch die Betreuer und Betreuerinnen der Arbeit.
Titel der Arbeit (in Druckschrift):
-_--__-_----_--._
i€fr-€=-="crS (>F ß.F.§\§FR=(§ILE:N{C-.2 :trrEl(} it{nchtr6,Er.tEtrit
:e§J HAS §*atO --sT§rE §.\HP- E}..S-=.R\HE§')TS
ii :
ii
Verfasst von {in Druckschrift):
Bei Gruppenarbeiten sind die Namen aller Vadasse innen und Vö$asser erfarde tficl', -
Name{n}:
AEF=T §C-HER
Vorname(n):
trA"T\\e-*\\J .bF*iE
lch bestätige mit meiner Unterschrift:
-
lch habe keine im Merkblatt -Zitier-Kniqoe" beschriebene Form des Plagiats begangen.-
lch habe alle Methoden, Daüen und Arbeitsabläufe wahrheitsgetreu dokumentiert.lch habe keine Daten manipuliert.
-
lch habe alle Personen enrähnt, welche die Arbeit wesentlich unterstützt haben.lch nehme zur Kenntniq dass die Arbeit mit elektrsnischen Hilfsmitteln auf Plagiate überprüft werden kann.
Or§ Datum
3Q*&'_isere_q_
Bei Gruppenarbeilen sind die Namen aller Vgiasseinnep un§
Veiasser erforderlich. Durc.h die lJnterschriften bürgen sie gemeinsam für den gesamten hheft dieser schriftlichen Arboit.
Contents
1 Introduction 1
2 Theory 2
2.1 Basic NMR Interactions . . . 2
2.1.1 The Zeeman Hamiltonian . . . 3
2.1.2 The Chemical-Shift Hamiltonian . . . 3
2.1.3 The Radio-Frequency Hamiltonian . . . 3
2.1.4 TheJ-Coupling Hamiltonian . . . 4
2.1.5 The Dipolar Coupling Hamiltonian . . . 4
2.2 Cartesian Spatial Tensors . . . 5
2.2.1 Euler Rotations . . . 6
2.3 Spherical Tensor Notation . . . 6
2.3.1 Rotation of Spherical Tensors . . . 7
2.4 Time Evolution of Spin Systems . . . 7
2.4.1 Interaction-Frame Representation . . . 8
2.5 The NMR Signal . . . 9
2.6 Origins of Time-Dependent NMR Hamiltonians . . . 9
2.6.1 MAS Modulation of the Spatial Tensor . . . 10
2.6.2 Radio-Frequency Interation-Frame Transformations . . . 11
2.7 Analysis of Time-Dependent NMR Hamiltonians . . . 14
2.7.1 Average-Hamiltonian Theory . . . 14
2.7.2 Floquet Theory . . . 15
2.7.3 Numerical Integration . . . 18
2.8 Pulse Sequences . . . 18
2.8.1 Single-Spin Systems: Nutation and Spin Lock . . . 18
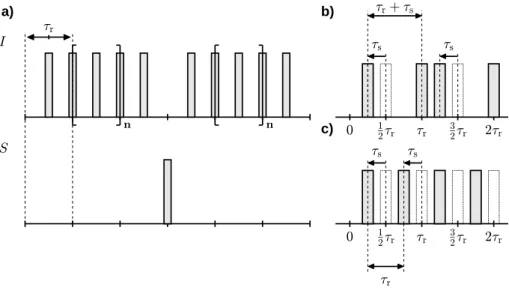
2.8.2 Rotational Echo Double Resonance . . . 19
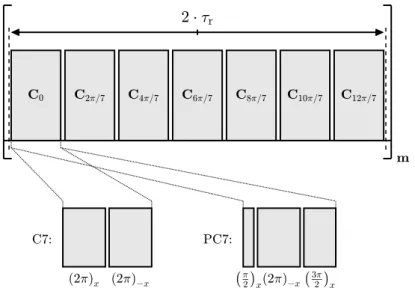
2.8.3 Symmetry-Based CN Recoupling . . . 22
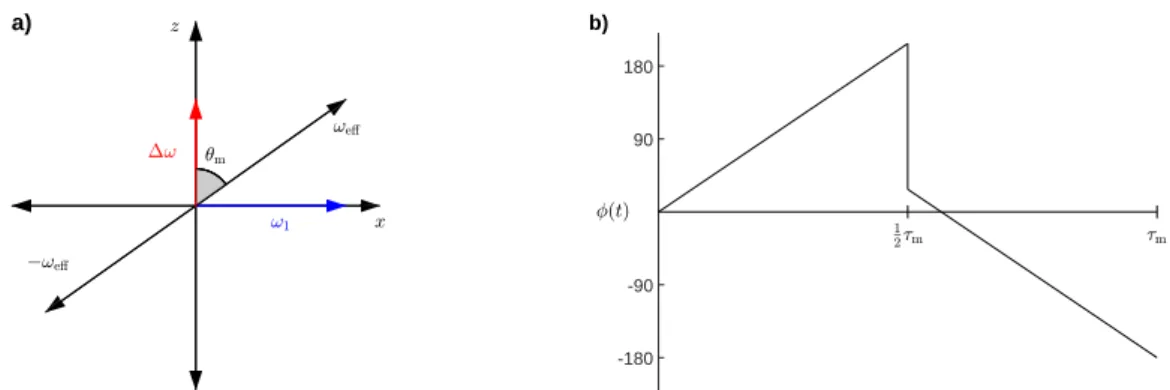
2.8.4 Frequency-Switched Lee-Goldburg Decoupling . . . 25
2.9 Radio-Frequency Fields in Solenoid Coils . . . 28
2.10 Theoretical Treatment of the Radio-Frequency-Field Inhomogeneity . . . 29
2.10.1 First-Order Effective Hamiltonian . . . 31
2.10.2 Second-Order Effective Hamiltonian . . . 32
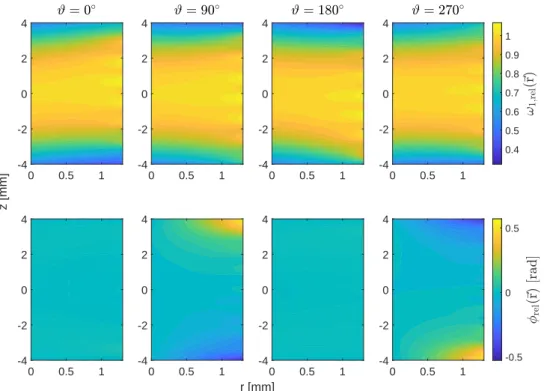
3 Methods and Materials 39 3.1 Spatial Radio-Frequency-Field Distributions . . . 39
3.2 Numerical Simulations . . . 43
3.3 Computation of Interaction-Frame Trajectories . . . 45
4 Results and Discussion 47 4.1 Spin Lock . . . 47
4.1.1 Numerical Simulations . . . 47
4.2 Nutation . . . 48
4.2.1 Analysis of Radio-Frequency Amplitude Modulations . . . 48
4.2.2 Interaction-Frame Trajectories: Phase Modulations . . . 50
4.2.3 Numerical Simulations . . . 52
4.3 Rotational Echo Double Resonance . . . 53
4.3.1 Numerical Simulations . . . 53
4.4 Symmetry-Based CN Recoupling - C7 and PC7 . . . 57
4.4.1 Floquet Analysis . . . 57
4.4.2 Numerical Simulations . . . 59
4.5 Frequency-Switched Lee-Goldburg Decoupling . . . 62
4.5.1 Floquet Analysis . . . 62
4.5.2 Numerical Simulations . . . 67
5 Nutation-Frequency-Selective Pulses in the Spin-Lock Frame 70 5.1 Introduction . . . 70
5.2 Theory . . . 70
5.3 Numerical simulations . . . 71
5.4 Experimental Results and Discussion . . . 74
5.4.1 Nutation Experiments . . . 74
5.4.2 Frequency-Switched Lee-Goldburg Decoupling . . . 77
5.5 Methods and Materials . . . 84
6 Conclusion and Outlook 86 Acknowledgements 87 Bibliography 87 A Appendices 93 A.1 NMR Hamiltonians: Tensor Operators . . . 93
Cartesian Rotation Matrices . . . 93
Spherical Tensor Operators . . . 93
A.2 Commutators of Spin Operators . . . 95
A.3 Additional Plots: Spatial Radio-Frequency-Field Distributions . . . 96
A.4 Basic Setup of Numerical Simulations . . . 99
A.5 Bessel Function Identities . . . 100
A.6 Computation of Interaction-Frame Trajectories . . . 100
Determination of ωeff . . . 100
Spherical One and Two-Spin Fourier Coefficients . . . 101
A.7 Additional Plots And Tables: Theoretical Results . . . 101
Spin Lock . . . 101
Spin System Parameters for Numerical Simulations . . . 102
A.8 Additional Plots and Tables: Nutation-Frequency-Selective Pulses . . . 103
Numerical Simulations of I-BURP-2 Pulses . . . 103
Nutation Experiments . . . 103
Frequency-Switched Lee-Goldburg Decoupling . . . 106
A.9 Source Code: Numerical Simulations: FSLG Decoupling . . . 107
A.10 Source Code: Interaction-Frame Trajectory Analysis: FSLG Decoupling . . . 114
Interaction-Frame Computation . . . 114
Extract Fourier Coefficients . . . 119
Compute Two-Spin Cartesian and Spherical Coefficients . . . 122
1 Introduction
In NMR spectroscopy, short pulses of linearly oscillating magnetic fields are applied to manip- ulate nuclear spins and generate non-equilibrium magnetization. The oscillation frequency of these magnetic fields is usually close to the Larmor frequency of the nuclei and thus in the radio-frequency (rf) range. Therefore, these pulses are commonly referred to as radio-frequency pulses. Generating well-defined rf fields is crucial for the precise control of spin dynamics and experimental imperfections often lead to the deterioration of the perfomance of pulse sequences.
Due to the characteristics of the electronic resonance circuit used for the generation of rf fields in NMR probes, phase transients [1] arise and pulses deviate from the rectangular pulses that would be required to realize ideal rotations. Moreover, the rf field is inhomogeneous and the field experienced by a spin packet thus depends on its position within the sample space.
In general, rf fields are generated by alternating current flowing through a coil wire and depending on the application, different coil designs have been developed. Helmholtz and saddle coils are often used in liquid-state NMR while solenoid coils that are wound around the rotor inside the magic-angle-spinning (MAS) stator are most commonly encountered in solid-state NMR probes. These coil designs can be integrated into multiple-resonance circuits and have the advantage of a large filling factor and high conversion ratio of rf power to field [2]. However, the fields thus generated suffer from a significant rf-field inhomogeneity observed over the sample volume [2]. Reduced rf inhomogeneity has been reported for solenoid coils with variable pitch angles [3] and wire diameters [4]. Furthermore, low-E probes, where the electric-field component of the rf field is minimized in order to avoid sample heating [5], have been developed that also show improved rf-field homogeneity. The magnitude of the inhomogeneity can be determined by a simple nutation experiment. The full spatial rf field distribution over the rotor can be determined by a ball-shift measurement [6] or characterized using either single- or triple axis gradients [7] or the z shim [8] for imaging. Alternatively, the spatial distribution can be com- puted numerically from the geometry of the rf coil and the properties of the sorrounding circuitry [2] [9]. Experimentally as well as numerically obtained rf-field distributions for solid-state NMR MAS probes show that the rf inhomogeneity is most pronounced along the rotor axis but sig- nificant radial contributions are also present. Spectral manifestations of this rf inhomogeneity include a reduction of the observed signal intensity in polarization-transfer experiments [10], line broadening in decoupling experiments [11] and a volume-selective magnetization transfer in cross-polarization experiments [12].
Based on experimental rf amplitude profiles, different models have been proposed to allow a more quantitative characterization of the rf inhomogeneity. The rf profile along the rotor axis can for example be modeled as a Gaussian [6] or by a semi-empirical power function model that was proposed more recently [12]. The functional form of this model is based on the Biot-Savart law for a cylinder carrying a homogeneous circular electrical current and is given by
ν1(p) =ν1cent−
ν1cent−ν1edge
· |p|, (1.1)
where ν1cent and ν1edge correspond to the rf amplitudes at the center and the edge of the coil respectively. The position along the coil axis is indicated by the variable p running from -1 to 1 along the sample length. The width of the profile is given by the exponent . Discrepancies between a real solenoid coil and the idealized cylindrical version used for the derivation of this model are absorbed into the fitting parameters. However, this only allows the characterization of the static rf-field distribution along the rotor axis and disregards radial field contributions.
In MAS experiments, this radial rf inhomogeneity will introduce a time dependence of the rf amplitude and phase experienced by a spin packet as it travels through areas with different rf
fields. These modulations are periodic with the rotor frequency and lead to radial-field side- bands in MAS spectra [13] [14]. Recently, an increase in signal intensities in NCO and NCA (factors 1.5 and 2 respectively) cross-polarization magnetization transfers has been reported [9]
for an optimal-control pulse sequence that was developed taking radial rf-field components and the resulting periodic modulations into account.
The aim of this Master thesis was to further explore the effects of the radial rf-field inhomo- geneity on the performance of various de- and recoupling sequences commonly used in solid-state NMR spectroscopy. The influence of time-dependent amplitude and phase modulations was stud- ied theoretically using Floquet theory and numerical simulations of spin dynamics performed.
Moreover, an implementation of band-selective pulses in the spin-lock frame is proposed that can be used to apply nutation-frequency-selective inversions to spin packets experiencing se- lected parts of the rf-amplitude distribution. This approach allows the restriction of the sample space in terms of the rf-field and represents an alternative to spatial sample restriction for the reduction of the rf-field inhomogeneity.
2 Theory
2.1 Basic NMR Interactions
All energies relevant for NMR spectroscopy arise from interactions that can be subdivided into two groups: interactions between nuclear spins and magnetic fields and interaction between nuclear spins and other spins [15]. A summary of the interactions considered in this work is given in Table 2.1 and expressions of the corresponding Hamiltonians will be discussed in the following.
Table 2.1: Summary of the spin-spin and spin-field interactions considered in this work.
Hˆ Interaction Description
HˆZ Zeeman Interaction Spin-field interaction with the static external magnetic field
Hˆrf rf field Interaction with the time-dependent rf field HˆCS Chemical shift Static external magnetic field is modified at site of
nucleus by electron cloud surrounding it
HˆJ ScalarJ coupling Indirect spin-spin coupling, mediated through bonding electrons
HˆDD Dipolar coupling Interaction between magnetic dipole moments of spins through space
The total Hamiltonian of a spin system is given by the sum of all Hamiltonians of the relevant interactions
Hˆtot= ˆHZ+ ˆHCS+ ˆHDD+ ˆHJ+ ˆHrf. (2.1) It should be noted that all Hamiltonians denoted with the ˆH symbol in this work are in angular frequency units.
In a Cartesian formulation, any of the spin-spin interaction Hamiltonians in Table 2.1 can be expressed as
Hˆ(p,q)=I~ˆp·A(p,q)·I~ˆq, (2.2)
for an interaction between two nuclear spins p and q. The spin vector operator consists of the Cartesian spin operators I~ˆ = ( ˆIx,Iˆy,Iˆz) that can be represented by the Pauli-matrices for a spin-1/2 nucleus. Spin-field interactions can generally be written as
Hˆ(p,B)=I~ˆp·A(p,B)·B ,~ (2.3)
where the magnetic field is described classically and denoted byB~. For both types of interactions, A is a 3x3 square matrix describing the strength and angular dependence of the interaction.
2.1.1 The Zeeman Hamiltonian
The Zeeman interaction is the interaction between the nuclear spins and the static external magnetic field. This external magnetic field is along the z axis in the laboratory frame and denoted as B~0= (0,0, B0). The general form of the Zeeman Hamiltonian is given by
HˆZ,Lab(p) =−γpBˆ0·~Iˆp =ω0(p)Iˆpz, (2.4) whereω(p)0 is the Larmor frequency of nucleusp, that is determined by its gyromagnetic ratioγp. The Zeeman interaction is the dominant term in the total NMR Hamiltonian in the laboratory frame. However, the theoretical description of NMR experiments is usually done in the so- called rotating frame that rotates about thez axis with the Larmor frequency of the nucleus of interest. This frame transformation removes the Zeeman term from the Hamiltonian and thus often simplifies the theoretical treatment.
2.1.2 The Chemical-Shift Hamiltonian
The local field at the position of each nucleus is modified by electrons in close proximity and thus deviates from the external static magnetic field. The actual field experienced by a nucleus can be expressed as the sum of this locally induced field B~ind and B~0
B~tot=B~0+B~ind=B~0+σ(p)B~0, (2.5) where, to a good approximation, the induced field depends linearly on the external magnetic field. The spin-field interaction with this additional magnetic field is described by the chemical- shift Hamiltonian
HˆCS,Lab(p) =~Iˆp·(−γp)σ(p)·B~0. (2.6) The chemical-shift tensor of rank twoσ(p)describes the strength and angular dependence of the interaction. In Cartesian representation this tensor is given by a 3x3 matrix with components σαβ (α, β = x, y, z). In the rotating frame, only the ˆIz component remains time-independent and transversal terms are usually neglected in the secular approximation. The chemical-shift Hamiltonian then simplifies to
HˆCS(p) =ω0(p)σzz(p)Iˆpz. (2.7) 2.1.3 The Radio-Frequency Hamiltonian
In NMR experiments, nuclear spins are manipulated by oscillating magnetic fields that are applied perpendicular to the static external field. These fields usually oscillate with frequencies in the rf range and are thus commmonly referred to as rf fields (denoted byB~1(t)). The general expression for a linearly polarized rf field in the laboratory frame is given by
B~1(t) = (2B1(t) cos(ωrft+φ(t)),0,0) (2.8)
with time-dependent rf amplitude of B1(t) and phase φ(t). The carrier frequency of the oscil- lating field is given by ωrf. The interaction of nuclear spins with this rf field can be expressed as
Hˆrf,Lab(t) =~Iˆp·(−γp)·B~1(t) =−2γpB1(t) cos(ωrft+φ(t)) ˆIpx. (2.9) For on-resonance irradiation, the rf modulation frequency corresponds to the Larmor frequency of the nuclei. Transforming this rf Hamiltonian into the rotating frame with ωrf results in two terms. One has a zero frequency and is static in the rotating frame while the second one rotates at twice the frequency and is usually neglected. It can, however, give rise to Bloch-Siegert effects [16]. Disregarding the counter-rotating part, the rotating-frame rf Hamiltonian to first order is given by
Hˆrf(t) =ω1(t)
cos(φ(t)) ˆIx+ sin(φ(t)) ˆIy
. (2.10)
Note, that the factor of two in front of B1(t) in Eq. (2.8) is just introduced for convenience to obtain an amplitude of B1(t) in the rotating frame. If the rf amplitude and phase are constant, this rf Hamiltonian in the rotating frame is now time-independent.
2.1.4 The J-Coupling Hamiltonian
The J coupling is the indirect spin-spin coupling that is mediated through electrons. In this work only the isotropic J coupling was considered and the corresponding general Hamiltonian can be written as
HˆJ,Lab = 2πJpq~IˆpI~ˆq, (2.11) whereJpq is the scalarJ coupling constant that is related to probability of finding an electron at the position of the nucleus. For homonuclear spin pairs, the form of theJ-coupling Hamiltonian in the rotating frame is the same as the one above, since the scalar product of two vectors is independent of the coordinate system used to represent the vectors. For heteronuclear spin pairs, the time-dependent transversal terms are neglected in the secular approximation when going in the rotating frame and only the ˆIpzIˆqz term remains. The J-coupling Hamiltonian is then given by
HˆJ = 2πJpqIˆpzIˆqz. (2.12) 2.1.5 The Dipolar Coupling Hamiltonian
The dipolar coupling describes the coupling of two nuclear spins through their magnetic dipole moments. For a pair of spins pand q, the corresponding Hamiltonian can be written as
HˆDD,Lab(p,q) =I~ˆpD(p,q)I~ˆq =−µ0
4π γpγq~
rpq3
3
I~ˆp·~rpq I~ˆp·~rpq
r2pq −I~ˆp·~Iˆq
, (2.13) where ~rpq is the internuclear vector and µ0 the permeability of vacuum. The Cartesian tensor D(p,q)can be expressed as a symmetric and traceless 3x3 square matrix. In a coordinate system in which D(p,q) is diagonal (z axis parallel to the internuclear axis) it is given by
D(p,q)=−2µ0
4π γpγq~
r3pq
−12 0 0 0 −12 0
0 0 1
=δpq
−12 0 0 0 −12 0
0 0 1
, (2.14)
where δpq corresponds to the anisotropy of the dipolar coupling tensor. Often, the dipolar coupling Hamiltonian is expanded in the so-called dipolar alphabet
HˆDD,Lab(p,q) = µ0 4π
γpγq~ rpq3
hAˆ+ ˆB+ ˆC+ ˆD+ ˆE+ ˆF i
, (2.15)
with
Aˆ= 2 ˆIpzIˆqz1−3 cos2θ
2 , (2.16)
Bˆ= 1 2
hIˆp+Iˆq−+ ˆIp−Iˆq+
i 3 cos2θ−1
2 , (2.17)
Cˆ=−h
Iˆp+Iˆqz+ ˆIpzIˆq+i3 sinθcosθe−iφ
2 , (2.18)
Dˆ =−h
Iˆp−Iˆqz+ ˆIpzIˆq−
i3 sinθcosθeiφ
2 , (2.19)
Eˆ=−1 2
hIˆp+Iˆq+i3 sin2θe−2iφ
2 , (2.20)
Fˆ=−1 2
hIˆp−Iˆq−
i3 sin2θe2iφ
2 , (2.21)
whereθandφdenote the polar and azimuthal angle describing the orientation of the internuclear vector. Transformation of this Hamiltonian into the rotating frame leads to a time dependence of the terms ˆC−Fˆ for homonuclear spin pairs. In the heteronuclear case, the ˆB term also becomes time-dependent. In the secular approximation, these time-dependent terms are neglected and the simplified dipolar Hamiltonian is given by
HˆDD(p,q)=−µ0 4π
γpγq~ r3pq
3 cos2θ−1 2
2 ˆIpzIˆqz−1 2
hIˆp+Iˆq−+ ˆIp−Iˆq+i
(2.22) for a homonuclear spin pair and by
HˆDD(p,q)=−µ0
4π γpγq~
r3pq
3 cos2θ−1 2
h 2 ˆIpzIˆqz
i
(2.23) for a heteronuclear spin pair.
2.2 Cartesian Spatial Tensors
The general 3x3 matrix representation of a Cartesian spatial tensorA can be decomposed into three components
A=A(0)+A(1)+A(2), (2.24)
namely the isotropic zeroth-rank component A(0), the anti-symmetric and traceless first-rank componentA(1)and the symmetric and traceless second-rank componentA(2). The components of the matrix representation of the spatial tensor depend on the coordinate frame and usually a frame in which its symmetric part is diagonal and characterized by the three diagonal values axx, ayy and azz is chosen. This is referred to as the Principal Axes System (PAS). Instead of the three principal components, the spatial tensor is often characterized by the isotropic average aiso, the anisotropyδ and the asymmetry η, where
aiso= 1
3TrA= axx+ayy+azz
3 , (2.25)
δ=azz −aiso, (2.26)
η= ayy−axx
δ . (2.27)
In this convention, the ordering of the principal components is chosen to be
|azz −aiso| ≤ |axx−aiso| ≤ |ayy−aiso|. (2.28) The spatial tensor can then be rotated into the laboratory or any other frame using Euler rotations.
2.2.1 Euler Rotations
Any coordinate transformation for a Cartesian tensor can be defined by a transformation matrix
R=
Rxx Rxy Rxz Ryx Ryy Ryz
Rzx Rzy Rzz
. (2.29)
In the description of NMR phenomena, rotations represent a crucial group of coordinate trans- formations. Often, they are described in terms of the three Euler angles α, β and γ and the overall rotation matrix is constructed from three consecutive rotations. In this work, the follow- ing convention for the three rotations is used: a rotation aroundz by α, followed by a rotation around the new y0 axis by β and finally a rotation by γ around the new z00 axis. The matrix describing the full coordinate frame transformation is thus given by
R(α, β, γ) =Rz00(γ)·Ry0(β)·Rz(α), (2.30) where the matrix representations of the rotation matricesRy/z around they and zaxes can be found in the Appendix (Section A.1). The inverse of this transformation is given by
R−1(α, β, γ) =R(−γ,−β,−α) =Rz00(−α)·Ry0(−β)·Rz(−γ). (2.31) Using these generalized rotation matrices, the transformation of any of the matrix represen- tations of the second-rank tensors introduced for the description of spin-spin and spin-field interactions from a coordinate frame F to a new oneF0 can be written as
AF0 =R(α, β, γ)AF R−1(α, β, γ). (2.32)
2.3 Spherical Tensor Notation
Thus far, the Hamiltonians of all relevant NMR interactions were represented using Cartesian spin and spatial tensors. However, this formulation is not particularly well-suited for the theo- retical description of NMR phenomena, where rotations in spin and real space are required. As an alternative, the spherical-tensor representation is often chosen, where tensors are expressed in terms of basis functions that have the same symmetry as spherical harmonics. In this formalism, any of the NMR interactions (i) introduced in Section 2.1 can be expressed as the sum of scalar products of irreducible spherical tensors [17]
Hˆ(i)=
2
X
l=0
A(i)l ·Tˆl(i) =
2
X
l=0 l
X
m=−l
(−1)mA(i)lm·Tˆl,−m(i) . (2.33) Each of these scalar products involve a spatial Al and a spin spherical tensor ˆTl of rankl com- posed of 2l+ 1 subcomponents. All basic NMR interactions can be described using tensors of maximum rank two. In analogy to the Cartesian formulation, the spatial spherical tensor characterizes the strength and angular dependence of the interaction. The components of Al and ˆTl can be obtained from the respective Cartesian representations. This is outlined further in the Appendix (Section A.1).
In high-field NMR, the Zeeman interaction is the dominant term in the total Hamiltonian (s. Eq. (2.1)). It can be removed by going into a coordinate frame that rotates about thez axis
with the Larmor frequency of the nucleus in question. As discussed in Section 2.1, this frame transformation leads to a time dependence of all terms that do not commute with the ˆIz spin operator. These terms are then neglected in the secular approximation. In spherical tensor notation, only the ˆTl0 terms remain time-independent and the Hamiltonian for an interaction in the high-field approximation is therefore given by
Hˆ(i)=A(i)00Tˆ00(i)+A(i)20Tˆ20(i). (2.34) The total Hamiltonian is then again the sum over all interactions.
2.3.1 Rotation of Spherical Tensors
A spherical tensor Gl can be rotated by multiplication with the Wigner rotation matrix of the same rank Dl. As the components of tensors of different ranks do not intermix under rotation, the transformation from an initial coordinate frame F to a new frame F0 can be written as
GFl,m0 =
l
X
m0=−l
Dml 0,m(α, β, γ)GFl,m0, (2.35) where α, β and γ denote the three Euler angles that characterize the transformation. The elements of the Wigner rotation matrix are given by
Dml 0,m(α, β, γ) = exp −im0α
dlm0m(β) exp(−imγ), (2.36) wheredlm0m(β) are the reduced Wigner matrix elements that only depend onβ. Elements of the Wigner rotation matrix can be obtained from the Cartesian rotation matrix by the appropriate basis transformation and are tabulated in most books about angular momentum, e.g. in Ref. 18.
2.4 Time Evolution of Spin Systems
As is known from basic quantum mechancis [19], the state of a quantum system can be rep- resented by a state vector |Ψ(t)i. This state vector can be expanded in terms of a set of orthonormal basis functions |φii
|Ψ(t)i=X
i
ci(t)|φii (2.37)
with time-dependent expansion coefficients ci(t). The time-evolution of this state vector is governed by the time-dependent Schr¨odinger equation
d
dt|Ψ(t)i=−iH(t)ˆ |Ψ(t)i , (2.38) shown here for a Hamiltonian operator in angular frequency units. In NMR spectroscopy, one is usually concerned with large ensembles of spins and the description using state vectors is not particularly practical. Instead, the state of such a spin ensemble is described by the density operator
ˆ
ρ(t) =X
i
X
j
ci(t)cj(t)∗|φii hφj|=X
k
pk|Ψk(t)i hΨk(t)|, (2.39) where pk corresponds to the probability that an individual spin system within the ensemble is found in state|Ψk(t)i. The time evolution of the density operator is governed by the Liouville- von Neumann equation
d
dtρ(t) =ˆ −ih H,ˆ ρ(t)ˆ
i
, (2.40)
where the Hamiltonian ˆH is again in angular frequency units. If the density operator commutes with the system Hamiltonian, the commutator on the right-hand side of this equation will be zero and the density operator will not evolve as a function of time. For non-commuting operators, the general solution to this equation is given by
ˆ
ρ(t) = ˆU(t) ˆρ(0) ˆU(t)−1, (2.41) where the propagation operator ˆU(t) solves the following differential equation
d dt
Uˆ(t) =−iH(t) ˆˆ U(t) (2.42)
and is given by
Uˆ(t) = ˆTexp
−i Z t
0
H(tˆ 0)dt0
. (2.43)
Tˆ is the Dyson time-ordering operator [20], that ensures proper time-ordering of non-commuting operators in products. For time-independent Hamiltonians, this integral can be solved easily and the propagator computed as
Uˆ(t) = exp
−iHtˆ
. (2.44)
For time-dependent Hamiltonians, the determination of the propagation operator becomes more complex and often no analytical solution can be obtained. However, several methods have been developed that can be used to derive approximate solutions. These strategies are discussed in Section 2.7 for periodically time-dependent Hamiltonians.
2.4.1 Interaction-Frame Representation
NMR phenomena are usually described in a coordinate frame rotating about the laboratory z axis. In this rotating frame, the Zeeman interaction, which would otherwise be dominant, is eliminated from the Hamiltonian. Generalizing this concept, the spin system can be described in an interaction-frame with respect to any interaction present in the Hamiltonian. This often simplifies the theoretical treatment to a great extent. In the following the basic principle and the governing equations for the time evolution in the interaction frame are discussed.
For a general interaction-frame transformation, the Hamiltonian is expressed as the sum of two time-dependent terms
H(t) = ˆˆ H0(t) + ˆH1(t), (2.45) where ˆH0(t) is the dominant part of the total Hamiltonian with respect to which the interaction- frame transformation is performed. The dynamics under the ˆH0(t) term should be known, such that the propagator ˆU0(t) can be determined as the solution of
d
dtUˆ0(t) =−iHˆ0(t) ˆU0(t). (2.46) that is given by
Uˆ0(t) = ˆTexp
−i Z t
0
Hˆ0(t0)dt0
, (2.47)
where ˆT is again the Dyson time-ordering operator [20]. The total propagator ˆU(t) can be defined as the product of ˆU0(t) and the interaction-frame propagatorUˆ˜(t)
U(t, tˆ 1) = ˆU0(t, t1)·Uˆ˜(t, t1). (2.48)
Inserting this ansatz into Eq. (2.42), the following differential equation for Uˆ˜(t, t1) is obtained d
dt ˆ˜
U(t, t1) =−i
Uˆ0(t, t1)†Hˆ1(t) ˆU0(t, t1)
| {z }
ˆ˜ H(t)
ˆ˜
U(t, t1), (2.49)
where the interaction-frame Hamiltonian Hˆ˜ has been defined [21].
In order to describe the time evolution of the spin system in this interaction frame, the density operator has to be transformed in full analogy to the system Hamiltonian
ˆ
ρ0(t) = ˆU0−1(t) ˆρ(t) ˆU0(t). (2.50) The equivalent of the Liouville-von Neumann equation (s. Eq. (2.40)) in this interaction frame is obtained by substitution of the interaction-frame density operator ˆρ0(t). This results in
d
dtρˆ0(t) = d dt
Uˆ0−1(t) ˆρ(t) ˆU0(t) =−ihHˆ˜ −Hˆ0,ρˆ0i
, (2.51)
where the governing Hamiltonian is given by Hˆ˜ −Hˆ0 and the dominant term thus removed.
2.5 The NMR Signal
In the theoretical treatment of NMR spectrocopy, the time-domain signal corresponds to the expectation value of an observable operator ˆO as a function of time. In the density operator formalism, such expectation values can easily be computed as [19]
Oˆ
(t) = Tr n
ˆ ρ(t) ˆO
o
. (2.52)
If the time evolution of the density operator is known, Oˆ
(t) can therefore be computed at any point in time. Generally, this observable operator corresponds to the ˆIx, ˆIy and ˆIz spin operators or a linear combination thereof.
In an experimental setup, the NMR signal corresponds to the current induced by oscillating transverse magnetization components in a coil. Usually, the same solenoid coil is used for the excitation of the spin system with rf fields and the signal detection. The sensitivity of this coil depends on the position within it and according to the reciprocity theorem [22] [2], the signal s(t) in the rotating frame is proportional to the transverse components of the magnetization vector M~ and the rf field of the receiving coilB~1 at a given position in the sample. The signal s(t) is thus given by
s(t)∝ Z
B~1(z, r, ϑ, t)·M~(z, r, ϑ)rdr dϑ dz , (2.53) where a point is space is defined by the set of cylindrical coordinates (z, r, ϑ). The coil sensitivity is simply given by the strength of the rf field it generates at a given position.
2.6 Origins of Time-Dependent NMR Hamiltonians
For static molecules and in the absence of rf irradiation, the Hamiltonian for any of the relevant interactions in the laboratory frame (s. Eq. (2.33)) is in principle time-independent. However,
time-dependent Hamiltonians in solid-state NMR arise from the sample rotation in magic-angle- spinning experiments and the application of time-dependent rf irradiation. In the following, these sources of time-dependent modulations of the Hamiltonian will be discussed in more detail.
In most experiments, the system is perturbed in a periodic manner and the resulting Hamil- tonian can be expressed as a Fourier series. For a single basic frequency ω, the Hamiltonian is given by
H(t) =ˆ
∞
X
n=−∞
Hˆ(n)einωt (2.54)
with the Fourier components ˆH(n). For a time dependence due to MAS, the basic frequency is equal to the rotor frequency, whereas it would correspond to the modulation frequency of the pulse scheme if the time dependence is caused by periodic rf irradiation. For multiple time-dependent modulations, this representation can easily be expanded using several basic frequencies.
2.6.1 MAS Modulation of the Spatial Tensor
In a MAS experiment, the sample is spun around an axis inclined by the magic angle θm = acos(1/√3)≈54.7456◦. The rapid spinning about this axis leads to the averaging of all anisotropic interactions [23] [24]. This makes MAS is a crucial tool for high-resolution solid-state NMR.
The sample spinning during MAS introduces time-dependent modulations of the spatial part of the Hamiltonian
H(t) =ˆ
2
X
l=0 l
X
m=−l
(−1)mAlm(t)·Tˆl,−m, (2.55) since the transformation of the spatial tensor from the PAS to the laboratory frame becomes- time-dependent. For convenience, this transformation is commonly expressed as two consecutive rotations: first a rotation from the PAS into a rotor-fixed frame in which the z axis is aligned with the magic angle, and second a rotation from this rotor-fixed frame to the laboratory frame.
This second rotation is periodically time-dependent with the rotor frequency ωr. In spherical- tensor notation, these two rotations can be expressed using Wigner rotation matrices and the spatial tensor in the laboratory frame is given by
ALlm(t) =
l
X
m0=−l
Dlm0,m(−ωrt,−θm,0)
| {z }
Rotor-fixed→Laboratory
l
X
m00=−l
Dml 00,m0(α, β, γ)ρPASlm00
| {z }
PAS→Rotor-fixed
=
l
X
m0=−l
Dlm0,m(−ωrt,−θm,0)ARlm0, (2.56) where ARlm0 denote the components of the spatial tensor in the rotor-fixed frame. This trans- formation of the PAS into the rotor-fixed frame is characterized by the set of Euler angles α,β and γ and theARlm0 components are given by
ARlm0 =
l
X
m00=−l
Dml 00,m0(α, β, γ)ρPASlm00
=
l
X
m00=−l
e−im00αdlm00,m0(β)e−im0γρPASlm00 . (2.57)
In the high-field approximation, only them = 0 components remains time-independent and all other terms are neglected in the secular approximation. The spatial tensor in the laboratory frame can thus be written as
ALl0(t) =
l
X
m0=−l
eim0ωrtdlm00(−θm)ARlm0. (2.58)
Substituting this into Eq. (2.55) yields H(t) =ˆ
l
X
m0=−l
eim0ωrtdlm00(−θm)ARlm0Tˆl0 =
l
X
m0=−l
Hˆ(m0)eim0ωrt, (2.59)
where ˆH(m0) are the Fourier components that are given by Hˆ(m0) =dlm00(−θm)ARlm0·Tˆl0
= dlm00(−θm)
l
X
m00=−l
e−im00αdlm00,m0(β)e−im0γρPASlm00
!
·Tˆl0. (2.60) Magic-angle spinning, therefore, leads to a periodic modulation of the spatial tensors with the rotor frequency and the summation index (m0) in the Fourier series representation is limited by the tensor rank. Thus, only frequency components up to ±2·ωr arise for second-rank spatial tensors like the chemical-shielding or dipolar-coupling tensors.
2.6.2 Radio-Frequency Interation-Frame Transformations
The second source of time-dependent Hamiltonians in the description of solid-state NMR exper- iments are time-dependent rf fields that are applied to manipulate nuclear spins. In contrast to MAS, that caused a time dependence of the spatial part, rf irradiation leads to a modulation of the spin part of the Hamiltonian
H(t) =ˆ
2
X
l=0 l
X
m=−l
(−1)mAlm·Tˆl,−m(t). (2.61)
The general form of a time-dependent rf Hamiltonian in the rotating frame is given by Hˆrf(t) =ω1(t)
cos(φ(t)) ˆIx+ sin(φ(t)) ˆIy
, (2.62)
where both the rf amplitude ω1(t) and phase φ(t) can be time-dependent depending on the irradiation scheme. The radial part of the rf inhomogeneity will lead to an additional modula- tion of both with the rotor frequency during MAS. The basic principle of an interaction-frame transformation was introduced in Section 2.4.1. This can now be applied and an interaction- frame transformation with respect to the time-dependent rf irradiation performed. The resulting interaction-frame Hamiltonian can be computed as
ˆ˜
H(t) = ˆUrf−1H(t) ˆˆ Urf, (2.63) where the propagator characterizing the transformation is given by
Uˆrf = ˆTexp −i Z t0
0
Hˆrf(t0)dt0
!
. (2.64)
Tˆ is again the Dyson time-ordering operator [20]. Such an interaction-frame transformation will affect all irradiated spins and lead to time-dependent modulations of the corresponding spin operators. If the rf irradiation is periodic with a period of τm, the spin operators will transform according to
ˆ˜
Iµ(t) = X
χ=x,y,z
aµχ(t) ˆIχ=X
χ
X
k
X
l
a(k,l)µχ eikωmteilωeffIˆχ, (2.65) ˆ˜
Tr,0(t) =
r
X
s=−r
ar,s(t) ˆTr,s=
r
X
s=−r
X
k
X
l
a(k,l)r,s eikωmteilωeffTˆr,s, (2.66) where the transformation behaviour of both the Cartesian and the spherical spin operators is shown above. The interaction-frame trajectories of these spin operators are characterized by the Fourier coefficients a(k,l)µχ anda(k,l)r,s respectively. These coefficients only depend on the rf irradia- tion scheme and are independent of the details of the spin system under investigation. Generally, two basic frequencies result: the modulation frequency of the pulse sequence ωm = 2π/τm and the additional effective nutation frequency ωeff that can be determined from the effective flip angle over a period of the rf pulse scheme ωeff = βeff/τm. If the propagator over a full cycle of the rf sequence is unity, no additional effective fields arise and ωeff = 0. Under MAS, the radial part of the inhomogeneity causes a modulation of the rf amplitude and phase with ωr
and the rf Hamiltonian will only be periodic over a finite interval if the basic frequency of the pulse sequence is commensurate with the rotor frequency. This will lead to an additional mod- ulation of the spin part of the Hamiltonian withωrand is discussed in more detail in Section 2.10.
Under MAS, these two frequencies along with the rotor frequency (modulation of the spatial tensor) constitute the three basic frequencies characterizing the interaction-frame Hamiltonian.
This Hamiltonian can again be expanded as a Fourier series ˆ˜
H(t) =X
n
X
k
X
l
Hˆ(n,k,l)einωrteikωmteilωefft, (2.67)
with Fourier components ˆH(n,k,l). As discussed in Section 2.6.1 the Fourier indexnof the rotor frequency is limited to±2.
In the following, general expressions for the Fourier components of the Hamiltonian for a heteronuclear spin system with NI I spins and NS S spins will be derived. Considering all interactions described in Section 2.1, the total Hamiltonian in the rotating frame under MAS is given by
H(t) =ˆ
NI
X
d=1
ωI(n)
d einωrtIˆz+
NS
X
p=1
ω(n)S
peinωrtSˆz+
NI
X
d=1 NS
X
p=1 2
X
n=−2
ωI(n)
dSpeinωr2 ˆIdzSˆpz +
NI
X
d<e 2
X
n=−2 n6=0
ω(n)I
dIeeinωrth
3 ˆIdzIˆez−~Iˆd·I~ˆei +
NI
X
d<e
ωI(0)
dIe
~ˆ Id·~Iˆe
+
NS
X
p<q 2
X
n=−2 n6=0
ω(n)S
pSqeinωrt h
3 ˆSpzSˆqz−S~ˆp·S~ˆq
i +
NS
X
p<q
ωS(0)
pSq
~ˆ
Sp·S~ˆq+ ˆHrf(t), (2.68)
where the secular approximation was invoked. Components of the spatial tensors ω(n) of the
chemical shift of a spin Sp and couplings between two spinsSp and Sq are given by
ωS(0)p = ΩSp (2.69)
ωS(n)
p = 2
√
6d2n,0(θm)e−inγ
2
X
m=−2
d2m,n(β)e−imαρ(S2,mp) (2.70) ωS(0)
pSq =πJpq (2.71)
ωS(n)pSq = 1
√
6d2n,0(θm)e−inγd20,n(β)ρ(S2,0qSp) (2.72) for the isotropic and anisotropic chemical shifts, the scalarJ and the anisotropic dipolar coupling.
Spatial tensors of isotropic interactions are of rank zero and invariant under rotation, therefore only components with n= 0 result. For irradiation of the I spins, the rf Hamiltonian is given by
Hˆrf(t) =ω1(t)
NI
X
d=1
cosφ(t) ˆIdx+ sinφ(t) ˆIdy
. (2.73)
The interaction-transformation with respect to this rf Hamiltonian (s. Eq. (2.64)) will lead to the time dependence of the I spin terms while leaving all S spin terms unaffected. Therefore, the interaction-frame Hamiltonian is given by
ˆ˜ H(t) =
NI
X
d=1
ω(n)I
d einωrtIˆ˜z(t) +
NS
X
p=1
ωS(n)
peinωrtSˆz+
NI
X
d=1 NS
X
p=1 2
X
n=−2
ω(n)I
dSpeinωr2Iˆ˜dz(t) ˆSpz +
NI
X
d<e 2
X
n=−2 n6=0
ωI(n)
dIeeinωrt h
3Iˆ˜dz(t)Iˆ˜ez(t)−I~ˆd·~Iˆe
i +
NI
X
d<e
ω(0)I
dIe
~ˆ Id·I~ˆe
+
NS
X
p<q 2
X
n=−2 n6=0
ωS(n)
pSqeinωrt h
3 ˆSpzSˆqz−S~ˆp·S~ˆq
i +
NS
X
p<q
ω(0)S
pSq
~ˆ
Sp·S~ˆq, (2.74)
The scalar product of vectors is independent of the coordinate frame and ~Iˆd·I~ˆe terms thus remain time-independent. The ˆIz spin operators will transform according to
ˆ˜
Iz(t) =X
χ
X
k
X
l
a(k,l)zχ eikωmteilωeffIˆχ. (2.75) For two-spin operators it is convenient to define general two-spin Fourier coefficients
a(l,k)µχ,µ0χ0 =X
k1
X
l1
a(kµµ10,l1)a(k−kχχ0 1,l−l1), (2.76) that can be computed as the convolution of the single-spin coefficients. Using these, the interaction-frame transformation of the ˆIdzIˆez terms can be written as
ˆ˜
Idz(t)Iˆ˜ez(t) =X
µ
X
χ
a(k,l)zz,µχeikωmteilωefftIˆdµIˆeχ. (2.77) Substitution of the expressions for the transformation behaviour of one and two-spin terms into Eq. (2.74) yields the Fourier componentsHˆ˜(n,k,l)of the Hamiltonian. Separating them according