Uniqueness and regularity for porous media equations with x-dependent coefficients
Volltext
Abbildung
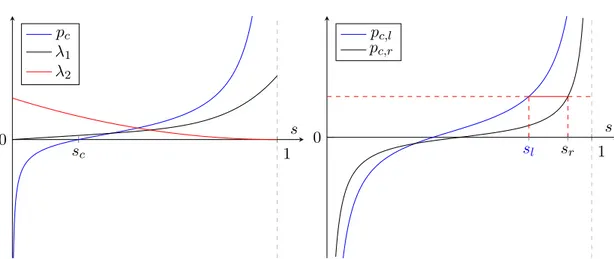
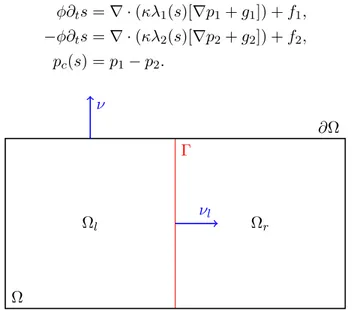
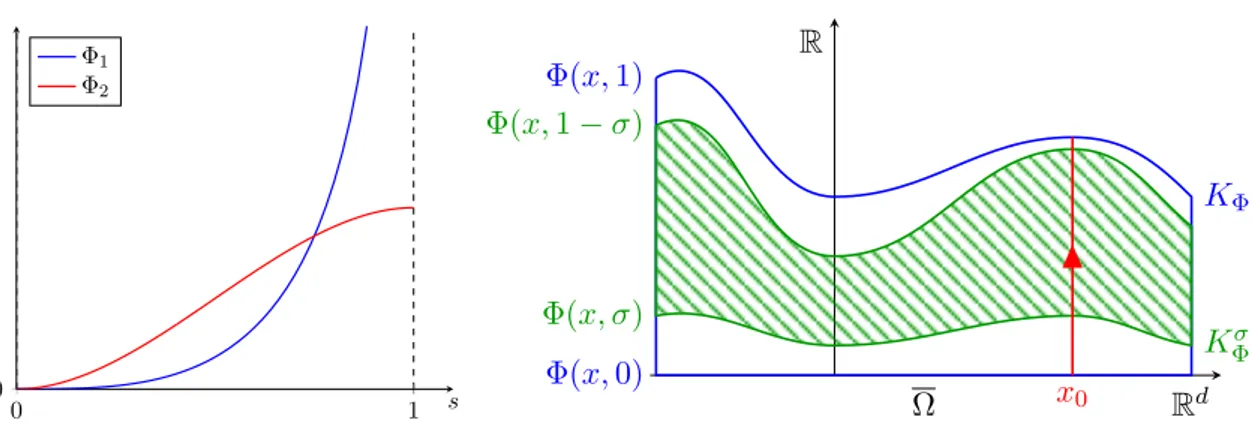
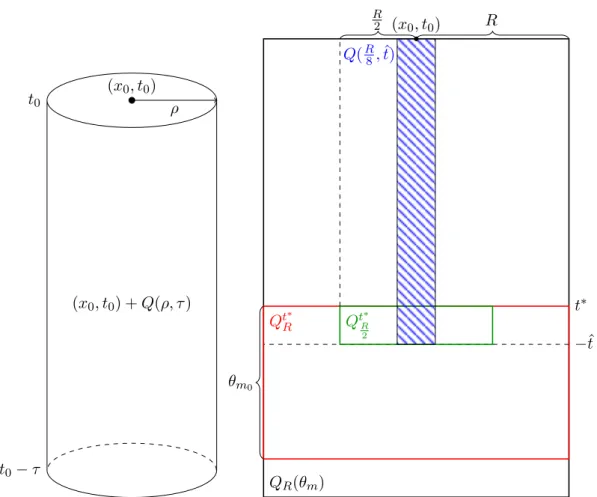
ÄHNLICHE DOKUMENTE
A map f dened on a given open convex set that is n + 1 times continuously dierentiable and is such that its derivatives are bounded is Lipschitz- n on that set (assuming that the
(1.6) A major step forward towards a full proof of the local continuity of solutions to (1.3) with p = 2 and β a general maximal monotone graph in R ×R, is represented by [11];
NEW EQUATIONS FOR THE TIME-DEPENDENT REGULATOR
The proof is based on the existence of R-bounded solution operators of the corresponding generalized resolvent problem which is shown with the help of an operator-valued
In this section we give several further examples of uniqueness of quadrature domains based on real comprehensive triangular decomposition and other computational meth- ods
Aus den magnetischen Untersuchungen wie auch aus einem Vergleich der Atomabstände läßt sich daher ableiten, daß im genannten Tem- peraturbereich in allen Verbindungen vom Typ SELi
That is, we will show that among the above class of nonlinear differential equa- tions, the KP and Boussinesq equations and their di- mensional reductions are the only
This paper is concerned with global existence, uniqueness, and asymptotic behavior of solutions to the linear inhomogeneous equations of one-dimensional thermoelasticity that model