Funktionales Programmieren Teil 9 Carl Philipp Reh
Volltext
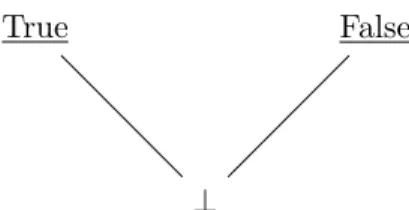
Abbildung
ÄHNLICHE DOKUMENTE
Zun¨ achst stellen wir fest, dass f¨ ur jede endliche Kette c : N → D das Supremum existiert, was das. ” letzte“ Element der Kette ist (Beweis:
Wenn man zeigen will, dass Funktionen stetig sind, kommt es oft vor, dass man mit mehreren Ketten auf einmal zu tun hat.. Diese Funktion ist stetig, weil sie
Er besagt, dass jede stetige Funktion einen kleinsten Fixpunkt hat und zeigt sogar, wie man diesen erh¨ alt..
Wir werden hierbei einige Einschr¨ ankungen vornehmen, die allerdings keine wirklichen Einschr¨ ankungen sind, da man alle anderen Haskell-Programme in unsere erlaubte Syntax
Wir m¨ ussten eigentlich noch zeigen, dass alle Funktionen, die wir in der Definition der Semantik benutzt haben, auch stetig sind.. Da dies allerdings sehr aufw¨ andig ist, m¨
Intuitiv geschieht dies, indem man Typvariablen so ersetzt, dass alle Typgleichungen von der Form τ = τ sind, also zum Beispiel α = Int wird zu Int = Int, indem man α durch
I ” nicht l¨ osbar“ liefert, wenn es keine L¨ osung f¨ ur E gibt, I und andernfalls eine allgemeinste L¨ osung f¨ ur E liefert.. Wir starten mit einer Substitution s, die am
Lehrstuhl Theoretische Informatik Carl Philipp Reh. Funktionales Programmieren